Effect of Alloying Elements on the α-γ Phase Transformation in Iron
Abstract
:1. Introduction
2. Method
2.1. Interatomic Interaction Potentials
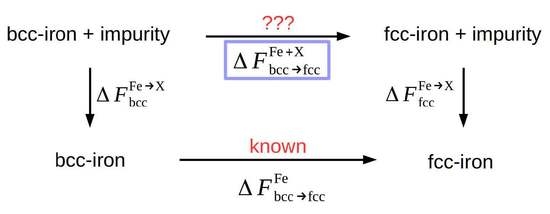
2.2. Free Energies
2.3. Simulation
3. Results
3.1. Transition Temperatures
3.2. Connection to Potentials
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Modified Johnson Potential
References
- Urbassek, H.M.; Sandoval, L. Molecular dynamics modeling of martensitic transformations in steels. In Phase Transformations in Steels; Diffusionless Transformations, High Strength Steels, Modelling and Advanced Analytical Techniques; Pereloma, E., Edmonds, D.V., Eds.; Woodhead Publishing Limited: Cambridge, UK, 2012; Volume 2, pp. 433–463. [Google Scholar]
- Ou, X. Molecular dynamics simulations of fcc-to-bcc transformation in pure iron: A review. Mater. Sci. Technol. 2017, 33, 822–835. [Google Scholar] [CrossRef]
- Körmann, F.; Dick, A.; Grabowski, B.; Hallstedt, B.; Hickel, T.; Neugebauer, J. Free energy of bcc iron: Integrated ab initio derivation of vibrational, electronic, and magnetic contributions. Phys. Rev. B 2008, 78, 033102. [Google Scholar] [CrossRef]
- Militzer, M.; Mecozzi, M.G.; Sietsma, J.; van der Zwaag, S. Three-dimensional phase field modelling of the austenite-to-ferrite transformation. Acta Mater. 2006, 54, 3961. [Google Scholar] [CrossRef]
- Schmidt, S.; Plate, C.; Müller, R.; Müller, R.; Meiser, J.; Urbassek, H.M. A phase field model for martensitic transformations with a temperature-dependent separation potential. Proc. Appl. Math. Mech. 2016, 16, 481–482. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.; Anderko, K. Constitution of Binary Alloys, 2nd ed.; McGraw-Hill: New York, NY, USA, 1958. [Google Scholar]
- Meyer, R.; Entel, P. Martensite-austenite transition and phonon dispersion curves of Fe1−xNix studied by molecular-dynamics simulations. Phys. Rev. B 1998, 57, 5140. [Google Scholar] [CrossRef]
- Müller, M.; Erhart, P.; Albe, K. Analytic bond-order potential for bcc and fcc iron—Comparison with established EAM potentials. J. Phys. Condens. Matter 2007, 19, 326220. [Google Scholar] [CrossRef]
- Lee, T.; Baskes, M.I.; Valone, S.M.; Doll, J.D. Atomistic modeling of thermodynamic equilibrium and polymorphism of iron. J. Phys. Condens. Matter 2012, 24, 225404. [Google Scholar] [CrossRef]
- Engin, C.; Sandoval, L.; Urbassek, H.M. Characterization of Fe potentials with respect to the stability of the bcc and fcc phase. Model. Simul. Mater. Sci. Eng. 2008, 16, 035005. [Google Scholar] [CrossRef]
- Ruda, M.; Farkas, D.; Abriata, J. Interatomic potentials for carbon interstitials in metals and intermetallics. Scr. Mater. 2002, 46, 349. [Google Scholar] [CrossRef]
- Lee, B.J. A modified embedded-atom method interatomic potential for the Fe-C system. Acta Mater. 2006, 54, 701–711. [Google Scholar] [CrossRef]
- Shibuta, Y.; Maruyama, S. Bond-order potential for transition metal carbide cluster for the growth simulation of a single-walled carbon nanotube. Comput. Mater. Sci. 2007, 39, 842–848. [Google Scholar] [CrossRef]
- Becquart, C.S.; Raulot, J.M.; Bencteux, G.; Domain, C.; Perez, M.; Garruchet, S.; Nguyen, H. Atomistic modeling of an Fe system with a small concentration of C. Comput. Mater. Sci. 2007, 40, 119–129. [Google Scholar] [CrossRef]
- Lau, T.T.; Först, C.J.; Lin, X.; Gale, J.D.; Yip, S.; Vliet, K.J.V. Many-Body Potential for Point Defect Clusters in Fe-C Alloys. Phys. Rev. Lett. 2007, 98, 215501. [Google Scholar] [CrossRef]
- Hepburn, D.J.; Ackland, G.J. Metallic-covalent interatomic potential for carbon in iron. Phys. Rev. B 2008, 78, 165115. [Google Scholar] [CrossRef]
- Henriksson, K.O.E.; Nordlund, K. Simulations of cementite: An analytical potential for the Fe-C system. Phys. Rev. B 2009, 79, 144107. [Google Scholar] [CrossRef]
- Ruda, M.; Farkas, D.; Garcia, G. Atomistic simulations in the Fe-C system. Comput. Mater. Sci. 2009, 45, 550. [Google Scholar] [CrossRef]
- Henriksson, K.O.E.; Björkas, C.; Nordlund, K. Atomistic simulations of stainless steels: A many-body potential for the Fe-Cr-C system. J. Phys. Condens. Matter 2013, 25, 445401. [Google Scholar] [CrossRef]
- Sak-Saracino, E.; Urbassek, H.M. Free energies of austenite and martensite Fe-C alloys: An atomistic study. Philos. Mag. 2014, 94, 933–945. [Google Scholar] [CrossRef]
- Johnson, R.A.; Dienes, G.J.; Damask, A.C. Calculations of the energy and migration characteristics of carbon and nitrogen in alpha-iron and vanadium. Acta Metall. 1964, 12, 1215. [Google Scholar] [CrossRef]
- Rosato, V. Comparative behavior of carbon in b.c.c. and f.c.c. iron. Acta Mater. 1989, 37, 2759. [Google Scholar] [CrossRef]
- Wang, B.; Sak-Saracino, E.; Gunkelmann, N.; Urbassek, H.M. Molecular-dynamics study of the α↔γ phase transition in Fe-C. Comput. Mater. Sci. 2014, 82, 399–404. [Google Scholar] [CrossRef]
- Zhang, X.; Hickel, T.; Rogal, J.; Fähler, S.; Drautz, R.; Neugebauer, J. Structural transformations among austenite, ferrite and cementite in Fe-C alloys: A unified theory based on ab initio simulations. Acta Mater. 2015, 99, 281–289. [Google Scholar] [CrossRef]
- Zhou, X.W.; Johnson, R.A.; Wadley, H.N.G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B 2004, 69, 144113. [Google Scholar] [CrossRef]
- Wadley, H.N.G.; Zhou, X.; Johnson, R.A.; Neurock, M. Mechanisms, Models and Methods of Vapor Deposition. Prog. Mater. Sci. 2001, 46, 329. [Google Scholar] [CrossRef]
- Zhou, X.W.; Wadley, H.N.G.; Johnson, R.A.; Larson, D.J.; Tabat, N.; Cerezo, A.; Petford-Long, A.K.; Smith, G.D.W.; Clifton, P.H.; Martens, R.L.; et al. Atomic Scale Structure of sputtered metal Multilayers. Acta Mater. 2001, 49, 4005. [Google Scholar] [CrossRef]
- Johnson, R.A. Analytic nearest-neighbor model for fcc metals. Phys. Rev. B 1988, 37, 3924. [Google Scholar] [CrossRef]
- Johnson, R.A. Alloy models with the embedded-atom method. Phys. Rev. B 1989, 39, 12–554. [Google Scholar] [CrossRef]
- Miller, M.A.; Reinhardt, W.P. Efficient free energy calculations by variationally optimized metric scaling: Concepts and applications to the volume dependence of cluster free energies and to solid-solid phase transitions. J. Chem. Phys. 2000, 113, 7035. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation, 2nd ed.; Academic: San Diego, CA, USA, 2002. [Google Scholar]
- Freitas, R.; Asta, M.; de Koning, M. Nonequilibrium free-energy calculation of solids using LAMMPS. Comput. Mater. Sci. 2016, 112, 333. [Google Scholar] [CrossRef]
- Frenkel, D.; Ladd, A.J.C. New Monte Carlo method to compute the free energy of arbitrary solids. Applications to the fcc and hcp phases of hard spheres. J. Chem. Phys. 1984, 81, 3188. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–9. [Google Scholar] [CrossRef]
- Bendick, W.; Pepperhoff, W. On the α/γ stability of Fe. Acta Metall. 1982, 30, 679. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420. [Google Scholar] [CrossRef]
- Chipot, C.; Pohorille, A. Free Energy Calculations, Springer Series in Chemical Physics, Springer: Berlin, Germany, 2007; Volume 86.
- Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distribution. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Landolt Börnstein—Group IV Physical Chemistry. Phase Equilibria, Crystallographic and Thermodynamic Data of Binary Alloys; Springer: Berlin, Germany, 1991; Volume 5. [Google Scholar] [CrossRef]
- Owen, E.A.; Yates, E.L.; Sully, A.H. An X-ray investigation of pure iron-nickel alloys. Part 4: The variation of lattice-parameter with composition. Proc. Phys. Soc. (Lond.) 1937, 49, 315. [Google Scholar] [CrossRef]
- Basinski, Z.S.; Hume-Rothery, W.; Sutton, A.L. The Lattice Expansion of Iron. Proc. Roy. Soc. (Lond.) A 1955, 229, 459. [Google Scholar]







| (eV) | Error (eV) | (eV) | |
|---|---|---|---|
| Pd | |||
| Au | |||
| Cu | |||
| Ni | |||
| Co | |||
| Fe | |||
| W | |||
| Mo |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meiser, J.; Urbassek, H.M. Effect of Alloying Elements on the α-γ Phase Transformation in Iron. Materials 2019, 12, 1355. https://doi.org/10.3390/ma12081355
Meiser J, Urbassek HM. Effect of Alloying Elements on the α-γ Phase Transformation in Iron. Materials. 2019; 12(8):1355. https://doi.org/10.3390/ma12081355
Chicago/Turabian StyleMeiser, Jerome, and Herbert M. Urbassek. 2019. "Effect of Alloying Elements on the α-γ Phase Transformation in Iron" Materials 12, no. 8: 1355. https://doi.org/10.3390/ma12081355
APA StyleMeiser, J., & Urbassek, H. M. (2019). Effect of Alloying Elements on the α-γ Phase Transformation in Iron. Materials, 12(8), 1355. https://doi.org/10.3390/ma12081355