Filling Capacity Evaluation of Self-Compacting Concrete in Rock-Filled Concrete
Abstract
:1. Introduction
2. Theoretical Model for Filling Capacity of SCC
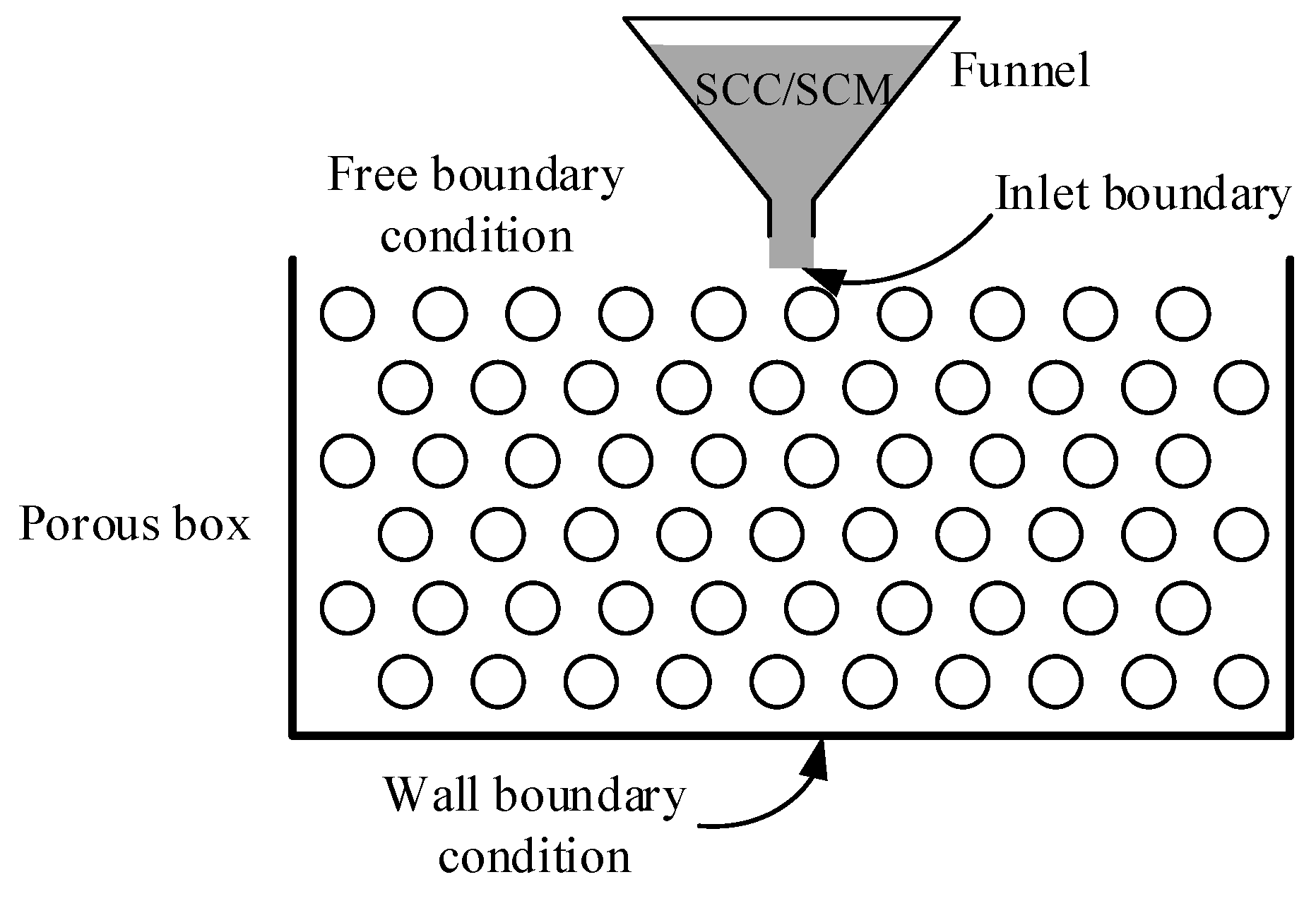
2.1. Porous Boxes
2.2. Numerical Model for SCC
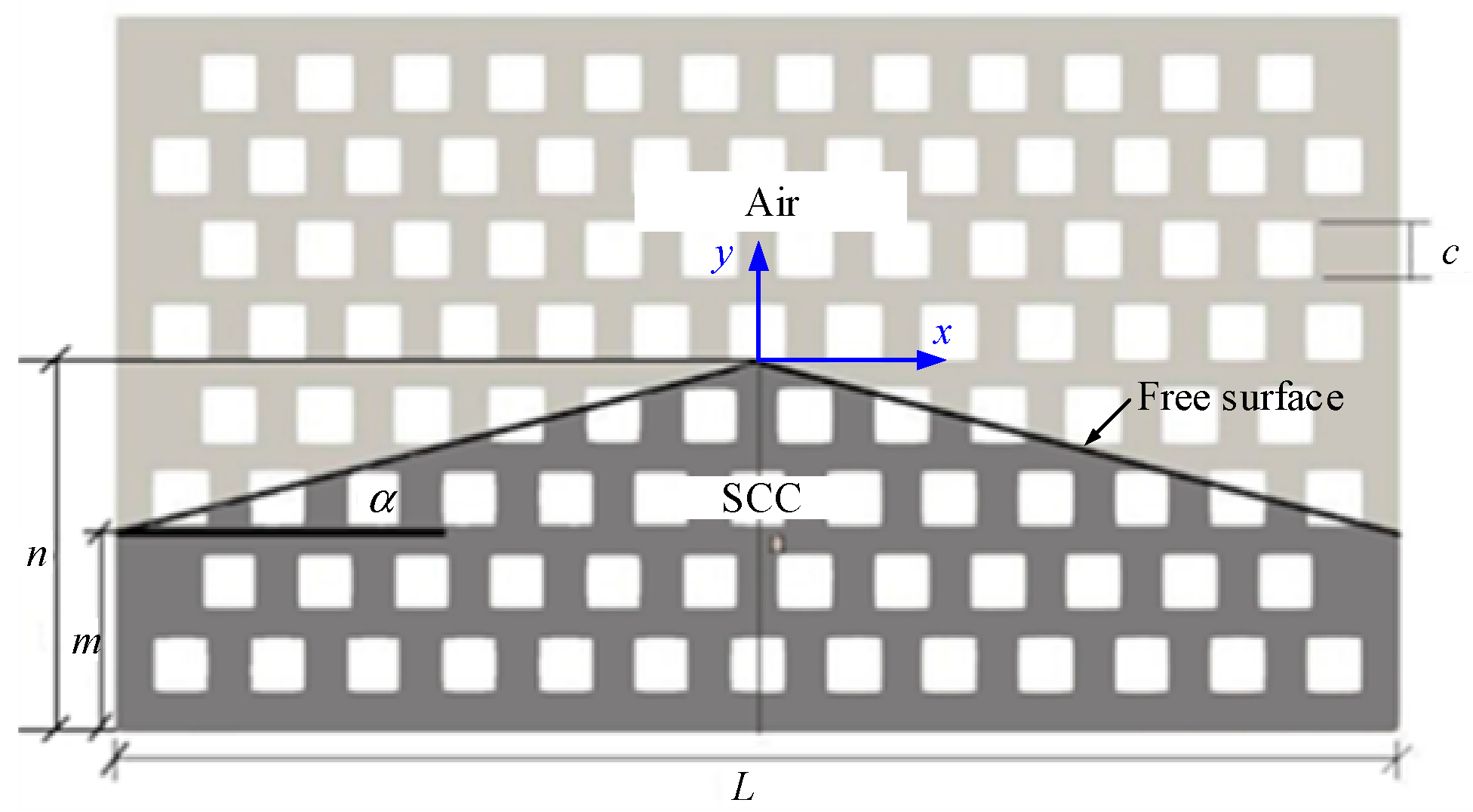
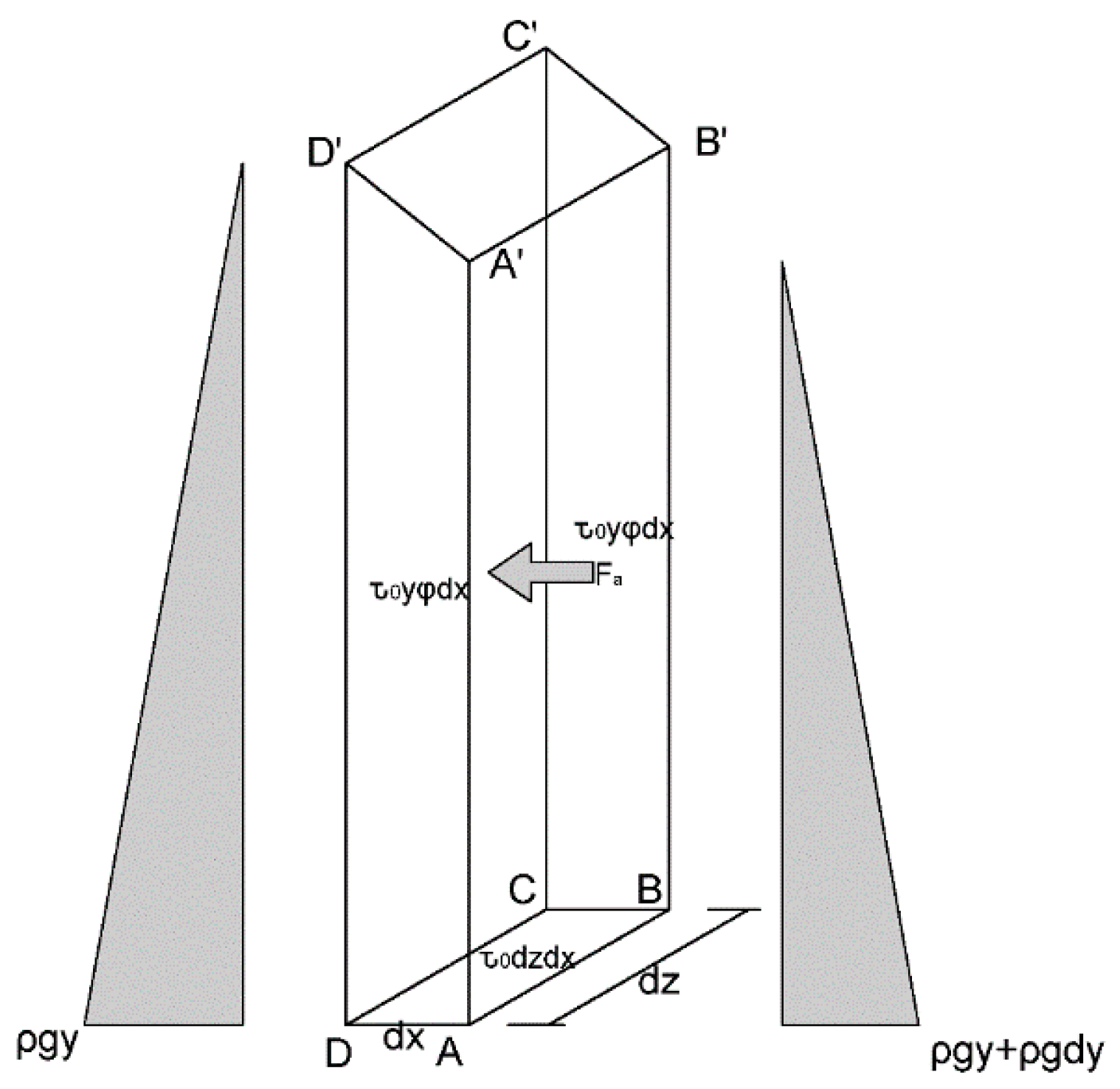
2.3. Derivation of the Theoretical Model
- (a)
- SCC is regarded as a homogeneous fluid.
- (b)
- When the flow stops, the SCC distribution in the porous box is symmetrical and its free surface in the cross-section is regarded as a straight line.
- (c)
- When the flow is about to stop, the main flow direction is horizontal and the vertical velocity is negligible.
3. Results and Discussions
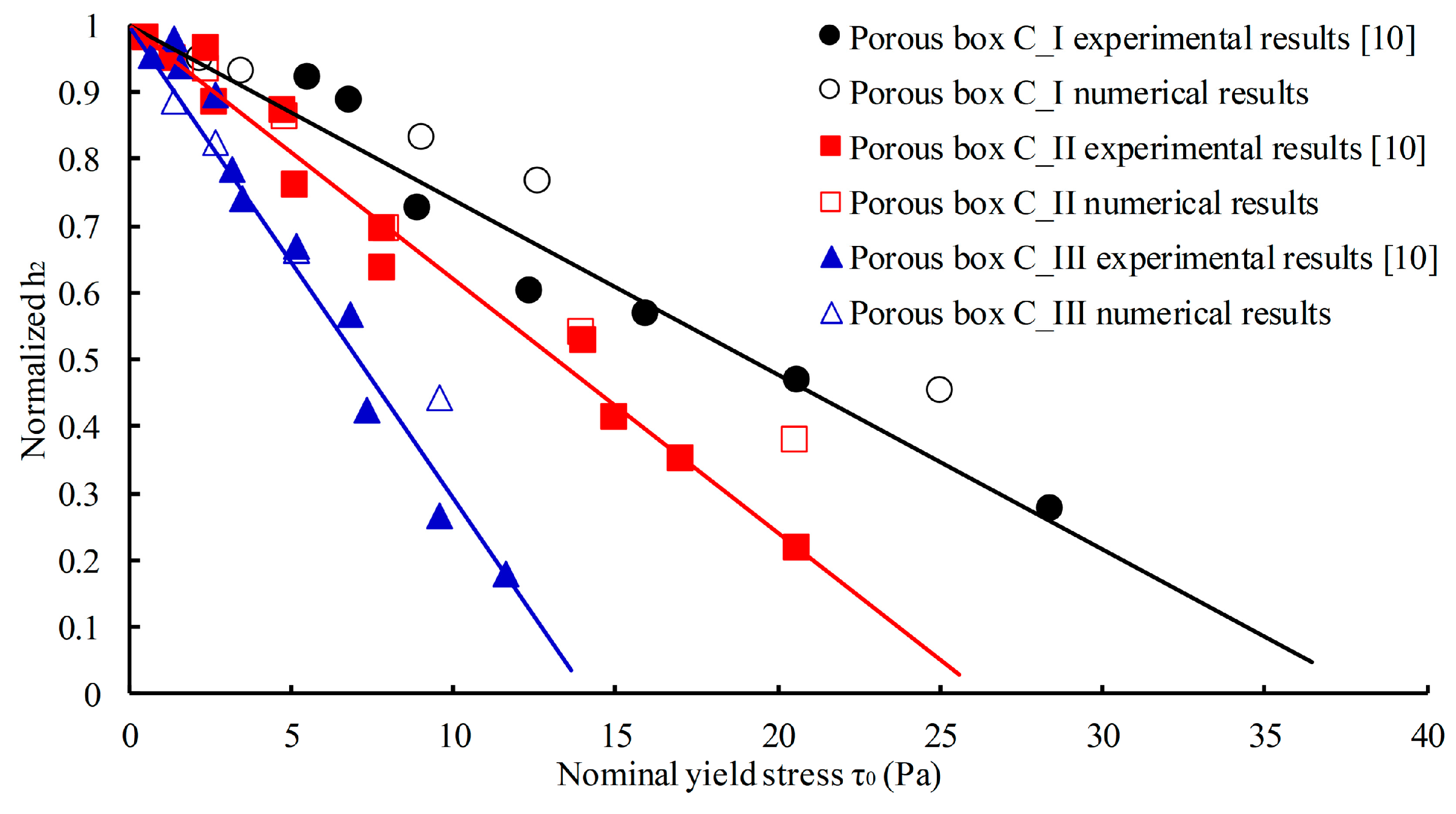
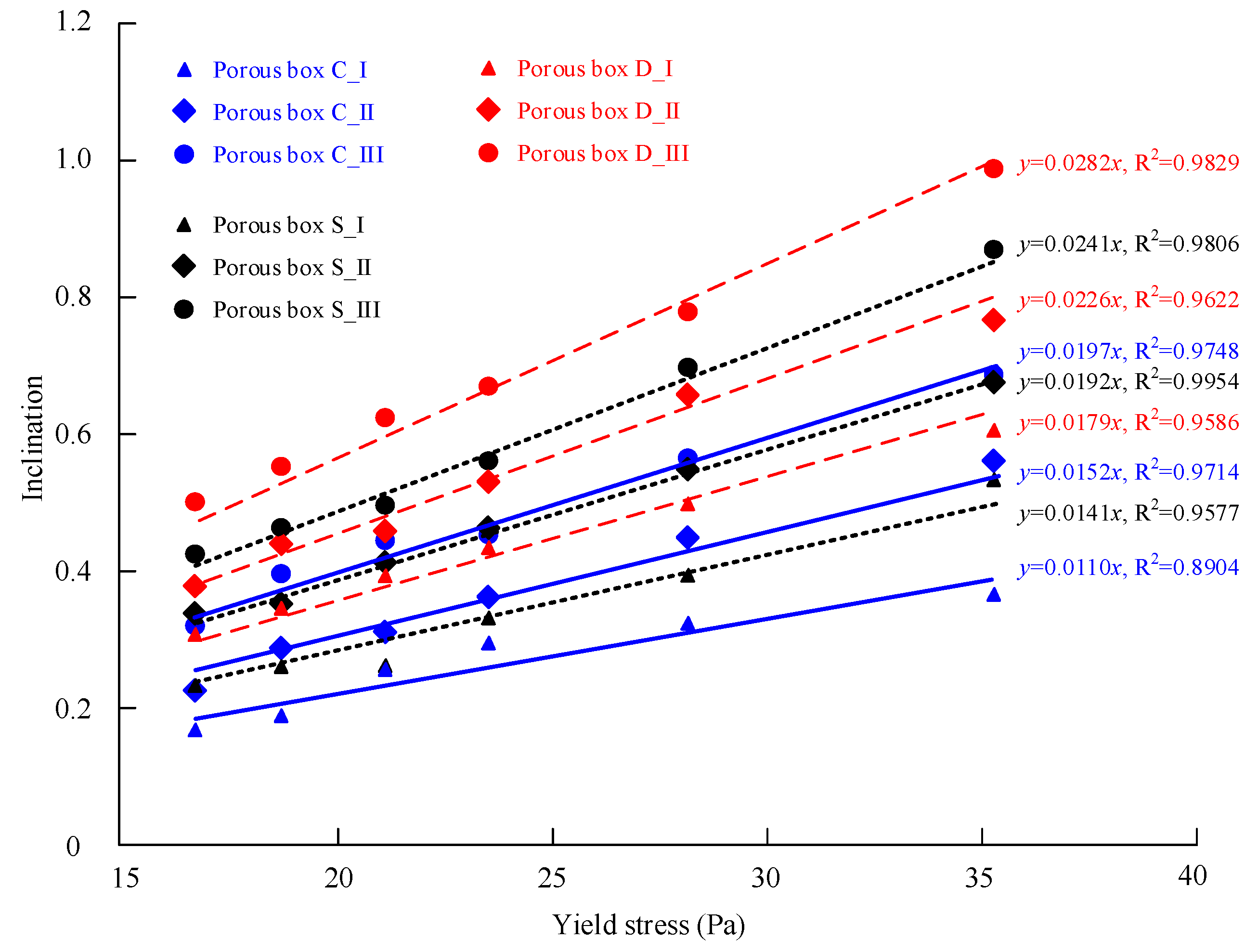
3.1. Effect of Yield Stress on Filling Capacity of SCC
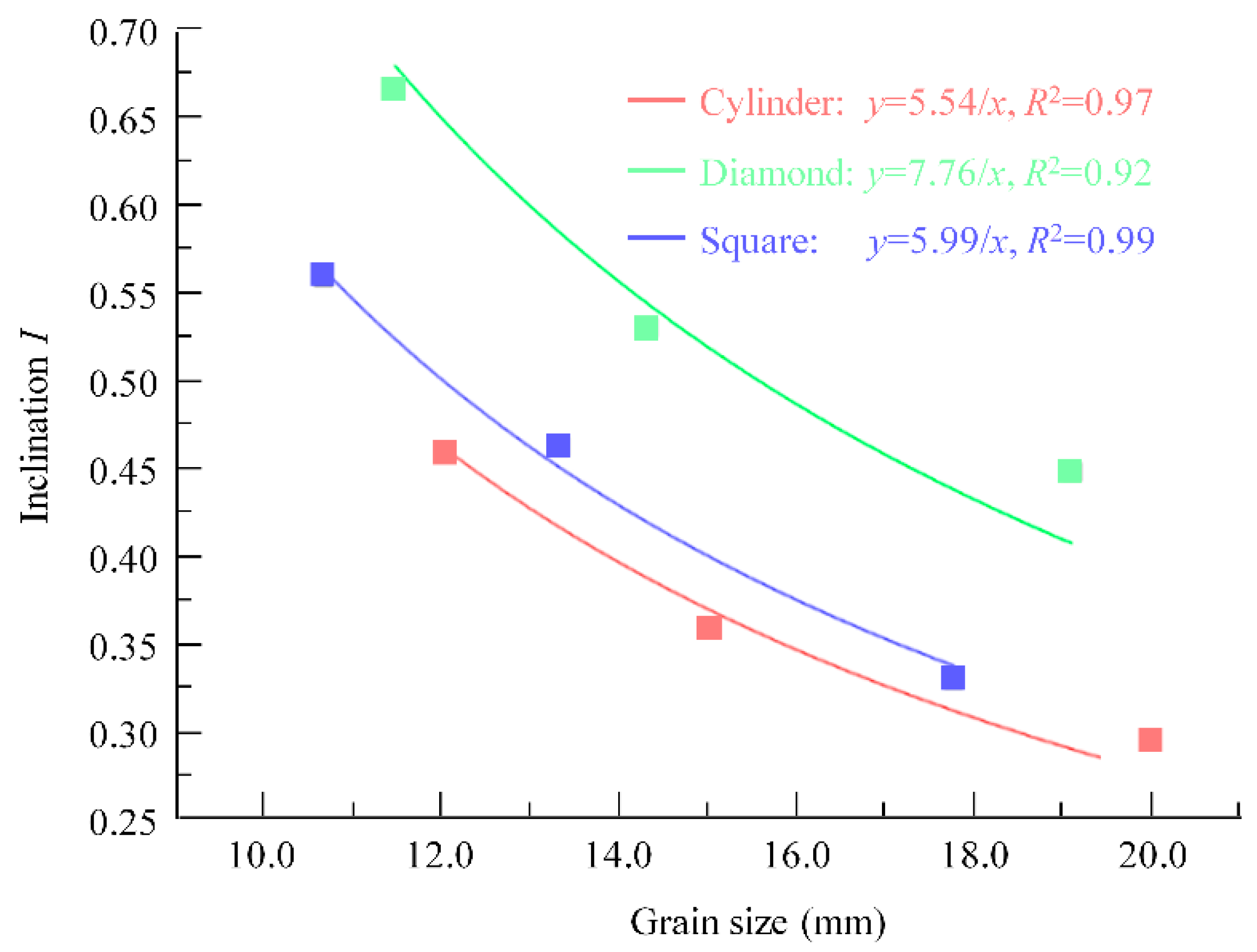
3.2. Effect of Grain Scale and Shape on Filling Capacity of SCC
4. Conclusions
- (1)
- The inclination I of the free surface of SCC distribution at flow stoppage is defined to evaluate the filling capacity of SCC in the porous media. A smaller value of inclination indicates a better filling capacity of the SCC. That is to say, an inclination of zero, corresponding to the fluid with zero yield stress such as water, means perfect filling performance.
- (2)
- The theoretical model, , is proposed for evaluation of filling capacity of SCC in porous media. The filling performance of SCC in porous media is determined by the yield stress of the SCC (τ0), the size (s) and the shape (M) of the grains in the porous media, and the grain accumulation parameter (K). The inclination is directly proportional to the yield stress of the SCC and is inversely proportional to the grain size. The value of MK is defined as blocking effect of grains on SCC flowing in the porous media. It only depends on the shape and accumulation of grains and is not affected by the pore scale. The numerical simulation of SCC flowing in the porous media provides consistent results with the theoretical model.
- (3)
- The theoretical model and numerical simulation suggest that a decrease in yield stress of SCC or an increase in size of grains results in better filling performance of SCC in porous media with the same pore ratio. In addition, SCC exhibits better filling capacity in porous media composed of grains with smooth shapes. These points are beneficial for quality control of RFC. It is expected to use rounded large rocks and SCC with low yield stress to ensure good quality of RFC.
Author Contributions
Funding
Conflicts of Interest
References
- An, X.; Wu, Q.; Jin, F.; Huang, M.; Zhou, H.; Chen, C.; Liu, C. Rock-filled concrete, the new norm of SCC in hydraulic engineering in China. Cem. Concr. Compos. 2014, 54, 89–99. [Google Scholar] [CrossRef]
- Kim, J.K.; Han, S.H.; Park, Y.D.; Noh, J.H. Material Properties of Self-Flowing Concrete. J. Mater. Civ. Eng. 1999, 10, 244–249. [Google Scholar] [CrossRef]
- Xie, Y.; Corr, D.J.; Chaouche, M.; Jin, F.; Shah, S.P. Experimental study of filling capacity of self-compacting concrete and its influence on the properties of rock-filled concrete. Cem. Concr. Res. 2014, 56, 121–128. [Google Scholar] [CrossRef]
- Roussel, N.; Coussot, P. Fifty-cent rheometer for yield stress measurements: From slump to spreading flow. J. Rheol. 2005, 49, 705–718. [Google Scholar] [CrossRef]
- Roussel, N.; Stefani, C.; Leroy, R. From mini-cone test to Abrams cone test: Measurement of cement-based materials yield stress using slump tests. Cem. Concr. Res. 2005, 35, 817–822. [Google Scholar] [CrossRef]
- Okamura, H.; Maekawa, K.; Ozawa, K. High Performance Concrete; Gihoudou Pub: Tokyo, Japan, 1993. [Google Scholar]
- Noguchi, T.; Oh, S.; Tomosawa, F. Rheological approach to passing ability between reinforcing bars of self-compacting concrete. In Self-Compacting Concrete, Proceedings of the First International RILEM Symposium, Stockholm, Sweden, 13–14 September 1999; RILEM Publications: Paris, France, 1999. [Google Scholar]
- Nepomuceno, M.C.; Pereira-de-Oliveira, L.A.; Lopes, S.M.R.; Franco, R.M.C. Maximum coarse aggregate’s volume fraction in self-compacting concrete for different flow restrictions. Constr. Build. Mater. 2016, 113, 851–856. [Google Scholar] [CrossRef]
- Khayat, K.H.; Assaad, J.; Daczko, J. Comparison of field-oriented test methods to assess dynamic stability of self-consolidating concrete. Mater. J. 2004, 101, 168–176. [Google Scholar]
- Wang, Y.Y.; Jin, F.F.; Pan, J.J.; Xie, Y.Y.; Wang, B.B. Grating-box test: A testing method for filling performance evaluation of self-compacting mortar in granular packs. Constr. Build. Mater. 2018, 181, 358–368. [Google Scholar] [CrossRef]
- De Schutter, G.; Gibbs, J.; Domone, P.; Bartos, P.J.M. Self-Compacting Concrete; Universiteit Ghent: Ghent, Belgium, 2008. [Google Scholar]
- Tattersall, G.; Banfill, P. The Rheology of Fresh Concrete, Pitman Adv.; Publ. Progr.: Boston, MA, USA, 1983. [Google Scholar]
- Domone, P.; Yongmo, X.; Banfill, P. Developments of the two-point workability test for high-performance concrete. Mag. Concr. Res. 1999, 51, 171–179. [Google Scholar] [CrossRef]
- Hosseinpoor, M.; Khayat, K.H.; Yahia, A. Numerical simulation of self-consolidating concrete flow as a heterogeneous material in L-Box set-up: Coupled effect of reinforcing bars and aggregate content on flow characteristics. Mater. Struct. 2017, 50, 163. [Google Scholar] [CrossRef]
- Cui, W.; Yan, W.S.; Song, H.F.; Wu, X.L. Blocking analysis of fresh self-compacting concrete based on the DEM. Constr. Build. Mater. 2018, 168, 412–421. [Google Scholar] [CrossRef]
- Chen, S.G.; Zhang, C.H.; Jin, F.; Cao, P.; Sun, Q.C.; Zhou, C.J. Lattice Boltzmann-Discrete Element Modeling Simulation of SCC Flowing Process. for Rock-Filled Concrete. Materials 2019, 12, 3128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vasilic, K.; Meng, B.; Kühne, H.C.; Roussel, N. Flow of fresh concrete through steel bars: A porous medium analogy. Cem. Concr. Res. 2011, 41, 496–503. [Google Scholar] [CrossRef]
- Shin, T.Y.; Kim, J.H.J.M. Prediction of concrete casting in steel-plate concrete panels. Structures 2019, 52, 15. [Google Scholar] [CrossRef]
- Ferraris, C.F.; de Larrard, F.O. Testing and Modelling of Fresh Concrete Rheology; US Department of Commerce, Technology Administration, National Institute of Standards and Technology: Gaithersburg, MD, USA, 1998. [Google Scholar]
- Chidiac, S.E.; Mahmoodzadeh, F. Plastic viscosity of fresh concrete—A critical review of predictions methods. Cem. Concr. Compos. 2009, 31, 535–544. [Google Scholar] [CrossRef]
- Laskar, A.I.; Talukdar, S. Rheological behavior of high performance concrete with mineral admixtures and their blending. Constr. Build. Mater. 2008, 22, 2345–2354. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ Library for Complex Physics Simulations. In International Workshop on Coupled Methods in Numerical Dynamics; IUC: Dubrovnik, Croatia, 2007. [Google Scholar]
- Ayachit, U. The Paraview Guide: A Parallel Visualization Application; Kitware, Inc.: Clifton Park, NY, USA, 2015. [Google Scholar]
- Brookes, G.; Whitmore, R. The static drag on bodies in Bingham plastics. Rheol. Acta 1968, 7, 188–193. [Google Scholar] [CrossRef]
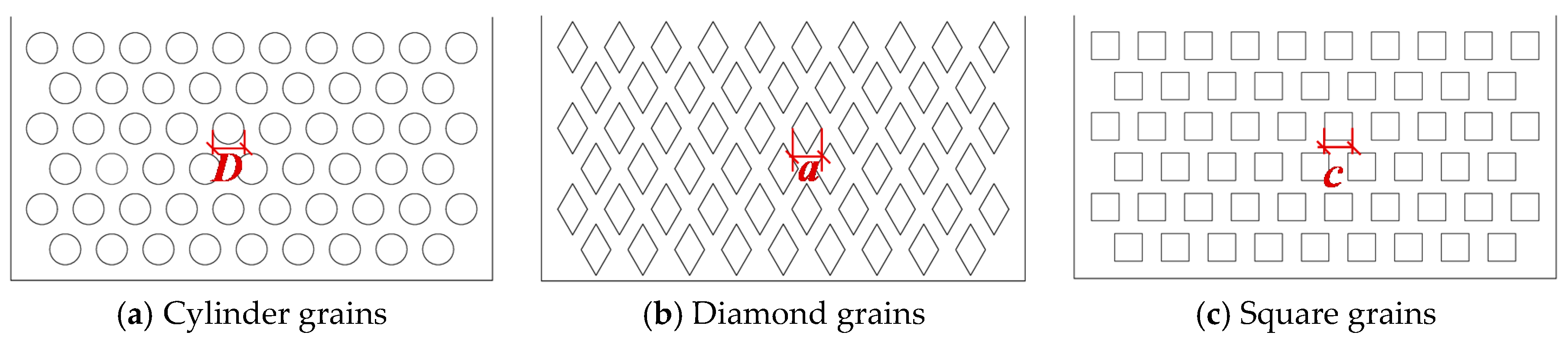

| Porous Box | Shape of Grains | Size of Grains * (mm) | Length of Box (mm) | Height of Box (mm) | Porosity |
|---|---|---|---|---|---|
| C_I | Cylinder | D = 20.00 | 312 | 168 | 0.644 |
| C_II | D = 15.00 | 307 | 171 | 0.663 | |
| C_III | D = 12.00 | 310 | 170 | 0.660 | |
| D_I | Diamond | a = 19.05 | 312 | 168 | 0.644 |
| D_II | a = 14.28 | 307 | 171 | 0.663 | |
| D_III | a = 11.43 | 310 | 170 | 0.660 | |
| S_I | Square | c = 17.72 | 312 | 168 | 0.644 |
| S_II | c = 13.29 | 307 | 171 | 0.663 | |
| S_III | c = 10.63 | 310 | 170 | 0.660 |
| Porous Box | Case | Spreading Diameter * (mm) | Flow Stoppage Time * (s) | Yields Stress (Pa) | Consistency Index (Pa·s m) # |
|---|---|---|---|---|---|
| C_I | 1 | 222.8 | 11 | 28.4 | 23.6 |
| 2 | 250.0 | 13 | 16.0 | 23.6 | |
| 3 | 263.0 | 14 | 12.4 | 23.6 | |
| 4 | 296.2 | 17 | 6.9 | 21.2 | |
| 5 | 308.8 | 19 | 5.5 | 18.8 | |
| C_II | 6 | 230.6 | 12 | 24.0 | 23.6 |
| 7 | 246.0 | 13 | 17.4 | 23.6 | |
| 8 | 268.0 | 14 | 11.2 | 23.6 | |
| 9 | 286.0 | 16 | 8.1 | 21.2 | |
| 10 | 306.6 | 19 | 5.8 | 18.8 | |
| C_III | 11 | 261.0 | 14 | 12.9 | 23.6 |
| 12 | 283.8 | 16 | 8.5 | 23.6 | |
| 13 | 304.0 | 19 | 6.0 | 21.2 | |
| 14 | 319.2 | 20 | 4.7 | 18.8 |
| Porous Box | Yield Stress (Pa) | |||||
|---|---|---|---|---|---|---|
| 16.72 | 18.84 | 21.2 | 23.55 | 28.26 | 35.33 | |
| C_I | 0.172 | 0.188 | 0.255 | 0.294 | 0.325 | 0.362 |
| C_II | 0.215 | 0.284 | 0.312 | 0.359 | 0.446 | 0.551 |
| C_III | 0.322 | 0.394 | 0.447 | 0.459 | 0.559 | 0.674 |
| D_I | 0.306 | 0.349 | 0.398 | 0.448 | 0.494 | 0.601 |
| D_II | 0.379 | 0.440 | 0.462 | 0.530 | 0.688 | 0.761 |
| D_III | 0.497 | 0.553 | 0.621 | 0.666 | 0.772 | 0.979 |
| S_I | 0.226 | 0.260 | 0.262 | 0.330 | 0.390 | 0.533 |
| S_II | 0.331 | 0.351 | 0.406 | 0.462 | 0.543 | 0.670 |
| S_III | 0.422 | 0.454 | 0.492 | 0.559 | 0.689 | 0.870 |
| Grain Shape | Porous Box | M | s | K | |
|---|---|---|---|---|---|
| Cylinder | C_I | 4/π | 20.00 | 111.89 | 152.91 |
| C_II | 15.00 | 122.50 | |||
| C_III | 12.00 | 125.89 | |||
| Diamond | D_I | 2.0 | 19.05 | 109.18 | 219.24 |
| D_II | 14.28 | 110.39 | |||
| D_III | 11.43 | 109.28 | |||
| Square | S_I | 1.0 | 17.72 | 162.94 | 170.40 |
| S_II | 13.29 | 174.56 | |||
| S_III | 10.63 | 173.70 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Pan, J. Filling Capacity Evaluation of Self-Compacting Concrete in Rock-Filled Concrete. Materials 2020, 13, 108. https://doi.org/10.3390/ma13010108
Liu W, Pan J. Filling Capacity Evaluation of Self-Compacting Concrete in Rock-Filled Concrete. Materials. 2020; 13(1):108. https://doi.org/10.3390/ma13010108
Chicago/Turabian StyleLiu, Wenju, and Jianwen Pan. 2020. "Filling Capacity Evaluation of Self-Compacting Concrete in Rock-Filled Concrete" Materials 13, no. 1: 108. https://doi.org/10.3390/ma13010108





