Investigation of Thermal Transport in Multi-Shaped Cu Nanomaterial-Based Nanofluids
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Formulation
2.1.1. Statement and Geometry of the Model
2.1.2. Governing Model and Similarity Transformations
2.2. Mathematical Analysis
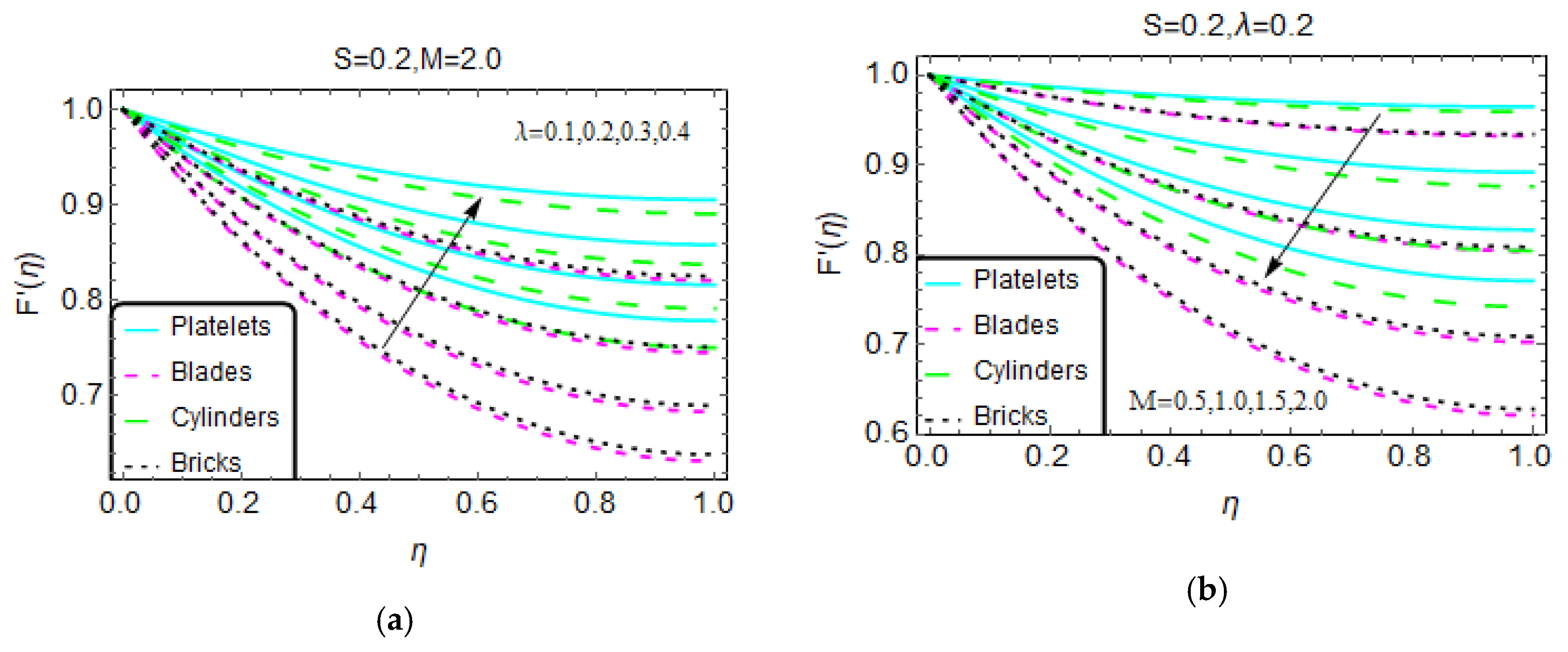
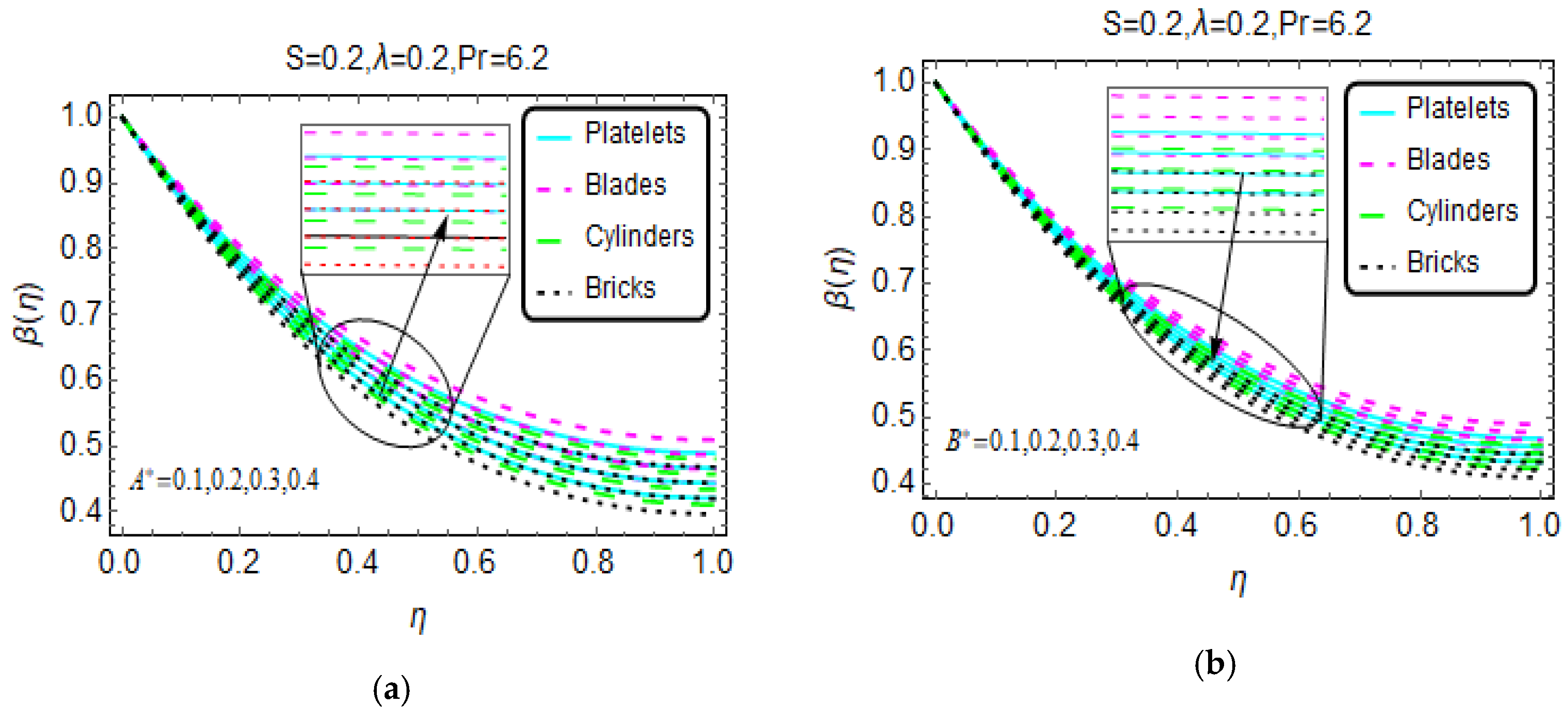
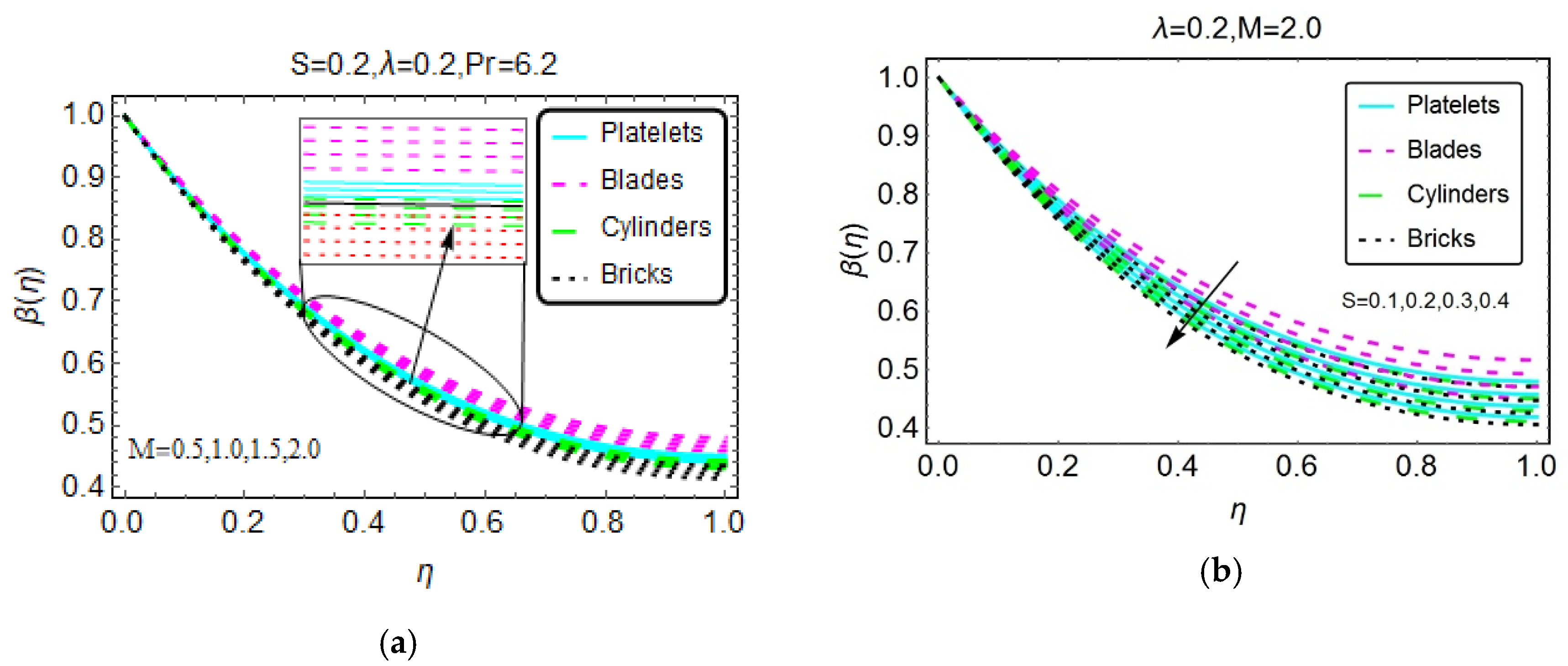
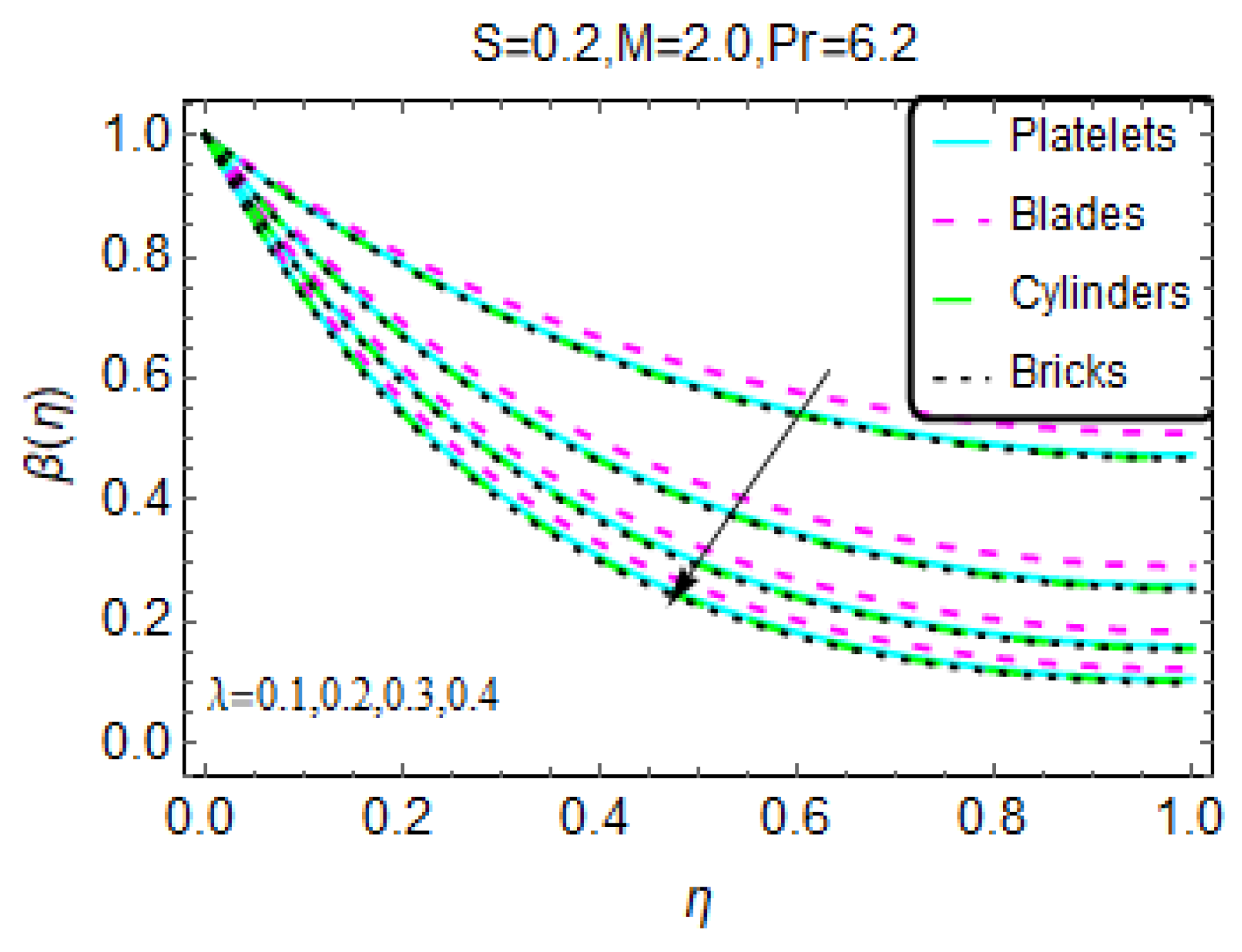
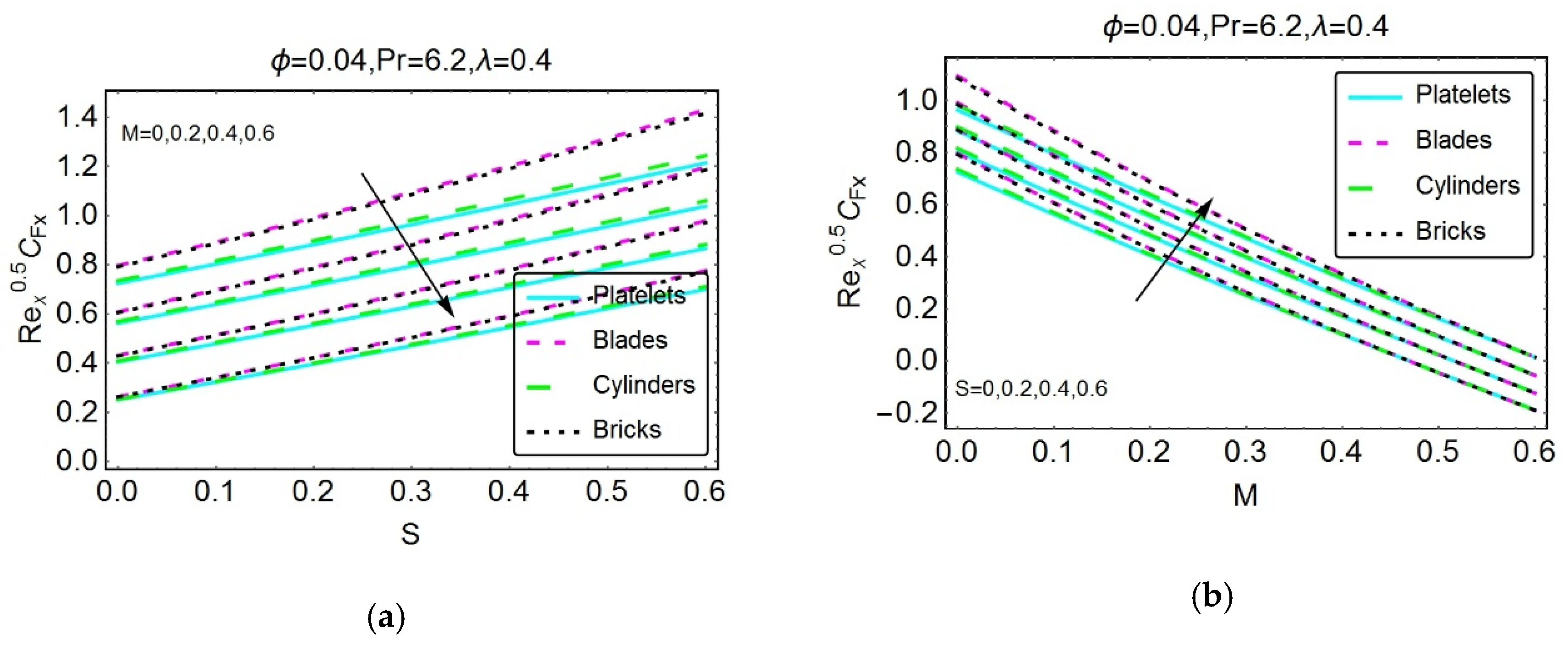
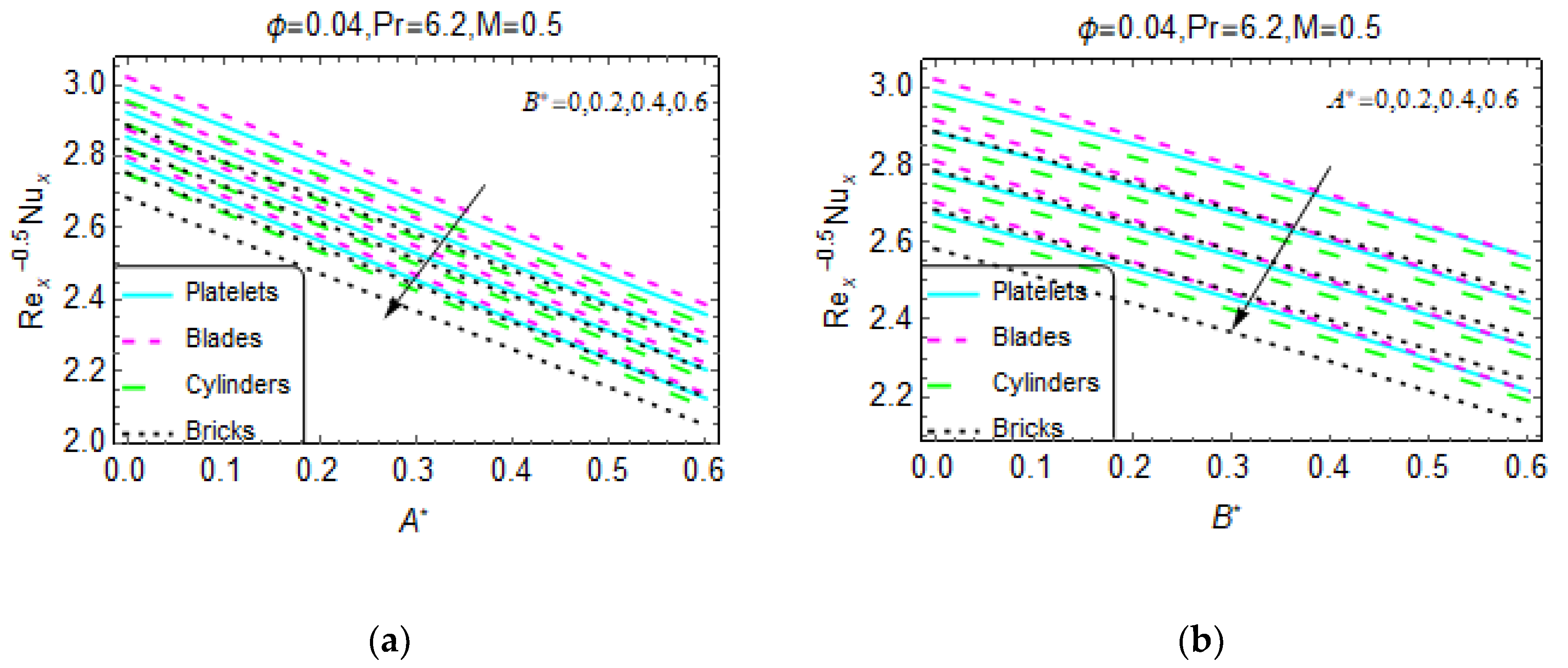
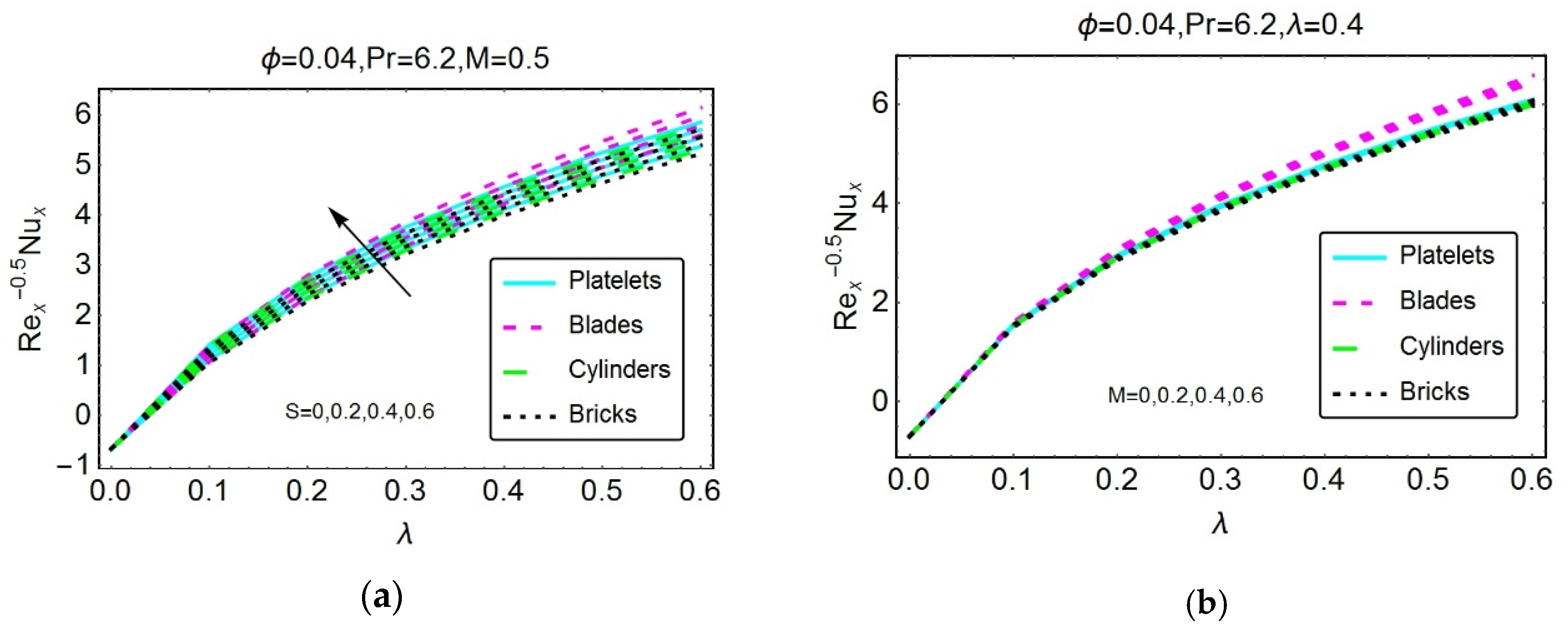
3. Physical Interpretation of the Results
4. Validation of the Analysis
5. Conclusions
6. Achievements
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| u, v | Velocities in the x- and y-directions, respectively (m/s) |
| x, y | Coordinates |
| To and Tr | Temperature at the slit surface and reference temperature, respectively (K) |
| Bo | Magnetic field (T) |
| and b | Constants |
| nf | Denotes the nanofluid |
| Nanofluid density (kg/m3) | |
| and | Densities of the tiny particles and host liquid, respectively (kg/m3) |
| Dynamic viscosity of the nanofluid (kg/ms) | |
| Electrical conductivity of the nanofluid (S/m) | |
| and | Electrical conductivities of the tiny particles and host liquid, respectively (S/m) |
| Specific heat capacity of the nanofluid (J/kg K) | |
| , | Specific heat capacities of the liquid and tiny particles, respectively (J/kg K) |
| Thermal conductivity of the nanofluid (W/m K) | |
| and | Thermal conductivities of the liquid and tiny particles, respectively (W/m K) |
| n | Shape factor of the particles |
| ϕ | Volume fraction of the particles |
| η | Invertible variable |
| F(η) | Dimensionless velocity |
| β(η) | Dimensionless temperature |
| λ | Dimensionless slit thickness |
| φ | Stream function |
| Pr | Prandtl number |
| M | Magnetic number |
| S | Unsteadiness number |
| CFx | Dimensionless skin friction coefficient |
| Nux | Dimensionless Nusselt number |
| and | Linear operators |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. Presented at the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA USA, 12–17 November 1995; Available online: https://www.osti.gov/servlets/purl/196525 (accessed on 1 October 1995).
- Shah, Z.; Dawar, A.; Kumam, P.; Khan, W.; Islam, S. Impact of nonlinear thermal radiation on MHD nanofluid thin film flow over a horizontally rotating disk. Appl. Sci. 2019, 9, 1533. [Google Scholar] [CrossRef] [Green Version]
- Ullah, A.; Shah, Z.; Kumam, P.; Ayaz, M.; Islam, S.; Jameel, M. Viscoelastic MHD nanofluid thin film flow over an unsteady vertical stretching sheet with entropy generation. Processes 2019, 7, 262. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, M.; Qi, S. Heat and Mass Transfer in a thin liquid film over an unsteady stretching surface in the presence of thermosolutal capillarity and variable magnetic field. Math. Probl. Eng. 2016, 2016, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Ramzan, M.; Mohammad, M.; Howari, F.; Chung, J.D. A thin film flow of nanofluid comprising carbon nanotubes influenced by Cattaneo-Christov heat flux and entropy generation. Coatings 2019, 9, 296. [Google Scholar] [CrossRef] [Green Version]
- Nasir, S.; Shah, Z.; Islam, S.; Bonyah, E.; Gul, T. Darcy forchheimer nanofluid thin film flow of SWCNTs and heat transfer analysis over an unsteady stretching sheet. AIP Adv. 2019, 9, 015223. [Google Scholar] [CrossRef] [Green Version]
- Fakour, M.; Rahbari, A.; Khodabandeh, E.; Ganji, D.D. Nanofluid thin film flow and heat transfer over an unsteady stretching elastic sheet by LSM. J. Mech. Sci. Technol. 2018, 32, 177–183. [Google Scholar] [CrossRef]
- Aaiza, G.; Khan, I.; Shafie, S. Energy transfer in mixed convection MHD flow of nanofluid containing different shapes of nanoparticles in a channel filled with saturated porous medium. Nanoscale Res. Lett. 2015, 10, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Khan, U.; Ahmed, N.; Mohyud-Din, S.T. Analysis of magnetohydrodynamic flow and heat transfer of Cu–water nanofluid between parallel plates for different shapes of nanoparticles. Neural Comput. Appl. 2016, 29, 695–703. [Google Scholar] [CrossRef]
- Gul, A.; Khan, I.; Shafie, S.; Khalid, A.; Khan, A. Heat transfer in MHD mixed convection flow of a ferrofluid along a vertical channel. PLoS ONE 2015, 10, e0141213. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hayat, T.; Alsaedi, A. Numerical study for external magnetic source influence on water based nanofluid convective heat transfer. Int. J. Heat Mass Transf. 2017, 106, 745–755. [Google Scholar] [CrossRef]
- Ahmed, N.; Adnan; Khan, U.; Mohyud-Din, S.T. Influence of thermal radiation and viscous dissipation on squeezed flow of water between Riga plates saturated with carbon nanotubes. Colloids Surf. A Physicochem. Eng. Asp. 2017, 522, 389–398. [Google Scholar] [CrossRef]
- Ullah, I.; Shafie, S.; Khan, I. Effects of slip condition and Newtonian heating on MHD flow of Casson fluid over a nonlinearly stretching sheet saturated in a porous medium. J. King Saud Univ. Sci. 2017, 29, 250–259. [Google Scholar] [CrossRef] [Green Version]
- Ullah, I.; Khan, I.; Shafie, S. MHD natural convection flow of casson nanofluid over nonlinearly stretching sheet through porous medium with chemical reaction and thermal radiation. Nanoscale Res. Lett. 2016, 11, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adnan; Khan, U.; Ahmed, N.; Mohyud-Din, S.T. Thermo-diffusion and diffusion-thermo effects on flow of second grade fluid between two inclined plane walls. J. Mol. Liq. 2016, 224, 1074–1082. [Google Scholar] [CrossRef]
- Adnan; Asadullah, M.; Khan, U.; Ahmed, N.; Mohyud-Din, S.T. Analytical and numerical investigation of thermal radiation effects on flow of viscous incompressible fluid with stretchable convergent/divergent channels. J. Mol. Liq. 2016, 224, 768–775. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liq. 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Zin, N.A.M.; Khan, I.; Shafie, S. The impact silver nanoparticles on MHD free convection flow of Jeffrey fluid over an oscillating vertical plate embedded in a porous medium. J. Mol. Liq. 2016, 222, 138–150. [Google Scholar]
- Ali, F.; Gohar, M.; Khan, I. MHD flow of water-based Brinkman type nanofluid over a vertical plate embedded in a porous medium with variable surface velocity, temperature and concentration. J. Mol. Liq. 2016, 223, 412–419. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S.A. Magnetohydrodynamic nanofluid convection in a porous encloure considering heat flux boundary condition. Int. J. Heat Mass Trans. 2017, 106, 1261–1269. [Google Scholar] [CrossRef]
- Sheikholeslami, M. CVFEM for magnetic nanofluid convective heat transfer in a porous curved enclosure. Eur. Phys. J. Plus 2016, 131. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Hashim, I. Thermocapillarity and magnetic field effects in a thin liquid film on an unsteady stretching surface. Int. J. Heat Mass Transf. 2010, 53, 2044–2051. [Google Scholar] [CrossRef]
- Wang, C.; Pop, I. Analysis of the flow of a power-law fluid film on an unsteady stretching surface by means of homotopy analysis method. J. Non-Newtonian Fluid Mech. 2006, 138, 161–172. [Google Scholar] [CrossRef]




| Model | Platelets | Blades | Cylinders | Bricks |
|---|---|---|---|---|
| 37.1 | 14.6 | 13.5 | 1.9 | |
| 612.6 | 123.3 | 904.4 | 471.4 |
| Model | Platelets | Blades | Cylinders | Bricks |
|---|---|---|---|---|
| 0.52 | 0.36 | 0.62 | 0.81 |
| Model | (kgm−3) | (kg−1k−1) | (wm−1k−1) | (10−5k−1) |
|---|---|---|---|---|
| 997.1 | 4179 | 0.613 | 21 | |
| 8933 | 385 | 401 | 1.67 |
| Error | |||||||
|---|---|---|---|---|---|---|---|
| η ↓ | F(η) | β(η) | ||||
|---|---|---|---|---|---|---|
| HAM | Numerical | Error | HAM | Numerical | Error | |
| 0.0 | ||||||
| 0.1 | ||||||
| 0.2 | ||||||
| 0.3 | ||||||
| 0.4 | ||||||
| 0.5 | ||||||
| 0.6 | ||||||
| 0.7 | ||||||
| 0.8 | ||||||
| 0.9 | ||||||
| 1.0 | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adnan; Ali Zaidi, S.Z.; Khan, U.; Abdeljawad, T.; Ahmed, N.; Mohyud-Din, S.T.; Khan, I.; Nisar, K.S. Investigation of Thermal Transport in Multi-Shaped Cu Nanomaterial-Based Nanofluids. Materials 2020, 13, 2737. https://doi.org/10.3390/ma13122737
Adnan, Ali Zaidi SZ, Khan U, Abdeljawad T, Ahmed N, Mohyud-Din ST, Khan I, Nisar KS. Investigation of Thermal Transport in Multi-Shaped Cu Nanomaterial-Based Nanofluids. Materials. 2020; 13(12):2737. https://doi.org/10.3390/ma13122737
Chicago/Turabian StyleAdnan, Syed Zulfiqar Ali Zaidi, Umar Khan, Thabet Abdeljawad, Naveed Ahmed, Syed Tauseef Mohyud-Din, Ilyas Khan, and Kottakkaran Sooppy Nisar. 2020. "Investigation of Thermal Transport in Multi-Shaped Cu Nanomaterial-Based Nanofluids" Materials 13, no. 12: 2737. https://doi.org/10.3390/ma13122737
APA StyleAdnan, Ali Zaidi, S. Z., Khan, U., Abdeljawad, T., Ahmed, N., Mohyud-Din, S. T., Khan, I., & Nisar, K. S. (2020). Investigation of Thermal Transport in Multi-Shaped Cu Nanomaterial-Based Nanofluids. Materials, 13(12), 2737. https://doi.org/10.3390/ma13122737






