The Effect of Transverse Shear in Symmetric and Asymmetric End Notch Flexure Tests–Analytical and Numerical Modeling
Abstract
:1. Introduction
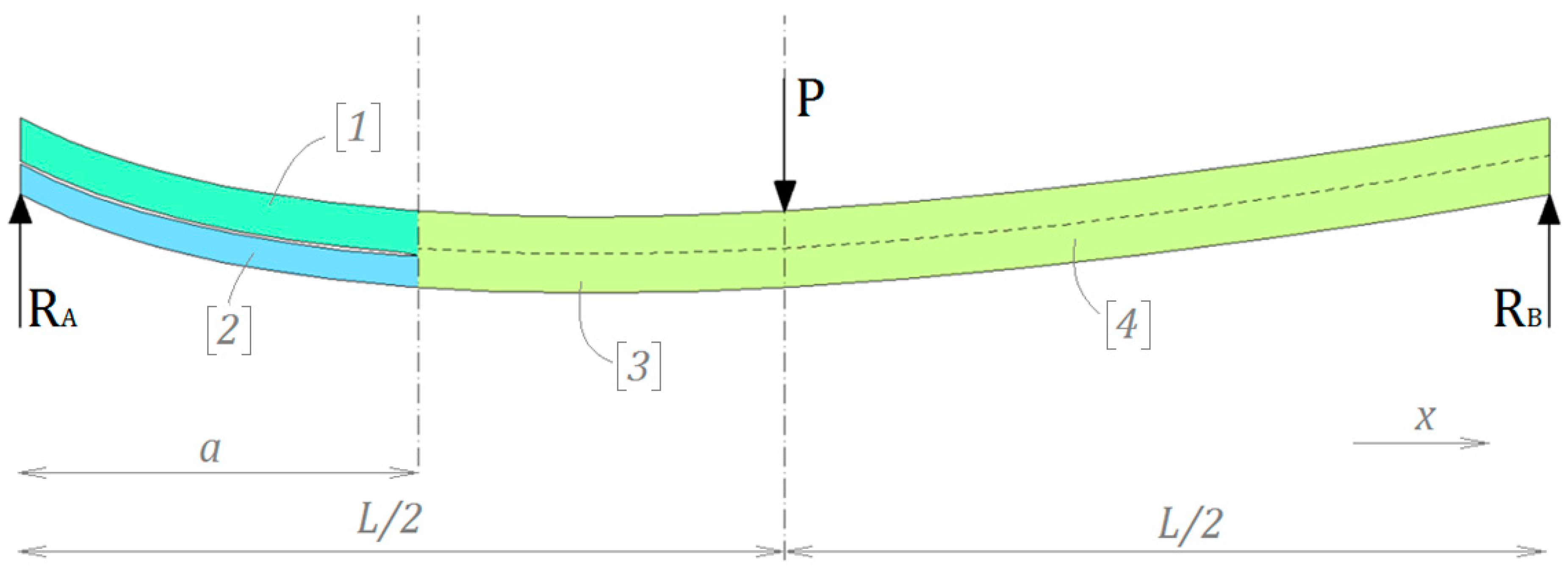
2. Problem Description
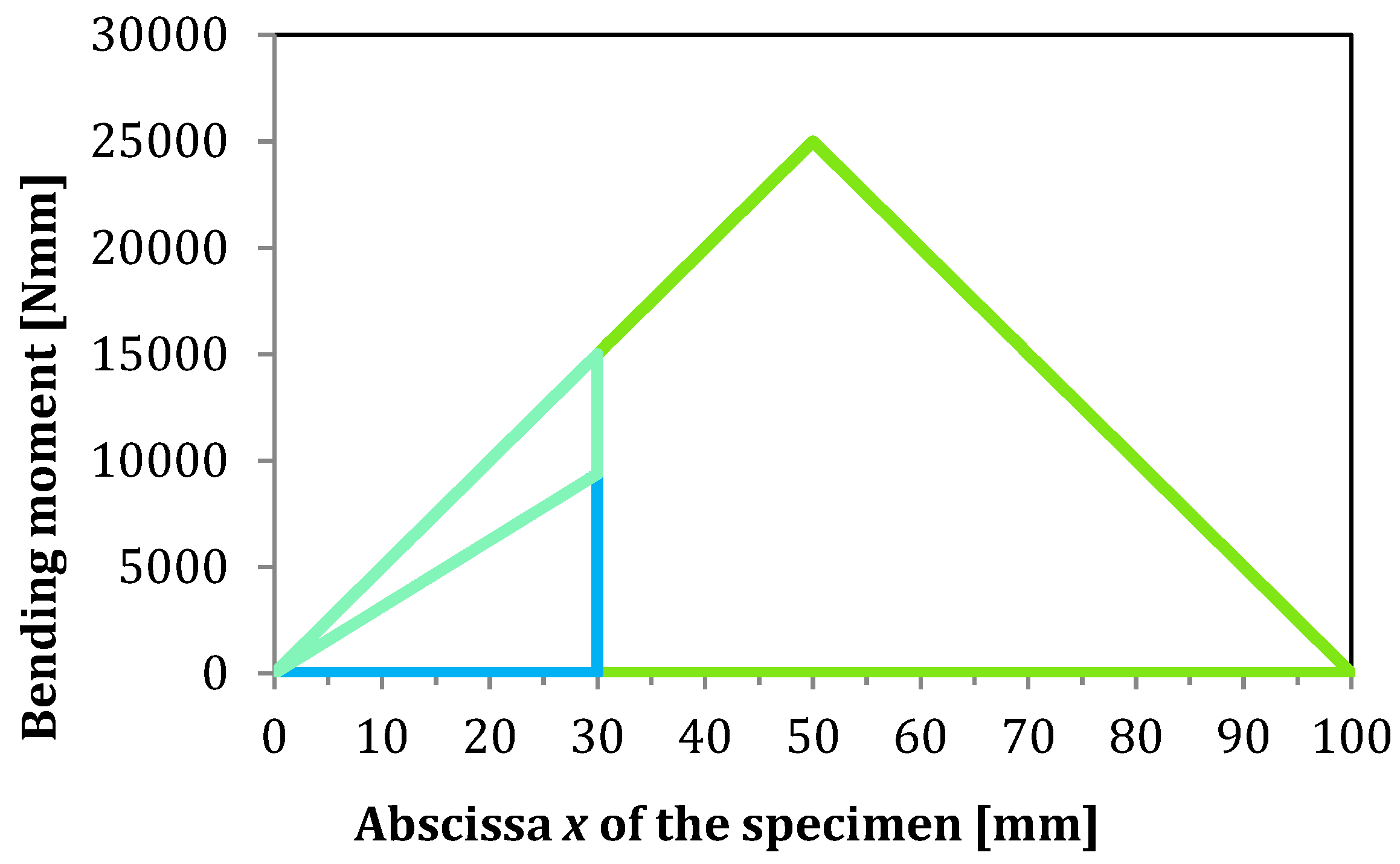
2.1. The Magnitude of Bending Moment Acting on Non-Cracked Part of the Beam
2.2. Shearing Forces and Bending Moment Acting on Delaminated Regions of the Specimen
3. Simple Beam Theory Solution
3.1. Deflection of Two Euler–Bernoulli Cantilever Beams Fixed at One End
3.2. Deflection Curve of the AENF Specimen
3.2.1. First Integrations of the Differential Equations for Beams Curvatures
3.2.2. First Boundary Conditions: Slopes of the Beams at Singular Points
3.2.3. Second Integration of the Beams Slope’s Equations.
3.2.4. Second Boundary Conditions: Beam Deflections at Specimen Ends
3.2.5. Third Boundary Conditions: Beam Deflections at Singular Points
3.3. Final Form of the Equation for AENF Deflection Curve by Euler–Bernoulli Beam Theory
3.4. Crack Length as a Function of AENF Specimen Deflection
4. Timoshenko Beam Theory Solution
4.1. Deflection of Two Timoshenko Cantilever Beams Fixed at One End
4.2. Deflection Curve of the AENF Specimen
4.2.1. First Integrations of the Differential Equations for Beams Curvatures
4.2.2. First Boundary Condition: Cross-Section Rotations of the Beams at Singular Points
4.2.3. Second Integration of the Beams Equations
4.2.4. Second Boundary Conditions: Beam Deflections at Specimen Ends
4.2.5. Third Boundary Conditions: Beam Deflections at Singular Points
4.2.6. Final Form of the Equation for AENF Deflection Curve by Timoshenko Beam Theory
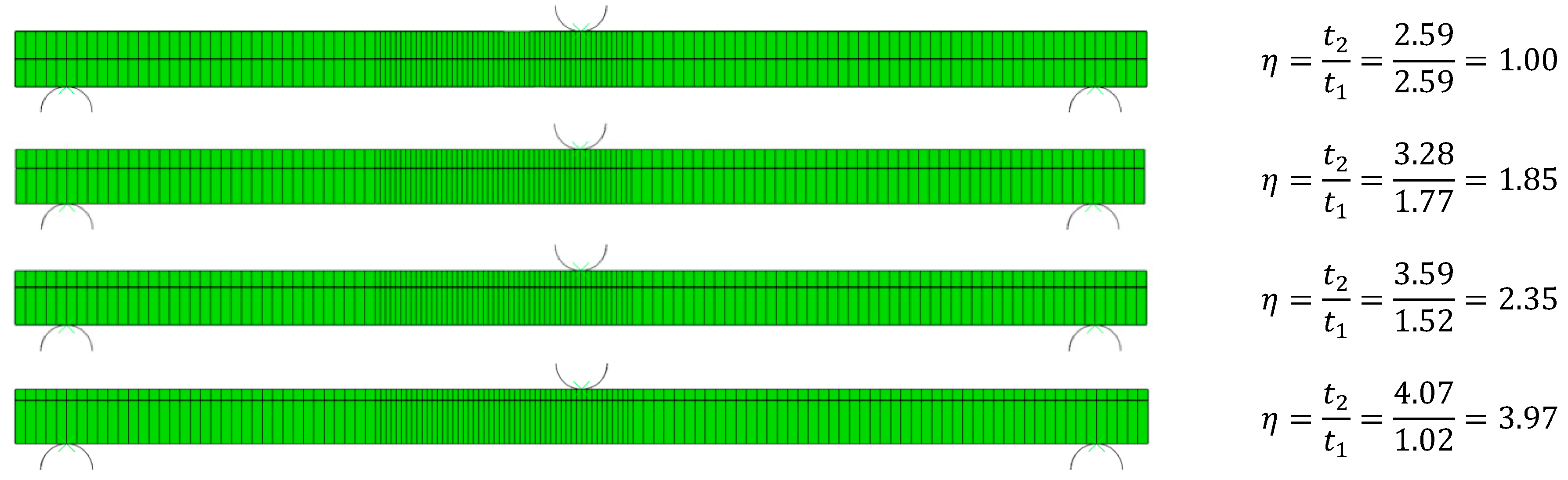
5. Experimental and Numerical Validation
5.1. Methodology
5.2. Deflection Profiles of the ENF and AENF Specimen
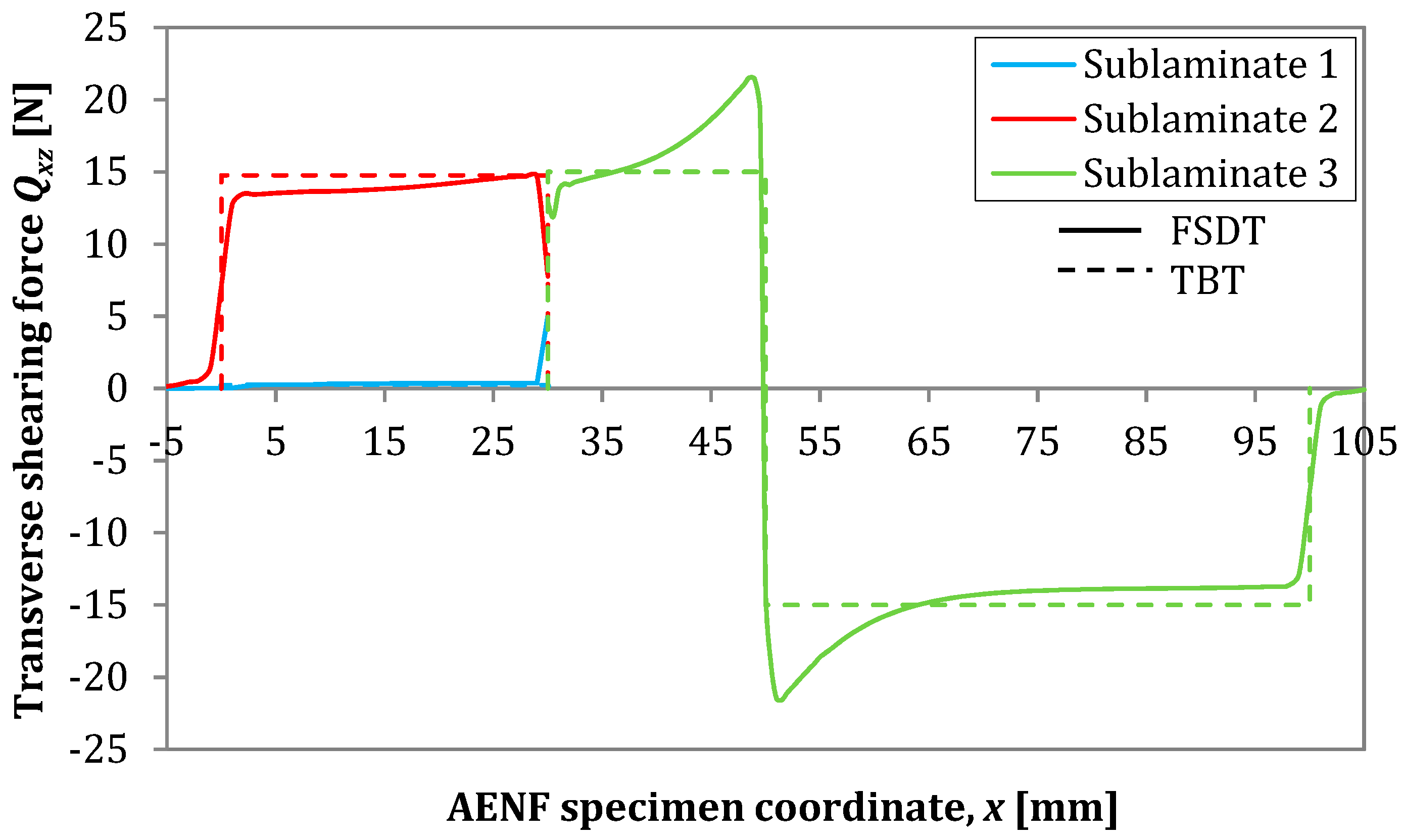
6. Influence of Cross-Section Rotation on the Internal Forces in AENF
6.1. Parametric Study-Simple vs. Timoshenko Beam Theory
6.2. Three-Dimensional Finite Element Analysis Modeling of AENF
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Sublaminate Equivalent Stiffness
References
- Barrett, J.D.; Foschi, R.O. Mode II Stress Intensity Factors for Cracked Wood Beams. Eng. Fract. Mech. 1977, 9, 371–378. [Google Scholar] [CrossRef]
- Russell, A.J.; Street, K.N. Moisture and temperature effects on the mixed-mode delamination fracture of unidirectional graphite/epoxy. In Delamination and Debonding of Materials; Johnson, W.S., Ed.; STP876-EB; ASTM International: West Conshohocken, NY, USA, 1985; pp. 349–370. [Google Scholar] [CrossRef]
- O’Brien, T.K.; Johnston, W.M.; Toland, G.J. Mode II Interlaminar Fracture Toughness and Fatigue Characterization of a Graphite Epoxy Composite Material; Technical Report; National Aeronautics and Space Administration Langley Research Center: Hampton, VA, USA, August 2010; p. 23681-2199.
- Sundararaman, V.; Davidson, B.D. An unsymmetric end-notched flexure test for interfacial fracture toughness determination. Eng. Fract. Mech. 1998, 60, 361–377. [Google Scholar] [CrossRef]
- Pereira, A.B.; de Morais, A.B.; Marques, A.T.; de Castro, P.T. Mode II interlaminar fracture of carbon/epoxy multidirectional laminates. Compos. Sci. Technol. 2004, 64, 1653–1659. [Google Scholar] [CrossRef]
- Adamos, L.; Tsokanas, P.; Loutas, T. An experimental study of the interfacial fracture behavior of Titanium/CFRP adhesive joints under mode I and mode II fatigue. Int. J. Fatigue 2020, 136, 105586. [Google Scholar] [CrossRef]
- Dadej, K.; Bieniaś, J.; Valvo, P.S. Experimental Testing and Analytical Modeling of Asymmetric End-Notched Flexure Tests on Glass-Fiber Metal Laminates. Metals 2020, 10, 56. [Google Scholar] [CrossRef] [Green Version]
- Bienias, J.; Dadej, K.; Surowska, B. Interlaminar fracture toughness of glass and carbon reinforced multidirectional fiber metal laminates. Eng. Fract. Mech. 2017, 175, 127–145. [Google Scholar] [CrossRef]
- ASTM D7905/D7905M-19. Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, NY, USA, 2019. [Google Scholar] [CrossRef]
- Davidson, B.D.; Teller, S.S. Recommendations for an ASTM Standardized Test for Determining GIIc of Unidirectional Laminated Polymeric Matrix Composites. J. ASTM Int. 2010, 7, 1–11. [Google Scholar] [CrossRef]
- Gillespie, J.M., Jr.; Carlsson, L.A.; Pipes, R.B. Finite element analysis of the end notched flexure specimen for measuring mode II fracture toughness. Compos. Sci. Technol. 1986, 27, 177–197. [Google Scholar] [CrossRef]
- Carlsson, L.A.; Gillespie, J.W., Jr.; Pipes, R.B. On the analysis and design of end notched flexure (ENF) for mode II testing. J. Compos. Mater. 1986, 20, 594–604. [Google Scholar] [CrossRef]
- Timoshenko, S.P. Strength of Materials, Vol. 1: Elementary Theory and Problems, 3rd ed.; D. Van Nostrand: New York, NY, USA, 1955. [Google Scholar]
- Valvo, P.S. The effects of shear on Mode II delamination: A critical review. Fract. Struct. Integr. 2018, 44, 123–139. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Wang, J.; Thouless, M.D. The effects of shear on delamination in layered materials. J. Mech. Phys. Solids 2004, 52, 193–214. [Google Scholar] [CrossRef]
- Andrews, M.G.; Massabò, R. The effects of shear and near tip deformations on energy release rate and mode mixity of edge-cracked orthotropic layers. Eng. Fract. Mech. 2007, 74, 2700–2720. [Google Scholar] [CrossRef]
- Wang, J.; Qiao, P. Mechanics of Bimaterial Interface: Shear Deformable Split Bilayer Beam Theory and Fracture. J. Appl. Mech. 2005, 72, 674–682. [Google Scholar] [CrossRef]
- Bennati, S.; Fisicaro, P.; Valvo, P.S. An enhanced beam-theory model of the mixed-mode bending (MMB) test—Part II: Applications and results. Meccanica 2013, 48, 465–484. [Google Scholar] [CrossRef] [Green Version]
- Reissner, E. The effect of transverse shear deformation on the bending of elastic plates. J. Appl. Mech. 1945, 12, 69–72. [Google Scholar]
- Mindlin, R.D. Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar]
- Jones, R.M. Mechanics of Composite Materials, 2nd ed.; Taylor & Francis: Philadelphia, PA, USA, 1999. [Google Scholar]
- Valvo, P.S. On the calculation of energy release rate and mode mixity in delaminated laminated beams. Eng. Fract. Mech. 2016, 165, 114–139. [Google Scholar] [CrossRef]
- Cubic Formula. Available online: https://mathworld.wolfram.com/CubicFormula.html (accessed on 7 July 2020).
- MATLAB, R2017a, Symbolic Math Toolbox; The MathWorks I.: Natick, MA, USA, 2019; Available online: https://www.mathworks.com/help/symbolic/ (accessed on 7 July 2020).
- Brunner, A.J.; Stelzer, S.; Pinter, G.; Terrasi, G.P. Mode II fatigue delamination resistance of advanced-reinforced polymer-matrix laminates: Towards the development of a standarized test procedure. Int. J. Fatigue 2013, 50, 57–62. [Google Scholar] [CrossRef]
- Blackman, B.R.K.; Brunner, A.J.; Williams, J.G. Mode II fracture testing of composites: A new look at an old problem. Eng. Fract. Mech. 2006, 73, 2443–2455. [Google Scholar] [CrossRef]
- Bienias, J.; Dadej, K. Fatigue delamination growth of carbon and glass reinforced fiber metal laminates in fracture mode II. Int. J. Fatigue 2020, 130, 105267. [Google Scholar] [CrossRef]
- Blackman, B.R.K.; Kinloch, A.J.; Paraschi, M. The determination of the mode II adhesive fracture resistance, GIIC, of structural adhesive joints: An effective crack length approach. Eng. Fract. Mech. 2005, 72, 877–897. [Google Scholar] [CrossRef] [Green Version]
- Jumel, J.; Budzik, M.K.; Ben Salem, N.; Shanahan, M.E.R. Instrumented End Notched Flexure—Crack propagation and process zone monitoring. Part I: Modelling and analysis. Int. J. Solid Struct. 2013, 50, 297–309. [Google Scholar] [CrossRef] [Green Version]
- Budzik, M.K.; Jumel, J.; Ben Salem, N.; Shanahan, M.E.R. Instrumented end notched flexure—Crack propagation and process zone monitoring Part II: Data reduction and experimental. Int. J. solid Struct. 2013, 50, 310–319. [Google Scholar] [CrossRef] [Green Version]
- Szekrenyes, A. Interlaminar stresses and energy release rates in delaminated orthotropic composite plates. Int. J. Solid Struct. 2012, 49, 2460–2470. [Google Scholar] [CrossRef] [Green Version]




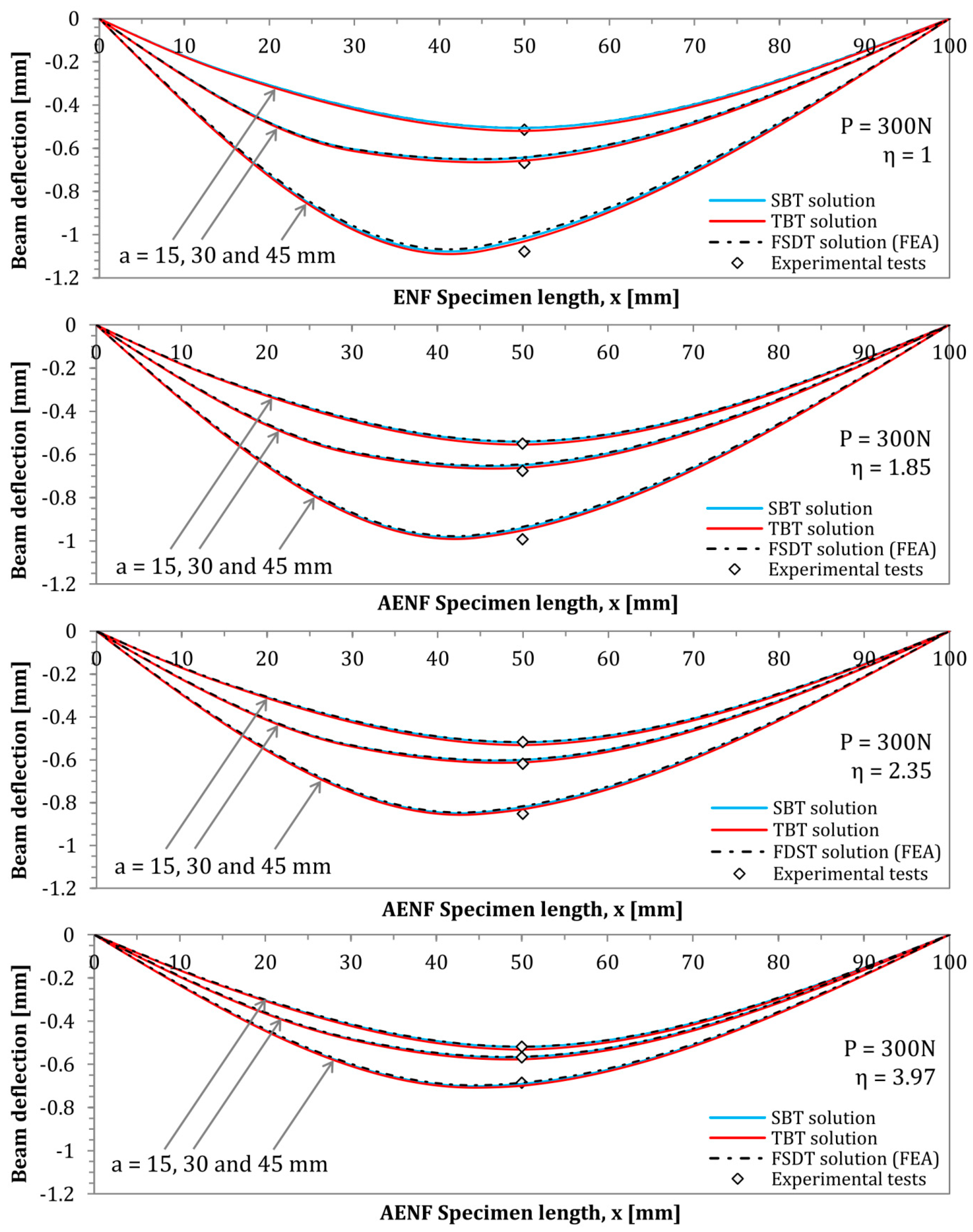
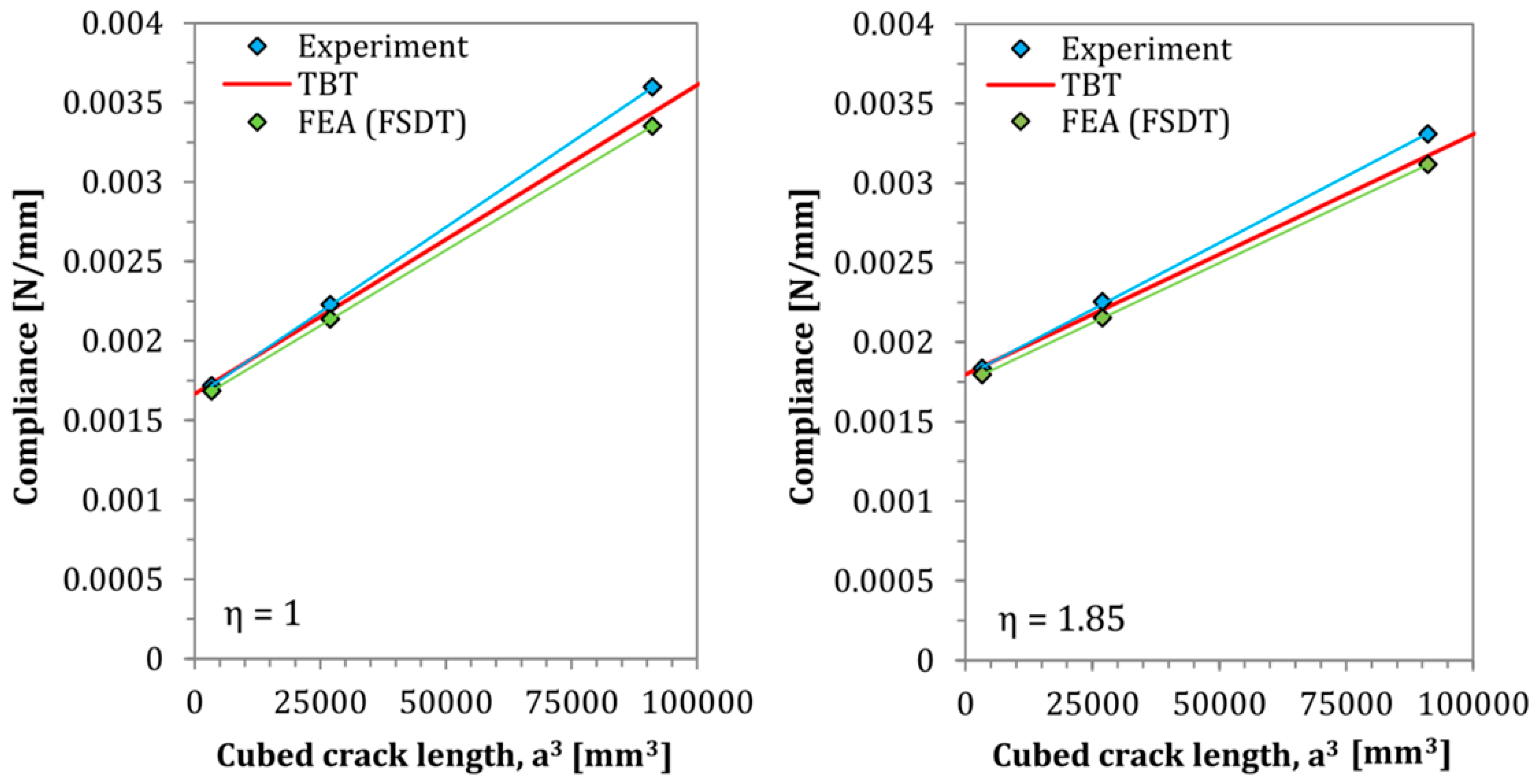


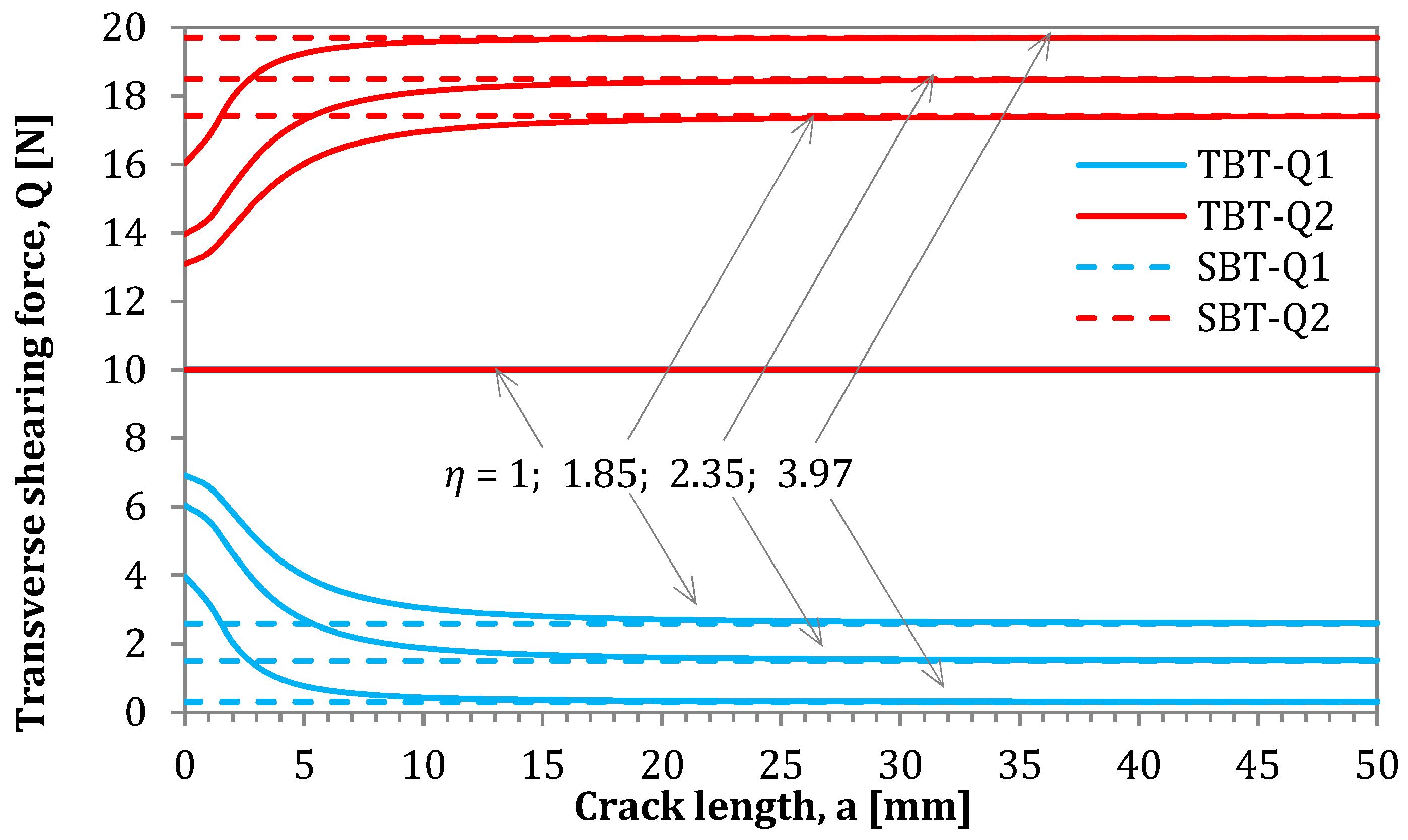
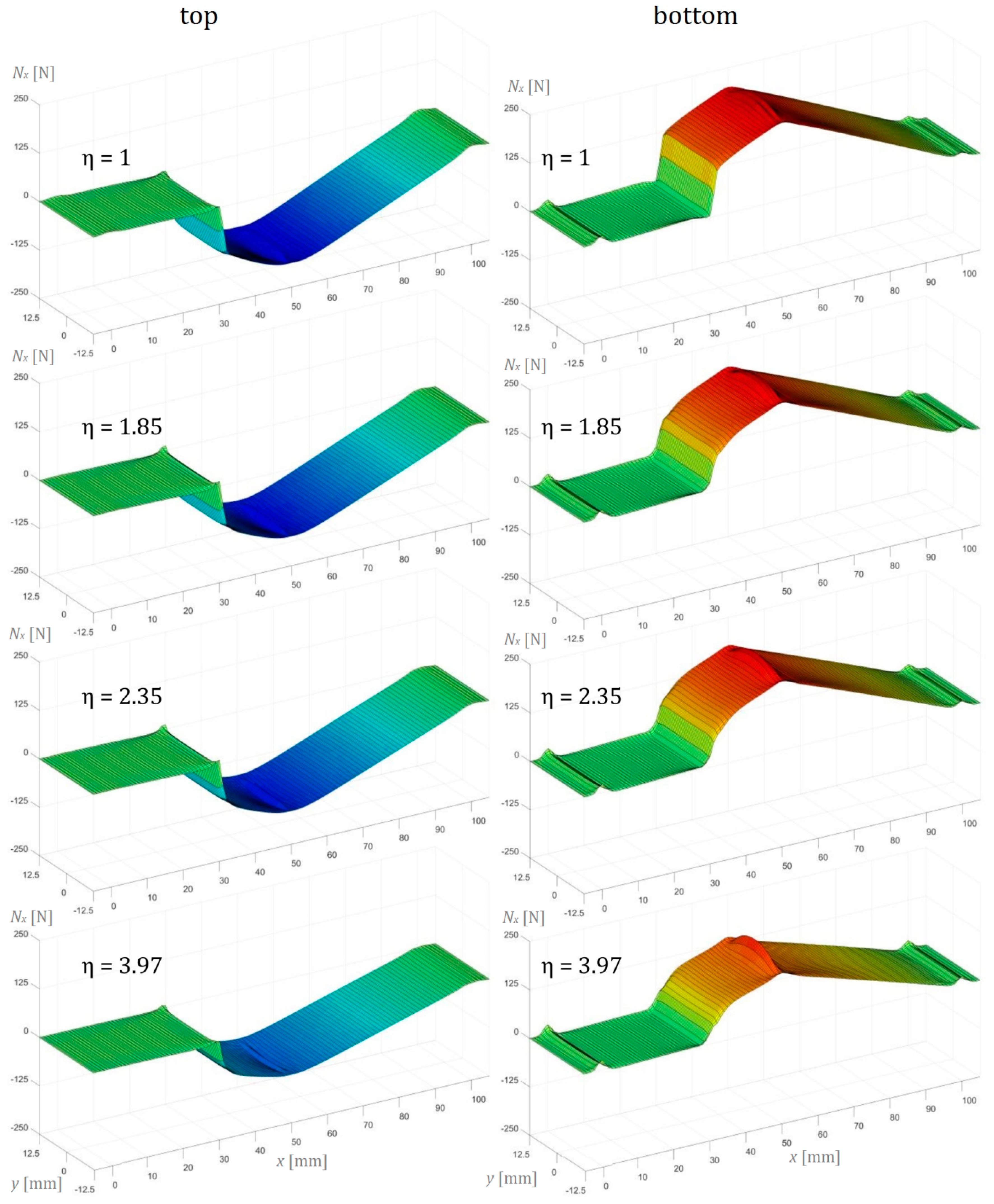

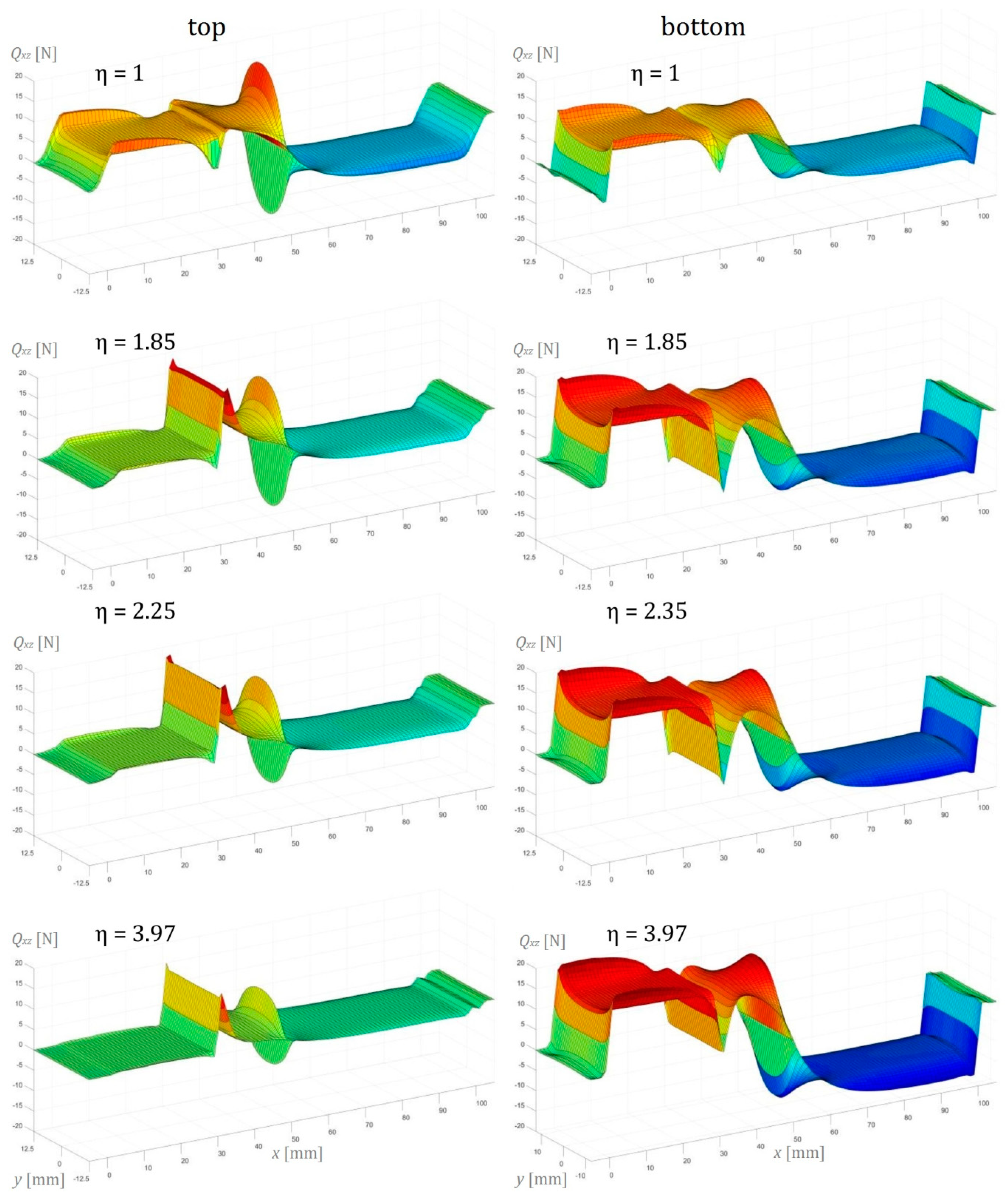
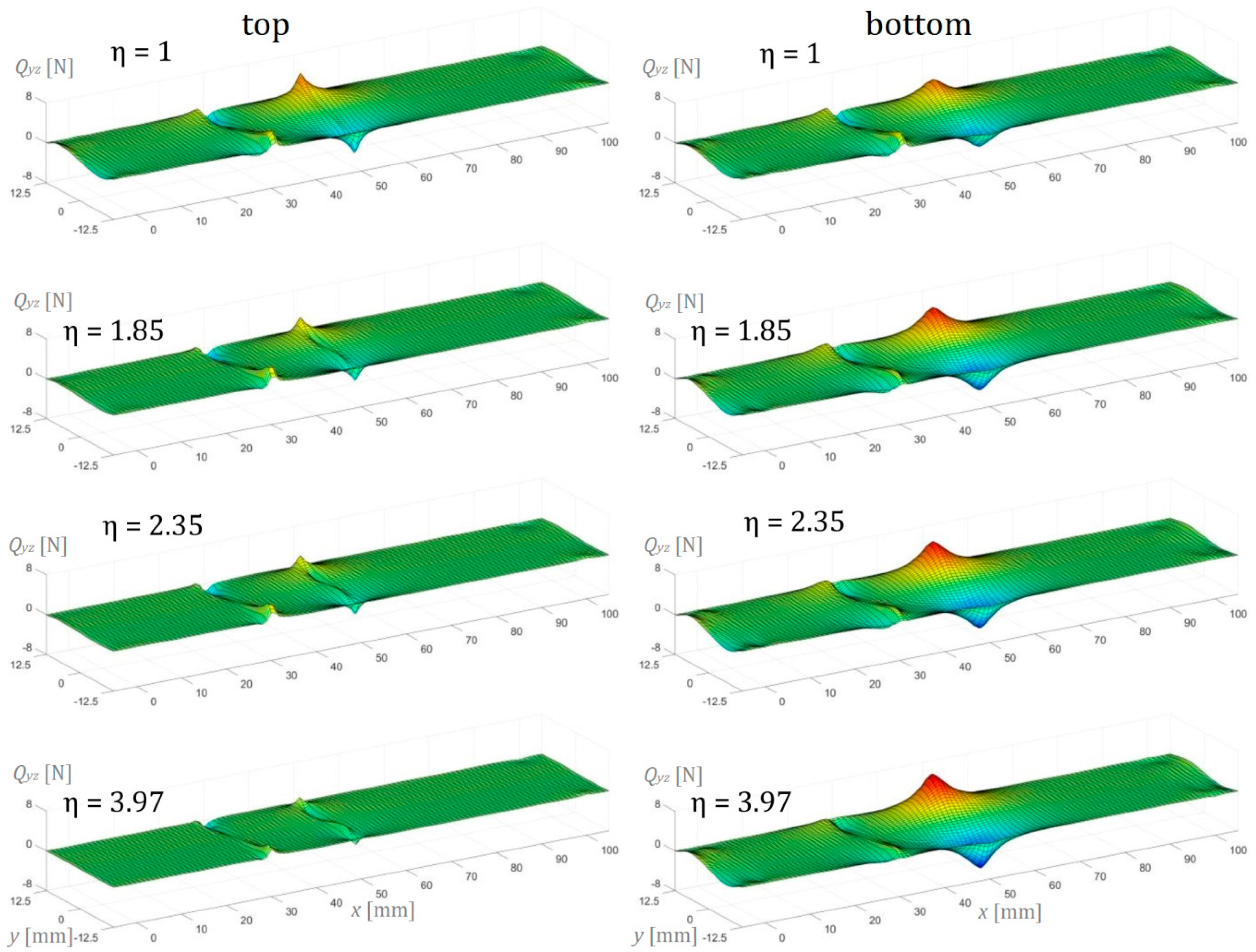
| Crack Length [mm] | 15 | 30 | 45 | 15 | 30 | 45 | 15 | 30 | 45 | 15 | 30 | 45 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Layup | η = 1 | η = 1.85 | η = 2.35 | η = 3.97 | ||||||||
| δEXP (mm) | 0.515 | 0.668 | 1.079 | 0.554 | 0.690 | 1.025 | 0.518 | 0.619 | 0.853 | 0.519 | 0.569 | 0.686 |
| δSBT (mm) | 0.506 | 0.643 | 1.017 | 0.540 | 0.647 | 0.936 | 0.516 | 0.597 | 0.815 | 0.517 | 0.562 | 0.684 |
| δTBT (mm) | 0.520 | 0.657 | 1.031 | 0.554 | 0.662 | 0.952 | 0.530 | 0.612 | 0.831 | 0.532 | 0.577 | 0.700 |
| δFEA (mm) | 0.532 | 0.671 | 1.045 | 0.569 | 0.698 | 0.965 | 0.547 | 0.647 | 0.854 | 0.550 | 0.606 | 0.723 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dadej, K.; Valvo, P.S.; Bieniaś, J. The Effect of Transverse Shear in Symmetric and Asymmetric End Notch Flexure Tests–Analytical and Numerical Modeling. Materials 2020, 13, 3046. https://doi.org/10.3390/ma13143046
Dadej K, Valvo PS, Bieniaś J. The Effect of Transverse Shear in Symmetric and Asymmetric End Notch Flexure Tests–Analytical and Numerical Modeling. Materials. 2020; 13(14):3046. https://doi.org/10.3390/ma13143046
Chicago/Turabian StyleDadej, Konrad, Paolo Sebastiano Valvo, and Jarosław Bieniaś. 2020. "The Effect of Transverse Shear in Symmetric and Asymmetric End Notch Flexure Tests–Analytical and Numerical Modeling" Materials 13, no. 14: 3046. https://doi.org/10.3390/ma13143046






