Investigation of Yield Surfaces Evolution for Polycrystalline Aluminum after Pre-Cyclic Loading by Experiment and Crystal Plasticity Simulation
Abstract
:1. Introduction
2. Material and Experimental Procedure
2.1. Experimental Material and Specimen
2.2. Experimental Procedure
3. Constitutive Relationships and Coupling Methodology
3.1. Constitutive Framework
3.2. Hardening Rules
3.3. Back Stress Evolution
4. Modeling
4.1. Finite Element Models at Different Scale
4.2. Parameters Calibration of Crystalline Plasticity Models
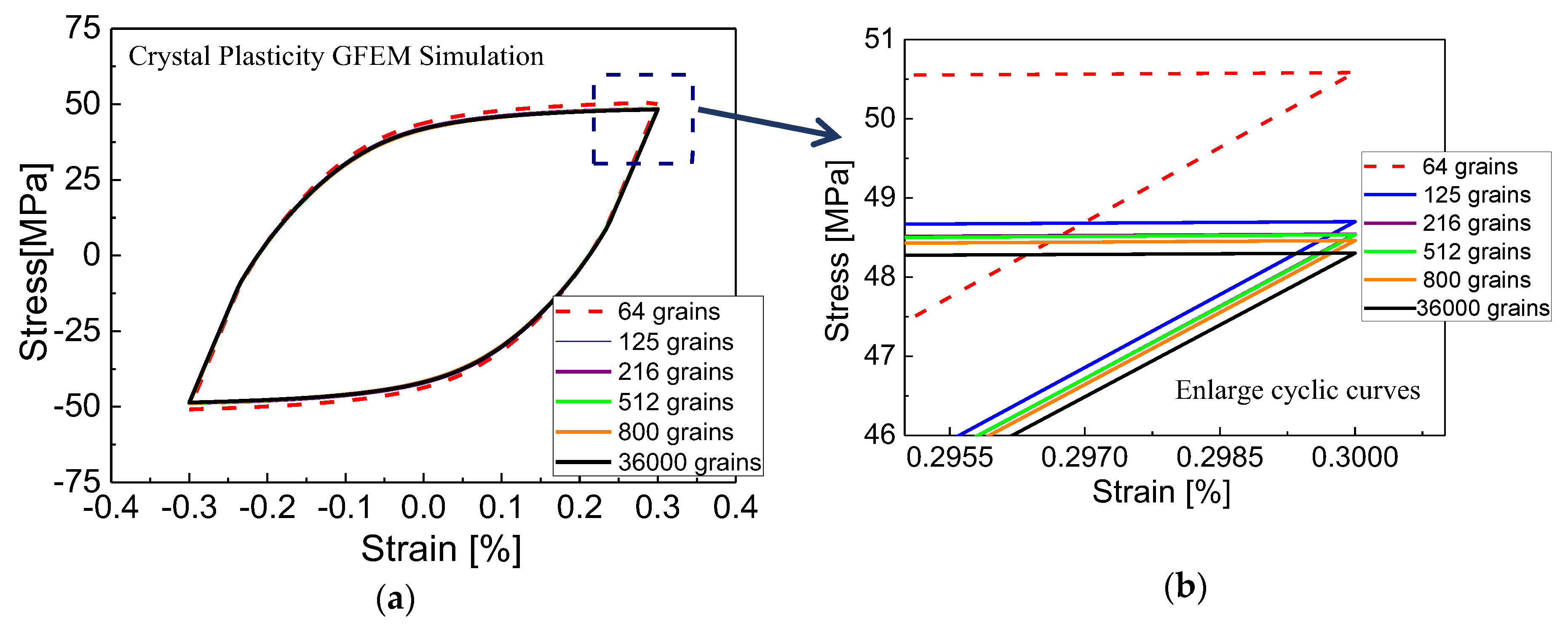
4.3. The Number of Grain effects on the Macroscopic Behavior
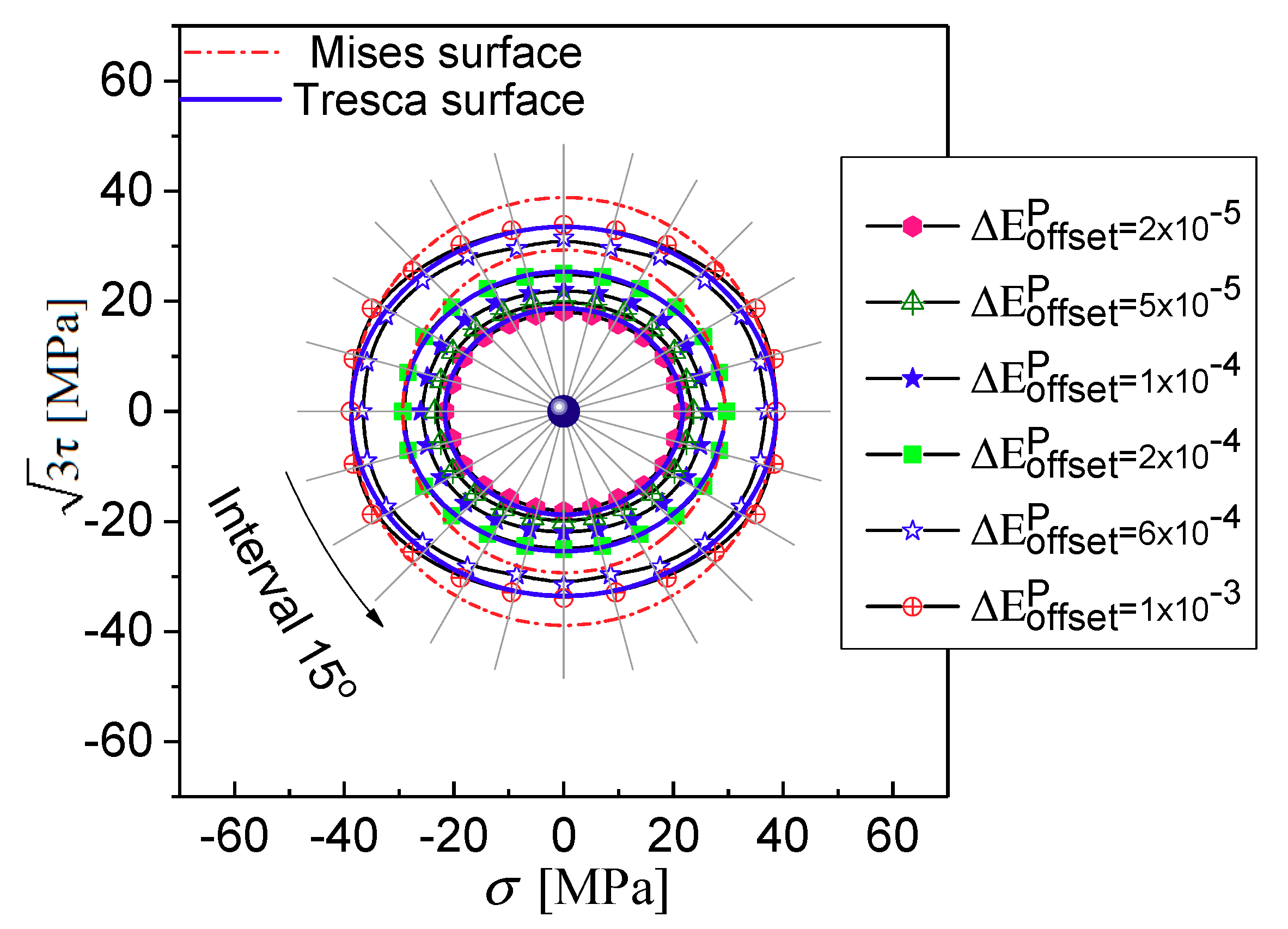
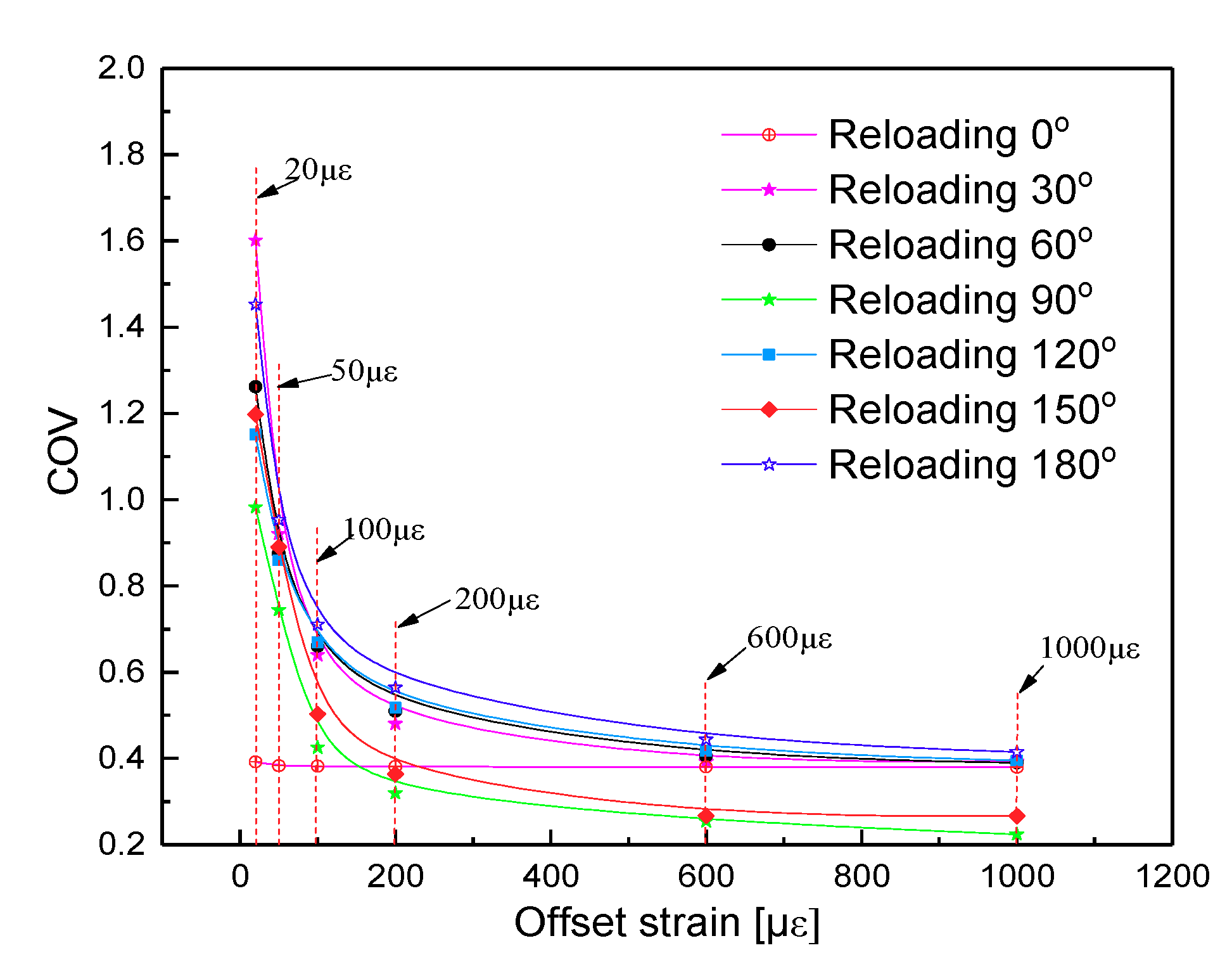
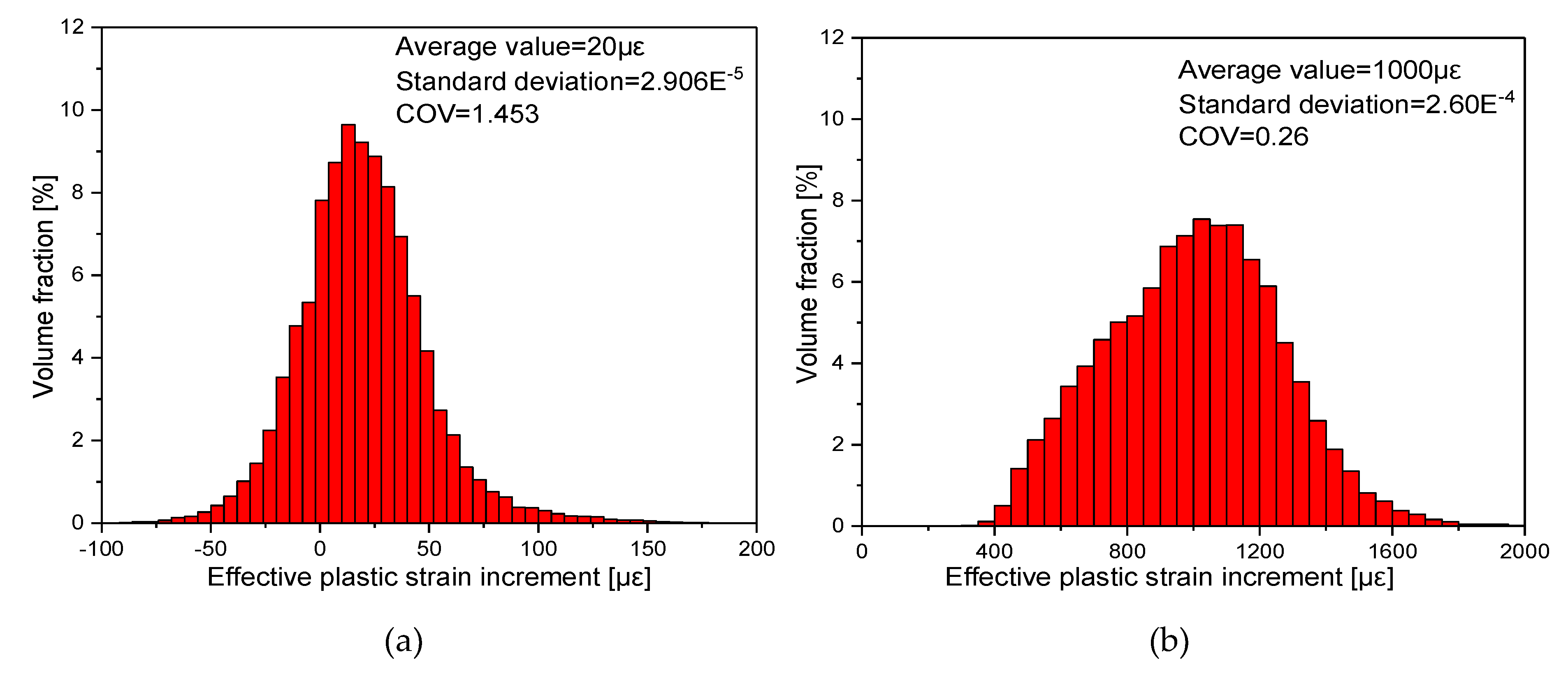
5. Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ohashi, Y.; Kawashima, K.; Yokochi, T. Anisotropy due to plastic deformation of initially isotropic mild steel and its analytical formulation. J. Mech. Phys. Solids 1975, 23, 277–294. [Google Scholar] [CrossRef]
- Kuwabara, T.; Yoshida, K.; Narihara, K.; Takahashi, S. Anisotropic plastic deformation of extruded aluminum tube under axial forces and internal pressure. Int. J. Plast. 2005, 42, 2225–2241. [Google Scholar] [CrossRef]
- Wu, H.C.; Yeh, W.C. On the experimental determination of yield surfaces and some results of annealed 304 stainless steel. Int. J. Plast. 1991, 7, 803–826. [Google Scholar] [CrossRef]
- Phillips, A.; Lu, W.Y. An experimental investigation of yield surfaces and loading surfaces of pure aluminum with stress-controlled and strain-controlled paths of loading. J. Eng. Mater. Technol. 1984, 106, 349–354. [Google Scholar] [CrossRef]
- Khan, A.S.; Kazmi, R.; Pandey, A.; Stoughton, T.B. Evolution of subsequent yield surfaces and elastic constants with finite plastic deformation. Part-I: A very low work hardening aluminum alloy (Al6061-T6511). Int. J. Plast. 2009, 25, 1611–1625. [Google Scholar] [CrossRef]
- Khan, A.S.; Pandey, A.; Stoughton, T. Evolution of subsequent yield surfaces and elastic constants with finite plastic deformation. Part II: A very high work hardening aluminum alloy (annealed 1100 Al). Int. J. Plast. 2010, 26, 1421–1431. [Google Scholar] [CrossRef]
- Khan, A.S.; Pandey, A.; Stoughton, T. Evolution of subsequent yield surfaces and elastic constants with finite plastic deformation. Part III: Yield surface in tension–tension stress space (Al 6061–T 6511 and annealed 1100 Al). Int. J. Plast. 2010, 26, 1432–1441. [Google Scholar] [CrossRef]
- Sung, S.J.; Liu, L.W.; Hong, H.K.; Wu, H.C. Evolution of yield surface in the 2D and 3D stress spaces. Int. J. Solids Struct. 2011, 48, 1054–1069. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Badreddine, H.; Saanouni, K. Thermomechanical modeling of distortional hardening fully coupled with ductile damage under non-proportional loading paths. Int. J. Solids Struct. 2018, 144–145, 123–136. [Google Scholar] [CrossRef]
- Zhang, K.S.; Shi, Y.K.; Xu, L.B. Anisotropy of yielding/hardening and microinhomogeneity of deforming/rotating for a polycrystalline metal under cyclic tension-compression. Acta Metall. Sin. 2011, 47, 1292–1300. [Google Scholar]
- Kowalewski, Z.L.; Sliwowski, M. Effect of cyclic loading on the yield surface evolution of 18G2A low-alloy steel. Int. J. Mech. Sci. 1997, 39, 51–68. [Google Scholar] [CrossRef]
- Rokhgireh, H.; Nayebi, A.; Chaboche, J.L. Application of a new distortional yield surface model in cyclic uniaxial and multiaxial loading. Int. J. Solids Struct. 2017, 110–111, 219–238. [Google Scholar] [CrossRef]
- Parma, S.; Pleek, J.; Marek, R.; Hruby, Z.; Feigenbaum, H.P.; Dafalias, Y.F. Calibration of a simple directional distortional hardening model for metal plasticity. Int. J. Solids Struct. 2018, 143, 113–124. [Google Scholar] [CrossRef]
- Stout, M.G.; Martin, P.L.; Helling, D.E.; Ganova, G.R. Multiaxial yield behavior of 1100 aluminum following various magnitudes of prestrain. Int. J. Plast. 1985, 1, 163–174. [Google Scholar] [CrossRef] [Green Version]
- Kan, A.S.; Wang, X. An experimental study on subsequent yield surface after finite shear pre-straining. Int. J. Plast. 1993, 9, 889–905. [Google Scholar] [CrossRef]
- Ishikawa, H.; Sasaki, K. Yield surfaces of SUS304 under cyclic loading. J. Eng. Techonol. 1988, ASME110, 364–371. [Google Scholar] [CrossRef]
- Ishikawa, H. Subsequent yield surface probed from its current center. Int. J. Plast. 1997, 13, 533–549. [Google Scholar] [CrossRef]
- Baltov, A.; Sawczuk, A. A rule of anisotropic hardening. Acta Mech. 1965, 1, 81–92. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Schick, D.; Tsakmakis, C. A simple model for describing yield surface evolution during plastic flow. Appl. Comput. Mech. 2002, 10, 169–201. [Google Scholar]
- Chen, J.Y.; Zhang, K.S.; Kuang, Z.; Hu, G.J.; Song, Q.; Chang, Y.J. The anisotropic distortional yield surface constitutive model based on the chaboche cyclic plastic model. Materials 2019, 12, 543. [Google Scholar] [CrossRef] [Green Version]
- Francois, M. A plasticity model with yield surface distortion for non proportional loading. Int. J. Plast. 2001, 17, 703–717. [Google Scholar] [CrossRef] [Green Version]
- Barlat, F.; Gracio, J.J.; Lee, M.G.; Rauch, E.F.; Vincze, G. An alternative to kinematic hardening in classical plasticity. Int. J. Plast. 2011, 27, 1309–1327. [Google Scholar] [CrossRef]
- Feigenbaum, H.P.; Dafalias, Y.F. Directional distortional hardening in metal plasticity within thermodynamics. Int. J. Solids Struct. 2007, 44, 7526–7542. [Google Scholar] [CrossRef]
- Lian, J.S.; Chen, J.W. Isotropic polycrystal yield surfaces of b.c.c. and f.c.c. metals: Crystallographic and continuum mechanics approaches. Acta Metall. Mater. 1991, 39, 2285–2294. [Google Scholar] [CrossRef]
- Daehli, L.E.B.; Hopperstad, O.S.; Benallal, A. Effective behaviour of porous ductile solids with a non-quadratic isotropic matrix yield surface. J. Mech. Phys. Solids 2019, 130, 56–81. [Google Scholar] [CrossRef]
- Hu, G.J.; Huang, S.H.; Lu, D.M.; Zhong, X.C.; Li, Z.H.; Wolfgang, B.; Zhang, K.S. Subsequent yielding of polycrystalline aluminum after cyclic tension-compression analyzed by experiments and simulations. Int. J. Solids Struct. 2015, 56–57, 142–153. [Google Scholar] [CrossRef]
- Zhang, K.S.; Huang, S.H.; Liu, G.L.; Lu, D.M. Measuring subsequent yield surface of pure copper by crystal plasticity simulation. Chin. J. Theor. Appl. Mech. 2017, 49, 870–879. [Google Scholar]
- Lee, E.H. Discussion: “Elastic-plastic deformation at finite strains”. J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J.R. Constitutive analysis of elastic–plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J.R. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef] [Green Version]
- Needleman, A.; Asaro, R.J.; Lemonds, J.; Peirce, D. Finite element analysis of crystalline solids. Comput. Meth. Appl. Mech. Eng. 1985, 52, 689–708. [Google Scholar] [CrossRef]
- Zhang, K.S.; Shi, Y.K.; Ju, J.W. Grain-level statistical plasticity analysis on strain cycle fatigue of a FCC metal. Mech. Mater. 2013, 64, 76–90. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Rice, J.R. Inelastic constitutive relations for solids: An internal variables theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. A Math. Phys. 1976, 348, 101–127. [Google Scholar]
- Hutchinson, J.W. Elastic-plastic behaviour of polycrystalline metals and composites. Proc. R. Soc. A Math. Phys. 1970, 319, 247–272. [Google Scholar]
- Chang, Y.W.; Asaro, R.J. An experimental study of shear localization in aluminum-copper single crystals. Acta Metall. 1981, 29, 241–257. [Google Scholar] [CrossRef]
- Walker, K.P. Research and Development Program for Non-linear Structural Modeling with Advanced Time-temperature Dependent Constitutive Relationships; Report PWA-5700-50; 1981; NASA CR-165533. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19820008207.pdf (accessed on 9 July 2020).
- Chaboche, J.L. On some modifications of kinematic hardening to improve the description of ratchetting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Segurado, J.; Llorca, J. Simulation of the deformation of polycrystalline nanostructured Ti by computational homogenization. Comput. Mater. Sci. 2013, 76, 3–11. [Google Scholar] [CrossRef] [Green Version]
- Phillips, A.; Juh-Ling, T. The effect of loading path on the yield surface at elevated temperatures. Int. J. Solids Struct. 1972, 8, 463–474. [Google Scholar] [CrossRef]
- Moon, H. An experimental study of the outer yield surface for annealed polycrystalline aluminium. Acta Mech. 1976, 24, 191–208. [Google Scholar] [CrossRef]

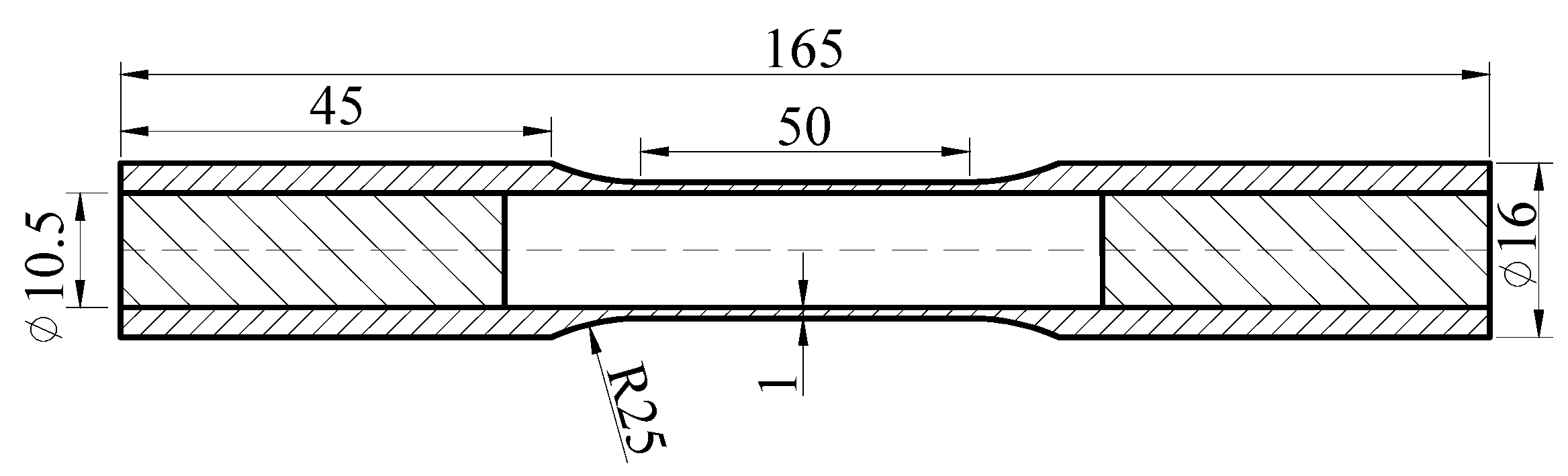
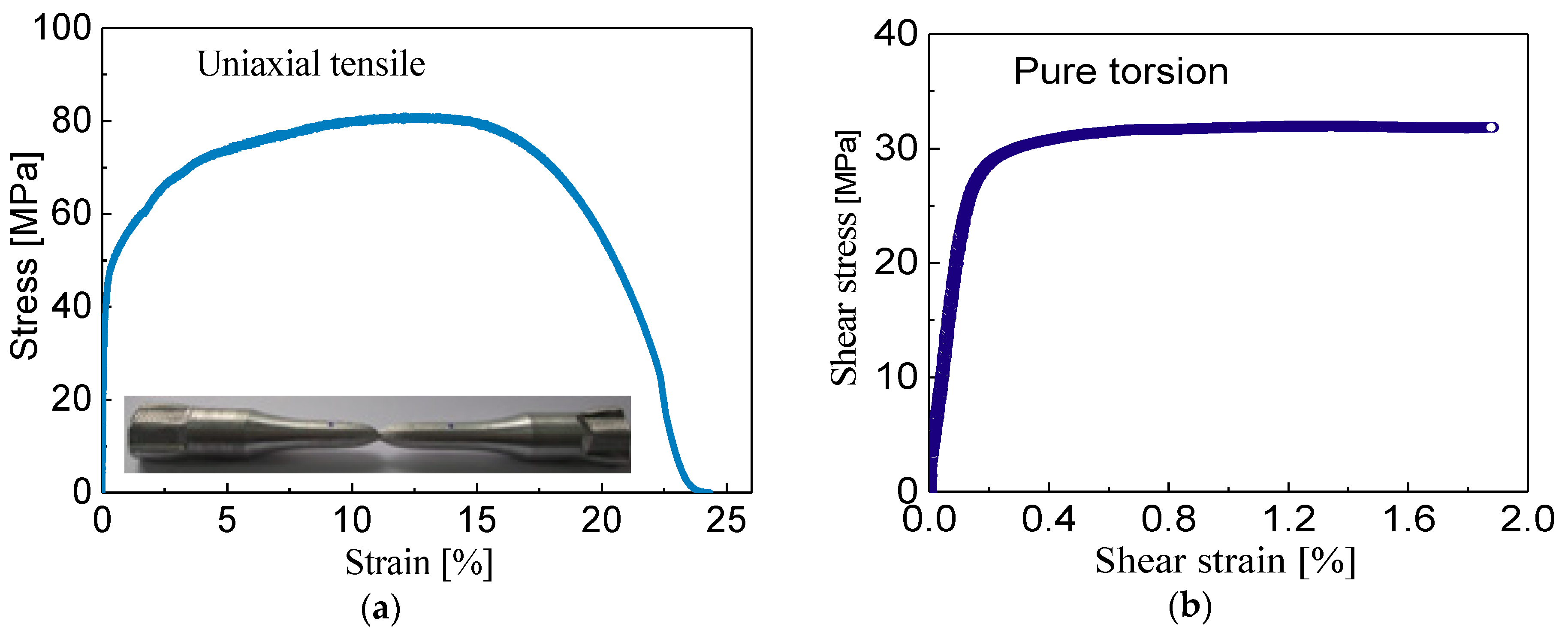
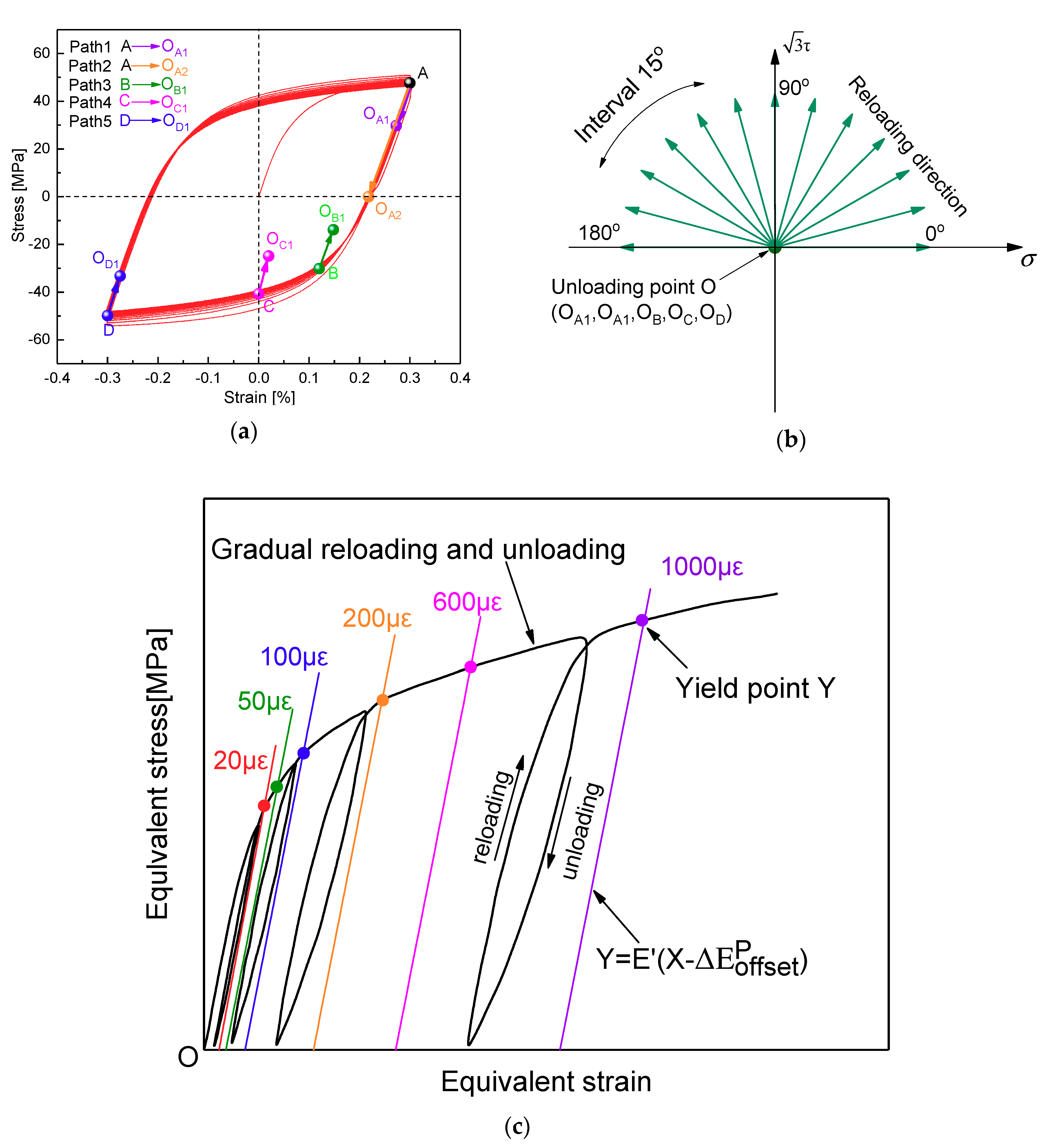
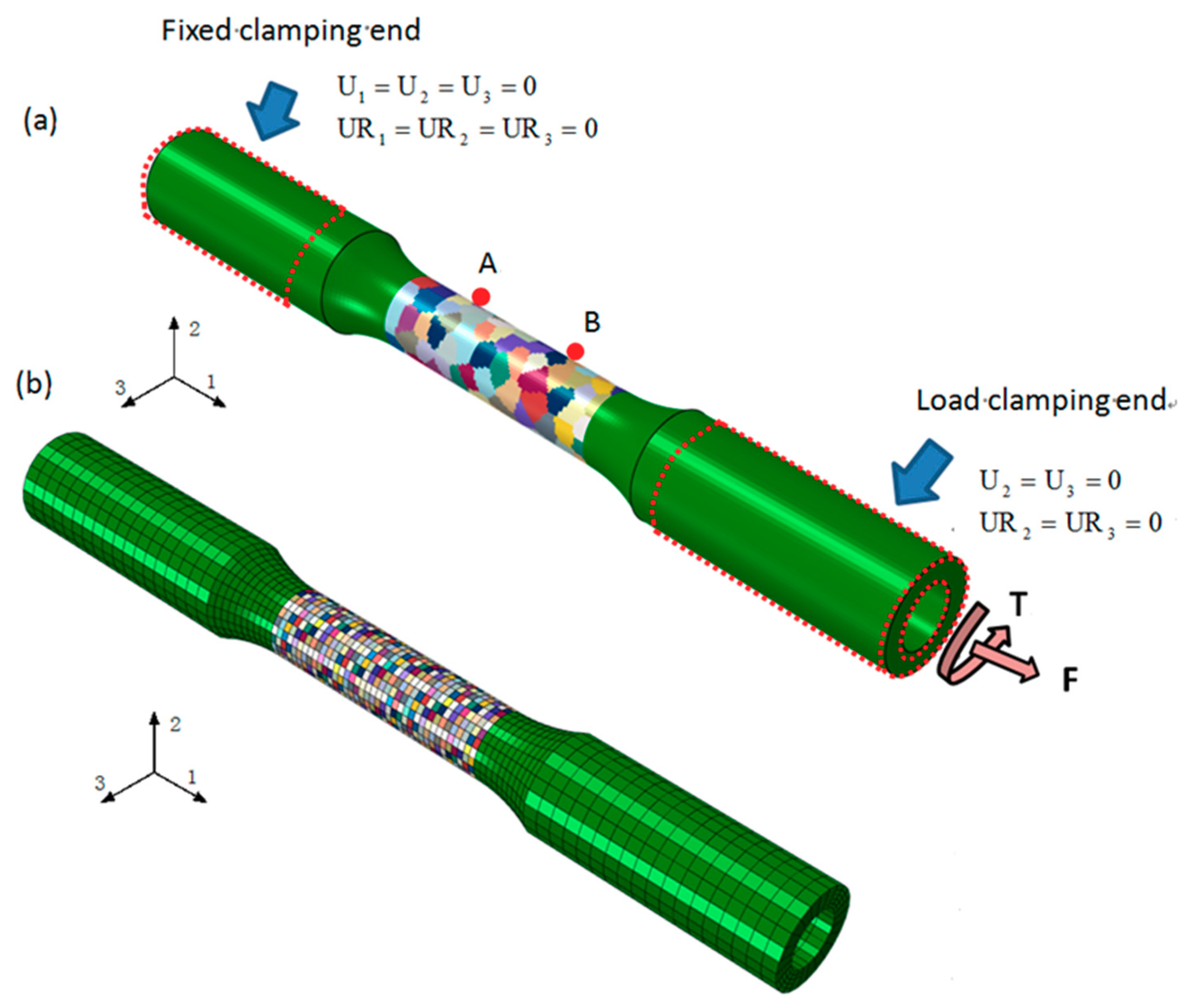






| Chemical Composition | Mechanical Properties | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Al/% | Cu/% | Mg/% | Si/% | Mn/% | Zn/% | E/GPa | G/GPa | |||
| 99.89 | 0.02 | 0.03 | 0.03 | 0.02 | 0.01 | 57 | 25 | 20 | 81 | 24% |
| /GPa | /GPa | /GPa | /MPa | /MPa | /MPa | /GPa | /GPa | /s−1 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 75.64 | 36.86 | 25.4 | 8.42 | 9.2 | 65 | 22.5 | 2.5 | 0.1 | 1.0 | 0 | 0.001 | 200 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, D.; Zhang, K.; Hu, G.; Lan, Y.; Chang, Y. Investigation of Yield Surfaces Evolution for Polycrystalline Aluminum after Pre-Cyclic Loading by Experiment and Crystal Plasticity Simulation. Materials 2020, 13, 3069. https://doi.org/10.3390/ma13143069
Lu D, Zhang K, Hu G, Lan Y, Chang Y. Investigation of Yield Surfaces Evolution for Polycrystalline Aluminum after Pre-Cyclic Loading by Experiment and Crystal Plasticity Simulation. Materials. 2020; 13(14):3069. https://doi.org/10.3390/ma13143069
Chicago/Turabian StyleLu, Damin, Keshi Zhang, Guijuan Hu, Yongting Lan, and Yanjun Chang. 2020. "Investigation of Yield Surfaces Evolution for Polycrystalline Aluminum after Pre-Cyclic Loading by Experiment and Crystal Plasticity Simulation" Materials 13, no. 14: 3069. https://doi.org/10.3390/ma13143069





