Validated Finite Element Models of Premolars: A Scoping Review
Abstract
1. Introduction
2. Materials and Methods
2.1. Protocol
2.2. Information Sources and Search Strategy
2.3. Data Charting Process
2.4. Screening
2.5. Eligibility
2.6. Data Analysis
3. Results
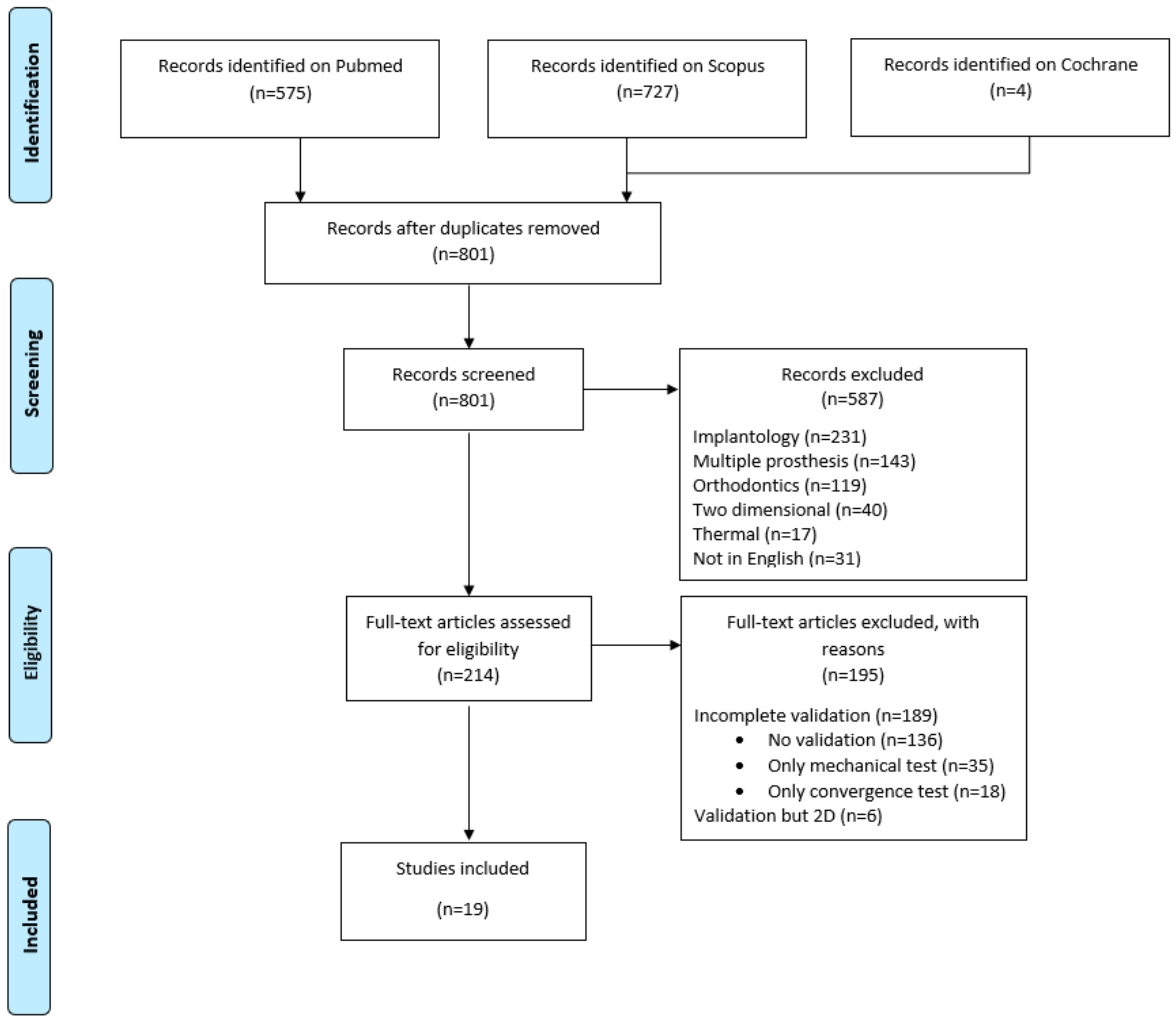
3.1. Selection of Sources of Evidence
3.2. Characteristics of the Studies and Their Objective
3.3. Scoping Synthesis of Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Almasri, M. Assessment of extracting molars and premolars after root canal treatment: A retrospective study. Saudi Dent. J. 2019, 31, 487–491. [Google Scholar] [CrossRef] [PubMed]
- Khasnis, S.A.; Kidiyoor, K.H.; Patil, A.B.; Kenganal, S.B. Vertical root fractures and their management. J. Conserv. Dent. 2014, 17, 103–110. [Google Scholar] [CrossRef] [PubMed]
- Yoshino, K.; Ito, K.; Kuroda, M.; Sugihara, N. Prevalence of vertical root fracture as the reason for tooth extraction in dental clinics. Clin. Oral Investig. 2015, 19, 1405–1409. [Google Scholar] [CrossRef] [PubMed]
- Reenen, J.; Reid, C. Maxillary premolar crown morphology. A preliminary study. J. Dent. Assoc. S. Afr. 1997, 51, 783–786. [Google Scholar]
- Raiden, G.; Costa, L.; Koss, S.; Hernández, J.L.; Aceñolaza, V. Residual thickness of root in first maxillary premolars with post space preparation. J. Endod. 1999, 25, 502–505. [Google Scholar] [CrossRef]
- Wang, C.H.; Du, J.K.; Li, H.Y.; Chang, H.C.; Chen, K.K. Factorial analysis of variables influencing mechanical characteristics of a post used to restore a root filled premolar using the finite element stress analysis combined with the Taguchi method. Int. Endod. J. 2016, 49, 690–699. [Google Scholar] [CrossRef]
- Govare, N.; Contrepois, M. Endocrowns: A systematic review. J. Prosthet. Dent. 2019, 23, 411–418. [Google Scholar] [CrossRef]
- Lee, Y.; Ogihara, N.; Lee, T. Assessment of finite element models for prediction of osteoporotic fracture. J. Mech. Behav. Biomed. Mater. 2019, 97, 312–320. [Google Scholar] [CrossRef]
- Rodrigues, Y.L.; Mathew, M.T.; Mercuri, L.G.; da Silva, J.S.P.; Henriques, B.; Souza, J.C.M. Biomechanical simulation of temporomandibular joint replacement (TMJR) devices: A scoping review of the finite element method. Int. J. Oral Maxillofac. Surg. 2018, 47, 1032–1042. [Google Scholar] [CrossRef]
- Diarra, A.; Mushegyan, V.; Naveau, A. Finite Element Analysis Generates an Increasing Interest in Dental Research: A Bibliometric Study. Open Dent. J. 2016, 10, 35–42. [Google Scholar] [CrossRef]
- Zadpoor, A.A.; Weinans, H. Patient-specific bone modeling and analysis: The role of integration and automation in clinical adoption. J. Biomech. 2015, 48, 750–760. [Google Scholar] [CrossRef] [PubMed]
- Li, C.H.; Wu, C.H.; Lin, C.L. Design of a patient-specific mandible reconstruction implant with dental prosthesis for metal 3D printing using integrated weighted topology optimization and finite element analysis. J. Mech. Behav. Biomed. Mater. 2020, 105, 103700. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Tambe, A.A.; Maeda, Y.; Wada, M.; Gonda, T. Finite element analysis of dental implants with validation: To what extent can we expect the model to predict biological phenomena? A literature review and proposal for classification of a validation process. Int. J. Implant. Dent. 2018, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Tseng, Z.J.; Mcnitt-Gray, J.L.; Flashner, H.; Wang, X.; Enciso, R. Model sensitivity and use of the comparative finite element method in mammalian jaw mechanics: Mandible performance in the Gray Wolf. PLoS ONE 2011, 6, 4. [Google Scholar] [CrossRef] [PubMed]
- Burkhart, T.A.; Andrews, D.M.; Dunning, C.E. Finite element modeling mesh quality, energy balance and validation methods: A review with recommendations associated with the modeling of bone tissue. J. Biomech. 2013, 46, 1477–1488. [Google Scholar] [CrossRef]
- Erdemir, A.; Guess, T.M.; Halloran, J.; Tadepalli, S.C.; Morrison, T.M. Considerations for reporting finite element analysis studies in biomechanics. J. Biomech. 2012, 45, 625–633. [Google Scholar] [CrossRef]
- Tricco, A.C.; Lillie, E.; Zarin, W.; O’Brien, K.K.; Colquhoun, H.; Levac, D.; Hempel, S. PRISMA extension for scoping reviews (PRISMA-ScR): Checklist and explanation. Ann. Intern. Med. 2018, 169, 467–473. [Google Scholar] [CrossRef]
- Kishore, M.; Panat, S.R.; Aggarwal, A.; Agarwal, N.; Upadhyay, N.; Alok, A. Evidence based dental care: Integrating clinical expertise with systematic research. J. Clin. Diagn Res. 2014, 8, 259–262. [Google Scholar] [CrossRef]
- Limjeerajarus, N.; Dhammayannarangsi, P.; Phanijjiva, A.; Tangsripongkul, P.; Jearanaiphaisarn, T.; Pittayapat, P.; Limjeerajarus, C.N. Comparison of ultimate force revealed by compression tests on extracted first premolars and FEA with a true scale 3D multi-component tooth model based on a CBCT dataset. Clin. Oral Investig. 2020, 24, 211–220. [Google Scholar] [CrossRef]
- MacHado, A.C.; Soares, C.J.; Reis, B.R.; Bicalho, A.A.; Raposo, L.H.A.; Soares, P.V. Stress-strain analysis of premolars with non-carious cervical lesions: Influence of restorative material, loading direction and mechanical fatigue. Oper. Dent. 2017, 42, 253–265. [Google Scholar] [CrossRef]
- Lin, C.L.; Chang, W.J.; Lin, Y.S.; Chang, Y.H.; Lin, Y.F. Evaluation of the relative contributions of multi-factors in an adhesive MOD restoration using FEA and the Taguchi method. Dent. Mater. 2009, 25, 1073–1081. [Google Scholar] [CrossRef] [PubMed]
- Tajima, K.; Chen, K.K.; Takahashi, N.; Noda, N.; Nagamatsu, Y.; Kakigawa, H. Three-dimensional finite element modeling from CT images of tooth and its validation. Dent. Mater. J. 2009, 28, 219–226. [Google Scholar] [CrossRef]
- Chang, Y.H.; Lin, W.H.; Kuo, W.C.; Chang, C.Y.; Lin, C.L. Mechanical interactions of cuspal-coverage designs and cement thickness in a cusp-replacing ceramic premolar restoration: A finite element study. Med. Biol. Eng. Comput. 2009, 47, 367–374. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.L.; Chang, Y.H.; Lin, Y.F. Combining structural-thermal coupled field FE analysis and the Taguchi method to evaluate the relative contributions of multi-factors in a premolar adhesive MOD restoration. J. Dent. 2008, 36, 626–636. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.L.; Chang, Y.H.; Liu, P.R. Multi-factorial analysis of a cusp-replacing adhesive premolar restoration: A finite element study. J. Dent. 2008, 36, 194–203. [Google Scholar] [CrossRef]
- Ausiello, P.; Rengo, S.; Davidson, C.L.; Watts, D.C. Stress distributions in adhesively cemented ceramic and resin-composite class II inlay restorations: A 3D-FEA study. Dent. Mater. 2004, 20, 862–872. [Google Scholar] [CrossRef]
- Lee, H.E.; Lin, C.L.; Wang, C.H.; Cheng, C.H.; Chang, C.H. Stresses at the cervical lesion of maxillary premolar—A finite element investigation. J. Dent. 2002, 30, 283–290. [Google Scholar] [CrossRef]
- Ausiello, P.; Apicella, A.; Davidson, C.L.; Rengo, S. 3D-finite element analyses of cusp movements in a human upper premolar, restored with adhesive resin-based composites. J. Biomech. 2001, 34, 1269–1277. [Google Scholar] [CrossRef]
- Toparli, M.; Gökay, N.; Aksoy, T. An investigation of the stress values on a tooth restored by amalgam. J. Oral Rehabil. 1999, 26, 259–263. [Google Scholar] [CrossRef]
- Chang, Y.H.; Lee, H.; Lin, C.L. Early resin luting material damage around a circular fiber post in a root canal treated premolar by using micro-computerized tomographic and finite element sub-modeling analyses. J. Mech. Behav. Biomed. Mater. 2015, 51, 184–193. [Google Scholar] [CrossRef]
- Zelic, K.; Vukicevic, A.; Jovicic, G.; Aleksandrovic, S.; Filipovic, N.; Djuric, M. Mechanical weakening of devitalized teeth: Three-dimensional finite element analysis and prediction of tooth fracture. Int. Endod. J. 2015, 48, 850–863. [Google Scholar] [CrossRef] [PubMed]
- Guimarães, J.C.; Soella, G.G.; Durand, L.B.; Horn, F.; Baratieri, L.N.; Monteiro Jr, S.; Belli, R. Stress amplifications in dental non-carious cervical lesions. J. Biomech. 2014, 47, 410–416. [Google Scholar] [CrossRef]
- Juloski, J.; Apicella, D.; Ferrari, M. The effect of ferrule height on stress distribution within a tooth restored with fibre posts and ceramic crown: A finite element analysis. Dent. Mater. 2014, 30, 1304–1315. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.L.; Chang, Y.H.; Hsieh, S.K.; Chang, W.J. Estimation of the failure risk of a maxillary premolar with different crack depths with endodontic treatment by computer-aided design/computer-aided manufacturing ceramic restorations. J. Endod. 2013, 39, 375–379. [Google Scholar] [CrossRef]
- Lin, C.L.; Pai, C.A. Numerical investigation of failure risk of cad/cam ceramic restoration for an endodontically treated maxillary premolar with mo preparation. Biomed. Eng. Appl. Basis Commun. 2010, 22, 327–335. [Google Scholar] [CrossRef]
- Barak, M.M.; Geiger, S.; Chattah, N.L.T.; Shahar, R.; Weiner, S. Enamel dictates whole tooth deformation: A finite element model study validated by a metrology method. J. Struct. Biol. 2009, 168, 511–520. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.L.; Chang, Y.H.; Pa, C.A. Estimation of the Risk of Failure for an Endodontically Treated Maxillary Premolar with MODP Preparation and CAD/CAM Ceramic Restorations. J. Endod. 2009, 35, 1391–1395. [Google Scholar] [CrossRef]
- Wood, S.A.; Strait, D.S.; Dumont, E.R.; Ross, C.F.; Grosse, I.R. The effects of modeling simplifications on craniofacial finite element models: The alveoli (tooth sockets) and periodontal ligaments. J. Biomech. 2011, 44, 1831–1838. [Google Scholar] [CrossRef] [PubMed]
- Guida, M.; Marulo, F.; Abrate, S. Advances in crash dynamics for aircraft safety. Prog. Aerosp. Sci. 2018, 98, 106–123. [Google Scholar] [CrossRef]
- Liu, X.; Guo, J.; Bai, C.; Sun, X.; Mou, R. Drop test and crash simulation of a civil airplane fuselage section. Chin. J. Aeronaut. 2015, 28, 447–456. [Google Scholar] [CrossRef]
- Lin, C.L.; Chang, C.H.; Ko, C.C. Multifactorial analysis of an MOD restored human premolar using auto-mesh Finite Element approach. J. Oral Rehabil. 2001, 28, 576–585. [Google Scholar] [CrossRef] [PubMed]
- Dar, F.H.; Meakin, J.R.; Aspden, R.M. Statistical methods in finite element analysis. J. Biomech. 2002, 35, 1155–1161. [Google Scholar] [CrossRef]
- Lauzeral, N.; Borzacchiello, D.; Kugler, M.; George, D.; Rémond, Y.; Hostettler, A.; Chinesta, F. Shape parametrization of bio-mechanical finite element models based on medical images. Comput. Methods BioMech. Biomed. Eng Imaging Vis. 2019, 7, 480–489. [Google Scholar] [CrossRef]
- Huysmans, M.C.D.N.J.M.; Van der Varst, P.G.T. Finite element analysis of quasistatic and fatigue failure of post and cores. J. Dent. 1993, 21, 57–64. [Google Scholar] [CrossRef]
- Pérez-González, A.; Iserte-Vilar, J.L.; González-Lluch, C. Interpreting finite element results for brittle materials in endodontic restorations. Biomed. Eng. 2011, 10, 44. [Google Scholar] [CrossRef] [PubMed]
- Mao, Q.; Su, K.; Zhou, Y.; Hossaini-Zadeh, M.; Lewis, G.S.; Du, J. Voxel-based micro-finite element analysis of dental implants in a human cadaveric mandible: Tissue modulus assignment and sensitivity analyses. J. Mech. Behav. Biomed. Mater. 2019, 94, 229–237. [Google Scholar] [CrossRef]
- Hohmann, A.; Kober, C.; Young, P.; Dorow, C.; Geiger, M.; Boryor, A.; Sander, F.G. Influence of different modeling strategies for the periodontal ligament on finite element simulation results. Am. J. Orthod. Dentofac. Orthop. 2011, 139, 775–783. [Google Scholar] [CrossRef]
- Ortún-Terrazas, J.; Cegoñino, J.; Santana-Penín, U.; Santana-Mora, U.; Pérez del Palomar, A. Approach towards the porous fibrous structure of the periodontal ligament using micro-computerized tomography and finite element analysis. J. Mech. Behav. Biomed. Mater. 2018, 79, 135–149. [Google Scholar] [CrossRef]
- Kinney, J.H.; Marshall, S.J.; Marshall, G.W. The mechanical properties of human dentin: A critical review and re-evaluation of the dental literature. Crit Rev. Oral Biol. Med. 2003, 14, 13–29. [Google Scholar] [CrossRef]
- Arola, D.D.; Reprogel, R.K. Tubule orientation and the fatigue strength of human dentin. Biomaterials 2006, 27, 2131–2140. [Google Scholar] [CrossRef]
- Wan, B.; Shahmoradi, M.; Zhang, Z.; Shibata, Y.; Sarrafpour, B.; Swain, M.; Li, Q. Modelling of stress distribution and fracture in dental occlusal fissures. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Mangado, N.; Piella, G.; Noailly, J.; Pons-Prats, J.; Ballester, M.Á.G. Analysis of uncertainty and variability in finite element computational models for biomedical engineering: Characterization and propagation. Front. Bioeng. Biotechnol. 2016, 4, 1–17. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Eggermont, F.; van der Wal, G.; Westhoff, P.; Laar, A.; de Jong, M.; Rozema, T.; Verdonschot, N. Patient-specific finite element computer models improve fracture risk assessments in cancer patients with femoral bone metastases compared to clinical guidelines. Bone 2020, 130, 115101. [Google Scholar] [CrossRef] [PubMed]
- Bernakiewicz, M.; Viceconti, M. The role of parameter identification in finite element contact analyses with reference to orthopaedic biomechanics applications. J. Biomech. 2002, 35, 61–67. [Google Scholar] [CrossRef]
- Murakami, N.; Wakabayashi, N. Finite element contact analysis as a critical technique in dental biomechanics: A review. J. Prosthodont Res. 2014, 58, 92–101. [Google Scholar] [CrossRef]
- Benazzi, S.; Grosse, I.R.; Gruppioni, G.; Weber, G.W.; Kullmer, O. Comparison of occlusal loading conditions in a lower second premolar using three-dimensional finite element analysis. Clin. Oral Investig. 2014, 18, 369–375. [Google Scholar] [CrossRef]
- Shahrbaf, S.; Van Noort, R.; Mirzakouchaki, B.; Ghassemieh, E.; Martin, N. Fracture strength of machined ceramic crowns as a function of tooth preparation design and the elastic modulus of the cement. Dent. Mater. 2014, 30, 234–241. [Google Scholar] [CrossRef]
- Fages, M.; Slangen, P.; Raynal, J.; Corn, S.; Turzo, K.; Margerit, J.; Cuisinier, F.J. Comparative mechanical behavior of dentin enamel and dentin ceramic junctions assessed by speckle interferometry (SI). Dent. Mater. 2012, 28, 229–238. [Google Scholar] [CrossRef]
- Lo, Y.J.; Chang, W.J.; Lee, S.Y.; Chang, K.J.; Lin, C.T.; Huang, H.M. Reductions in the effects of damping on stress concentration in premolars by post-endodontic restorations: A non-linear finite element study. Proc. Inst. Mech. Eng. Part H J. Eng Med. 2009, 223, 555–565. [Google Scholar] [CrossRef]
| Database | Search |
|---|---|
| MEDLINE [PubMed] | “finite element model premolar” OR “finite element analysis premolar” OR “finite element model premolar [Mesh]” OR “finite element analysis premolar [Mesh]” |
| SciVerse Scopus | “TITLE – ABS -KEY + finite + AND + element + AND + analysis + AND + premolar + OR + TITLE – ABS – KEY + finite + AND + element + AND + model + AND + premolar” |
| Cochrane Library | “TITLE – ABS -KEY + finite + AND + element + AND + analysis + AND + premolar + OR + TITLE – ABS – KEY + finite + AND + element + AND + model + AND + premolar” |
| Reference First Author Year | Aim | Technique | Number, Type of Elements, and Convergence | Law | Enamel | Dentine | Boundary | Loading | Experimental Comparison |
|---|---|---|---|---|---|---|---|---|---|
| [19] Limjeerajarus et al. 2019 | Intact tooth, setting-up of a new FEM, principal stress | Micro CT, NURBS | 1,062,233 TET10 Convergence | Elastic, linear | Orthotropic Εs: 73.7 GPa ν: 0.23 Εc: 63.3 GPa ν: 0.45?Εa: 63.3 GPa ν: 0.23 | Orthotropic Εs: 17.1 GPa ν: 0.30?Εc: 5.6 GPa ν: 0.33?Εa: 5.6 GPa ν: 0.30 | Ligament only | Axial, contact with a modeled indenter | F/d values in vitro Exp/num graphs 6.0 mm ball indenter, 30 intact teeth embedded in silicone |
| [20] MacHado et al. 2017 | Cervical lesion, analysis of multi factors, von Mises stress | Scan, literature data, NURBS | 1,709,931 TET10 | Elastic, linear | Orthotropic Εs: 73.7 GPa ν: 0.23 Εc: 63.3 GPa ν: 0.45?Εa: 63.3 GPa ν: 0.23 | Orthotropic Εs: 17.1 GPa ν: 0.30?Εc: 5.6 GPa ν: 0.33?Εa: 5.6 GPa ν: 0.30 | Ligament only | Axial and oblique, forces: 150 N | σ/ε values in vitro Exp/num graphs 4.0 mm ball indenter, 25 intact teeth embedded in polyether |
| [30] Chang et al. 2015 | Post and crown, analysis of multi factors, principal stress | Micro CT, segmentation | 607,890 TET4 Convergence | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.33 | Isotropic E: 18.6 GPa ν: 0.31 | Cortical spongy bone and ligament | Axial and oblique, forces: 200 N | σ/ε values in vitro Δε exp/num < 6% 5 intact teeth embedded in epoxy resin |
| [31] Zelic et al. 2014 | Coronal restorations, analysis of multi factors, principal stress | CT, segmentation | 124,768 139,284 112,828 119,492 HEX8 | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.33 | Isotropic E: 18.6 GPa ν: 0.31 | Ligament only | Axial, force: 1025 N | F/d values in vitro Exp/num graphs 1 intact and 1 restored tooth embedded in silicone |
| [32] Guimarães et al. 2014 | Cervical lesion, analysis of multi factors, principal stress | Measurement of tooth slices, NURBS | 122,996 TET4 | Elastic, linear | Isotropic E: 72.7 GPa ν: 0.33 | Isotropic E: 18.6 GPa ν: 0.31 | Cortical spongy bone and ligament | Axial, force: 105 N | F/d values in vitro Δε exp/num < 4.6% 6.0 mm ball indenter, teeth embedded in epoxy resin |
| [33] Juloski et al. 2014 | Post and crown, analysis of multi factors, principal stress | Scan, literature data, NURBS | 31,240 TET4 Convergence | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.33 | Orthotropic Εs: 25 GPa ν: 0.45 Εc: 23.2 GPa ν: 0.29 | Cortical spongy bone and ligament | Oblique, force: 200 N | σ/ε values in vivo Exp/num graphs one patient in vivo |
| [34] Lin et al. 2013 | Post and crown, analysis of multi factors, principal stress | Micro CT, segmentation | 134,810 HEX8 Convergence | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.33 | Isotropic E: 18.6 GPa ν: 0.31 | Cortical spongy bone and ligament | Axial, force: 2000 N | σ/ε values in vitro Δε exp/num = 18% 4 intact teeth |
| [35] Lin et al. 2009 | Post and crown, analysis of multi factors, principal stress | Micro CT, segmentation | 39,728 HEX8 Convergence | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.33 | Isotropic E: 18.6 GPa ν: 0.31 | Cortical spongy bone and ligament | Axial, force: 100 N | σ/ε values in vitro Δε exp/num < 10% 5 restored teeth embedded in epoxy resin |
| [36] Barak et al. 2009 | Intact tooth, setting-up of a new FEM, strain alone | Micro CT, segmentation | 438,638 TET4 | Elastic, linear | Isotropic E: 75 GPa ν: 0.3 | Isotropic E: 15 GPa ν: 0.3 | No ligament or bone | Axial, force: 200 N | Interferometry Δε exp/num = [11–85%] 4 intact teeth embedded in epoxy resin composite |
| [37] Lin et al. 2009 | Post and crown, analysis of multi factors, principal stress | Micro CT, segmentation | 39,728 HEX8 Convergence | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.33 | Isotropic E: 18.6 GPa ν: 0.31 | Cortical spongy bone and ligament | Axial, force: 100 N | σ/ε values in vitro Δε exp/num < 10% 5 restored teeth |
| [21] Lin et al. 2009 | Coronal restorations, statistical analysis of multi factors, principal stress | Scan, literature data, NURBS | 205,720 TET4 | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.2 | Isotropic E: 18.6 GPa ν: 0.31 | Cortical spongy bone and ligament | Axial and oblique, forces: 200 N | σ/ε values in vitro Δε exp/num < 10% 5.0 mm ball indenter, 5 restored teeth embedded in epoxy resin |
| [22] Tajima et al. 2009 | Intact tooth, setting-up of a new FEM, von Mises stress | CT, segmentation, NURBS | 20,773 TET10 | Elastic, linear | Isotropic E: 60.6 GPa ν: 0.3 | Isotropic E: 18.3 GPa ν: 0.3 | No ligament or bone | Axial, force: 88.3 N | σ/ε values in vitro Δε exp/num = 6% 5 intact teeth embedded in dental stone |
| [23] Chang et al. 2008 | Coronal restorations, analysis of multi factors, principal stress | Scan, literature data, NURBS | 197,527 TET4 Convergence | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.2 | Isotropic E: 18.6 GPa ν: 0.31 | Cortical spongy bone and ligament | Axial, force: 200 N | σ/ε values in vitro Δε exp/num < 10% 6.0 mm ball indenter, 5 restored teeth embedded in epoxy resin |
| [24] Lin et al. 2008 | Coronal restorations, analysis of multi factors, principal stress | Scan, literature data, NURBS | 205,720 TET4 | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.33 | Isotropic E: 18.6 GPa ν: 0.31 | Cortical spongy bone and ligament | Axial, force: 200 N | σ/ε values in vitro Δε exp/num < 10% 6.0 mm ball indenter, 5 restored teeth embedded in epoxy resin |
| [25] Lin et al. 2008 | Coronal restorations, statistical analysis of multi factors, principal stress | Scan, literature data, NURBS | 197,527 TET4 Convergence | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.2 | Isotropic E: 18.6 GPa ν: 0.31 | Cortical spongy bone and ligament | Axial, force: 200 N | σ/ε values in vitro Δε exp/num < 10% 6.0 mm ball indenter, 5 restored teeth embedded in epoxy resin |
| [26] Ausiello et al. 2004 | Coronal restorations, analysis of multi factors, von Mises stress | Scan, literature data, NURBS | 24,818 HEX8 | Elastic, linear | Isotropic E: 48 GPa ν: 0.23 | Isotropic E: 18 GPa ν: 0.2 | No ligament or bone | Axial, force: 400 N | F/d values in vitro Exp/num graphs 6.0 mm ball indenter, 10 restored teeth embedded in composite |
| [27] Lee et al. 2002 | Cervical lesion, analysis of multi factors, principal stress | Measurement of tooth slices, NURBS | 5921 HEX8 Convergence | Elastic, linear | Isotropic E: 84.1 GPa ν: 0.2 | Isotropic E: 18.6 GPa ν: 0.31 | Spongy bone and ligament | Axial, force: 170 N | σ/ε values in vitro Δε exp/num < 10% one intact tooth embedded in epoxy resin |
| [28] Ausiello et al. 2001 | Coronal restorations, analysis of multi factors, von Mises stress | Scan, literature data, NURBS | 7894 HEX8 | Elastic, linear | Isotropic E: 48 GPa ν: 0.23 | Isotropic E: 18 GPa ν: 0.2 | No ligament or bone | Axial, force: 400 N | F/d values in vitro Exp/num graphs 6.0 mm ball indenter one restored tooth embedded in epoxy resin |
| [29] Toparli et al. 1999 | Coronal restorations, analysis of multi factors, stress | Measurement of tooth slices, NURBS | 840 HEX8 | Elastic, linear | Isotropic E: 41.4 GPa ν: 0.3 | Isotropic E: 18.6 GPa ν: 0.31 | No ligament or bone | Axial, force: 300 N | σ/ε values in vitro Δε exp/num < 10% 2.0 mm ball indenter, 2 restored teeth |
| Section | Parameters | Most Frequently Used Choice | N/Ntotal—% |
|---|---|---|---|
| Study | Objective | Coronal reconstruction | 8/19–42.1% |
| Number of factors studied | Multifactorial | 16/19–84.2% | |
| Statistical approach | No statistical approach | 17/19–89.5% | |
| Failure criteria | Principal Stress | 13/19–68.4% | |
| Model construction | Reconstruction technique | Literature data | 9/19–47.4% |
| Element type | TET4/HEX8 | 8/19–42.1% | |
| Mesh Quality | Convergence test | 9/19–47.4% | |
| Presence of model for bone and ligament | Bone and ligament simulated | 11/19–57.9% | |
| Material law | Enamel law | Isotropy | 17/19–89.5% |
| Enamel Young’s modulus | 84.1 GPa | 11/17–64.7% | |
| Enamel Poisson’s ratio | 0.3 or 0.33 | 11/17–64.7% | |
| Dentine law | Isotropy | 16/19–84.2% | |
| Dentine Young’s modulus | 18-18.6 GPa | 15/16–93.8% | |
| Dentine Poisson’s ratio | 0.3 or 0.31 | 14/16–84.5% | |
| Ligament law | Isotropy | 10/11–92.9% | |
| Bone law | Isotropy | 13/14–90.9% | |
| Boundary and loading | Type of loading | Force | 18/19–94.7% |
| Force intensity | 200 N | 7/18–38.8% | |
| Force orientation | Axial | 15/18–78.9% | |
| Validation process | In vitro/in vivo | in vitro | 18/19–94.7% |
| Experimental test | Strain gauge | 13/19–68.4% | |
| Comparison process | Exp/num error | 13/19–68.4% | |
| Sample size | 5 teeth | 8/18–44.4% | |
| Tooth type | Restored | 9/18–50.0% | |
| Tooth fixation | Epoxy resin | 9/17–52.9% | |
| Loading | 6 mm ball indenter | 7/10–70.0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richert, R.; Farges, J.-C.; Tamimi, F.; Naouar, N.; Boisse, P.; Ducret, M. Validated Finite Element Models of Premolars: A Scoping Review. Materials 2020, 13, 3280. https://doi.org/10.3390/ma13153280
Richert R, Farges J-C, Tamimi F, Naouar N, Boisse P, Ducret M. Validated Finite Element Models of Premolars: A Scoping Review. Materials. 2020; 13(15):3280. https://doi.org/10.3390/ma13153280
Chicago/Turabian StyleRichert, Raphaël, Jean-Christophe Farges, Faleh Tamimi, Naim Naouar, Philippe Boisse, and Maxime Ducret. 2020. "Validated Finite Element Models of Premolars: A Scoping Review" Materials 13, no. 15: 3280. https://doi.org/10.3390/ma13153280
APA StyleRichert, R., Farges, J.-C., Tamimi, F., Naouar, N., Boisse, P., & Ducret, M. (2020). Validated Finite Element Models of Premolars: A Scoping Review. Materials, 13(15), 3280. https://doi.org/10.3390/ma13153280









