Numerical Analysis of Fatigue Crack Growth Path and Life Predictions for Linear Elastic Material
Abstract
:1. Introduction
2. Numerical Predication of Mixed-Mode Fatigue Life
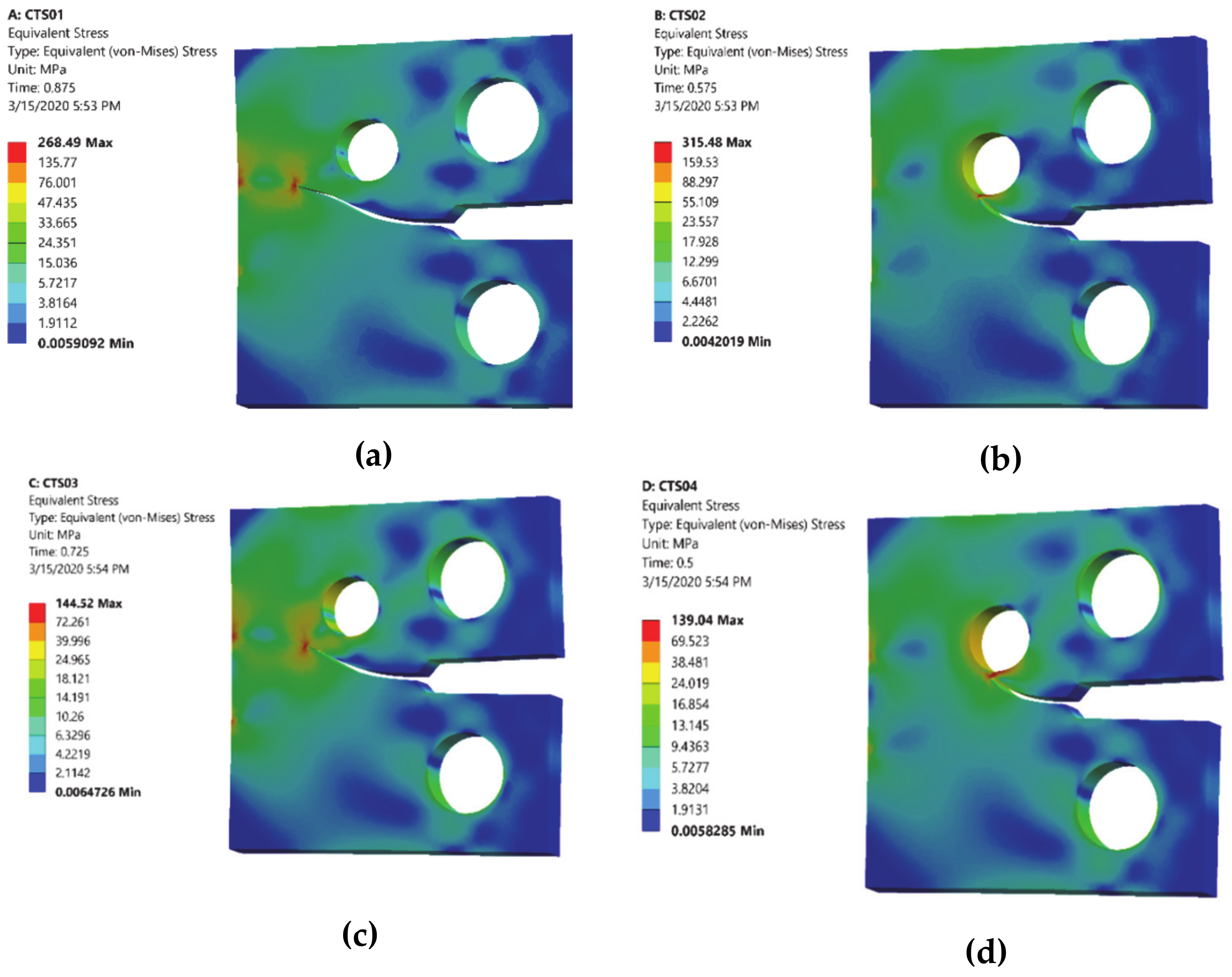
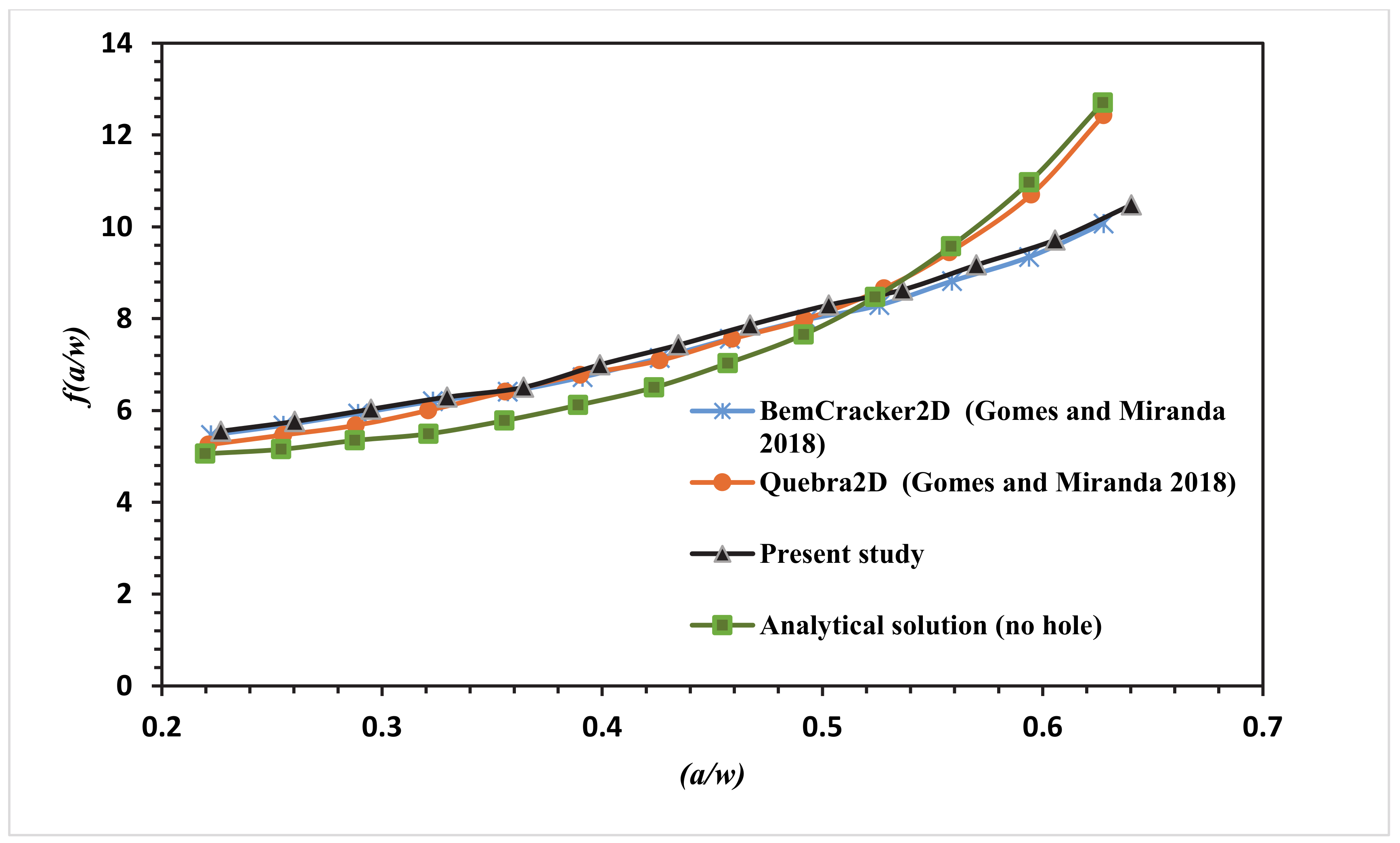
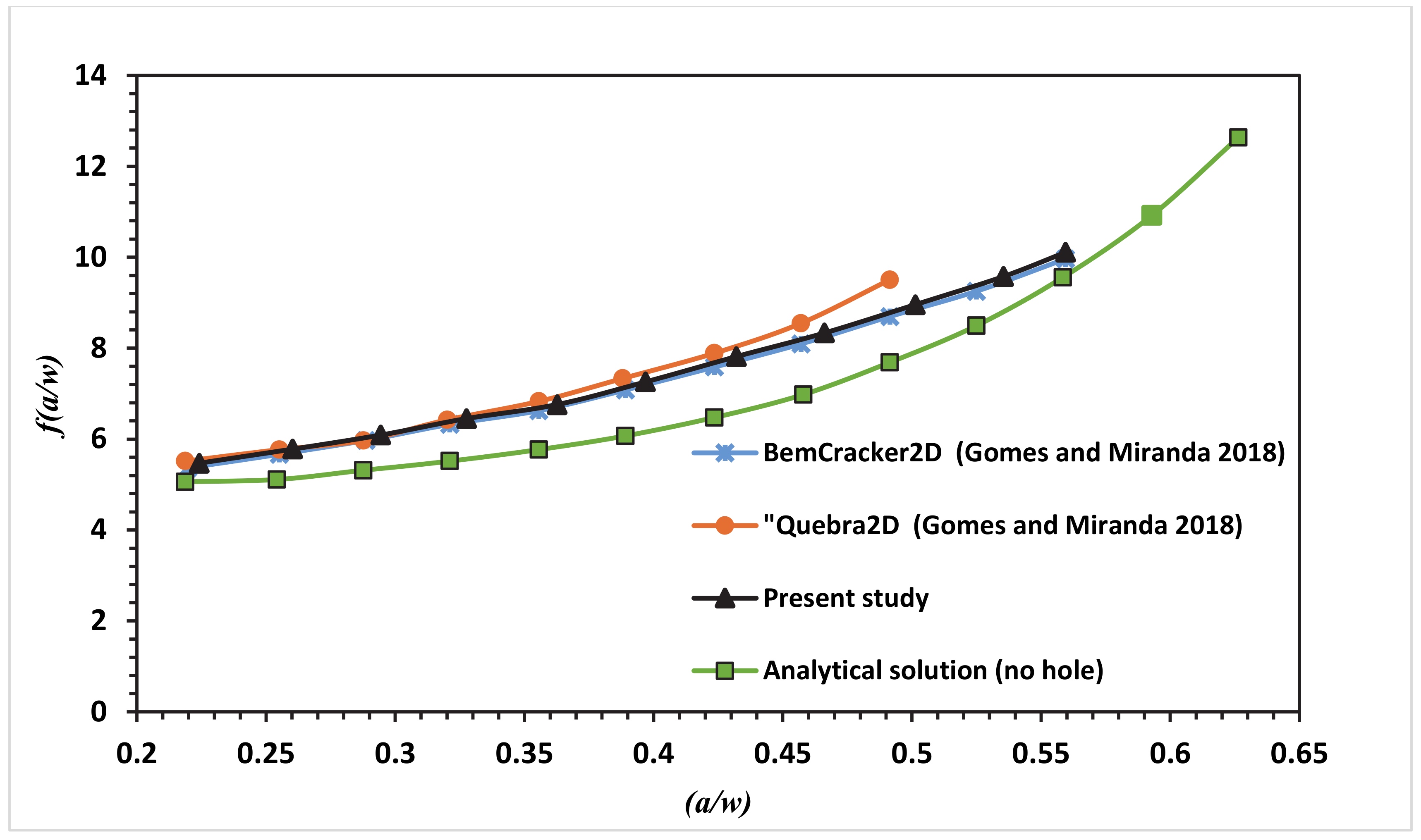
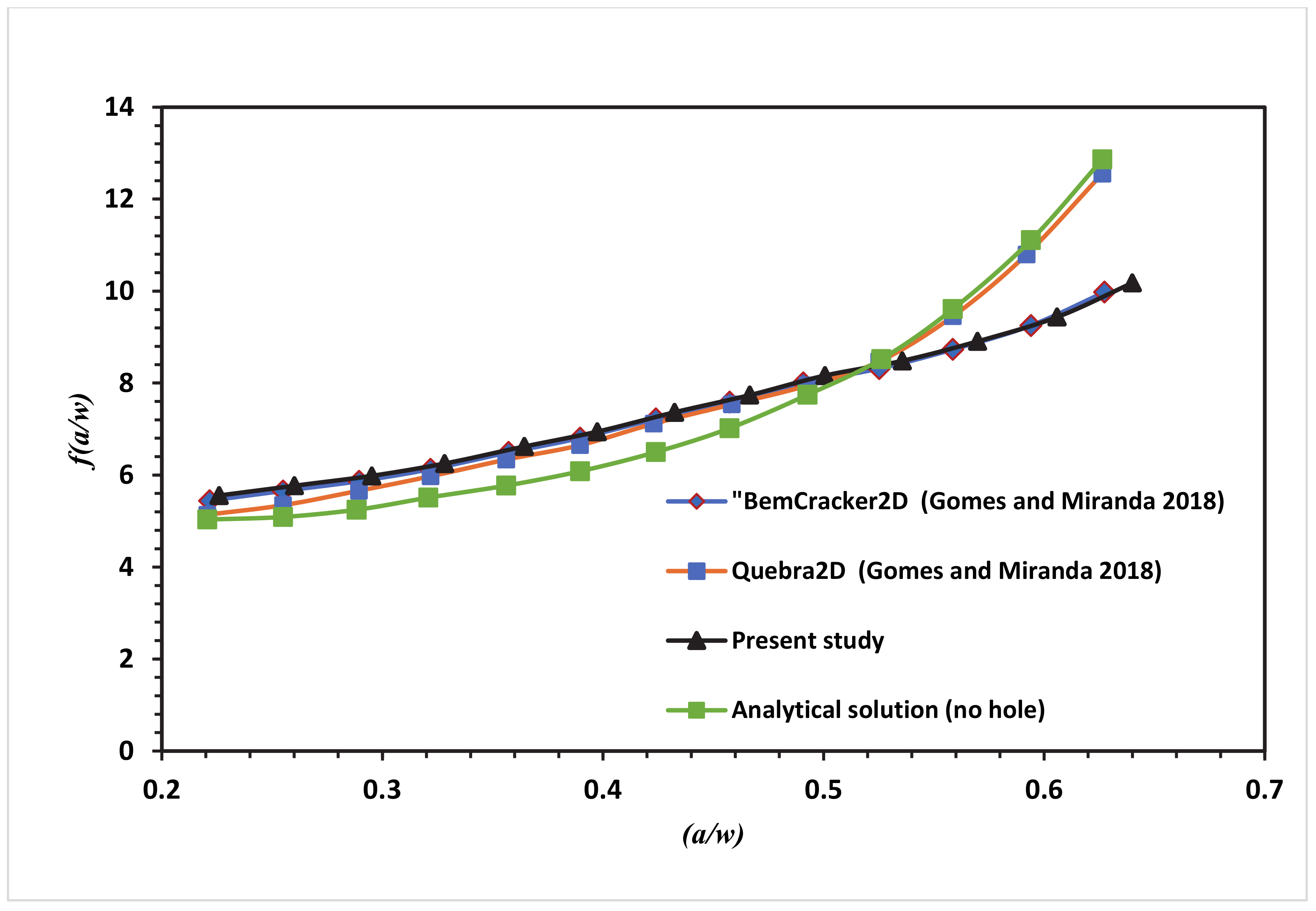
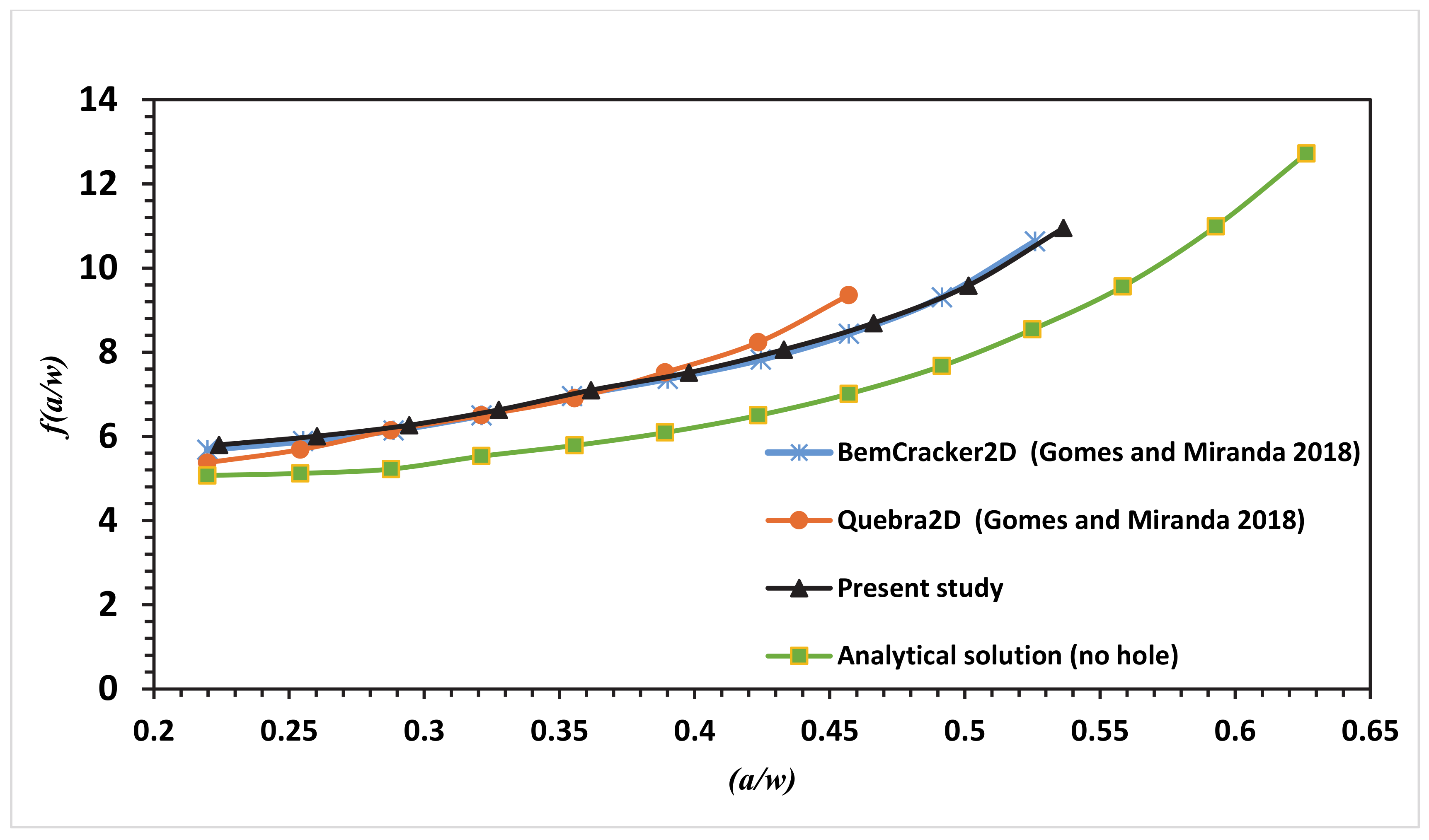
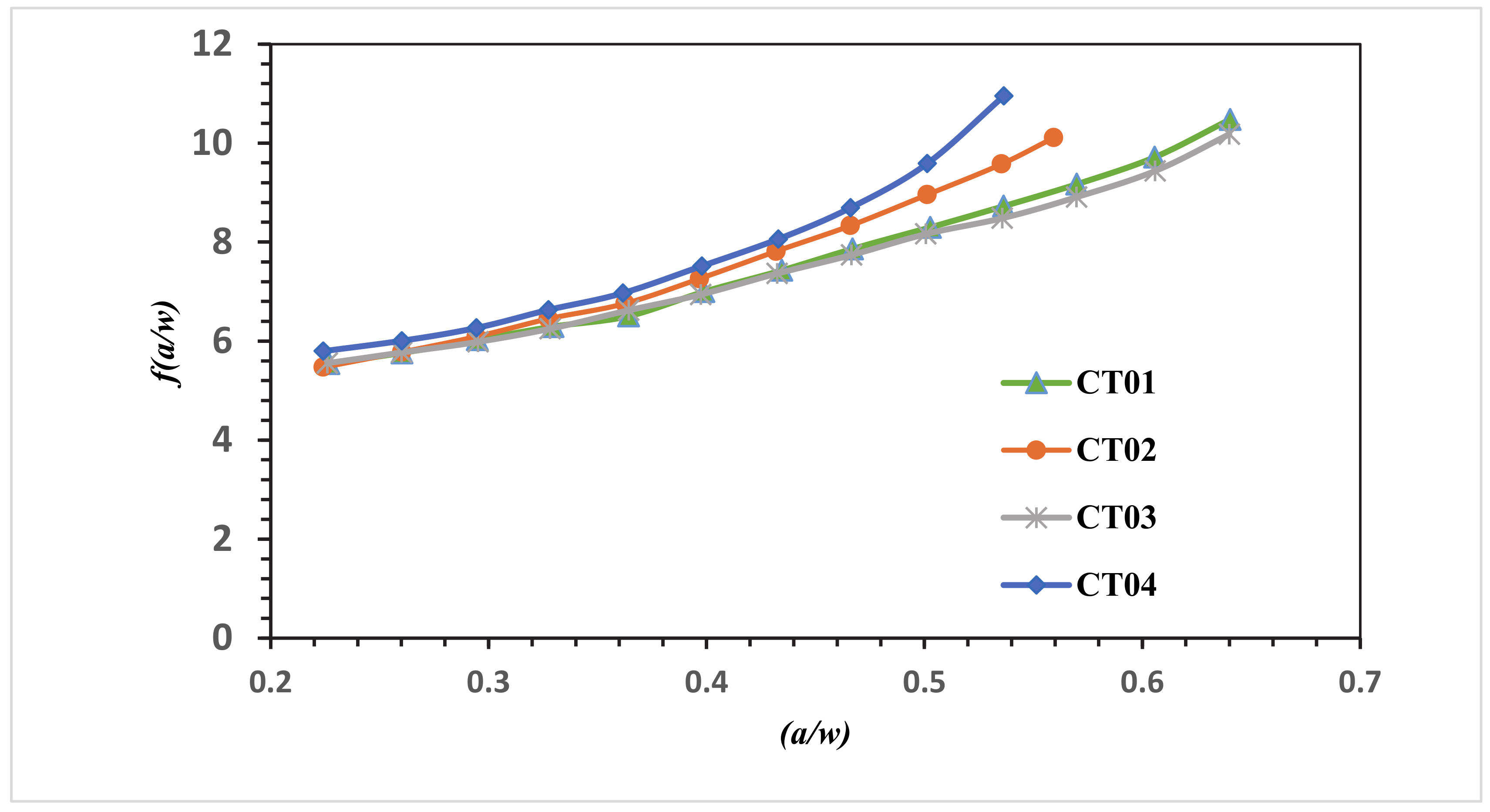
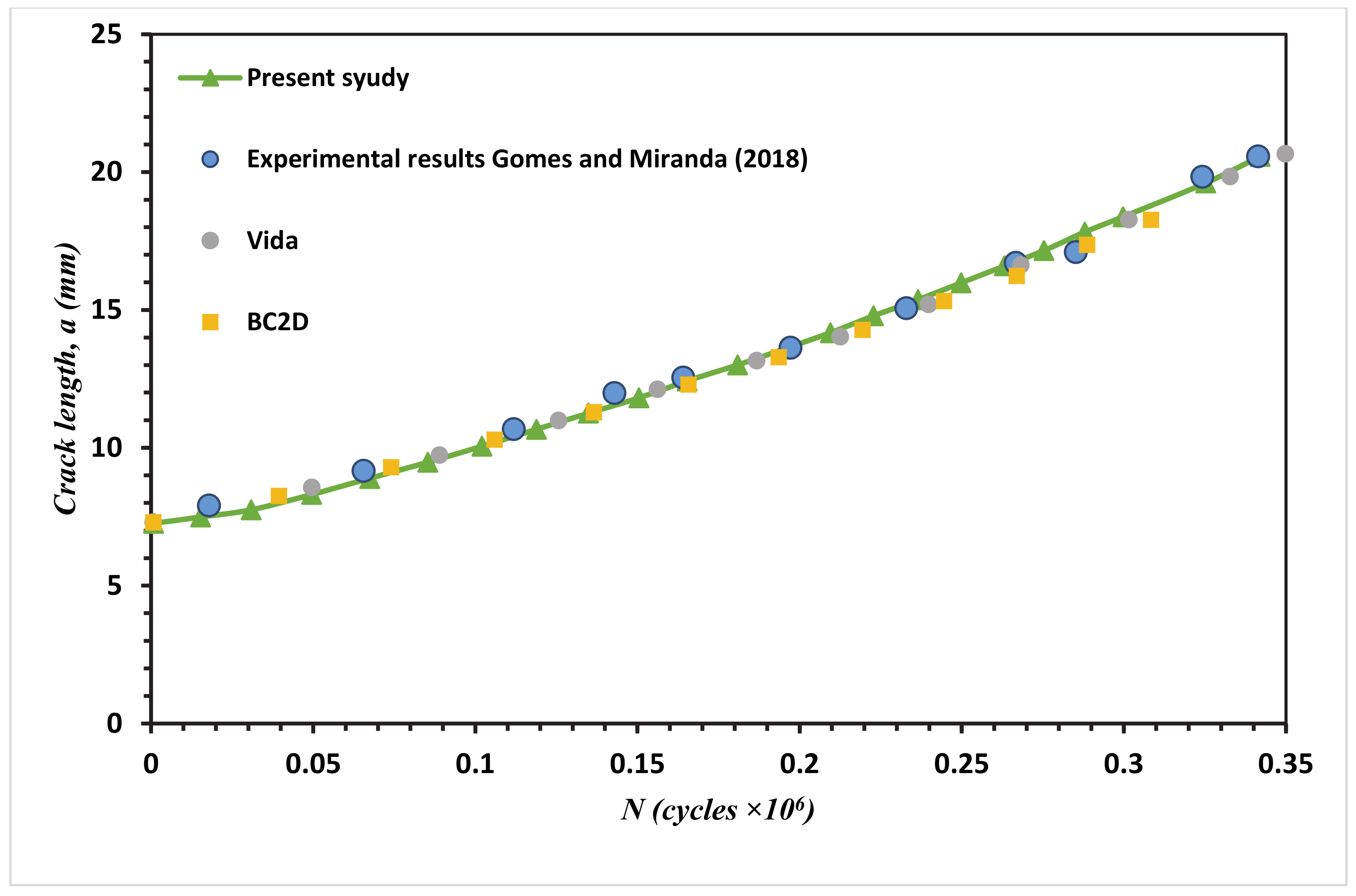
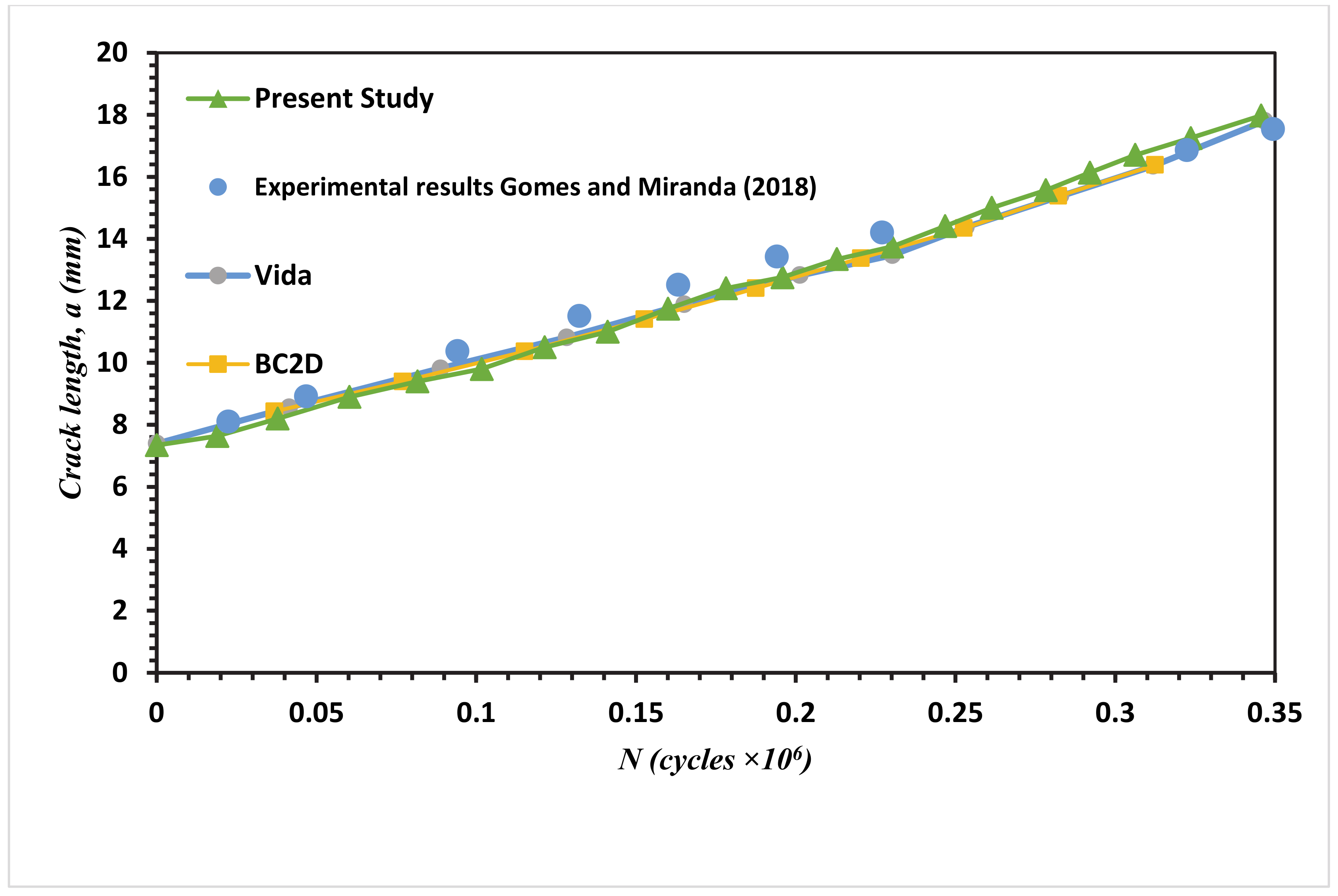
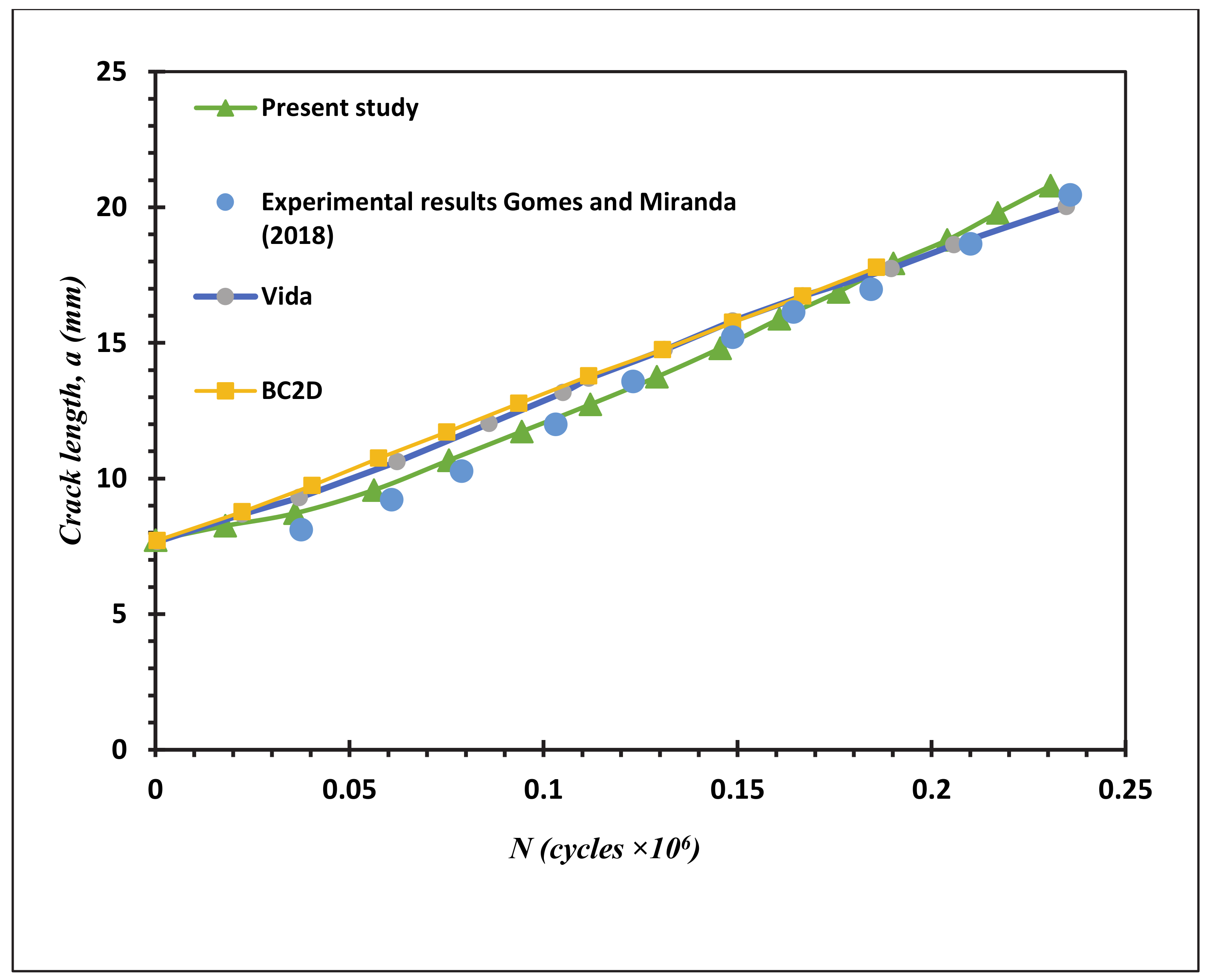
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alegre, J.M.; Preciado, M.; Ferreño, D. Study of the fatigue failure of an anti-return valve of a high pressure machine. Eng. Fail. Anal. 2007, 14, 408–416. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Finite element procedures for the numerical simulation of fatigue crack propagation under mixed mode loading. Struct. Eng. Mech. 2010, 35, 283–299. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Comprehensive comparisons of two and three-dimensional numerical estimation of stress intensity factors and crack propagation in linear elastic analysis. Int. J. Integr. Eng. 2019, 11, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Alshoaibi, A.M.; Bin Ghouth, A.; Fageehi, Y.A. Three-dimensional simulation of crack propagation using finite element method. Intern. J. Eng. Adv. Technol. 2019, 9, 892–897. [Google Scholar]
- Alshoaibi, A.M.; Fageehi, Y.A. 2D finite element simulation of mixed mode fatigue crack propagation for CTS specimen. J. Mater. Res. Technol. 2020, 9, 7850–7861. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- ASTM. Standard Test Method for Measurement of Fatigue Crack Growth Rates; E647-13-08; American Society for Testing and Materials: West Consonance, PA, USA, 2013; Volume 712. [Google Scholar]
- Barsom, J.; Rolfe, S. Fracture and Fatigue in Structure: Application of Fracture Mechanics; American Society for Testing and Materials: Philadelphia, PA, USA, 1999. [Google Scholar]
- Boyce, B.L.; Ritchie, R.O. Effect of load ratio and maximum stress intensity on the fatigue threshold in Ti–6Al–4V. Eng. Fract. Mech. 2001, 68, 129–147. [Google Scholar] [CrossRef]
- Broek, D. Elementary Engineering Fracture Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Chandran, K.S.R. Net-section based approach for fatigue crack growth characterization using compact tension specimen: Physical correlation of mean stress or stress ratio effects. Int. J. Fatigue 2019, 124, 473–482. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Q.; Zeng, W.; Liu, G.; Sun, J.; He, L.; Bui, T.Q. Dynamic brittle crack propagation modeling using singular edge-based smoothed finite element method with local mesh rezoning. Eur. J. Mech. A/Solids 2019, 76, 208–223. [Google Scholar] [CrossRef]
- Coffin, L. Cyclic Deformation and Fatigue of Metals; IZO: Moscow, Russia, 1963. [Google Scholar]
- Demir, O.; Ayhan, A.O.; Iriç, S. A new specimen for mixed mode-I/II fracture tests: Modeling, experiments and criteria development. Eng. Fract. Mech. 2017, 178, 457–476. [Google Scholar] [CrossRef]
- Dirik, H.; Yalçinkaya, T. Crack path and life prediction under mixed mode cyclic variable amplitude loading through XFEM. Int. J. Fatigue 2018, 114, 34–50. [Google Scholar] [CrossRef]
- Fageehi, Y.A.; Alshoaibi, A.M. Numerical simulation of mixed-mode fatigue crack growth for compact tension shear specimen. Adv. Mater. Sci. Eng. 2020, 2020, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Gomes, G.O.; Miranda, A.C. Analysis of crack growth problems using the object-oriented program bemcracker2D. Frat. Ed Integrità Strutt. 2018, 12, 67–85. [Google Scholar] [CrossRef] [Green Version]
- Hellan, K.; Saunders, H. Introduction to Fracture Mechanics. J. Vib. Acoust. 1987, 109, 325–326. [Google Scholar] [CrossRef] [Green Version]
- Hussain, M.; Pu, S.; Underwood, J. Strain Energy Release Rate for a Crack Under Combined Mode I and Mode II, Proceedings of the National Symposium on Fracture Mechanics, Vancouver, BC, Canada, 20–22 May 2009; ASTM International: Conshohocken, PA, USA, 2009; p. 2. [Google Scholar]
- Liu, A.F. Mechanics and Mechanisms of Fracture: An Introduction; ASM International: Cleveland, OH, USA, 2005. [Google Scholar]
- Miranda, A.; Meggiolaro, M.A.; De Castro, J.T.P.; Martha, L.; Bittencourt, T. Fatigue life and crack path predictions in generic 2D structural components. Eng. Fract. Mech. 2003, 70, 1259–1279. [Google Scholar] [CrossRef] [Green Version]
- Newman, J. Stress Analysis of the Compact Specimen Including the Effects of Pin Loading. Proceedings of the National Symposium on Fracture Mechanics, Vancouver, BC, Canada, 20–22 May 2009; ASTM International: Conshohocken, PA, USA, 2009; p. 105. [Google Scholar]
- Newman, J.C., Jr.; Ruschau, J.J.; Hill, M.R. Improved test method for very lowfatigue-crack-growth-rate data. Fatigue. Fract. Eng. Mater. Struct. 2011, 34, 270–279. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Qi, S.; Cai, L.; Bao, C.; Chen, H.; Shi, K.; Wu, H. Analytical theory for fatigue crack propagation rates of mixed-mode I–II cracks and its application. Int. J. Fatigue 2019, 119, 150–159. [Google Scholar] [CrossRef]
- Richard, H.A.; Sander, M.; Fulland, M.; Kullmer, G. Development of fatigue crack growth in real structures. Eng. Fract. Mech. 2008, 75, 331–340. [Google Scholar] [CrossRef]
- Sajith, S.; Murthy, K.; Robi, P.S. Prediction of Accurate Mixed Mode Fatigue Crack Growth Curves using the Paris’ Law. J. Inst. Eng. (India) Ser. C. 2017, 100, 165–174. [Google Scholar] [CrossRef]
- Schijve, J. Fatigue of Structures and Materials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Sih, G.; Liebowitz, H. Mathematical Fundamentals; Fracture, Academic Press: New York, NY, USA, 1968; Volume 2, pp. 67–190. [Google Scholar]
- Srawley, J.E. Wide range stress intensity factor expressions for ASTM E 399 standard fracturetoughness specimens. Int. J. Fract. 1976, 12, 475–476. [Google Scholar]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook, 3rd ed.; ASME International: New York, NY, USA, 2000. [Google Scholar]
- Tanaka, K. Fatigue crack propagation from a crack inclined to the cyclic tensile axis. Eng. Fract. Mech. 1974, 6, 493–507. [Google Scholar] [CrossRef]
- Wöhler, A. Versuche zur Ermittlung der auf die Eisenbahnwagenachsen einwirkenden Kräfte und die Widerstandsfähigkeit der Wagen-Achsen. Zeitschrift für Bauwesen 1860, 10, 583–614. [Google Scholar]

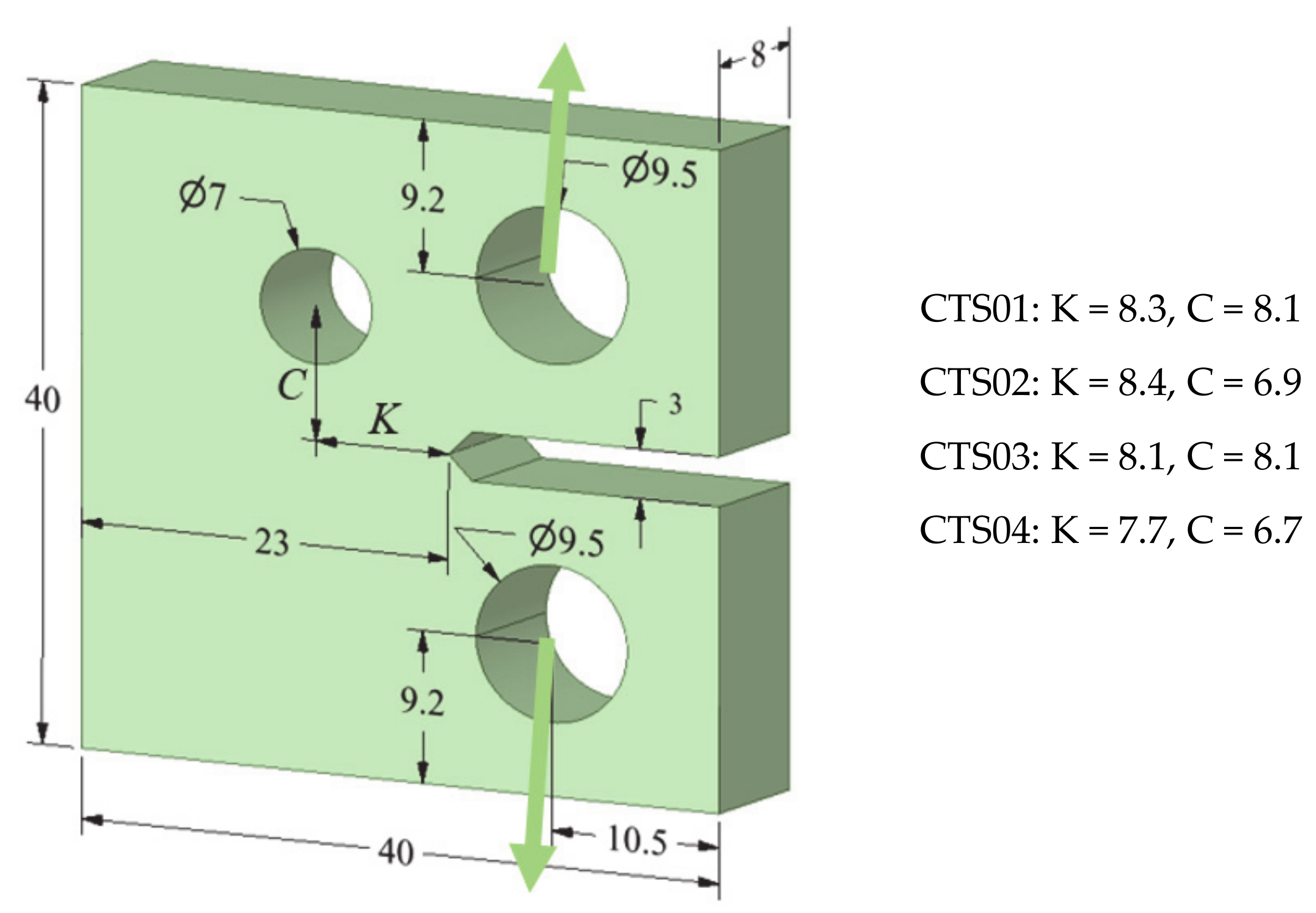


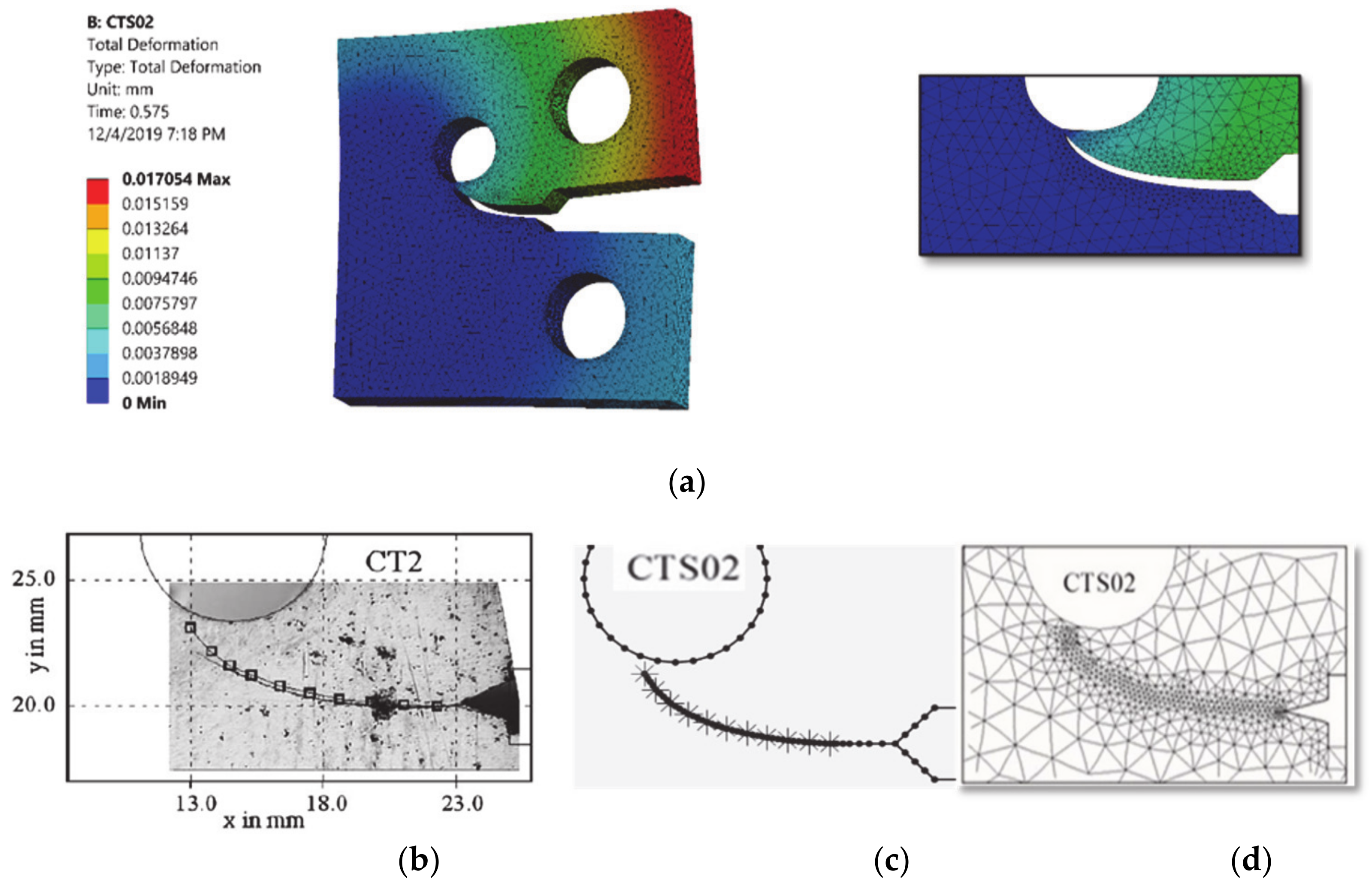
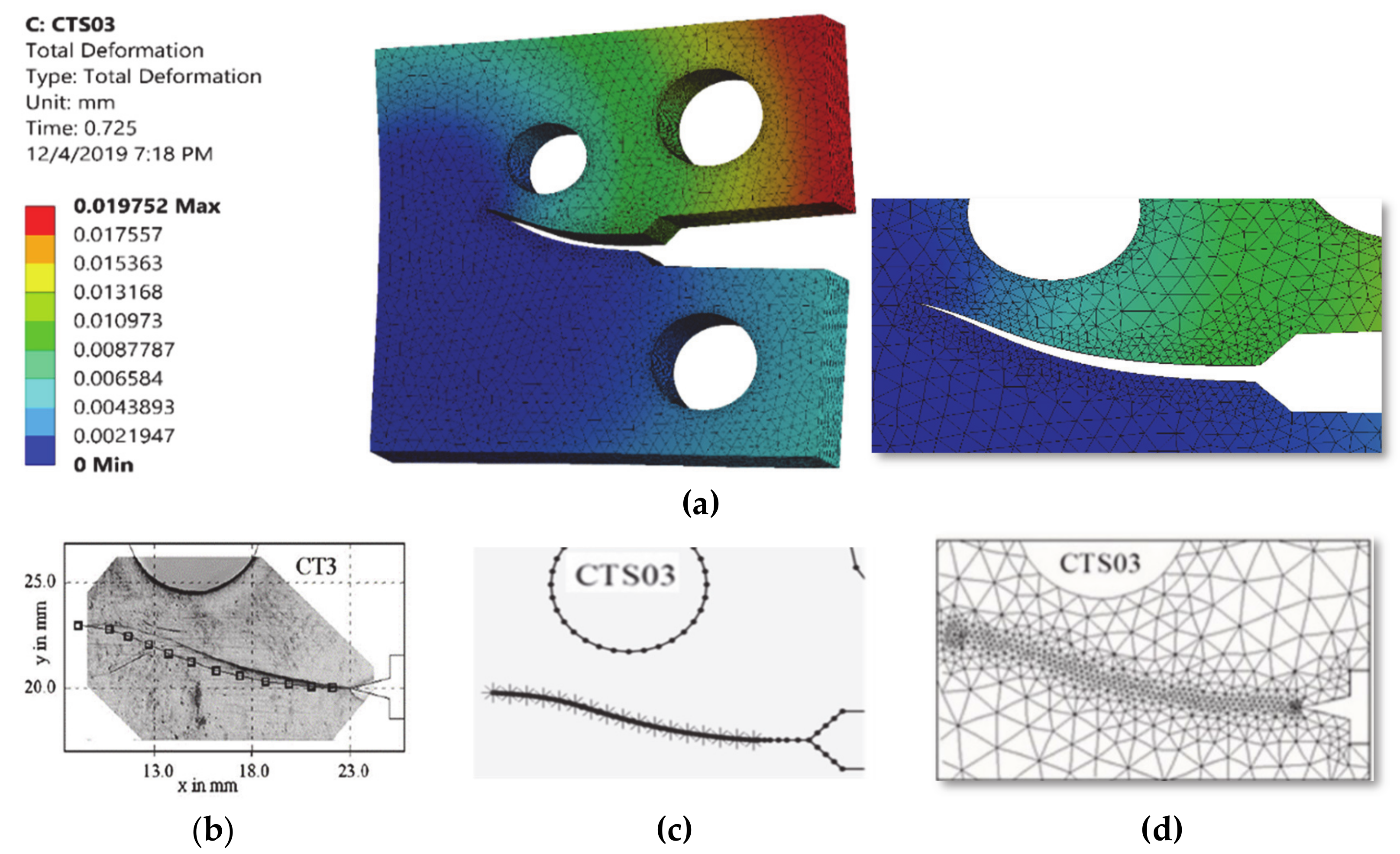

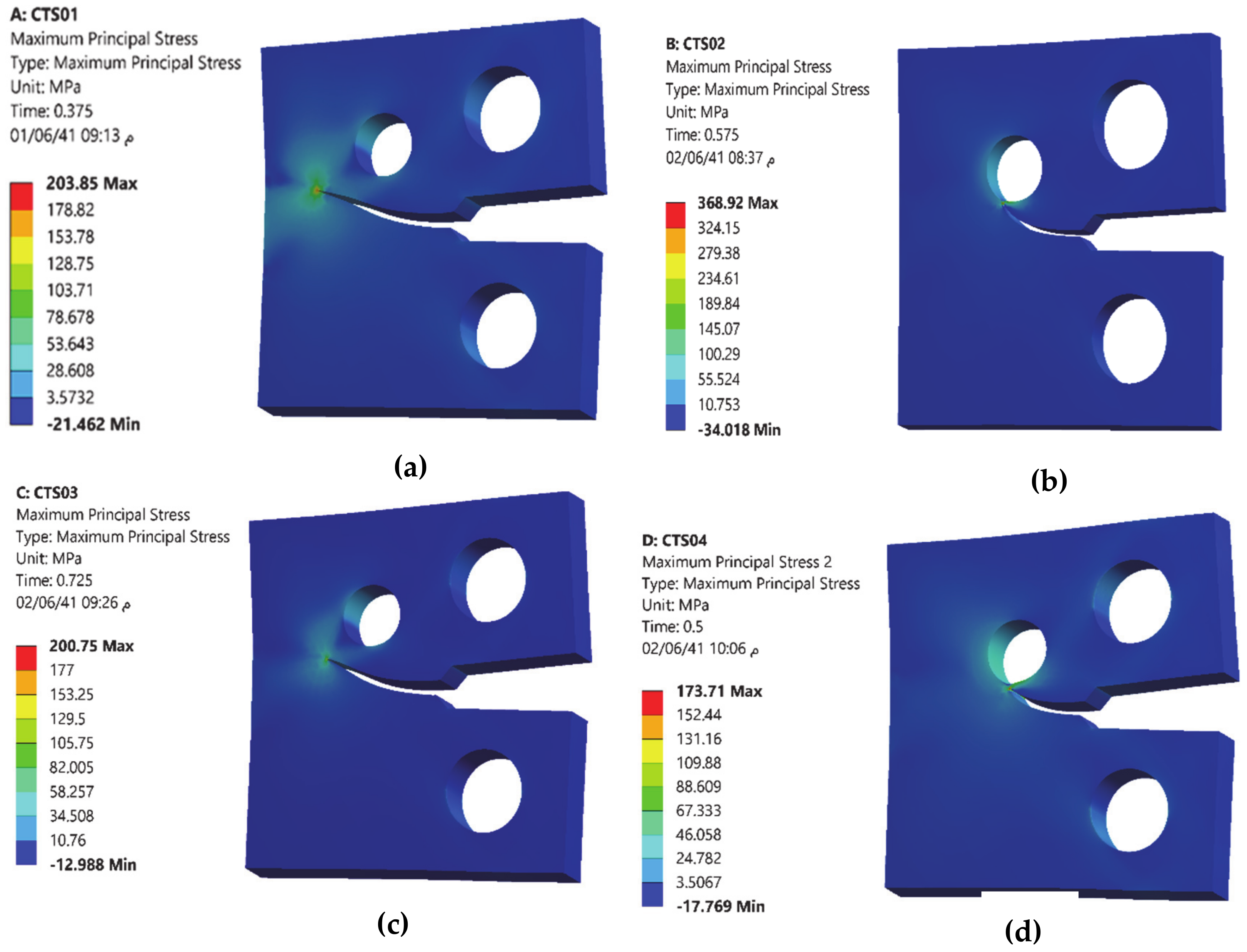

| Property | Value in Metric Unit |
|---|---|
| Modulus of elasticity, E | 205 GPa |
| Poisson’s ratio, υ | 0.29 |
| Yield strength, σy | 285 MPa |
| Ultimate strength, σu | 491 MPa |
| Paris’ law coefficient, C | 8.59 × 10−14 |
| Paris law exponent m | 4.26 |
| MCTS# | Number of Elements | Number of Nodes |
|---|---|---|
| MCTS01 | 120,097 | 182,971 |
| MCTS02 | 130,710 | 198,991 |
| MCTS03 | 119,370 | 181,989 |
| MCTS04 | 121,409 | 184,850 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshoaibi, A.M.; Fageehi, Y.A. Numerical Analysis of Fatigue Crack Growth Path and Life Predictions for Linear Elastic Material. Materials 2020, 13, 3380. https://doi.org/10.3390/ma13153380
Alshoaibi AM, Fageehi YA. Numerical Analysis of Fatigue Crack Growth Path and Life Predictions for Linear Elastic Material. Materials. 2020; 13(15):3380. https://doi.org/10.3390/ma13153380
Chicago/Turabian StyleAlshoaibi, Abdulnaser M., and Yahya Ali Fageehi. 2020. "Numerical Analysis of Fatigue Crack Growth Path and Life Predictions for Linear Elastic Material" Materials 13, no. 15: 3380. https://doi.org/10.3390/ma13153380
APA StyleAlshoaibi, A. M., & Fageehi, Y. A. (2020). Numerical Analysis of Fatigue Crack Growth Path and Life Predictions for Linear Elastic Material. Materials, 13(15), 3380. https://doi.org/10.3390/ma13153380






