The Effect of Periodic Spatial Perturbations on the Emission Rates of Quantum Dots near Graphene Platforms
Abstract
:1. Introduction
- Excitation of the chromophore (here, the QDs) by a pump laser at frequency ωL. The chromophore is relaxed and transfers energy at frequency ωE to a 2-D graphene surface guide on a hole-patterned oxide substrate. The graphene is coated with a thin oxide (hafnia). A surface mode is sustained due to the large refractive index of graphene (ngraphene~2.6), QDs and hafnia, but not necessarily through a plasmonic mode for which the dielectric constant of graphene needs to be negative [24].
- The excited QD dipole is coupled non-radiatively to a charge dipole in the graphene via energy transfer [9,10,11] at the rate of Γi1→f1 with i1—the initial, excited state of QD and f1—the final state, the excited dipole in the graphene. The final state, f1 may transfer its energy to another QD nearby or thermally relax. If the graphene is coupled to a resonator (the periodic spatial pattern), then the QD may relax at a rate of Γi1→f2 with i1—the initial, excited state of the QD and f2—the final electromagnetic state within the surface resonator. That mode may propagate back and forth along the surface resonator and eventually be coupled to free space modes or back to the lossy graphene film. Coherence in our case is achieved when the surface mode is at resonance with the local periodic perturbations.
- A third interaction channel between the standing surface mode and the dipole generated in the graphene may be possible. Its mutual coupling may be sensitive to nonlinear photonic, or phononic effects [25] and could result in energy exchange. We will not dwell on such effect but a discussion is provided in the Supplementary information Section (SI). Overall, our measurements were carried for fluorescence intensity values that were linear with respect to the laser intensity.
- The surface mode is coupled to free-space radiation modes and detected by a faraway detector.
- Furthermore,
- (a)
- when all the other parameters are kept the same, the emission rate of a chromophore coupled to a 2-D system is smaller than a chromophore coupled to a 3-D system;
- (b)
- the conductive graphene increases the emission rate through non-radiative energy transfer process, which is enabled by charge screening;
- (c)
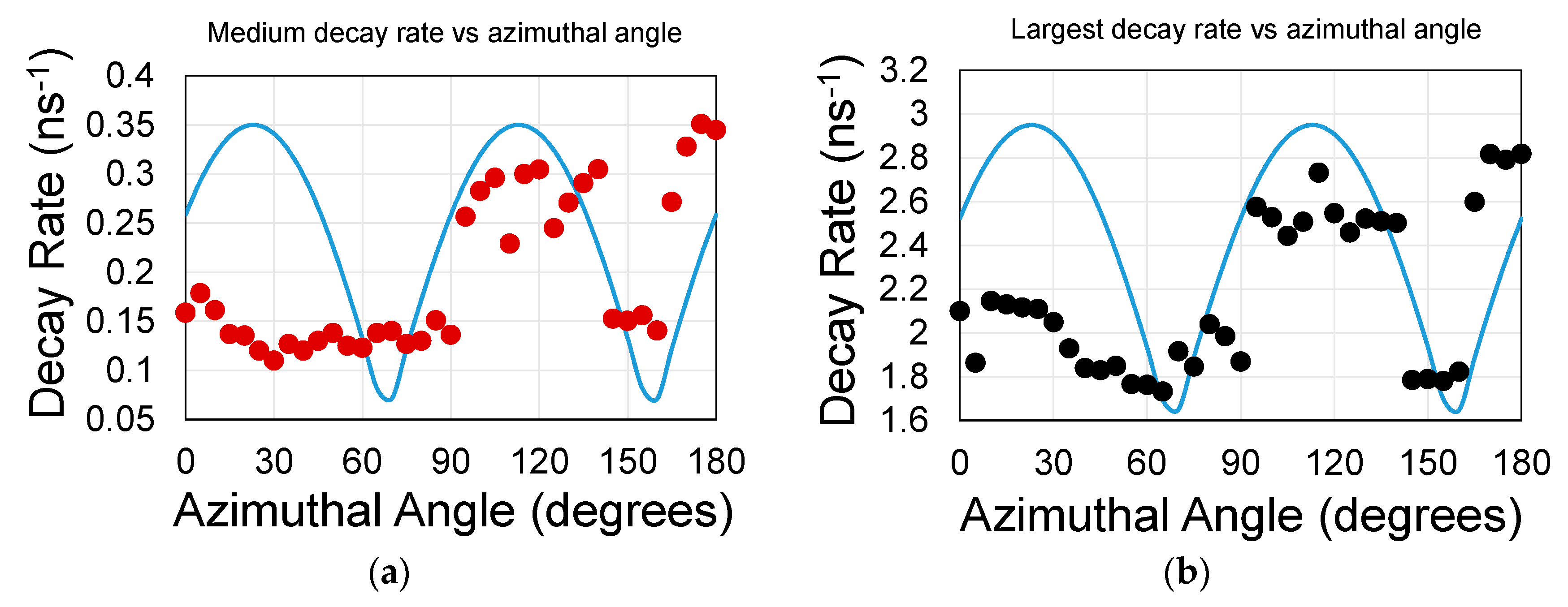
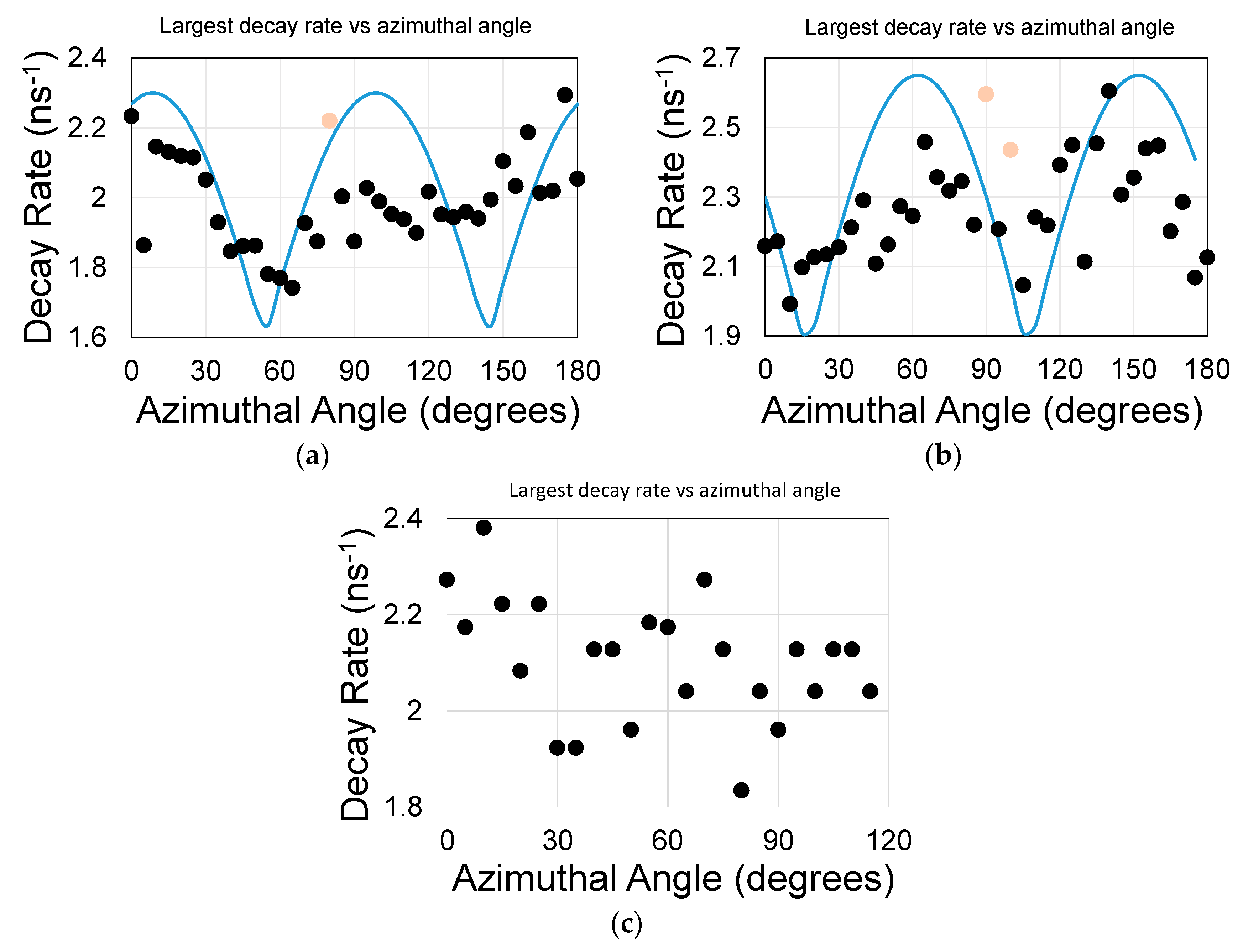
- the effect of a resonating spatial perturbation is to further increase the emission rate of the chromophore due to an increase in the DOS near resonance [20]. The measured rate is ΓET = Γi1→f1 + Γi1→f2 in the absence of other nonlinear processes (see SI Section). The process efficiency is E~ΓET/(ΓET + ΓD), where ΓET and ΓD are, respectively, the non-radiative rate of energy transfer and the radiative decay rate of a stand-alone donor. Thus, increasing or decreasing of ΓET provides an active control over the entire process. Long lifetime donors (small ΓD) are preferred;
- (d)
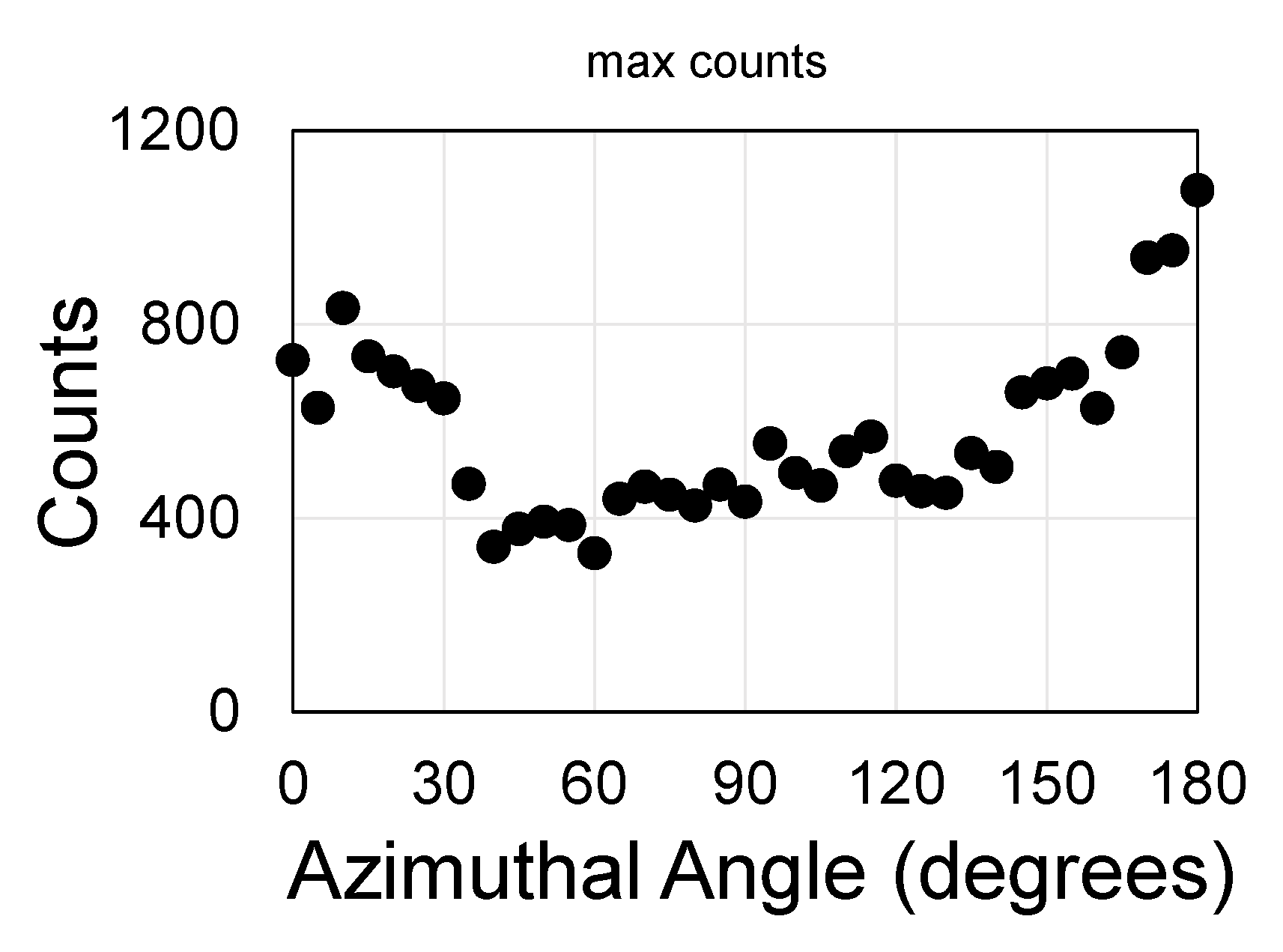
- the efficiency of the coupling between the QDs and the surface mode is enhanced because the resonating electromagnetic mode is mostly confined to the structure holes as we shall see below. A photon travelling back and forth within a resonating structure (namely, the surface guide with periodic perturbations) forms a standing wave at resonance conditions. The resonance conditions result in enhanced intensity at some particular tilt and azimuthal rotation angles with respect to the nano-hole array [16,26].
2. Methods and Experiments
- (1).
- The geometrical effect of the laser spot on the overall emission rate assessment is not straight forward. The Gaussian beam has features of a plane wave only at the focal point; yet, excitations of the dots with varying degrees of efficiency occur with the unfocused beam as well.
- (2).
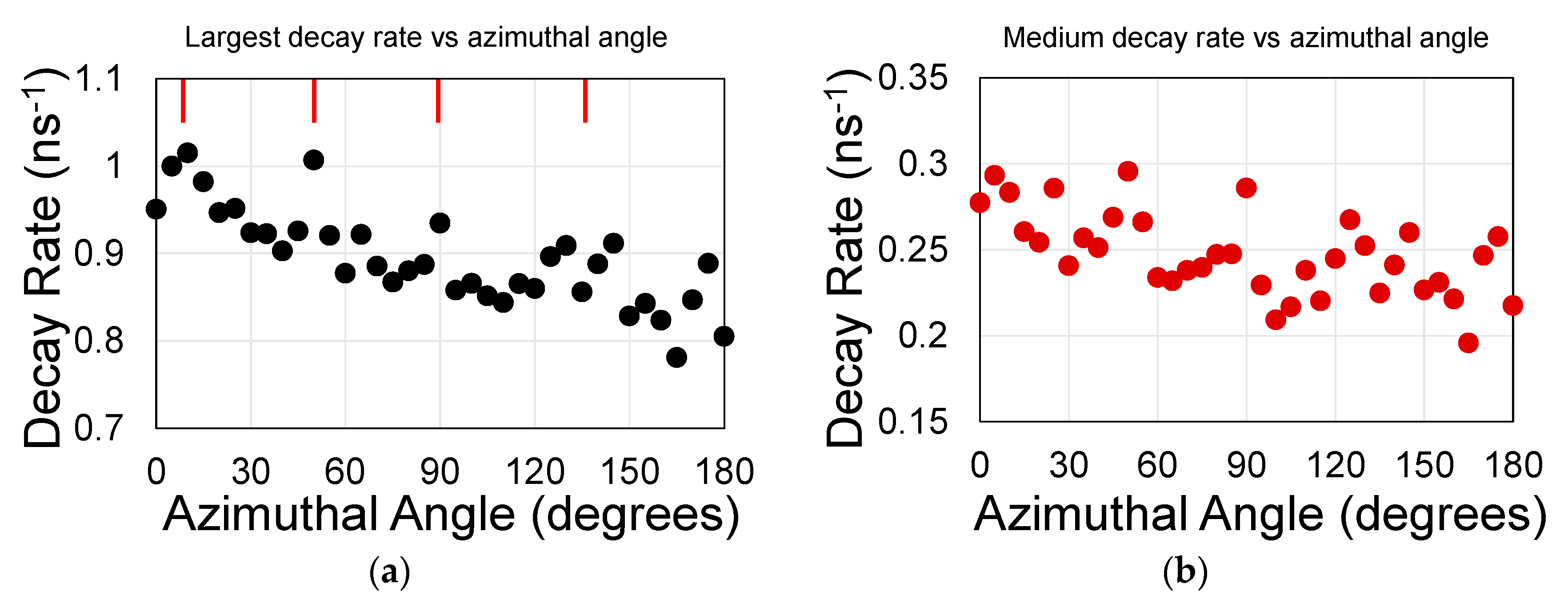
- Limiting the fit to mainly one time component that is prevalent in a finite time range (namely, limiting the fit, say, to a window of 10 ns after excitation) runs the risk that the solution will be affected by the boundaries of the time window.
- (3).
- Having too many time constants may blur the physics of the processes.
- (4).
- Considering the fit quality by only its R-square value is insufficient. One needs to consider the distribution of the residuals about the fitting parameter (see SI Section). The residual distribution has to be evenly spread above and below the mean.
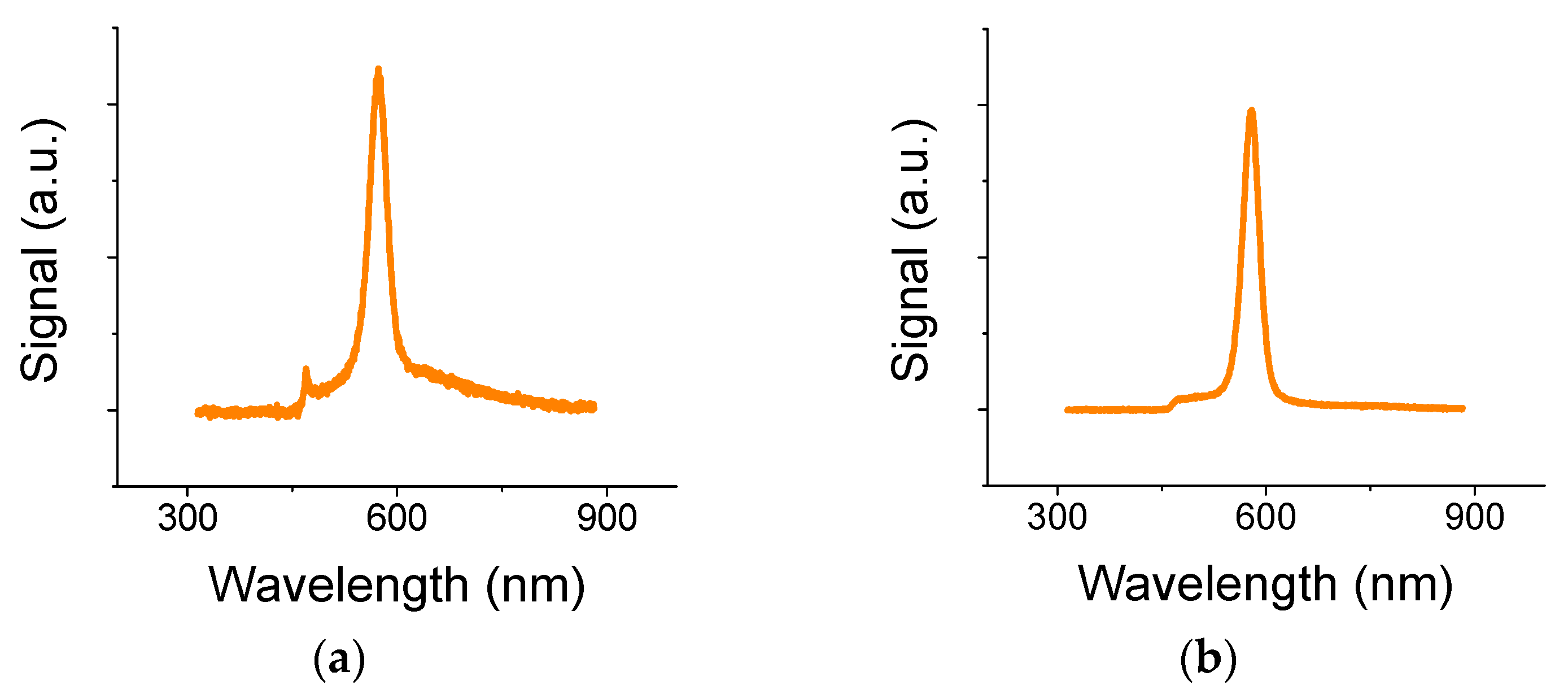
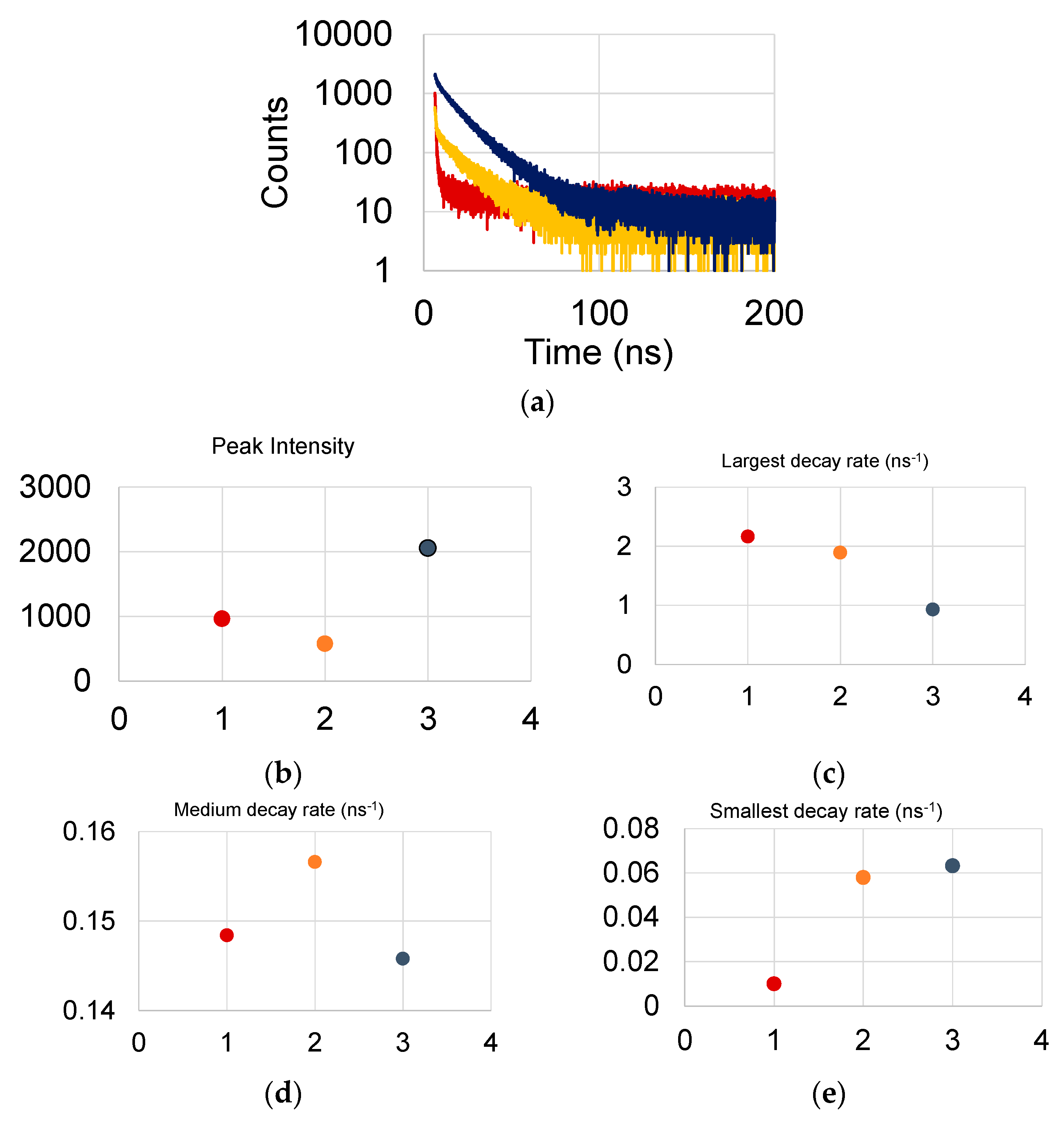
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Persson, B.N.J.; Lang, N.D. Electron-hole-pair quenching of excited-states near a metal. Phys. Rev. B 1982, 26, 5409. [Google Scholar] [CrossRef]
- Barnes, W.L. Fluorescence near interfaces: The role of photonic mode density. J. Mod. Opt. 1998, 45, 661. [Google Scholar] [CrossRef]
- Morales-Narváez, E.; Merkoçi, A. Graphene oxide as an optical biosensing platform. Adv. Mater. 2012, 24, 3298–3308. [Google Scholar] [CrossRef] [PubMed]
- Klekachev, A.V.; Nourbakhsh, A.; Asselberghs, I.; Stesmans, A.L.; Heyns, M.M.; De Gendt, S. Electron accumulation in graphene by interaction with optically excited quantum dots. Physica E 2011, 43, 1046–1049. [Google Scholar] [CrossRef]
- Dong, H.; Gao, W.; Yan, F.; Ji, H.; Ju, H. Fluorescence resonance energy transfer between quantum dots and graphene oxide for sensing biomolecules. Anal. Chem. 2010, 82, 5511–5517. [Google Scholar] [CrossRef]
- Kasry, A.; Ardakani, A.A.; George, S.; Menges, T.B.; Copel, M.; Vyklicky, L. Highly efficient fluorescence quenching with graphene. J. Phys. Chem. C 2012, 116, 2858–2862. [Google Scholar] [CrossRef]
- Salihoglu, O.; Kakenov, N.; Balci, O.; Balci, S.; Kocabas, C. Graphene as a reversible and spectrally selective fluorescence quencher. Sci. Rep. 2016, 6, 33911. [Google Scholar] [CrossRef]
- Lin, W.; Tian, B.; Zhuang, P.; Yin, J.; Zhang, C.; Li, Q.; Shih, T.M.; Cai, W. Graphene-based fluorescence-quenching-related fermi level elevation and electron-concentration surge. Nano Letts. 2016, 16, 5737–5741. [Google Scholar] [CrossRef]
- Konstantatos, G.; Badioli, M.; Gaudreau, L.; Osmond, J.; Bernechea, M.; De Arquer, F.P.; Gatti, F.; Koppens, F.H. Hybrid graphene-quantum dot phototransistors with ultrahigh gain. Nat. Nanotechnol. 2012, 7, 363–368. [Google Scholar] [CrossRef]
- Zhu, M.; Liu, Q.; Chen, W.; Yin, Y.; Ge, L.; Li, H.; Wang, K. Boosting the visible-light photoactivity of BiOCl/BiVO4/N-GQD ternary heterojunctions based on internal Z-scheme charge transfer of N-GQDs: Simultaneous band gap narrowing and carrier lifetime prolonging. ACS Appl. Mater. Interfaces 2017, 9, 38832–38841. [Google Scholar] [CrossRef]
- Zhu, Y.; Meng, X.; Cui, H.; Jia, S.; Dong, J.; Zheng, J.; Zhao, J.; Wang, Z.; Li, L.; Zhang, L.; et al. Graphene frameworks promoted electron transport in quantum dot-sensitized solar cells. ACS Appl. Mater. Interfaces 2014, 6, 13833–13840. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Berciaud, S.; Nuckolls, C.; Tony, F.H.; Brus, L.E. Graphene channels interfaced with an array of individual quantum dots. arXiv Prepr. 2017, arXiv:1705.05910. [Google Scholar] [CrossRef] [Green Version]
- Rogez, B.; Yang, H.; Le Moal, E.; Leveque-Fort, S.; Boer-Duchemin, E.; Yao, F.; Lee, Y.H.; Zhang, Y.; Wegner, K.D.; Hildebrandt, N.; et al. Fluorescence lifetime and blinking of individual semiconductor nanocrystals on graphene. J. Phys. Chem. C 2014, 118, 18445–18452. [Google Scholar] [CrossRef]
- Li, R.; Schneider, L.M.; Heimbrodt, W.; Wu, H.; Koch, M.; Rahimi-Iman, A. Gate tuning of Förster resonance energy transfer in a graphene—quantum dot FET photo-detector. Sci. Rep. 2016, 6, 28224. [Google Scholar] [CrossRef] [Green Version]
- The linear absorption coefficient of QD is A ~ 105 /cm and a typical dot diameter is D = 3 nm. If we assume that the absorption behaves as [1-exp(A∙D)] ~ A∙D, then the absorption of a QD monolayer is ~3%.
- Miao, X.; Gosztola, D.J.; Sumant, A.V.; Grebel, H. Lifetime and linewidth of individual quantum dots interfaced with grapheme. Nanoscale 2018, 10, 7040–7046. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lunz, M.; Bradley, A.L.; Chen, W.Y.; Gerard, V.A.; Byrne, S.J.; Gun’ko, Y.K.; Lesnyak, V.; Gaponik, N. Influence of quantum dot concentration on Förster resonant energy transfer in monodispersed nanocrystal quantum dot monolayers. Phys. Rev. B 2010, 81, 205316. [Google Scholar] [CrossRef]
- Lunz, M.; Bradley, A.L.; Gerard, V.A.; Byrne, S.J.; Gun’ko, Y.K.; Lesnyak, V.; Gaponik, N. Concentration dependence of Förster resonant energy transfer between donor and acceptor nanocrystal quantum dot layers: Effect of donor-donor interactions. Phys. Rev. B 2011, 83, 115423. [Google Scholar] [CrossRef]
- Shung, K.W. Dielectric function and plasmon structure of stage-1 intercalated graphite. Phys. Rev. B 1986, 34, 979. [Google Scholar] [CrossRef]
- Purcell, E.M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 1946, 69, 681. [Google Scholar]
- Joulain, K.; Carminati, R.; Mulet, J.P.; Greffet, J.J. Definition and measurement of the local density of electromagnetic states close to an interface. Phys. Rev. B 2003, 68, 245405. [Google Scholar] [CrossRef] [Green Version]
- Lunnemann, P.; Koenderink, A.F. The local density of optical states of a metasurface. Sci. Rep. 2016, 6, 20655. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jander, S.; Kornowski, A.; Weller, H. Energy transfer from CdSe/CdS Nanorods to amorphous carbon. Nano Lett. 2011, 11, 5179–5183. [Google Scholar] [CrossRef] [PubMed]
- Low, T.; Avouris, P. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banerjee, A.; Grebel, H. Nonlinear behavior of vibrating molecules on suspended graphene waveguides. Opt. Lett. 2013, 38, 226–228. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, A.; Grebel, H. Depositing graphene films on solid and perforated. Substr. Nanotechnol. 2008, 19, 365303. [Google Scholar] [CrossRef]
- Li, R.; Banerjee, A.; Grebel, H. The possibility for surface plasmons lasers. Opt. Exp. 2009, 17, 1622–1627. [Google Scholar] [CrossRef]
- Perrin, M.F.; de Fluorescence, P.L. Vie moyenne de molecules dans l’etat excite. J. Phys. Radium 1926, 7, 390–401. [Google Scholar] [CrossRef]
- Paraskevaidis, C.; Kuykendall, T.; Melli, M.; Weber-Bargioni, A.; Schuck, P.J.; Schwartzberg, A.; Dhuey, S.; Cabrini, S.; Grebel, H. Gain and raman line-broadening with graphene coated diamond-shape nano-antennas. Nanoscale 2015, 7, 15321–15331. [Google Scholar] [CrossRef] [PubMed]
- Grebel, H.; Stan, L.; Sumant, A.V.; Liu, Y.; Gosztola, D.; Ocola, L.; Fisher, B. Transfer of graphene with protective oxide layers. Chem. Eng. 2018, 2, 58. [Google Scholar] [CrossRef] [Green Version]
- Gaigalas, A.K.; DeRose, P.; Wang, L.; Zhang, Y.-Z. Optical properties of CdSe/ZnS Nanocrystals. J. Res. Natl. Inst. Stand. Technol. 2014, 119, 610. [Google Scholar] [CrossRef]
- Gromova, Y.; Alaferdov, A.; Rackauskas, S.; Ermakov, V.; Orlova, A.; Maslov, V.; Moshkalev, S.; Baranov, A.; Fedorov, A. Photoinduced electrical response in quantum dots/graphene hybrid structure. J. Appl. Phys. 2015, 118, 104305. [Google Scholar] [CrossRef]
- Li, M.; Zhang, T.; Wang, P.; Li, M.; Wang, J.; Liu, Z. Temperature characteristics of a pressure sensor based on BN/graphene/BN heterostructure. Sensors 2019, 19, 2223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Linh, D.K.; Khánh, N.Q. Electrical conductivity of bilayer-graphene double layers at finite temperature. Superlattices Microstruct. 2018, 114, 406–415. [Google Scholar] [CrossRef]
- Miao, X.; Trivedi, S.; Grebel, H. Electrical and photo-induced effects in graphene channels when interfaced with quantum dots. MRS Online Proc. Libr. Arch 2015, mrsf14-1727-k05-08. [Google Scholar] [CrossRef]
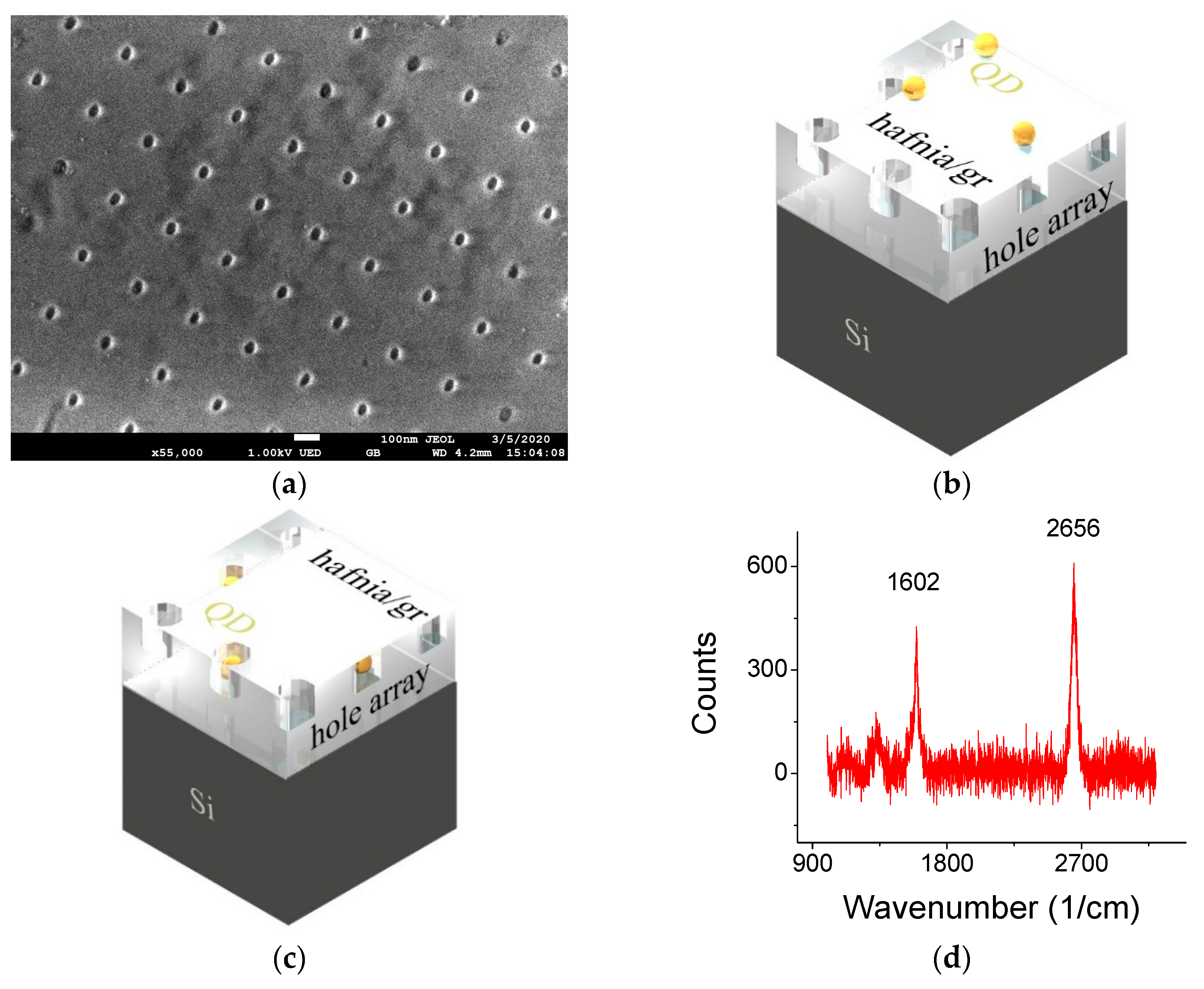

| Sample | QD Deposition Method | Placement of QD | Concentration | Spacer/Top Coat |
|---|---|---|---|---|
| S2 | spin | in holes | High | no/PMMA |
| S7 | dip | on spacer | High | yes/no |
| S8 | spin | in holes | Low | yes/no |
| S9 | spin | on spacer | Low | yes/no |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, X.; Gosztola, D.J.; Ma, X.; Czaplewski, D.; Stan, L.; Grebel, H. The Effect of Periodic Spatial Perturbations on the Emission Rates of Quantum Dots near Graphene Platforms. Materials 2020, 13, 3504. https://doi.org/10.3390/ma13163504
Miao X, Gosztola DJ, Ma X, Czaplewski D, Stan L, Grebel H. The Effect of Periodic Spatial Perturbations on the Emission Rates of Quantum Dots near Graphene Platforms. Materials. 2020; 13(16):3504. https://doi.org/10.3390/ma13163504
Chicago/Turabian StyleMiao, Xin, David J. Gosztola, Xuedan Ma, David Czaplewski, Liliana Stan, and Haim Grebel. 2020. "The Effect of Periodic Spatial Perturbations on the Emission Rates of Quantum Dots near Graphene Platforms" Materials 13, no. 16: 3504. https://doi.org/10.3390/ma13163504
APA StyleMiao, X., Gosztola, D. J., Ma, X., Czaplewski, D., Stan, L., & Grebel, H. (2020). The Effect of Periodic Spatial Perturbations on the Emission Rates of Quantum Dots near Graphene Platforms. Materials, 13(16), 3504. https://doi.org/10.3390/ma13163504