Experimental Analysis of the Function of a Window with a Phase Change Heat Accumulator
Abstract
:1. Introduction
- Incorrect selection of PCMs used in the application location in question;
- Unsealing forms moulds with PCMs applied;
- Change of physicochemical properties of PCMs after many phase transformation cycles;
- Insufficient ability of solid-state PCMs to conduct heat.
2. Materials and Methods
2.1. Materials
- 2 mm thick aluminum sheet, covered with matt black paint.
2.2. Apparatus
- Almemo 2890-9 recorder, company Ahlborn, Ilmenau, Germany;
- Pt1000 temperature sensor, company Salus, Kobielice, Poland;
- Heat flux density sensor: FQA020C, company Ahlborn, Ilmenau, Germany;
- LT 019008 thermocouple, company Ahlborn, Ilmenau, Germany;
- Almemo FLA 613 GS pyranometer, company Ahlborn, Ilmenau, Germany.
2.3. Resarch Method
2.4. Experimental Tests
2.5. Mathematical Model
3. Results
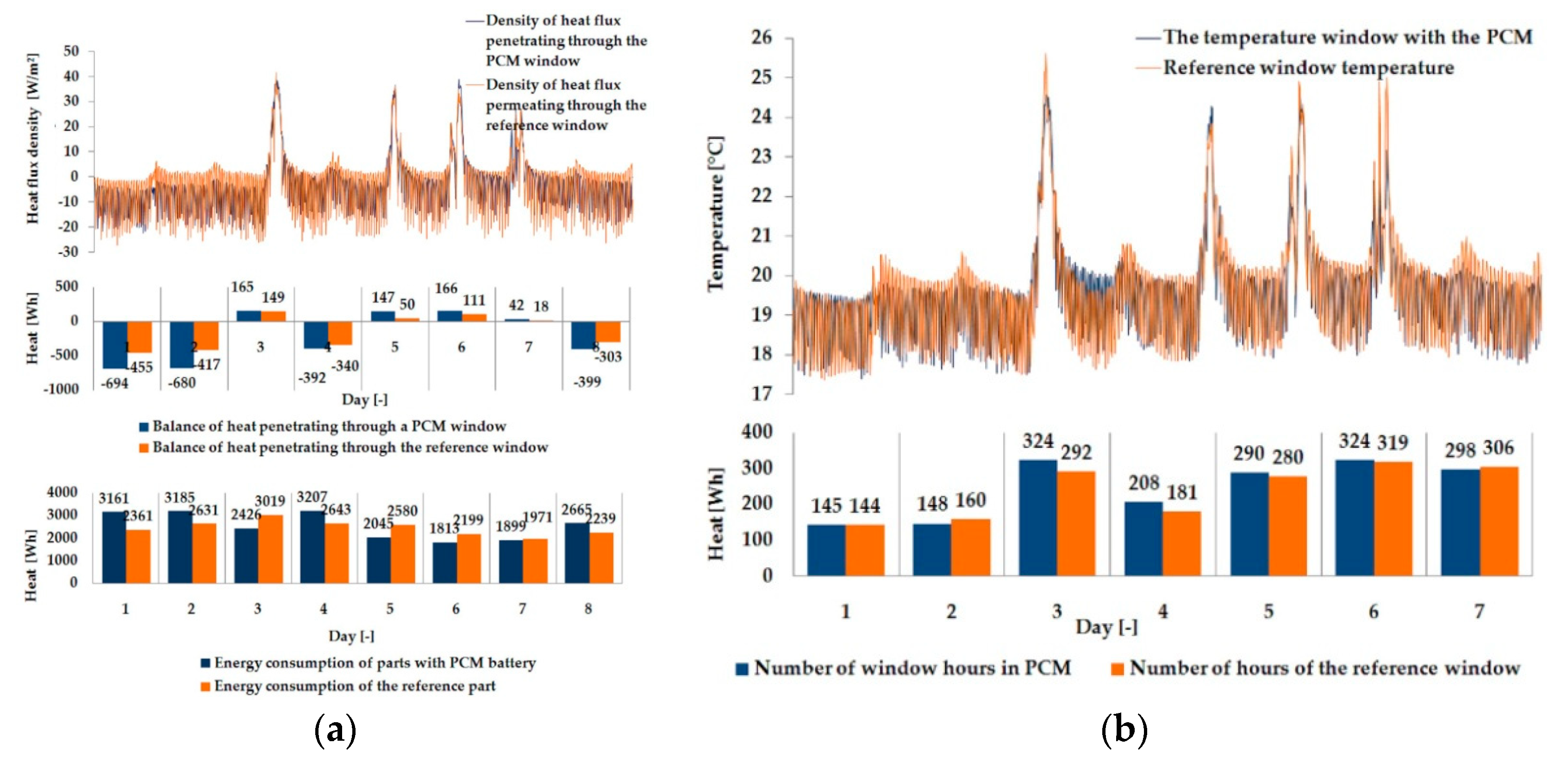
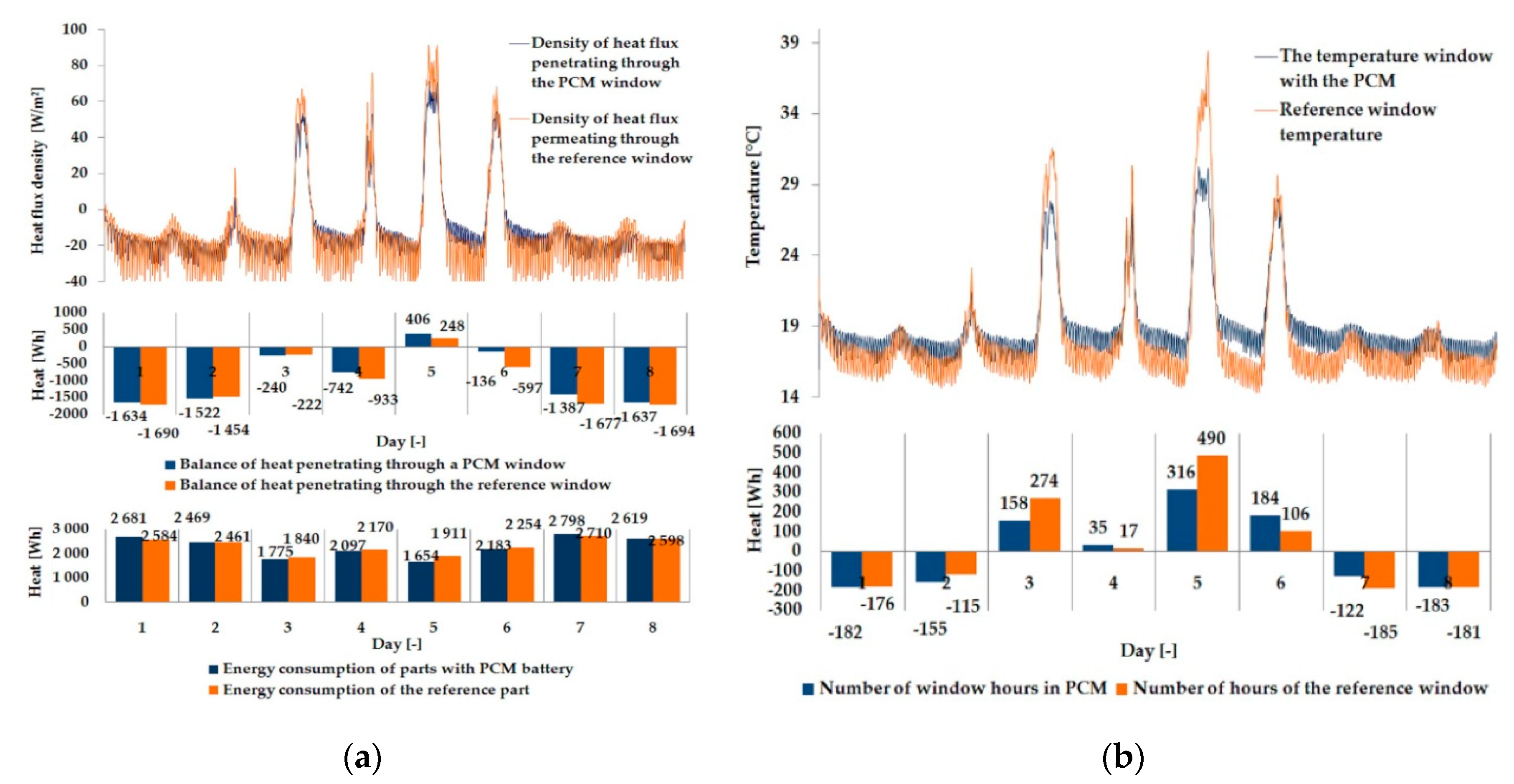
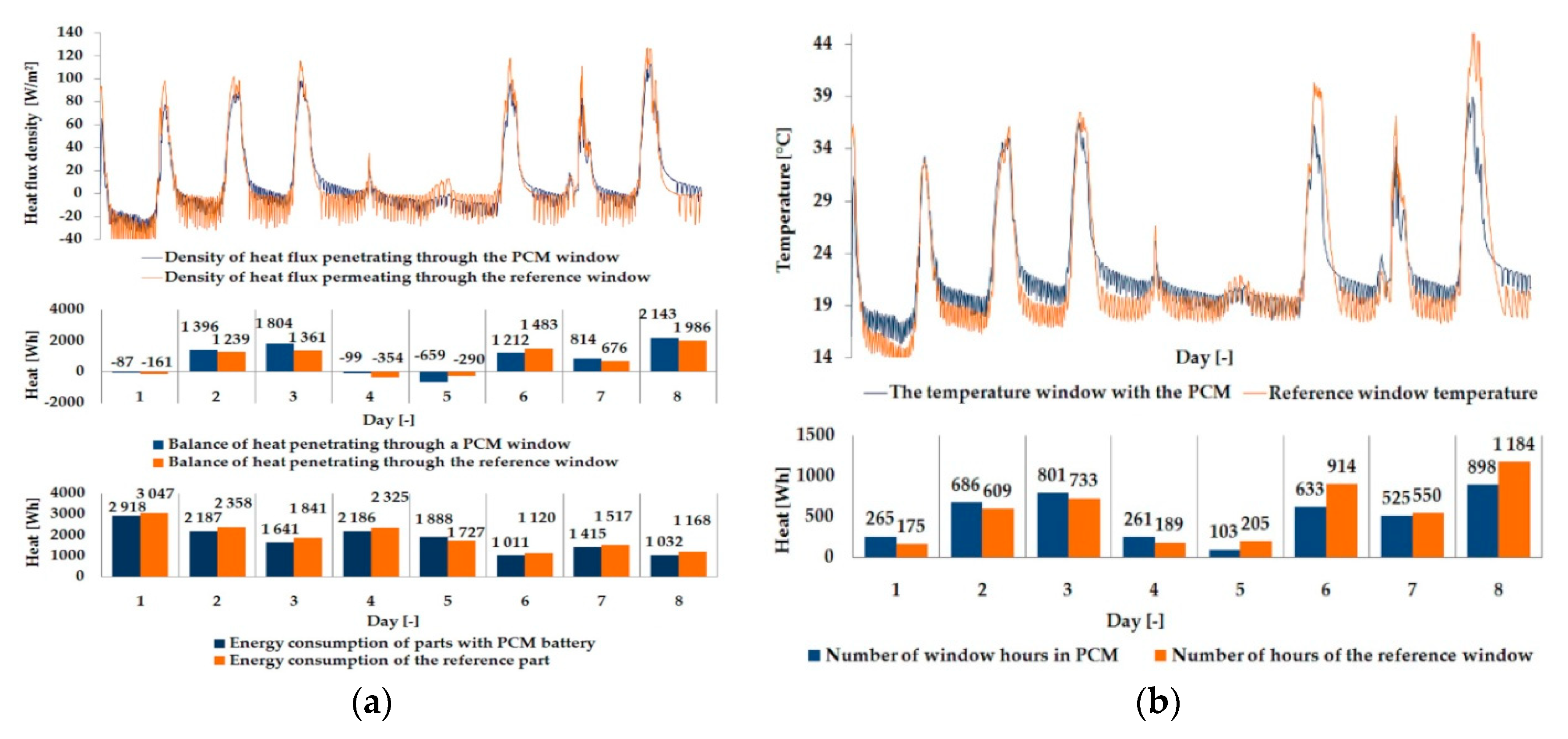
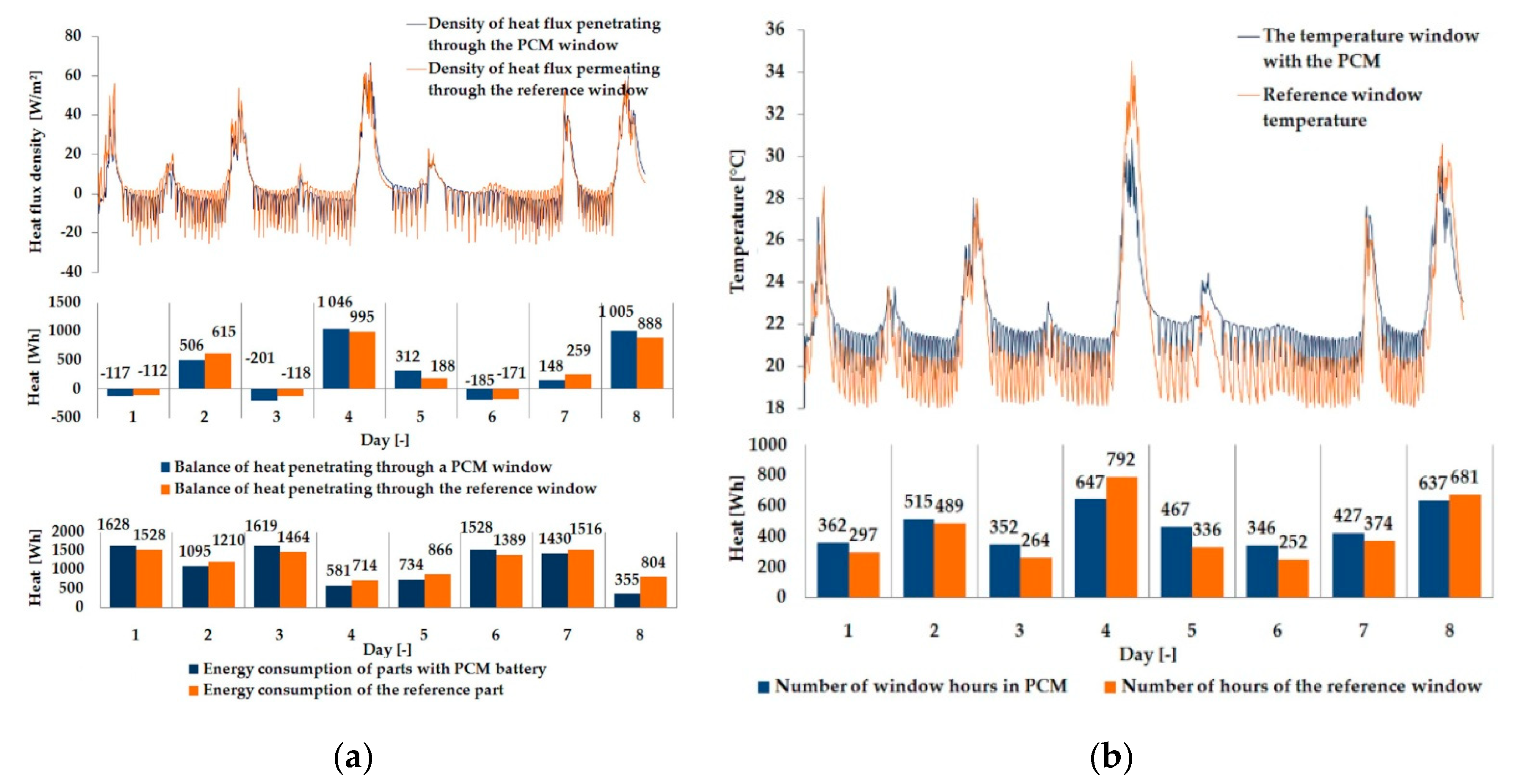
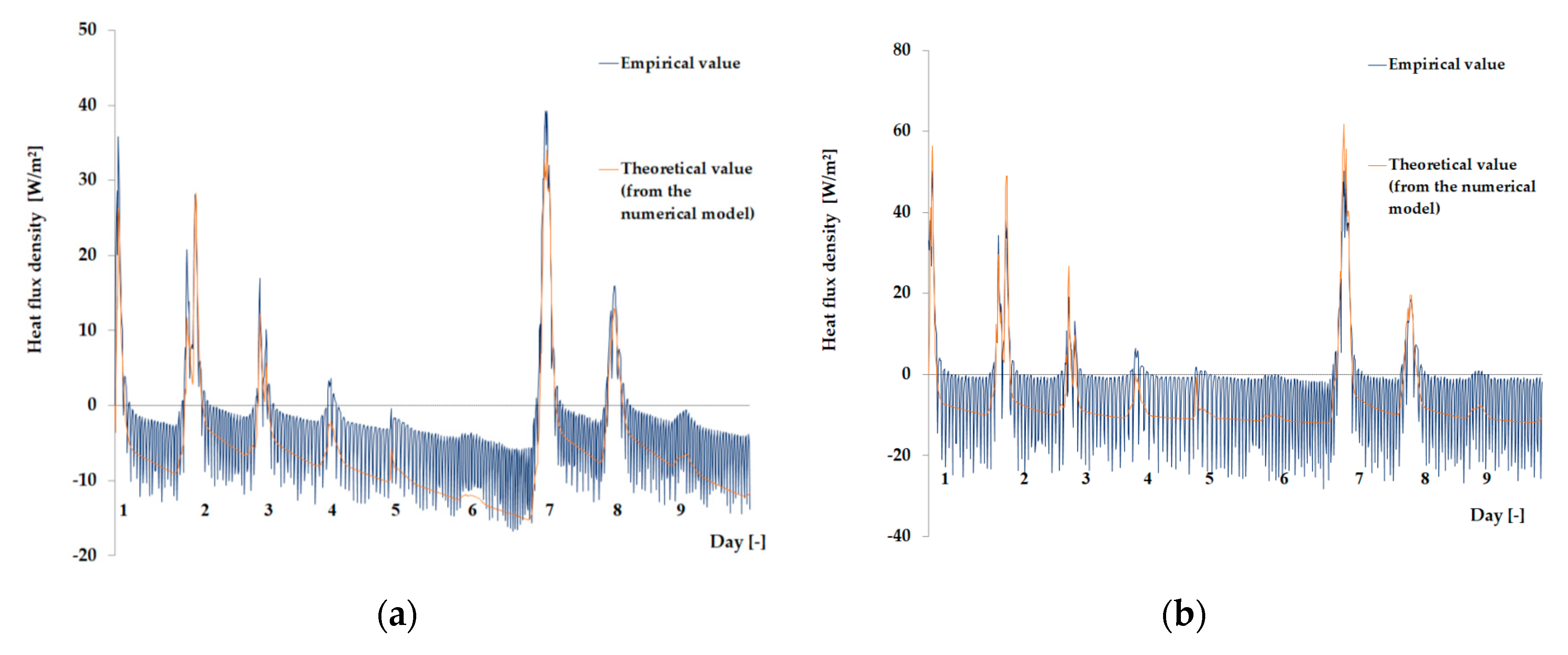
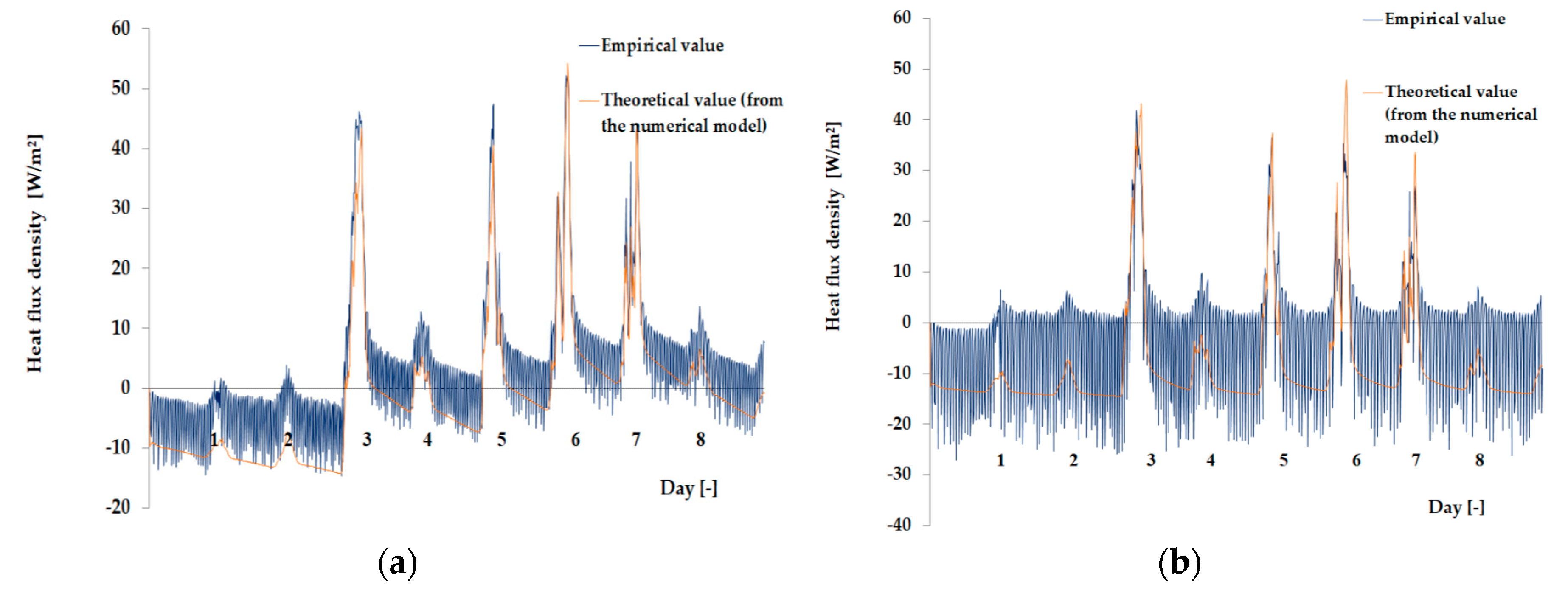
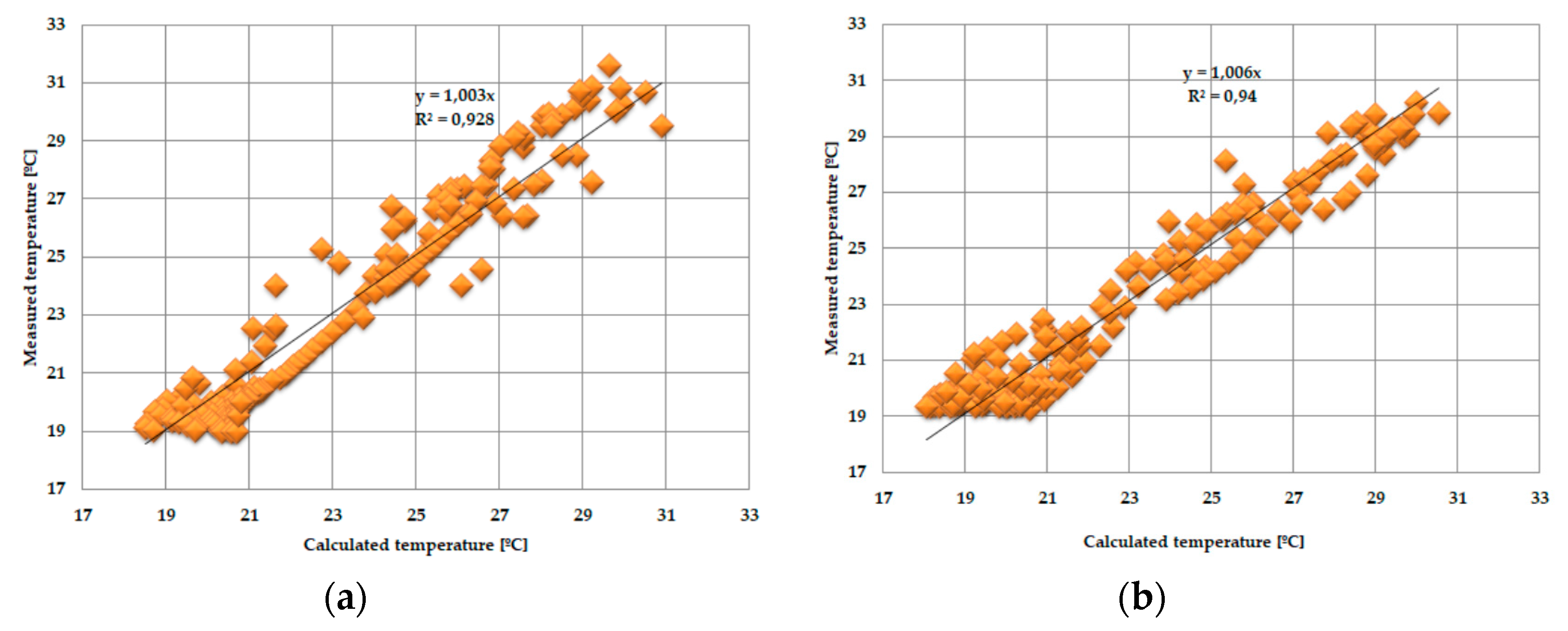
3.1. Experimental Results
3.2. Results of the Mathematical Simulation
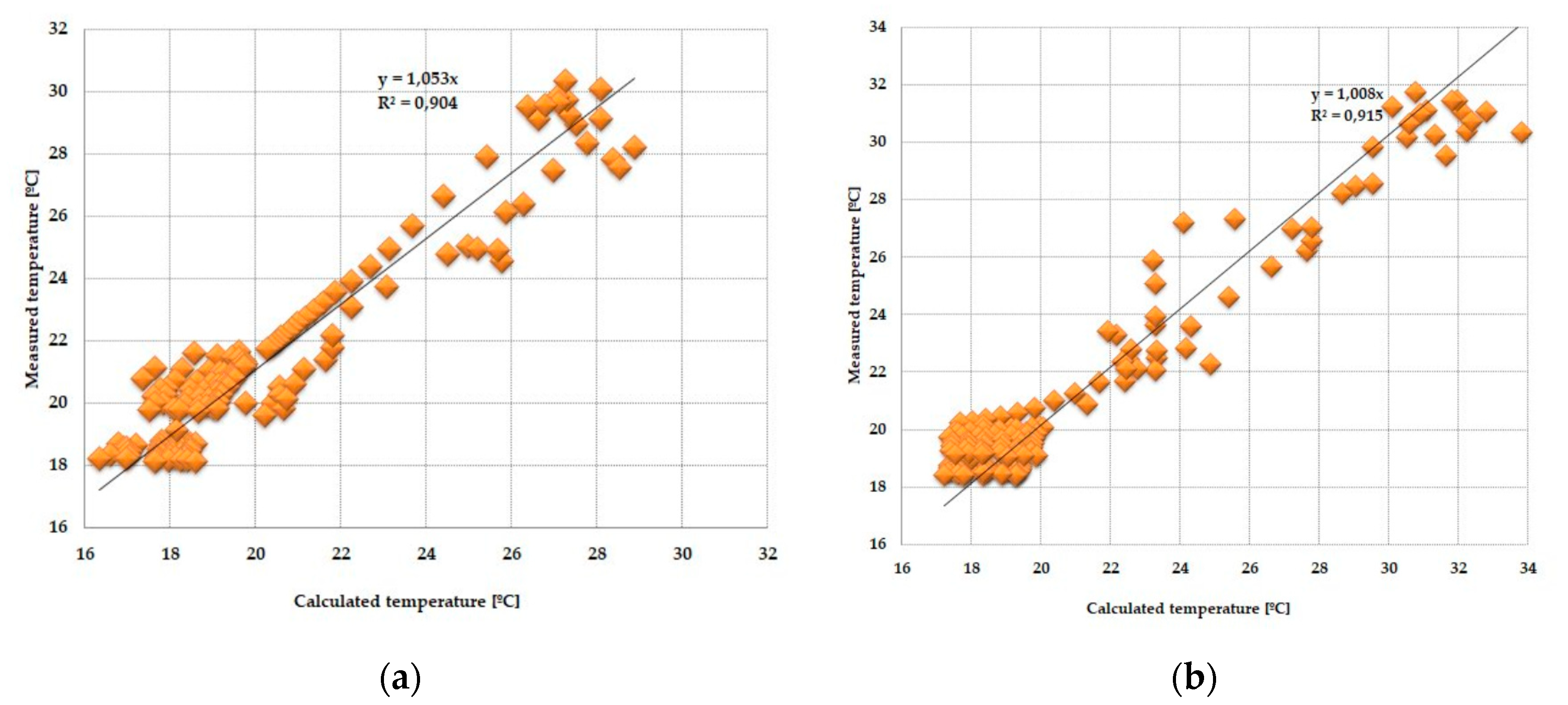
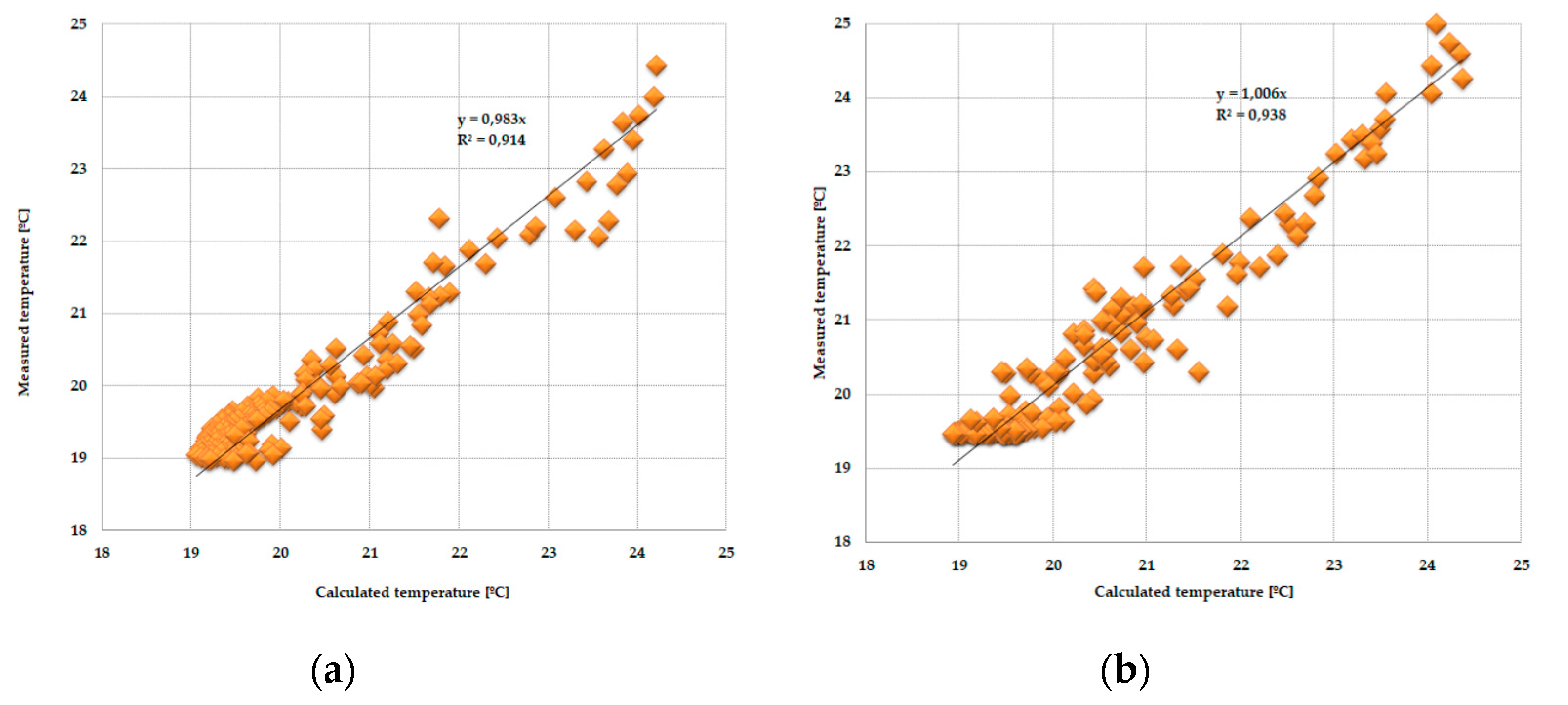
3.3. Statistical Analysis
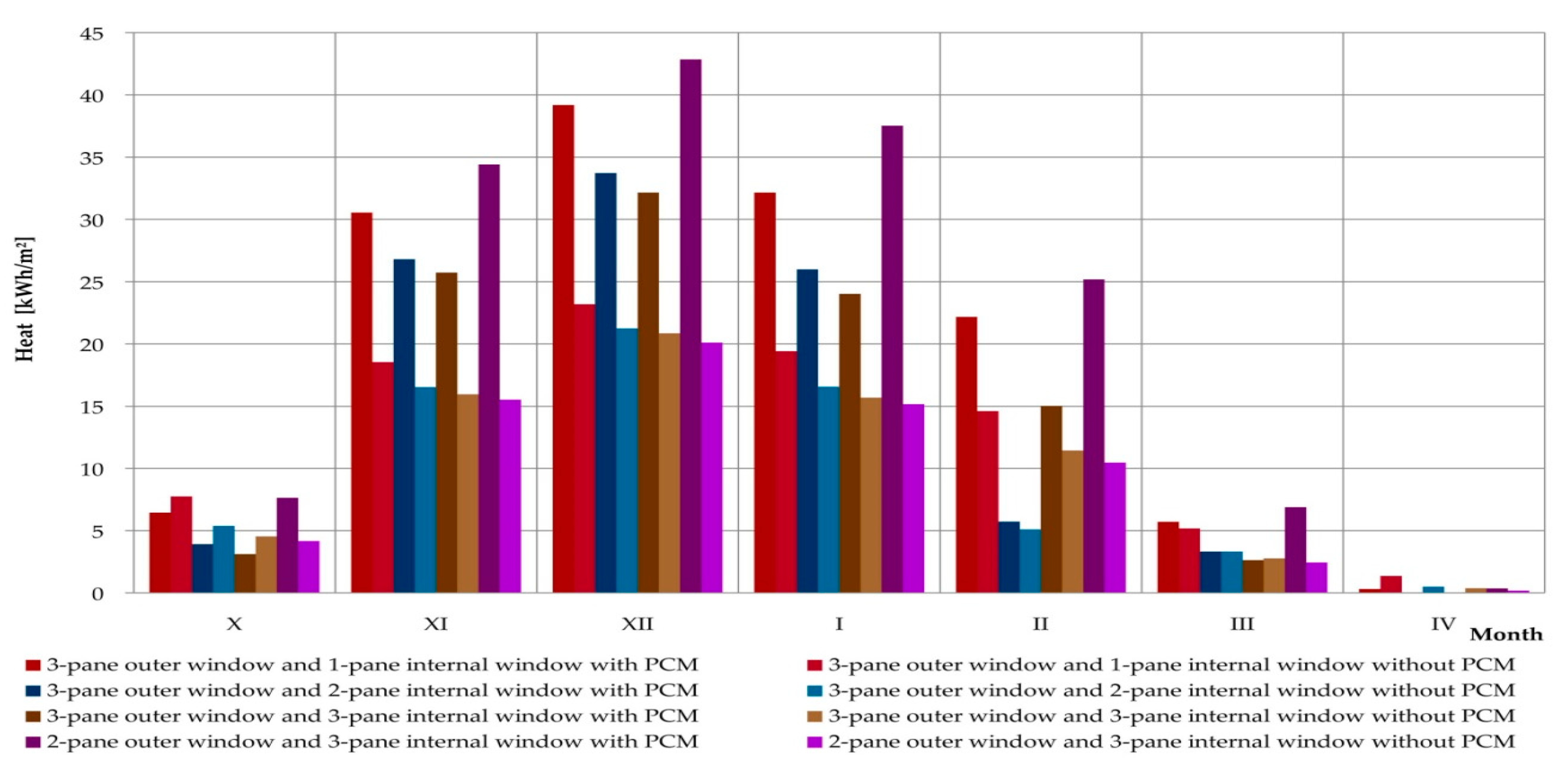
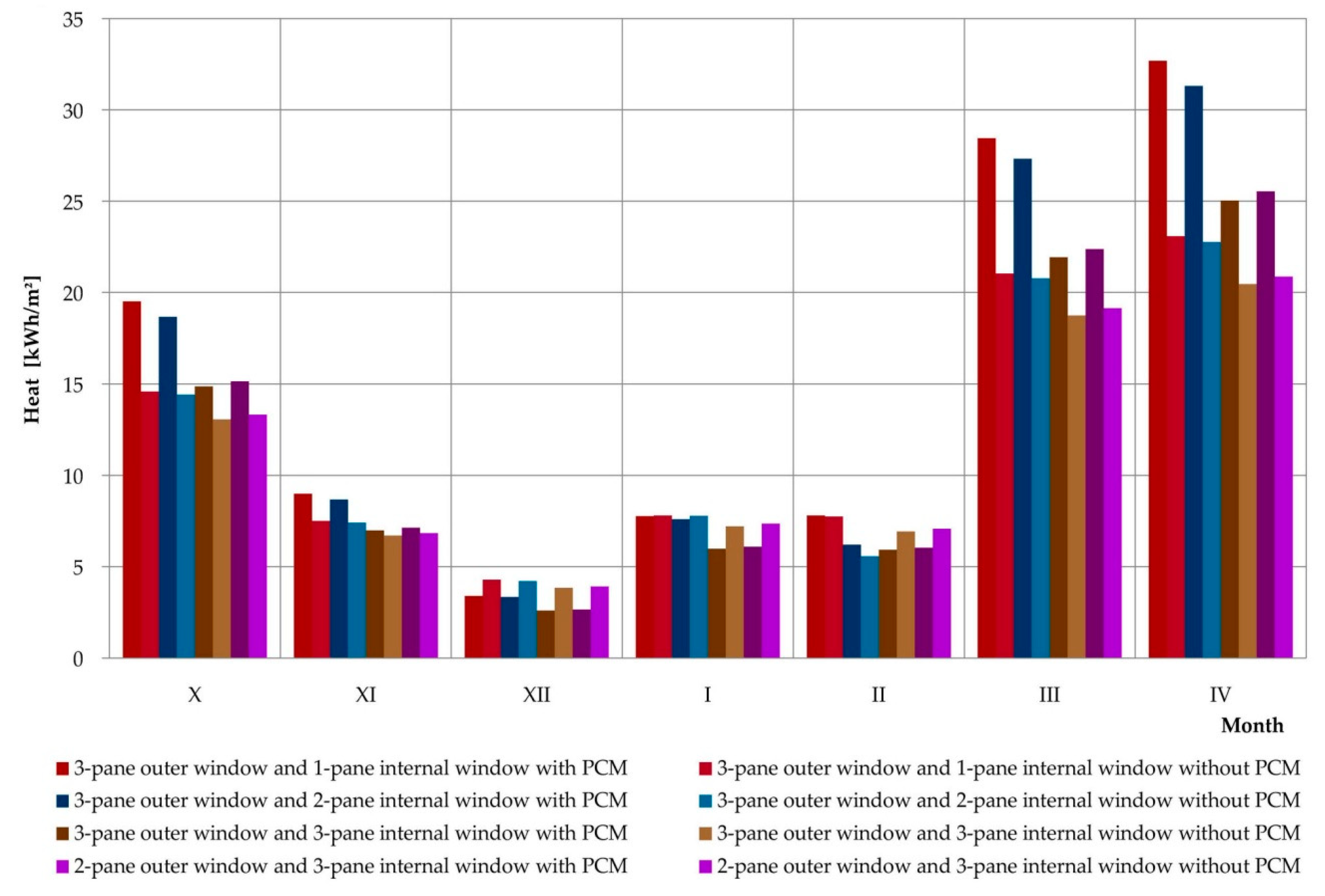
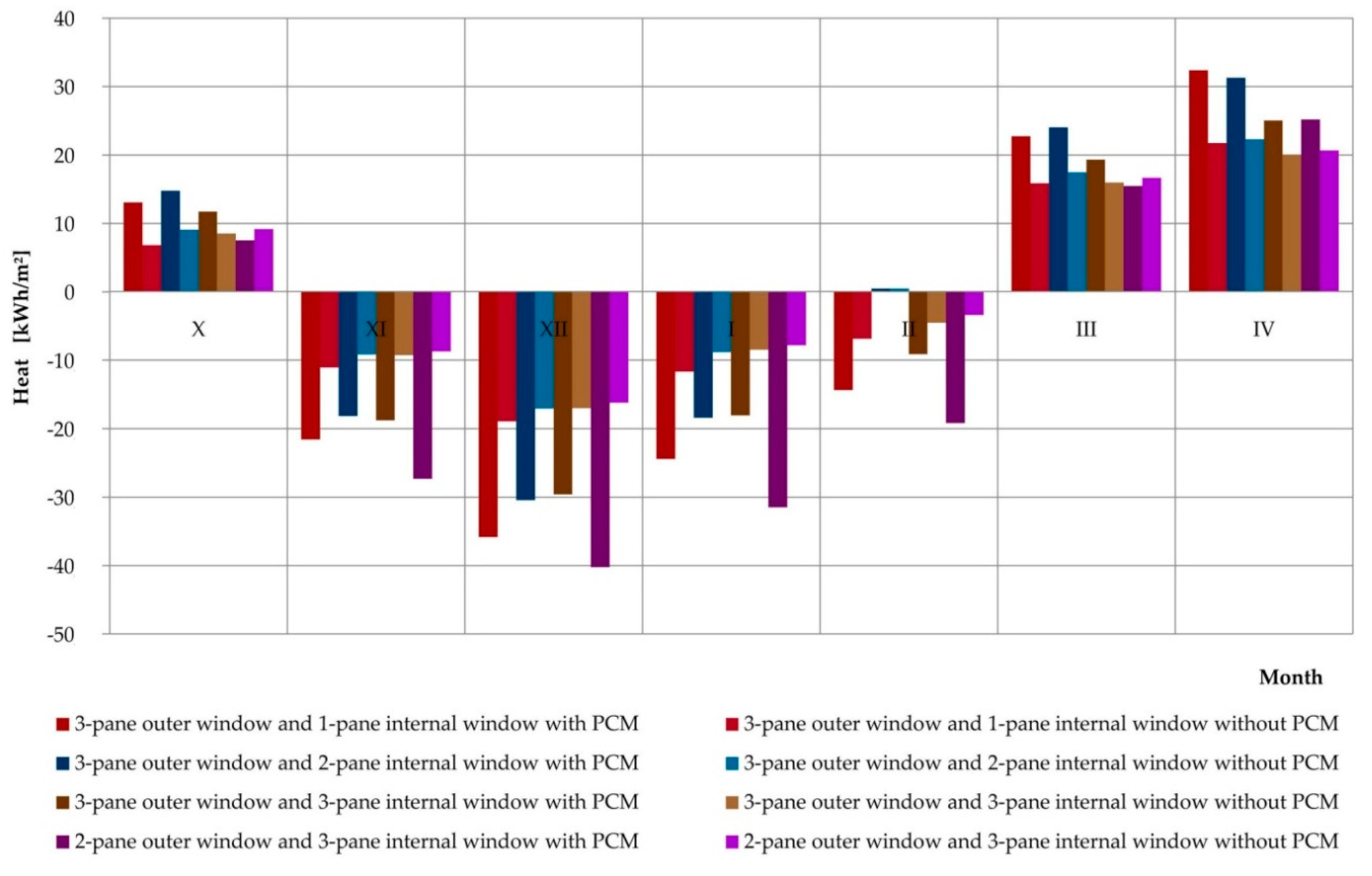
3.4. Simulations of the Operation of a Composite Window with a Phase Change Heat Accumulator for Data of a Typical Meteorological Year in Rzeszów
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jachimowicz, L. Xenophon Socratic Letters. Memories of Socrates; Translation from the Greek original; Polish scientific publisher: Warsaw, Poland, 1967; pp. 22–78. (In Polish) [Google Scholar]
- Wehle-Strzelecka, S. Development of solar energy gaining concept in architectural and urban solutions: First generation of solar architecture. Tech. Transac. Arch. 2008, 7, 149–185. (In Polish) [Google Scholar]
- Czarnecki, L.; Kaproń, M.; Piasecki, M.; Wall, S. Sustainable construction means construction of future. Eng. Const. 2012, 68, 18–21. (In Polish) [Google Scholar]
- Pawłowski, A.; Pawłowski, L. Sustainable Development in Contemporary Civilisation. Part 1: The Environment and Sustainable Development. Prob. Sustainab. Develop. 2008, 3, 53–65. (In Polish) [Google Scholar]
- Pos. 926 Amending the Regulation on the Technical Conditions to be Met by Buildings and Their Location; Regulation of the Minister of Transport, Construction and Maritime Economy: Warsaw, Poland, 2013. (In Polish)
- Smolec, W. Photothermal Solar Energy Conversion; Polish Scientific Publisher: Warsaw, Poland, 2000. (In Polish) [Google Scholar]
- Chwieduk, D. Solar Energy Building; Arkady: Warsaw, Poland, 2011. (In Polish) [Google Scholar]
- Klemm, P. General Construction 2. Building Physics; Arkady: Warsaw, Poland, 2005. (In Polish) [Google Scholar]
- Dylla, A. Buildings’ Thermal Physics in Practice; Polish scientific publisher: Warsaw, Poland, 2015. (In Polish) [Google Scholar]
- Chwieduk, D.; Jaworski, M. Renewable Energy in Construction. Heat Storage; Polish scientific publisher: Warsaw, Poland, 2018. (In Polish) [Google Scholar]
- Vogel, A.I. Organic Preparation; Polish scientific publisher: Warsaw, Poland, 2006. (In Polish) [Google Scholar]
- Busico, V.; Cafagna, C.; Salerno, V.; Vacatello, M.; Fittipaldi, F. The layer perovskites as thermal energy storage systems. Sol. Energy 1980, 24, 575. [Google Scholar] [CrossRef]
- Benson, D.K.; Burrows, R.W.; Webb, J.B. Solid state phase transitions in pentaerythriol and related polyhydric alcohols. Sol. Energy Mater. 1986, 13, 133–152. [Google Scholar] [CrossRef]
- Memon, S.A. Phase change materials integrated in building walls: A state of the art review. Renew. Sustain. Energy Rev. 2014, 31, 870–906. [Google Scholar] [CrossRef]
- Zalba, B.; Marın, J.M.; Cabeza, L.F.; Mehling, H. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications. Appl. Therm. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Farid, M.; Khudhair, A.M.; Razack, S.A.K.; Al-Hallaj, S. A review on phase change energy storage: Materials and applications. Energy Convers. Manag. 2004, 45, 1597–1615. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, C.; Tian, Y. Review on thermal energy storage with phase change materials (PCMs) in building applications. Appl. Energy 2012, 92, 593–605. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Ubinas, E.; Valero, L.R.; Vega, S.; Neila, J. Applications of Phase Change Material in highly energy-efficient houses. Energy Build. 2012, 50, 49–62. [Google Scholar] [CrossRef]
- Lichołai, L.; Musiał, M. Useof copolymers of vinyl acetate and alkyl acrylates for coating organic phase change materials. Przem. Chem. 2018, 97, 1852. [Google Scholar] [CrossRef]
- Pigoń, K.; Ruzewicz, Z. Physical Chemistry Part 1; Polish scientific publisher: Warsaw, Poland, 1993. (In Polish) [Google Scholar]
- Lane, G.A. Solar Heat Storage; Latent Heat Materials; CRC Press: Boca Raton, FL, USA, 1983. [Google Scholar] [CrossRef]
- Schröder, J.; Gawron, K. Latent Heat Storage. Int. J. Energy Res. 1981, 5, 103. [Google Scholar] [CrossRef]
- Tyagi, V.; Buddhi, D. PCM thermal storage in buildings: A state of art. Renew. Sustain. Energy Rev. 2007, 11, 1146–1166. [Google Scholar] [CrossRef]
- Kenisarin, M.; Mahkamov, K. Solar energy storage using phase change materials. Renew. Sustain. Energy Rev. 2007, 11, 1913–1965. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, G.; Lin, K.; Zhang, Q.; Di, H. Application of latent heat thermal energy storage in buildings: State-of-the-art and outlook. Build. Environ. 2007, 42, 2197–2209. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.; Chen, C.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Musiał, M. Use of organic aliphatic esters to obtain an energy-efficient eutectic mixture. Przem. Chem. 2018, 97, 1855. [Google Scholar] [CrossRef]
- Musiał, M. Phase-Change Material and Method of Producing Phase-Change Material. PL Patent Application No. P.425,190, 12 April 2018. [Google Scholar]
- Dalenbäck, J.O.; Tech, L. The Säro Projekt: A solar heating plant with seasonal storage. In Energy Conservation in Buildings; University of Reading: Reading, UK, 1990; pp. 254–259. [Google Scholar] [CrossRef]
- Bankston, C.A. The Status and Potential of Central Solar Heating Plants with Seasonal Storage; American Solar Energy Society: Boulder, CO, USA, 1986. [Google Scholar]
- Lin, W.; Huang, R.; Fang, X.; Zhang, Z. Improvement of thermal performance of novel heat exchanger with latent heat storage. Int. J. Heat Mass Transf. 2019, 140, 877–885. [Google Scholar] [CrossRef]
- Ardahaie, S.S.; Hosseini, M.; Ranjbar, A.; Rahimi, M. Energy storage in latent heat storage of a solar thermal system using a novel flat spiral tube heat exchanger. Appl. Therm. Eng. 2019, 159, 113900. [Google Scholar] [CrossRef]
- Taler, D.; Dzierwa, P.; Trojan, M.; Sacharczuk, J.; Kaczmarski, K.; Taler, J. Numerical modeling of transient heat transfer in heat storage unit with channel structure. Appl. Therm. Eng. 2019, 149, 841–853. [Google Scholar] [CrossRef]
- Soares, N.; Costa, J.J.; Gaspar, A.R.; Santos, P. Review of passive PCM latent heat thermal energy storage systems towards building’s energy efficiency. Energy Build. 2013, 59, 82–103. [Google Scholar] [CrossRef]
- Vigna, I.; Bianco, L.; Goia, F.; Serra, V. Phase Change Materials in Transparent Building Envelopes: A Strengths, Weakness, Opportunities and Threats (SWOT) Analysis. Energies 2018, 11, 111. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Heiselberg, P.K. A new ventilated window with PCM heat exchanger—Performance analysis and design optimization. Energy Build. 2018, 169, 185–194. [Google Scholar] [CrossRef]
- Weinläder, H.; Beck, A.; Fricke, J. PCM-facade-panel for daylighting and room heating. Sol. Energy 2005, 78, 177–186. [Google Scholar] [CrossRef]
- Li, S.; Zou, K.; Sun, G.; Zhang, X. Simulation research on the dynamic thermal performance of a novel triple-glazed window filled with PCM. Sustain. Cities Soc. 2018, 40, 266–273. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Liu, C.; Zhang, G.; Arıcı, M. Numerical investigation of thermal and optical performance of window units filled with nanoparticle enhanced PCM. Int. J. Heat Mass Transf. 2018, 125, 1321–1332. [Google Scholar] [CrossRef]
- Musiał, M. Analysis of the impact of selected factors on the effectiveness of using PCM in mobile window insulation. E3S Web Conf. 2018, 49, 00073. [Google Scholar] [CrossRef] [Green Version]
- Musiał, M. Evaluation of the energy efficiency of an internal blind containing PCM. E3S Web Conf. 2018, 49, 00074. [Google Scholar] [CrossRef] [Green Version]
- Lichołai, L.; Musiał, M.; Szyszka, J. International Patent Application. PL Patent Application No. P.15461528.0, 4 May 2015. [Google Scholar]
- Mehling, H. Strategic project ‘Innovative PCM-Technology’—Results and future perspectives. In Proceedings of the 8th Expert Meeting and Workshop, Kizkalesi, Turkey, 18–25 April 2005; pp. 18–20. [Google Scholar]
- Weinlaeder, H.; Koerner, W.; Heidenfelder, M. Monitoring results of an interior sun protection system with integrated latent heat storage. Energy Build. 2011, 43, 2468–2475. [Google Scholar] [CrossRef]
- Li, Y.; Darkwa, J.; Kokogiannakis, G.; Su, W. Phase change material blind system for double skin façade integration: System development and thermal performance evaluation. Appl. Energy 2019, 252, 113376. [Google Scholar] [CrossRef]
- Bontemps, A.; Ahmad, M.; Johannes, K.; Sallee, H. Experimental and modelling study of twin cells with latent heat storage walls. Energy Build. 2011, 43, 2456–2461. [Google Scholar] [CrossRef]
- Jaworski, M.; Abeid, S. Thermal conductivity of gypsum with incorporated phase change material (PCM) for building applications. J. Power Technol. 2011, 91, 49–53. [Google Scholar]
- Wnuk, R.; Jaworski, M. Investigation of thermal characteristics of heat accumulating building elements containing PCM (phase change materials). Polish Solar Energy 2010, 2, 5–11. (In Polish) [Google Scholar]
- Cabeza, L.F.; Castellón, C.; Nogués, M.; Medrano, M.; Leppers, R.; Zubillaga, O. Use of microencapsulated PCM in concrete walls for energy savings. Energy Build. 2007, 39, 113–119. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Medrano, M.; Castellón, C.; Castell, A.; Solé, C.; Roca, J.; Nogués, M. Thermal energy storage with phase change materials in building envelopes. Contrib. Sci. 2007, 3, 501–510. [Google Scholar] [CrossRef]
- Zhu, N.; Wang, S.; Xu, X.; Ma, Z. A simplified dynamic model of building structures integrated with shaped-stabilized phase change materials. Int. J. Therm. Sci. 2010, 49, 1722–1731. [Google Scholar] [CrossRef]
- Xiao, M.; Feng, B.; Gong, K. Preparation and performance of shape stabilized phase change thermal storage materials with high thermal conductivity. Energy Convers. Manag. 2002, 43, 103–108. [Google Scholar] [CrossRef]
- Sarı, A. Form-stable paraffin/high density polyethylene composites as solid–liquid phase change material for thermal energy storage: Preparation and thermal properties. Energy Convers. Manag. 2004, 45, 2033–2042. [Google Scholar] [CrossRef]
- Xiao, M.; Feng, B.; Gong, K. Thermal performance of a high conductive shape-stabilized thermal storage material. Sol. Energy Mater. Sol. Cells 2001, 69, 293–296. [Google Scholar] [CrossRef]
- Zhou, G.; Yang, Y.; Xu, H. Energy performance of a hybrid space-cooling system in an office building using SSPCM thermal storage and night ventilation. Sol. Energy 2011, 85, 477–485. [Google Scholar] [CrossRef]
- Musiał, M. Analysis of the impact of PCM elements’ geometry on their heat storage efficiency. Bauphysik 2019, 6, 324–330. [Google Scholar] [CrossRef]
- Charach, C.; Zarmi, Y.; Zemel, A. Simpel Method for Assessing the Thermal Performance of PCM Panels; Biennial Congress of the International Solar Energy Society: Hamburg, Germany, 1987. [Google Scholar] [CrossRef]
- Taler, J.; Duda, P. Solving Simple and Inverse Heat Conduction Problems; Scientific and Technical Publishing House: Warsaw, Poland, 2006. (In Polish) [Google Scholar]
- Zastawna-Rumin, A.; Kisilewicz, T.; Berardi, U. Novel Simulation Algorithm for Modeling the Hysteresis of Phase Change Materials. Energies 2020, 13, 1200. [Google Scholar] [CrossRef] [Green Version]
- Heim, D.; Mrowiec, A.; Prałat, K. Determination of heat conductivity of liquit organic acids by the hot wire method. Chem. Eng. Equipm. 2010, 49, 51–52. (In Polish) [Google Scholar]
- Pogorzelski, J.A. Building Thermal Physics; Polish scientific publisher: Warsaw, Poland, 1976. (In Polish) [Google Scholar]
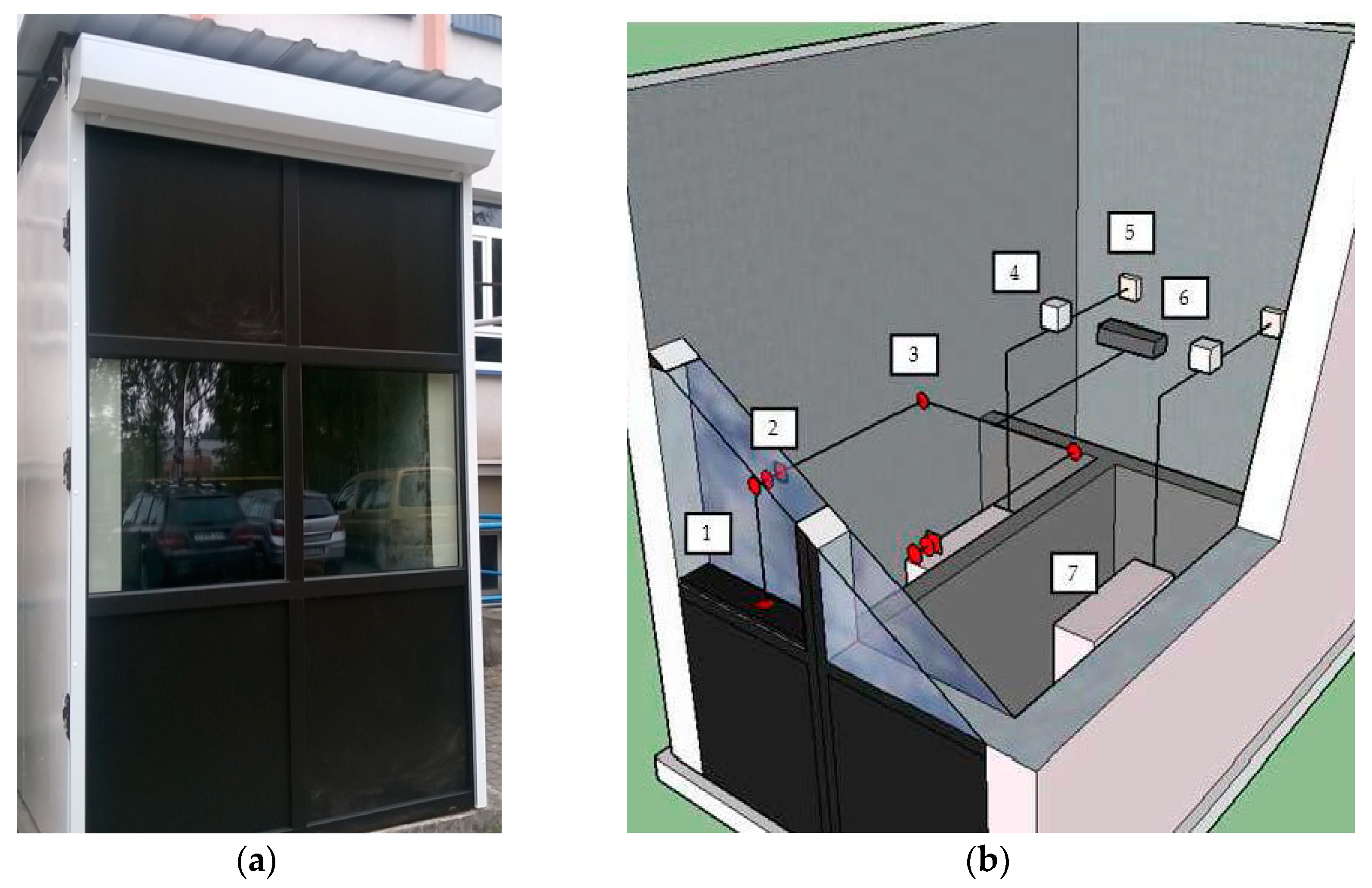
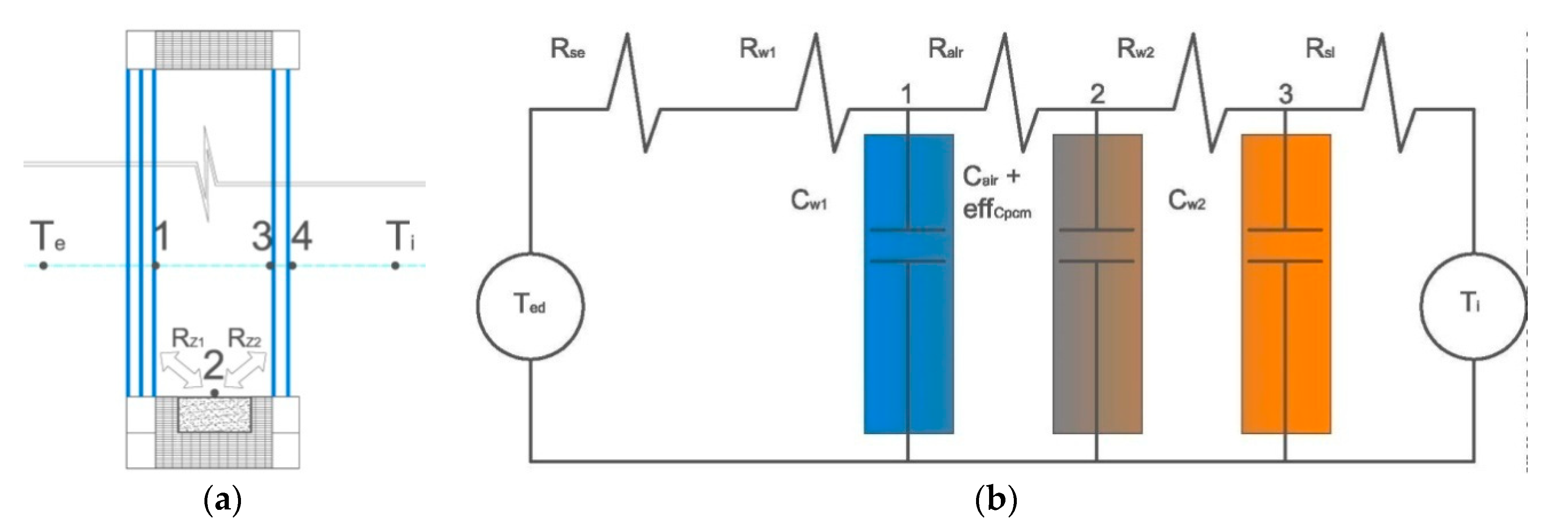
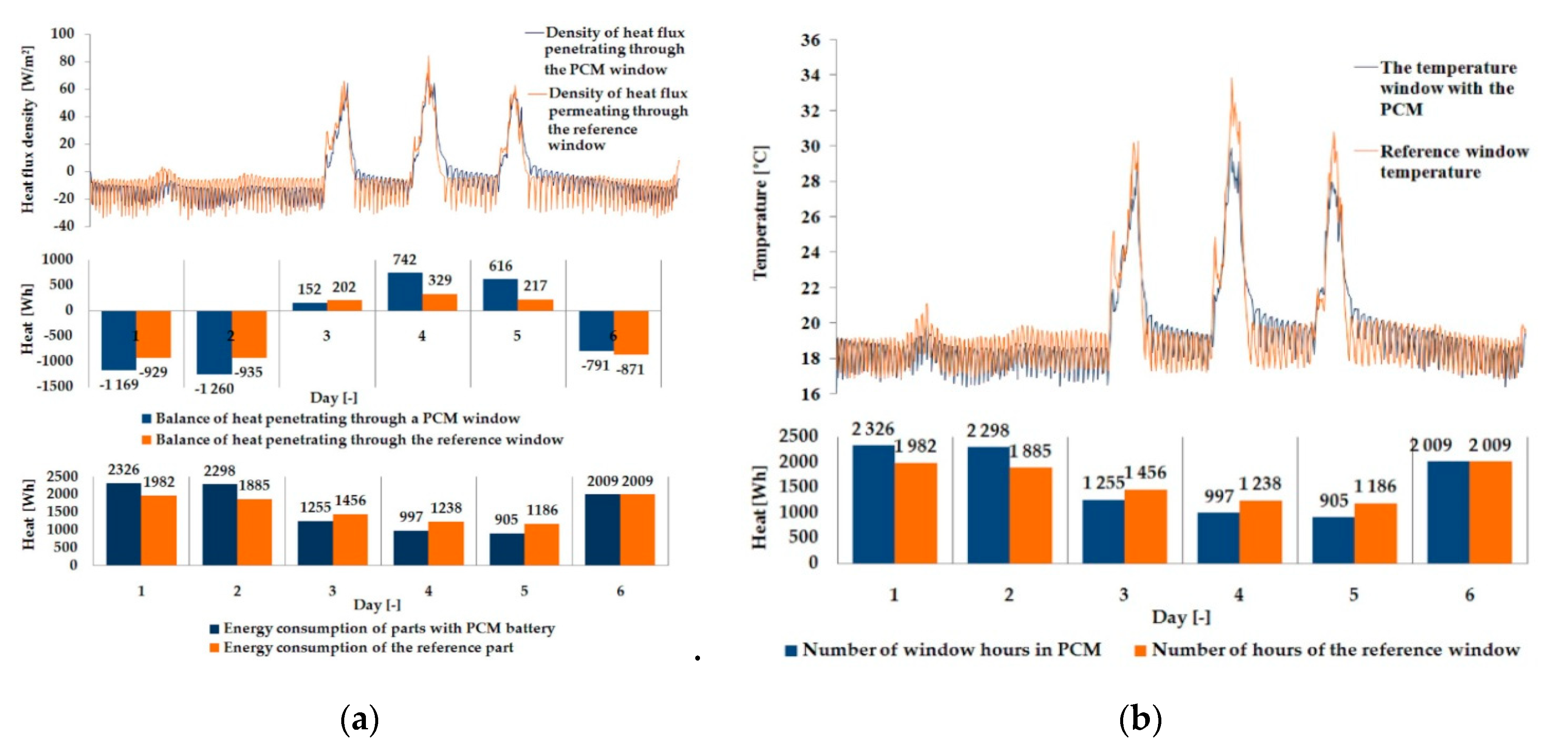
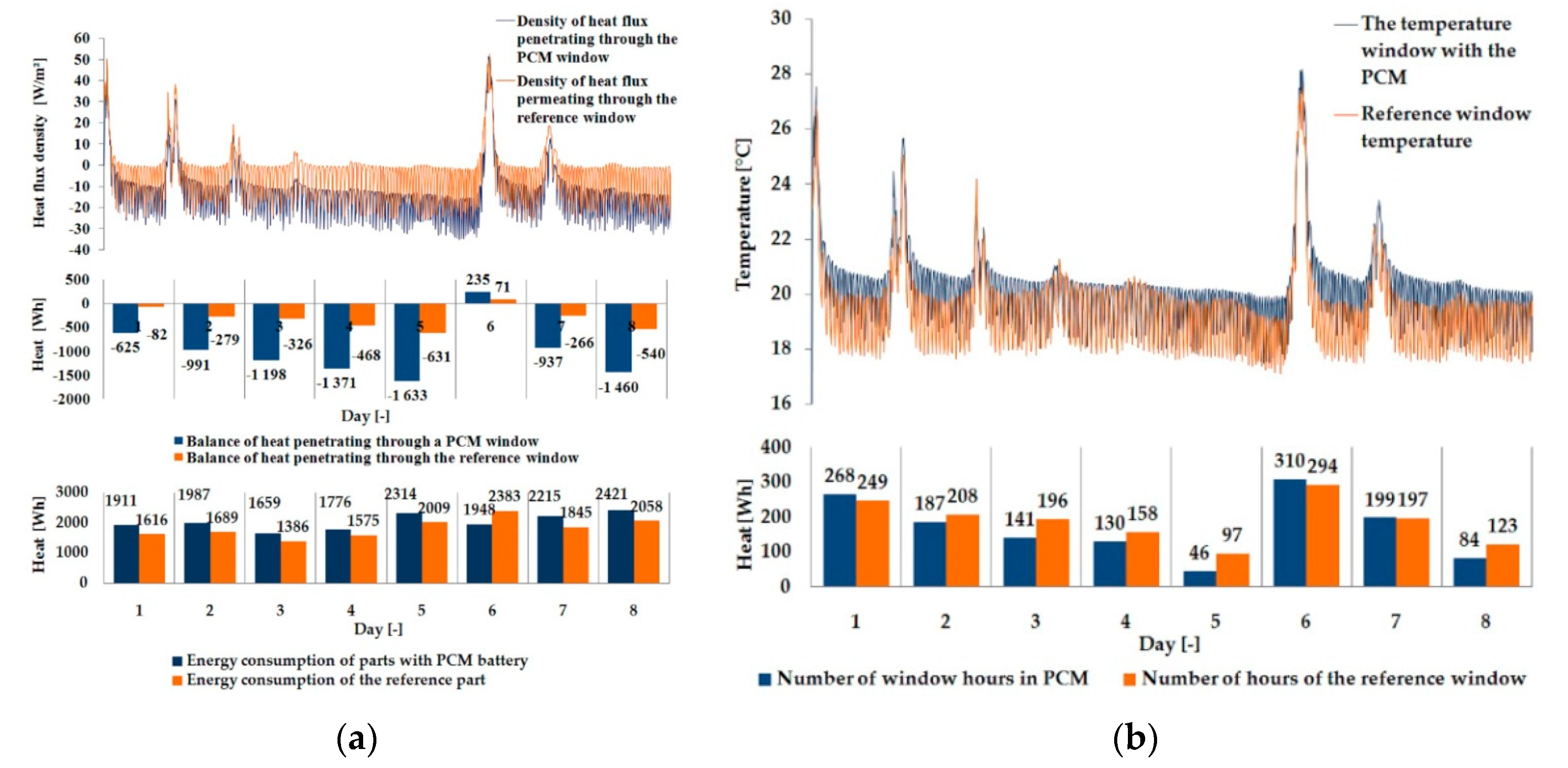






| Parameter | Single Glazing | Double Glazing Unit | Triple Glazing Unit |
|---|---|---|---|
| Heat transfer coefficient (W/m2·K) | 5 | 1.1 | 0.7 |
| Transmittance (-) | 0.82 | 0.75 | 0.5 |
| Light permeability (-) | 0.89 | 0.78 | 0.6 |
| Construction of glazing unit (mm) | /4/ | /4/16 Ar/4/ | /4/16Ar/4/16 Ar/4/ |
| Sets of Glazing Units | Quotient of Variance for PCM Part | Critical Value | Quotient of Variance for the Reference Part | Critical Value |
|---|---|---|---|---|
| FPCM (α,f1,f2) | Fkr | FRef (α,f1,f2) | Fkr | |
| 3–1 | 1.0485 | 1.1100 | 1.0306 | 1.1100 |
| 3–2 | 1.1021 | 1.1100 | 1.0213 | 1.1100 |
| 3–3 | 1.1027 | 1.1100 | 1.0900 | 1.1100 |
| 2–1 | 1.2242 | 1.1100 | 1.0337 | 1.1100 |
| 2–2 | 1.2241 | 1.1100 | 1.1000 | 1.1100 |
| 2–3 | 1.0943 | 1.1100 | 1.0155 | 1.1100 |
| Exterior Window | Triple Glazing Unit | Double Glazing Unit | ||||||
|---|---|---|---|---|---|---|---|---|
| Inner Window | Single Glazing | Double Glazing Unit | Triple Glazing Unit | Triple Glazing Unit | ||||
| Window with PCM | Reference Window | Window with PCM | Reference Window | Window with PCM | Reference Window | Window with PCM | Reference Window | |
| Month | (kWh) | |||||||
| X | 13.06 | 6.82 | 14.73 | 9.03 | 11.71 | 8.510 | 7.49 | 9.13 |
| XI | −21.57 | −11.04 | −18.13 | −9.14 | −18.74 | −9.254 | −27.29 | −8.70 |
| XII | −35.81 | −18.91 | −30.39 | −17.03 | −29.56 | −17.008 | −40.21 | −16.20 |
| I | −24.39 | −11.63 | −18.38 | −8.78 | −18.05 | −8.472 | −31.44 | −7.82 |
| II | −14.37 | −6.87 | 0.46 | 0.47 | −9.11 | −4.524 | −19.15 | −3.40 |
| III | 22.71 | 15.85 | 23.99 | 17.44 | 19.29 | 15.970 | 15.47 | 16.67 |
| IV | 32.36 | 21.72 | 31.26 | 22.26 | 25.02 | 20.073 | 25.17 | 20.67 |
| Sum | −19.45 | 5.30 | 3.55 | 14.25 | −−19.45 | 5.295 | −69.97 | 10.36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lichołai, L.; Musiał, M. Experimental Analysis of the Function of a Window with a Phase Change Heat Accumulator. Materials 2020, 13, 3647. https://doi.org/10.3390/ma13163647
Lichołai L, Musiał M. Experimental Analysis of the Function of a Window with a Phase Change Heat Accumulator. Materials. 2020; 13(16):3647. https://doi.org/10.3390/ma13163647
Chicago/Turabian StyleLichołai, Lech, and Michał Musiał. 2020. "Experimental Analysis of the Function of a Window with a Phase Change Heat Accumulator" Materials 13, no. 16: 3647. https://doi.org/10.3390/ma13163647





