Sound Transmission Loss of a Sandwich Plate with Adjustable Core Layer Thickness
Abstract
1. Introduction
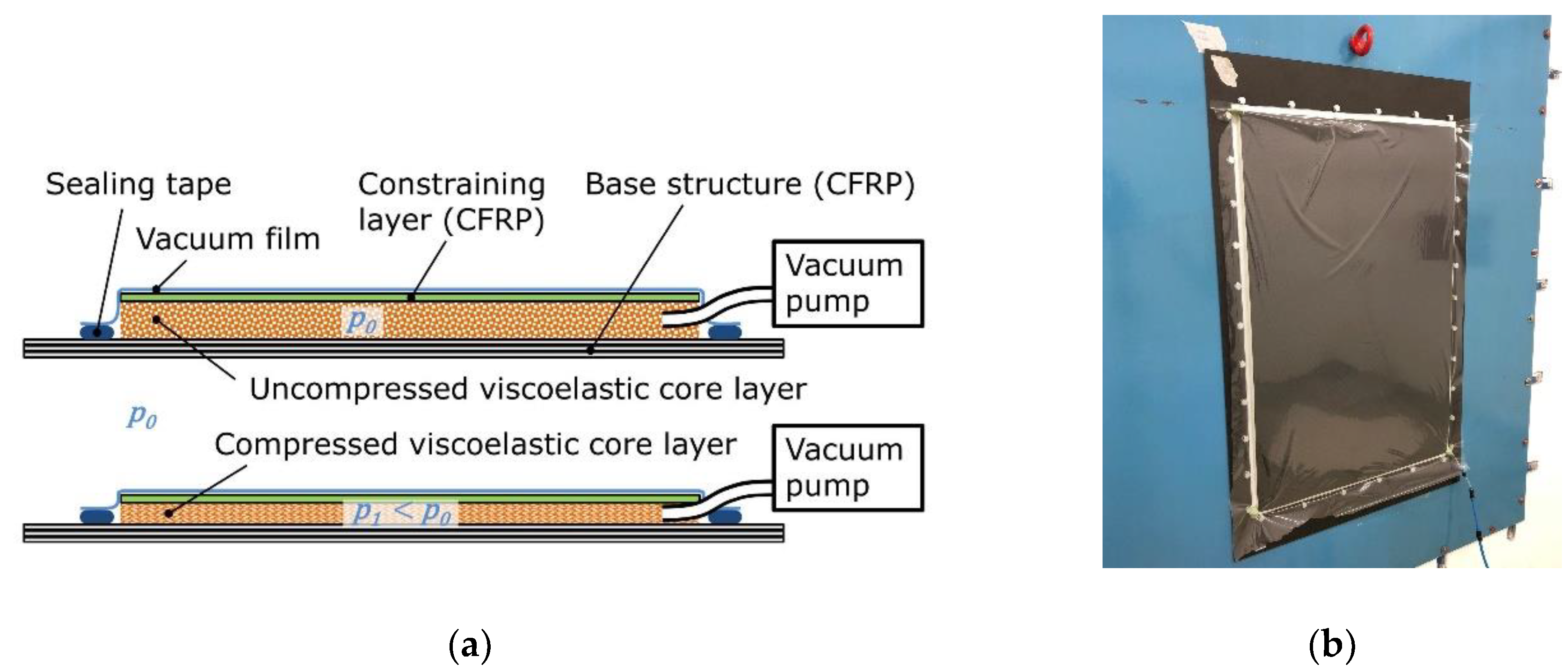
1.1. Operating Principle of Compressible Constrained Layer Damping
1.2. Sound Transmission Loss of Sandwich Structures
2. Materials and Test Set-up Configuration
2.1. Materials
2.2. CCLD Test Set-up Configuration
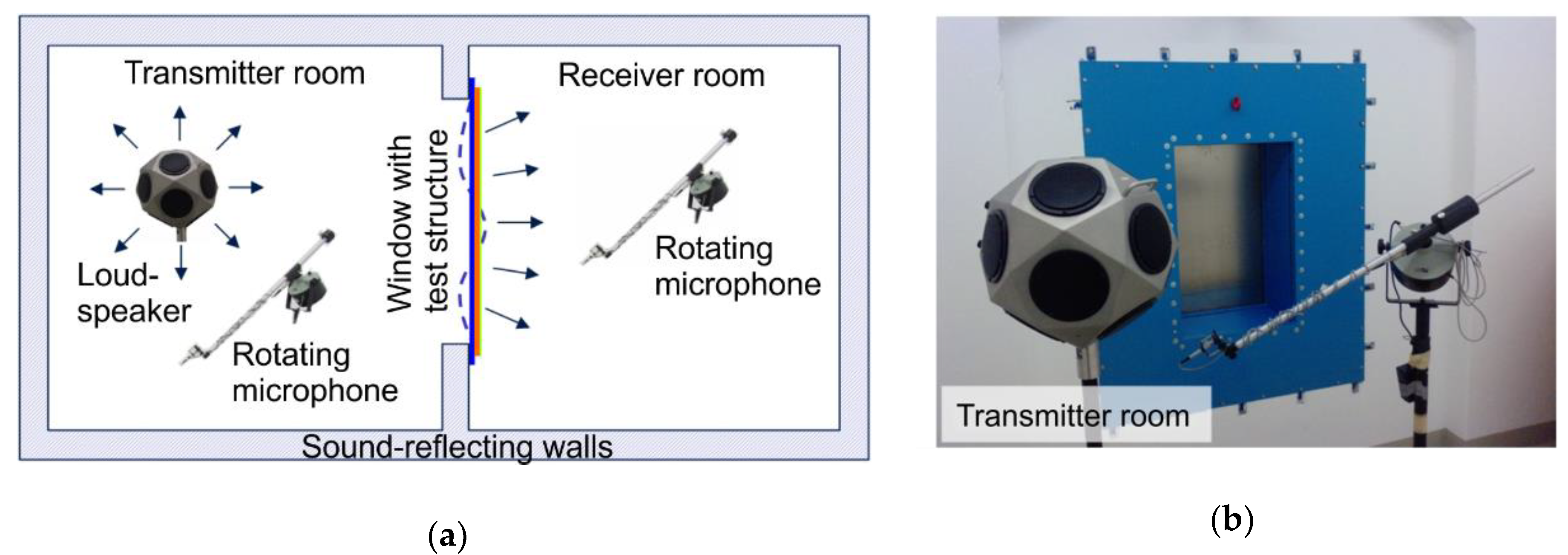
2.3. Sound Transmission Loss Measurements
3. Sound Transmission Loss Calculation of the Base Structure
4. Results and Discussion
4.1. Base Structure
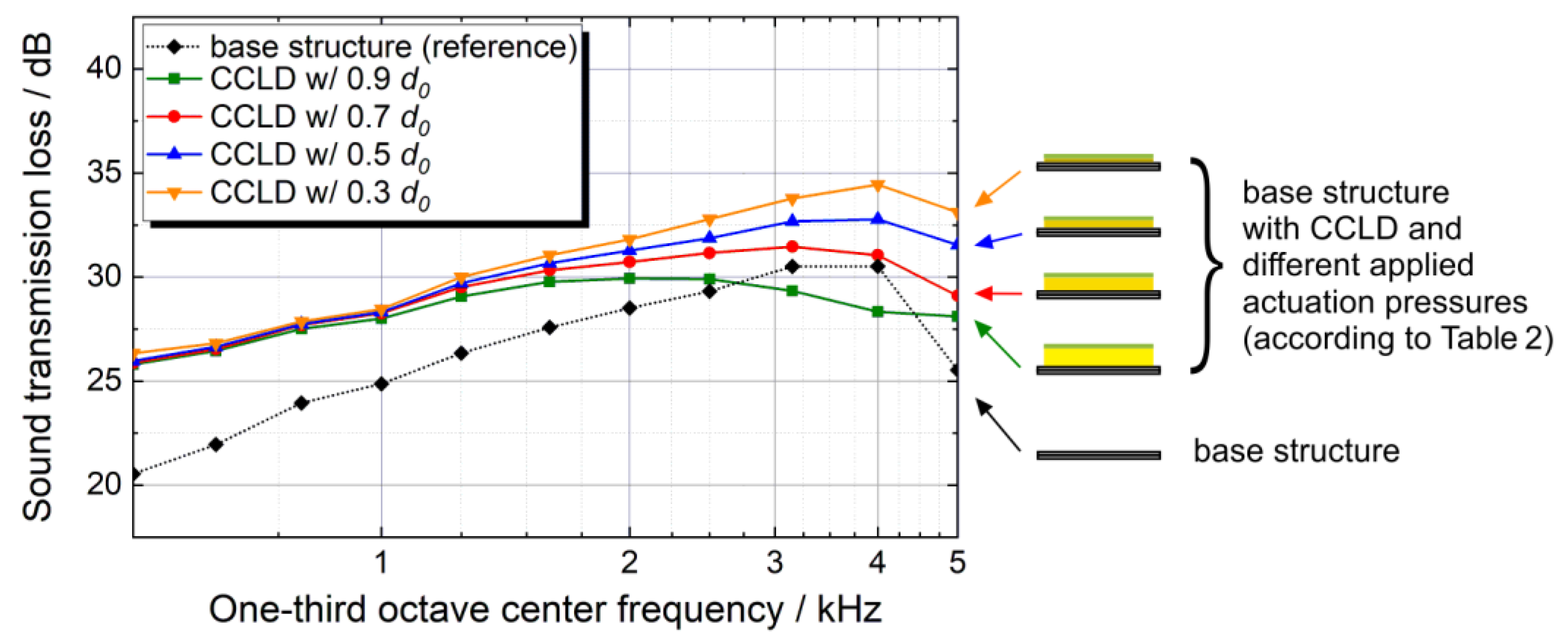
4.2. Base Structure with CCLD Treatment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hufenbach, W. Textile Verbundbauweisen und Fertigungstechnologien für Leichtbaustrukturen des Maschinen-und Fahrzeugbaus: SPP 1123; Sächsisches Druck-und Verlagshaus: Dresden, Germany, 2007. [Google Scholar]
- Kostka, P.; Holeczek, K.; Filippatos, A.; Hufenbach, W. Integration of health monitoring system for composite rotors. In Proceedings of the 18th International Conference on Composite Materials (ICCM18), Jeju, Korea, 21–26 August 2011. [Google Scholar]
- Kostka, P.; Holeczek, K.; Hufenbach, W. Structure-integrated Active Damping System: Integral Strain-based Design Strategy for the Optimal Placement of Functional Elements. Int. J. Compos. Mater. 2013, 3, 53–58. [Google Scholar] [CrossRef]
- Adams, R.D.; Bacon, D.G.C. Effect of fibre orientation and laminate geometry on the dynamic properties of CFRP. J. Compos. Mater. 1973, 7, 402–428. [Google Scholar] [CrossRef]
- Alam, N.; Asnani, N.T. Vibration and damping analysis of fibre reinforced composite material plates. J. Compos. Mater. 1986, 20, 2–18. [Google Scholar] [CrossRef]
- Dannemann, M.; Täger, O.; Modler, N. Combined semi-analytical and numerical vibro-acoustic design approach for anisotropic fibre-reinforced composite structures. J. Sound Vib. 2017, 404, 1–14. [Google Scholar] [CrossRef]
- Hanselka, H.; Hoffmann, U. Damping characteristics of fibre reinforced polymers. Tech. Mech. 1999, 10, 91–101. [Google Scholar]
- Holeczek, K.; Starke, E.; Winkler, A.; Dannemann, M.; Modler, N. Numerical and experimental characterisation of fibre-reinforced thermoplastic composite structures with embedded piezoelectric sensor-actuator-arrays for ultra-sonic applications. Appl. Sci. 2016, 6, 55. [Google Scholar] [CrossRef]
- Hurlebaus, S.; Gaul, L. Smart structure dynamics. Mech. Syst. Signal Process. 2006, 20, 255–281. [Google Scholar] [CrossRef]
- Marakakis, K.; Tairidis, G.K.; Koutsianitis, P.; Stavroulakis, G.E. Shunt Piezoelectric Systems for Noise and Vibration Control: A Review. Front. Built Environ. 2019, 5, 64. [Google Scholar] [CrossRef]
- Preumont, A. Vibration Control of Active Structures. An Introduction, 3rd ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Rao, M.D.; Echempati, R.; Nadella, S. Dynamic analysis and damping of composite structures embedded with viscoelastic layers. Compos. B Eng. 1997, 28, 547–554. [Google Scholar] [CrossRef]
- Trindade, M.A.; Benjeddou, A. Hybrid Active-Passive Damping Treatments Using Viscoelastic and Piezoelectric Materials: Review and Assessment. J. Vib. Control 2002, 8, 699–745. [Google Scholar] [CrossRef]
- Zeller, P. Handbuch Fahrzeugakustik. Grundlagen, Auslegung, Berechnung, Versuch, 1st ed.; Vie-weg+Teubner Verlag: Wiesbaden, Germany, 2009. [Google Scholar]
- Ehrig, T.; Holeczek, K.; Kostka, P. Experimental investigations of lightweight structures with fluidically actuated Compressible Constrained Layer Damping. Mater. Today Commun. 2018, 16, 204–211. [Google Scholar] [CrossRef]
- Holeczek, K.; Koschichow, R.; Schlieter, T.; Ehrig, T.; Kostka, P. Numerical investigations of polymer-based fibre-reinforced structures with fluidically actuated Compressible Constrained Layer Damping. Proc. Appl. Math. Mech. 2018, 18, e201800260. [Google Scholar] [CrossRef]
- Ehrig, T.; Holeczek, K.; Modler, N.; Kostka, P. Dynamic Behaviour Adaptation of Lightweight Structures by Compressible Constrained Layer Damping with Embedded Polymeric Foams and Nonwovens. Appl. Sci. 2019, 9, 3490. [Google Scholar] [CrossRef]
- Holeczek, K.; Zhou, B.; Kostka, P. Evanescent morphing for tuning the dynamic behavior of composite lightweight structures: Theoretical assessment. Mech. Adv. Mater. Struct. 2019, 10, 1–10. [Google Scholar] [CrossRef]
- D’Alessandro, V.; Petrone, G.; Franco, F.; Rosa, S. A review of the vibroacoustics of sandwich panels: Models and experiments. J. Sandw. Struct. Mater. 2013, 15, 541–582. [Google Scholar] [CrossRef]
- Isaac, C.W.; Pawelczyk, M.; Wrona, S. Comparative Study of Sound Transmission Losses of Sandwich Composite Double Panel Walls. Appl. Sci. 2020, 10, 1543. [Google Scholar] [CrossRef]
- Dym, C.L.; Lang, D.C. Transmission loss of damped asymmetric sandwich panels with orthotropic cores. J. Sound Vib. 1983, 88, 299–319. [Google Scholar] [CrossRef]
- Shengchun, W.; Zhaoxiang, D.; Weidong, S. Sound transmission loss characteristics of unbounded orthotropic sandwich panels in bending vibration considering transverse shear deformation. Compos. Struct. 2010, 92, 2885–2889. [Google Scholar] [CrossRef]
- Ehrig, T.; Modler, N.; Kostka, P. Compression and frequency dependence of the viscoelastic shear properties of flexible open-cell foams. Polym. Test. 2018, 70, 151–161. [Google Scholar] [CrossRef]
- Hufenbach, W.; Blanchet, D.; Dannemann, M.; Kolbe, F. Integrated Calculation of Transmission Loss of Sandwich Structures using Coupled Finite and Boundary Element Method. In Proceedings of the 1st ESI Global Users Conference and Exhibition on Simulation-Based Design, Munich, Germany, 19–20 May 2010. [Google Scholar]
- Liu, Y.; Sebastian, A. Effects of external and gap mean flows on sound transmission through a double-wall sandwich panel. J. Sound Vib. 2015, 344, 399–415. [Google Scholar] [CrossRef]
- Liu, Y. Sound transmission through triple-panel structures lined with poroelastic materials. J. Sound Vib. 2015, 339, 376–395. [Google Scholar] [CrossRef]
- Du, S.; An, F.; Liu, B. On the sound transmission loss of finite plates with constrained viscoelastic layer. Appl. Acoust. 2019, 149, 32–38. [Google Scholar] [CrossRef]
- DIN EN ISO 10140-4:2010. Acoustics–Laboratory Measurement of Sound Insulation of Building Elements–Part 4: Measurement procedures and requirements, German version; Beuth Verlag GmbH: Berlin, Germany, 2010. [Google Scholar]
- DIN EN ISO 717-1:2013. Acoustic–Rating of Sound Insulation in Buildings and of Building Elements–Part 1: Airborne Sound Insulation, German version; Beuth Verlag GmbH: Berlin, Germany, 2013. [Google Scholar]
- Fahy, F.J.; Gardonio, P. Sound and Structural Vibration: Radiation, Transmission and Response, 2nd ed.; Acadmic Press: Boston, MA, USA, 2007. [Google Scholar]
- Cremer, L.; Heckl, M.; Petersson, B.A.T. Structure-Borne Sound: Structural Vibrations and Sound Radiation at Audio Frequencies, 3rd ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Leissa, A.W. Vibration of Plates; National Aeronautics and Space Administration: Washington, DC, USA, 1969. [Google Scholar]
- Carboplast Faserverbund-Werkstoffe, TDB-CFK_Platte2mmCarboplast, Product Datasheet, Nov. 2009. Available online: https://www.carboplast.de/index.php?controller=attachment&id_attachment=107 (accessed on 31 January 2020).


| Layer | Material | Manufacturer | Density ρ | Length a | Width b | Thickness d | Mass m | Mass per Unit Area |
|---|---|---|---|---|---|---|---|---|
| kg/m³ | mm | mm | mm | kg | kg/m² | |||
| Base structure | CFRP (HTA-CF, EP) | Carboplast | 1550 | 1100 | 700 | 2 | 2.41 | 3.13 |
| Visco-elastic layer | Viscoelastic foam Confor CF-47M | Aearo Technologies LLC | 96 | 880 | 580 | 10 | 0.56 | 1.10 |
| Constrain-ing layer | CFRP (HT-CF, EP) | R&G | 1550 | 880 | 580 | 0.2 | 0.18 | 0.35 |
| Applied Actuation Pressure p1 | −3.9 kPa | −5.9 kPa | −7.6 kPa | −16.0 kPa |
|---|---|---|---|---|
| Core layer thickness d1 | 0.9 d0 | 0.7 d0 | 0.5 d0 | 0.3 d0 |
| 0.9 d0 | 0.7 d0 | 0.5 d0 | 0.3 d0 | Base Structure |
|---|---|---|---|---|
| 28.9 dB | 29.4 dB | 29.8 dB | 30.1 dB | 26.1 dB |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ehrig, T.; Dannemann, M.; Luft, R.; Adams, C.; Modler, N.; Kostka, P. Sound Transmission Loss of a Sandwich Plate with Adjustable Core Layer Thickness. Materials 2020, 13, 4160. https://doi.org/10.3390/ma13184160
Ehrig T, Dannemann M, Luft R, Adams C, Modler N, Kostka P. Sound Transmission Loss of a Sandwich Plate with Adjustable Core Layer Thickness. Materials. 2020; 13(18):4160. https://doi.org/10.3390/ma13184160
Chicago/Turabian StyleEhrig, Tom, Martin Dannemann, Ron Luft, Christian Adams, Niels Modler, and Pawel Kostka. 2020. "Sound Transmission Loss of a Sandwich Plate with Adjustable Core Layer Thickness" Materials 13, no. 18: 4160. https://doi.org/10.3390/ma13184160
APA StyleEhrig, T., Dannemann, M., Luft, R., Adams, C., Modler, N., & Kostka, P. (2020). Sound Transmission Loss of a Sandwich Plate with Adjustable Core Layer Thickness. Materials, 13(18), 4160. https://doi.org/10.3390/ma13184160









