Innovative Controllable Torsional Damper Based on Vacuum Packed Particles
Abstract
1. Introduction
2. Vacuum Packed Particles
3. Experiments
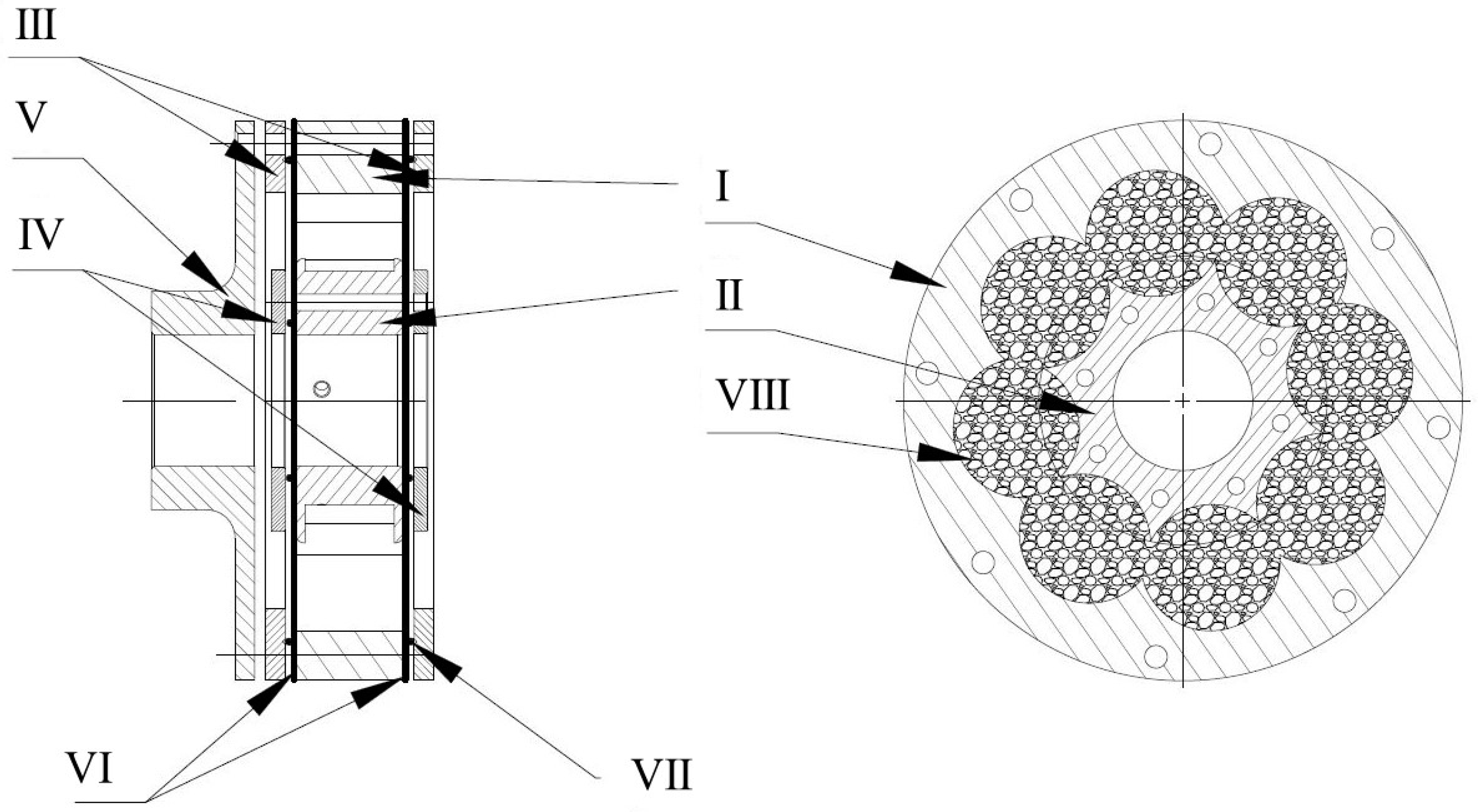
3.1. VPP Torsional Damper Prototype
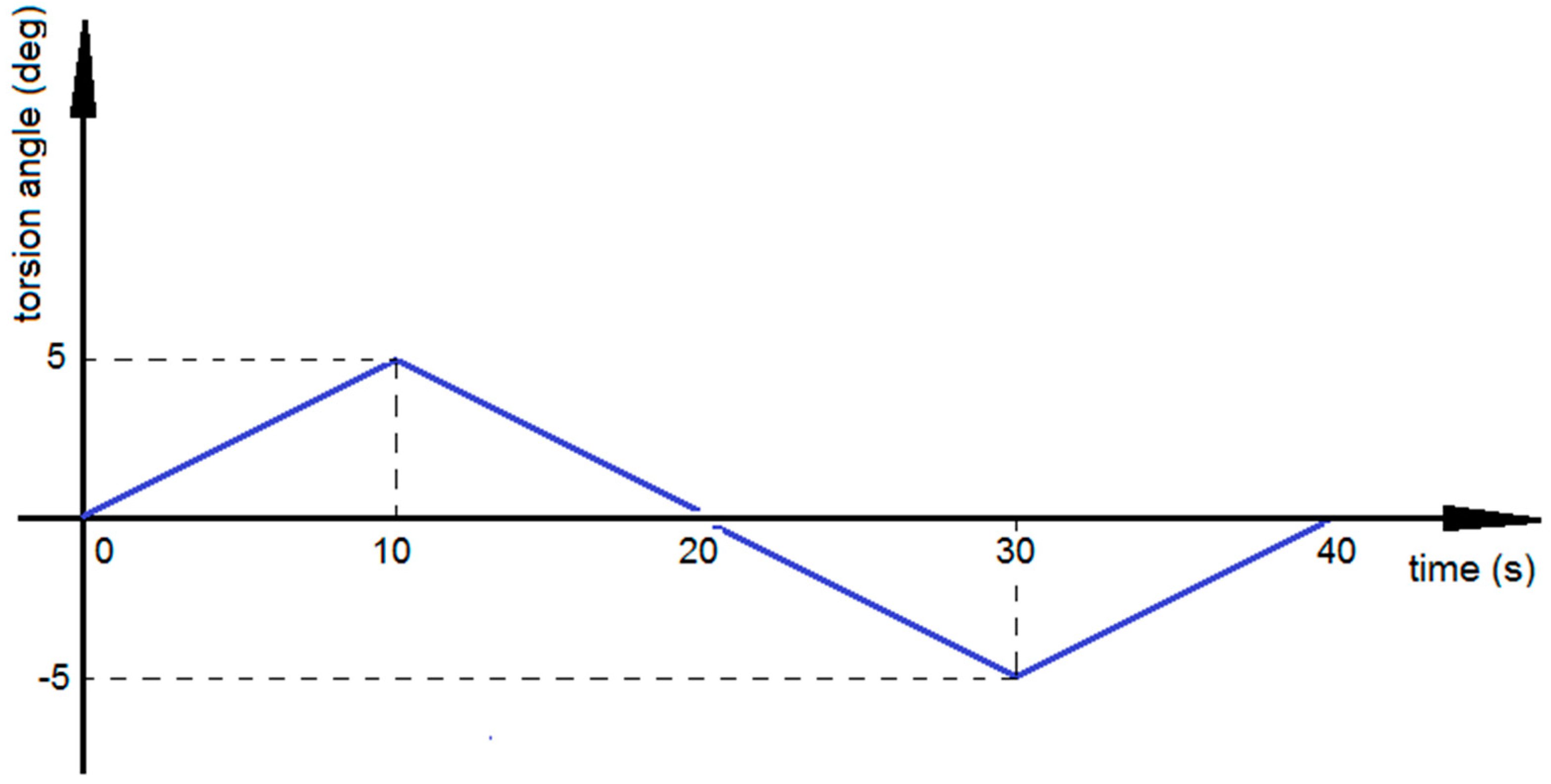
3.2. Research Plan
3.3. Test Stand
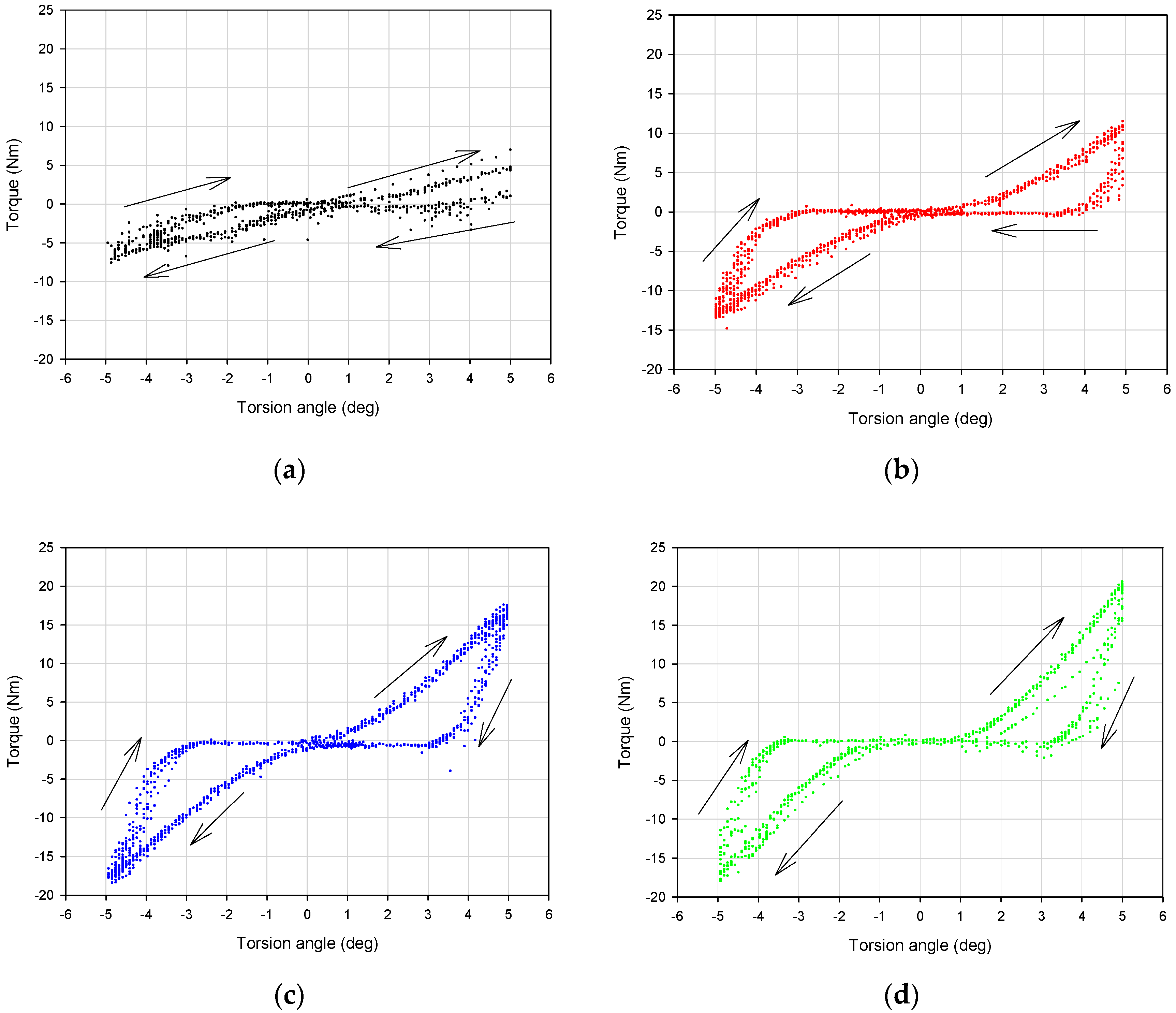
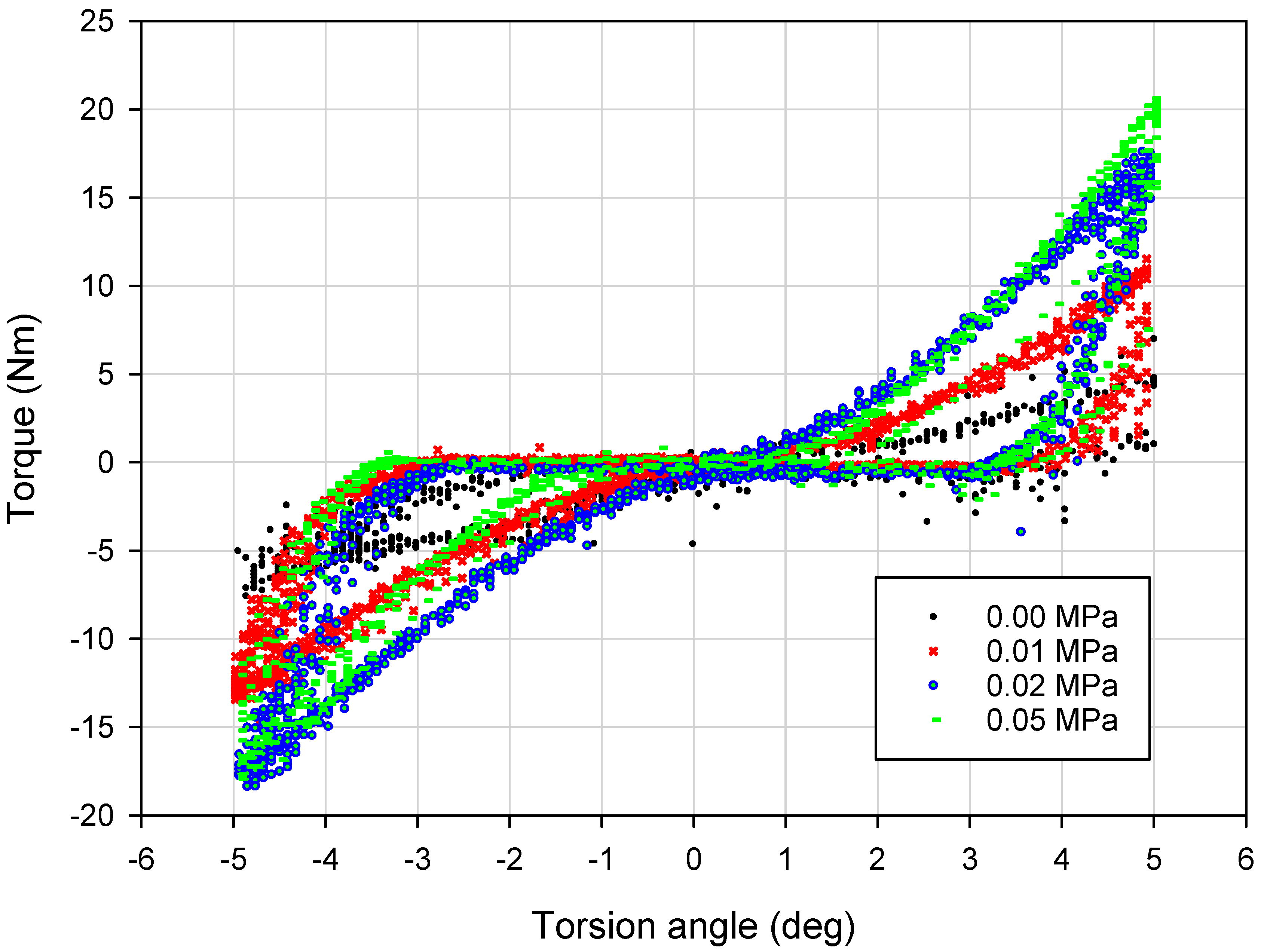
3.4. Results
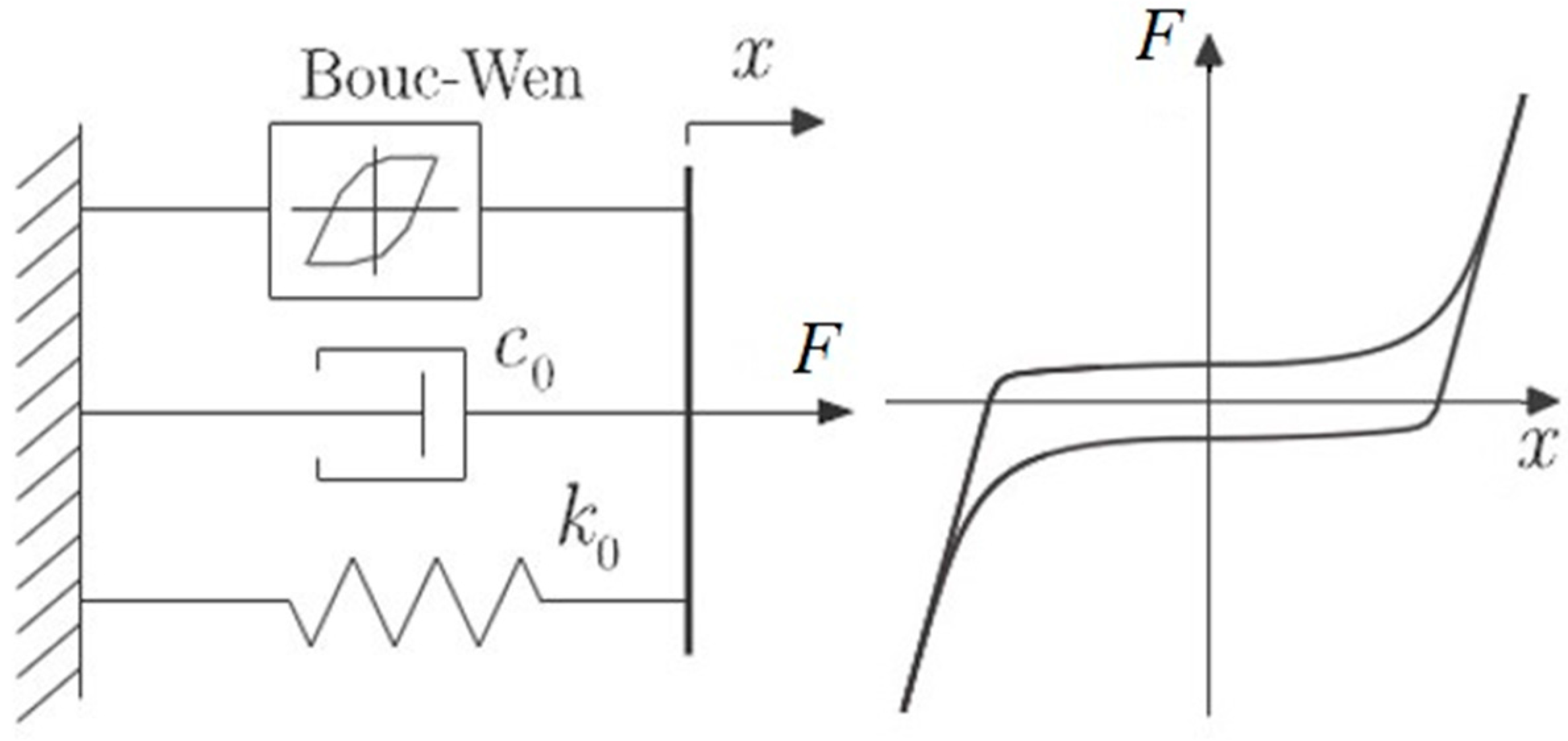
4. The Bouc–Wen Model
- F(t) = force function;
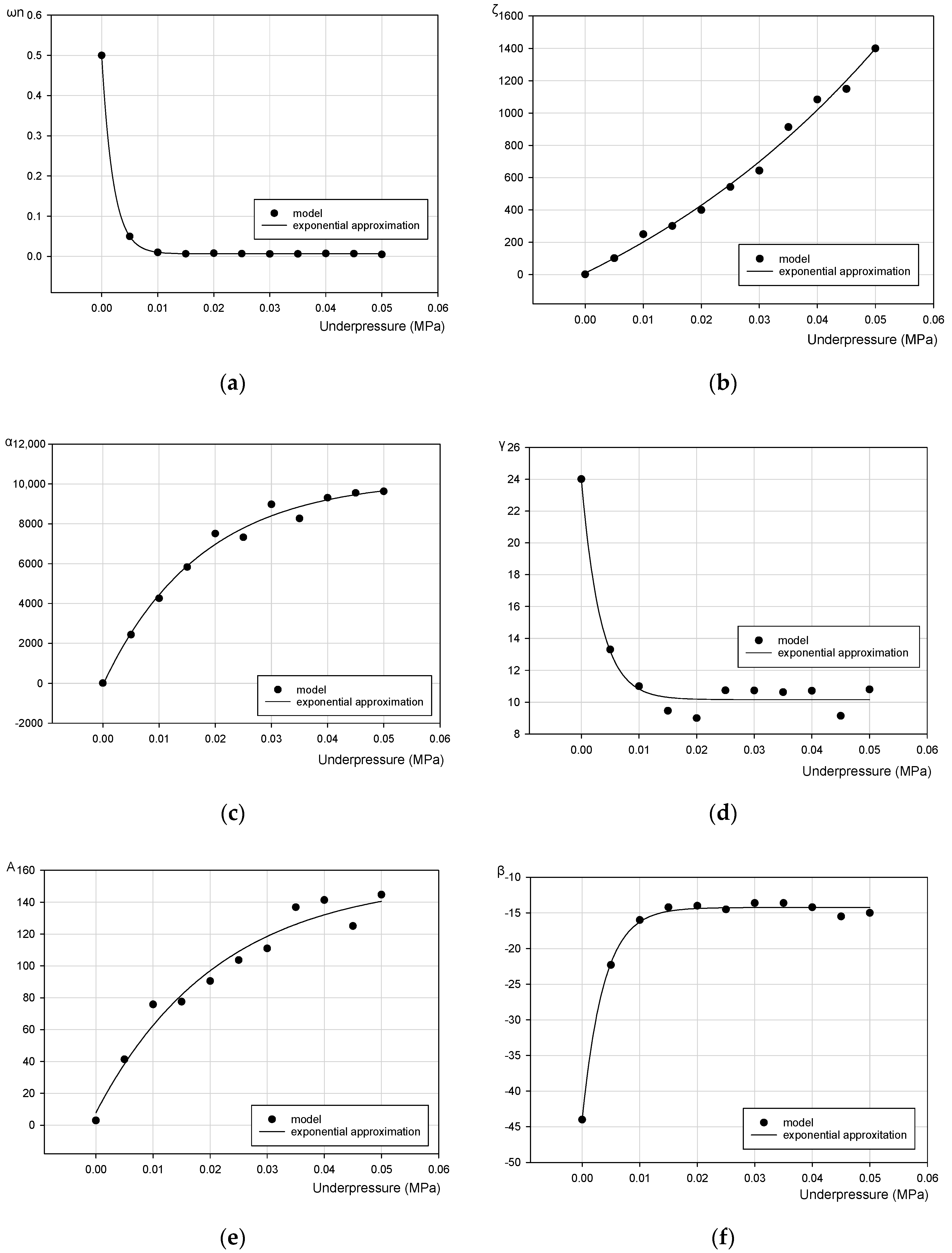
- ξ = linear viscous damping ratio;
- ωn = pseudo-natural frequency of the system;
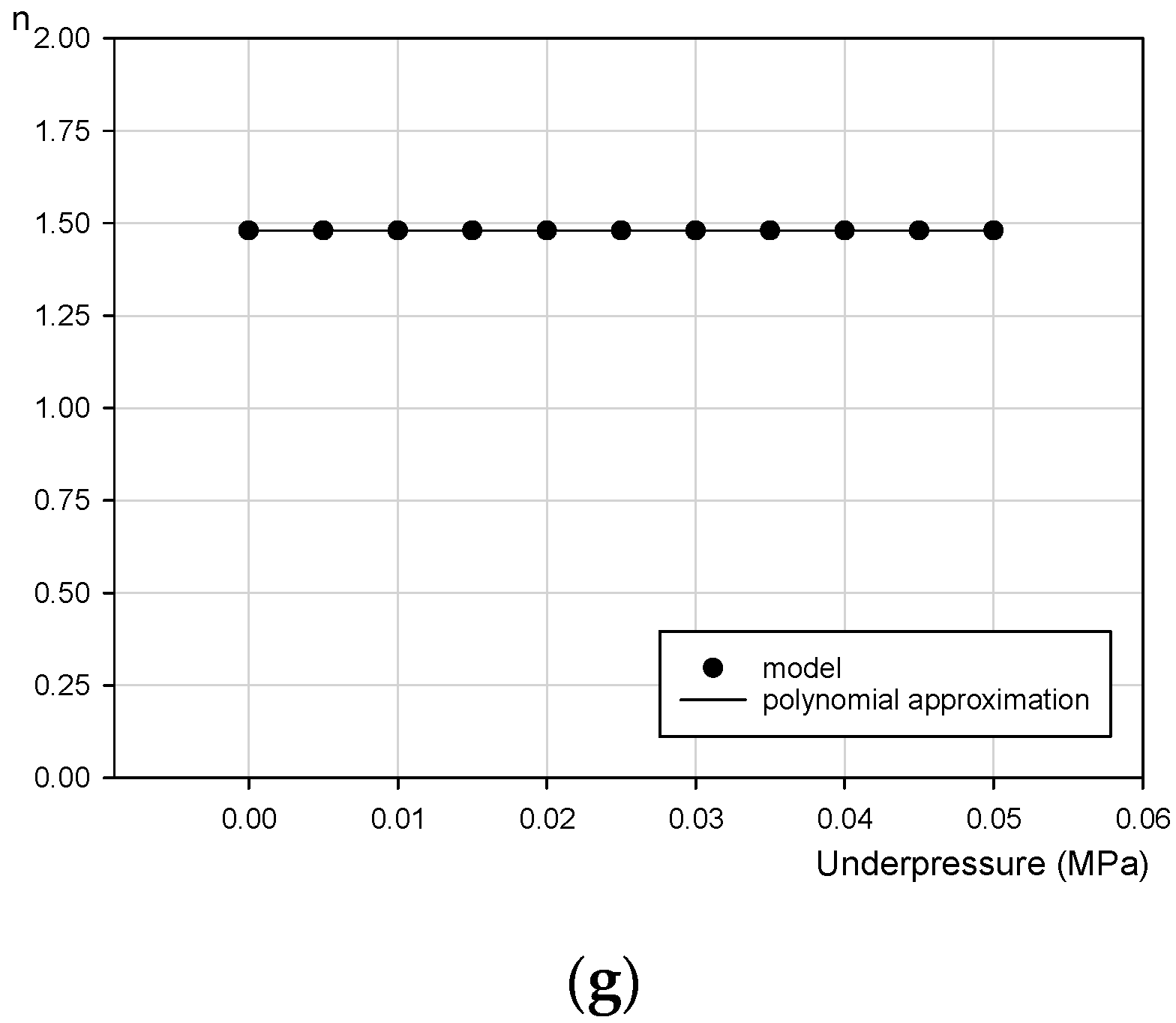
- n = degree of polynomial; and
- α; γ; β; A = parameters of hysteresis loop shape.
5. Result Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dyniewicz, B.; Pręgowska, A.; Czesław Bajer, I. Adaptive control of a rotating system. Mech. Syst. Signal Process. 2014, 43, 90–102. [Google Scholar] [CrossRef]
- Pisarski, D.; Szmidt, T.; Bajer, C.I.; Dyniewicz, B.; Bajkowski, J.M. Vibration control of double beam system with multiple smart damping members. Shock Vib. 2016, 2438902. [Google Scholar] [CrossRef]
- Spencer, B.F., Jr. Reliability of Randomly Excited Hysteretic Structures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 21. [Google Scholar]
- Shi, W.; Wang, L.; Lu, Z. Study on self-adjustable tuned mass damper with variable mass. Struct. Control Health Monit. 2018, 25, e2114. [Google Scholar] [CrossRef]
- Gao, P.; Xiang, C.; Liu, H.; Walker, P.; Zhang, N. Design of the frequency tuning scheme for a semi-active vibration absorber. Mech. Mach. Theory 2019, 140, 641–653. [Google Scholar] [CrossRef]
- Lin, G.L.; Lin, C.C.; Chen, B.C.; Soong, T.T. Vibration control performance of tuned mass dampers with resettable variable stiffness. Eng. Struct. 2015, 83, 187–197. [Google Scholar] [CrossRef]
- Wasilewski, M.; Pisarski, D.; Konowrocki, R.; Bajer, C.I. A new efficient adaptive control of torsional vibrations induced by switched nonlinear disturbances. Int. J. Appl. Math. Comput. Sci. 2019, 29, 285–303. [Google Scholar] [CrossRef]
- Szmidt, T.; Pisarski, D.; Konowrocki, R.; Awietjan, S.; Boczkowska, A. Adaptive Damping of a Double-Beam Structure Based on Magnetorheological Elastomer. Shock Vib. 2019, 2019, 8526179. [Google Scholar] [CrossRef]
- Szmidt, T. Shear deformation damping of a double-beam structure. J. Sound Vib. 2016, 370, 163–175. [Google Scholar] [CrossRef]
- Nayak, B.; Dwivedy, S.K.; Murthy, K.S.K.R. Dynamic analysis of magnetorheological elastomer-based sandwich beam with conductive skins under various boundary conditions. J. Sound Vib. 2011, 330, 1837–1859. [Google Scholar] [CrossRef]
- Boczkowska, A.; Awietjan, S.F.; Pietrzko, S.; Kurzydłowski, K.J. Mechanical properties of magneto-rheological elastomers under shear deformation. Compos. Part B Eng. 2012, 43, 636–640. [Google Scholar] [CrossRef]
- Wen, J.M.; Shen, D.Z.; Wang, R.M.; Li, J.P.; Ma, J.J. A two-fixed-end beam piezoelectric inertial actuator using electromagnet controlled magnetorheological fluid (MRF) for friction regulation. Smart Mater. Struct. 2020, 29, 065011. [Google Scholar] [CrossRef]
- Khanouki, M.A.; Sedaghati, R.; Hemmatian, M. Multidisciplinary Design Optimization of a Novel Sandwich Beam-Based Adaptive Tuned Vibration Absorber Featuring Magnetorheological Elastomer. Materials 2020, 13, 2261. [Google Scholar] [CrossRef]
- Bartkowski, P.; Zalewski, R. A concept of smart multiaxial impact damper made of vacuum packed particles. In MATEC Web of Conferences; EDP Sciences: Les Ulis, Frances, 2018; Volume 157, p. 05001. [Google Scholar]
- Jiang, A.; Aste, T.; Dasgupta, P.; Althoefer, K.; Nanayakkara, T. Granular Jamming with Hydraulic Control. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Portland, OR, USA, 4–7 August 2013. [Google Scholar]
- Mozeika, A.; Steltz, E.; Jaeger, M.H. The first steps of a robot based on jamming skin enabled locomotion. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 408–409. [Google Scholar]
- Brown, E.; Rodenberg, N.; Amend, J.; Mozeika, A.; Steltz, E.; Zakin, M.R.; Lipson, H.; Jaeger, H.M. Universal robotic gripper based on the jamming of granular material. Proc. Natl. Acad. Sci. USA 2010, 107, 18809–18814. [Google Scholar] [CrossRef]
- Zalewski, R.; Szmidt, T. Application of special granular structures for semi-active damping of lateral beam vibrations. Eng. Struct. 2014, 65, 13–20. [Google Scholar] [CrossRef]
- Skalski, P.; Zalewski, R. Viscoplastic properties of an MR fluid in a damper. J. Theor. Appl. Mech. 2014, 52, 1061–1070. [Google Scholar] [CrossRef][Green Version]
- Wang, J.; Meng, G. Magnetorheological fluid devices: Principles, characteristics and applications in mechanical engineering. Proc. Inst. Mech. Eng. L Mater. J. Des. Appl. 2001, 215, 165–174. [Google Scholar] [CrossRef]
- Zalewski, R.; Chodkiewicz, P. Semi-active linear vacuum packed particles damper. J. Theor. Appl. Mech. 2016, 54, 311–316. [Google Scholar] [CrossRef]
- Luscombe, M.; Williams, J. Comparison of a long spinal board and vacuum mattress for spinal immobilization. Emerg. Med. J. 2003, 20, 476–478. [Google Scholar] [CrossRef]
- Loeve, A.J.; van de Ven, O.S.; Vogel, J.G.; Breedveld, P.; Dankelman, J. Vacuum packed particles as flexible endoscope guides with controllable rigidity. Granul. Matter 2010, 12, 543–554. [Google Scholar] [CrossRef]
- Szmidt, T.; Zalewski, R. Inertially excited beam vibrations damped by vacuum packed particles. Smart Mater. Struct. 2014, 23, 105026. [Google Scholar] [CrossRef]
- Bajkowski, J.M.; Bajer, C.I.; Dyniewicz, B.; Pisarski, D. Vibration control of adjacent beams with pneumatic granular coupler: An experimental study. Mech. Res. Commun. 2016, 78, 51–56. [Google Scholar] [CrossRef]
- Bajkowski, J.; Dyniewicz, B.; Bajer, C. Corrigendum to “damping properties of a beam with vacuum-packed granular damper”. J. Sound Vib. 2015, 341, 74–85. [Google Scholar] [CrossRef]
- Bouc, R. Forced vibrations of mechanical systems with hysteresis. In Proceedings of the Fourth Conference on Nonlinear Oscillations, Prague, Czech Republic, 5–9 September 1967. [Google Scholar]
- Bartkowski, P.; Zalewski, R.; Chodkiewicz, P. Parameter identification of Bouc-Wen model for vacuum packed particles based on genetic algorithm. Ach. Civil. Mech. Eng. 2019, 19, 322–333. [Google Scholar] [CrossRef]
- Weber, F.; Maślanka, M. Precise Stiffness and Damping Emulation with MR Dampers and its Application to Semi-active Tuned Mass Dampers of Wolgograd Bridge. Smart Mater. Struct. 2014, 23, 015019. [Google Scholar] [CrossRef]
- Zalewski, R.; Chodkiewicz, P.; Shillor, M. Vibrations of a mass spring system using a granular-material damper. Appl. Math. Model. 2016, 40, 8033–8047. [Google Scholar] [CrossRef]
- Zalewski, R. Analysis of Mechanical Properties of Vacuum Packed Particles. Ph.D. Thesis, Warsaw University of Technology, Warsaw, Poland, 2005. (In Polish). [Google Scholar]
- Bartkowski, P. Empirical Research and Modeling of Energy Dissipators Working on the Basis of Vacuum Packed Particles. Ph.D. Thesis, Warsaw University of Technology, Warsaw, Poland, 2019. (In Polish). [Google Scholar]
- Spencer, B., Jr.; Dyke, S.; Sain, M.; Carlson, J. Phenomenological model for magnetorheological dampers. Eng. J. Mech. 1997, 123, 230–238. [Google Scholar] [CrossRef]
- Yang, G.; Spencer, B.F., Jr.; Jung, H.-J.; Carlson, J.D. Dynamic modeling of large-scale magnetorheological damper systems for civil engineering applications. Eng. J. Mech. 2004, 130, 1107–1114. [Google Scholar] [CrossRef]
- Holnicki-Szulc, J.; Graczykowski, C.; Mikułowski, G.; Mróz, A.; Pawłowski, P.; Wiszowaty, R. Adaptive Impact Absorption—The Concept and Potential Applications. Int. J. Prot. Struct. 2015, 6, 357–377. [Google Scholar] [CrossRef]
- Gamota, D.; Filisko, F. Dynamic mechanical studies of electrorheological materials: Moderate frequencies. Rheol. J. 1991, 35, 399–425. [Google Scholar] [CrossRef]
- Lederer, D.; Igarashi, H.; Kost, A.; Honma, T. On the parameter identification and application of the Jiles-Atherton hysteresis model for numerical modeling of measured characteristics. IEEE Trans. Magnet. 1999, 35, 1211–1214. [Google Scholar] [CrossRef]
- Asif Zaman, M.; Hansen, C.; Neustock, P.T.; Padhy, L.; Hesselink, P.L. Adjoint Method for Estimating Jiles-Atherton Hysteresis Model Parameters. J. Appl. Phys. 2016, 120, 093903. [Google Scholar] [CrossRef]
- Bertotti, G. Dynamic generalization of the scalar Preisach model of hysteresis. IEEE Trans. Magnet. 1992, 28, 2599–2601. [Google Scholar] [CrossRef]
- Ismail, M.; Ikhouane, F.; Rodellar, J. The hysteresis Bouc-Wen model, a survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Wen, Y.-K. Method for random vibration of hysteretic systems. Eng. J. Mech. Div. 1976, 102, 249–263. [Google Scholar]
- Dong, H.; Han, Q.; Du, X. Application of an extended Bouc-Wen model for hysteretic behavior of the RC structure with SCEBs. Struct. Eng. Mech. 2019, 71, 683–697. [Google Scholar]
- Kirkpatrick, S.; Gelatt, D., Jr.; Vecchi, P.M. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X. Parameter estimation of the Bouc-Wen hysteresis model using particle swarm optimization. Smart Mater. Struct. 2007, 16, 2341. [Google Scholar] [CrossRef]
- Asif Zaman, M.; Sikder, U. Bouc-Wen hysteresis model identification using modified firefly algorithm, Magnet. J. Magnet. Mater. 2015, 395, 229–233. [Google Scholar] [CrossRef]
- Pyrz, M.; Krzywoblocki, M. Crashworthiness optimization of thin-walled tubes using macro element method and evolutionary algorithm. Thin-Walled Struct. 2017, 112, 12–19. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer: New York, NY, USA, 1999; ISBN 0-387-98793-2. [Google Scholar]



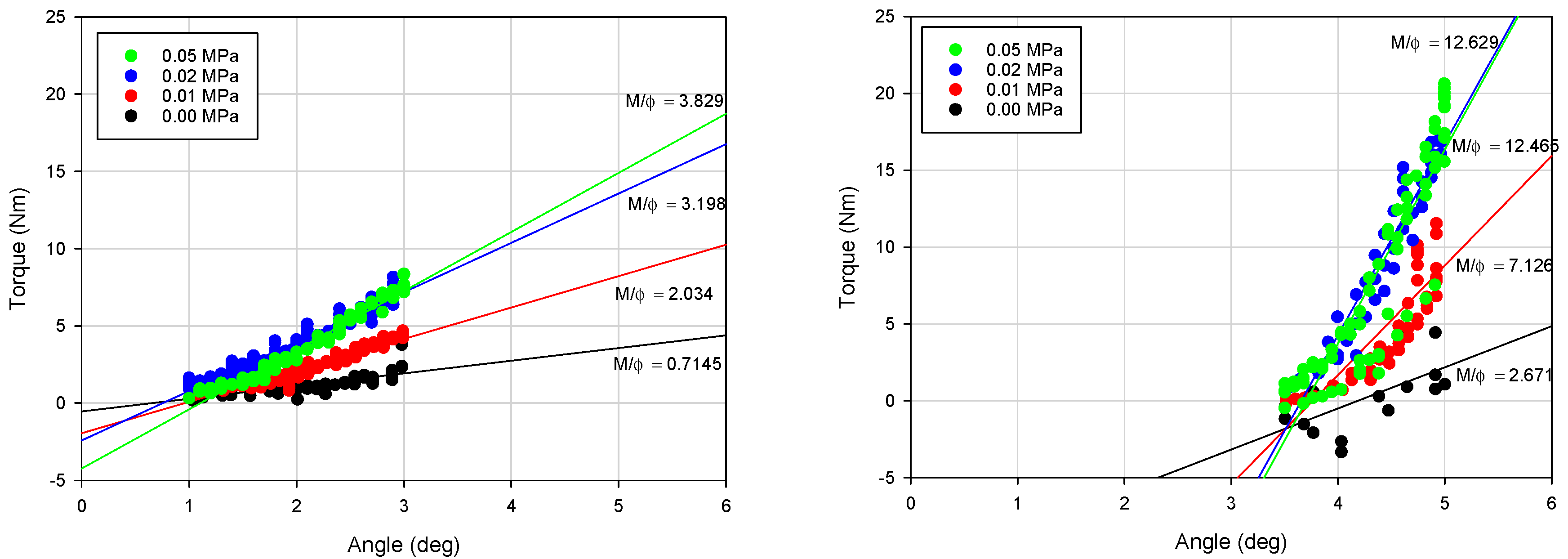
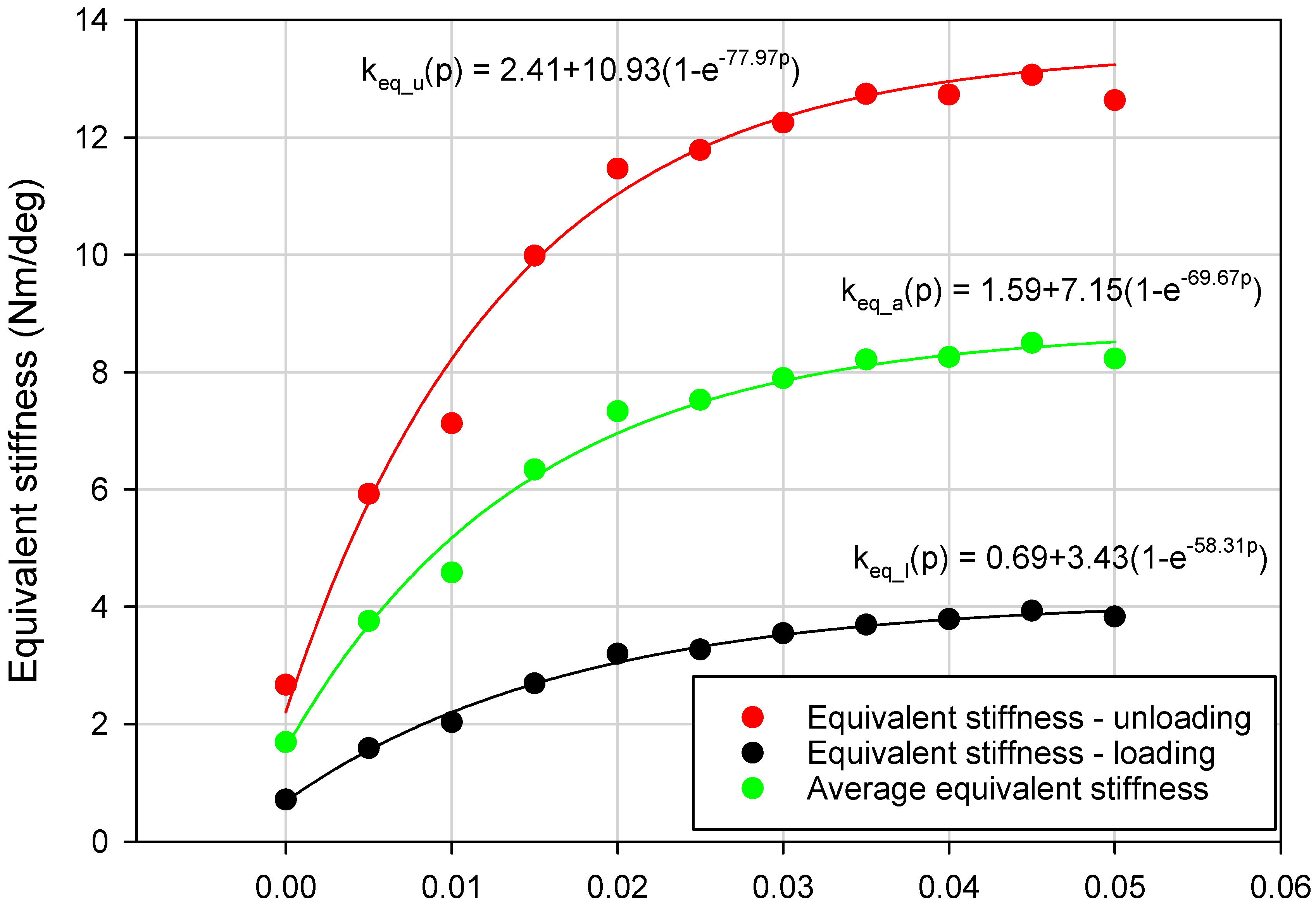
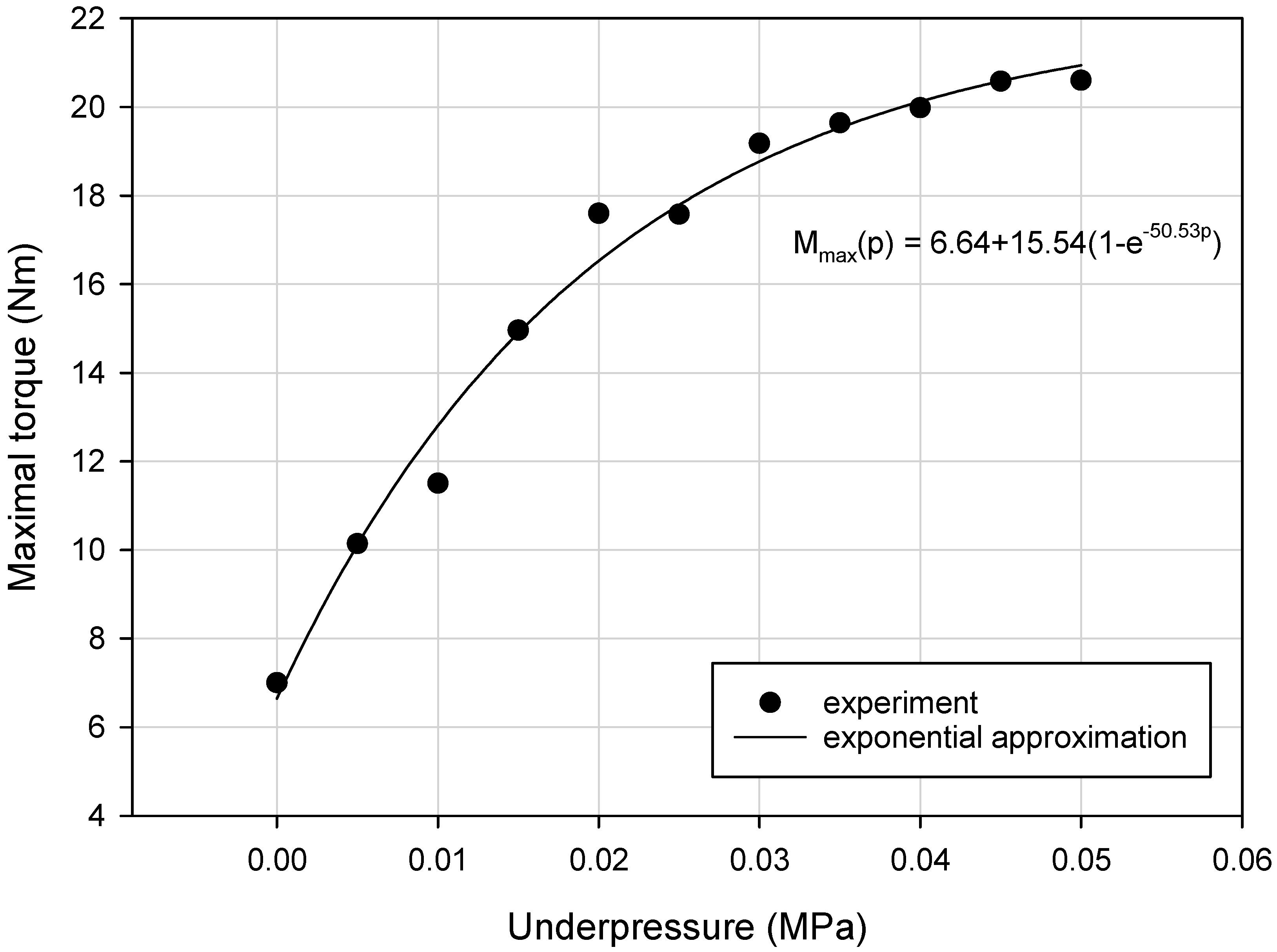
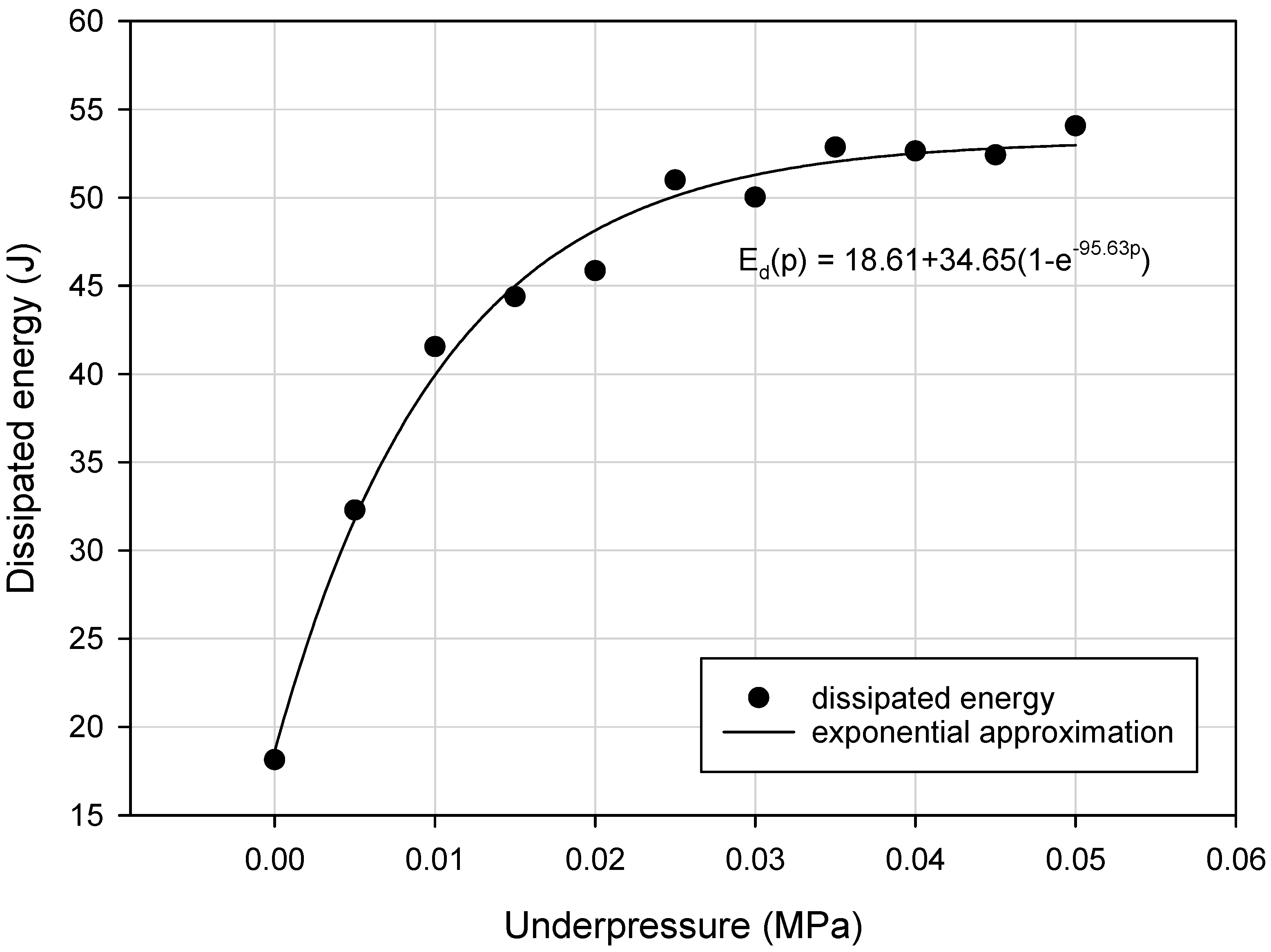

| Underpressure (MPa) | Equivalent Loading Stiffness keq_l (Nm/deg) | Equivalent Unloading Stiffness keq_u (Nm/deg) | Equivalent Stiffness keq_a (Nm/deg) | Maximum Torque Mmax (Nm) | Dissipated Energy (Nm/deg) |
|---|---|---|---|---|---|
| 0.000 | 0.72 | 2.67 | 1.69 | 7.00 | 18.13 |
| 0.005 | 1.59 | 5.92 | 3.75 | 10.14 | 32.28 |
| 0.01 | 2.03 | 7.13 | 4.58 | 11.50 | 41.55 |
| 0.015 | 2.69 | 9.98 | 6.34 | 14.96 | 44.38 |
| 0.02 | 3.20 | 11.47 | 7.33 | 17.60 | 45.86 |
| 0.025 | 3.27 | 11.78 | 7.53 | 17.56 | 50.99 |
| 0.03 | 3.55 | 12.25 | 7.90 | 19.18 | 50.02 |
| 0.035 | 3.69 | 12.74 | 8.21 | 19.64 | 52.85 |
| 0.04 | 3.79 | 12.72 | 8.26 | 19.98 | 52.64 |
| 0.045 | 3.93 | 13.06 | 8.50 | 20.58 | 52.41 |
| 0.05 | 3.83 | 12.63 | 8.23 | 20.60 | 54.06 |
| p (MPa) | ωn (1/s) | ξ (Nm∙s/°) | α (Nm/°) | γ (deg−2) | A (-) | β (deg−2) | n (-) | R2 (-) | Error (%) |
|---|---|---|---|---|---|---|---|---|---|
| 0.000 | 0.5000 | 2 | 13 | 24.01 | 3.00 | −44.00 | 1.48 | 0.857 | 19.2 |
| 0.005 | 0.0503 | 106 | 2877 | 12.88 | 36.19 | −21.25 | 1.48 | 0.902 | 18.1 |
| 0.01 | 0.0100 | 250 | 4259 | 11.00 | 75.83 | −16.00 | 1.48 | 0.931 | 14.7 |
| 0.015 | 0.0065 | 292 | 5646 | 10.98 | 77.54 | −13.92 | 1.48 | 0.950 | 13.5 |
| 0.02 | 0.0080 | 400 | 7511 | 9.00 | 90.50 | −14.00 | 1.48 | 0.962 | 13.3 |
| 0.025 | 0.0066 | 603 | 7401 | 9.05 | 101.40 | −13.64 | 1.48 | 0.970 | 16.1 |
| 0.03 | 0.0065 | 720 | 9235 | 9.04 | 112.17 | −14.78 | 1.48 | 0.976 | 15.6 |
| 0.035 | 0.0062 | 887 | 9797 | 10.43 | 118.76 | −15.07 | 1.48 | 0.979 | 13.5 |
| 0.04 | 0.0064 | 992 | 8660 | 10.82 | 122.51 | −15.07 | 1.48 | 0.981 | 13.4 |
| 0.045 | 0.0063 | 1280 | 9646 | 10.33 | 134.74 | −13.62 | 1.48 | 0.983 | 12.9 |
| 0.05 | 0.0050 | 1400 | 9630 | 10.8 | 144.70 | −15.00 | 1.48 | 0.984 | 12.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodak, D.; Zalewski, R. Innovative Controllable Torsional Damper Based on Vacuum Packed Particles. Materials 2020, 13, 4356. https://doi.org/10.3390/ma13194356
Rodak D, Zalewski R. Innovative Controllable Torsional Damper Based on Vacuum Packed Particles. Materials. 2020; 13(19):4356. https://doi.org/10.3390/ma13194356
Chicago/Turabian StyleRodak, Dominik, and Robert Zalewski. 2020. "Innovative Controllable Torsional Damper Based on Vacuum Packed Particles" Materials 13, no. 19: 4356. https://doi.org/10.3390/ma13194356
APA StyleRodak, D., & Zalewski, R. (2020). Innovative Controllable Torsional Damper Based on Vacuum Packed Particles. Materials, 13(19), 4356. https://doi.org/10.3390/ma13194356





