Impact Resistance Study of Three-Dimensional Orthogonal Carbon Fibers/BMI Resin Woven Composites
Abstract
1. Introduction
2. Materials and Experiments
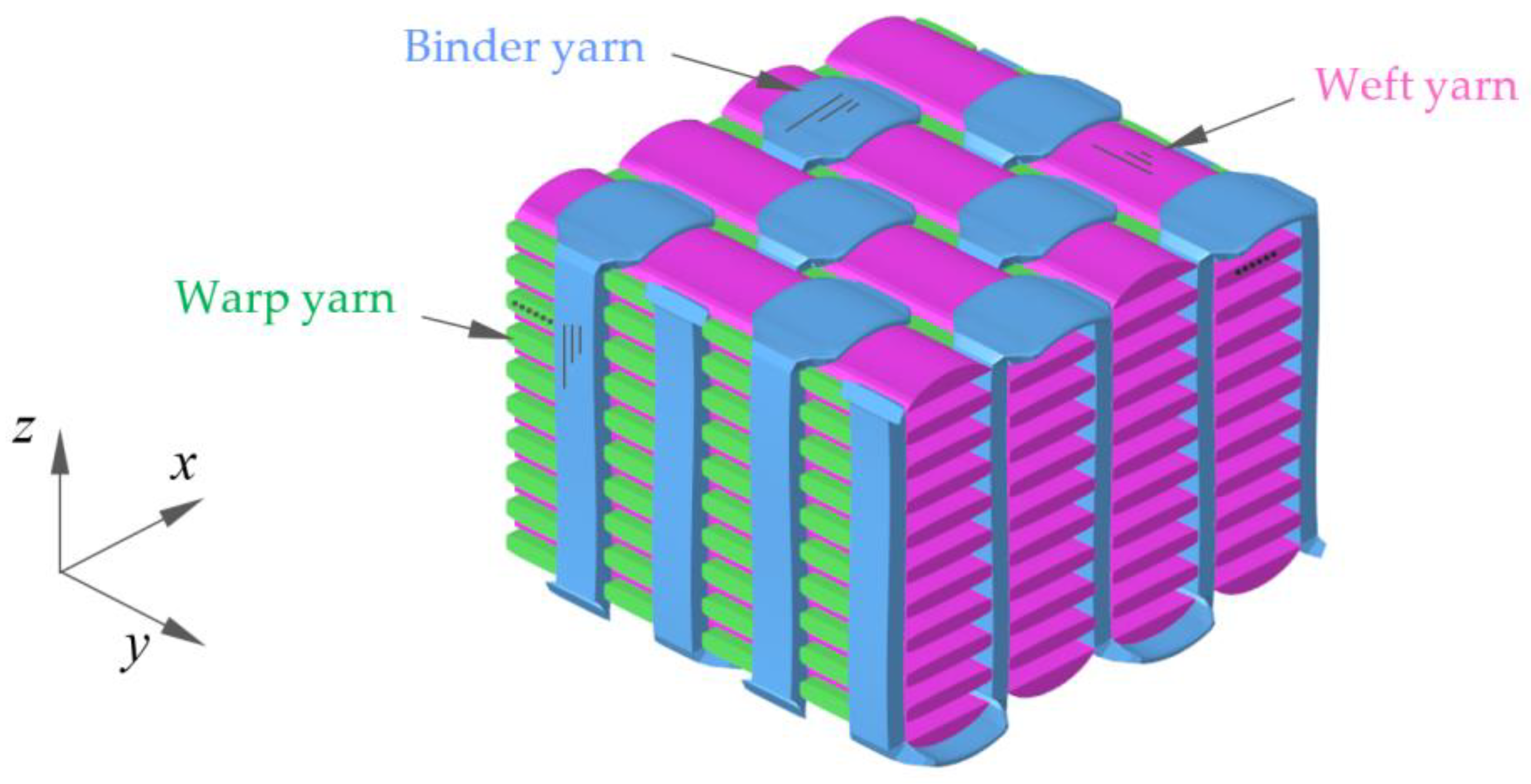
2.1. Materials
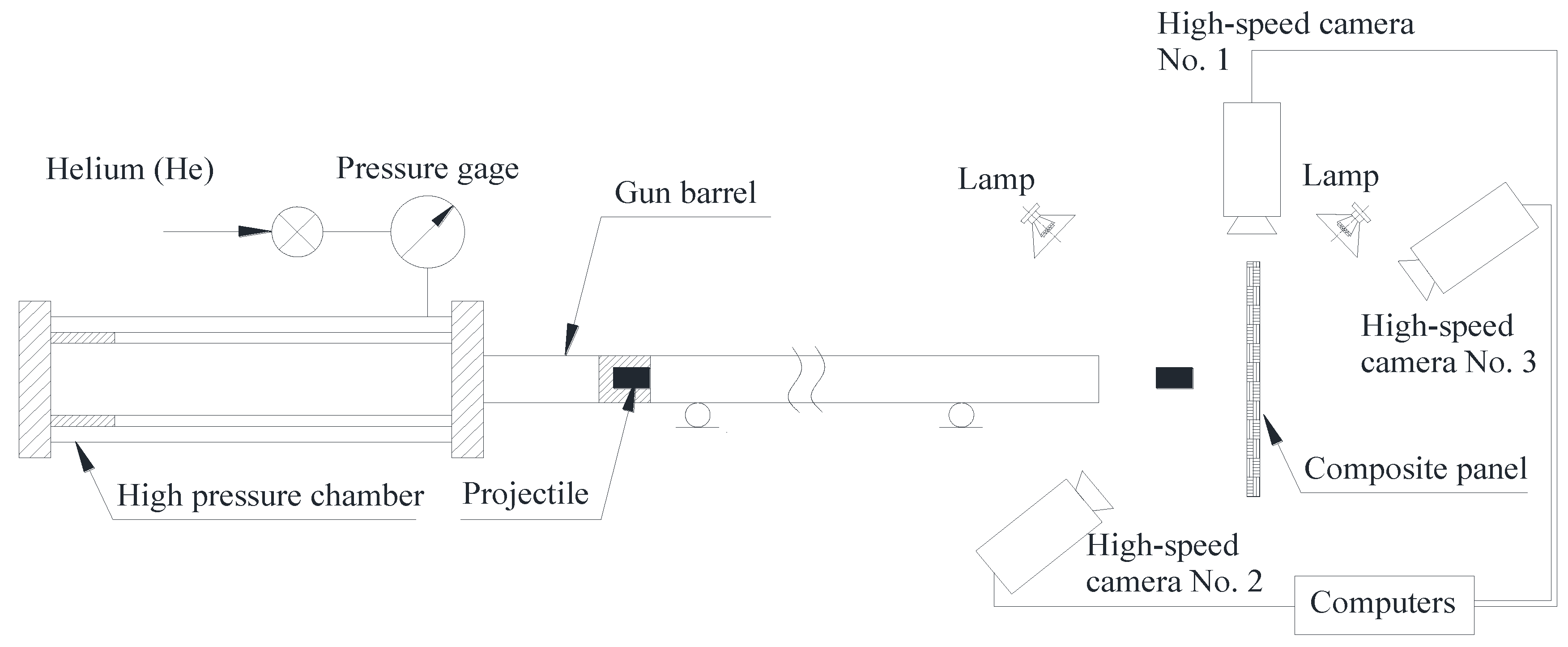
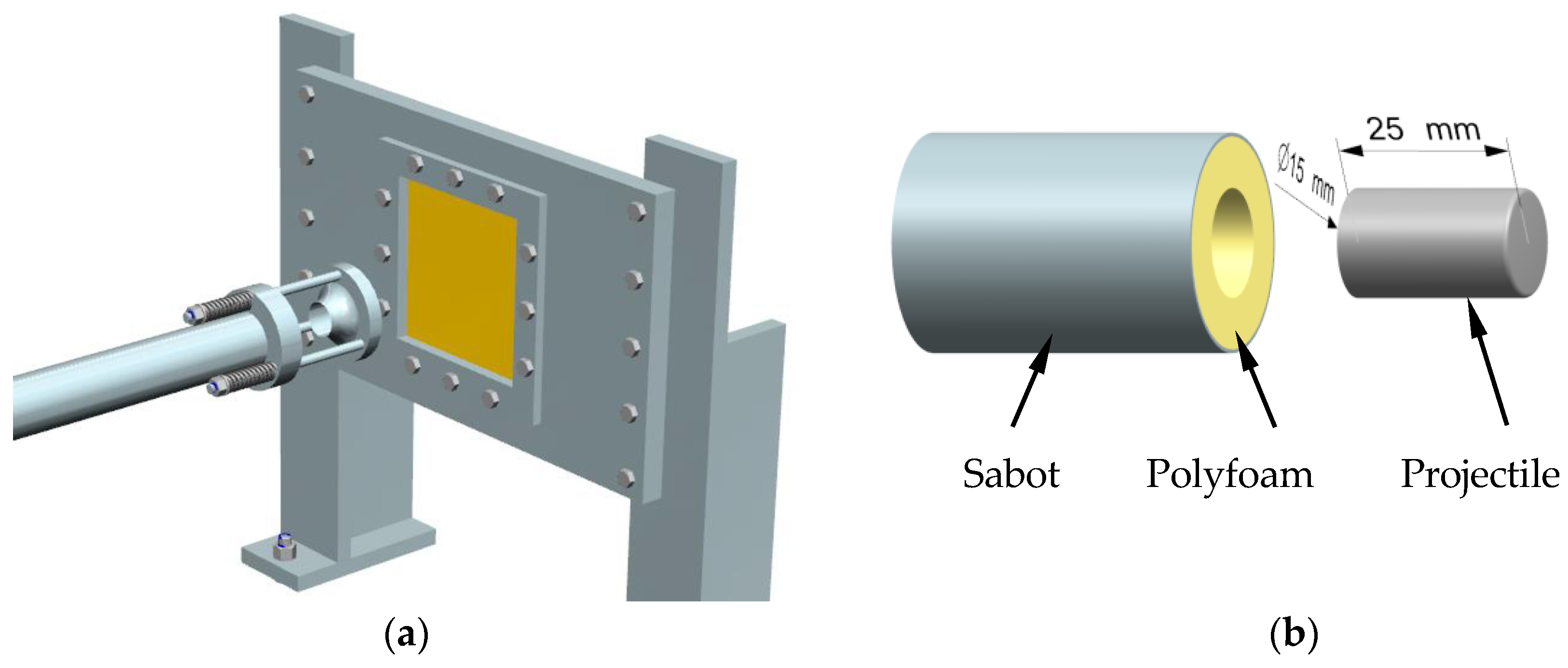
2.2. Impact Test
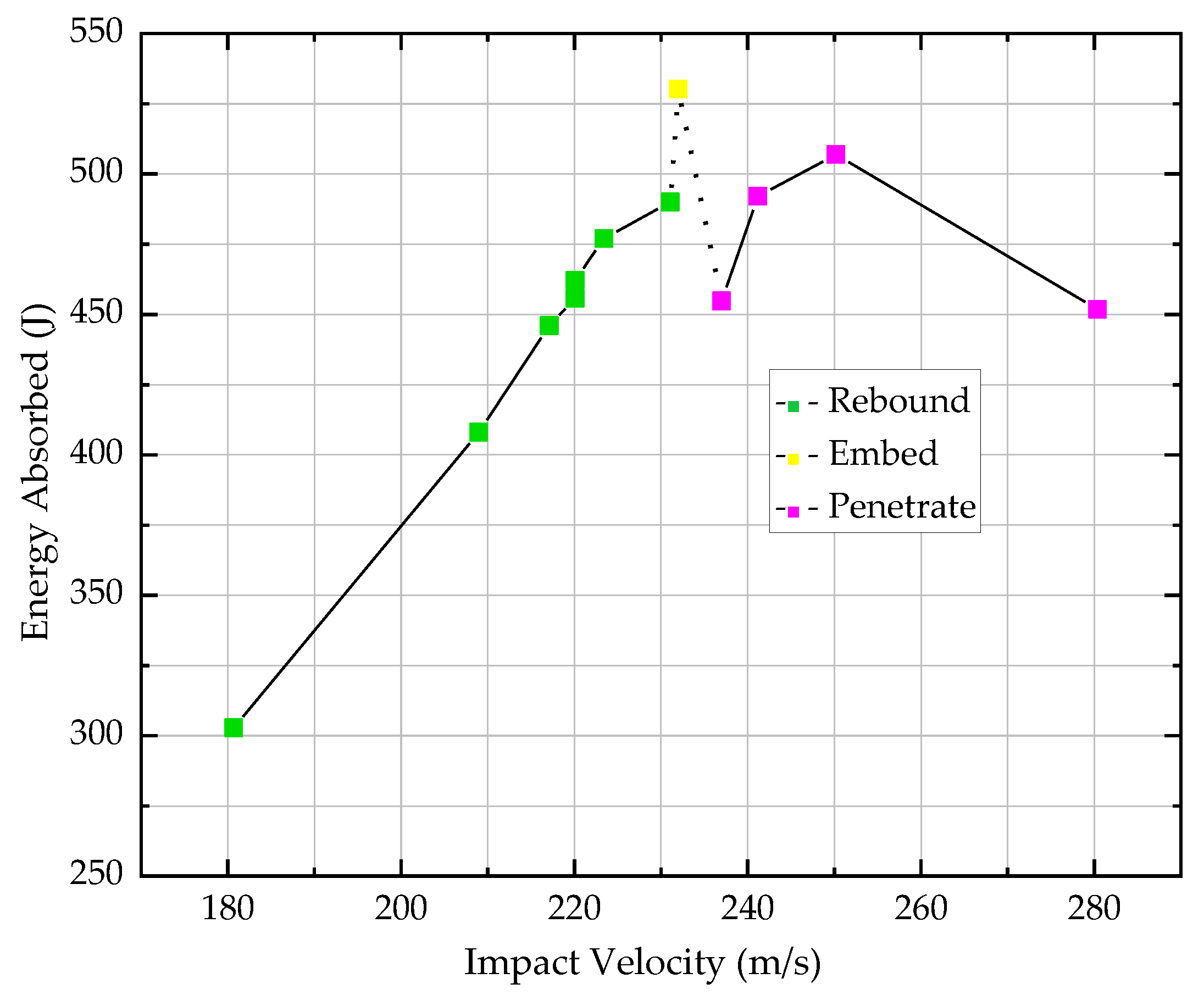
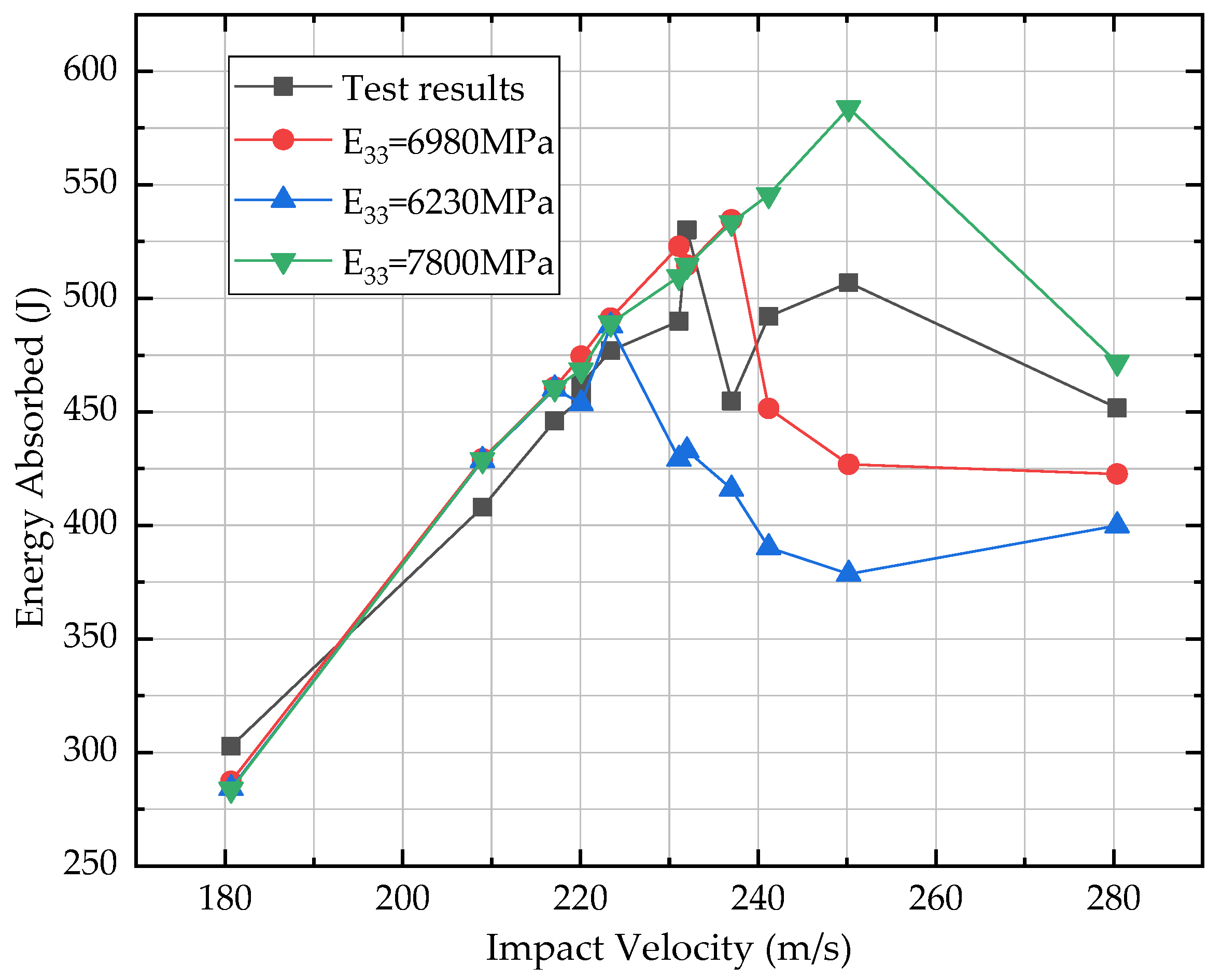
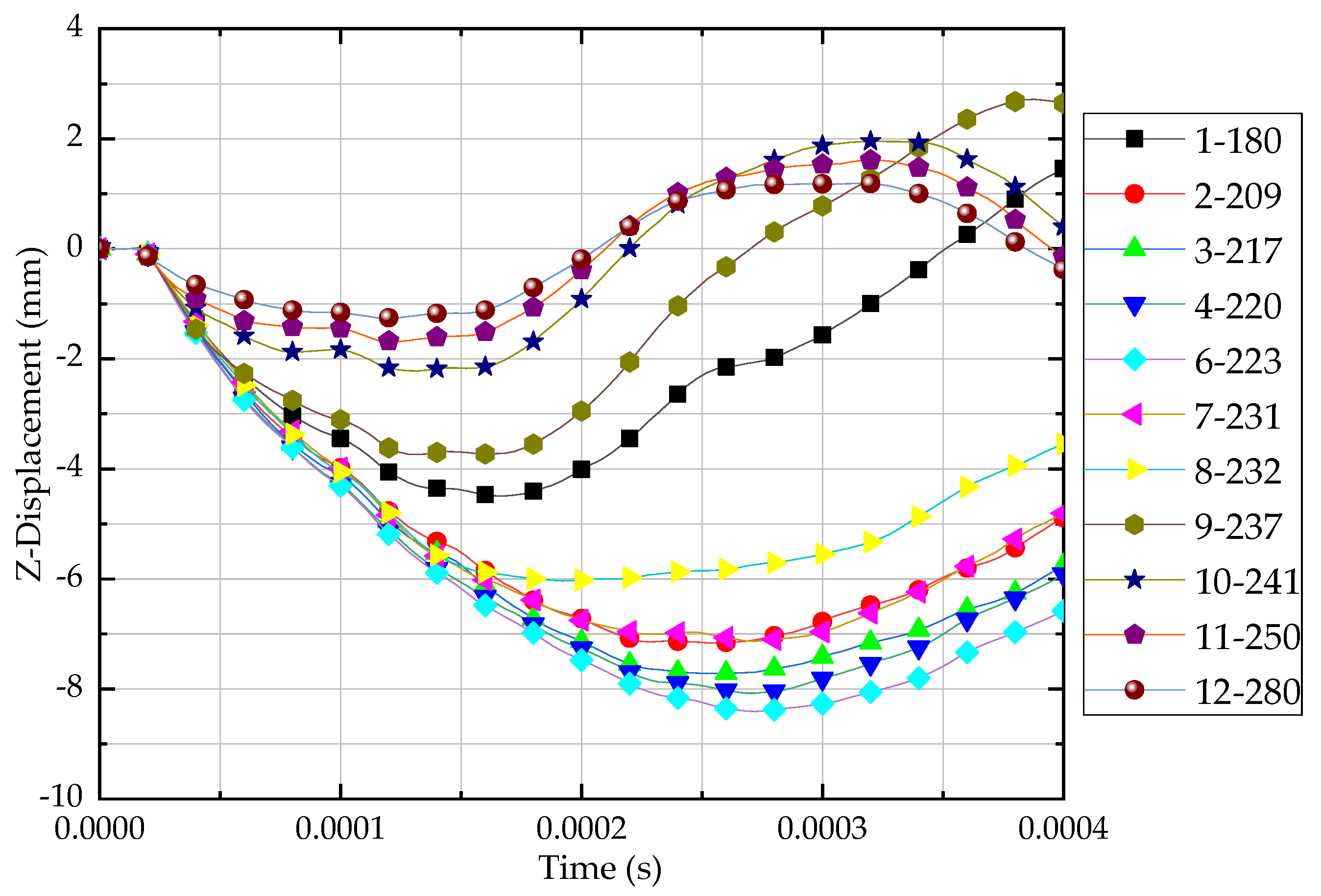
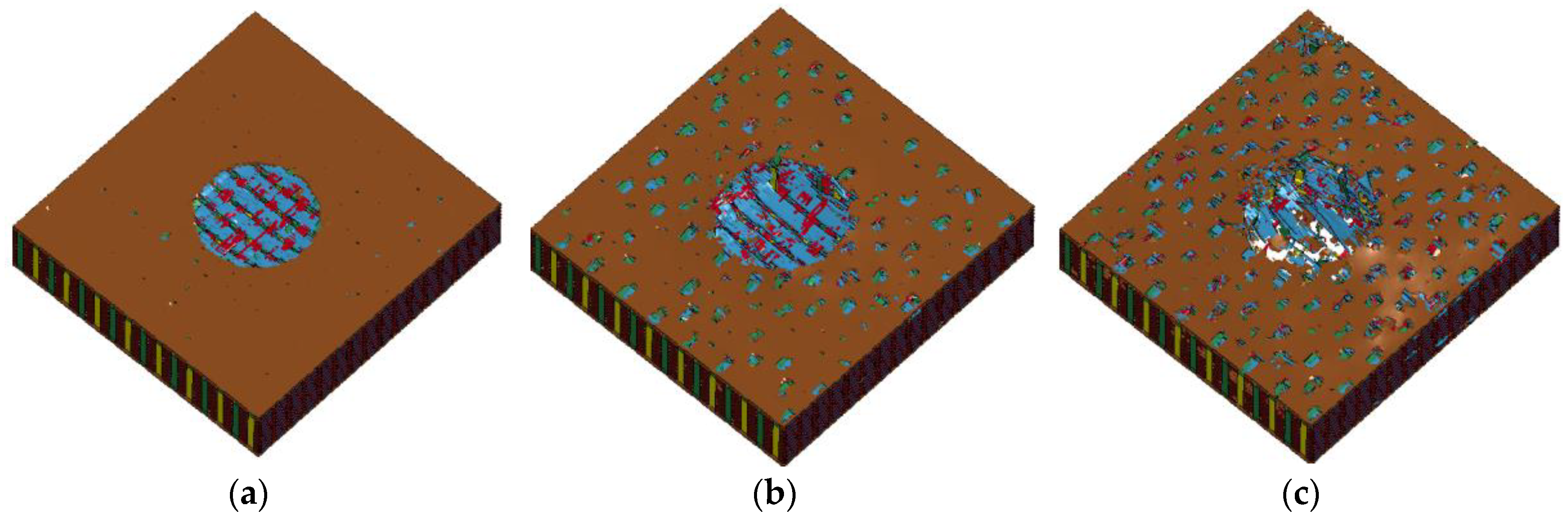
2.3. Test Results
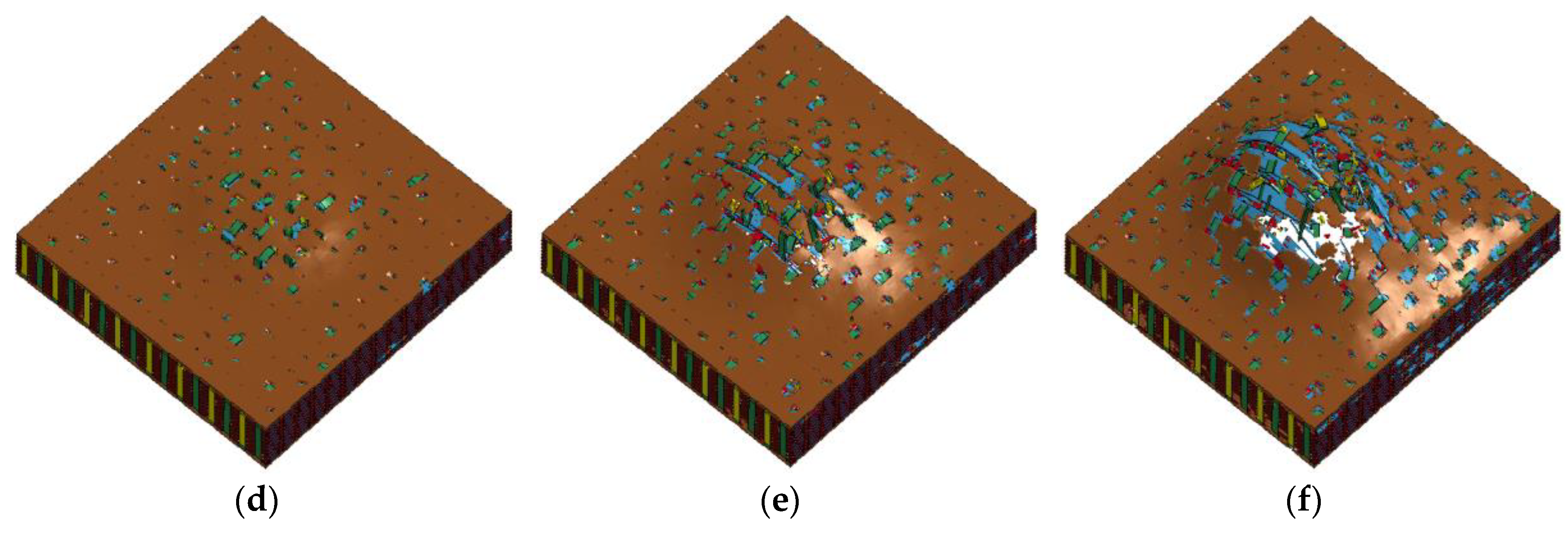
3. Finite Element Simulation
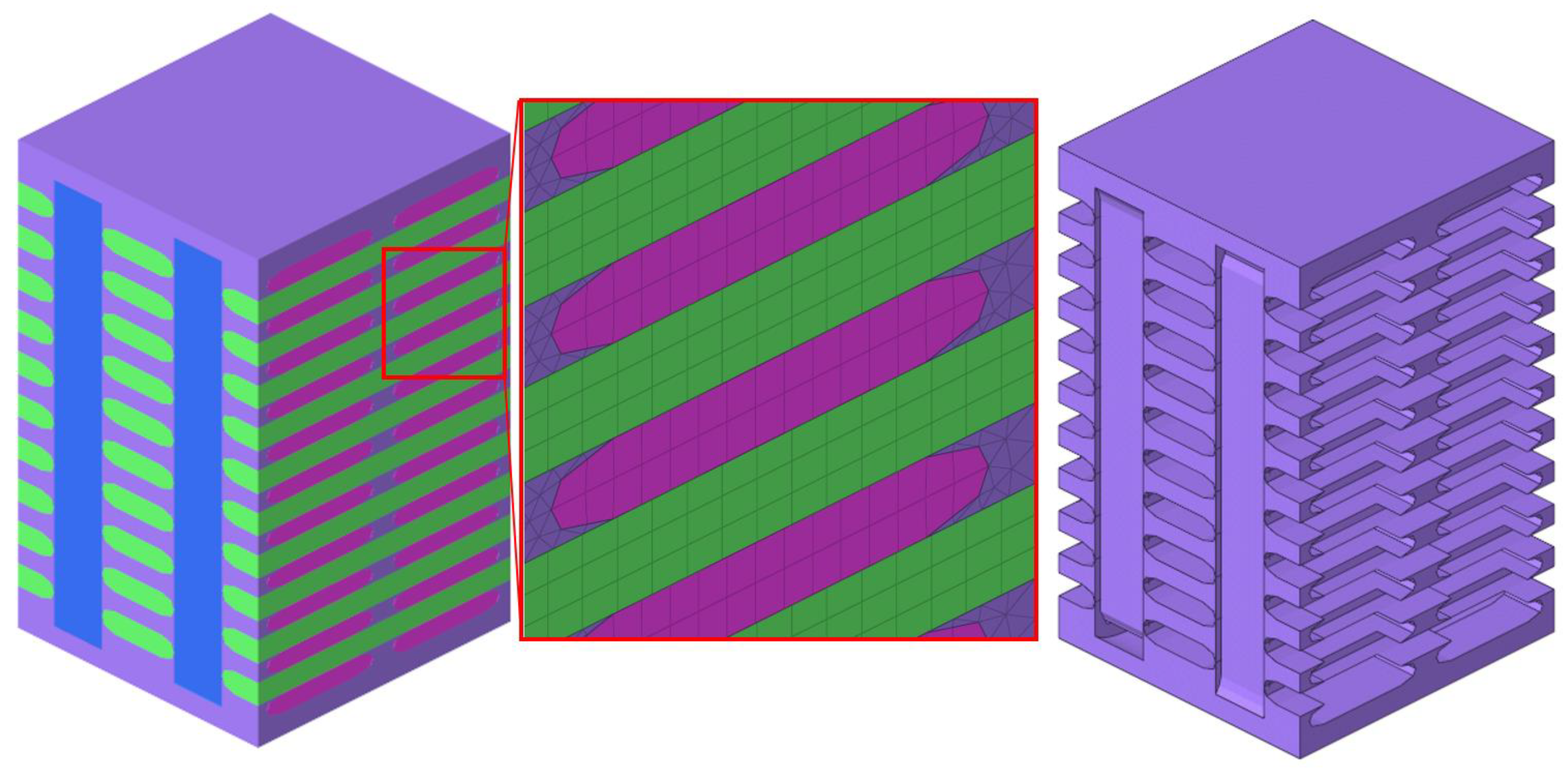
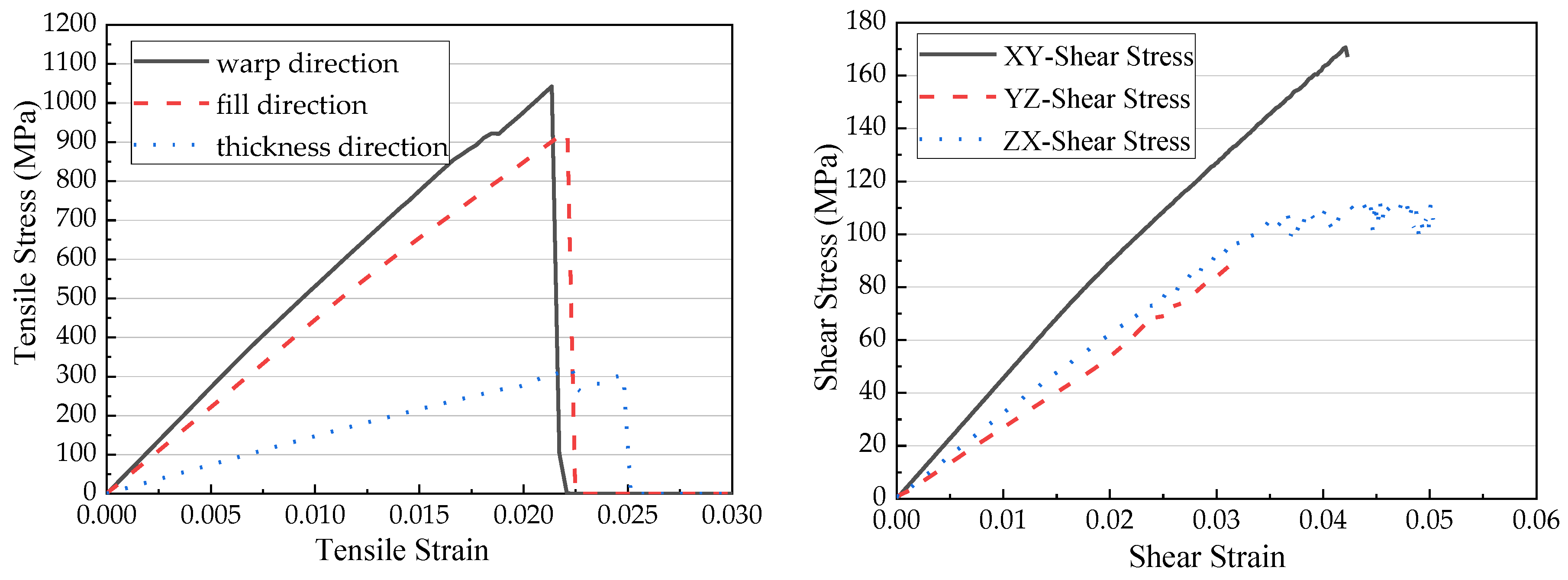
3.1. Micromchanical Modeling and Unit Cell Analysis
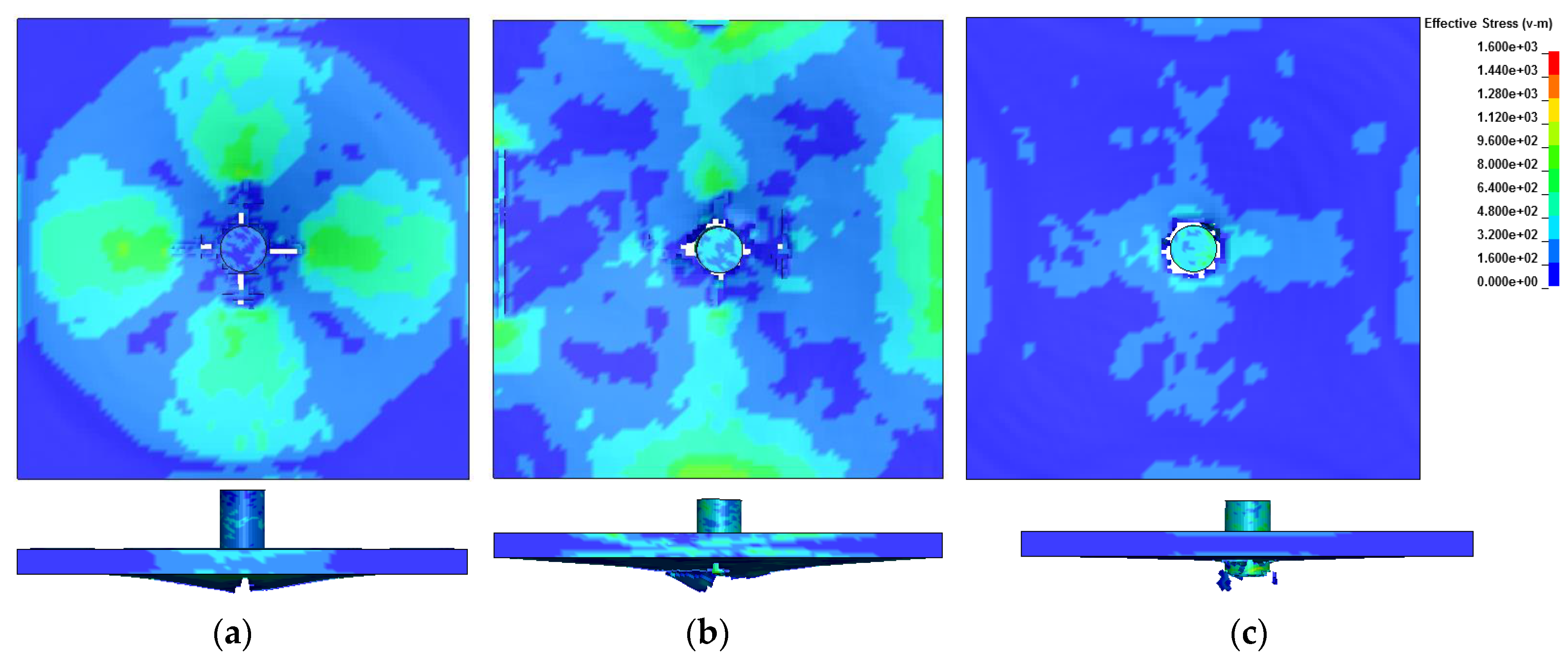
3.2. Macroscale Modeling
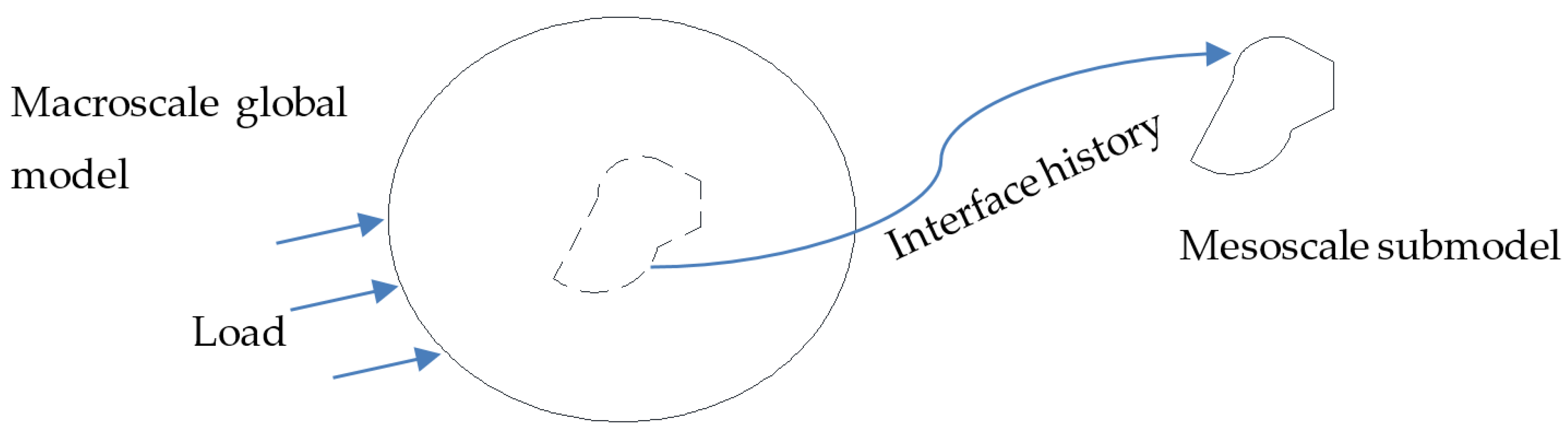
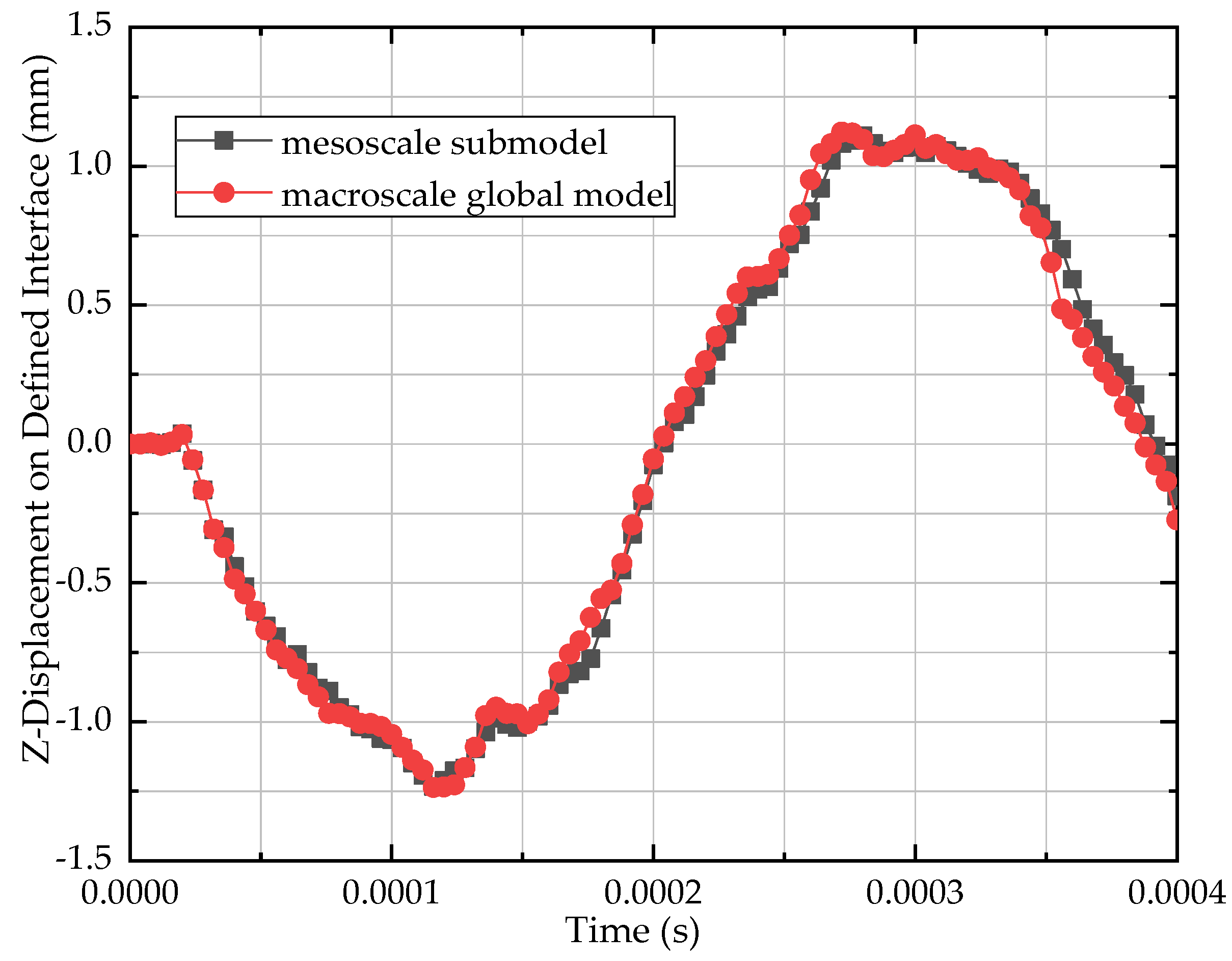
3.3. Combined Meso-Macroscale Modeling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saleh, M.N.; Soutis, C. Recent advancements in mechanical characterization of 3D woven composites. Mech. Adv. Mater. Mod. Process. 2017, 3, 12. [Google Scholar] [CrossRef]
- Goering, J.; McClain, M. Recent Developments In 3D Woven Pi Preforms. In Proceedings of the American Society for Composites, 22nd Technical Conference, Seattle, WA USA, 17–19 September 2007. [Google Scholar]
- Gardiner, G. 3D Preformed Composites: The Leap into LEAP. 2014. Available online: https://www.compositesworld.com/articles/3-d-preformed-composites-the-leap-into-leap (accessed on 30 September 2020).
- CCAR-33, Airworthiness Standards: Aircraft Engines; Civil Aviation Administration of China: Beijing, China, 2005. (In Chinese)
- Potluri, P.; Hogg, P.; Arshad, M. Influence of fibre architecture on impact damage tolerance in 3D woven composites. Appl. Compos. Mater. 2012, 19, 799–812. [Google Scholar] [CrossRef]
- Bahei-El-Din, Y.A.; Zikry, M.A. Impact-induced deformation fields in 2D and 3D woven composites. Compos. Sci. Technol. 2003, 63, 923–942. [Google Scholar] [CrossRef]
- Luo, Y. Transverse impact behavior and energy absorption of three-dimensional orthogonal hybrid woven composites. Compos. Struct. 2007, 81, 202–209. [Google Scholar] [CrossRef]
- Lv, L.; Sun, B.; Qiu, Y.; Gu, B. Energy absorptions and failure modes of 3D orthogonal hybrid woven composite struck by flat-ended rod. Polym. Compos. 2006, 27, 410–416. [Google Scholar] [CrossRef]
- Hao, A.; Sun, B.; Qiu, Y. Dynamic properties of 3-D orthogonal woven composite T-beam under transverse impact. Compos. A Appl. Sci. Manuf. 2008, 39, 1073–1082. [Google Scholar] [CrossRef]
- Tsai, P.; Jeng, Y.; Lee, J.; Stachiv, I.; Pittner, P. Effects of carbon nanotube reinforcement and grain size refinement mechanical properties and wear behaviors of carbon nanotube/copper composites. Diam. Relat. Mater. 2017, 74, 197–204. [Google Scholar] [CrossRef]
- Xuan, H.; Liu, L.; Chen, G. Impact Response and damage evolution of triaxial braided carbon/epoxy composites. Part I: Ballistic impact testing. J. Text. Res. 2013, 83, 1703–1716. [Google Scholar]
- Cater, C.R.; Xiao, X.; Goldberg, R.K.; Kohlman, L.W. Single ply and multi-ply braided composite response predictions using modified subcell approach. J. Aerosp. Eng. 2015, 28, 04014117. [Google Scholar] [CrossRef]
- Antin, K.N.; Laukkanen, A.; Andersson, T.; Smyl, D.; Vilaca, P. A multiscale modeling approach for estimating the effect of defects in unidirectional carbon fiber reinforced polymer composites. Materials 2019, 12, 1885. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, D.S.; Baudry, F.; Broucke, B.V.D.; Lomov, S.V.; Xie, H.; Verpoest, I. Failure analysis of triaxial braided composite. Compos. Sci. Technol. 2009, 69, 1372–1380. [Google Scholar] [CrossRef]
- Littell, J.D.; Binienda, W.K.; Roberts, G.D.; Goldbert, R.K. Characterization of damage in triaxial braided compos-ites under tensile loading. J. Aerosp. Eng. 2009, 22, 270–279. [Google Scholar] [CrossRef]
- Kohlman, L.W.; Bail, J.L.; Roberts, G.D.; Salem, J.A.; Martin, R.E.; Binienda, W.K. A notched coupon approach for tensile testing of braided composites. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1680–1688. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Binienda, W.K. Mesomechanical Model for Numerical Study of Two-Dimensional Triaxially Braided Composite. J. Eng. Mech. 2010, 136, 1366–1379. [Google Scholar]
- Hu, Y.; Binienda, W.K. Combined multiscale modeling of two-dimensional triaxially braided composites. In Proceedings of the Internationals Symposium on Structural Integrity, Nanjing, China, 2–5 November 2018. [Google Scholar]
- Nie, Z. Advanced Mesomechanical Modeling of Triaxially Braided Composites for Dynamic Impact Analysis with Fialure. Ph.D. Thesis, University of Akron, Akron, OH, USA, 2014. [Google Scholar]
- Sun, M. Multiscale Hybrid Element Modeling of Triaxial Braided Composite; University of Akron: Akron, OH, USA, 2018. [Google Scholar]
- Iredale, R.J.; Ward, C.; Hamerton, I. Modern advances in bismaleimide resin technology: A 21st century perspective on the chemistry of addition polyimides. Prog. Polym. Sci. 2017, 69, 1–21. [Google Scholar] [CrossRef]
- Calladine, C.R. Simple ideas in the large-deflection plastic theory of plates and slabs. In Engineering Plasticity; Heyman, J., Lechie, F.A., Eds.; Cambridge University Press: Cambridge, UK, 1968; pp. 93–127. [Google Scholar]
- Yu, T.; Qiu, X. Impact Dynamics, 1st ed.; Tsinghua University Press: Beijing, China, 2011; pp. 171–184. (In Chinese) [Google Scholar]
- Ma, P.; Jin, L.; Wu, L. Experimental and numerical comparisons of ballistic impact behaviors between 3D angle-interlock woven fabric and its reinforced composite. J. Ind. Text. 2019, 48, 1044–1058. [Google Scholar] [CrossRef]
- Li, Z.; Sun, B.; Gu, B. FEM simulation of 3D angle-interlock woven composite under ballistic impact from unit cell approach. Comput. Mater. Sci. 2010, 49, 171–183. [Google Scholar] [CrossRef]
- Chamis, C.C. Simplified composite micromechanics equations for strength, fracture toughness, and environmental effects. In Proceedings of the 29th Annual Conference of the Society of the Plastics Industry, Houston, TX, USA, 16–20 January 1984. [Google Scholar]
- Chamis, C.C. Mechanics of composite materials: Past, present and future. J. Compos. Tech. Res. 1989, 11, 3–14. [Google Scholar]
- Aboudi, J.; Arnold, S.M.; Bednarcyk, B.A. Micromechanics of Composite Materials: A Generalized Multiscale Analysis Approach, 1st ed.; Elsevier: Waltham, MA, USA, 2013; pp. 148–180. [Google Scholar]
- Bednarcyk, B.A.; Arnold, S.M. MAC/GMC 4.0 User’s Manuals-Keywords Manual, NASA/TM-2002-212-77/VOL2; NASA Glenn Research Center: Cleveland, OH, USA, 2002. [Google Scholar]
- Mishnaevsky, L., Jr.; Schmauder, S. Continuum mesomechanical finite element modeling in materials development: A state-of-the-art review. Appl. Mech. Rev. 2001, 54, 49–74. [Google Scholar] [CrossRef]
- LS-DYNA Keyword User’s Manual, Volume II Material Models; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2019.
- Harrington, J. Using Virtual Testing for Characterization of Composite Materials. Master’s Thesis, Arizona State University, Phoenix, AZ, USA, 2015. [Google Scholar]
- Liu, L. Research on the Containment of 2D Carbon Fiber Triaxial Braided Tape Wound Composite Casing. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2013. [Google Scholar]
- Lomov, S.V.; Bogdanovich, A.E.; Karahan, M.; Mungalov, D.; Verpoest, I. Mechanical behaviour of non-crimp 3D woven carbon/epoxy composite under in-plane tensile loading. In Proceedings of the 18th International Conference of Composite Materials, Jeju Island, Korea, 21–26 August 2011; Volume 18, pp. 1–5. [Google Scholar]
- Bogdanovich, A.E.; Karahan, M.; Lomov, S.V.; Verpoest, I. Quasi-static tensile behavior and damage of carbon/epoxy composite reinforced with 3D non-crimp orthogonal woven fabric. Mech. Mater. 2013, 62, 14–31. [Google Scholar] [CrossRef]
- LS-DYNA Keyword User’s Manual, Volume I; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2019.



| Property 1 | Fiber | Matrix |
|---|---|---|
| Material type | Toray T700 | BMI-A resin |
| Density (g/cm3) | 1.8 | 1.27 |
| Axial modulus (GPa) | 230 | 4.03 |
| Transverse modulus (GPa) | 15 | 4.03 |
| Shear modulus (GPa) | 24 (Axial)/5.03 (Transverse) | 101 |
| Tensile strength (MPa) | 4900 | 107.1 |
| Shear strength (MPa) | - | 100.7 |
| Filament diameter (μm) | 7 | - |
| Glass transition temperatures (°C) | - | ~250 |
| Parameters | Composites Studied | Parameters | Composites Studied |
|---|---|---|---|
| Textile type | 3D orthogonal woven | Density in weft (yarns/cm) | 3.8 |
| Fibers per yarn | 12k | Thickness (mm) | ~8 |
| Density in warp (yarns/cm) | 4 | Fiber volume fraction (%) | ~54 |
| Test No. | Projectile Velocity (Vi, m/s) | Initial Kinetic Energy (J) | Residual Velocity 1 (Vr, m/s) | Absorbed Energy (J) |
|---|---|---|---|---|
| 1 | 180.7 | 319.99 | −41.9 | 302.79 |
| 2 | 209.0 | 430.26 | −47.5 | 408.03 |
| 3 | 217.1 | 461.90 | −40.3 | 445.98 |
| 4 | 220.1 | 474.75 | −44.1 | 455.69 |
| 5 | 220.1 | 474.75 | −35.9 | 462.12 |
| 6 | 223.4 | 491.59 | −38.5 | 476.99 |
| 7 | 231.1 | 523.39 | −58.4 | 489.97 |
| 8 | 232.0 | 530.17 | 0 | 530.17 |
| 9 | 237.0 | 553.26 | 100 | 454.76 |
| 10 | 241.2 | 570.14 | 89.3 | 491.99 |
| 11 | 250.2 | 613.48 | 104.3 | 506.87 |
| 12 | 280.4 | 774.45 | 181 | 451.75 |
| Property 1 | Fiber Yarn |
|---|---|
| Elastic Modulus , MPa | 180,287 |
| Elastic modulus , MPa | 11,381 |
| Poisson ratio, | 0.24356 |
| Shear modulus , MPa | 7863 |
| Shear modulus , MPa | 3962 |
| Tension strength , MPa | 3841 |
| Tension strength , MPa | 356 |
| Compression strength , MPa | 1538 |
| Compression strength , MPa | 422 |
| Shear strength , MPa | 2302 |
| E (GPa) | ν | ρ (kg/m3) | Tm (K) | Tr (K) | Cp (J/kg*K) | (s−1) | A (MPa) | B (MPa) |
| 113 | 0.33 | 4.43 × 103 | 1878 | 293 | 580 | 1 | 1089 | 1083 |
| C | n | m | D1 | D2 | D3 | D4 | D5 | |
| 0.014 | 0.93 | 1.1 | −0.09 | 0.27 | 0.48 | 0.014 | 3.87 |
| ρ (kg/m3) | E11 (GPa) 1 | E22 (GPa) | E33 (GPa) | v21 | v32 |
| 1.563 × 10−9 | 55.4 | 50.21 | 6.98 | 0.1618 | 0.1535 |
| G12 (MPa) | G23 (MPa) | G31 (MPa) | |||
| 3580 | 2220 | 2440 | 0.021 | 0.021 | 0.025 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; He, Z.; Xuan, H. Impact Resistance Study of Three-Dimensional Orthogonal Carbon Fibers/BMI Resin Woven Composites. Materials 2020, 13, 4376. https://doi.org/10.3390/ma13194376
Hu Y, He Z, Xuan H. Impact Resistance Study of Three-Dimensional Orthogonal Carbon Fibers/BMI Resin Woven Composites. Materials. 2020; 13(19):4376. https://doi.org/10.3390/ma13194376
Chicago/Turabian StyleHu, Yanqi, Zekan He, and Haijun Xuan. 2020. "Impact Resistance Study of Three-Dimensional Orthogonal Carbon Fibers/BMI Resin Woven Composites" Materials 13, no. 19: 4376. https://doi.org/10.3390/ma13194376
APA StyleHu, Y., He, Z., & Xuan, H. (2020). Impact Resistance Study of Three-Dimensional Orthogonal Carbon Fibers/BMI Resin Woven Composites. Materials, 13(19), 4376. https://doi.org/10.3390/ma13194376




