Study of the Fracture Behavior of Tetragonal Zirconia Polycrystal with a Modified Phase Field Model
Abstract
:1. Introduction
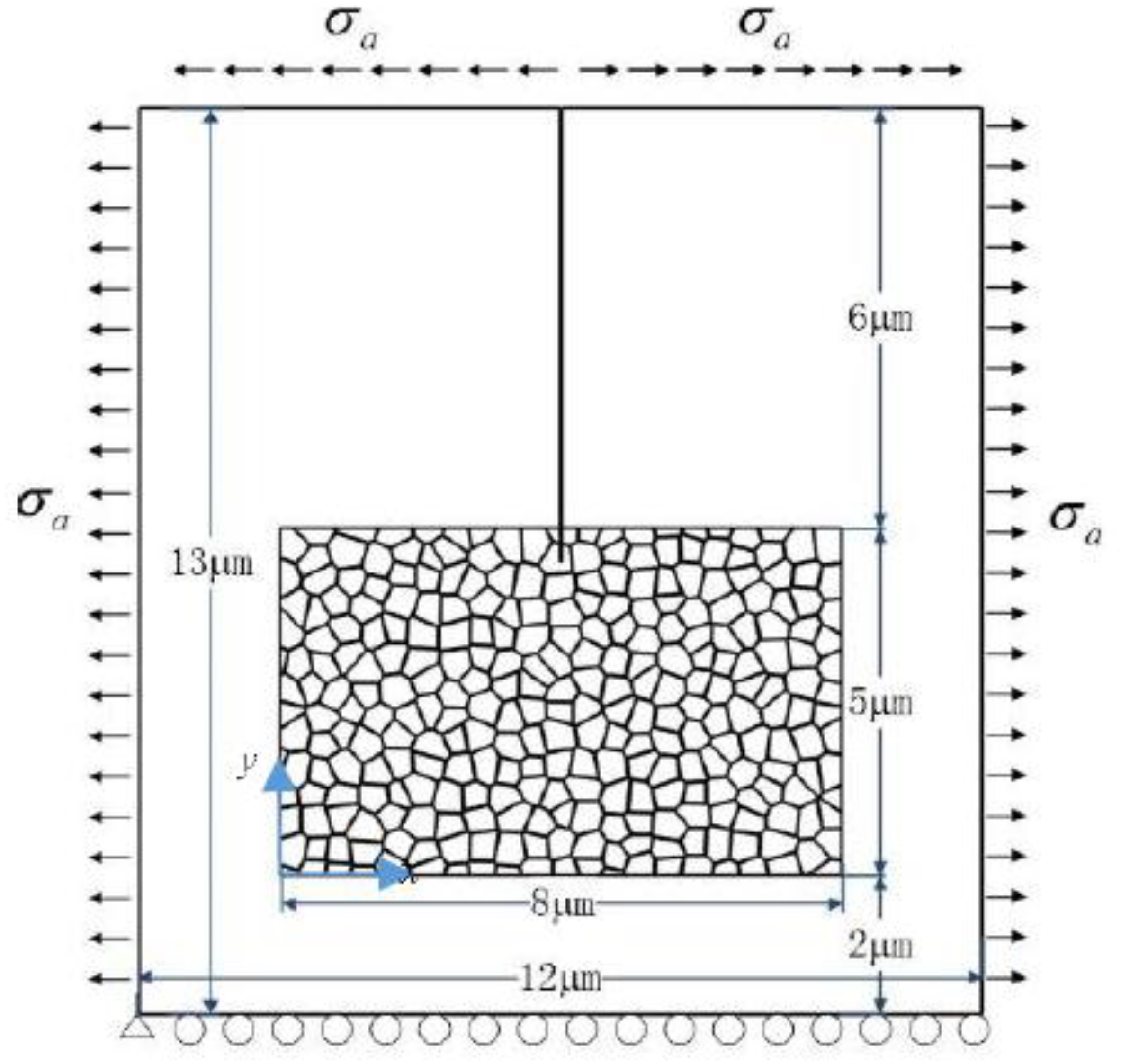
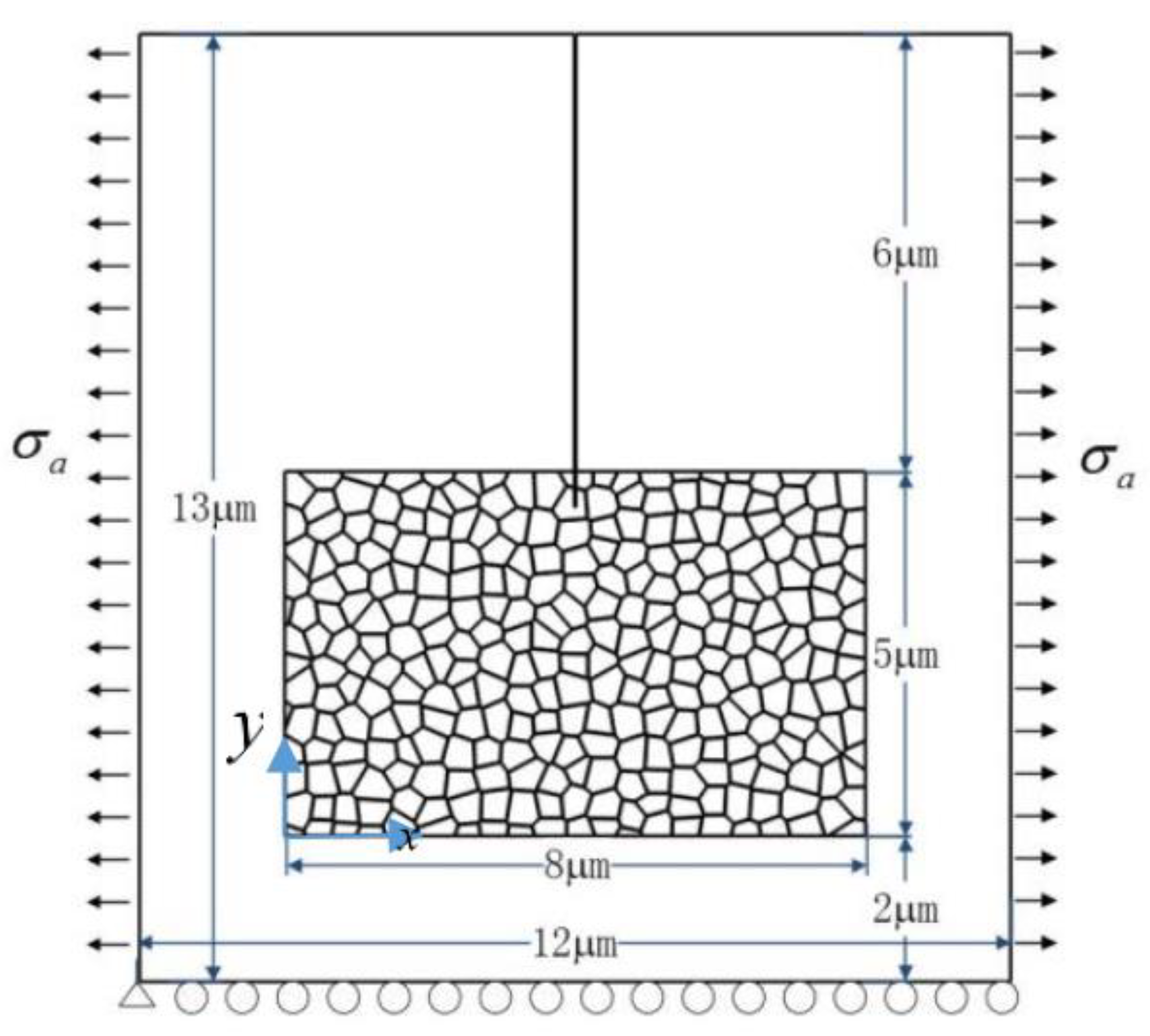
2. The Coupled PF Model for Crack Propagation in TZP
3. Results and Discussion
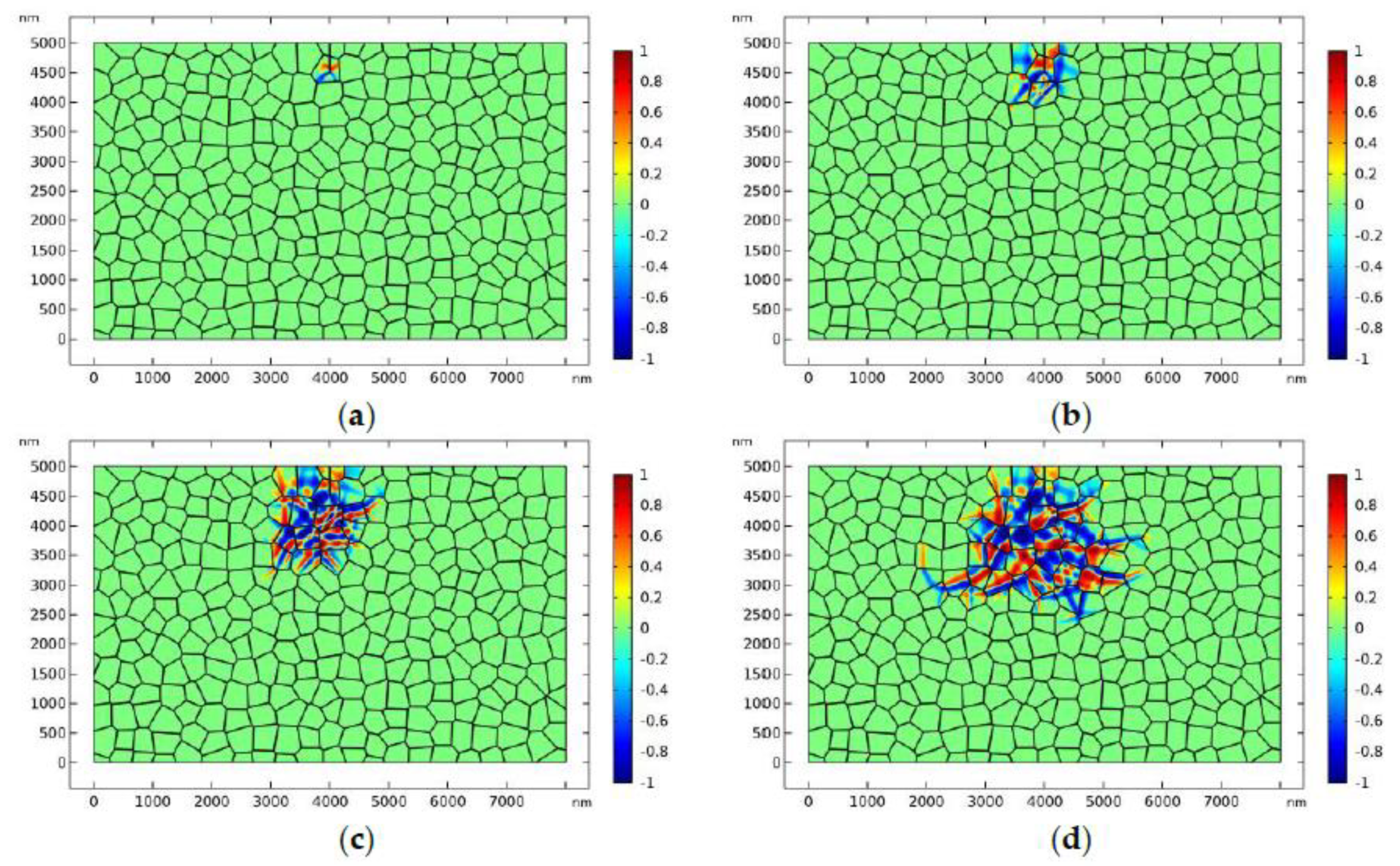
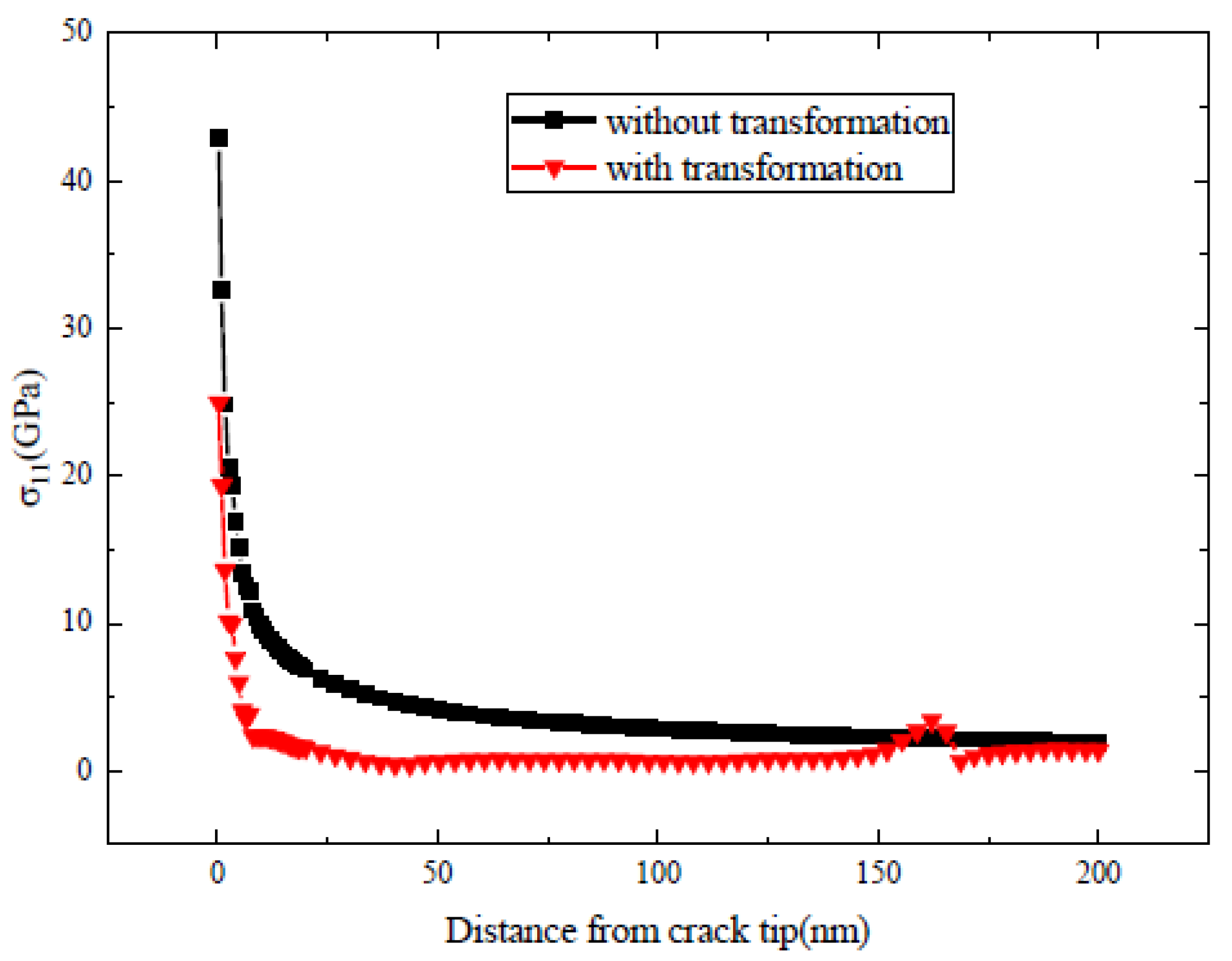
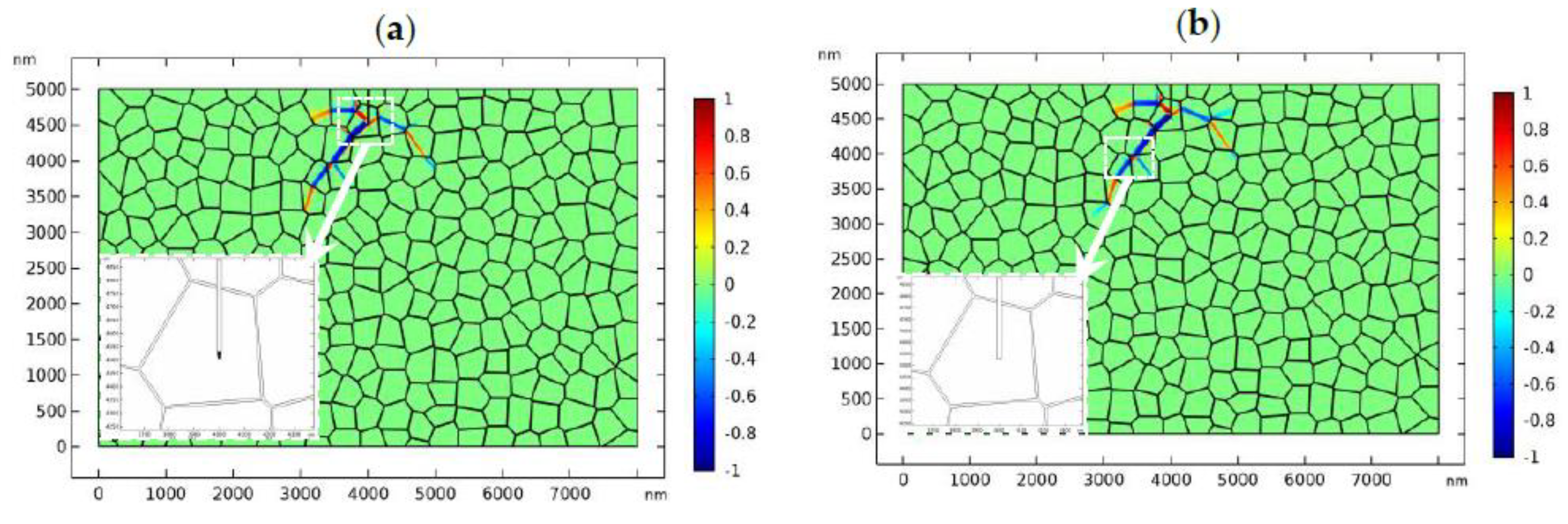
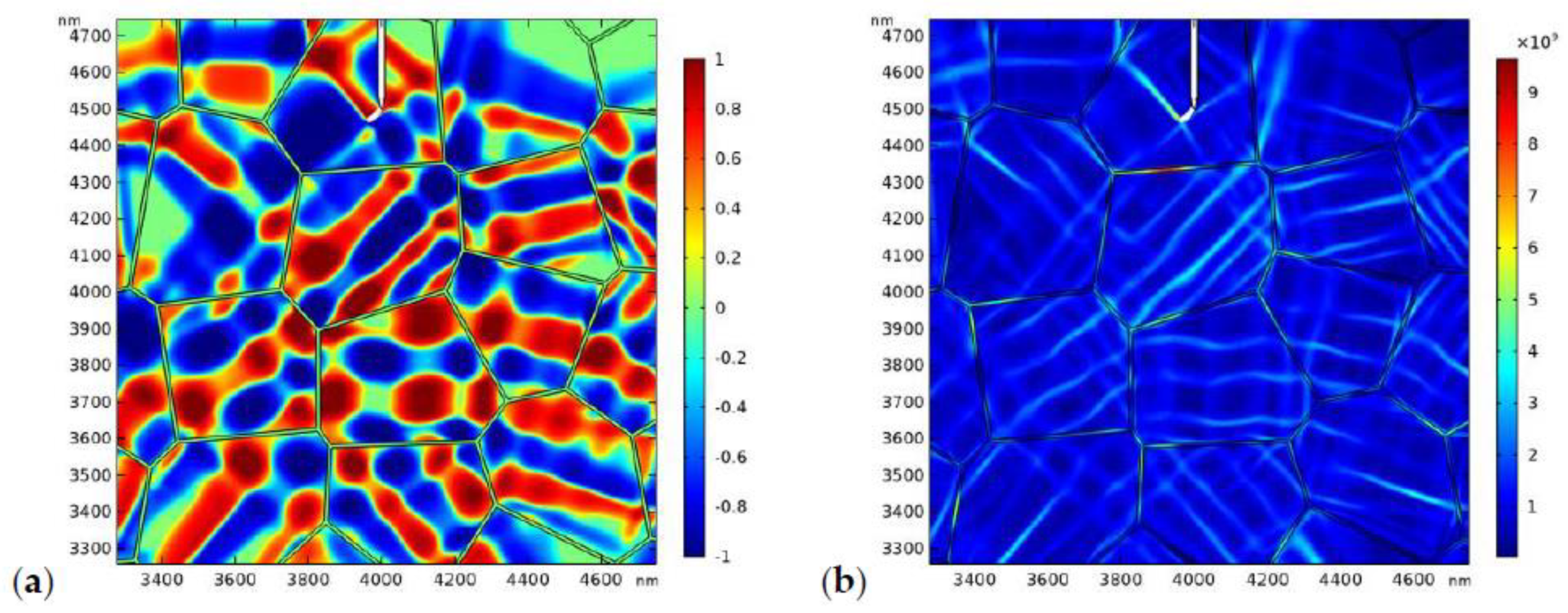
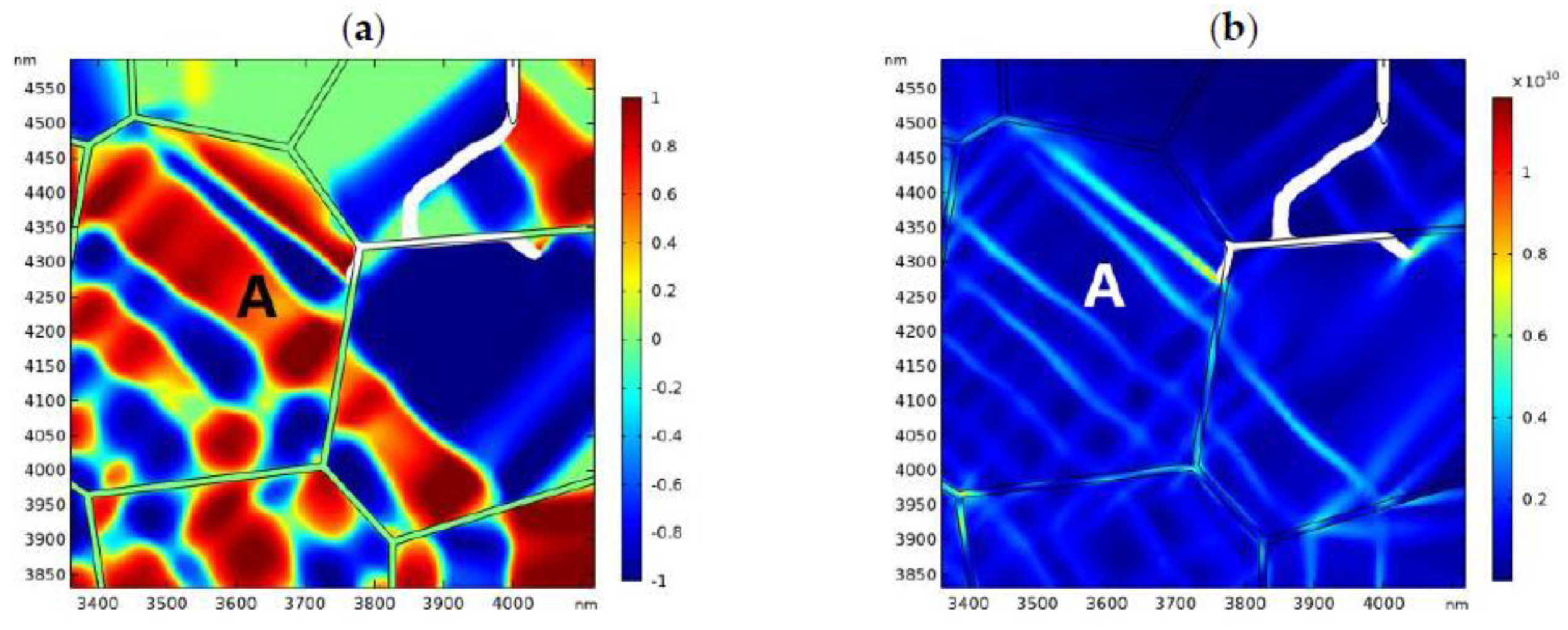
3.1. Transformation Zone around a Static Crack
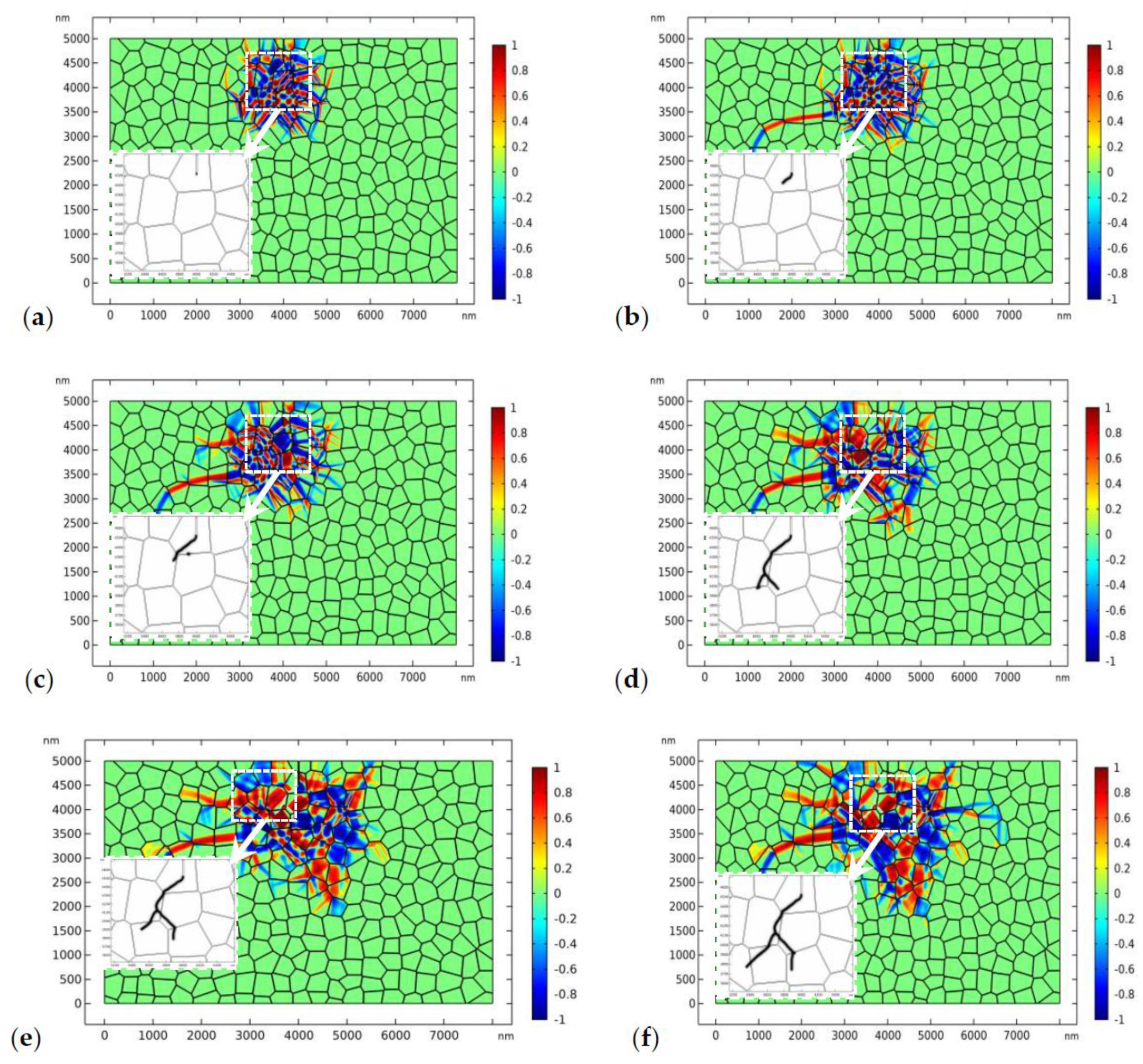
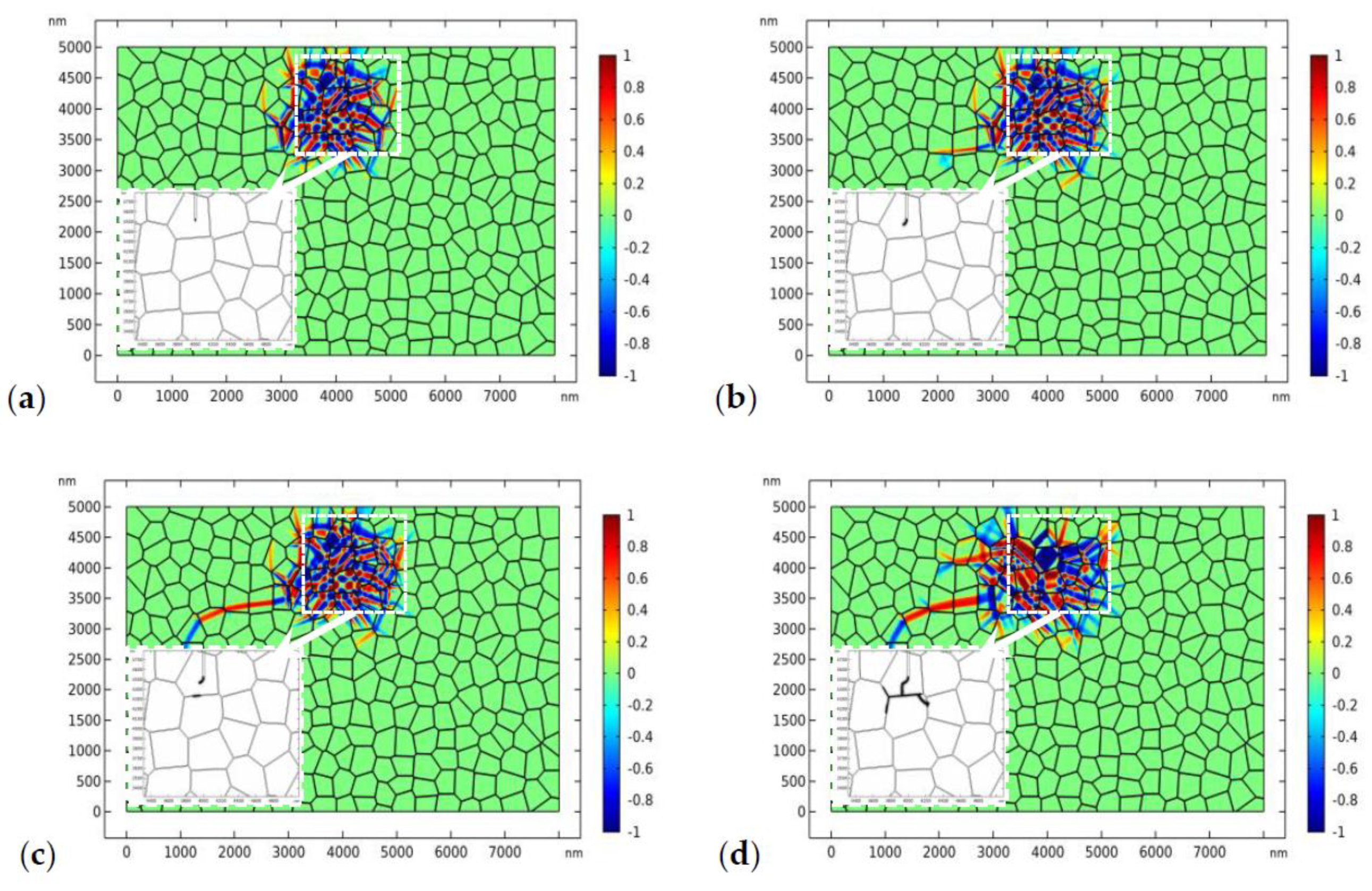
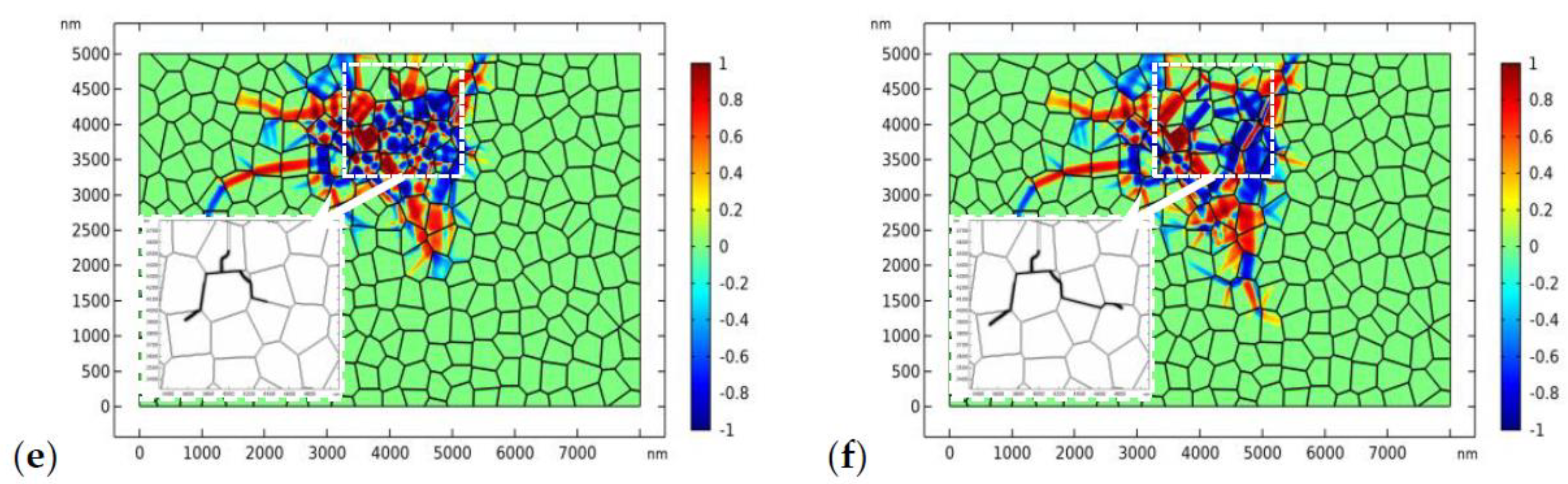
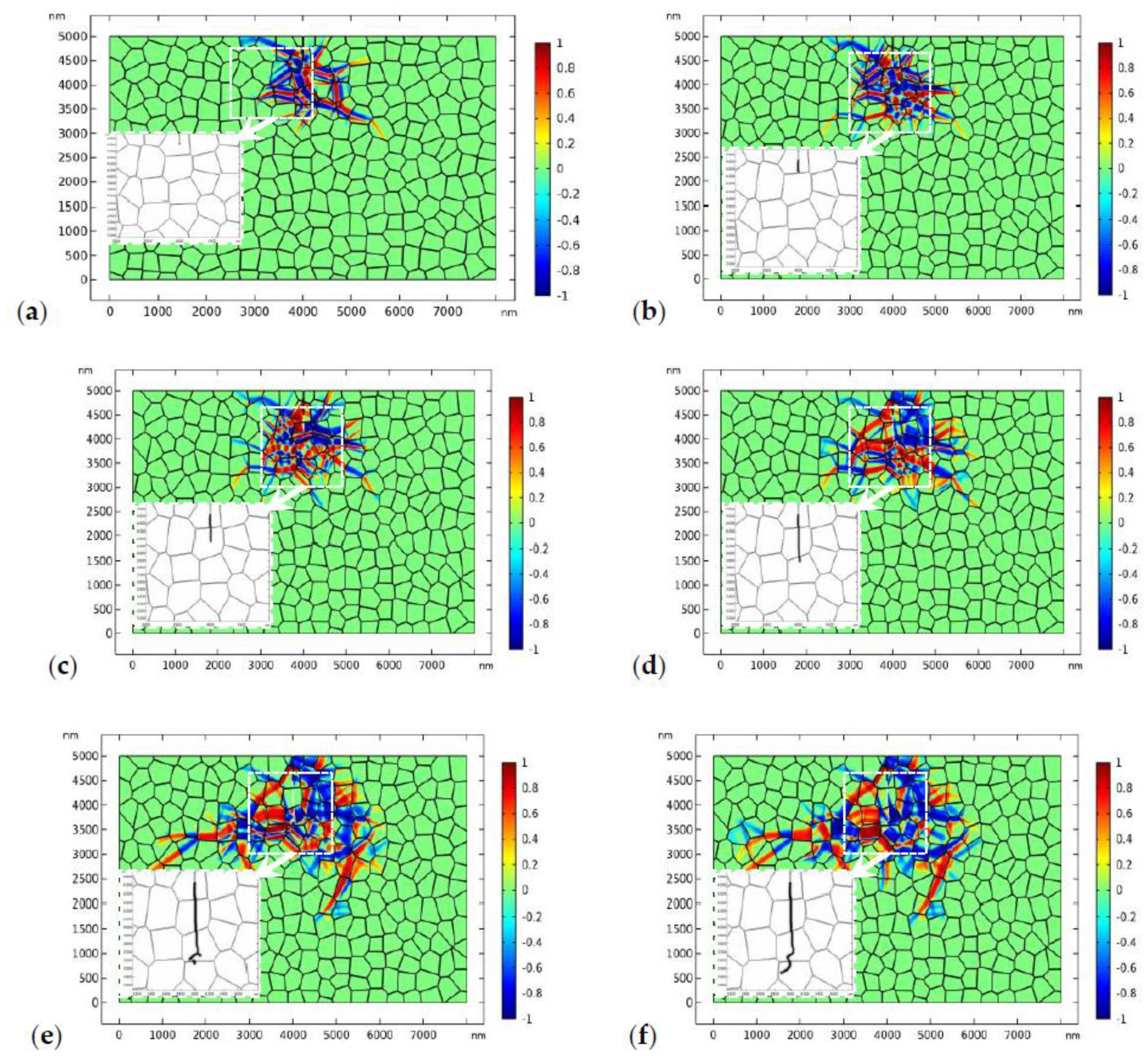
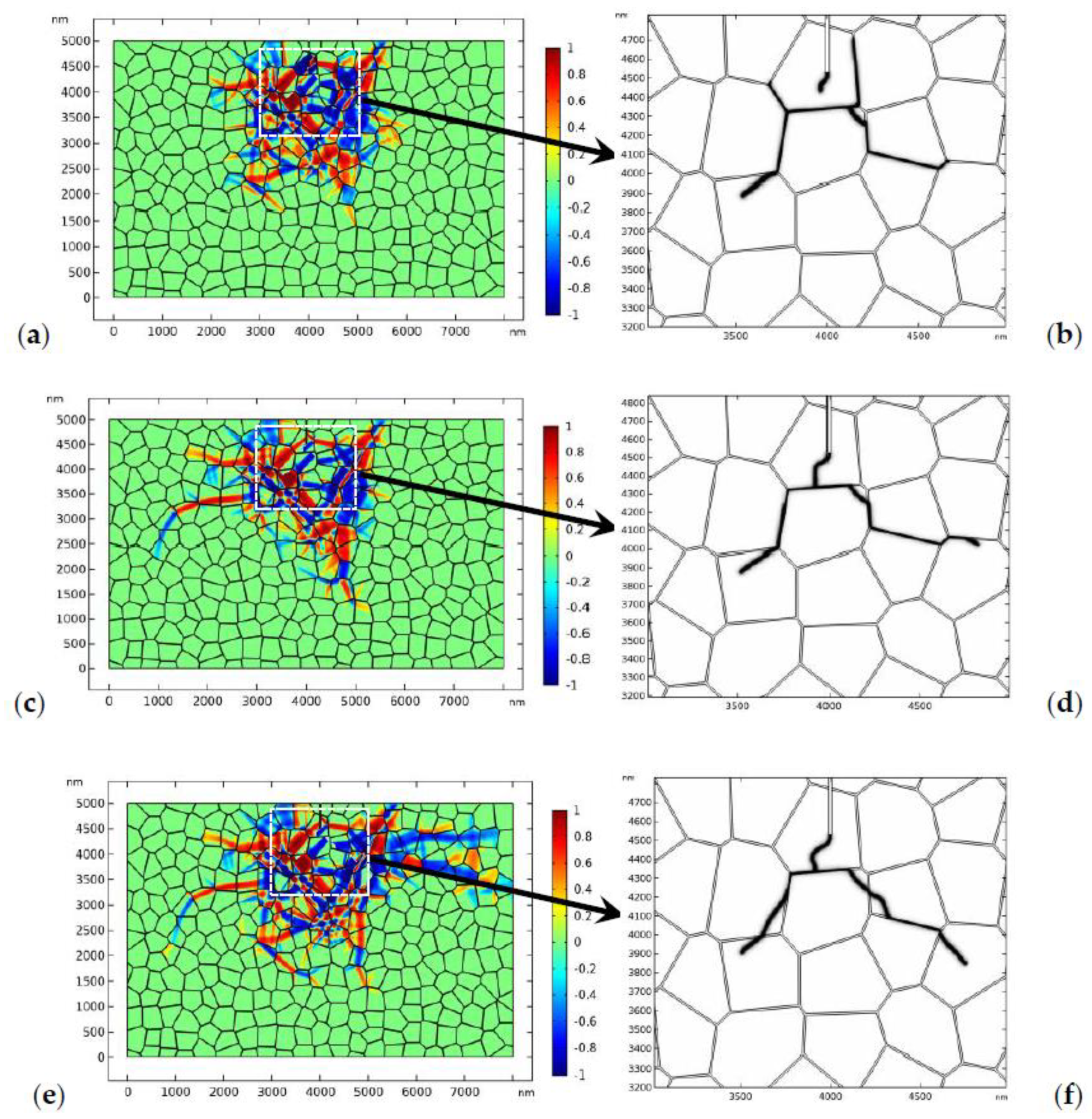
3.2. Crack Propagation in TZP
4. Conclusions
- The phase evolution process around the crack tip can be directly characterized with the PF model. The shape and size of the phase transformation zone around the crack tip are firstly predicted with the mesoscale PF model.
- The phase transformation can decrease the stress around the static crack tip and retards its propagation. The toughening effect of phase transformation on the initial crack has been confirmed by the crack propagation model (Figure 7).
- For crack propagation in TZP, the phase patterns and the crack evolve simultaneously. The crack may experience deflection or branching due to the perturbation of the stress field by the complex phase patterns.
- The crystal orientation, the fracture toughness of the GBs, and the external load all have important influences on the topology of crack propagation in TZP. For TZP with strong GBs, the crack tends to propagate transgranularly, while the crack is more likely to propagate intergranularly for TZP with low GB fracture toughness. Under higher loads, the crack has the tendency to propagate transgranularly.
Author Contributions
Funding
Conflicts of Interest
References
- Garvie, R.C.; Hannink, R.H.; Pascoe, R.T. Ceramic steel? Nature 1975, 258, 703–704. [Google Scholar] [CrossRef]
- Marshall, D.B.; Shaw, M.C.; Dauskardt, R.H.; Ritchie, R.O.; Readey, M.J.; Heuer, A.H. Crack-Tip Transformation Zones in Toughened Zirconia. J. Am. Ceram. Soc. 1990, 73, 2659–2666. [Google Scholar] [CrossRef]
- Wang, J.S.; Tsai, J.F.; Shetty, D.K.; Virkar, A.V. Effect of MnO on the microstructures, phase stability, and mechanical properties of ceria-partially-stabilized zirconia (Ce–TZP) and Ce–TZP–Al2O3 composites. J. Mater. Res. 1990, 5, 1948–1957. [Google Scholar] [CrossRef]
- Yu, C.S.; Shetty, D.K. Transformation Zone Shape, Size, and Crack-Growth-Resistance [R-Curve] Behavior of Ceria-Partially-Stabilized Zirconia Polycrystals. J. Am. Ceram. Soc. 1989, 72, 921–928. [Google Scholar] [CrossRef]
- Yu, C.S.; Shetty, D.K. Transformation yielding, plasticity and crack-growth-resistance (R-curve) behaviour of CeO2-TZP. J. Mater. Sci. 1990, 25, 2025–2035. [Google Scholar] [CrossRef]
- Yu, C.S.; Shetty, D.K.; Shaw, M.C.; Marshall, D.B. Transformation Zone Shape Effects on Crack Shielding in Ceria-Partially-Stabilized Zirconia (Ce-TZP)-Alumina Composites. J. Am. Ceram. Soc. 1992, 75, 2991–2994. [Google Scholar] [CrossRef]
- Tsai, J.F.; Yu, C.S.; Shetty, D.K. Role of Autocatalytic Transformation in Zone Shape and Toughening of Ceria-Tetragonal-Zirconia-Alumina (Ce-TZP/Al2O3) Composites. J. Am. Ceram. Soc. 1991, 74, 678–681. [Google Scholar] [CrossRef]
- Tsai, J.F.; Chon, U.; Ramachandran, N.; Shetty, D.K. Transformation Plasticity and Toughening in CeO2-Partially-Stabilized Zirconia-Alumina (Ce-TZP/Al2O3) Composites Doped with MnO. J. Am. Ceram. Soc. 1992, 75, 1229–1238. [Google Scholar] [CrossRef]
- Becher, P.F.; Swain, M.V. Grain-Size-Dependent Transformation Behavior in Polycrystalline Tetragonal Zirconia. J. Am. Ceram. Soc. 1992, 75, 493–502. [Google Scholar] [CrossRef]
- Deville, S.; El Attaoui, H.; Chevalier, J. Atomic force microscopy of transformation toughening in ceria-stabilized zirconia. J. Eur. Ceram. Soc. 2005, 25, 3089–3096. [Google Scholar] [CrossRef] [Green Version]
- Rose, L.R.F.; Swain, M.V. Transformation zone shape in ceria partially-stabilized zirconia. Acta Met. 1988, 36, 955–962. [Google Scholar] [CrossRef]
- McMeeking, R.M.; Evans, A.G. Mechanics of Transformation-Toughening in Brittle Materials. J. Am. Ceram. Soc. 1982, 65, 242–246. [Google Scholar] [CrossRef]
- Budiansky, B.; Hutchinson, J.W.; Lambropoulos, J.C. Continuum Theory of Dilatant Transformation Toughening in Ceramics. Int. J. Solids Struct. 1983, 19, 337–355. [Google Scholar] [CrossRef]
- Lambropoulos, J.C. Effect of Nucleation on Transformation Toughening. J. Am. Ceram. Soc. 1986, 69, 218–222. [Google Scholar] [CrossRef]
- Chen, I.W.; Morel, P.E.R. Implications of Transformation Plasticity in ZrO2-Containing Ceramics: I, Shear and Dilatation Effects. J. Am. Ceram. Soc. 1986, 69, 181–189. [Google Scholar] [CrossRef]
- Rose, L.R.F. The Mechanics of Transformation Toughening. Proc. R. Soc. London. Ser. A 1987, 412, 169–197. [Google Scholar] [CrossRef]
- Chen, I.W. Model of Transformation Toughening in Brittle Materials. J. Am. Ceram. Soc. 1991, 74, 2564–2572. [Google Scholar] [CrossRef]
- Sun, Q.P.; Hwang, K.C.; Yu, S.W. A micromechanics constitutive model of transformation plasticity with shear and dilatation effect. J. Mech. Phys. Solids 1991, 39, 507–524. [Google Scholar] [CrossRef]
- Stam, G.T.M.; van der Giessen, E.; Meijers, P. Effect of transformation-induced shear strains on crack growth in zirconia-containing ceramics. Int. J. Solids Struct. 1994, 31, 1923–1948. [Google Scholar] [CrossRef] [Green Version]
- Luo, J.; Xiao, Z.M. Transformation toughening behavior of two edge cracks emanating from a circular hole in zirconia ceramics. Int. J. Fract. 2005, 131, 351–366. [Google Scholar] [CrossRef]
- Tian-Fu, G.; Qing-Ping, S.; Xing, Z. The role of autocatalysis and transformation shear in crack tip zone shape and toughening of zirconia ceramics. Int. J. Solids Struct. 1997, 34, 4213–4236. [Google Scholar] [CrossRef]
- Liu, B.; Liu, N.; Luo, J.; Xiao, Z. Study of Transformation Toughening Behavior of an Edge Through Crack in Zirconia Ceramics with the Cohesive Zone Model. Int. J. Appl. Mech. 2018, 10, 1850066. [Google Scholar] [CrossRef]
- Hannink, R.H.J.; Kelly, P.M.; Muddle, B.C. Transformation Toughening in Zirconia-Containing Ceramics. J. Am. Ceram. Soc. 2000, 83, 461–487. [Google Scholar] [CrossRef]
- Kelly, P.M.; Rose, L.R.F. The martensitic transformation in ceramics—its role in transformation toughening. Prog. Mater. Sci. 2002, 47, 463–557. [Google Scholar] [CrossRef]
- Basu, B. Toughening of yttria-stabilised tetragonal zirconia ceramics. Int. Mater. Rev. 2005, 50, 239–256. [Google Scholar] [CrossRef]
- Evans, A.G.; Heuer, A.H. REVIEW—Transformation Toughening in Ceramics: Martensitic Transformations in Crack-Tip Stress Fields. J. Am. Ceram. Soc. 1980, 63, 241–248. [Google Scholar] [CrossRef]
- Heuer, A.H.; Lange, F.F.; Swain, M.V.; Evans, A.G. Transformation Toughening: An Overview. J. Am. Ceram. Soc. 1986, 69, i–iv. [Google Scholar] [CrossRef]
- Lambropoulos, J.C. Shear, shape and orientation effects in transformation toughening. Int. J. Solids Struct. 1986, 22, 1083–1106. [Google Scholar] [CrossRef]
- Chen, I.W.; Reyes-Morel, P.E. Transformation Plasticity and Transformation Toughening in Mg-PSZ and Ce-TZP. MRS Proc. 1986, 78, 75. [Google Scholar] [CrossRef]
- Rauchs, G.; Fett, T.; Munz, D.; Oberacker, R. Tetragonal-to-monoclinic phase transformation in CeO2-stabilized zirconia under multiaxial loading. J. Eur. Ceram. Soc. 2002, 22, 841–849. [Google Scholar] [CrossRef]
- Chen, L.Q. Phase-Field Models for Microstructure Evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef] [Green Version]
- Boettinger, W.J.; Warren, J.A.; Beckermann, C.; Karma, A. Phase-Field Simulation of Solidification. Annu. Rev. Mater. Res. 2002, 32, 163–194. [Google Scholar] [CrossRef]
- Zaeem, M.A.; El Kadiri, H.; Wang, P.T.; Horstemeyer, M.F. Investigating the effects of grain boundary energy anisotropy and second-phase particles on grain growth using a phase-field model. Comput. Mater. Sci. 2011, 50, 2488–2492. [Google Scholar] [CrossRef]
- Wu, R.; Sandfeld, S. A dislocation dynamics-assisted phase field model for Nickel-based superalloys: The role of initial dislocation density and external stress during creep. J. Alloy. Compd. 2017, 703, 389–395. [Google Scholar] [CrossRef]
- Wu, R.; Yue, Z.; Wang, M. Effect of initial γ/γ′ microstructure on creep of single crystal nickel-based superalloys: A phase-field simulation incorporating dislocation dynamics. J. Alloy. Compd. 2019, 779, 326–334. [Google Scholar] [CrossRef]
- Wu, R.; Zhao, Y.; Liu, Y.; Ai, X. High temperature creep mechanisms of a single crystal superalloy: A phase-field simulation and microstructure characterization. Prog. Nat. Sci. 2020. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, L.; Yue, P.; Sun, W. Fracture failure in crack interaction of asphalt binder by using a phase field approach. Mater. Struct. 2015, 48, 2997–3008. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Zhao, T.; Zhu, J.; Luo, J. Study of crack propagation behavior in single crystalline tetragonal zirconia with the phase field method. Eng. Fract. Mech. 2016, 159, 155–173. [Google Scholar] [CrossRef]
- Zhu, J.; Luo, J. Study of transformation induced intergranular microcracking in tetragonal zirconia polycrystals with the phase field method. Mater. Sci. Eng. A 2017, 701, 69–84. [Google Scholar] [CrossRef]
- Khachaturyan, A.G. Theory of Structural Transformation in Solids; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Wang, Y.; Khachaturyan, A.G. Three-dimensional field model and computer modeling of martensitic transformations. Acta Mater. 1997, 45, 759–773. [Google Scholar] [CrossRef]
- Wang, Y.U.; Jin, Y.M.; Khachaturyan, A.G. Phase field microelasticity theory and simulation of multiple voids and cracks in single crystals and polycrystals under applied stress. J. Appl. Phys. 2002, 91, 6435. [Google Scholar] [CrossRef]
- Mamivand, M.; Zaeem, M.A.; El Kadiri, H.; Chen, L.Q. Phase field modeling of the tetragonal-to-monoclinic phase transformation in zirconia. Acta Mater. 2013, 61, 5223–5235. [Google Scholar] [CrossRef] [Green Version]
- Mamivand, M.; Zaeem, M.A.; El Kadiri, H. Phase field modeling of stress-induced tetragonal-to-monoclinic transformation in zirconia and its effect on transformation toughening. Acta Mater. 2014, 64, 208–219. [Google Scholar] [CrossRef]
- Mamivand, M.; Zaeem, M.A.; El Kadiri, H. Effect of variant strain accommodation on the three-dimensional microstructure formation during martensitic transformation: Application to zirconia. Acta Mater. 2015, 87, 45–55. [Google Scholar] [CrossRef]
- Zhu, J.; Luo, J.; Sun, Y. Phase field study of the grain size and temperature dependent mechanical responses of tetragonal zirconia polycrystals: A discussion of tension-compression asymmetry. Comput. Mater. Sci. 2020, 172, 109326. [Google Scholar] [CrossRef]
- Sun, Y.; Luo, J.; Zhu, J. Phase field study of the microstructure evolution and thermomechanical properties of polycrystalline shape memory alloys: Grain size effect and rate effect. Comput. Mater. Sci. 2018, 145, 252–262. [Google Scholar] [CrossRef]
- Sun, Y.; Luo, J.; Zhu, J.; Zhou, K. A non-isothermal phase field study of the shape memory effect and pseudoelasticity of polycrystalline shape memory alloys. Comput. Mater. Sci. 2019, 167, 65–76. [Google Scholar] [CrossRef]
- Kuhn, C.; Müller, R. A continuum phase field model for fracture. Eng. Fract. Mech. 2010, 77, 3625–3634. [Google Scholar] [CrossRef]
- Kuhn, C.; Schlüter, A.; Müller, R. On degradation functions in phase field fracture models. Comput. Mater. Sci. 2015, 108, 374–384. [Google Scholar] [CrossRef]
- Abdollahi, A.; Arias, I. Numerical simulation of intergranular and transgranular crack propagation in ferroelectric polycrystals. Int. J. Fract. 2012, 174, 3–15. [Google Scholar] [CrossRef]
- Abdollahi, A.; Arias, I. Three-dimensional simulation of crack propagation in ferroelectric polycrystals: Effect of combined toughening mechanisms. Acta Mater. 2014, 65, 106–117. [Google Scholar] [CrossRef]
- Schmitt, R.; Kuhn, C.; Skorupski, R.; Smaga, M.; Eifler, D.; Müller, R. A combined phase field approach for martensitic transformations and damage. Arch. Appl. Mech. 2015, 85, 1459–1468. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Moshkelgosha, E.; Mamivand, M. Phase field modeling of crack propagation in shape memory ceramics—Application to zirconia. Comput. Mater. Sci. 2020, 174, 109509. [Google Scholar] [CrossRef]
- Landau, L.D.; Ter-Haar, D. Collected Papers of L.D. Landau; Pergamon: Oxford, UK, 1965; ISBN 978-0-08-010586-4. [Google Scholar]
- Levitas, V.I.; Javanbakht, M. Surface Tension and Energy in Multivariant Martensitic Transformations: Phase-Field Theory, Simulations, and Model of Coherent Interface. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef]
- Levitas, V.I.; Javanbakht, M. Phase-field approach to martensitic phase transformations: Effect of martensite–martensite interface energy. Int. J. Mater. Res. 2011, 102, 652–665. [Google Scholar] [CrossRef]
- Javanbakht, M.; Barati, E. Martensitic phase transformations in shape memory alloy: Phase field modeling with surface tension effect. Comput. Mater. Sci. 2016, 115, 137–144. [Google Scholar] [CrossRef]
- Mamivand, M.; Zaeem, M.A.; El Kadiri, H. Shape memory effect and pseudoelasticity behavior in tetragonal zirconia polycrystals: A phase field study. Int. J. Plast. 2014, 60, 71–86. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.-J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Malik, A.; Amberg, G.; Borgenstam, A.; Ågren, J. Phase-field modelling of martensitic transformation: The effects of grain and twin boundaries. Modell. Simul. Mater. Sci. Eng. 2013, 21, 085003. [Google Scholar] [CrossRef]
- Liu, N.; Su, Y.; Weng, G.J. A phase-field study on the hysteresis behaviors and domain patterns of nanocrystalline ferroelectric polycrystals. J. Appl. Phys. 2013, 113, 204106. [Google Scholar] [CrossRef]
- Ahluwalia, R.; Quek, S.S.; Wu, D.T. Simulation of grain size effects in nanocrystalline shape memory alloys. J. Appl. Phys. 2015, 117, 244305. [Google Scholar] [CrossRef]
- Zhao, X.S.; Shang, S.L.; Liu, Z.K.; Shen, J.Y. Elastic properties of cubic, tetragonal and monoclinic ZrO2 from first-principles calculations. J. Nucl. Mater. 2011, 415, 13–17. [Google Scholar] [CrossRef]
- Coyle, T.W.; Coblenz, W.S.; Bender, B.A. Transformation Toughening in Large-Grain-Size CeO2-Doped ZrO2 Polycrystals. J. Am. Ceram. Soc. 1988, 71, C-88–C-92. [Google Scholar] [CrossRef]
- Kirchner, H.P.; Gruver, R.M.; Swain, M.V.; Garvie, R.C. Crack Branching in Transformation-Toughened Zirconia. J. Am. Ceram. Soc. 1981, 64, 529–533. [Google Scholar] [CrossRef]
- Chevallier, J.; Olagnon, C.; Gremillard, L.; Fantozzi, G. Crack Propagation in TZP Ceramics. Key Eng. Mater. 1998, 161–163, 563–568. [Google Scholar] [CrossRef]
- Attaoui, H.E.; Saâdaoui, M.; Chevalier, J.; Fantozzi, G. Static and cyclic crack propagation in Ce-TZP ceramics with different amounts of transformation toughening. J. Eur. Ceram. Soc. 2007, 27, 483–486. [Google Scholar] [CrossRef]
- Tsai, J.F.; Belnap, J.D.; Shetty, D.K. Crack Shielding in Ce-TZP/Al2O3 Composites: Comparison of Fatigue and Sustained Load Crack Growth Specimens. J. Am. Ceram. Soc. 1994, 77, 105–117. [Google Scholar] [CrossRef]
- Alcalá, J.; Anglada, M. High-temperature crack growth in Y-TZP. Mater. Sci. Eng. A 1997, 232, 103–109. [Google Scholar] [CrossRef]
- Lee, J.K.; Kim, H. Surface crack initiation in 2Y-TZP ceramics by low temperature aging. Ceram. Int. 1994, 20, 413–418. [Google Scholar] [CrossRef]





| Correspondence | ||||
|---|---|---|---|---|
| ABC |
| (K) (equilibrium temperature) | 1367 |
| () (kinetic coefficient) | 10 |
| () (Mobility parameter) | 0.1 |
| () (gradient energy coefficient) | 2.5 × 10− |
| 0.95 | |
| () (grain boundary energy coefficient) | 2 × 108 |
| C () (energy barrier coefficient) | 5.4 × 107 |
| 13 | |
| 18 | |
| Interfacial thickness, () | 4 |
| () (Young’s modulus) | 202 |
| (Poisson’s ratio) | 0.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Luo, J.; Sun, Y. Study of the Fracture Behavior of Tetragonal Zirconia Polycrystal with a Modified Phase Field Model. Materials 2020, 13, 4430. https://doi.org/10.3390/ma13194430
Zhu J, Luo J, Sun Y. Study of the Fracture Behavior of Tetragonal Zirconia Polycrystal with a Modified Phase Field Model. Materials. 2020; 13(19):4430. https://doi.org/10.3390/ma13194430
Chicago/Turabian StyleZhu, Jingming, Jun Luo, and Yuanzun Sun. 2020. "Study of the Fracture Behavior of Tetragonal Zirconia Polycrystal with a Modified Phase Field Model" Materials 13, no. 19: 4430. https://doi.org/10.3390/ma13194430




