Configuration Optimisation of Laser Tracker Location on Verification Process
Abstract
:1. Introduction
2. Materials and Methods
2.1. LT as Verification Measurement System
2.1.1. Error Sources in an LT
2.1.2. LT Location in the Verification Process
2.1.3. Influence of LT Location on MT Volumetric Verification
2.2. LT Location Algorithm
2.2.1. Working Principles
- Nominal MT verification points.
- LT characteristics and limitations.
- Limits of LT location.
- Optimisation criteria to minimise the influence of uncertainty.
- Number of Monte Carlo tests used to determine the location area.
2.2.2. Case Study
3. Results
3.1. Uncertainty Due to LT Location
3.2. Influence of Design Conditions on Location Results
- Number of tests (100, 1000, or 10,000).
- Number of points (48 or 175).
- Distribution of points (mesh or cloud).
- Available workspace (narrow or wide).
- Number of LTs (1 or 2).
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Schwenke, H.; Knapp, W.; Haitjema, H.; Weckenmann, A.; Schmitt, R.; Delbressine, F. Geometric error measurement and compensation of machines-An update. CIRP Ann.-Manuf. Technol. 2008, 57, 660–675. [Google Scholar] [CrossRef]
- Aguado, S.; Santolaria, J.; Samper, D.; Aguilar, J.J.; Velázquez, J. Improving a real milling machine accuracy through an indirect measurement of its geometric errors. J. Manuf. Syst. 2016, 40, 26–36. [Google Scholar] [CrossRef]
- Aguado, S.; Velazquez, J.; Samper, D.; Santolaria, J. Modelling of computer-assisted machine tool volumetric verification process. Int. J. Simul. Model. 2016, 15, 497–510. [Google Scholar] [CrossRef]
- Aguado, S.; Pérez, P.; Albajez, J.A.; Santolaria, J.; Velázquez, J. Study on Machine Tool Positioning Uncertainty Due to Volumetric Verification. Sensors 2019, 19, 2847. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Shao, Z.; Fan, Z.; Han, Z. Optimization of laser trackers locations for position measurement. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, X.; Zheng, L.; Tang, X. Configuration Optimization of Laser Tracker Stations for Large-scale Components in Non-uniform Temperature Field Using Monte-carlo Method. Procedia CIRP 2016, 56, 261–266. [Google Scholar] [CrossRef] [Green Version]
- ASME B89.4.19-2005 Performance Evaluation of Laser Based Spherical Coordinate Measurement Systems; AmericanSociety of Mechanical Engineer: New York, NY, USA, 2005.
- VDI/VDE 2617 Part 10. Accuracy of Coordinate Measuring Machines−Characteristics and their Checking−Acceptance and Reverification Tests of Laser Trackers; VDI/VDE Innovation + Technik GmbH: Berlin, Germany, 2008. [Google Scholar]
- ISO 10360-10:2016. Geometrical Product Specifications (GPS)−Acceptance and Reverification Tests for Coordinate Measuring Systems (CMS)−Part 10: Laser Trackers for Measuring Point-to-Point Distances; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- Gallagher, B.B. Optical Shop Applications for Laser Tracker Metrology Systems; The University of Arizona Press: Tucson, AZ, USA, 2003; p. 205. [Google Scholar]
- Knapp, W. Measurement Uncertainty and Machine Tool Testing. CIRP Ann. 2002, 51, 459–462. [Google Scholar] [CrossRef]
- Pérez Muñoz, P.; Albajez García, J.A.; Santolaria Mazo, J. Analysis of the initial thermal stabilization and air turbulences effects on Laser Tracker measurements. J. Manuf. Syst. 2016, 41, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Muske, S.; Salisbury, D.; Salerno, R.; Calkins, J. 747 Data Management SystemDevelopment and Implementation. In Proceedings of the CMSC Conference and the 2000 Boeing Large Scale Metrology Conference, Long Beach, CA, USA, 23–24 February 2000. [Google Scholar]
- Costa, D.; Albajez, J.A.; Yagüe-Fabra, J.A.; Velázquez, J. Verification of Machine Tools Using Multilateration and Geometrical Approach. Nanomanuf. Metrol. 2018. [Google Scholar] [CrossRef]
- Aguado, S.; Samper, D.; Santolaria, J.; Aguilar, J.J. Volumetric verification of multiaxis machine tool using laser tracker. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ISO/IEC Guide 98-3:2008—Uncertainty of Measurement—Part. 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995); ISO: Geneva, Switzerland, 2008.
- Mason, R.L.; Gunst, R.F.; Hess, J.L. Statical Design and Analysis of Experiments with Applications to Engineering and Sicicence, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2003; ISBN 0-471-37216-1. [Google Scholar]
- Weisberg, S. Applied Linear Regressions; John Wiley & Sons: New York, NY, USA, 2005; ISBN 9-780-471-70409-6. [Google Scholar]









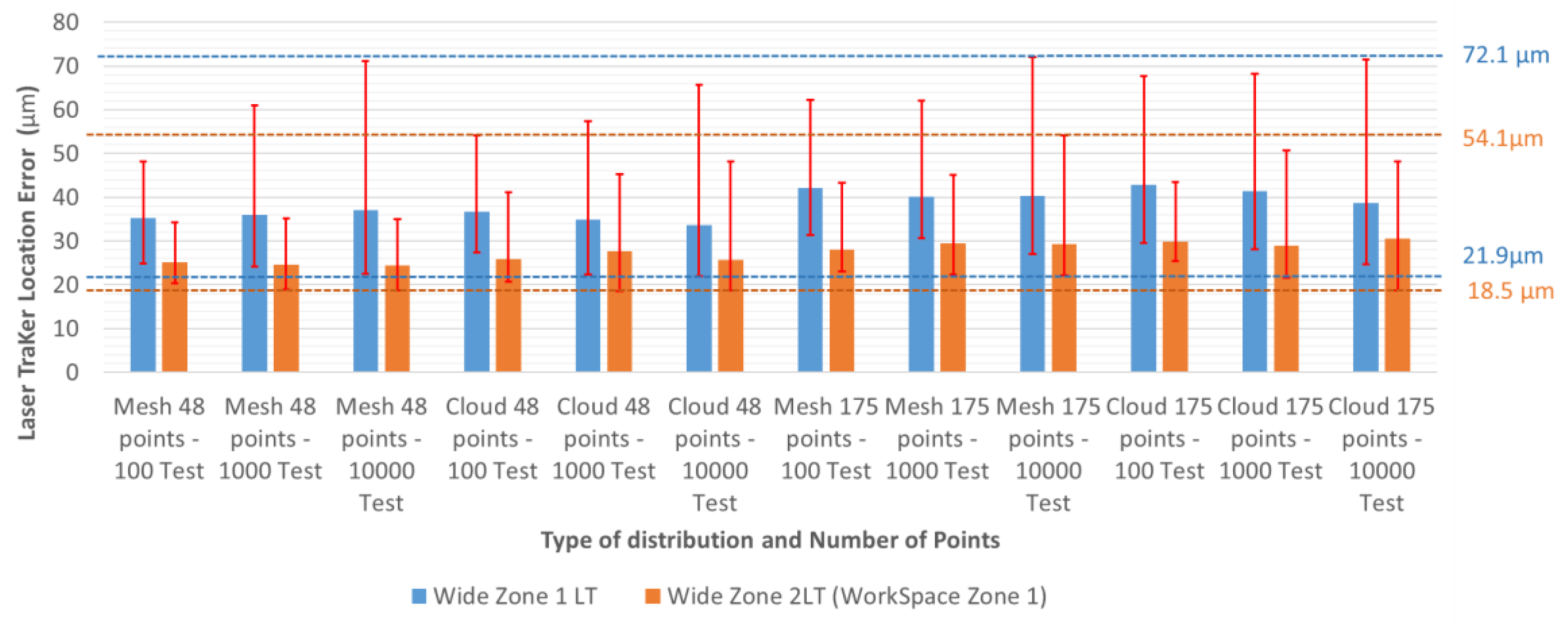
| Zones | Workspace Divided Into Two Zones; Two LTs | Workspace 1 Zone, 1 LT | ||||
|---|---|---|---|---|---|---|
| Min. Error (µm) | Max. Error (µm) | Min. Error (µm) | Max. Error (µm) | |||
| Space 1 | Space 2 | Space 1 | Space 2 | Unique Workspace | Unique Workspace | |
| Narrow | 20.6 | 54.0 | 47.1 | 167.9 | 56.2 | 170.5 |
| Wide | 22.1 | 23.7 | 54.1 | 49.9 | 27.1 | 72.0 |
| Points | Tests | Time | Points | Tests | Time |
|---|---|---|---|---|---|
| 48 | 100 | 1′35″ | 175 | 100 | 4′20″ |
| 48 | 1000 | 14′32″ | 175 | 1000 | 42′31″ |
| 48 | 10,000 | 2 h 3′11″ | 175 | 10,000 | 6 h 37′56″ |
| Configuration | Real Value | Estimated Value | ||||
|---|---|---|---|---|---|---|
| Type | Points | Tests | Mean (µm) | Max. (µm) | Mean (µm) | Max. (µm) |
| Mesh | 48 | 1000 | 36.1 | 60.9 | 35.3 | 49.4 |
| Cloud | 48 | 1000 | 34.8 | 57.4 | 36.4 | 55.2 |
| Mesh | 175 | 1000 | 40.2 | 72.0 | 42.2 | 63.1 |
| Cloud | 175 | 1000 | 41.3 | 68.2 | 42.5 | 67.9 |
| Configuration | Wide Zone-Workspace Zone 1 | Wide Zone-Workspace Zone 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Type | Points | Tests | Mean (µm) | Max. (µm) | Min. (µm) | Mean (µm) | Max. (µm) | Min. (µm) |
| Mesh | 48 | 100 | 25.2 | 34.3 | 20.3 | 25.2 | 34.3 | 20.3 |
| Mesh | 48 | 1000 | 24.6 | 35.1 | 18.9 | 24.6 | 35.1 | 18.9 |
| Mesh | 48 | 10,000 | 24.4 | 35.1 | 18.6 | 21.3 | 35.1 | 18.6 |
| Cloud | 48 | 100 | 25.9 | 41.2 | 20.8 | 24.8 | 41.2 | 19.4 |
| Cloud | 48 | 1000 | 27.6 | 45.3 | 18.5 | 27.1 | 45.4 | 18.7 |
| Cloud | 48 | 10,000 | 25.7 | 48.1 | 18.7 | 25.3 | 48.2 | 18.90 |
| Mesh | 175 | 100 | 28.1 | 43.3 | 23.0 | 31.9 | 44.3 | 25.3 |
| Mesh | 175 | 1000 | 29.5 | 45.1 | 22.3 | 30.4 | 46.2 | 23.3 |
| Mesh | 175 | 10,000 | 29.2 | 54.1 | 22.1 | 29.5 | 49.8 | 23.7 |
| Cloud | 175 | 100 | 29.9 | 43.4 | 25.4 | 29.5 | 44.6 | 25.5 |
| Cloud | 175 | 1000 | 28.9 | 50.7 | 21.6 | 29.7 | 51.4 | 22.5 |
| Cloud | 175 | 10,000 | 30.5 | 48.1 | 18.7 | 30.1 | 48.2 | 19.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguado, S.; Pérez, P.; Albajez, J.A.; Santolaria, J.; Velázquez, J. Configuration Optimisation of Laser Tracker Location on Verification Process. Materials 2020, 13, 331. https://doi.org/10.3390/ma13020331
Aguado S, Pérez P, Albajez JA, Santolaria J, Velázquez J. Configuration Optimisation of Laser Tracker Location on Verification Process. Materials. 2020; 13(2):331. https://doi.org/10.3390/ma13020331
Chicago/Turabian StyleAguado, Sergio, Pablo Pérez, José Antonio Albajez, Jorge Santolaria, and Jesús Velázquez. 2020. "Configuration Optimisation of Laser Tracker Location on Verification Process" Materials 13, no. 2: 331. https://doi.org/10.3390/ma13020331
APA StyleAguado, S., Pérez, P., Albajez, J. A., Santolaria, J., & Velázquez, J. (2020). Configuration Optimisation of Laser Tracker Location on Verification Process. Materials, 13(2), 331. https://doi.org/10.3390/ma13020331






