Tensile Notch Sensitivity of Additively Manufactured IN 625 Superalloy
Abstract
:1. Introduction
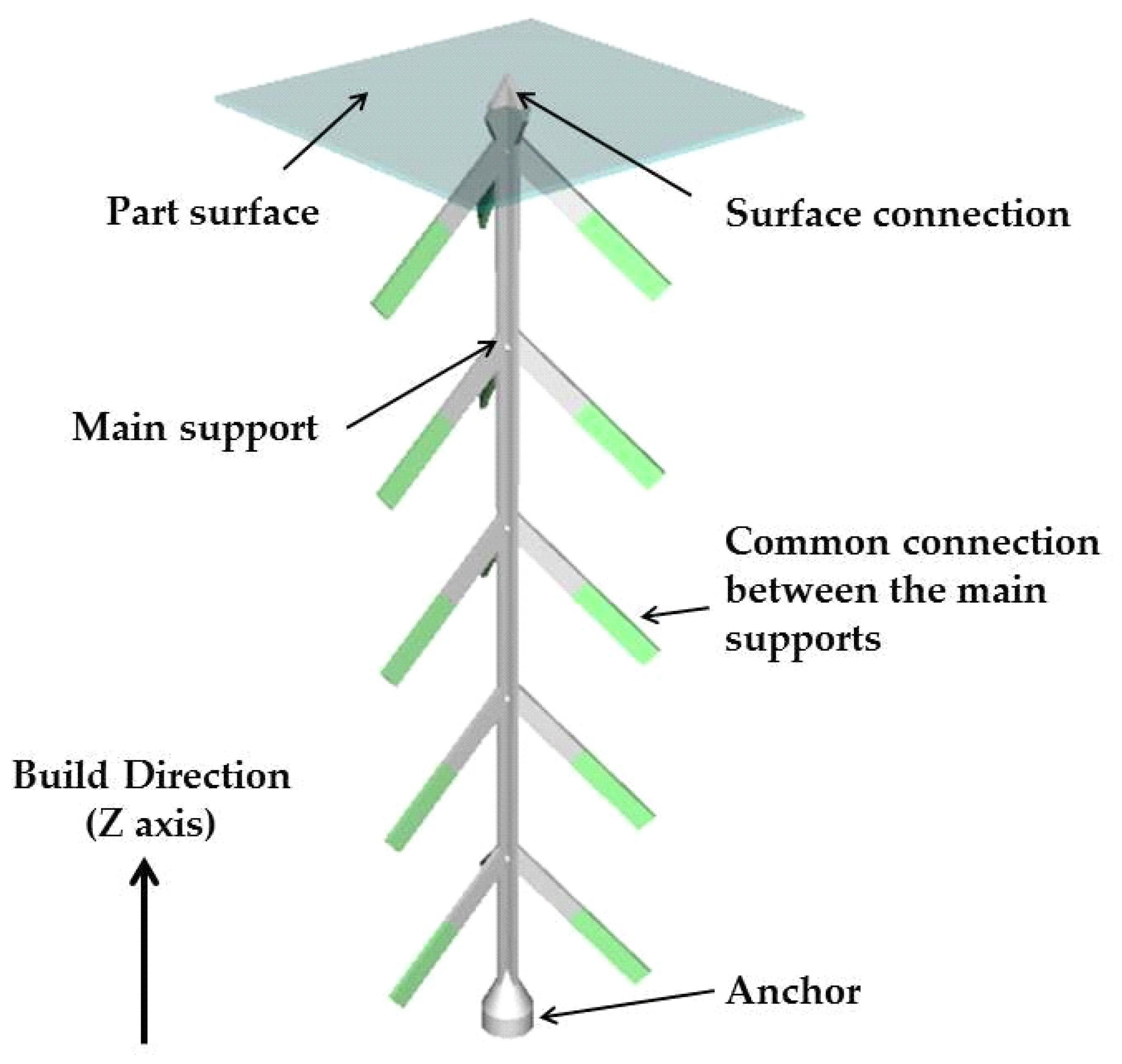
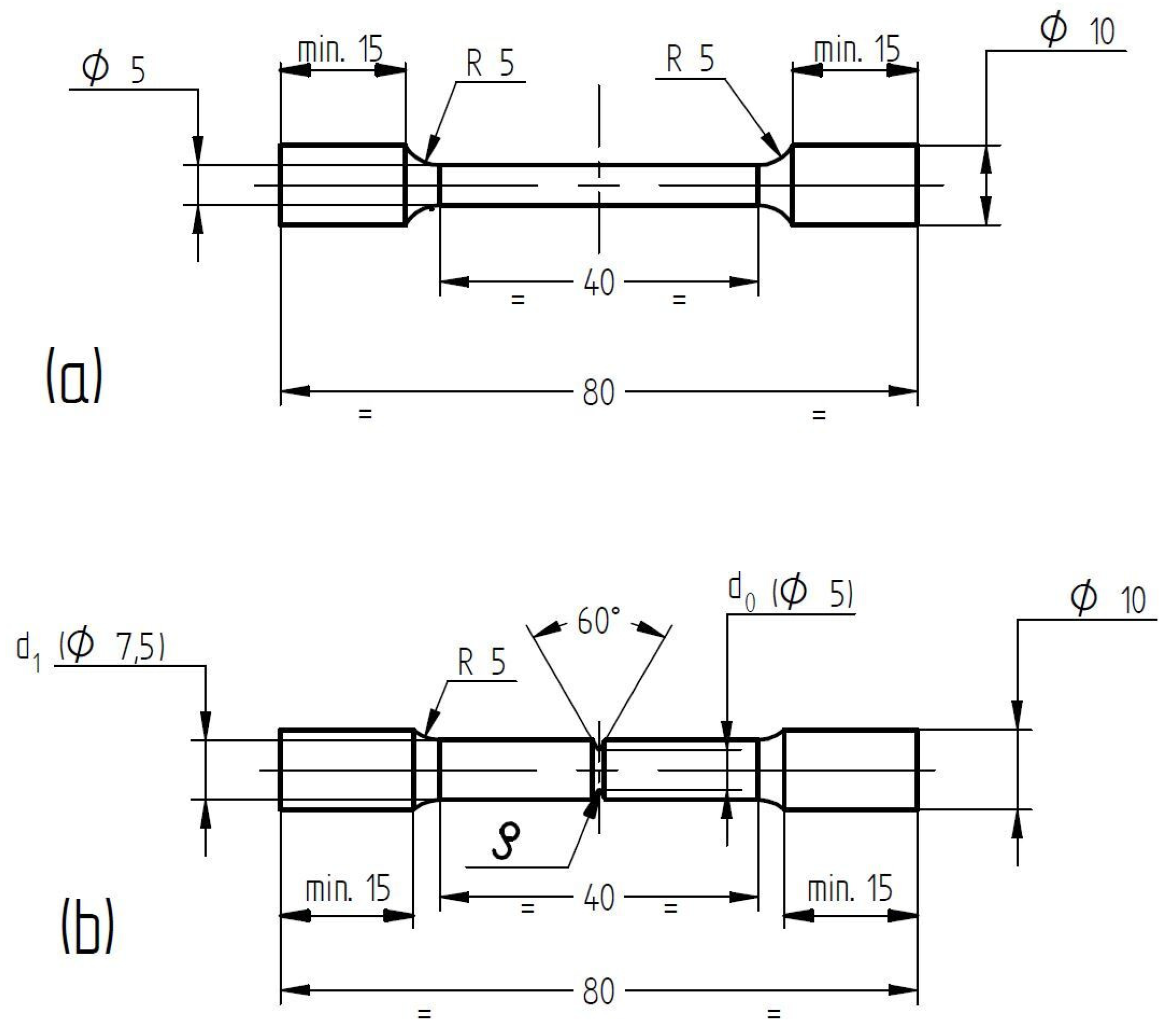
2. Materials and Methods
3. Results and Discussion
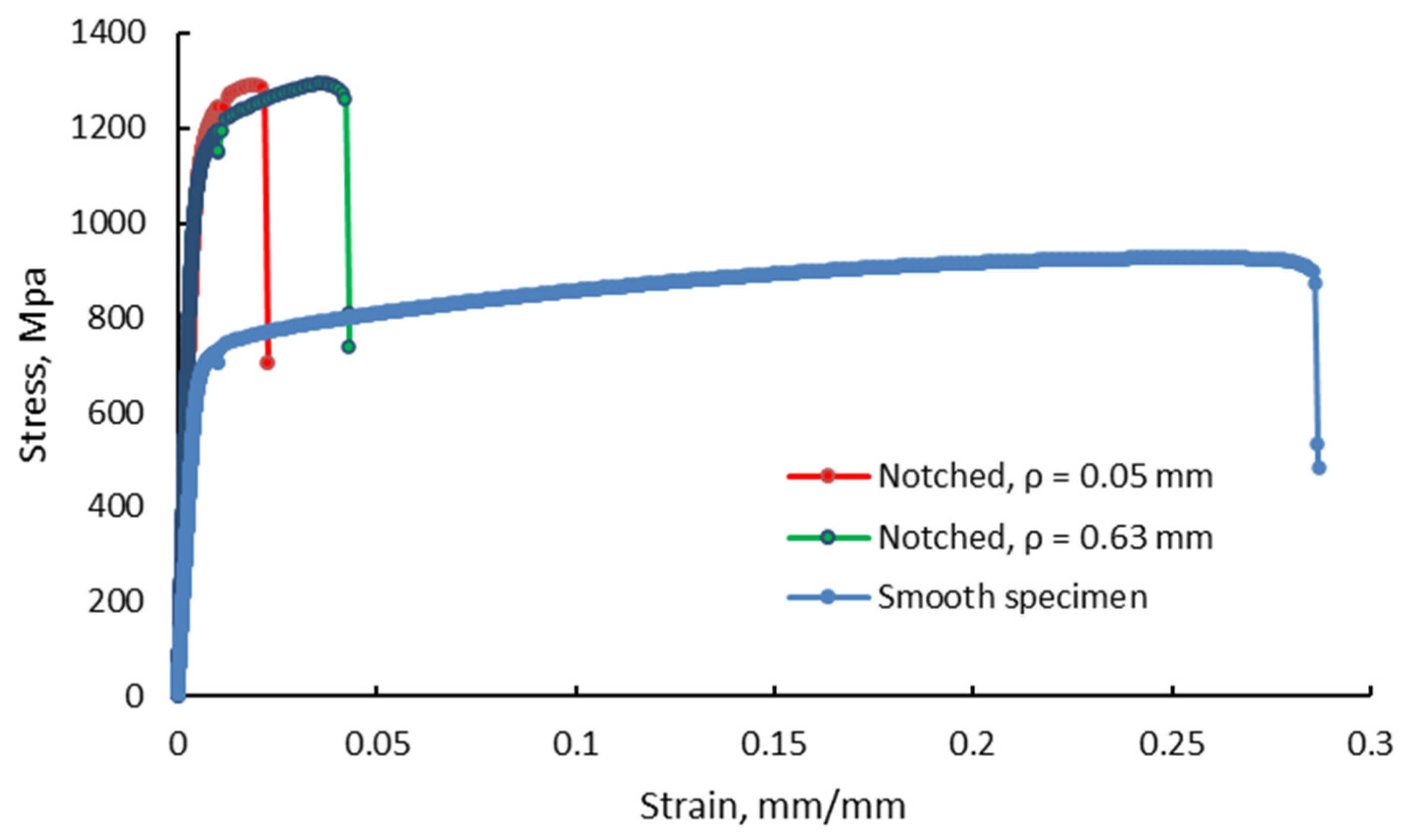
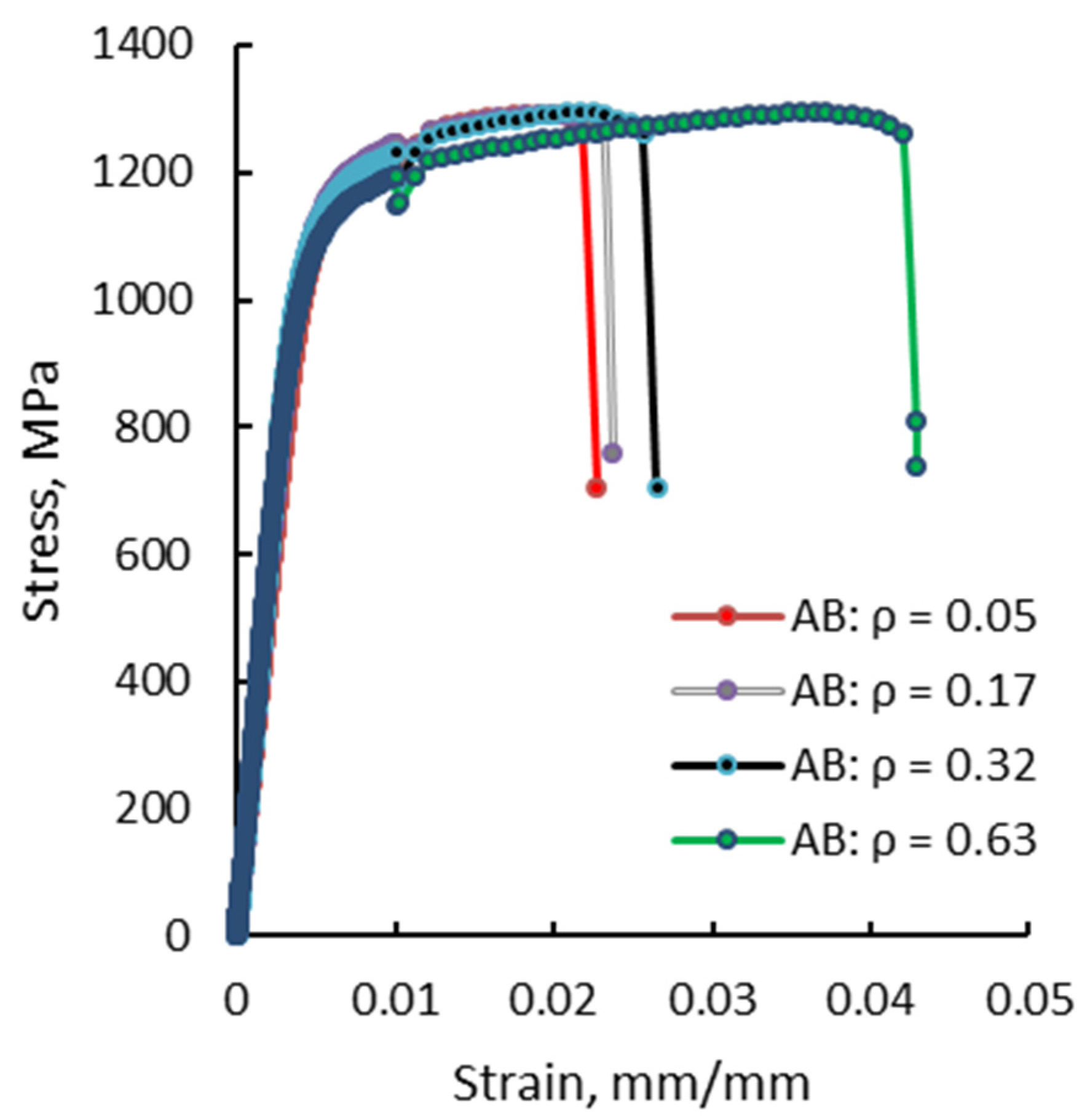
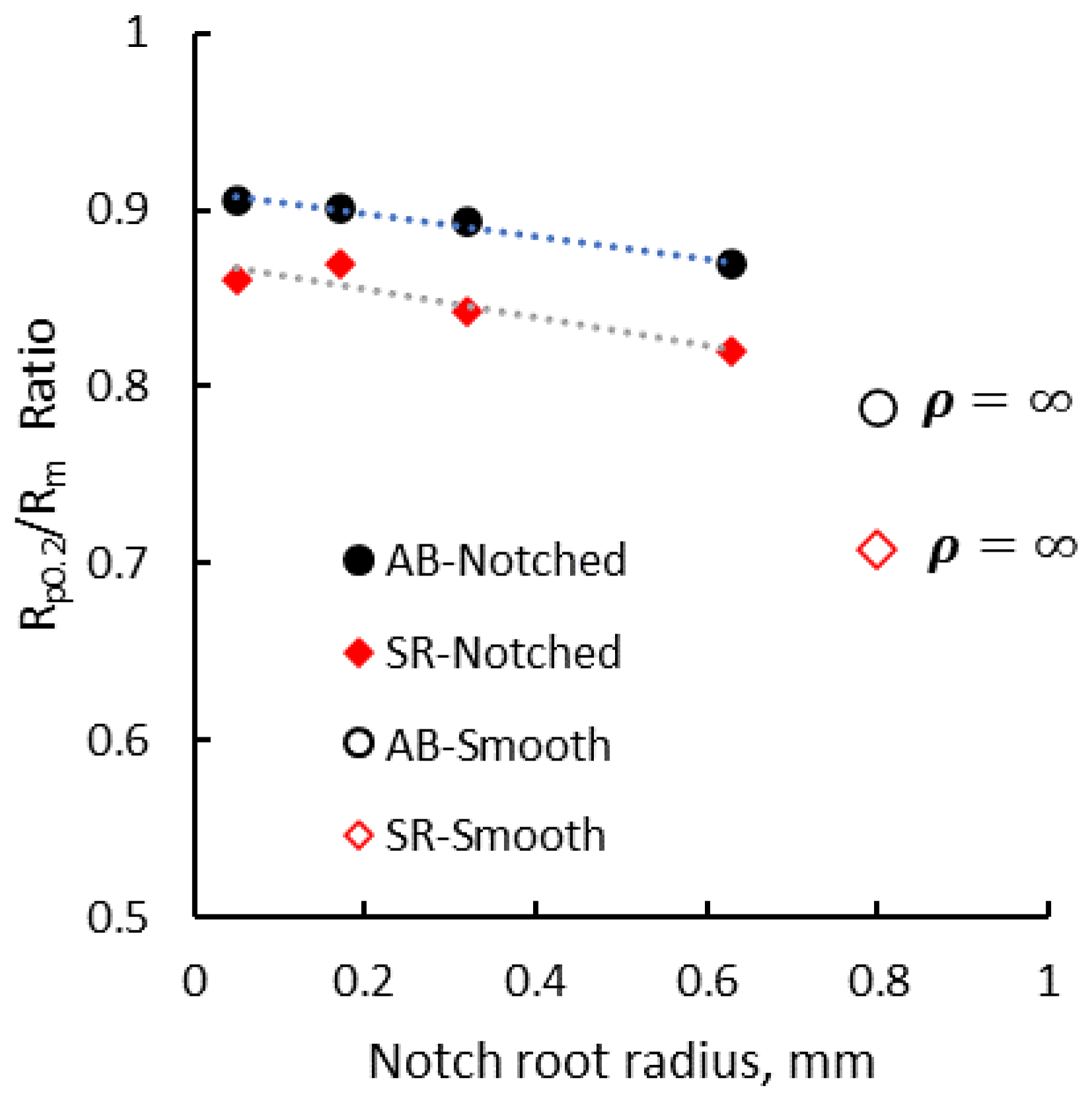
3.1. Notch Sensitivity
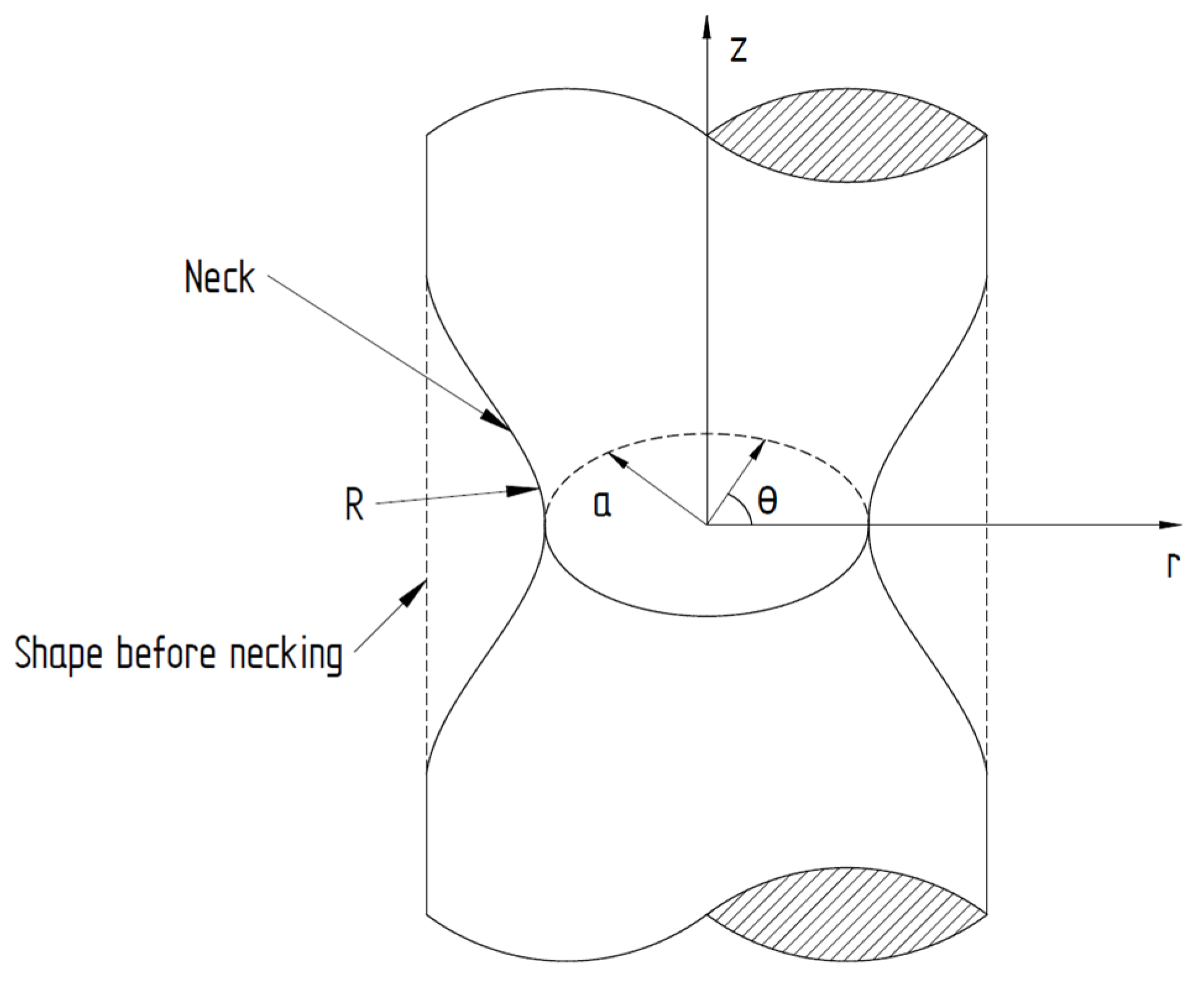
3.2. Stress Triaxiality
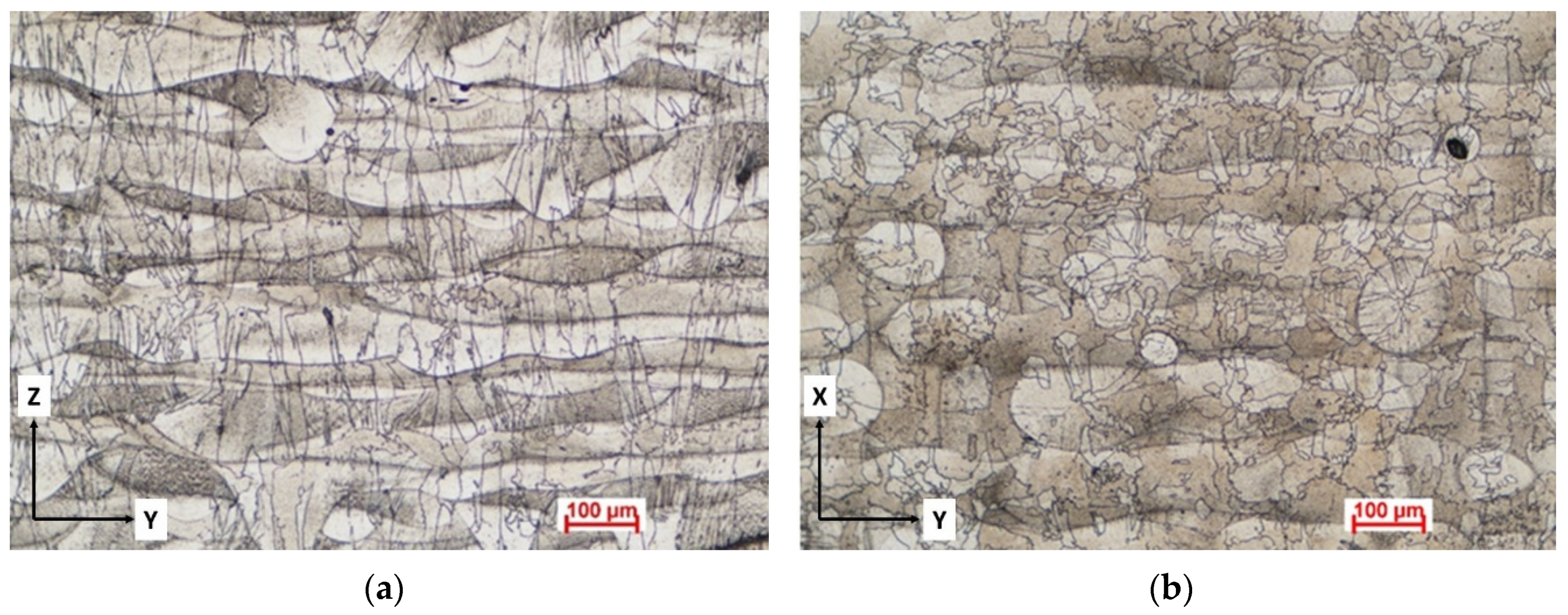
3.3. Microstructure
3.4. Fractographic Investigation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| No. | Notch Root Radius ρ, mm | Cylindrical Diameter d1, mm | Initial Diameter d0, mm | Diameter at Fracture d0f, mm | Tensile Strength Rm, MPa | Proof Strength Rp0.2, MPa |
|---|---|---|---|---|---|---|
| 1 | 0.05 | 7.448 | 5.280 | 5.080 | 1286 | 1164 |
| 2 | 0.06 | 7.520 | 5.240 | 4.958 | 1290 | 1170 |
| 3 | 0.16 | 7.510 | 5.297 | 5.000 | 1265 | 1134 |
| 4 | 0.15 | 7.515 | 5.284 | 5.028 | 1290 | 1170 |
| 5 | 0.32 | 7.480 | 5.118 | 4.885 | 1294 | 1153 |
| 6 | 0.33 | 7.500 | 5.109 | 4.963 | 1325 | 1187 |
| 7 | 0.65 | 7.490 | 5.217 | 4.790 | 1295 | 1116 |
| 8 | 0.65 | 7.520 | 5.210 | 4.909 | 1297 | 1136 |
| 9 | 5.010 | 5.010 | 4.373 | 864 | 681 |
| No. | Notch Root Radius ρ, mm | Cylindrical Diameter d1, mm | Initial Diameter d0, mm | Diameter at Fracture d0f, mm | Tensile Strength Rm, MPa | Proof Strength Rp0.2, MPa |
|---|---|---|---|---|---|---|
| 1 | 0.05 | 7.515 | 5.205 | 4.895 | 1165 | 1003 |
| 2 | 0.05 | 7.501 | 5.192 | 4.972 | 1175 | 1010 |
| 3 | 0.17 | 7.512 | 5.260 | 4.908 | 1139 | 996 |
| 4 | 0.17 | 7.525 | 5.268 | 4.984 | 1163 | 1004 |
| 5 | 0.32 | 7.500 | 5.169 | 4.857 | 1198 | 1005 |
| 6 | 0.32 | 7.520 | 5.174 | 4.862 | 1189 | 1007 |
| 7 | 0.68 | 7.514 | 5.153 | 4.797 | 1172 | 967 |
| 8 | 0.68 | 7.502 | 5.140 | 4.835 | 1206 | 983 |
| 9 | 5.017 | 5.017 | 3.982 | 824 | 583 |
Appendix B
| α = 0.05 | |||||
|---|---|---|---|---|---|
| Kt | Rm | Sum | Average | Variance | |
| As-Built | Stress-Relieved | ||||
| 10.31235738 | 1286 | 1164.7 | 2450.7 | 1225.35 | 7356.845 |
| 9.717797887 | 1290 | 1175.01 | 2465.01 | 1232.505 | 6611.35 |
| 6.259515187 | 1265 | 1139.39 | 2404.39 | 1202.195 | 7888.936 |
| 6.454050483 | 1290 | 1163.23 | 2453.23 | 1226.615 | 8035.316 |
| 4.842199891 | 1294 | 1197.94 | 2491.94 | 1245.97 | 4613.762 |
| 4.806692671 | 1325 | 1188.8 | 2513.8 | 1256.9 | 9275.22 |
| 3.644588088 | 1295 | 1172.41 | 2467.41 | 1233.705 | 7514.154 |
| 3.666025564 | 1297 | 1205.94 | 2502.94 | 1251.47 | 4145.962 |
| As-built | 10.342 | 1292.75 | 270.7857 | ||
| Stress-relieved | 9407.42 | 1175.928 | 455.2126 | ||
| Source of Variation | Sum of Squares (SS) | Degrees of Freedom (df) | (Mean Squares) MS | F-Ratio (F) | Probability Value (p-Value) | F Critical | SS% |
|---|---|---|---|---|---|---|---|
| Rows | 4230.429 | 7 | 604.347 | 4.967863 | 0.025356 | 3.787044 | 7.089474 |
| Columns | 54,589.99 | 1 | 54,589.99 | 448.7415 | 1.31 × 10−7 | 5.591448 | 91.48346 |
| Error | 851.5592 | 7 | 121.6513 | 1.427067 | |||
| Total | 59,671.97 | 15 |
| Source of Variation | Sum of Squares (SS) | Degrees of Freedom (df) | (Mean Squares) MS | F-Ratio (F) | Probability Value (p-Value) | F Critical | SS% |
|---|---|---|---|---|---|---|---|
| Between Groups | 54,589.99 | 1 | 54,589.99 | 150.386 | 7.08 × 10−9 | 4.60011 | 91.48346 |
| Within Groups | 5081.988 | 14 | 362.9992 | ||||
| Total | 59,671.97 | 15 |
| Kt Gropus | Rm Sum (As-Built + Stress-Relieved) | Average | Variance |
|---|---|---|---|
| 3–5 | 9976.09 | 1247.011 | 3734.388 |
| 5–7 | 4857.62 | 1214.405 | 5506.863 |
| 7–9 | 0 | 0 | 0 |
| 9–11 | 4915.71 | 1228.928 | 4673.13 |
| Source of Variation | Sum of Squares (SS) | Degrees of Freedom (df) | (Mean Squares) MS | F-Ratio (F) | Probability Value (p-Value) | F Critical |
|---|---|---|---|---|---|---|
| Between Groups | 2991.282 | 3 | 997.094 | 0.211097 | 0.886778 | 3.490295 |
| Within Groups | 56,680.69 | 12 | 4723.391 | |||
| Total | 59,671.97 | 15 |
| Groups | Sum | Average | Variance | ||||
|---|---|---|---|---|---|---|---|
| Kt | 49.70323 | 6.212903 | 6.584174 | ||||
| Rm As-built | 10,342 | 1292.75 | 270.7857 | ||||
| Source of Variation | Sum of Squares (SS) | Degrees of Freedom (df) | (Mean Squares) MS | F-ratio (F) | Probability Value (p-value) | F Critical | SS% |
| Between Groups | 6,620,711 | 1 | 6,620,711 | 47,739.22 | 3.9 × 10−26 | 4.60011 | 99.97068 |
| Within Groups | 1941.589 | 14 | 138.6849 | ||||
| Total | 6,622,652 | 15 |
| Groups | Sum | Average | Variance | ||||
|---|---|---|---|---|---|---|---|
| Kt | 49.70323 | 6.212903 | 6.584174 | ||||
| Rm Stress-relieved | 9407.42 | 1,175,928 | 455.2126 | ||||
| Source of Variation | Sum of Squares (SS) | Degrees of Freedom (df) | (Mean Squares) MS | F-Ratio (F) | Probability Value (p-value) | F Critical | SS% |
| Between Groups | 5,472,929 | 1 | 5,472,929 | 23,702.76 | 5.23 × 10−24 | 4.60011 | 99.94097 |
| Within Groups | 3,232,578 | 14 | 230.8984 | ||||
| Total | 5,476,162 | 15 |
| Kt | As-Built | |
|---|---|---|
| Kt | 1 | |
| As-built | −0.34825 | 1 |
| Kt | Stress-relieved | |
| Kt | 1 | |
| Stress-relieved | −0.44278 | 1 |
References
- Qu, R.; Zhang, P.; Zhang, Z. Notch Effect of Materials: Strengthening or Weakening? J. Mater. Sci. Technol. 2014, 30, 599–608. [Google Scholar] [CrossRef]
- Lei, X.; Li, C.; Shi, X.; Xu, X.; Wei, Y. Notch strengthening or weakening governed by transition of shear failure to normal mode fracture. Sci. Rep. 2015, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Hertzberg, R.W. Deformation and Fracture Mechanics of Engineering Materials, 4th ed.; John Wiley & Sons: Chichester, UK, 1996; pp. 274–275. [Google Scholar]
- Budynas, R.C.; Nisbett, J.K. Shigley’s Mechanical Engineering Design, 9th ed.; McGraw-Hill Education: Singapore, 2011; pp. 110–113. [Google Scholar]
- Atzori, B.; Zappalorto, M.; Berto, F. A theoretical treatise for notch and defect sensitivity under torsion. Mech. Res. Commun. 2010, 37, 173–176. [Google Scholar] [CrossRef]
- Sapora, A.; Cornetti, P.; Campagnolo, A.; Meneghetti, G. Fatigue limit: Crack and notch sensitivity by Finite Fracture Mechanics. Theor. Appl. Fract. Mech. 2020, 105, 1–6. [Google Scholar] [CrossRef]
- Hu, X.; Zhao, G.; Yang, X.; Shi, D. Finite element analysis and life modeling of a notched superalloy under thermal mechanical fatigue loading. Int. J. Press. Vessel. Pip. 2018, 165, 51–58. [Google Scholar] [CrossRef]
- Fan, J.; Chen, X.; Wang, D.; Li, S.; Zhao, Y. Infrared thermographic analysis of notch effects on tensile behavior of 30CrMnSiA steel. Infrared Phys. Technol. 2019, 101, 110–118. [Google Scholar] [CrossRef]
- Santus, C.; Taylor, D.; Benedetti, M. Experimental determination and sensitivity analysis of the fatigue critical distance obtained with rounded V-notched specimens. Int. J. Fatigue 2018, 11, 113–125. [Google Scholar] [CrossRef]
- Sajadifar, S.V.; Wegener, T.; Yapici, G.G.; Niendrof, T. Effect of Grain Size on the Very High Cycle Fatigue Behavior and Notch Sensitivity of Titanium. Theor. Appl. Fract. Mech. 2019, 104, 1–7. [Google Scholar] [CrossRef]
- Cai, D.; Zhang, W.; Nie, P.; Liu, W.; Yao, M. Dissolution kinetics of δ phase and its influence on the notch sensitivity of Inconel 718. Mater. Charact. 2007, 58, 220–225. [Google Scholar] [CrossRef]
- Chapetti, M.D.; Guerrero, A.O. Estimation of notch sensitivity and size effect on fatigue resistance. Procedia Eng. 2013, 66, 323–333. [Google Scholar] [CrossRef] [Green Version]
- Telesman, J.; Gabb, T.P.; Ghosn, L.J.; Gayda, J. Effect of notches on creep–fatigue behavior of a P/M nickel-based superalloy. Int. J. Fatigue 2016, 87, 311–325. [Google Scholar] [CrossRef]
- Hsu, H.H.; Wu, Y.C.; Tsay, L.W. Notch brittleness of Ti–15V–3Cr–3Sn–3Al alloys. Mater. Sci. Eng. A 2012, 545, 20–25. [Google Scholar] [CrossRef]
- Owolabi, G.; Okeyoyin, O.; Bamiduro, O.; Olasumboye, A.; Whitworth, H. The effects of notch size and material microstructure on the notch sensitivity factor for notched components. Eng. Fract. Mech. 2015, 145, 181–196. [Google Scholar] [CrossRef] [Green Version]
- Sanyal, G.; Das, A.; Singh, J.B.; Charavartty, J.K. Effect of notch geometry on fracture features. Mater. Sci. Eng. A 2015, 641, 210–214. [Google Scholar] [CrossRef]
- Lorenzino, P.; Navarro, A. Grain size effects on notch sensitivity. Int. J. Fatigue 2015, 70, 205–215. [Google Scholar] [CrossRef]
- Peron, M.; Torgersen, J.; Ferro, P.; Berto, F. Fracture behaviour of notched as-built EBM parts: Characterization and interplay between defects and notch strengthening behaviour. Theor. Appl. Fract. Mech. 2018, 98, 178–185. [Google Scholar] [CrossRef] [Green Version]
- Peron, M.; Torgersen, J.; Berto, P. Rupture Predictions of Notched Ti-6Al-4V Using Local Approaches. Materials 2018, 11, 663. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Huang, S.; Zhang, G.; Qin, R.; Liu, W.; Xiong, H.; Shi, G.; Blackburn, J. Progress in additive manufacturing on new materials: A review. J. Mater. Sci. Technol. 2019, 35, 242–269. [Google Scholar] [CrossRef]
- Murr, L.E. Frontiers of 3D Printing/Additive Manufacturing: From Human Organs to Aircraft Fabrication. J. Mater. Sci. Technol. 2016, 32, 987–995. [Google Scholar] [CrossRef]
- Shougat, R.; Sabuz, E.H.; Najmul Quader, G.M.; Mahboo, M. Effect of Building Orientation & Post Processing Material on Mechanical Properties of 3D Printed Parts. In Proceedings of the International Conference on Mechanical, Industrial and Energy Engineering, Khulna, Bangladesh, 26–27 December 2016; pp. 160110-1–160110-5. [Google Scholar]
- Hartunian, P.; Eshraghi, M. Effect of Build Orientation on the Microstructure and Mechanical Properties of Selective Laser-Melted Ti-6Al-4V Alloy. J. Manuf. Mater. Process. 2018, 2, 69. [Google Scholar] [CrossRef] [Green Version]
- Simonelli, M.; Tse, Y.Y.; Tuck, C. Effect of the build orientation on the mechanical properties and fracture modes of SLM Ti–6Al–4V. Mater. Sci. Eng. A 2014, 616, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Nicoletto, G. Smooth and notch fatigue behavior of selectively laser melted Inconel 718 with as-built surfaces. Int. J. Fatigue 2019, 128, 105211. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Ferro, P.; Berto, F.; Torgersen, J. Fatigue strength of blunt V-notched specimens produced by selective laser melting of Ti-6Al-4V. Theor. Appl. Fract. Mech. 2018, 97, 376–384. [Google Scholar] [CrossRef] [Green Version]
- Razavi, S.M.J.; Berto, F. Fatigue strength of notched specimens made of Ti-6Al-4V produced by Selected Laser Melting technique. J. Pro. Str. 2018, 13, 74–78. [Google Scholar] [CrossRef]
- Konecna, R.; Nicoletto, G.; Riva, E. Notch fatigue behavior of Inconel 718 produced by selective laser melting. J. Pro. Str. 2019, 17, 138–145. [Google Scholar]
- Benedetti, M.; Santus, C. Notch fatigue and crack growth resistance of Ti-6Al-4V ELI additively manufactured via selective laser melting: A critical distance approach to defect sensitivity. J. Pro. Str. 2019, 121, 281–292. [Google Scholar] [CrossRef]
- Solberg, K.; Berto, F. Notch-defect interaction in additively manufactured Inconel 718. J. Pro. Str. 2019, 122, 35–45. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, D.; Yang, B.; Chen, C.; Li, Y.; Zhou, K.; Jiang, L.; Liu, R. Microstructural evolution and defect formation in a powder metallurgy nickel based superalloy processed by selective laser melting. J. Mater. Sci. Technol. 2020, 36, 7–17. [Google Scholar] [CrossRef]
- Yan, Q.; Song, B.; Shi, Y. Comparative study of performance comparison of AlSi10Mg alloy prepared by selective laser melting and casting. J. Mater. Sci. Technol. 2020, 41, 199–202. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Davis, J.R. Tensile Testing, 2nd ed.; Davis, J.R., Ed.; ASM International: Novelty, OH, USA, 2004. [Google Scholar]
- Noda, N.; Takase, Y. Stress concentration formula useful for all notch shape in a round bar (comparison between torsion, tension and bending). J. Pro. Str. 2006, 28, 151–163. [Google Scholar] [CrossRef]
- ASTM F3056 Standard Specification for Additive Manufacturing Nickel Alloy (UNS N06625) with Powder Bed Fusion; ASTM International: Conshohocken, PA, USA, 2014.
- ASTM B443 Standard Specification for Nickel-Chromium-Molybdenum-Columbium Alloy and Nickel-Chromium-Molybdenum-Silicon Alloy Plate, Sheet, and Strip; ASTM International: Conshohocken, PA, USA, 2019.
- Sinha, S.; Komarasamy, M.; Wang, T.; Haridas, R.S.; Agrawal, P.; Shukla, S.; Thapliyal, S.; Frank, M.; Mishra, R.S. Notch-tensile behavior of Al0.1CrFeCoNi high entropy alloy. Mater. Sci. Eng. A 2020, 774, 138918. [Google Scholar] [CrossRef]
- Solberg, K.; Berto, F. The effect of defects and notches in quasi-static and fatigue loading of Inconel 718 specimens produced by selective laser melting. Int. J. Fatigue 2020, 137, 105637. [Google Scholar] [CrossRef]
- Hopperstad, O.S.; Borvik, T.; Langseth, M.; Labibes, K.; Albertini, C. On the Influence of Stress Triaxiality and Strain Rate on the Behaviour of a Structural Steel. Part I. Experiments. Eur. J. Mech. A Solids 2003, 22, 1–13. [Google Scholar] [CrossRef]
- Handcock, J.W.; Mackenzie, A.C. On the mechanisms of ductile failure in high-strength steels subjected to multi-axial stress-states. J. Mech. Phys. Solids 1976, 24, 147–169. [Google Scholar] [CrossRef]
- Wang, J.; Guo, W.; Guo, J.; Wang, Z.; Lu, S. The Effects of Stress Triaxiality, temperature and Strain rate on the Fracture Characteristics of a Nickel-Base Superalloy. J. Mater. Eng. Perform. 2016, 25, 2043–2052. [Google Scholar] [CrossRef]
- Bao, Y. Dependence of ductile crack formation in tensile tests on stress triaxiality, stress and strain ratios. Eng. Fract. Mech. 2005, 72, 505–522. [Google Scholar] [CrossRef]
- Condruz, M.R.; Matache, G.; Paraschiv, A.; Frigioescu, T.F.; Badea, T. Microstructural and tensile properties anisotropy of Selective Laser Melting manufactured IN 625. Materials. under review. [CrossRef]
- Marchese, G.; Lorusso, M.; Parizia, S.; Bassini, E.; Lee, J.W.; Calignano, F.; Manfredi, D.; Terner, M.; Hong, H.K.; Ugues, D.; et al. Influence of heat treatments on microstructure evolution and mechanical properties of Inconel 625 processed by laser powder bed fusion. Mater. Sci. Eng. A. 2018, 729, 64–75. [Google Scholar] [CrossRef]
- Ni, M.; Chen, C.; Wang, X.; Wang, P.; Li, R.; Zhang, X.; Zhou, K. Anisotropic tensile behavior of in situ precipitation strengthened Inconel 718 fabricated by additive manufacturing. Mater. Sci. Eng. A 2017, 701, 344–351. [Google Scholar] [CrossRef]
- Nguejio, J.; Szmytka, F.; Hallais, S.; Tanguy, A.; Nardone, S.; Godino Martinez, M. Comparison of microstructure features and mechanical properties for additive manufactured and wrought nickel alloys 625. Mater. Sci. Eng. A 2019, 764, 138214. [Google Scholar] [CrossRef]
- Brenne, F.; Niendorf, T. Effect of notches on the deformation behavior and damage evolution of additively manufactured 316L specimens under uniaxial quasi-static and cyclic loading. Int. J. Fatigue 2019, 127, 175–189. [Google Scholar] [CrossRef]











| Element | Al | C | Co | Cr | Fe | Mn | Mo | Nb | Si | Ti | Ni |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Specification | <0.4 | <0.1 | <1.0 | 20–23 | 3–5 | <0.5 | 8–10 | 3.15–4.15 | <0.5 | <0.4 | Bal. |
| Actual composition | 0.06 | 0.02 | 0.1 | 20.7 | 4.1 | 0.01 | 8.9 | 3.77 | 0.01 | 0.07 | Bal. |
| Notch Root Radius, , mm | 0.05 | 0.06 | 0.16 | 0.15 | 0.32 | 0.33 | 0.65 | 0.65 |
|---|---|---|---|---|---|---|---|---|
| Kt | 10.312 | 9.718 | 6.260 | 6.454 | 4.842 | 4.807 | 3.645 | 3.666 |
| NSR | 1.49 | 1.49 | 1.46 | 1.49 | 1.50 | 1.53 | 1.50 | 1.50 |
| Notch Root Radius, , mm | 0.05 | 0.05 | 0.17 | 0.17 | 0.32 | 0.32 | 0.68 | 0.68 |
|---|---|---|---|---|---|---|---|---|
| Kt | 10.612 | 10.61 | 6.102 | 6.123 | 4.811 | 4.853 | 3.631 | 3.634 |
| NSR | 1.41 | 1.43 | 1.38 | 1.41 | 1.45 | 1.44 | 1.42 | 1.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matache, G.; Paraschiv, A.; Condruz, M.R. Tensile Notch Sensitivity of Additively Manufactured IN 625 Superalloy. Materials 2020, 13, 4859. https://doi.org/10.3390/ma13214859
Matache G, Paraschiv A, Condruz MR. Tensile Notch Sensitivity of Additively Manufactured IN 625 Superalloy. Materials. 2020; 13(21):4859. https://doi.org/10.3390/ma13214859
Chicago/Turabian StyleMatache, Gheorghe, Alexandru Paraschiv, and Mihaela Raluca Condruz. 2020. "Tensile Notch Sensitivity of Additively Manufactured IN 625 Superalloy" Materials 13, no. 21: 4859. https://doi.org/10.3390/ma13214859
APA StyleMatache, G., Paraschiv, A., & Condruz, M. R. (2020). Tensile Notch Sensitivity of Additively Manufactured IN 625 Superalloy. Materials, 13(21), 4859. https://doi.org/10.3390/ma13214859





