A Novel Method for Changing the Dynamics of Slender Elements Using Sponge Particles Structures
Abstract
:1. Introduction
2. Preliminary Modeling and Analysis of Mass Redistribution on the System Dynamics
- —acceleration;
- —natural frequency;
- x—displacement;
- A—excitation amplitude;
- —excitation frequency.
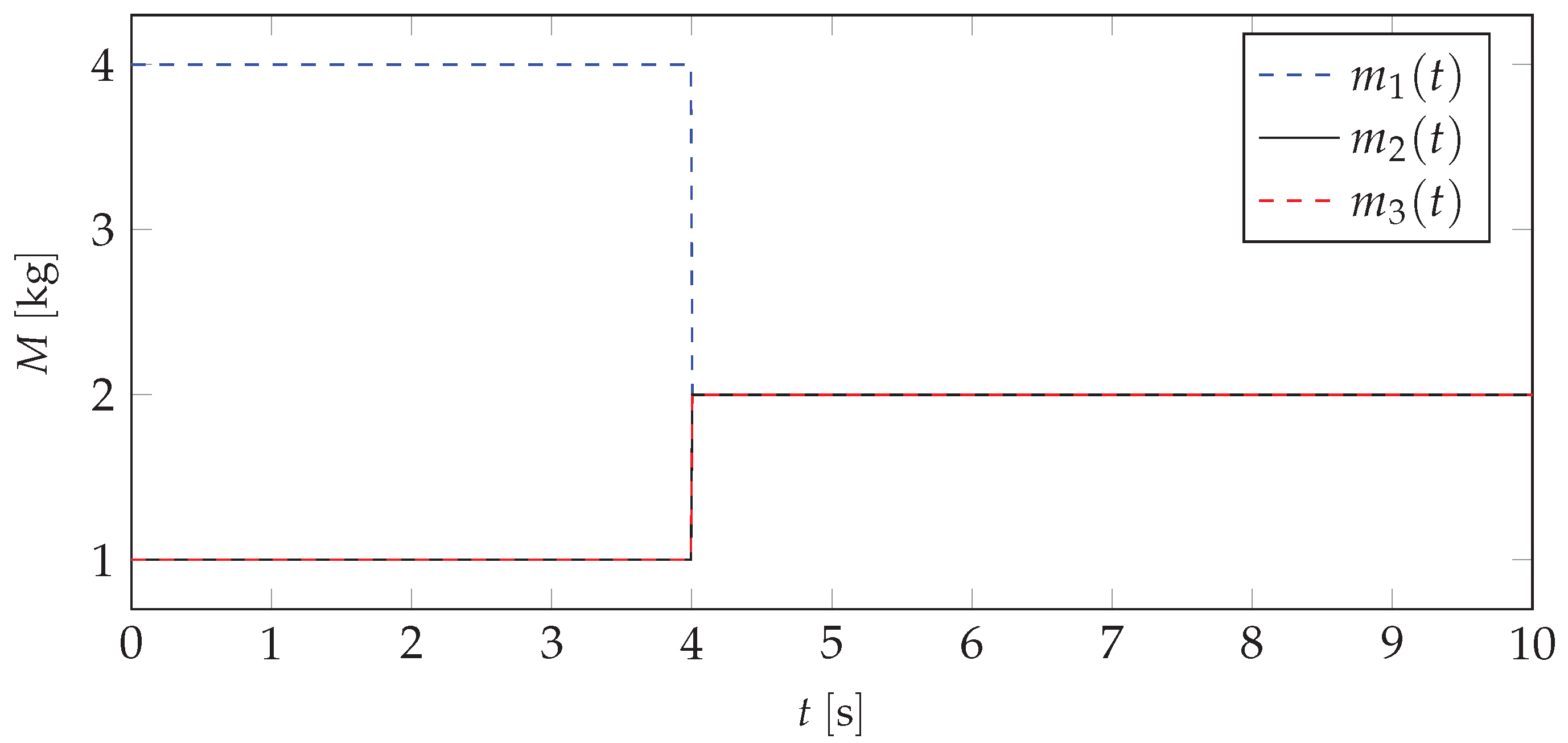
- —varying mass;
- —initial mass;
- —Heaviside function;
- —redistribution process starting time.
3. A Proposition of Modeling and Shaping of Beams Dynamics
- —flexibility matrix;
- —unit bending moment;
- —bending moment;
- E—Young modulus;
- J—moment of inertia.
- K—stiffness matrix.
- M—inertia matrix;
- n—number of nodes;
- —nodal masses.
- Basic mass distribution: ;
- First mass distribution: ;
- Second mass distribution: ;
- Third mass distribution: ;
- Youngs modulus: ;
- Moment of inertia: ;
- Inner diameter of the beam: ;
- Outer diameter of the beam: .
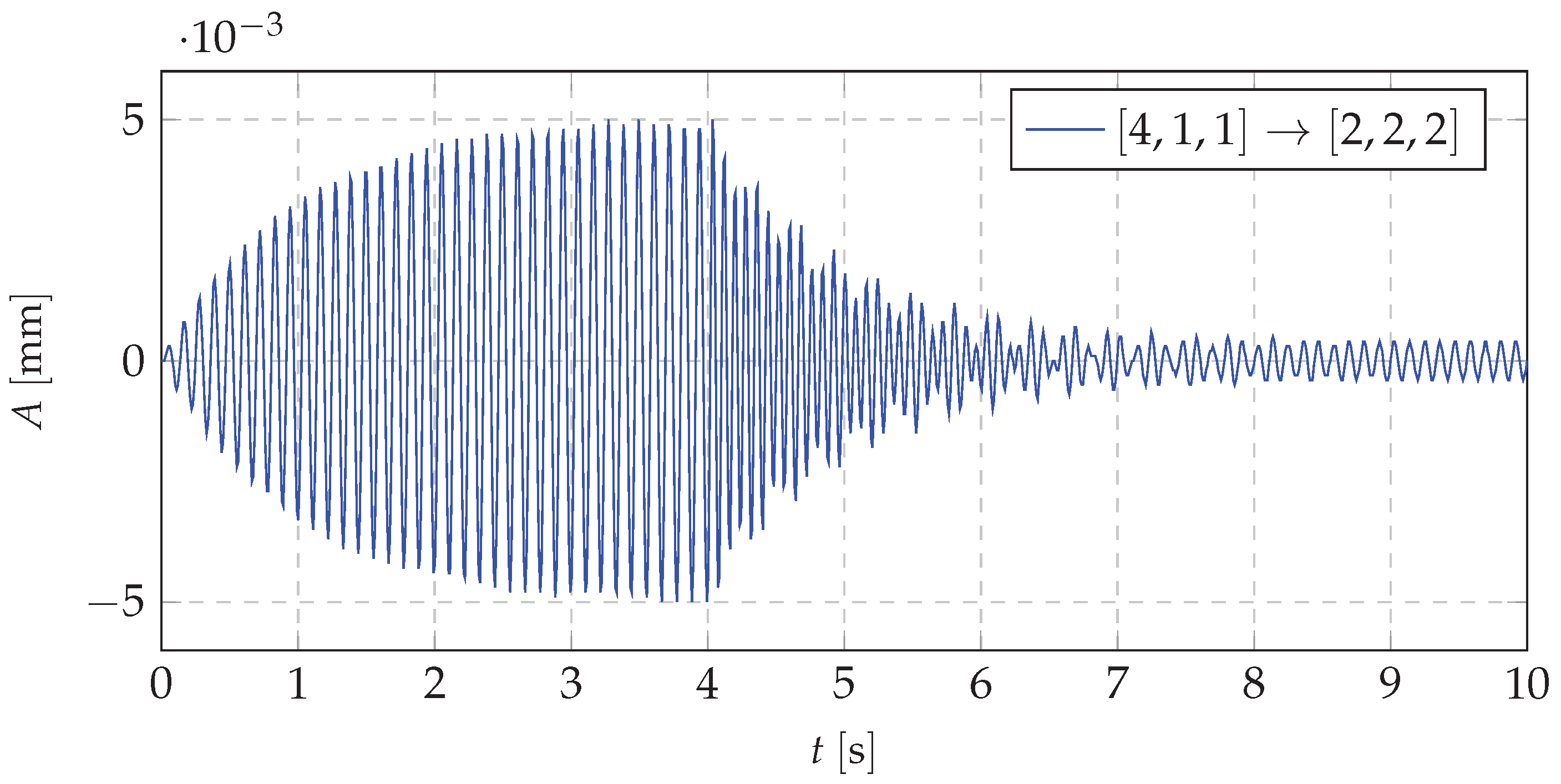
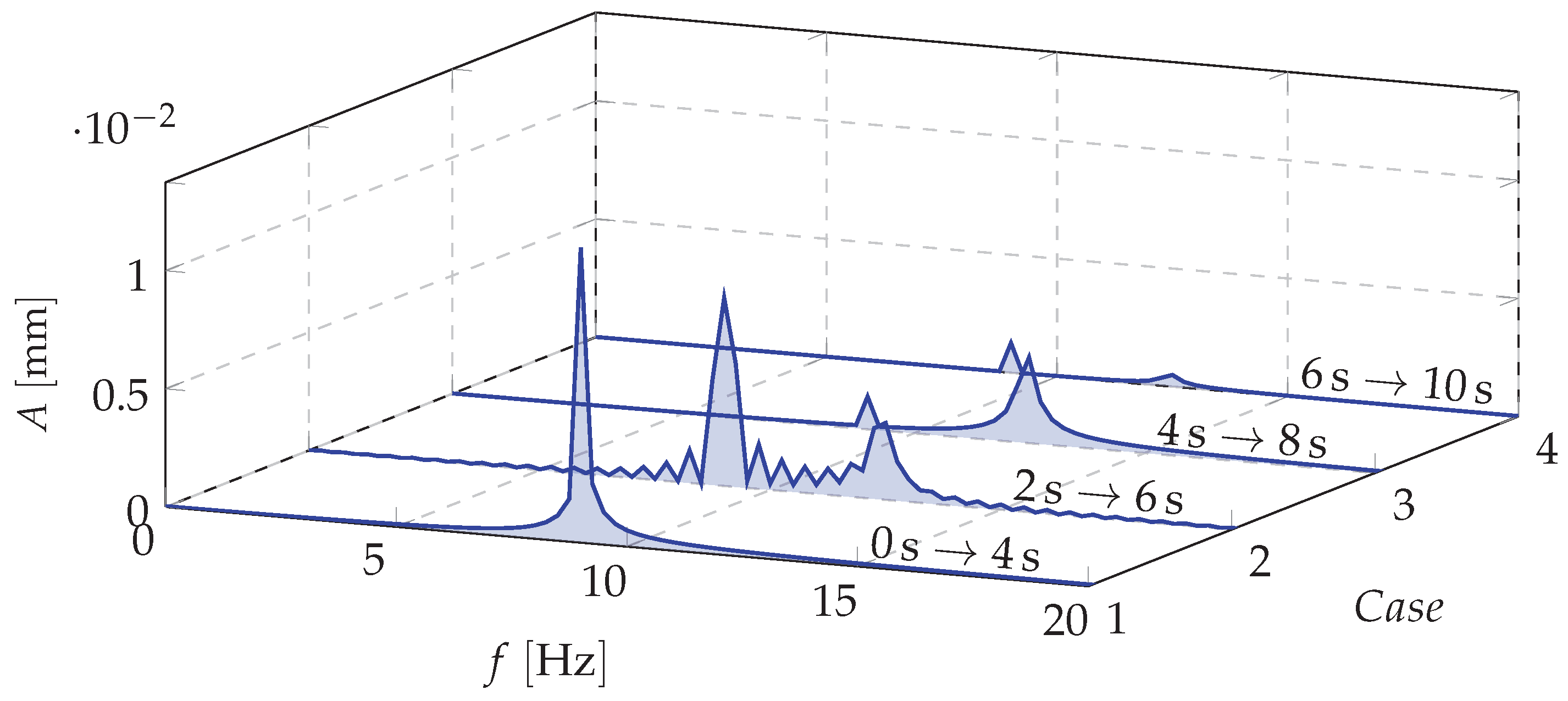
4. Simulations
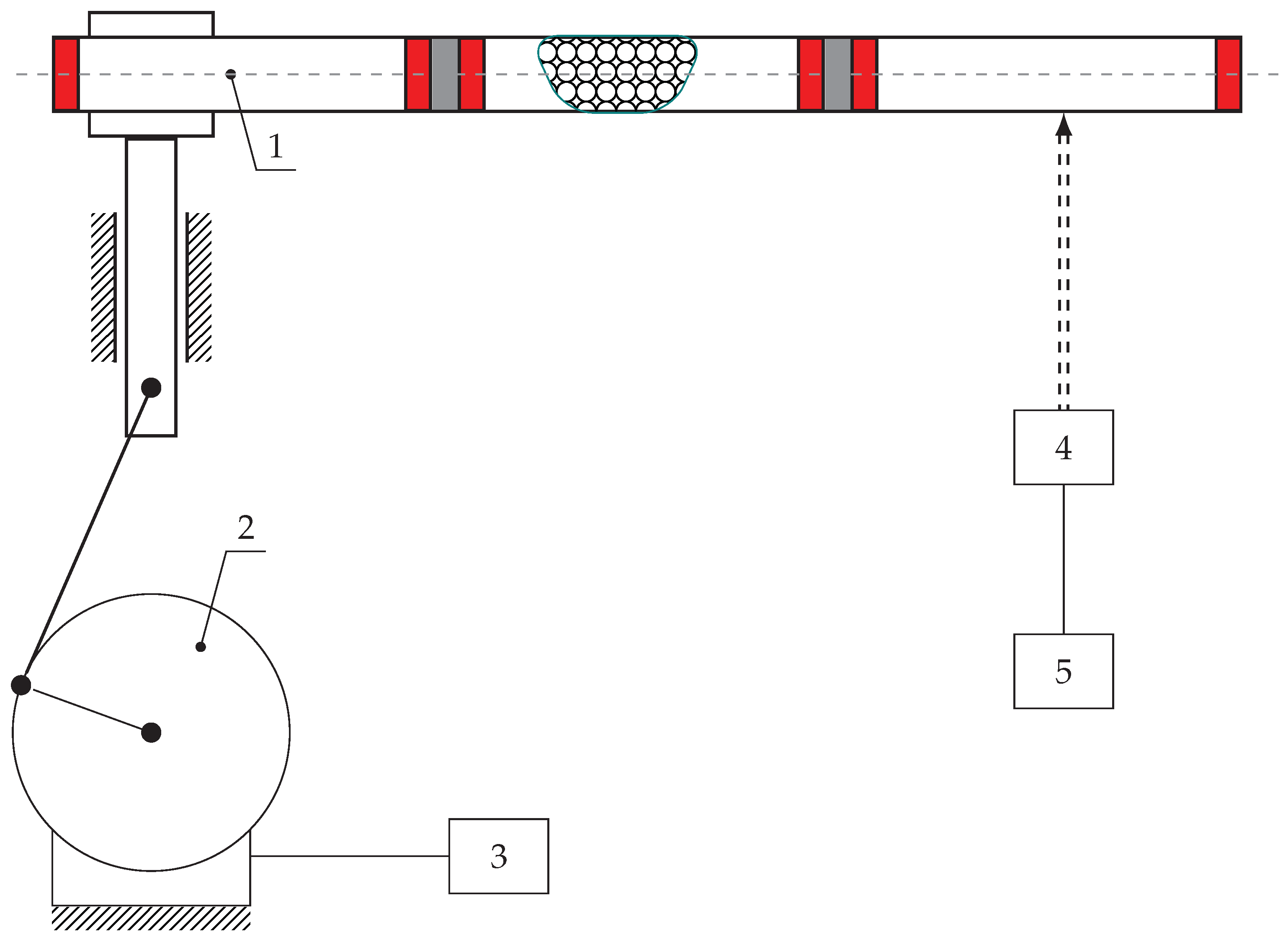
5. Test Stand
6. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Osiński, J. Damping of Vibrations; A.A.Balkema: Rotterdam, The Netherlands, 1998. [Google Scholar]
- Parulekar, Y.M. Passive response control systems for seismic response reduction: A state-of-the-art review. Int. J. Struct. Stab. Dyn. 2009, 9. [Google Scholar] [CrossRef]
- Diez-Jimenez, E.; Rizzo, R. Review of Passive Electromagnetic Devices for Vibration Damping and Isolation. Shock Vib. 2019, 11. [Google Scholar] [CrossRef]
- Bankar, V.K.; Aradhye, A. A Review on Active, Semi-active and Passive Vibration Dampin. Int. J. Curr. Eng. Technol. 2016, 6. [Google Scholar] [CrossRef]
- Chuaqui, T.R.; Roque, C.M.; Ribeiro, P. Active vibration control of piezoelectric smart beams with radial basis function generated finite difference collocation method. J. Intell. Mater. Syst. Struct. 2018, 29, 2728–2743. [Google Scholar] [CrossRef]
- Allien, J.V.; Kumar, H.; Desai, V. Semi-active vibration control of SiC-reinforced Al6082 metal matrix composite sandwich beam with magnetorheological fluid core. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 234, 408–424. [Google Scholar] [CrossRef]
- Mojtaba, B.; Gromada, M.S.F. Optimal configuration of piezoelectric sensors and actuators for active vibration control of a plate using a genetic algorithm. Acta Mech. 2015, 226, 3451–3462. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.; Krishna, Y.B.P. Damping in beams using viscoelastic layers. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2015, 229, 117–125. [Google Scholar] [CrossRef]
- Ashkan, H.; Quenneville, P. Large-scale testing of low damage rocking Cross Laminated Timber (CLT) wall panels with friction dampers. Eng. Struct. 2020, 206. [Google Scholar] [CrossRef]
- Cherif, S.; Trigui, M. Design parameters optimization of a particles impact damper. Int. J. Interact. Des. Manuf. 2018, 12, 1283–1297. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Z.; Masri, S.F.; Lu, X. Particle impact dampers: Past, present, and future. Struct. Control Health Monit. 2018, 25, e2058. [Google Scholar] [CrossRef]
- Gagnon, L.; Morandini, M. A review of particle damping modeling and testing. J. Sound Vib. 2019, 459. [Google Scholar] [CrossRef]
- Du, Y.; Guan, Z. Research on a New Particle Impact Damper. In Proceedings of the 4th Annual International Workshop on Materials Science and Engineering (IWMSE2018), Xi’an, China, 18–20 May 2018; Volume 381, pp. 1283–1297. [Google Scholar] [CrossRef]
- Panossian, H. Structural damping enhancement via non-obstructive particle damping technique. J. Vib. Acoust. 1992, 114, 101–105. [Google Scholar] [CrossRef]
- Ehrgott, R.H.; Panossian, G.D. Modelling techniques for evaluating the effectiveness of particle damping in turbomachinery. Pratt Whitney Rocket. 2009. [Google Scholar] [CrossRef]
- Simonian, S. Particle beam damper. Proc. SPIE 1995, 2445, 149–160. [Google Scholar] [CrossRef]
- Ashley, S. A new racket shakes up tennis. Mech. Eng. 1995, 117, 80–81. [Google Scholar]
- Mohamed, G.; Karkoub, M. Experimental Investigation of Linear Particle Chain Impact Dampers in Free-Vibration Suppression. J. Struct. Eng. 2017, 143, 407–417. [Google Scholar] [CrossRef]
- Toshihiko, K.; Iwata, Y. A combined approach for modeling particle behavior in granular impact damper using discrete element method and cellular automata. Int. J. Mech. Mater. Des. 2017, 13, 407–417. [Google Scholar] [CrossRef]
- Panossian, H. Non-obstructive Particle Damping Experience and Capabilities. Proc. SPIE Int. Soc. Opt. Eng. 2002, 2, 936–941. [Google Scholar] [CrossRef]
- Olson, S.E. An analytical particle damping model. J. Sound Vib. 2003, 264, 1155–1166. [Google Scholar] [CrossRef]
- Fowler, B.L.; Flint, E.M.; Olson, S.E. Effectiveness and Predictability of Particle Damping. Smart Struct. Mater. 2000. [Google Scholar] [CrossRef]
- Fowler, B.L.; Flint, E.M.; Olson, S.E. Design Methodology for Particle Damping. SPIE Conf. Smart Struct. Mater. 2001. [Google Scholar] [CrossRef]
- Mao, K.; Wang, M.Y. DEM simulation of particle damping. Powder Technol. 2004, 142, 154–165. [Google Scholar] [CrossRef]
- Szmidt, T.; Zalewski, R. Inertially excited beam vibrations damped by Vacuum Packed Particles. Smart Mater. Struct. 2014, 23. [Google Scholar] [CrossRef]
- Szmidt, T.; Zalewski, R. Application of Special Granular Structures for semi-active damping of lateral beam vibrations. Eng. Struct. 2014, 65, 13–20. [Google Scholar] [CrossRef]
- Ahamed, R.; Choi, S.B.; Ferdaus, M.M. A state of art on magneto-rheological materials and their potential applications. J. Intell. Mater. Syst. Struct. 2018, 29, 2051–2095. [Google Scholar] [CrossRef]
- Mojtaba, A.; Kouchakzadeh, M.A. Aeroelastic characteristics of magneto-rheological fluid sandwich beams in supersonic airflow. Compos. Struct. 2016, 143, 93–102. [Google Scholar] [CrossRef]


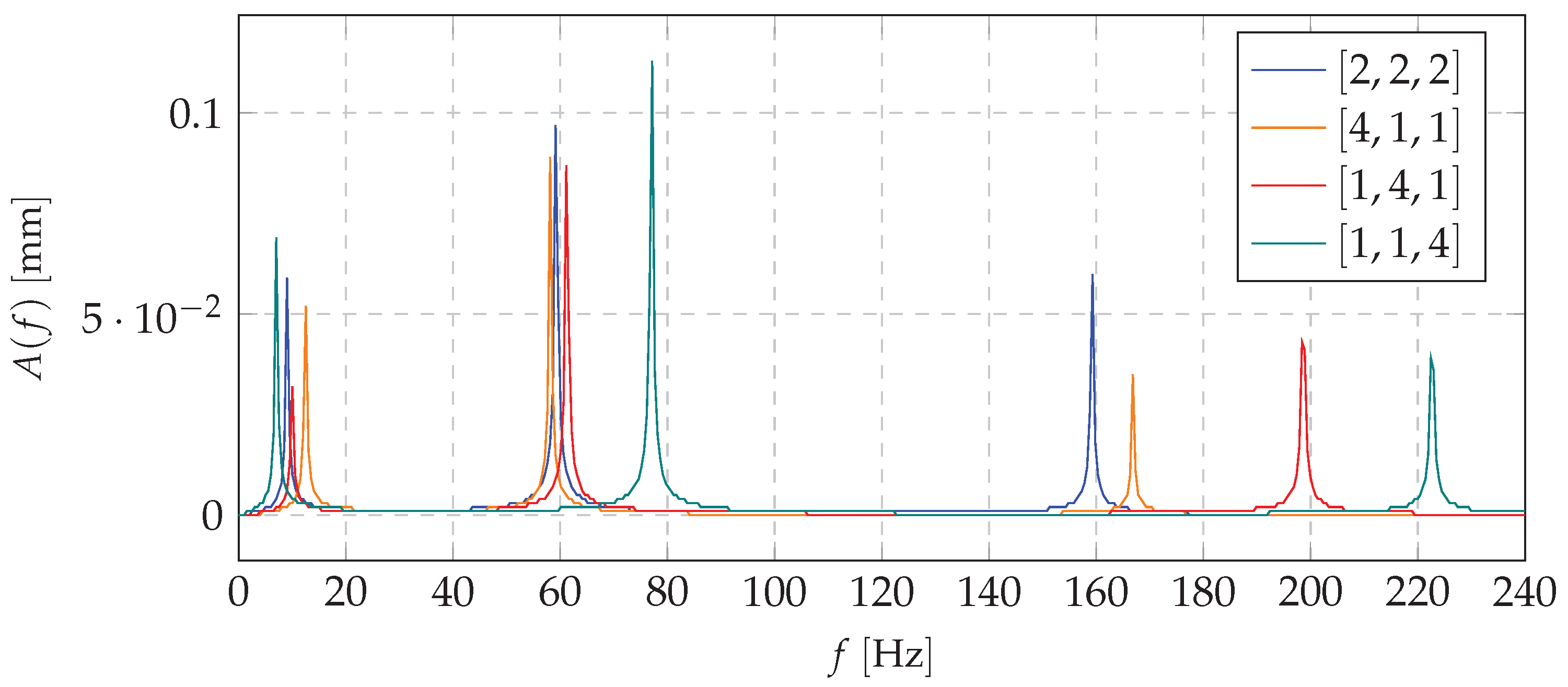
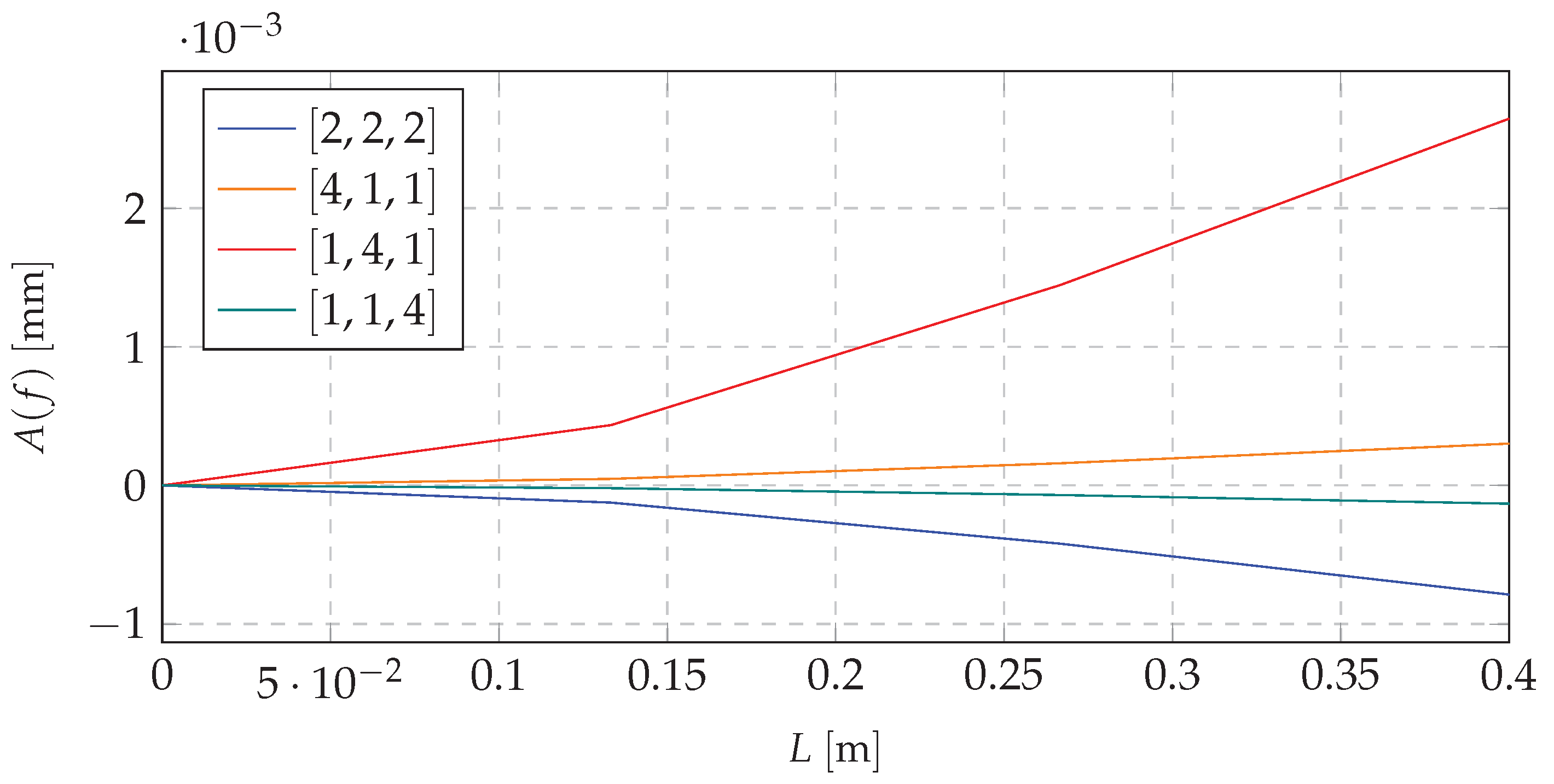
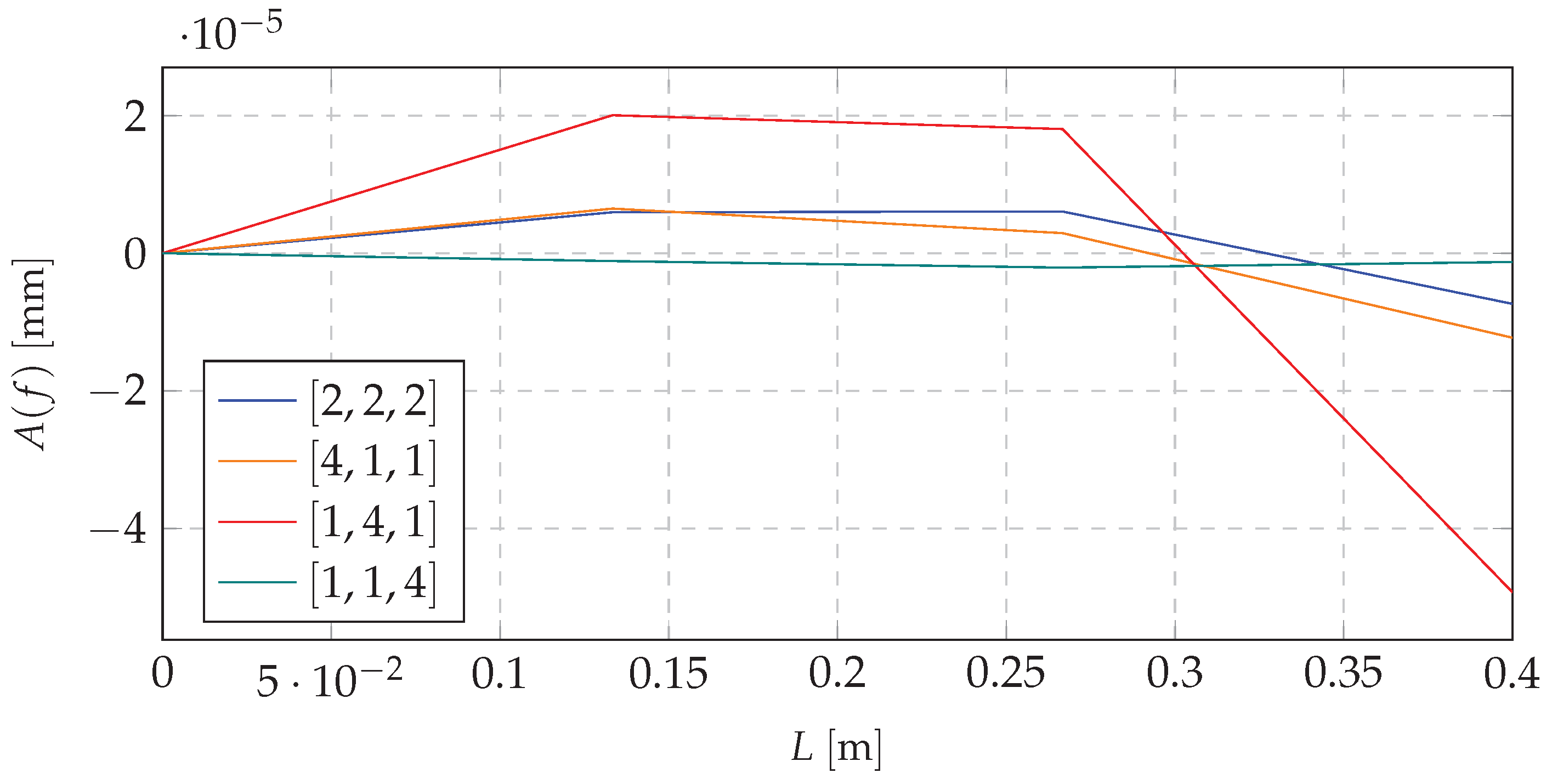
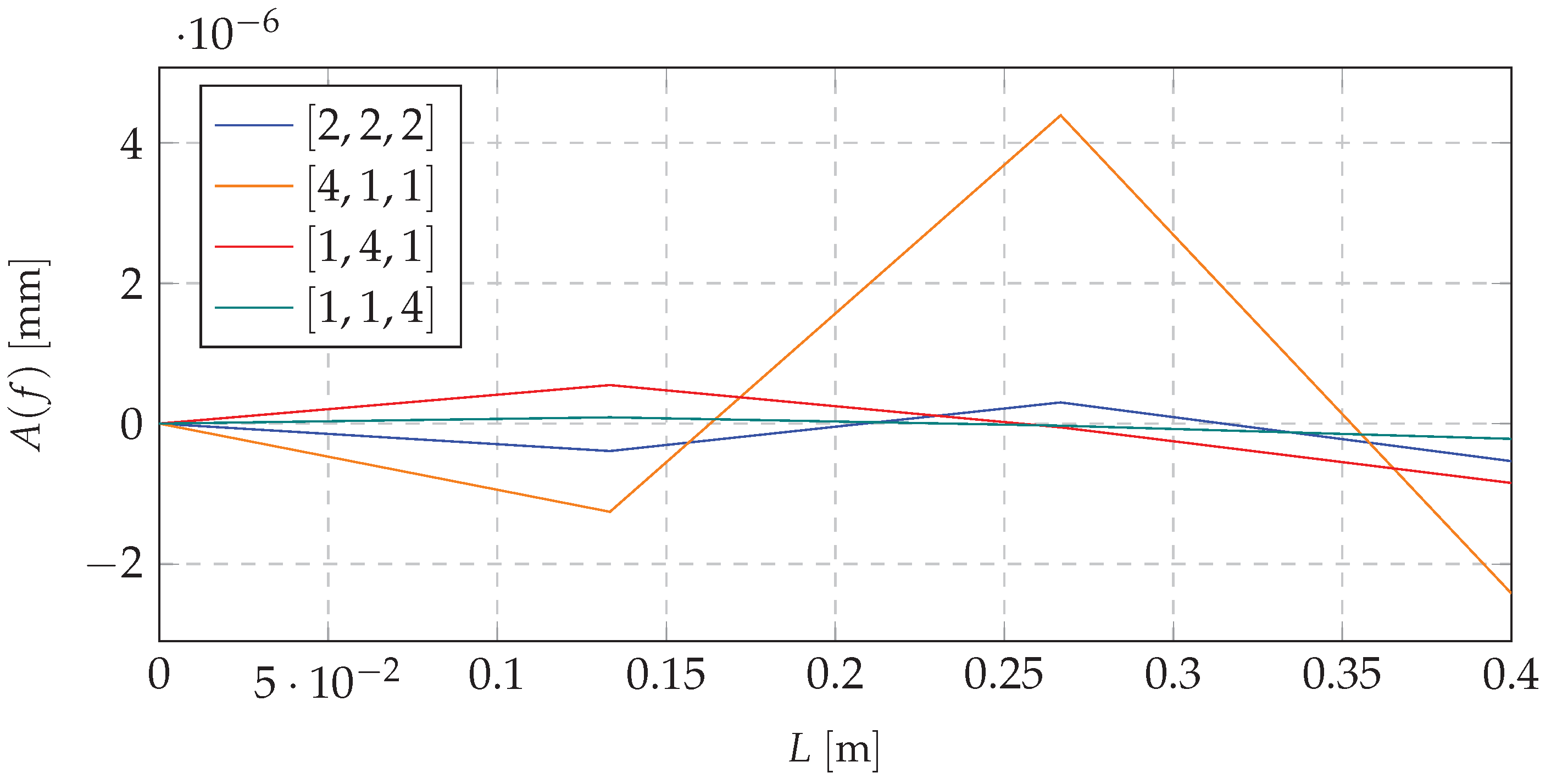
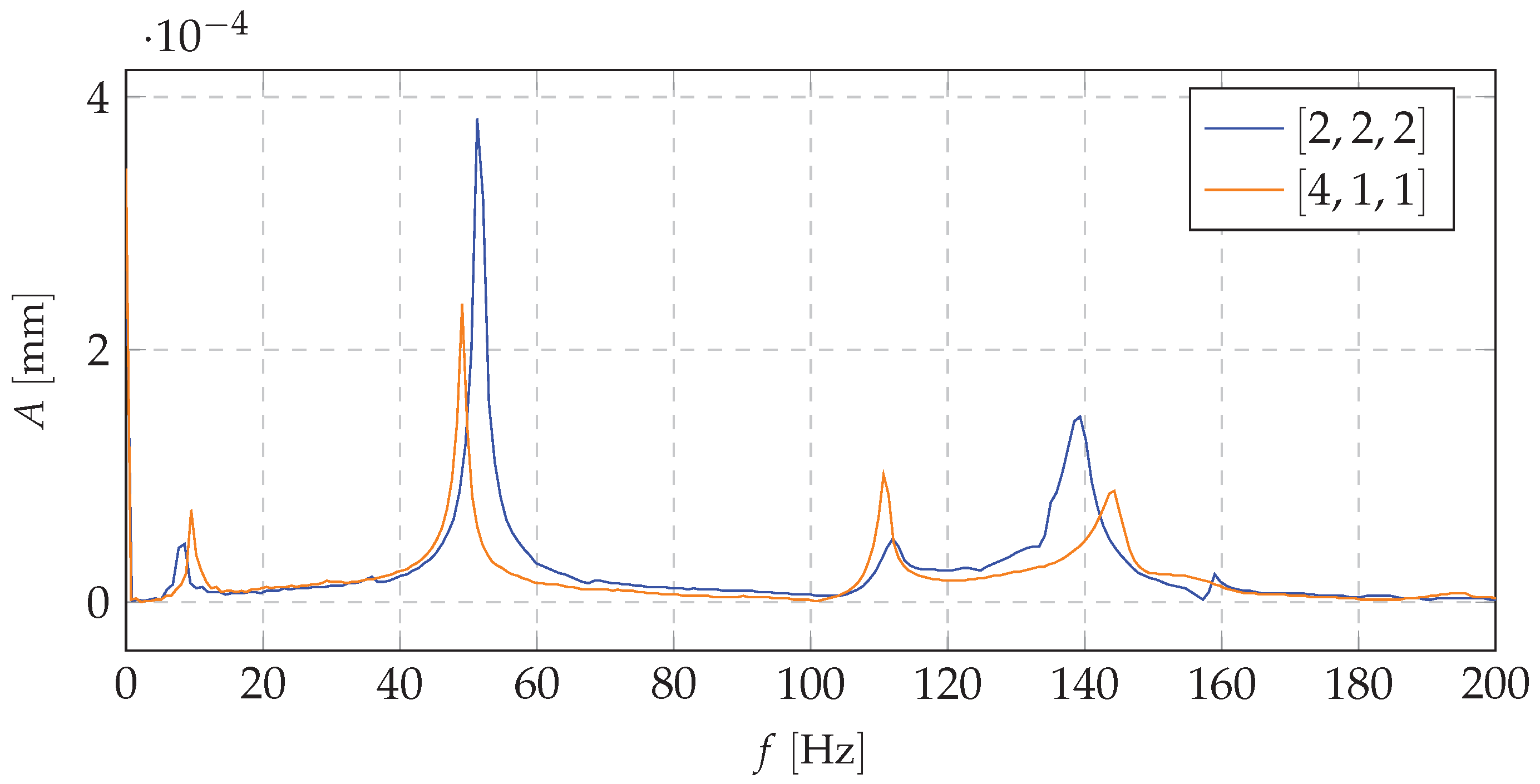

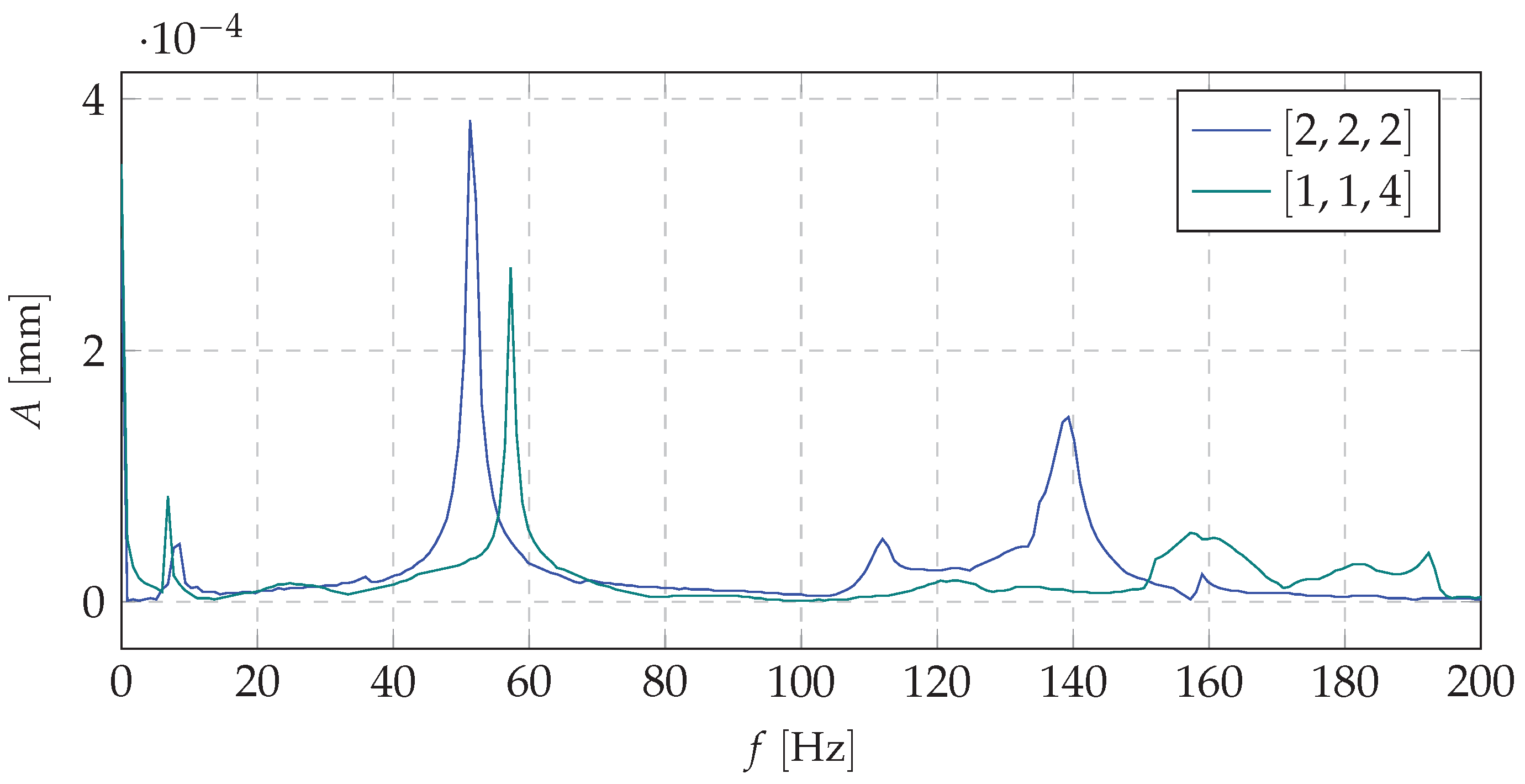
| No | 3 Nodes | 5 Nodes | 7 Nodes | 9 Nodes | 10 Nodes | |
|---|---|---|---|---|---|---|
| 8.1 | 8.5 | 8.9 | 9.2 | 9.23 | ||
| 53.1 | 54.1 | 56.4 | 57.8 | 58.4 | ||
| 142.7 | 153.4 | 159.1 | 162.6 | 163.9 |
| No | 3 Nodes | 5 Nodes | 7 Nodes | 9 Nodes | 10 Nodes | |
|---|---|---|---|---|---|---|
| 11 | 11.2 | 11.3 | 12.7 | 13.2 | ||
| 52.1 | 55 | 57.3 | 64.5 | 68.2 | ||
| 149.6 | 160.5 | 166.2 | 168.6 | 169.8 |
| Component | Parameter | Value |
|---|---|---|
| Cantilever beam | Length: | |
| Size | Inner diameter: | |
| Outer diameter: | ||
| Material | Steel | |
| Sponge | Density | |
| Material | Poliuretan | |
| Size | Diameter: | |
| Grains | Material | Steel |
| Density | ||
| Size | ||
| Balloon | Pressure | |
| Material | Rubber |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żurawski, M.; Chiliński, B.; Zalewski, R. A Novel Method for Changing the Dynamics of Slender Elements Using Sponge Particles Structures. Materials 2020, 13, 4874. https://doi.org/10.3390/ma13214874
Żurawski M, Chiliński B, Zalewski R. A Novel Method for Changing the Dynamics of Slender Elements Using Sponge Particles Structures. Materials. 2020; 13(21):4874. https://doi.org/10.3390/ma13214874
Chicago/Turabian StyleŻurawski, Mateusz, Bogumił Chiliński, and Robert Zalewski. 2020. "A Novel Method for Changing the Dynamics of Slender Elements Using Sponge Particles Structures" Materials 13, no. 21: 4874. https://doi.org/10.3390/ma13214874
APA StyleŻurawski, M., Chiliński, B., & Zalewski, R. (2020). A Novel Method for Changing the Dynamics of Slender Elements Using Sponge Particles Structures. Materials, 13(21), 4874. https://doi.org/10.3390/ma13214874





