SPR Effect Controlled by an Electric Field in a Tapered Optical Fiber Surrounded by a Low Refractive Index Nematic Liquid Crystal
Abstract
1. Introduction
- λ—wavelength of the incident light,
- ncore, nenviroment—refractive index of the new core and the external environment (dielectric medium),
- θi—incident angle of a wave.
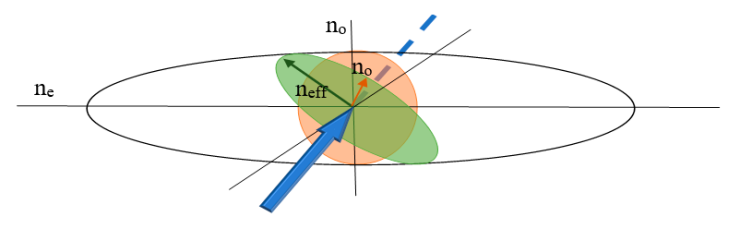
Physics of Surface Plasmon Resonance
- εm, εs—dielectric constants of metal and dielectric medium,
- ω, c—frequency and light velocity in the vacuum, respectively.
- KEW—the propagation constant of EW,
- —dielectric constant of the fiber material,
- θ—incident angle of a TM wave.
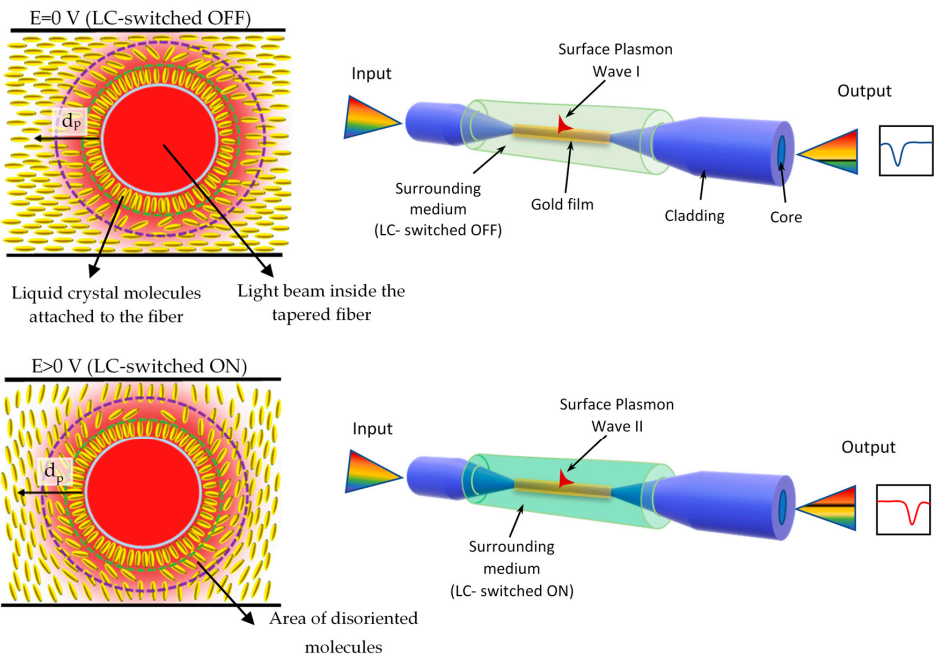
2. Materials and Methods
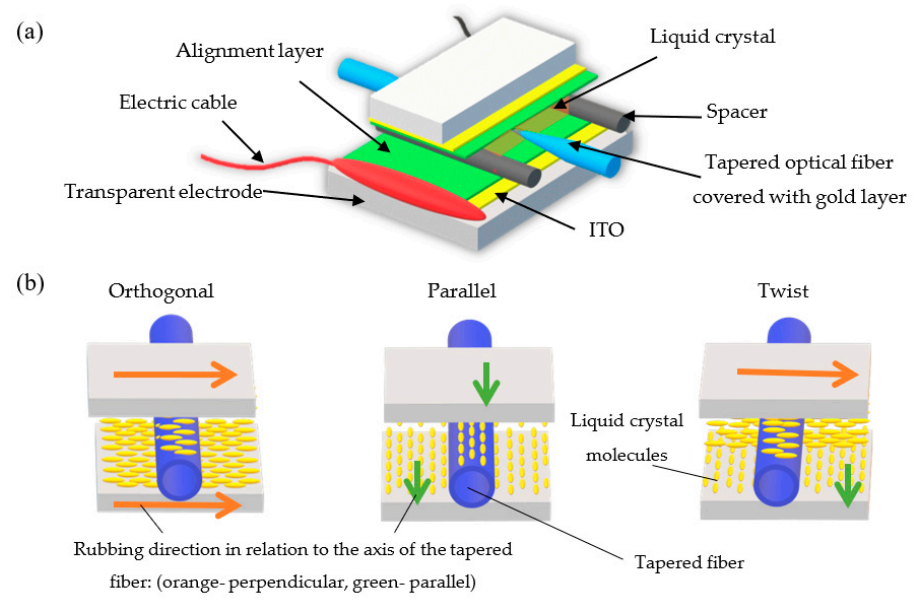
2.1. Preparation of Liquid Crystal Cells
2.2. Materials
2.3. Experimental
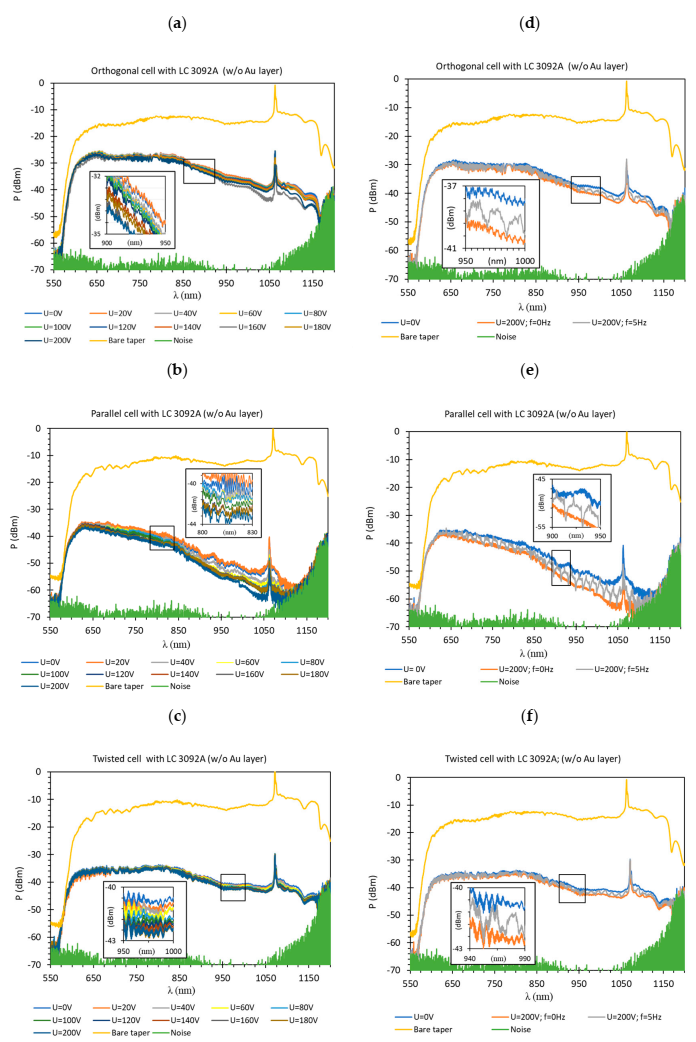
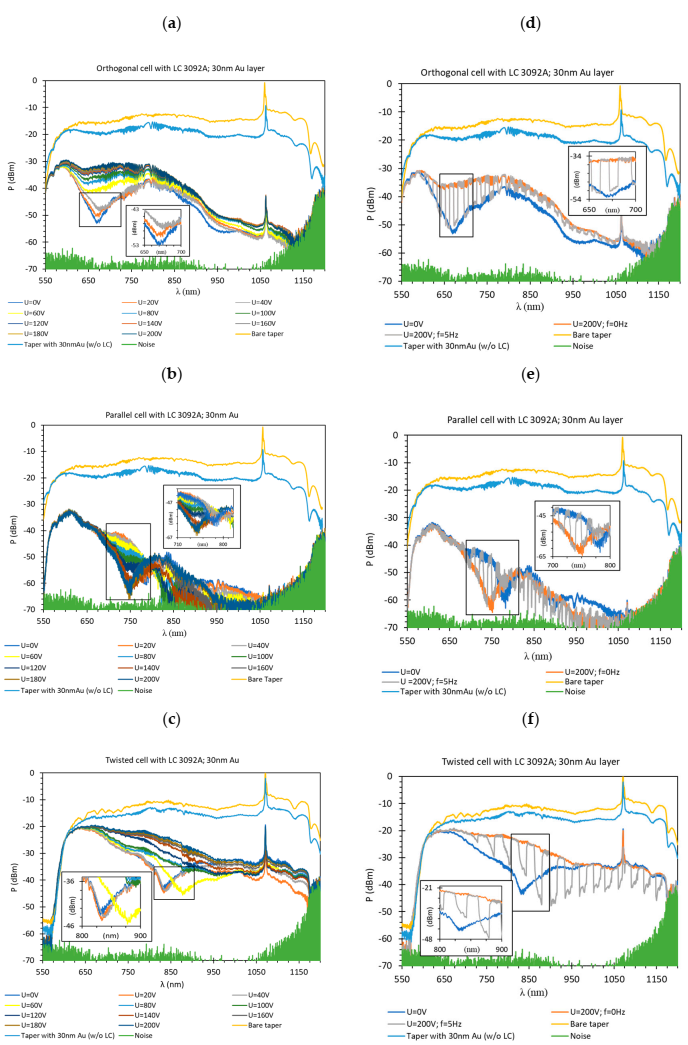
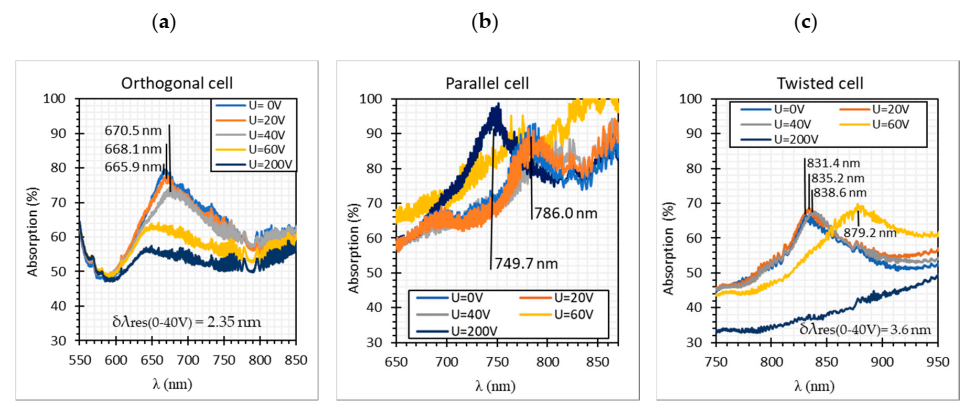
3. Results
4. Conclusions
- The sensing possibility of constructed system depended on cell type (orthogonal, parallel, and twist), and the used metallic layer.
- The initial molecules arrangement inside the LC cell had a significant influence on the occurrence and location of the resonant peak. For the orthogonal cell a resonant peak occurred at 660 nm, for the parallel cell at 770 nm and for the twisted cell at 840 nm.
- The highest resonant peak absorption occurred for the parallel cell and equaled 95% when the cell was switched off and 98% when it was switched on.
- Dynamic response (switching on/off) visible in the whole spectrum obtained for LC cells with the deposited metallic layer proved that it was possible to modify the light beam propagation properties including the resonant area.
- The resulting structure can be used in the future as a sensor of factors to which LC were sensitive, especially temperature and electric field. Additionally, it can be a filter for selected wavelengths depending on the type of cell used.
Author Contributions
Funding
Conflicts of Interest
References
- Mulchan, N.; Rodriguez, M.; O’Shea, K.; Darici, Y. Application of a high-resolution SPR technique for monitoring real-time metal/dielectric interactions. Sens. Actuators B Chem. 2003, 88, 132–137. [Google Scholar] [CrossRef]
- Piliarik, M.; Homola, J. SPR Sensor Instrumentation. In Surface Plasmon Resonance Based Sensors; Springer: Berlin/Heidelberg, Germany, 2006; pp. 95–114. [Google Scholar]
- Li, L.; Liang, Y.; Guang, J.; Cui, W.; Zhang, X.; Masson, J.F.; Peng, W. Dual Kretschmann and Otto configuration fiber surface plasmon resonance biosensor. Opt. Express 2017, 25, 26950. [Google Scholar] [CrossRef] [PubMed]
- Gupta, B.D.; Shrivastav, A.M.; Usha, S.P. Surface Plasmon Resonance-Based Fiber Optic Sensors Utilizing Molecular Imprinting. Sensors 2016, 16, 1381. [Google Scholar] [CrossRef]
- Lim, K.S.; Harun, S.W.; Arof, H.; Ahmad, H. Fabrication and Applications of Microfiber. Sel. Top. Opt. Fiber Technol. 2012, 17, 473–508. [Google Scholar]
- Brambilla, G. Optical fibre nanowires and microwires: A review. J. Opt. 2010, 12, 043001. [Google Scholar] [CrossRef]
- Villatoro, J.; Monzon-Hernandez, D.; Mejıa, E. Fabrication and modelling of uniform-waist single-mode tapered optical fiber sensors. Appl. Opt. 2003, 42, 2278–2283. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.; Hench, L. Effect of taper geometries and launch angle on evanescent wave penetration depth in optical fibers. Biosens. Bioelectron. 2005, 20, 1312–1319. [Google Scholar] [CrossRef]
- Tong, L.; Lou, J.; Mazur, E. Single-mode guiding properties of subwavelength-diameter silica and silicon wire waveguides. Opt. Express 2004, 12, 1025–1035. [Google Scholar] [CrossRef] [PubMed]
- Chen, G. A Review of Microfiber and Nanofiber Based Optical Sensors. Open Opt. J. 2014, 7, 32. [Google Scholar] [CrossRef]
- Martin-Fernandez, M.; Tynan, C.; Webb, S. A ‘pocket guide’ to total internal reflection fluorescence. J. Microsc. 2013, 252, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Gupta, B.D.; Verma, R.K. Surface Plasmon Resonance-Based Fiber Optic Sensors: Principle, Probe Designs, and Some Applications. J. Sens. 2009, 2009, 979761. [Google Scholar] [CrossRef]
- Gandhi, M.; Chu, S.; Senthilnathan, K.; Babu, P.; Nakkeeran, K.; Li, Q. Recent Advances in Plasmonic Sensor-Based Fiber Optic Probes for Biological Applications. Appl. Sci. 2019, 9, 949. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Xu, W. Surface plasmon polaritons: Physics and applications. J. Phys. D Appl. Phys. 2012, 45, 113001. [Google Scholar] [CrossRef]
- Liang, G.; Luo, Z.; Liu, K.; Wang, Y.; Dai, J.; Duan, Y. Fiber Optic Surface Plasmon Resonance–Based Biosensor Technique: Fabrication, Advancement, and Application. Crit. Rev. Anal. Chem. 2015, 46, 213–223. [Google Scholar] [CrossRef] [PubMed]
- Wieduwilt, T.; Kirsch, K.; Dellith, J.; Willsch, R.; Bartelt, H. Optical Fiber Micro-Taper with Circular Symmetric Gold Coating for Sensor Applications Based on Surface Plasmon Resonance. Plasmonics 2012, 8, 545–554. [Google Scholar] [CrossRef]
- Wang, D.; Loo, J.; Chen, J.; Yam, Y.; Chen, S.C.; He, H.; Ho, H. Recent Advances in Surface Plasmon Resonance Imaging Sensors. Sensors 2019, 19, 1266. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, X.; Niu, L.Y.; Fan, X.C. Enhanced sensitivity of bimetallic optical fiber SPR sensor based on MoS2 nanosheets. Opt. Lasers Eng. 2020, 128, 105997. [Google Scholar] [CrossRef]
- Gupta, B.D.; Kant, R. Recent advances in surface plasmon resonance based fiber optic chemical and biosensors utilizing bulk and nanostructures. Opt. Laser Technol. 2018, 101, 144–161. [Google Scholar] [CrossRef]
- Zeni, L.; Perri, C.; Cennamo, N.; Arcadio, F.; D’Agostino, G.; Salmona, M.; Beeg, M.; Gobbi, M. A portable optical-fibre-based surface plasmon resonance biosensor for the detection of therapeutic antibodies in human serum. Sci. Rep. 2020, 10, 11154. [Google Scholar] [CrossRef]
- Yuk, J.S.; Guignon, E.; Lynes, M. Sensitivity enhancement of a grating-based surface plasmon-coupled emission (SPCE) bionsor chip using gold thickness. Chem. Phys. Lett. 2014, 591, 5–9. [Google Scholar] [CrossRef]
- Raynes, E.P. Electro-Optic and Thermo-Optic Effects in Liquid Crystals. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1983, 309, 167–178. [Google Scholar]
- Muševič, I. Nematic Liquid-Crystal Colloids. Materials 2018, 11, 24. [Google Scholar] [CrossRef]
- Ko, M.; Kim, S.J.; Kim, J.H.; Lee, B.W.; Jeon, M.Y. Measurement of Effective Refractive Index of Nematic Liquid Crystal in Fabry-Perot Etalon. J. Opt. Soc. Korea 2015, 19, 346–350. [Google Scholar] [CrossRef]
- Polynkin, P.; Polynkin, A.; Peyghambarian, N.; Mansuripur, M. Evanescent field-based optical fiber sensing device for measuring the refractive index of liquids in microfluidic channels. Opt. Lett. 2005, 30, 1273. [Google Scholar] [CrossRef]
- Ahn, H.; Song, H.; Choi, J.-R.; Kim, K. A Localized Surface Plasmon Resonance Sensor Using Double-Metal-Complex Nanostructures and a Review of Recent Approaches. Sensors 2018, 18, 98. [Google Scholar] [CrossRef]
- Kaur, D.; Sharma, V.K.; Kapoor, A. High sensitivity lossy mode resonance sensors. Sens. Actuators B Chem. 2014, 198, 366–376. [Google Scholar] [CrossRef]
- Reshetnyak, V.; Pinkevych, I.; Zadorozhnii, V.; Evans, D. Liquid Crystal Control of Surface Plasmon Resonance Sensor Based on Nanorods. Mol. Cryst. Liq. Cryst. 2015, 613, 110–120. [Google Scholar] [CrossRef]
- Welford, K.R.; Sambles, J.R.; Clark, M.G. Guided modes and surface plasmon-polaritons observed with a nematic liquid crystal using attenuated total reflection. Liq. Cryst. 1987, 2, 91–105. [Google Scholar] [CrossRef]
- Korec, J.; Stasiewicz, K.A.; Jaroszewicz, L.R.; Piecek, W.; Kula, P. Temperature and voltage sensing based on a tapered optical fiber device with the liquid crystal cladding. Opt. Fiber Technol. 2020, 56, 102190. [Google Scholar] [CrossRef]
- Dabrowski, R.; Garbat, K.; Urban, S.; Woliński, T.R.; Dziaduszek, J.; Ogrodnik, T.; Siarkowska, A. Low-birefringence liquid crystal mixtures for photonic liquid crystal fibres application. Liq. Cryst. 2017, 44, 1911–1928. [Google Scholar] [CrossRef]
- Piecek, W.; Raszewski, Z.; Perkowski, P.; Morawiak, P.; Pajchrowski, G.; Ying, W. Transient Light Scattering Mode of an Orthoconic Antiferroelectric Liquid Crystal. Mol. Cryst. Liq. Cryst. 2008, 507, 150–160. [Google Scholar] [CrossRef]
- Varshneya, A.K.; Mauro, J.C. Fundamentals of Inorganic Glasses, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 595–606. ISBN 9780128162262. [Google Scholar]
- Kim, Y.; Lee, M.; Wang, H.S.; Song, K. The effect of surface polarity of glass on liquid crystal alignment. Liq. Cryst. 2017, 45, 757–764. [Google Scholar] [CrossRef]
- Francisco, A. Sensors Based on Nanostructured Materials; Springer: New York, NY, USA, 2009; p. 276. ISBN 9780387777535. [Google Scholar]
- Choudhury, P.K.; Soon, W. Te mode propagation through tapered core liquid crystal optical fibers. Prog. Electromagn. Res. 2010, 104, 449–463. [Google Scholar] [CrossRef]
- Choudhury, P.K.; Soon, W. On the transmission by liquid crystal tapered optical fibers. Opt. Int. J. Light Electron Opt. 2011, 122, 1061–1068. [Google Scholar] [CrossRef]
- Moś, J.E.; Korec, J.; Stasiewicz, K.A.; Jankiewicz, B.; Bartosewicz, B.; Jaroszewicz, L.R. Research on Optical Properties of Tapered Optical Fibers with Liquid Crystal Cladding Doped with Gold Nanoparticles. Crystals 2019, 9, 306. [Google Scholar] [CrossRef]
- Florek, M.; Stasiewicz, K.; Korec, J.; Moś, J.; Strzeżysz, O.; Garbat, K.; Jaroszewicz, L. Tapered fiber optic devices with liquid crystal cladding. Proc. SPIE 2019, 11045, 110450E. [Google Scholar]
- Henninot, J.F.; Louvergneaux, D.; Tabiryan, N.; Warenghem, M. Controlled Leakage of a Tapered Optical Fiber with Liquid Crystal Cladding. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1996, 282, 297–308. [Google Scholar] [CrossRef]
- Korposh, S.; James, S.W.; Lee, S.-W.; Tatam, R.P. Tapered Optical Fibre Sensors: Current Trends and Future Perspectives. Sensors 2019, 19, 2294. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, K.; Sharma, S.C.; Hozhabri, N. High performance surface plasmon sensors: Simulations and measurements. J. Appl. Phys. 2015, 118, 093105. [Google Scholar] [CrossRef]




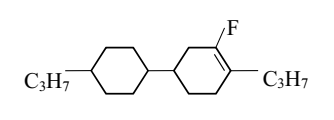
| No | Substrates | Properties | ||
|---|---|---|---|---|
| R1 | R2 | |||
| Ia | C3H7 | CH3 | cl. p (°C) | 63.2 |
| Ib | C3H7 | C2H5 | (1 kHz) (1 kHz) | 3.17 3.66 |
| Ic | C5H11 | CH3 | ∆ε (1 kHz) | 0.49 |
| Id | C5H11 | C2H5 | no (589 nm) | 1.4507 |
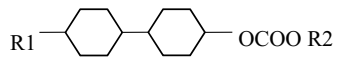 | ne (589 nm) | 1.5062 | ||
| II | C3H7 | CH2CF3 | ∆n (589 nm) | 0.056 |
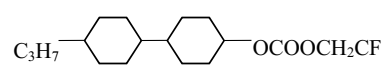 | ||||
| III | C3H7 | C3H7 | ||
 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korec, J.; Stasiewicz, K.A.; Jaroszewicz, L.R.; Garbat, K. SPR Effect Controlled by an Electric Field in a Tapered Optical Fiber Surrounded by a Low Refractive Index Nematic Liquid Crystal. Materials 2020, 13, 4942. https://doi.org/10.3390/ma13214942
Korec J, Stasiewicz KA, Jaroszewicz LR, Garbat K. SPR Effect Controlled by an Electric Field in a Tapered Optical Fiber Surrounded by a Low Refractive Index Nematic Liquid Crystal. Materials. 2020; 13(21):4942. https://doi.org/10.3390/ma13214942
Chicago/Turabian StyleKorec, Joanna, Karol A. Stasiewicz, Leszek R. Jaroszewicz, and Katarzyna Garbat. 2020. "SPR Effect Controlled by an Electric Field in a Tapered Optical Fiber Surrounded by a Low Refractive Index Nematic Liquid Crystal" Materials 13, no. 21: 4942. https://doi.org/10.3390/ma13214942
APA StyleKorec, J., Stasiewicz, K. A., Jaroszewicz, L. R., & Garbat, K. (2020). SPR Effect Controlled by an Electric Field in a Tapered Optical Fiber Surrounded by a Low Refractive Index Nematic Liquid Crystal. Materials, 13(21), 4942. https://doi.org/10.3390/ma13214942







