Modelling, Analysis, and Optimization of the Effects of Pulsed Electrophoretic Deposition Parameters on TiO2 Films Properties Using Desirability Optimization Methodology
Abstract
1. Introduction
2. Materials and Methods
2.1. Substrate Preparation
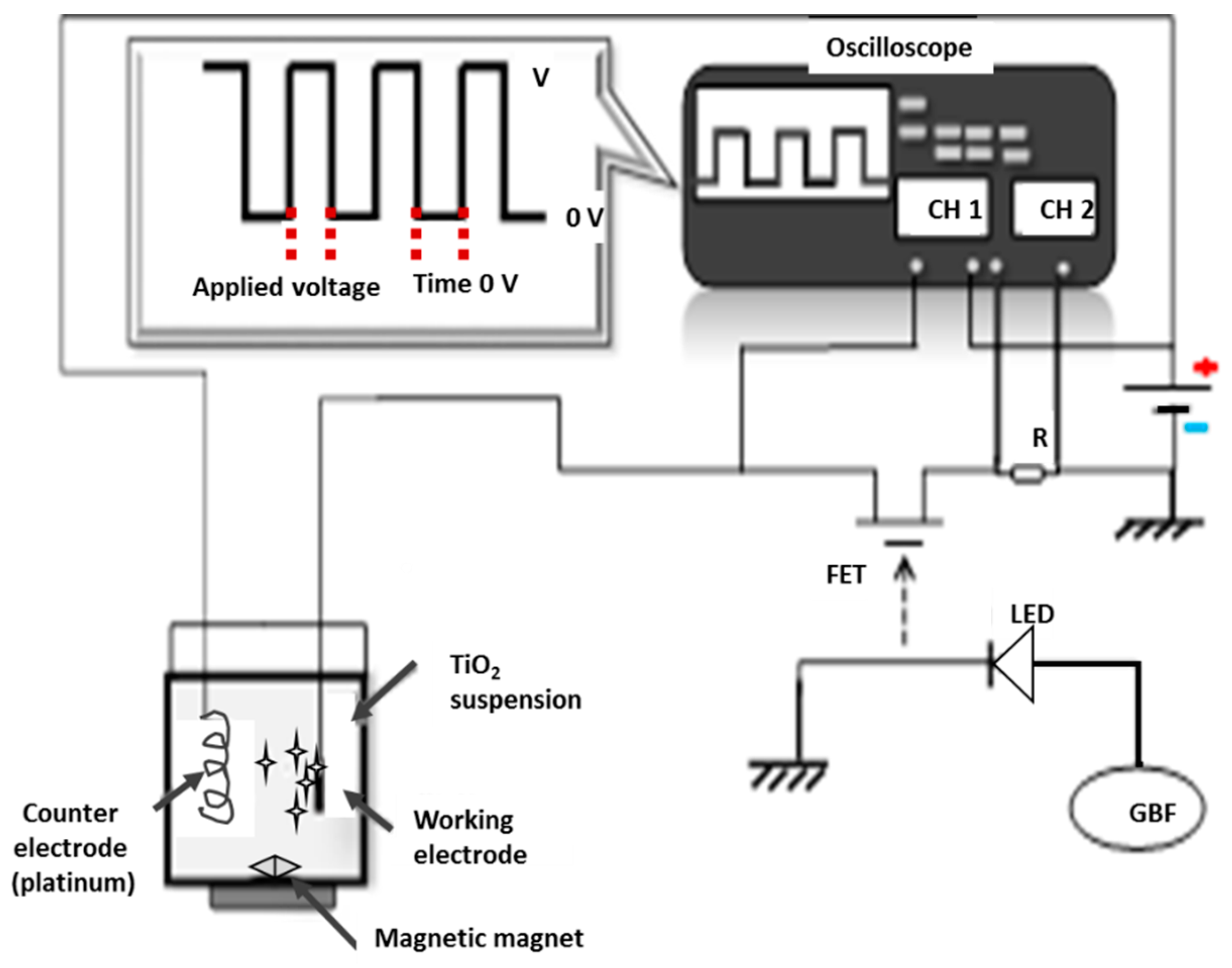
2.2. Pulsed Electrophoretic Deposition
2.3. Characterization of the Film
2.4. Degradation Experiments
2.5. Experimental Design
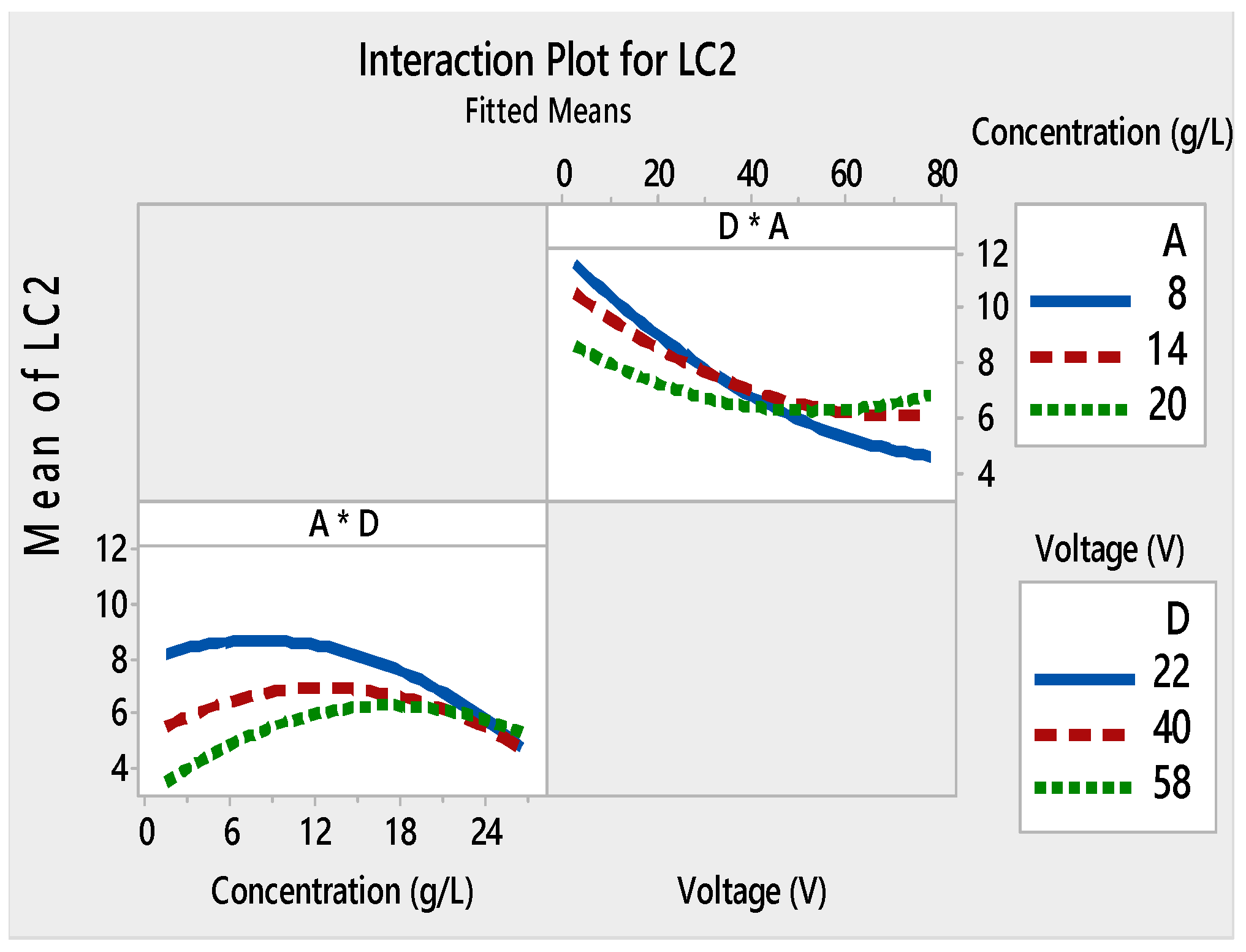
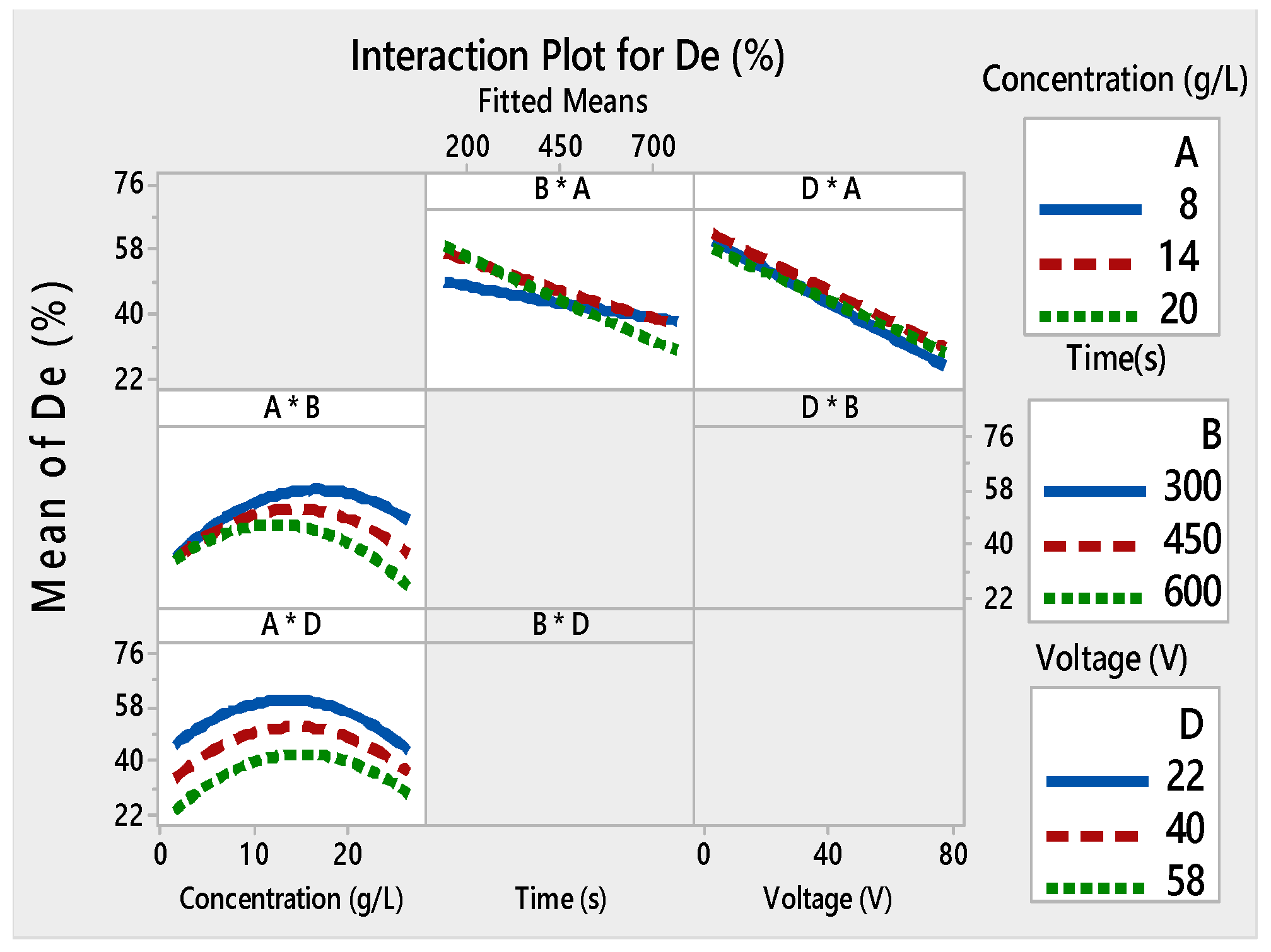
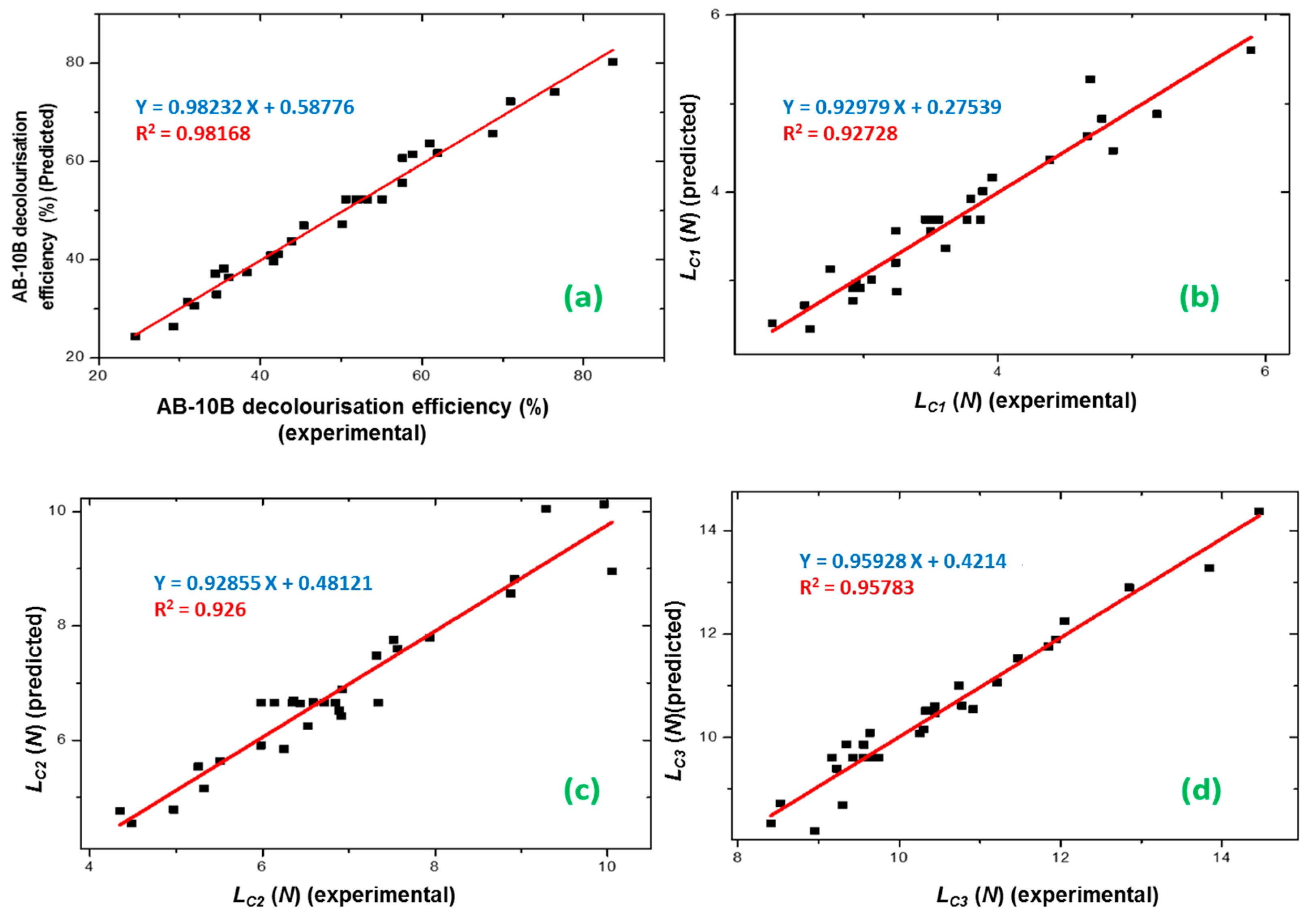
3. Results and Discussion
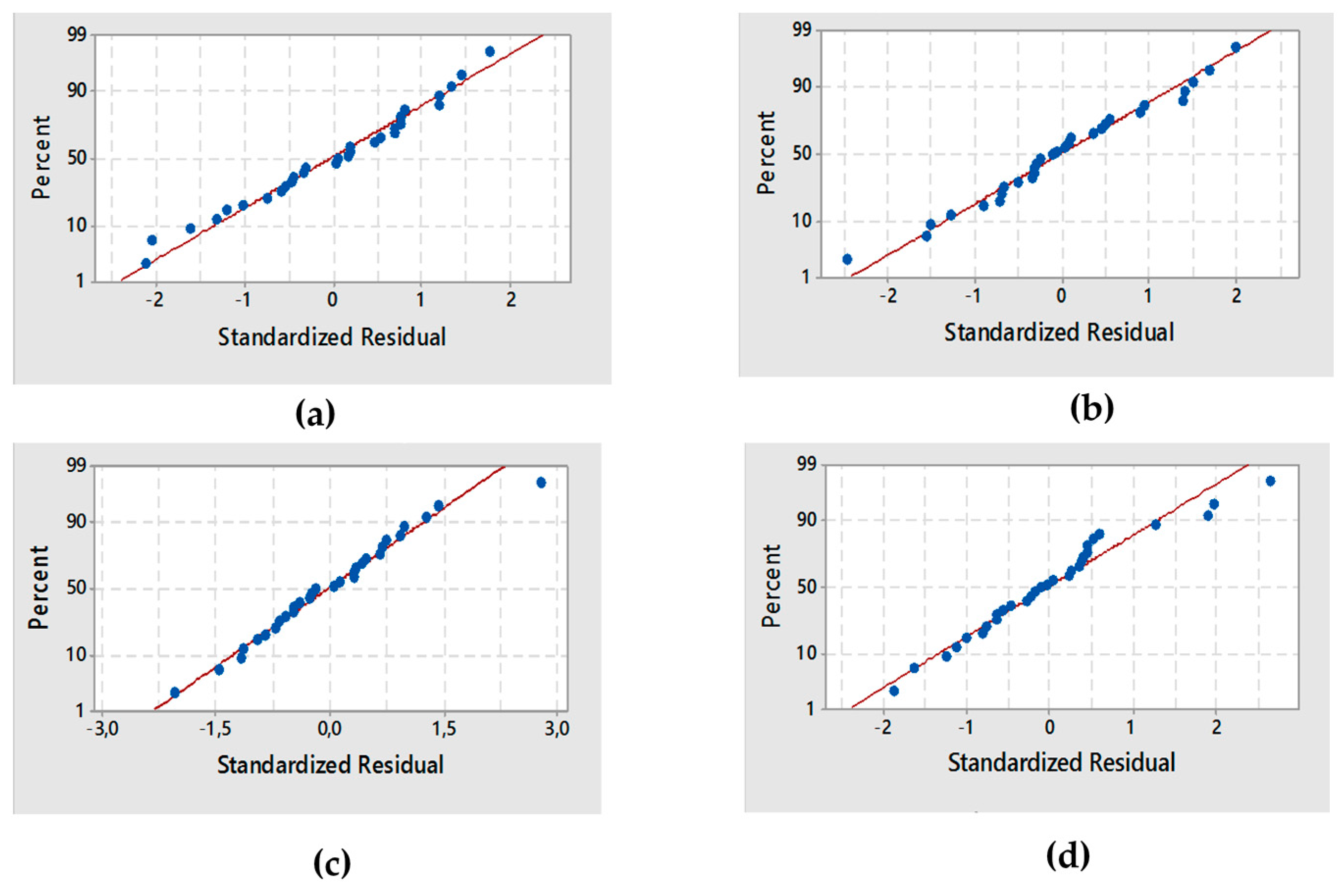
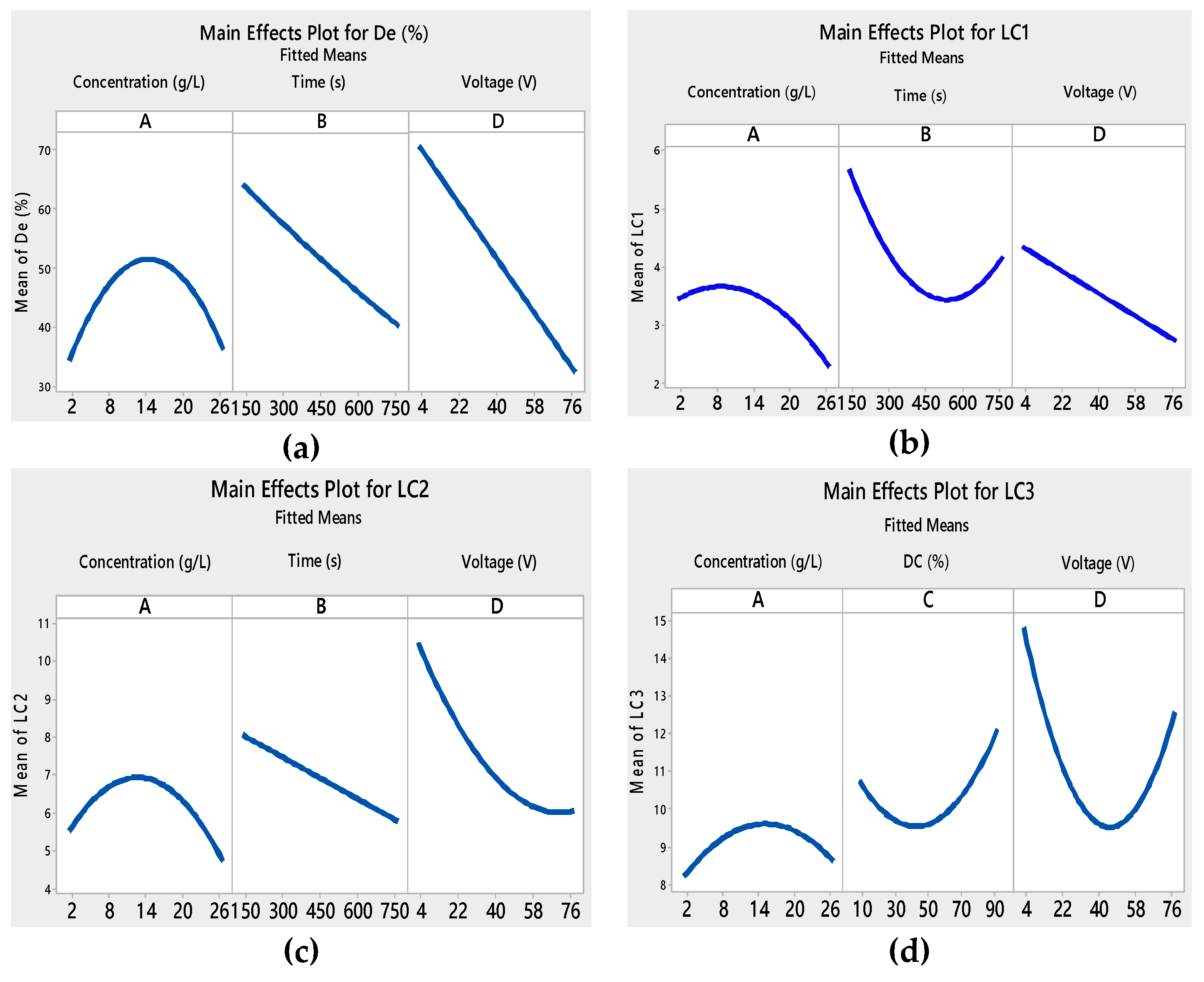
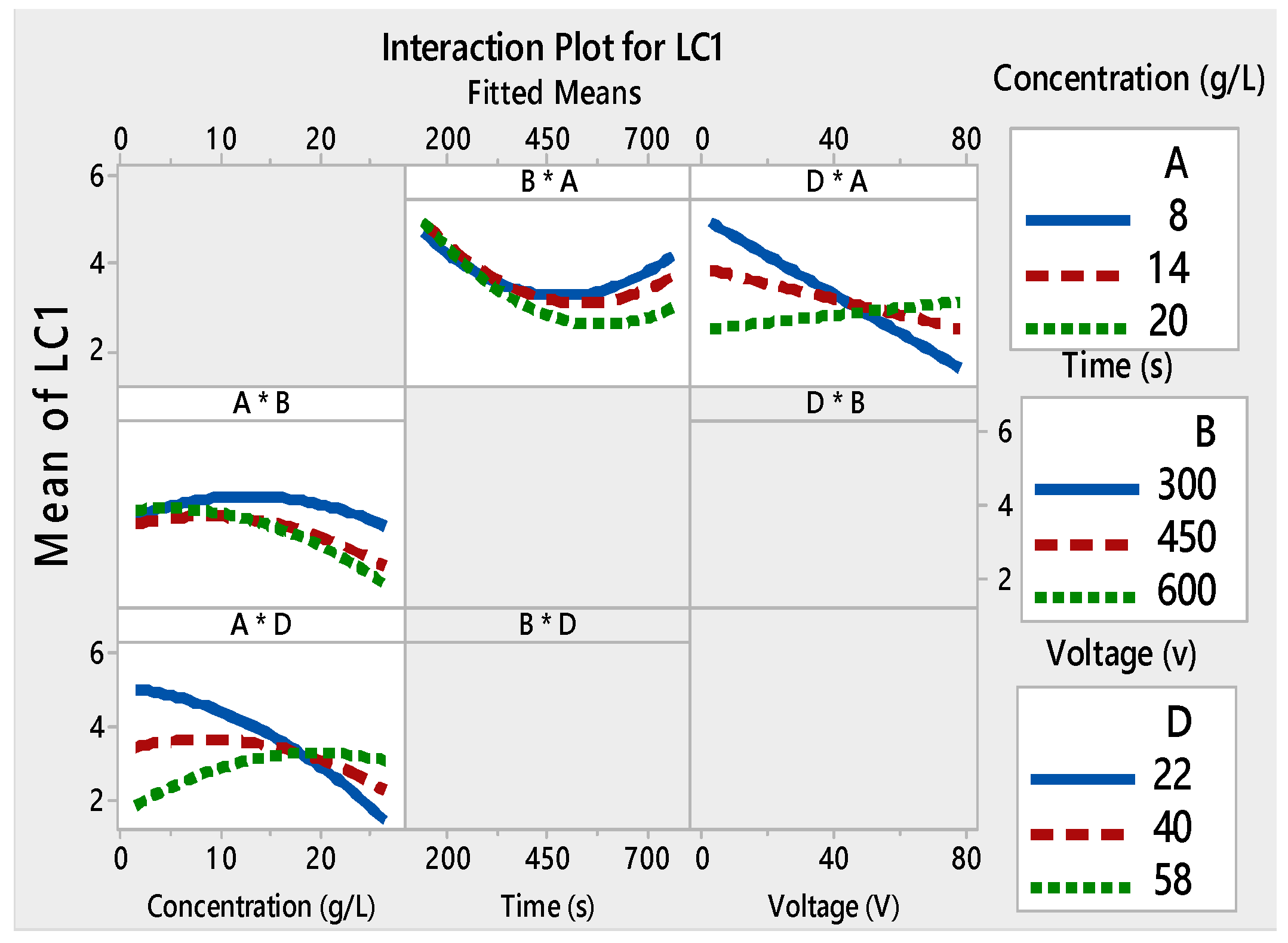
3.1. Analysis of Variance (ANOVA) and Response Surface Analysis
3.2. Optimization and Verification of the Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gao, F.; Sherwood, P. Photoelectron spectroscopic studies of the formation of hydroxyapatite films on 316L. Surf. Interface Anal. 2012, 44, 1587–1600. [Google Scholar] [CrossRef]
- Choy, C.; Shan, X.; Hou, K. Corrosion resistance of TiO2 films grown on stainless steel by atomic layer Deposition. Surf. Coat. Technol. 2008, 202, 2399–2402. [Google Scholar]
- Krishna, D.; Chena, Y.; Sun, Z. Magnetron sputtered TiO2 films on a stainless steel substrate: Selective rutile phase formation and its tribological and anti-corrosion performance. Thin Solid Films 2011, 519, 4860–4864. [Google Scholar] [CrossRef]
- de Sousa, R.R.M.; de Araújo, F.O.; da Costa, J.A.P.; Nishimoto, A.; Viana, B.C.; Alves, C., Jr. Deposition of TiO2 film on duplex stainless steel substrate using the cathodic cage plasma technique. Mater. Res. 2016, 19, 1207–1212. [Google Scholar] [CrossRef][Green Version]
- Pawar, N.; Bhargava, A.; Dayal, S.; Kumar, C. Synthesis and characterization of pure anatase phase nanocrystalline TiO2 thin film by magnetron sputtering method. In Proceedings of the AIP Conference Proceedings, Bikaner, India, 30–31 October 2015; AIP Publishing: Rajasthan, India, 2016; Volume 1728, p. 020561. [Google Scholar]
- Chen, W.; Koshy, P.; Sorrell, C. Effects of film topology and contamination as a function of thickness on the photo-induced hydrophilicity of transparent TiO2 thin films deposited on glass substrates by spin coating. J. Mater. Sci. 2016, 51, 2465–2480. [Google Scholar] [CrossRef]
- Vanaraja, M.; Muthukrishnan, K.; Boomadevi, S.; Karn, R.; Singh, V.; Singh, P.; Pandiyan, K. Dip coated TiO2 nanostructured thin film: Synthesis and application. Phase Transit. A Multi. J. 2016, 89, 107–114. [Google Scholar] [CrossRef]
- Atyaoui, A.; Bousselmi, L.; Cachet, H.; Peng, P.; Sutter, E. Influence of geometric and electronic characteristics of TiO2 electrodes with nanotubular array on their photocatalytic efficiencies. J. Photochem. Photobiol. A Chem. 2011, 224, 71–79. [Google Scholar] [CrossRef]
- Atyaoui, A.; Cachet, H.; Sutter, E.; Bousselmi, L. Effect of the anodization voltage on the dimensions and photoactivity of titania nanotubes arrays. Surf. Interface Anal. 2013, 45, 1751–1759. [Google Scholar] [CrossRef]
- Li, T.; Ding, D. Ni/Si-codoped TiO2 nanostructure photoanode for enhanced photoelectrochemical water splitting. Materials 2019, 112, 4102. [Google Scholar] [CrossRef]
- Zhou, M.; Roualdès, S.; Zhao, J.; Autès, V.; Ayral, A. Nanocrystalline TiO2 thin film prepared by low-temperature plasma-enhanced chemical vapor deposition for photocatalytic applications. Thin Solid Films 2015, 589, 770–777. [Google Scholar] [CrossRef]
- Wang, N.; Wang, J.; Zheng, F.; Wu, Y.; Hou, B. A comparison of diamond-like carbon films properties obtained by plasma enhanced chemical vapor deposition and electro-deposition. Mater. Sci. Forum 2016, 852, 1029–1033. [Google Scholar] [CrossRef]
- Sasinska, A.; Singh, T.; Wang, S.; Mathur, S.; Kraehnert, R. Enhanced photocatalytic performance in atomic layer deposition grown TiO2 thin films via hydrogen plasma treatment. J. Vac. Sci. Technol. 2015, 33, 01A152. [Google Scholar] [CrossRef]
- Eshaghi, A.; Aghaei, A. Determination of optical properties in nanostructured TiO2 thin film fabricated by electron beam physical vapor deposition. J. Opt. Technol. 2016, 83, 26–29. [Google Scholar] [CrossRef]
- Ruzybayev, A.I.; Yassitepe, E.; Karim, A.; Shah, S.I.; Bhatti, A. Phase transformations in the pulsed laser deposition grown TiO2 thin films as a consequence of O2 partial pressure and Nd doping. J. Phys. Chem. C 2015, 119, 11578–11587. [Google Scholar]
- Purcell-Milton, F.; Curutchet, A.; Gun’ko, Y. Electrophoretic deposition of quantum dots and characterisation of composites. Materials 2019, 12, 4089. [Google Scholar] [CrossRef]
- Fiołek, A.; Zimowski, S.; Kopia, A.; Łukaszczyk, A.; Moskalewicz, T. Electrophoretic Co-deposition of polyetheretherketone and graphite particles: Microstructure, electrochemical corrosion resistance, and coating adhesion to a titanium alloy. Materials 2020, 13, 3251. [Google Scholar] [CrossRef]
- Pascall, A.J.; Mora, J.; Jackson, J.; Kuntz, J. Light directed electrophoretic deposition for additive manufacturing: Spatially localized deposition control with photoconductive counter electrodes. Key Eng. Mater. 2015, 654, 261–267. [Google Scholar] [CrossRef]
- Lin, C.K.; Yang, T.; Feng, Y.; Tsung, T.; Su, C. Characterization of elecrophoretically deposited nanocrystalline titanium dioxide films. Surf. Coat. Technol. 2006, 200, 3184. [Google Scholar] [CrossRef]
- Santillán, M.; Membrives, F.; Quaranta, N.; Boccaccini, A. Characterization of TiO2 nanoparticle suspensions for electrophoretic deposition. J. Nanoparticle Res. 2008, 10, 787. [Google Scholar] [CrossRef]
- Lebrette, S.; Pagnoux, C.; Abélard, P. Stability of aqueous TiO2 suspensions: Influence of ethanol. J. Colloid Interface Sci. 2004, 280, 400. [Google Scholar] [CrossRef]
- Hanaor, D.; Michelazzi, M.; Veronesi, P.; Leonelli, C.; Romagnoli, M.; Sorrell, C. Anodic aqueous electrophoretic deposition of titanium dioxide using carboxylic acids as dispersing agents. J. Eur. Ceram. Soc. 2011, 31, 1041–1047. [Google Scholar] [CrossRef]
- Besra, L.; Uchikoshi, T.; Suzuki, T.; Sakka, Y. Application of constant current pulse to suppress bubble incorporation and control deposit morphology during aqueous electrophoretic deposition (EPD). J. Eur. Ceram. Soc. 2009, 29, 1837–1845. [Google Scholar] [CrossRef]
- Tang, F.; Uchikoshi, T.; Ozawa, K.; Sakka, Y. Effect of polyethylenimine on the dispersion and electrophoretic deposition of nano-sized titania aqueous suspensions. J. Eur. Ceram. Soc. 2006, 26, 1555–1560. [Google Scholar] [CrossRef]
- Nurhayati, E.; Yang, H.; Chen, C.; Liu, C.; Juang, Y.; Huang, C.; Hu, C. Electro-photocatalytic fenton decolorization of orange G using mesoporous TiO2/stainless steel mesh photo-electrode prepared by the sol-gel dip-coating method. Int. J. Electrochem. Sci. 2016, 11, 3615. [Google Scholar] [CrossRef]
- Barbana, N.; Youssef, A.B.; Dhiflaoui, H.; Bousselmi, L. Preparation and characterization of photocatalytic TiO2 films on functionalized stainless steel. J. Mater. Sci. 2018, 53, 3341–3364. [Google Scholar] [CrossRef]
- Toh, A.; Cai, R.; Butler, D. The influence of surface topography on the photocatalytic activity of electrophoretically deposited titanium dioxide thin films. Wear 2009, 266, 585–588. [Google Scholar] [CrossRef]
- Khataee, A.R.; Fathinia, M.; Aber, S.; Zarei, M. Optimization of photocatalytic treatment of dye solution on supported TiO2nanoparticles by central compositedesign: Intermediates identification. J. Hazard. Mater. 2010, 181, 886–897. [Google Scholar] [CrossRef]
- Alim, M.; Lee, J.; Akoh, C.; Choi, M.; Jeon, M.; Shin, J.; Lee, K. Enzymatic transesterification of fractionated rice bran oil with conjugated linoleic acid: Optimization by response surface methodology. LWT Food Sci. Technol. 2008, 41, 764–770. [Google Scholar] [CrossRef]
- Vaez, M.; Moghaddam, A.; Alijani, S. Optimization and modeling of photocatalytic degradation of azo dye using a response surface methodology (RSM) based on the central composite design with immobilized titania nanoparticles. Ind. Eng. Chem. Res. 2012, 51, 4199–4207. [Google Scholar] [CrossRef]
- Shafiq, N.; Kumar, R.; Zahid, M.; Tufail, R. Effects of modified metakaolin using nano-silica on the mechanical properties and durability of concrete. Materials 2019, 12, 2291. [Google Scholar] [CrossRef]
- Derringer, G. Balancing act: Optimizing a product’s properties. Qual. Prog. 1994, 27, 51–58. [Google Scholar]
- Bansal, P.; Verma, A.; Mehta, C.; Singla, J.; Toor, A. Assessment of integrated binary process by coupling photocatalysis and photo-Fenton for the removal of cephalexin from aqueous solution. J. Mater. Sci. 2018, 53, 7326–7343. [Google Scholar] [CrossRef]
- Seo, T.; Weon, J. Influence of weathering and substrate roughness on the interfacial adhesion of acrylic coating based on an increasing load scratch test. J. Mater. Sci. 2012, 47, 2234–2240. [Google Scholar] [CrossRef]
- Hare, B.A.; Moyse, A.; Sue, H. Analysis of scratch-induced damages in multi-layer packaging film systems. J. Mater. Sci. 2012, 47, 1389–1398. [Google Scholar] [CrossRef]
- Vaz, F.; Machado, P.; Rebouta, L.; Cerqueira, P.; Goudeau, P.; Rivière, J.; Alves, E.; Pischow, K.; Rijk, J. Mechanical characterization of reactively magnetron-sputtered TiN films. Surf. Coat. Technol. 2003, 174–175, 375–382. [Google Scholar] [CrossRef]
- Oliver, W.; Pharr, G. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564. [Google Scholar] [CrossRef]
- Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Ser. B 1951, 13, 1–45. [Google Scholar] [CrossRef]
- Hamaker, H.; Verwey, E. The role of the forces between the particles in electrodeposition and other phenomena. Trans. Faraday Soc. 1940, 36, 180–185. [Google Scholar] [CrossRef]
- Nyongesa, F.; Aduda, B. Electrophoretic deposition of titanium dioxide thin films for photocatalytic water purification systems. Adv. Mater. 2017, 6, 31–37. [Google Scholar] [CrossRef][Green Version]
- Mohammadi, M.; Vossoughi, M.; Feilizadeh, M.; Rashtchian, D.; Moradi, S.; Alemzadeh, I. Effects of electrophoretic deposition parameters on the photocatalytic activity of TiO2 films: Optimization by response surface methodology. Colloids Surf. A Physicochem. Eng. Asp. 2014, 452, 1–8. [Google Scholar] [CrossRef]
- Bezerra, M.; Santelli, R.; Oliveira, E.; Villar, L.; Escaleira, L. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef] [PubMed]
- Adeli, H.; Zein, S.; Tan, S.; Ahmad, A. Optimization of the mechanical strength properties of Poly (Llactide)/multi-walled carbon nanotube scaffolds using response surface methodology. Nano Brief Rep. Rev. 2011, 6, 113–122. [Google Scholar]
- Fu, J.; Zhao, Y.; Wu, Q. Optimising photoelectrocatalytic oxidation of fulvic acid using response surface methodology. J. Hazard. Mater. 2007, 144, 499–505. [Google Scholar] [CrossRef] [PubMed]
- Benehkohal, N.P. Innovations in Electrophoretic Deposition of Nanotitania-Based Photoanodes for Use in Dye-Sensitized Solar Cells. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2013. [Google Scholar]
- Chiou, C.; Juang, R. Photocatalytic degradation of phenol in aqueous solutions by Pr-doped TiO2 nanoparticles. J. Hazard. Mater. 2007, 149, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Noorsuhana, M.Y.; Hidayah, A.A.N. Electrophoretic deposition of titanium dioxide (TiO2) nanoparticles on ceramic membrane. Adv. Mater. Res. 2014, 974, 20–25. [Google Scholar] [CrossRef]
- Uchikoshi, T.; Ozawa, K.; Hatton, B.; Sakka, Y. Dense bubble-free ceramic deposits from aqueous suspensions by electrophoretic deposition. J. Mater. Res. 2001, 16, 321. [Google Scholar] [CrossRef]
- Besra, L.; Liu, M. A review on fundamentals and applications of electrophoretic deposition (EPD). Prog. Mater. Sci. 2007, 52, 1–61. [Google Scholar] [CrossRef]
- Abdullah, H.; Sorrell, C.C. TiO2 thick films by electrophoretic deposition. J. Aust. Ceram. Soc. 2008, 44, 12–16. [Google Scholar]
- Chang, H.; Su, H.; Chen, W.; Huang, K.D.; Chien, S.; Chen, S.; Chen, C. Fabrication of multilayer TiO2 thin films for dye-sensitized solar cellswith high conversion efficiency by electrophoresis deposition. Sol. Energy 2010, 84, 130–136. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Q. Synthesis and characterization of Fe-doped TiO2films by elec-trophoretic method and its photocatalytic activity toward methyl orange. Solid State Sci. 2013, 16, 16–20. [Google Scholar] [CrossRef]
- Benyounis, K.; Olabi, A.; Hashmi, M. Multi-response optimization of CO2 laser welding process of austenitic stainless steel. Opt. Laser Technol. 2008, 40, 76–87. [Google Scholar] [CrossRef]
- Dzepina, B.; Sigalas, I.; Herrmann, M.; Nilen, R. The aqueous electrophoretic deposition (EPD) of diamond–diamond laminates. Int. J. Refract. Met. Hard Mater. 2013, 36, 126–129. [Google Scholar] [CrossRef]
- Besra, L.; Uchikoshi, T.; Suzuki, T.; Sakka, Y. Bubble-free aqueous electrophoretic deposition (EPD) by pulse-potential application. J. Am. Ceram. Soc. 2008, 91, 3154. [Google Scholar] [CrossRef]
- Palmer, T. Investigation of Electrophoretic Deposition as a Fabrication Technique for High Performance Composites. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]



| Coded Variables | Factors | Units | Coded Level | ||||
|---|---|---|---|---|---|---|---|
| −α | −1 | 0 | +1 | +α | |||
| A | Initial Concentration | g/L | 2 | 8 | 14 | 20 | 26 |
| B | Time | s | 150 | 300 | 450 | 600 | 750 |
| C | Duty Cycle (DC) | % | 10 | 30 | 50 | 70 | 90 |
| D | Voltage | V | 4 | 22 | 40 | 58 | 76 |
| Variables | Responses | |||||||
|---|---|---|---|---|---|---|---|---|
| Stander Order | A | B | C | D | De (%) | LC1(N) | LC2(N) | LC3(N) |
| 1 | −1 | −1 | −1 | −1 | 76.39 | 4.69 | 8.88 | 9.23 |
| 2 | 1 | −1 | −1 | −1 | 83.57 | 3.89 | 7.56 | 9.56 |
| 3 | −1 | 1 | −1 | −1 | 68.77 | 4.67 | 7.32 | 10.74 |
| 4 | 1 | 1 | −1 | −1 | 58.87 | 2.32 | 6.89 | 13.84 |
| 5 | −1 | −1 | 1 | −1 | 57.58 | 4.78 | 9.29 | 11.21 |
| 6 | 1 | −1 | 1 | −1 | 61.96 | 3.24 | 7.52 | 11.47 |
| 7 | −1 | 1 | 1 | −1 | 31.82 | 5.19 | 10.05 | 10.78 |
| 8 | 1 | 1 | 1 | −1 | 29.23 | 2.92 | 6.59 | 12.85 |
| 9 | −1 | −1 | −1 | 1 | 30.96 | 3.61 | 6.53 | 9.64 |
| 10 | 1 | −1 | −1 | 1 | 38.36 | 4.39 | 7.94 | 8.96 |
| 11 | −1 | 1 | −1 | 1 | 43.9 | 2.56 | 5.32 | 10.92 |
| 12 | 1 | 1 | −1 | 1 | 41.68 | 3.25 | 6.36 | 10.45 |
| 13 | −1 | −1 | 1 | 1 | 42.26 | 2.97 | 5.51 | 11.85 |
| 14 | 1 | −1 | 1 | 1 | 50.09 | 3.8 | 6.25 | 9.35 |
| 15 | −1 | 1 | 1 | 1 | 34.42 | 2.94 | 4.48 | 10.3 |
| 16 | 1 | 1 | 1 | 1 | 34.62 | 2.75 | 4.35 | 10.26 |
| 17 | 0 | 0 | 0 | 0 | 52.09 | 3.46 | 6.35 | 9.56 |
| 18 | 0 | 0 | 0 | 0 | 51.89 | 3.56 | 7.34 | 9.17 |
| 19 | 0 | 0 | 0 | 0 | 50.57 | 3.55 | 6.14 | 9.75 |
| 20 | 0 | 0 | 0 | 0 | 53.24 | 3.87 | 6.71 | 9.64 |
| 21 | 0 | 0 | 0 | 0 | 55.09 | 3.52 | 5.98 | 9.43 |
| 22 | 0 | 0 | 0 | 0 | 51.84 | 3.77 | 6.85 | 9.58 |
| 23 | −α | 0 | 0 | 0 | 36.13 | 3.5 | 5.26 | 8.41 |
| 24 | +α | 0 | 0 | 0 | 35.52 | 2.6 | 4.97 | 8.53 |
| 25 | 0 | -α | 0 | 0 | 60.96 | 5.89 | 8.92 | 9.3 |
| 26 | 0 | +α | 0 | 0 | 41.31 | 3.96 | 6.44 | 10.33 |
| 27 | 0 | 0 | −α | 0 | 70.95 | 3.24 | 6.92 | 10.45 |
| 28 | 0 | 0 | +α | 0 | 45.37 | 3.06 | 6.911 | 11.94 |
| 29 | 0 | 0 | 0 | −α | 57.62 | 4.86 | 9.96 | 14.46 |
| 30 | 0 | 0 | 0 | +α | 24.56 | 2.92 | 5.98 | 12.05 |
| De% | LC1 | LC2 | LC3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Source of Variation | Sum of Squares | Df | Mean Square | p-Value | Sum of Squares | Df | Mean Square | p-Value | Sum of Squares | Df | Mean Square | p-Value | Sum of Squares | Df | Mean Square | p-Value |
| A | 5.09682 | 1 | 5.09682 | 0.2039 | 1.8426 | 1 | 1.8426 | 0.0004 | 0.84375 | 1 | 0.84375 | 0.1282 | 0.222337 | 1 | 0.222337 | 0.0664 |
| B | 783.869 | 1 | 783.869 | 0.0000 | 3.1032 | 1 | 3.1032 | 0.0001 | 7.1286 | 1 | 7.1286 | 0.0032 | 4.9777 | 1 | 4.9777 | 0.0001 |
| C | 958.618 | 1 | 958.618 | 0.0000 | 0.0551042 | 1 | 0.0551042 | 0.2039 | 0.321554 | 1 | 0.321554 | 0.3119 | 2.47684 | 1 | 2.47684 | 0.0006 |
| D | 1980.53 | 1 | 1980.53 | 0.0000 | 3.6115 | 1 | 3.6115 | 0.0001 | 26.7126 | 1 | 26.7126 | 0.0002 | 6.7947 | 1 | 6.7947 | 0.0000 |
| A × A | 395.026 | 1 | 395.026 | 0.0001 | 0.820288 | 1 | 0.820288 | 0.0024 | 3.90084 | 1 | 3.90084 | 0.0112 | 2.02907 | 1 | 2.02907 | 0.0009 |
| A × B | 106.606 | 1 | 106.606 | 0.0011 | 0.718256 | 1 | 0.718256 | 0.0033 | 3.28516 | 1 | 3.28516 | 0.0003 | ||||
| A × C | 1.7689 | 1 | 1.7689 | 0.0461 | 0.387506 | 1 | 0.387506 | 0.0272 | ||||||||
| A × D | 5.14156 | 1 | 5.14156 | 0.0000 | 6.3001 | 1 | 6.3001 | 0.0042 | 5.58141 | 1 | 5.58141 | 0.0001 | ||||
| B × B | 2.47966 | 1 | 2.47966 | 0.0002 | 2.01107 | 1 | 2.01107 | 0.0375 | ||||||||
| B × C | 270.109 | 1 | 270.109 | 0.0001 | 0.486506 | 1 | 0.486506 | 0.0074 | 4.25391 | 1 | 4.25391 | 0.0002 | ||||
| B × D | 438.484 | 1 | 438.484 | 0.0000 | 0.195806 | 1 | 0.195806 | 0.0401 | 1.32826 | 1 | 1.32826 | 0.0023 | ||||
| C × C | 93.5315 | 1 | 93.5315 | 0.0015 | 0.598163 | 1 | 0.598163 | 0.0048 | 4.75407 | 1 | 4.75407 | 0.0001 | ||||
| C × D | 805.141 | 1 | 805.141 | 0.0000 | 0.228006 | 1 | 0.228006 | 0.0311 | 4.3681 | 1 | 4.3681 | 0.0090 | ||||
| D × D | 166.676 | 1 | 166.676 | 0.0004 | 3.24633 | 1 | 3.24633 | 0.0160 | 24.064 | 1 | 24.064 | 0.0000 | ||||
| Lack-of-fit | 96.7267 | 13 | 7.44052 | 0.1085 | 0.912965 | 12 | 0.0760804 | 0.1206 | 3.17031 | 14 | 0.226451 | 0.6075 | 1.97794 | 12 | 0.164828 | 0.0663 |
| Pure error | 11.9433 | 5 | 2.38867 | 0.129083 | 5 | 0.0258167 | 1.27188 | 5 | 0.254377 | 0.203083 | 5 | 0.0406167 | ||||
| Total | 6144.9 | 29 | 20.8783 | 29 | 62.1753 | 29 | 63.0796 | 29 | ||||||||
| R 2 | 98% | 95% | 92% | 96% | ||||||||||||
| R 2 (adj) | 97% | 91% | 89.09% | 94% | ||||||||||||
| S | 1.54 | 0.16 | 0.504358 | 0.201536 | ||||||||||||
| Mean absolute error | 1.58 | 0.15 | 0.297567 | 0.200067 | ||||||||||||
| DW-statistic | 1.76 (p = 0.08) | 2.15 (p = 0.43) | 2.56707 (p = 0.9315) | 2.15913 (p = 0.6006) | ||||||||||||
| Lag 1 residual autocorrelation | 0.09 | −0.13 | −0.297881 | −0.0798249 | ||||||||||||
| Response | Goal | Lower | Target | Upper | Weight | Importance |
|---|---|---|---|---|---|---|
| LC3 | Maximum | 8.41 | 14.46 | 14.46 | 1 | 1 |
| LC2 | Maximum | 4.35 | 10.05 | 10.05 | 1 | 1 |
| LC1 | Maximum | 2.32 | 5.89 | 5.89 | 1 | 1 |
| De (%) | Maximum | 24.56 | 83.57 | 83.57 | 1 | 1 |
| Optimal Responses | Exp 1 | Exp 2 | Exp 3 | Exp 4 | |
|---|---|---|---|---|---|
| LC1 | 5.9 | 5.2 | 4.8 | 5.3 | 5 |
| LC2 | 12.5 | 10.5 | 11.3 | 12 | 11.8 |
| LC3 | 16.7 | 14.3 | 14 | 14.8 | 14.5 |
| De (%) | 82.75 | 75.3 | 78 | 86 | 81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbana, N.; Ben Youssef, A.; Rezgui, M.A.; Bousselmi, L.; Al-Addous, M. Modelling, Analysis, and Optimization of the Effects of Pulsed Electrophoretic Deposition Parameters on TiO2 Films Properties Using Desirability Optimization Methodology. Materials 2020, 13, 5160. https://doi.org/10.3390/ma13225160
Barbana N, Ben Youssef A, Rezgui MA, Bousselmi L, Al-Addous M. Modelling, Analysis, and Optimization of the Effects of Pulsed Electrophoretic Deposition Parameters on TiO2 Films Properties Using Desirability Optimization Methodology. Materials. 2020; 13(22):5160. https://doi.org/10.3390/ma13225160
Chicago/Turabian StyleBarbana, Nesrine, Adel Ben Youssef, Mohamed Ali Rezgui, Latifa Bousselmi, and Mohammad Al-Addous. 2020. "Modelling, Analysis, and Optimization of the Effects of Pulsed Electrophoretic Deposition Parameters on TiO2 Films Properties Using Desirability Optimization Methodology" Materials 13, no. 22: 5160. https://doi.org/10.3390/ma13225160
APA StyleBarbana, N., Ben Youssef, A., Rezgui, M. A., Bousselmi, L., & Al-Addous, M. (2020). Modelling, Analysis, and Optimization of the Effects of Pulsed Electrophoretic Deposition Parameters on TiO2 Films Properties Using Desirability Optimization Methodology. Materials, 13(22), 5160. https://doi.org/10.3390/ma13225160





