First-Principles Study on Structural, Mechanical, Anisotropic, Electronic and Thermal Properties of III-Phosphides: XP (X = Al, Ga, or In) in the P6422 Phase
Abstract
:1. Introduction
2. Calculation Methods
3. Results and Discussion
3.1. Structural Properties
3.2. Stability and Mechanical Properties
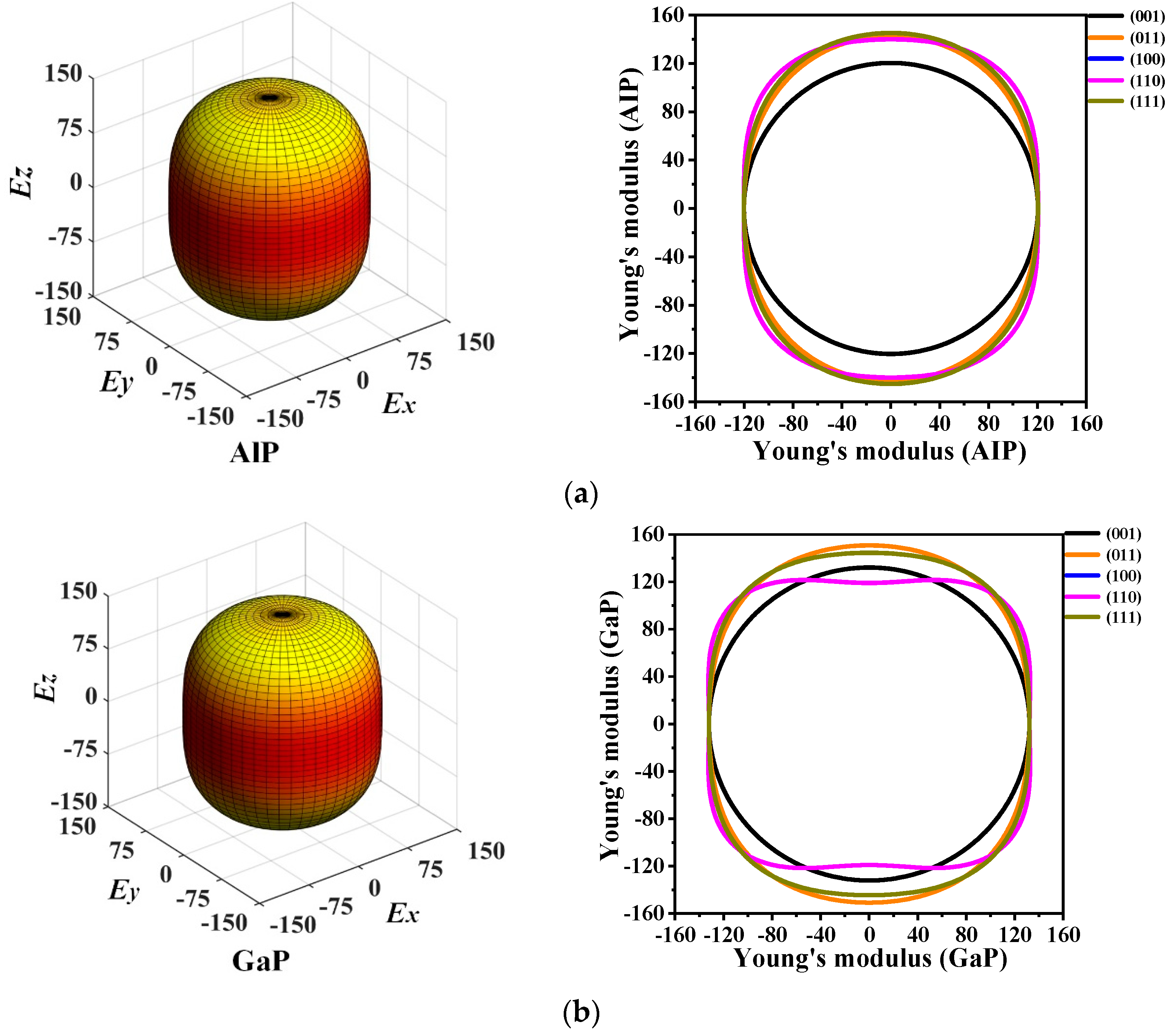
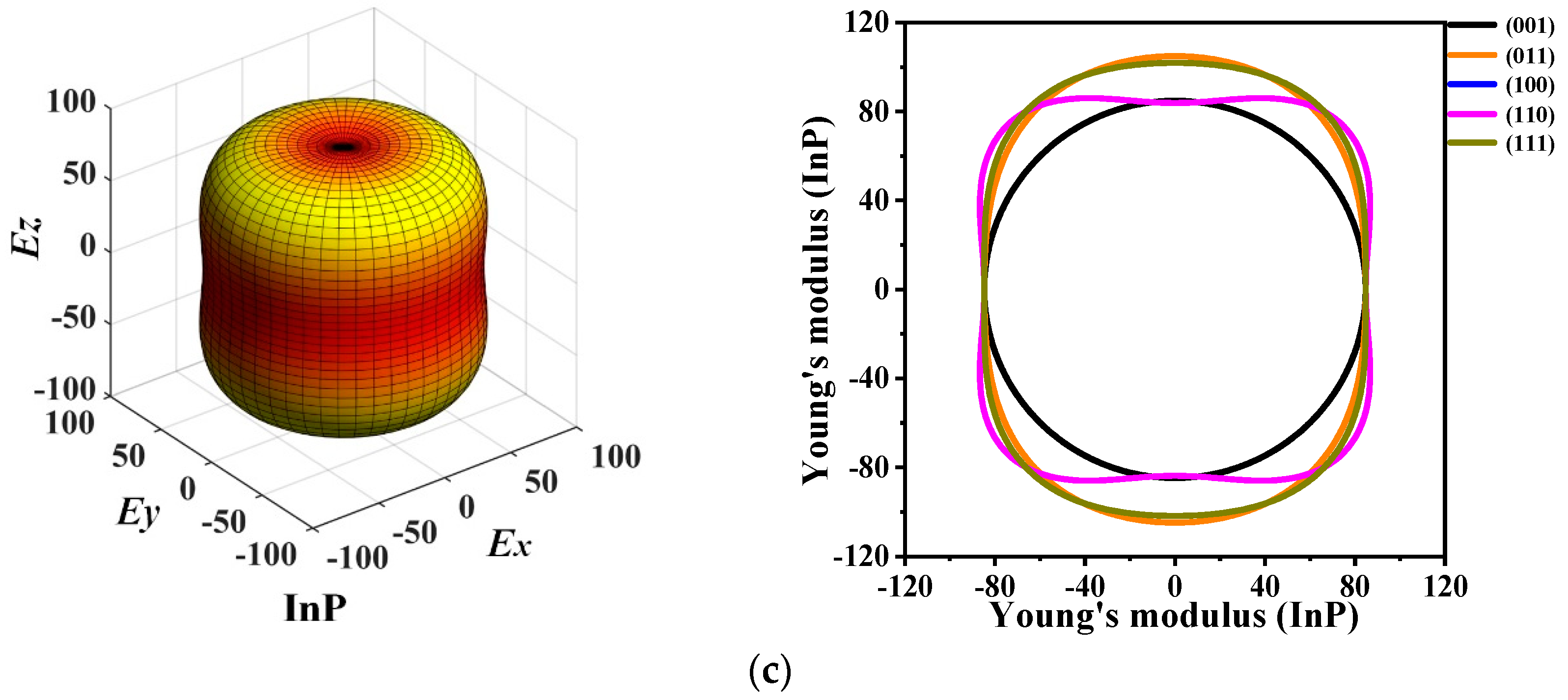
3.3. Mechanical Anisotropic Properties
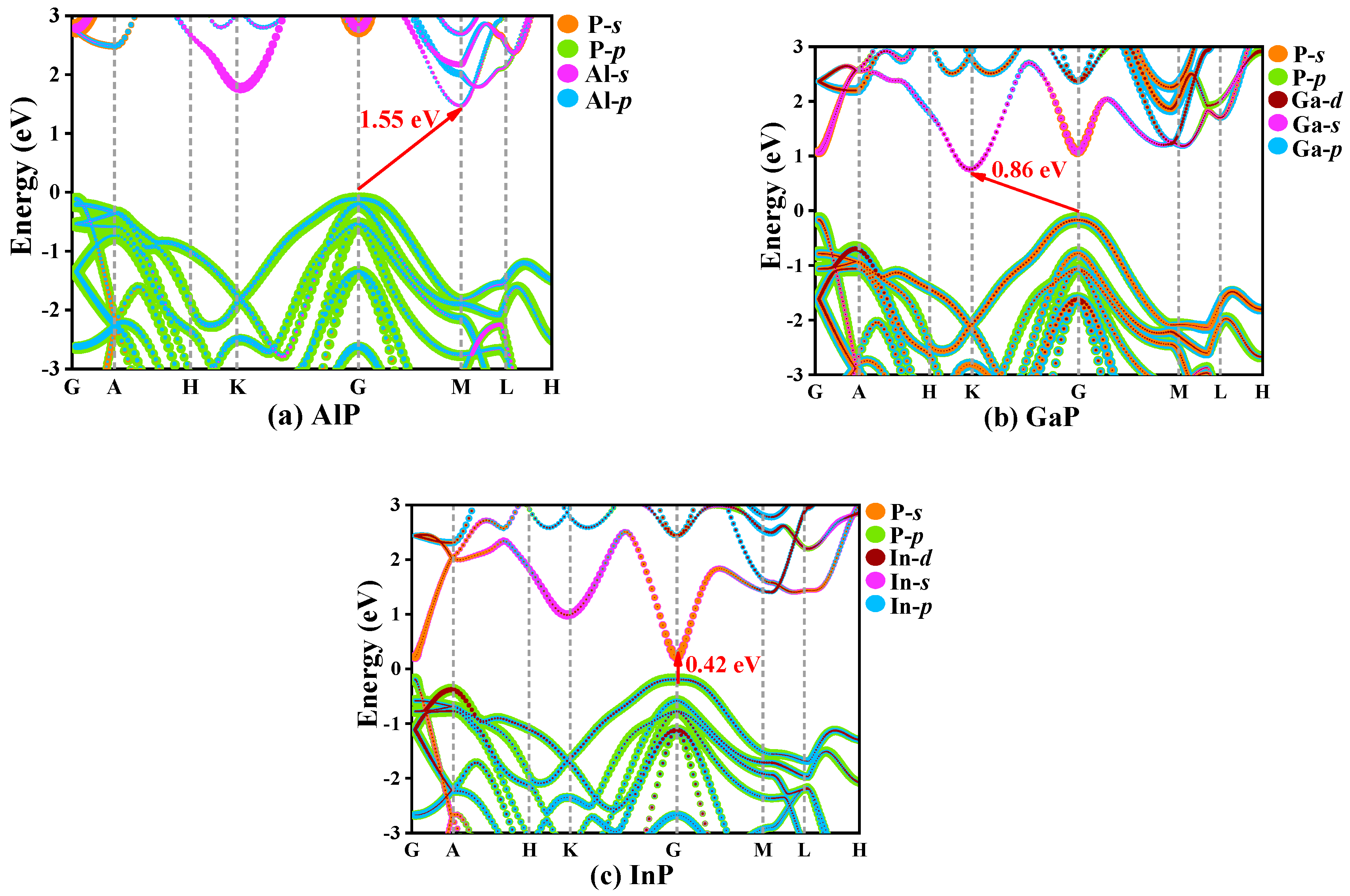
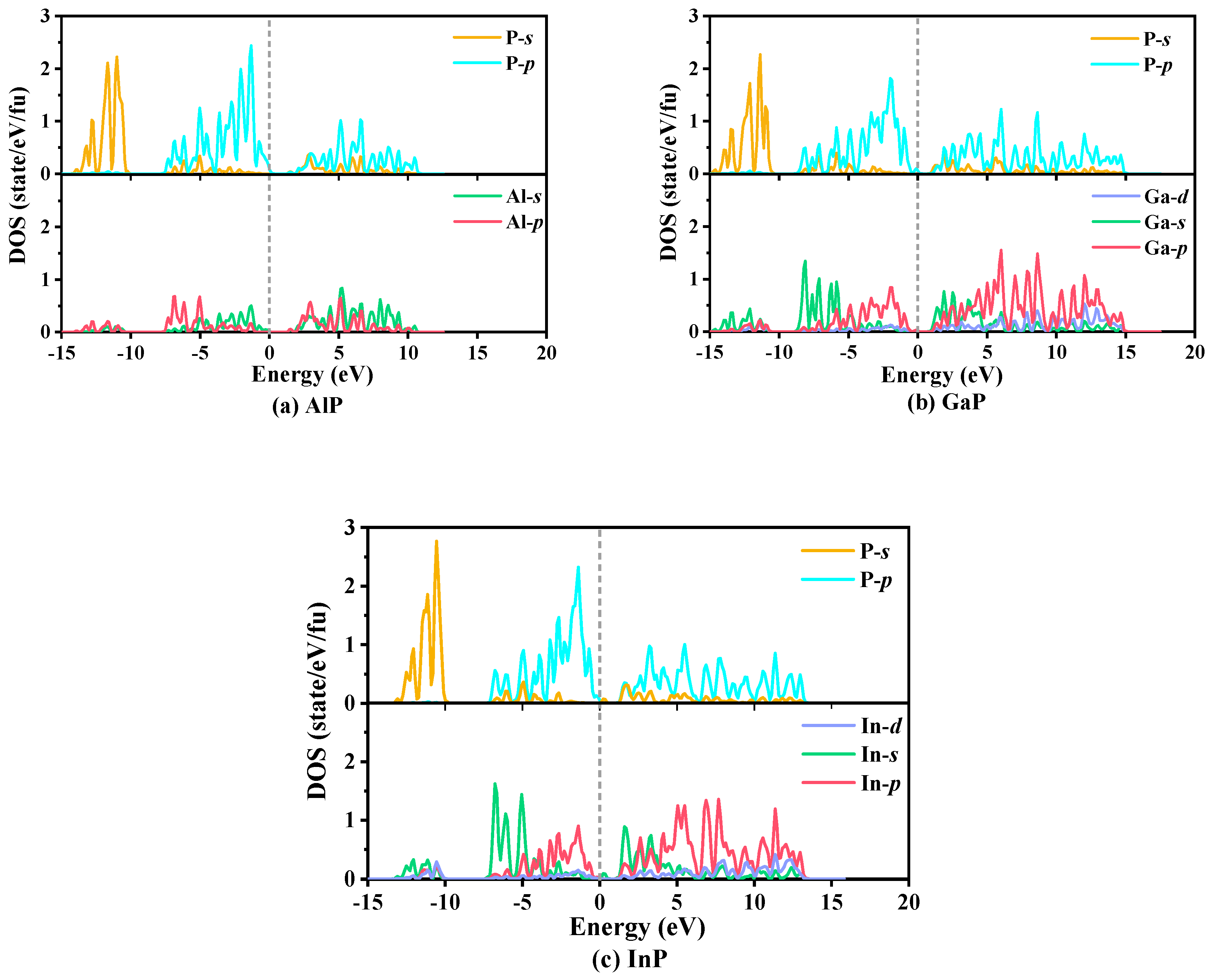
3.4. Electrical and Thermal Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jiao, Z.-Y.; Ma, S.-H.; Guo, Y.-L. Simulation of optical function for phosphide crystals following the DFT band structure calculations. Comput. Theor. Chem. 2011, 970, 79–84. [Google Scholar] [CrossRef]
- Lakel, S.; Okbi, F.; Meradji, H. Optical and electronic properties of BxAl1−xP alloys: A first principles study. Optik 2016, 127, 3755–3761. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, W.; Cheng, X. First-principles study of phase transition and thermodynamic properties of InP. Phys. B 2010, 405, 4536–4540. [Google Scholar] [CrossRef]
- Lin, L.; Woods, G.T.; Callcott, T.A. Soft-X-ray fluorescence spectra of III−V phosphides BP, GaP, and InP. Phys. Rev. B 2001, 63, 235107. [Google Scholar] [CrossRef]
- Xu, L.F.; Bu, W. Mechanical and thermodynamic properties of AlX (X = N, P, As) compounds. Int. J. Mod. Phys. B 2017, 31, 1750167. [Google Scholar] [CrossRef]
- Liu, C.; Ma, M.; Yuan, X.; Sun, H.; Ying, P.; Xu, B.; Zhao, Z.; He, J. Metastable phases, phase transformation and properties of AlAs based on first-principle study. Comput. Mater. Sci. 2017, 128, 337–342. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.; Zhu, C.; Wei, Q.; Zhang, D. First-principles study on phases of AlP. Solid State Commun. 2017, 267, 23–28. [Google Scholar] [CrossRef]
- Baida, A.; Ghezali, M. Structural, electronic and optical properties of InP under pressure: An ab-initio study. Comput. Condens. Matter 2018, 17, e00333. [Google Scholar] [CrossRef]
- Arbouche, O.; Belgoumène, B.; Soudini, B.; Azzaz, Y.; Bendaoud, H.; Amara, K. First-principles study on structural properties and phase stability of III-phosphide (BP, GaP, AlP and InP). Comput. Mater. Sci. 2010, 47, 685–692. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Chai, C.; Fan, Q.; Song, Y.; Yang, Y. PBCF-graphene: A 2D sp2 hybridized honeycomb carbon allotrope with a direct band gap. ChemNanoMat 2020, 6, 139–147. [Google Scholar] [CrossRef] [Green Version]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Fuer Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Chai, C.; Song, Y.; Fan, Q.; Yang, Y. Anisotropic, and Thermal Properties of AlAs in oC12 and hP6 Phases under Pressure. Materials 2018, 11, 740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, Q.; Niu, R.; Zhang, W.; Zhang, W.; Ding, Y.; Yun, S. t-Si64: A Novel Silicon Allotrope. ChemPhysChem 2019, 20, 128–133. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of Crystals with the Quasi-Newton Method. J. Comput. Phys. 1997, 131, 233. [Google Scholar] [CrossRef] [Green Version]
- Baroni, S.; de Gironcoli, S.; dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515. [Google Scholar] [CrossRef] [Green Version]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- Fan, Q.; Xu, J.; Zhang, W.; Song, Y.; Yun, S. Physical properties of group 14 semiconductor alloys in orthorhombic phase. J. Appl. Phys. 2019, 126, 045709. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmed, R.; Hashemifar, S.J.; Akbarzadeh, H. First-principles study of the structural and electronic properties of III-phosphides. Phys. B Condens. Matter. 2008, 403, 1876–1881. [Google Scholar] [CrossRef]
- Giesecke, G.; Pfister, H. Präzisionsbestimmung der Gitterkonstanten von AIIIBv-Verbindungen. Acta Crystallogr. 1958, 11, 369–371. [Google Scholar] [CrossRef]
- Kishino, S. Improved Techniques of Lattice Parameter Measurements Using two X-ray Beams. Adv. X-ray Anal. 1972, 16, 367–378. [Google Scholar] [CrossRef]
- Wang, C.C.; Zaheeruddin, M.; Spinar, L.H. Preparation and properties of aluminum phosphide. J. Inorg. Nucl. Chem. 1963, 25, 326. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Fan, Q.; Zhang, W.; Yun, S.; Xu, J.; Song, Y. III-Nitride Polymorphs: XN (X = Al, Ga, In) in the Pnma Phase. Chem. Eur. J. 2018, 24, 17280–17287. [Google Scholar] [CrossRef]
- Zhang, X.D.; Ying, C.H.; Li, Z.J.; Shi, G.M. First-principles calculations of structural stability, elastic, dynamical and thermodynamic properties of SiGe, SiSn, GeSn. Superlattices Microstruct. 2012, 52, 459–469. [Google Scholar] [CrossRef]
- Zhang, W.; Chai, C.; Fan, Q.; Weng, K.; Yang, Y. Theoretical investigations of Ge1−xSnx alloys (x = 0, 0.333, 0.667, 1) in P42/ncm phase. J. Mater. Sci. 2018, 53, 9611–9626. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Lond. 1952, 65, 349. [Google Scholar] [CrossRef]
- Yang, R.K.; Zhu, C.S.; Wei, Q.; Du, Z. Investigations on structural, elastic, thermodynamic and electronic properties of TiN, Ti2N and Ti3N2 under high pressure by first-principles. J. Phys. Chem. Solids 2016, 98, 10–19. [Google Scholar] [CrossRef]
- Zhang, W.; Chai, C.; Fan, Q.; Song, Y.; Yang, Y. Two novel superhard carbon allotropes with honeycomb structures. J. Appl. Phys. 2019, 126, 145704. [Google Scholar] [CrossRef]
- Ishii, I.; Fujiwara, T. Electronic structures and cohesion mechanism of Cd-based quasicrystals. J. Noncryst. Solids. 2002, 312, 494–497. [Google Scholar] [CrossRef]
- Muramatsu, S.; Kitahara, M. Simple expressions for elastic constants c11, c12, and c44 and internal displacements of semiconductors. J. Appl. Phys. 1993, 73, 4270. [Google Scholar] [CrossRef]
- Weil, R.; Groves, W.O. The Elastic Constants of Gallium Phosphide. J. Appl. Phys. 1968, 39, 4049. [Google Scholar] [CrossRef]
- Borcherds, P.H.; Kunc, K. The lattice dynamics of indium pnictides. J. Phys. C Solid State Phys. 1978, 11, 4145. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Yan, H.Y.; Zhang, M.G.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Elastic and electronic properties of Pbca-BN: First-principles calculations. Comput. Mater. Sci. 2014, 85, 80. [Google Scholar] [CrossRef]
- Hu, W.C.; Liu, Y.; Li, D.J.; Zeng, X.Q.; Xu, C.S. First-principles study of structural and electronic properties of C14-type Laves phase Al2Zr and Al2Hf. Comput. Mater. Sci. 2014, 83, 27–34. [Google Scholar] [CrossRef]
- Deng, R.P.; Ozsdolay, B.D.; Zheng, P.Y.; Khare, S.V.; Gall, D. Optical and transport measurement and first-principles determination of the ScN band gap. Phys. Rev. B 2015, 91, 045104. [Google Scholar] [CrossRef] [Green Version]
- Li, X.Z.; Xing, M.J. Prediction of a novel carbon allotrope from first-principle calculations: A potential superhard material in monoclinic symmetry. Mater. Chem. Phys. 2020, 242, 122480. [Google Scholar] [CrossRef]
- Clarke, D.R. Materials selection guidelines for low thermal conductivity thermal barrier coatings. Surf. Coat. Technol. 2003, 163, 67–74. [Google Scholar] [CrossRef]
- Cahill, D.G.; Watson, S.K.; Pohl, R.O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 1992, 46, 6131–6140. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, E.; Anderson, O.L.; Soga, N. Elastic Constants and Their Measurements; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Li, C.X.; Duan, Y.H.; Hu, W.C. Electronic structures, elastic anisotropy, thermal conductivity and optical properties of calcium apatite Ca5(PO4)3X (X = F, Cl or Br). J. Alloys Compd. 2015, 619, 66–77. [Google Scholar] [CrossRef]

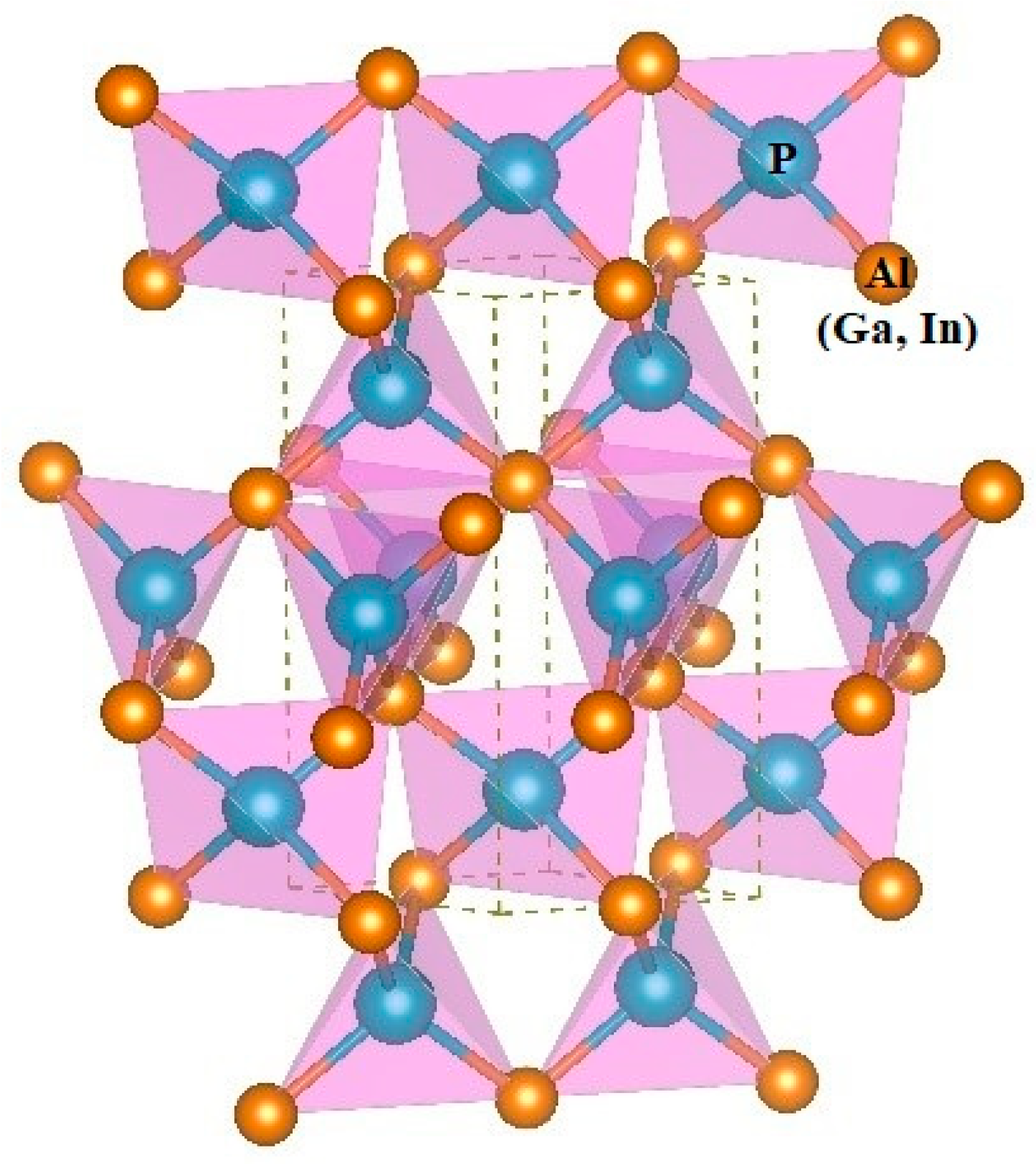
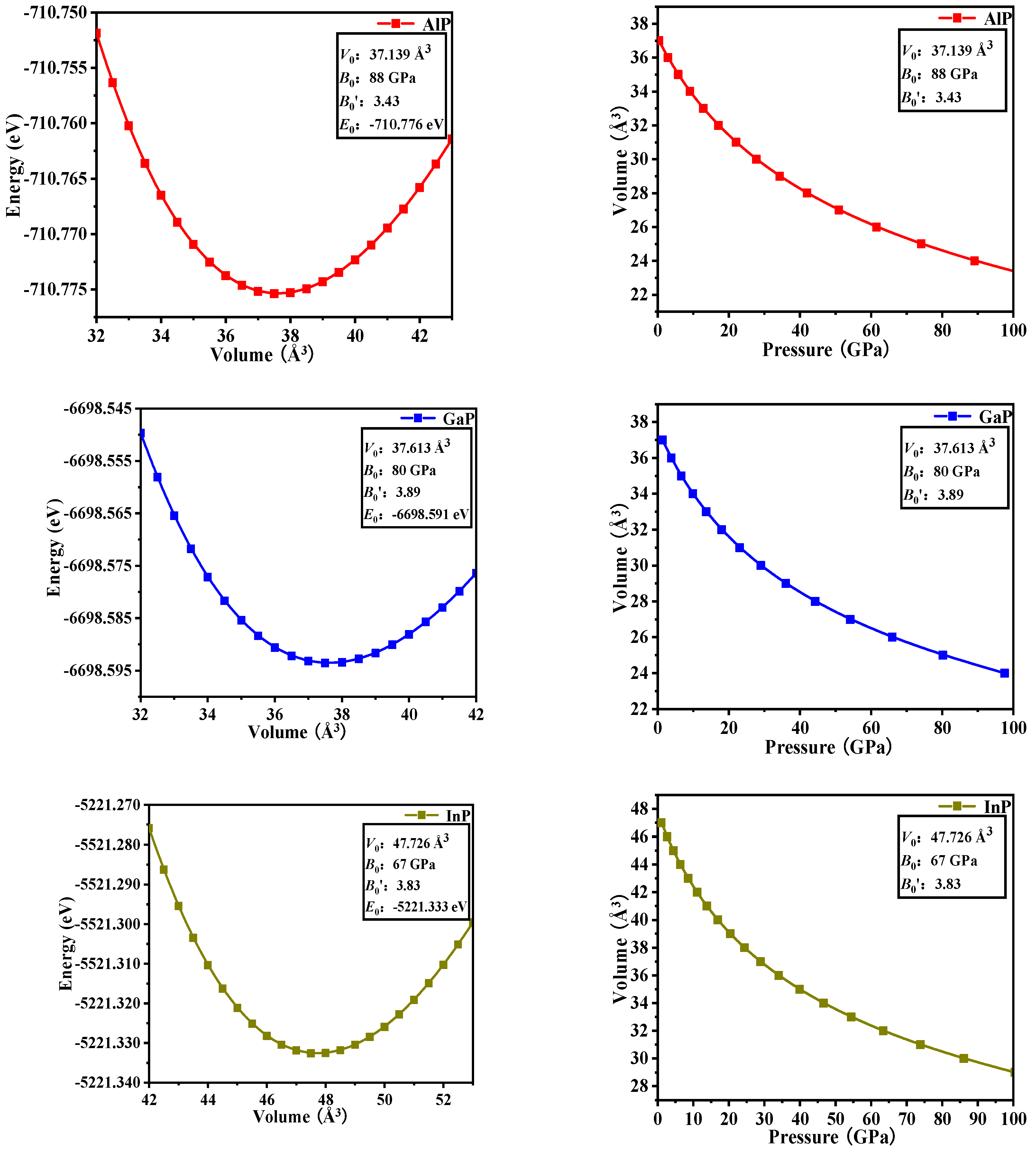
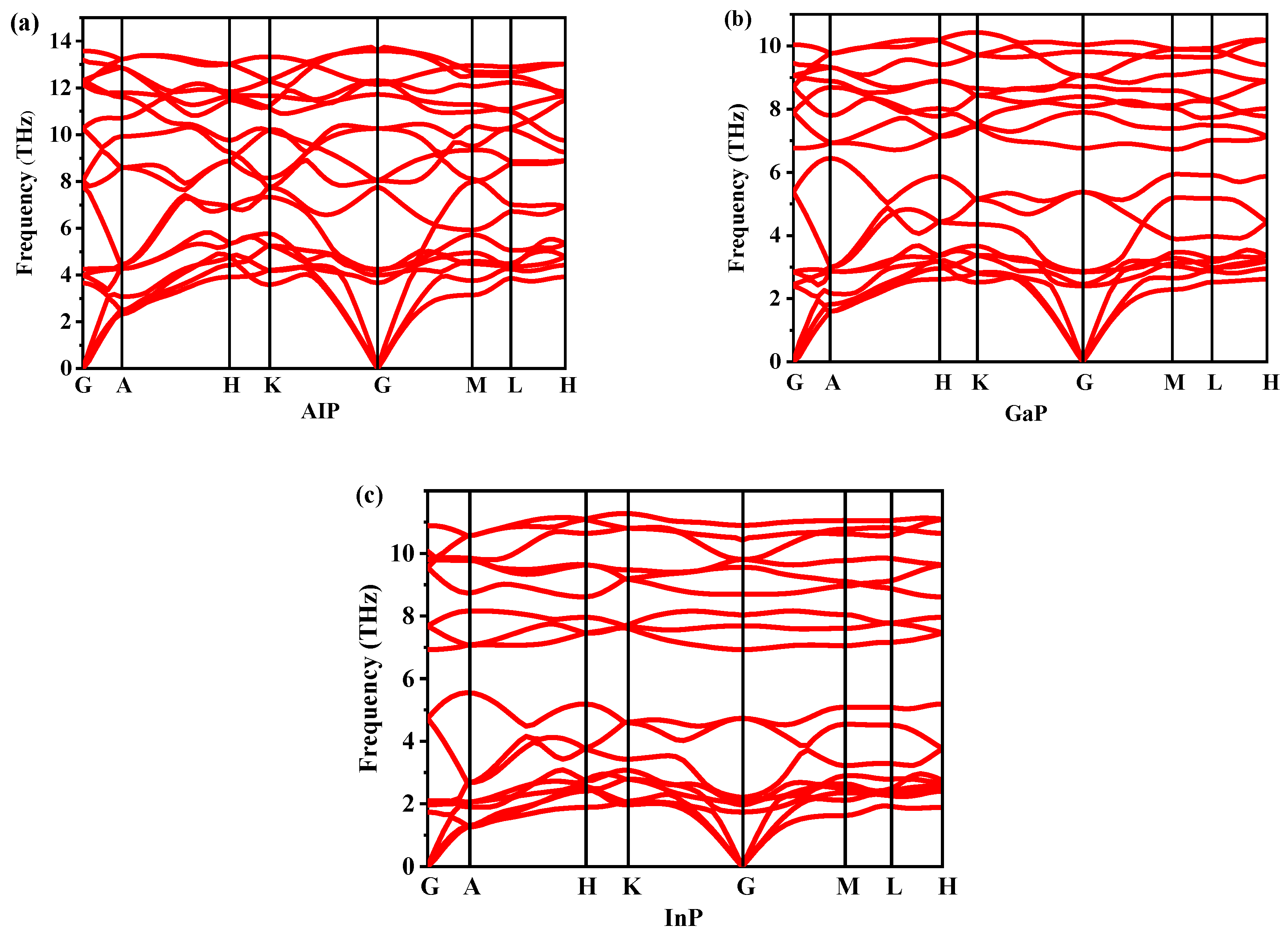
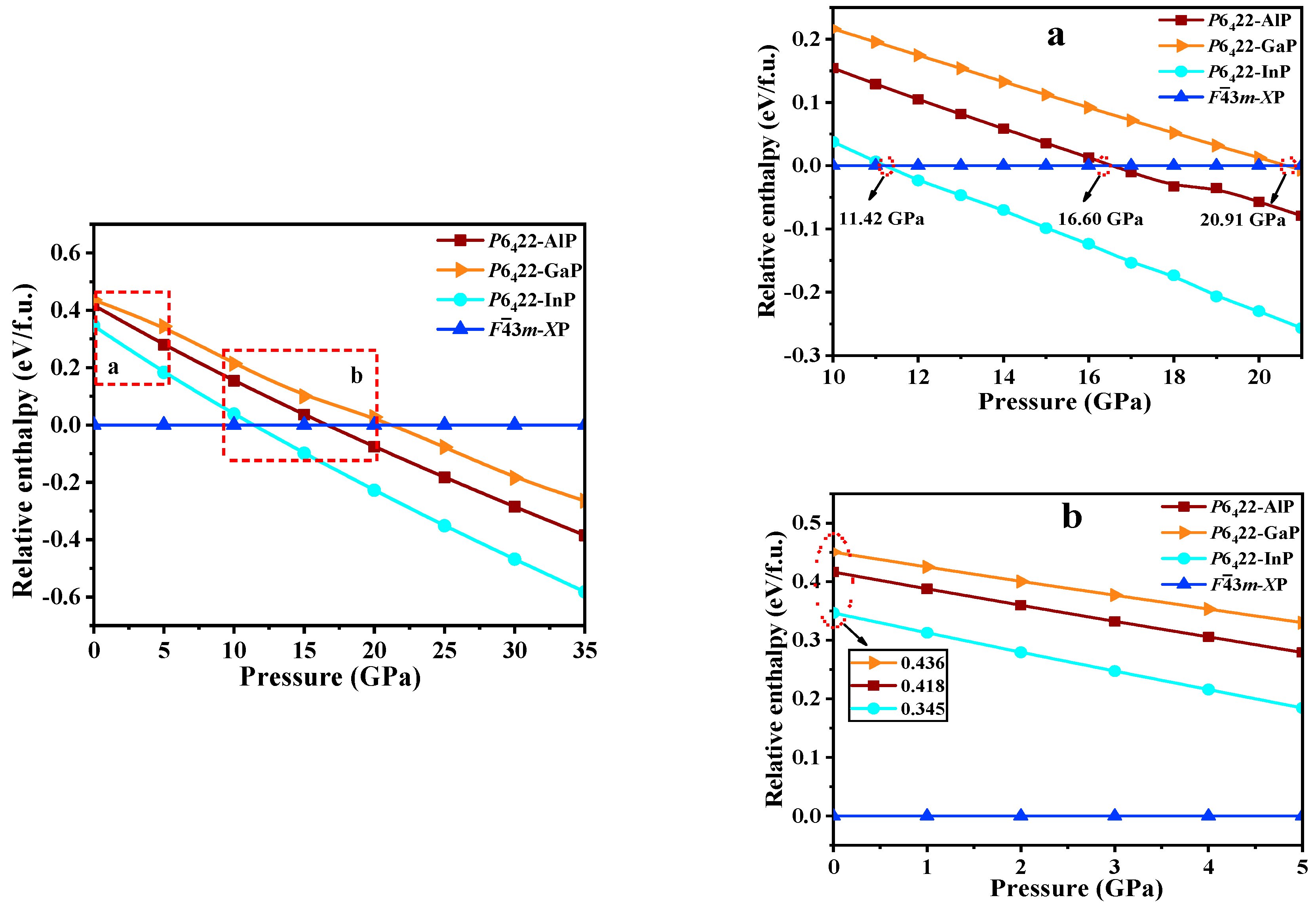
| Space Group | Methods | a [Å] | c [Å] | V [Å3 molecule−1] | ρ [g cm−3] | |
|---|---|---|---|---|---|---|
| AlP | P6422 | PBE | 3.849 | 8.683 | 37.139 | 2.591 |
| DFT-D2 | 3.790 | 8.669 | 35.942 | 2.678 | ||
| Fm | PBE | 5.510 | 41.822 | 2.301 | ||
| DFT-D2 | 5.442 | 40.297 | 2.388 | |||
| Fm[a] | Exp. | 5.467 | 40.773 | 2.360 | ||
| GaP | P6422 | PBE | 3.899 | 8.570 | 37.613 | 4.446 |
| DFT-D2 | 3.818 | 8.553 | 35.996 | 4.646 | ||
| Fm | PBE | 5.505 | 41.717 | 4.009 | ||
| DFT-D2 | 5.412 | 39.631 | 4.220 | |||
| Fm[b] | Exp. | 5.451 | 40.488 | 4.130 | ||
| InP | P6422 | PBE | 4.190 | 9.416 | 47.726 | 5.073 |
| DFT-D2 | 4.064 | 9.298 | 44.330 | 5.461 | ||
| Fm | PBE | 5.973 | 53.263 | 4.545 | ||
| DFT-D2 | 5.854 | 51.162 | 4.876 | |||
| Fm[c] | Exp. | 5.869 | 50.540 | 4.790 |
| Space Group | Methods | P | C11 | C12 | C13 | C33 | C44 | C66 | B | G | B/G | E | ʋ | AU |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P6422-AlP | PBE | 0 | 147 | 51 | 58 | 174 | 60 | 48 | 88 | 53 | 1.68 | 132 | 0.25 | 0.064 |
| 5 | 169 | 67 | 77 | 190 | 66 | 51 | 107 | 56 | 1.91 | 143 | 0.28 | 0.095 | ||
| 10 | 190 | 83 | 96 | 224 | 64 | 53 | 127 | 58 | 2.19 | 151 | 0.30 | 0.060 | ||
| 15 | 207 | 98 | 114 | 245 | 59 | 54 | 144 | 56 | 2.57 | 149 | 0.33 | 0.032 | ||
| 20 | 226 | 113 | 132 | 267 | 57 | 56 | 161 | 57 | 2.82 | 153 | 0.34 | 0.029 | ||
| 25 | 240 | 128 | 148 | 290 | 55 | 56 | 177 | 56 | 3.16 | 152 | 0.36 | 0.039 | ||
| 30 | 257 | 143 | 166 | 313 | 50 | 57 | 194 | 55 | 3.53 | 151 | 0.37 | 0.064 | ||
| 35 | 267 | 161 | 181 | 333 | 38 | 53 | 208 | 48 | 4.33 | 134 | 0.39 | 0.235 | ||
| Fm-AlP | PBE | 0 | 123 | 58 | 60 | 80 | 47 | 1.70 | 118 | 0.25 | 0.494 | |||
| Fm-AlP [a] | Exp. | 0 | 129 | 56 | 52 | |||||||||
| P6422-GaP | PBE | 0 | 152 | 37 | 49 | 144 | 67 | 57 | 80 | 58 | 1.38 | 140 | 0.21 | 0.087 |
| 5 | 178 | 54 | 56 | 150 | 75 | 62 | 92 | 64 | 1.44 | 156 | 0.22 | 0.117 | ||
| 10 | 213 | 82 | 116 | 228 | 82 | 65 | 140 | 66 | 2.12 | 171 | 0.30 | 0.234 | ||
| 15 | 230 | 91 | 115 | 222 | 88 | 69 | 147 | 70 | 2.10 | 181 | 0.29 | 0.217 | ||
| 20 | 250 | 108 | 111 | 207 | 92 | 71 | 151 | 73 | 2.07 | 189 | 0.29 | 0.211 | ||
| 25 | 271 | 125 | 143 | 248 | 96 | 73 | 179 | 75 | 2.39 | 197 | 0.32 | 0.245 | ||
| 30 | 291 | 140 | 167 | 273 | 102 | 76 | 200 | 76 | 2.63 | 202 | 0.33 | 0.319 | ||
| 35 | 310 | 156 | 181 | 285 | 104 | 77 | 216 | 77 | 2.81 | 206 | 0.34 | 0.332 | ||
| Fm-GaP | PBE | 0 | 134 | 60 | 70 | 80 | 59 | 1.39 | 131 | 0.21 | 0.500 | |||
| Fm-GaP [b] | Exp. | 0 | 141 | 62 | 70 | |||||||||
| P6422-InP | PBE | 0 | 108 | 37 | 49 | 117 | 45 | 36 | 67 | 37 | 1.81 | 94 | 0.27 | 0.124 |
| 5 | 130 | 53 | 64 | 135 | 48 | 38 | 84 | 40 | 2.10 | 104 | 0.29 | 0.120 | ||
| 10 | 151 | 76 | 94 | 171 | 48 | 38 | 110 | 40 | 2.75 | 107 | 0.34 | 0.157 | ||
| 15 | 168 | 93 | 108 | 187 | 55 | 37 | 126 | 42 | 3.00 | 113 | 0.35 | 0.257 | ||
| 20 | 190 | 112 | 129 | 209 | 59 | 39 | 146 | 43 | 3.40 | 117 | 0.37 | 0.298 | ||
| 25 | 211 | 127 | 148 | 230 | 53 | 42 | 165 | 44 | 3.75 | 121 | 0.38 | 0.164 | ||
| 30 | 225 | 148 | 168 | 251 | 48 | 38 | 186 | 41 | 4.54 | 115 | 0.40 | 0.118 | ||
| 35 | 245 | 161 | 188 | 273 | 56 | 42 | 201 | 44 | 4.57 | 123 | 0.40 | 0.233 | ||
| Fm-InP | PBE | 0 | 96 | 55 | 49 | 59 | 35 | 1.69 | 88 | 0.25 | 0.924 | |||
| Fm-InP [c] | Exp. | 0 | 102 | 56 | 47 |
| Planes | Materials | Emax | Emin | Ratio | Planes | Materials | Emax | Emin | Ratio |
|---|---|---|---|---|---|---|---|---|---|
| (001) | P6422-AlP | 120.333 | 120.333 | 1.000 | (110) | P6422-AlP | 145.147 | 120.334 | 1.206 |
| P6422-GaP | 132.093 | 132.093 | 1.000 | P6422-GaP | 151.508 | 119.008 | 1.273 | ||
| P6422-InP | 84.764 | 84.764 | 1.000 | P6422-InP | 104.849 | 83.797 | 1.251 | ||
| (011) | P6422-AlP | 142.751 | 120.334 | 1.186 | (111) | P6422-AlP | 145.081 | 120.334 | 1.205 |
| P6422-GaP | 151.508 | 132.093 | 1.147 | P6422-GaP | 151.508 | 132.093 | 1.147 | ||
| P6422-InP | 104.849 | 84.764 | 1.237 | P6422-InP | 104.849 | 84.764 | 1.237 | ||
| (100) | P6422-AlP | 145.147 | 120.334 | 1.206 | (010) | P6422-AlP | 145.147 | 120.334 | 1.206 |
| P6422-GaP | 151.508 | 119.008 | 1.273 | P6422-GaP | 151.508 | 119.008 | 1.273 | ||
| P6422-InP | 104.849 | 83.797 | 1.251 | P6422-InP | 104.849 | 83.797 | 1.251 |
| Clark | Cahill | |||||
|---|---|---|---|---|---|---|
| Ma × 10−23 | kmin | νt | νl | p × 1028 | kmin | |
| P6422-AlP | 4.817 | 1.222 | 4.523 | 7.825 | 5.379 | 1.338 |
| Fm-AlP | 4.817 | 1.132 | 4.520 | 7.874 | 4.777 | 1.240 |
| P6422-GaP | 8.389 | 0.972 | 3.381 | 5.569 | 6.047 | 1.058 |
| Fm-GaP | 8.389 | 0.904 | 3.836 | 6.291 | 4.779 | 1.024 |
| P6422-InP | 12.126 | 0.610 | 2.885 | 5.115 | 3.666 | 0.669 |
| Fm-InP | 12.126 | 0.592 | 2.775 | 4.822 | 3.748 | 0.647 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, J.; Chai, C.; Zhang, W.; Song, Y.; Yang, Y. First-Principles Study on Structural, Mechanical, Anisotropic, Electronic and Thermal Properties of III-Phosphides: XP (X = Al, Ga, or In) in the P6422 Phase. Materials 2020, 13, 686. https://doi.org/10.3390/ma13030686
Miao J, Chai C, Zhang W, Song Y, Yang Y. First-Principles Study on Structural, Mechanical, Anisotropic, Electronic and Thermal Properties of III-Phosphides: XP (X = Al, Ga, or In) in the P6422 Phase. Materials. 2020; 13(3):686. https://doi.org/10.3390/ma13030686
Chicago/Turabian StyleMiao, Junjie, Changchun Chai, Wei Zhang, Yanxing Song, and Yintang Yang. 2020. "First-Principles Study on Structural, Mechanical, Anisotropic, Electronic and Thermal Properties of III-Phosphides: XP (X = Al, Ga, or In) in the P6422 Phase" Materials 13, no. 3: 686. https://doi.org/10.3390/ma13030686
APA StyleMiao, J., Chai, C., Zhang, W., Song, Y., & Yang, Y. (2020). First-Principles Study on Structural, Mechanical, Anisotropic, Electronic and Thermal Properties of III-Phosphides: XP (X = Al, Ga, or In) in the P6422 Phase. Materials, 13(3), 686. https://doi.org/10.3390/ma13030686






