Hydro-Mechanical Behaviour of an Unbound Granular Base Course Material Used in Low Traffic Pavements
Abstract
:1. Introduction
2. Materials Studied
3. Repeated Load Triaxial Test (RLTT)
3.1. Sample Preparation and Test Equipment
- An axial force transducer;
- A cell pressure transducer;
- An external LVDT;
- Two inner Hall effect transducers (axial);
- An inner Hall effect transducer (radial).
3.2. Monotonic Triaxial Test
3.3. Two Methods for Fixing Displacement Transducers
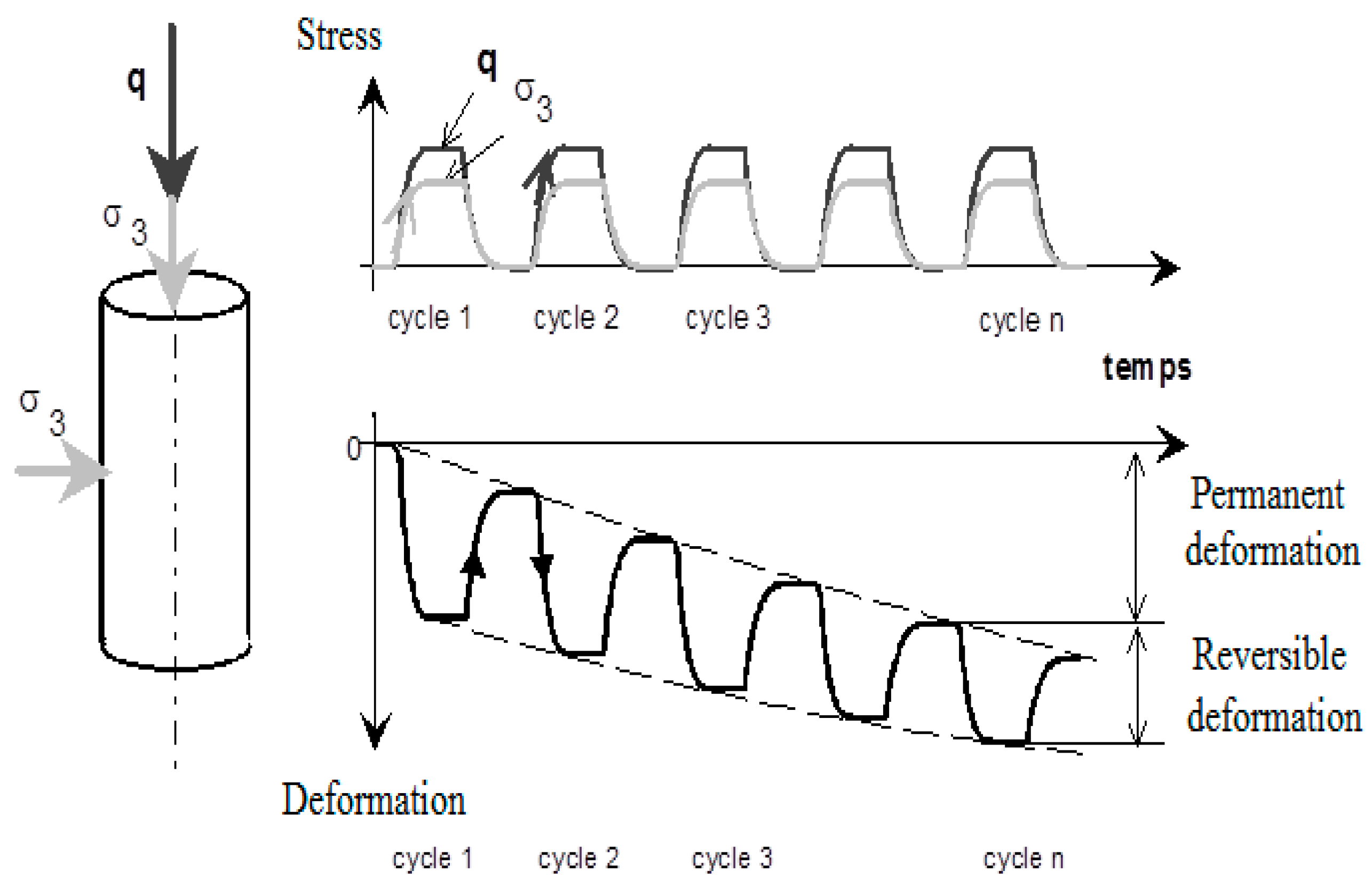
3.4. Test Procedures
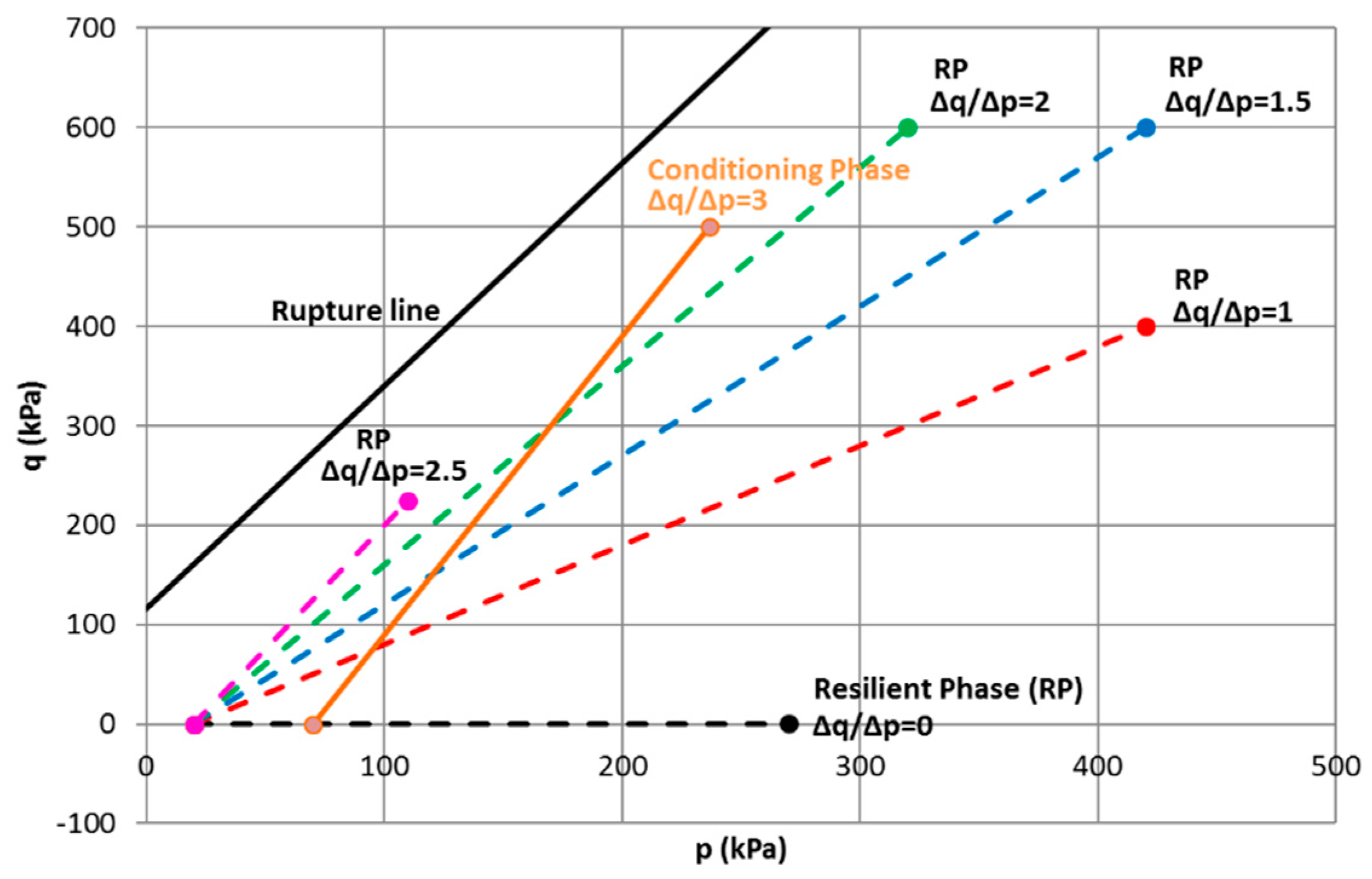
- For the conditioning phase, the cyclic stress path of Δq/Δp = 3 (Δp = 166.67 kPa, Δq = 500 kPa) from an initial stress state (p0 = 70 kPa, q0 = 0 kPa) is applied at a frequency of f = 0.5 Hz. The number of cycles is chosen as N = 20,000 cycles. When the permanent deformation rate Δε1p/ΔN is lower than 1 × 10−7, we can state that the permanent deformation achieves the equilibrium state [24].
- For the following resilient phase, five stress paths (Δq/Δp = 0; 1; 1.5; 2; 2.5) are applied on the same sample in sequence from an initial stress state (p0 = 20 kPa, q0 = 0 kPa). Each stress path contains 100 loading and unloading cycles, with a frequency of f = 0.05 Hz.
4. Results and Discussions
4.1. Permanent Deformation
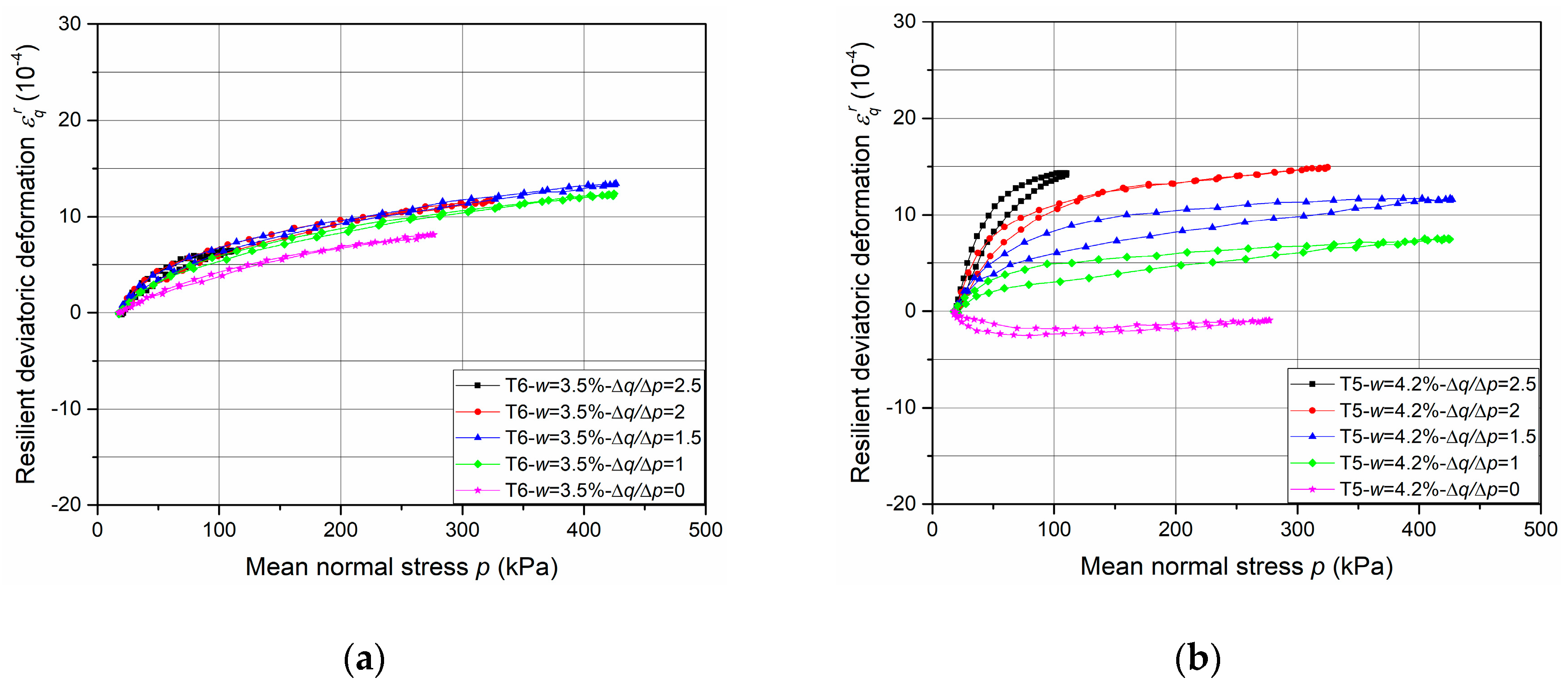
4.2. Resilient Deformation
- The cycles show that the behaviour of the UGM is nonlinear, and depends on the mean stress p and the stress ratio Δq/Δp. It can be stated that εqr increases while εvr decreases with the ratio Δq/Δp increases.
- The effect of water content on resilient deformations is observed: εvr and εqr increase with the water content and present the largest values at the water content (4.6%) in all stress paths nearly.
- The very slight hysteresis for the cycles suggests that the behaviour is close to pure elasticity and the measurements with tube method is more accurate enough compared to that with the metallic inserts/screws.
5. Modelling of Permanent and Resilient Behaviour
5.1. Determination of Permanent Axial Deformation with Water Content and Suction
5.2. Determination of Resilient Deformation with Modified Boyce Model
6. Conclusions
- -
- Both approaches based on water content/suction have a good capacity to describe the permanent deformation behaviour of UGM at different water contents. However, the modelling accuracy is decreasing gradually with increasing particle size with suction-based model.
- -
- For the resilient behaviour of UGM, the improved Boyce–Hornych model has a good ability to capture the changing anisotropy caused by the various water contents or fine contents under repeated loading.
- -
- The two methods of fixing the sensors on the materials with large particles for RLTTs are proposed and compared with each other. The results suggest that the tube method is more suitable for the large particle UGM as the accurate measurement and good adaptability during the RLTT.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chazallon, C.; Koval, G.; Hornych, P.; Allou, F.; Mouhoubi, S. Modeling of rutting of two flexible pavements with the shakedown theory and the finite element method. Comput. Geotech. 2009, 36, 798–809. [Google Scholar] [CrossRef]
- Cerni, G.; Cardone, F.; Virgili, A.; Camilli, S. Characterisation of permanent deformation behavior of unbound granular materials under repeated triaxial loading. Constr. Build. Mater. 2012, 28, 79–87. [Google Scholar] [CrossRef]
- Erlingsson, S.; Rahman, S.; Salour, F. Characteristic of unbound granular materials and subgrades based on multi stage RLT testing. Transp. Geotech. 2017, 13, 28–42. [Google Scholar] [CrossRef]
- Jing, P.; Nowamooz, H.; Chazallon, C. Permanent Deformation Behavior of a Granular Material Used in Low Traffic Pavements. Road Mater. Pavement Des. 2018, 19, 289–314. [Google Scholar] [CrossRef]
- Jing, P.; Nowamooz, H.; Chazallon, C. Effect of Anisotropy on the Resilient Behavior of a Granular Material in Low Traffic Pavement. Materials 2017, 10, 1382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dawson, A.R. Introduction to Soils & Granular Materials. Lecture Notes from Residential Course, Bituminous Pavements: Materials, Design and Evaluation; University of Nottingham: Nottingham, UK, 1990. [Google Scholar]
- Gidel, G.; Breysse, D.; Denis, A. Influence de l’état hydrique et des sollicitations routières sur l’évolution du comportement des graves non traitées calcaires utilisées en assise de chaussée. Revue Française De Génie Civil 2002, 6, 789–799. [Google Scholar] [CrossRef]
- Uthus, L.; Hermansson, Å.; Horvli, I.; Hoff, I. A study on the influence of water and fines on the deformation properties and frost heave of unbound aggregates. In Proceedings of the 13th International Conference on Cold Regions Engineering, Orono, ME, USA, 23–26 July 2006; pp. 1–13. [Google Scholar] [CrossRef]
- Trinh, V.N.; Tang, A.M.; Cui, Y.J.; Dupla, J.C.; Canou, J.; Calon, N.; Lambert, L.; Robinet, A.; Schoen, O. Mechanical characterisation of the fouled ballast in ancient railway track substructure by large-scale triaxial tests. Soils Found. 2012, 52, 511–523. [Google Scholar] [CrossRef]
- Duong, T.V.; Tang, A.M.; Cui, Y.J.; Trinh, V.N.; Dupla, J.C.; Calon, N.; Canou, J.; Robinet, A. Effects of Fines and Water Contents on the Mechanical Behavior of Interlayer Soil in Ancient Railway Sub-structure. Soils Found. 2013, 53, 868–878. [Google Scholar] [CrossRef] [Green Version]
- Salour, F.; Erlingsson, S. Resilient Modulus Modeling of Unsaturated Subgrade Soils: Laboratory Investigation of Silty Sand Subgrade. Road Mater. Pavement Des. 2015, 16, 553–568. [Google Scholar] [CrossRef]
- Salour, F.; Erlingsson, S. Permanent deformation characteristics of silty sand subgrades from multistage RLT tests. Int. J. Pavement Eng. 2017, 18, 236–246. [Google Scholar] [CrossRef]
- Jing, P.; Nowamooz, H.; Chazallon, C. Unsaturated Mechanical Behavior of a Granular Material. Road Mater. Pavement Des. 2019, 20, 1429–1451. [Google Scholar] [CrossRef]
- Xiao, Y.J.; Zhang, Z.; Chen, L.X.; Zheng, K.Y. Modeling stress path dependency of cyclic plastic strain accumulation of unbound granular materials under moving wheel loads. Mater. Des. 2018, 137, 9–21. [Google Scholar] [CrossRef]
- Xiao, Y.J.; Zheng, K.Y.; Chen, L.X.; Mao, J.F. Shakedown analysis of cyclic plastic deformation characteristics of unbound granular materials under moving wheel loads. Constr. Build. Mater. 2018, 167, 457–472. [Google Scholar] [CrossRef]
- Zhalehjoo, N.; Tolooiyan, A.; Mackay, R.; Bodin, D. The effect of instrumentation on the determination of the resilient modulus of unbound granular materials using advanced repeated load triaxial testing. Transp. Geotech. 2018, 14, 190–201. [Google Scholar] [CrossRef]
- Association Française de Normalisation (AFNOR). Sols: Reconnaissance et Essais—Détermination des Références de Compactage d’un Matériau—Essai Proctor Normal. In Essai Proctor Modifié; NF P94-093; AFNOR: Saint-Denis La Plaine, France, 2014. [Google Scholar]
- ASTM. ASTM D5298-10—Standard Test Method for Measurement of Soil Potential (Suction); ASTM International: West Conshohocken, PA, USA, 2010. [Google Scholar]
- Ben Mahmoud, A. Modélisation des Chaussés Construites Par des Matériaux Granulaires Compactés Non-Saturés. Master’s Thesis, Nancy University, Nancy, France, 2010. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Arsenie, I.M. Interprétation en Contraintes Effectives du Comportement Réversible des Matériaux Granulaires Compactés Non-Saturés Sous Sollicitations Triaxiales Cycliques. Master’s Thesis, INSA-Strasbourg, Strasbourg, France, 2009. [Google Scholar]
- Association Française de Normalisation (AFNOR). Mélanges Traités et Mélanges non Traités aux Liants Hydrauliques. In Méthodes L’essai Pour la Masse Volumique de Référence et la Teneur en Eau en Laboratoire—Marteau Vibrant; NF EN 13286-4; AFNOR: Saint-Denis La Plaine, France, 2003. [Google Scholar]
- Jing, P. Etudes de L’effet des Fines et de la Teneur en eau sur le Comportement Hydromecanique des Materiaux Granulaires. Doctoral Thesis, University of Strasbourg, Strasbourg, France, 2017. [Google Scholar]
- Association Française de Normalisation (AFNOR). Melanges Avec ou Sans Liant Hydraulique Essai Triaxial Sous Charge Cyclique Pour Melanges Sans Liant Hydraulique; NF EN 13286-7; AFNOR: Saint-Denis La Plaine, France, 2004. [Google Scholar]
- Boyce, H.R. A Non-linear Model for the Elastic Behavior of Granular Materials under Repeated Loading. In Proceedings of the International Symposium on Soils under Cyclic and Transient Loading, Swansea, UK, 7–11 January 1980; pp. 285–294. [Google Scholar]
- Hornych, P.; Kazai, A.; Piau, J.M. Study of the Resilient Behavior of Unbound Granular Material. In Proceedings of the 5th Conference on Bearing Capacity of Roads and Airfields, Trondheim, Norway, 6–8 July 1998; pp. 1277–1287. [Google Scholar]






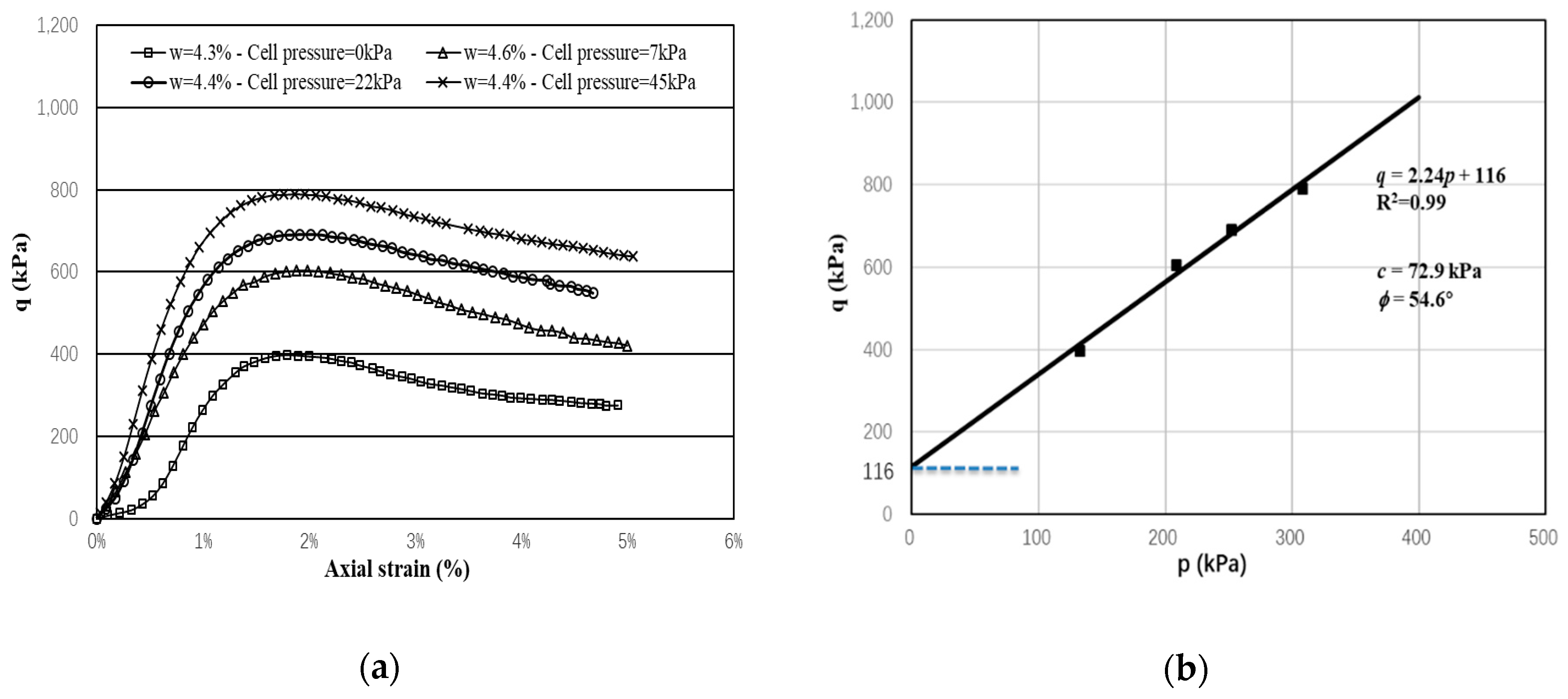







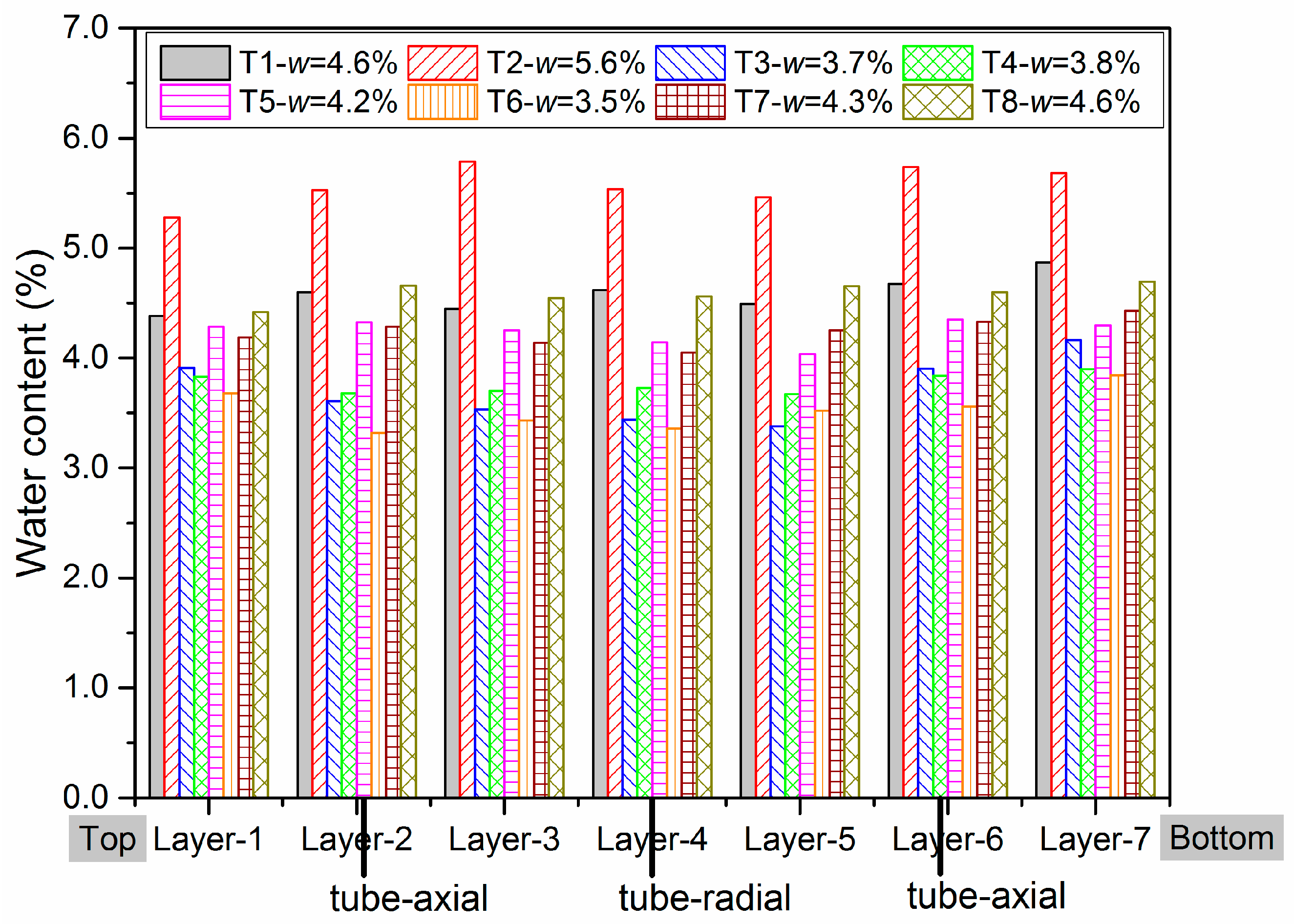

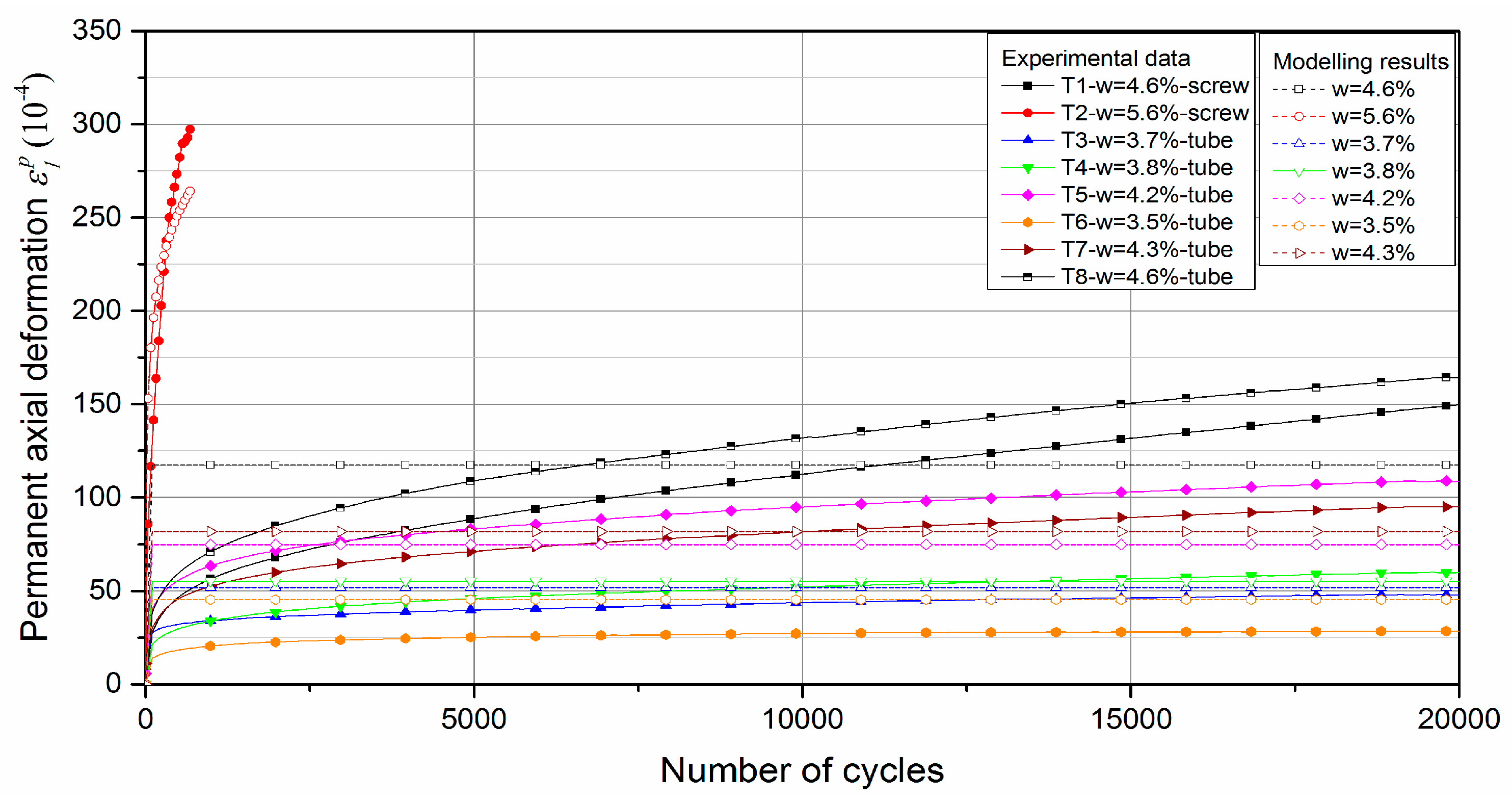
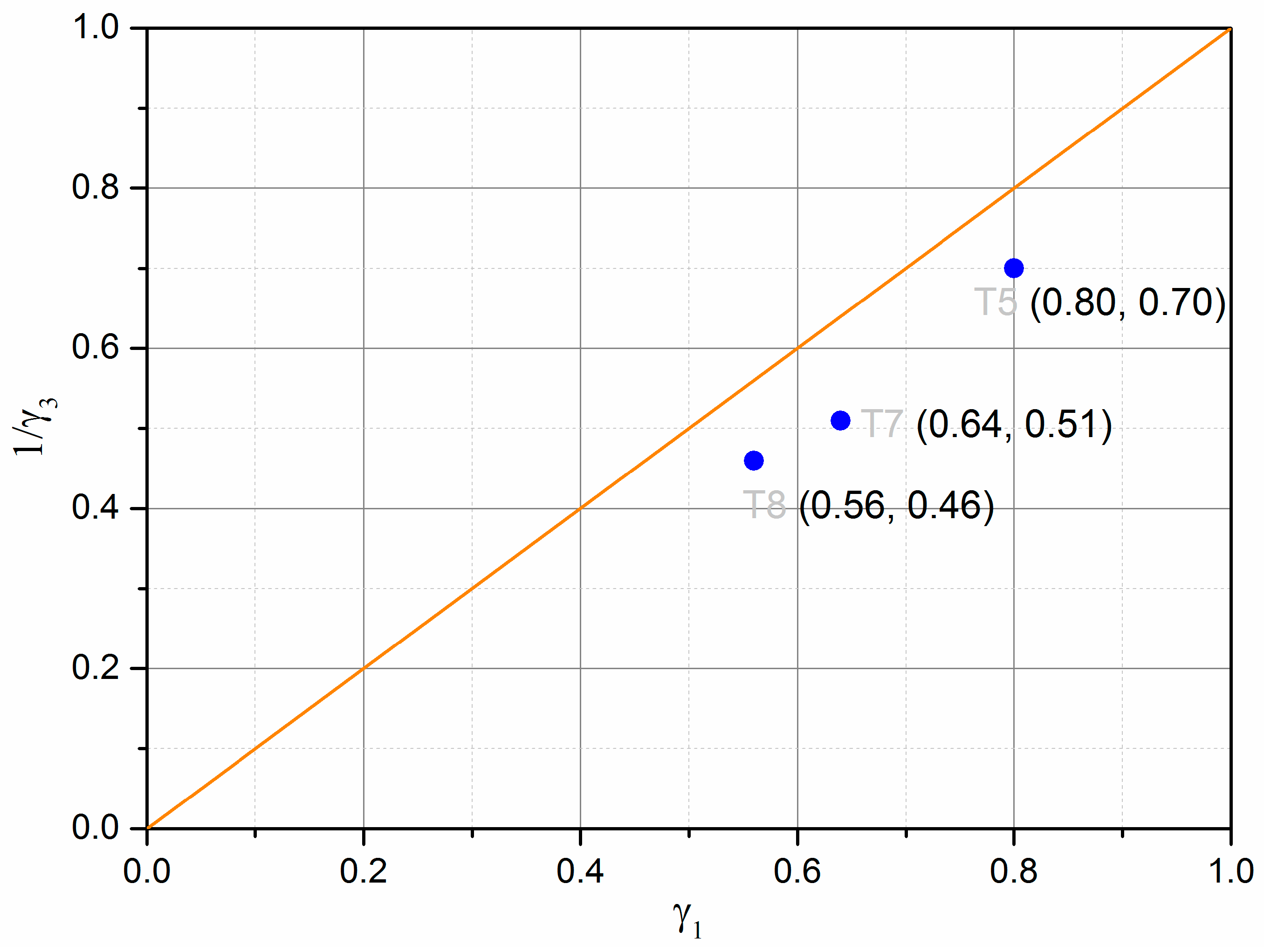


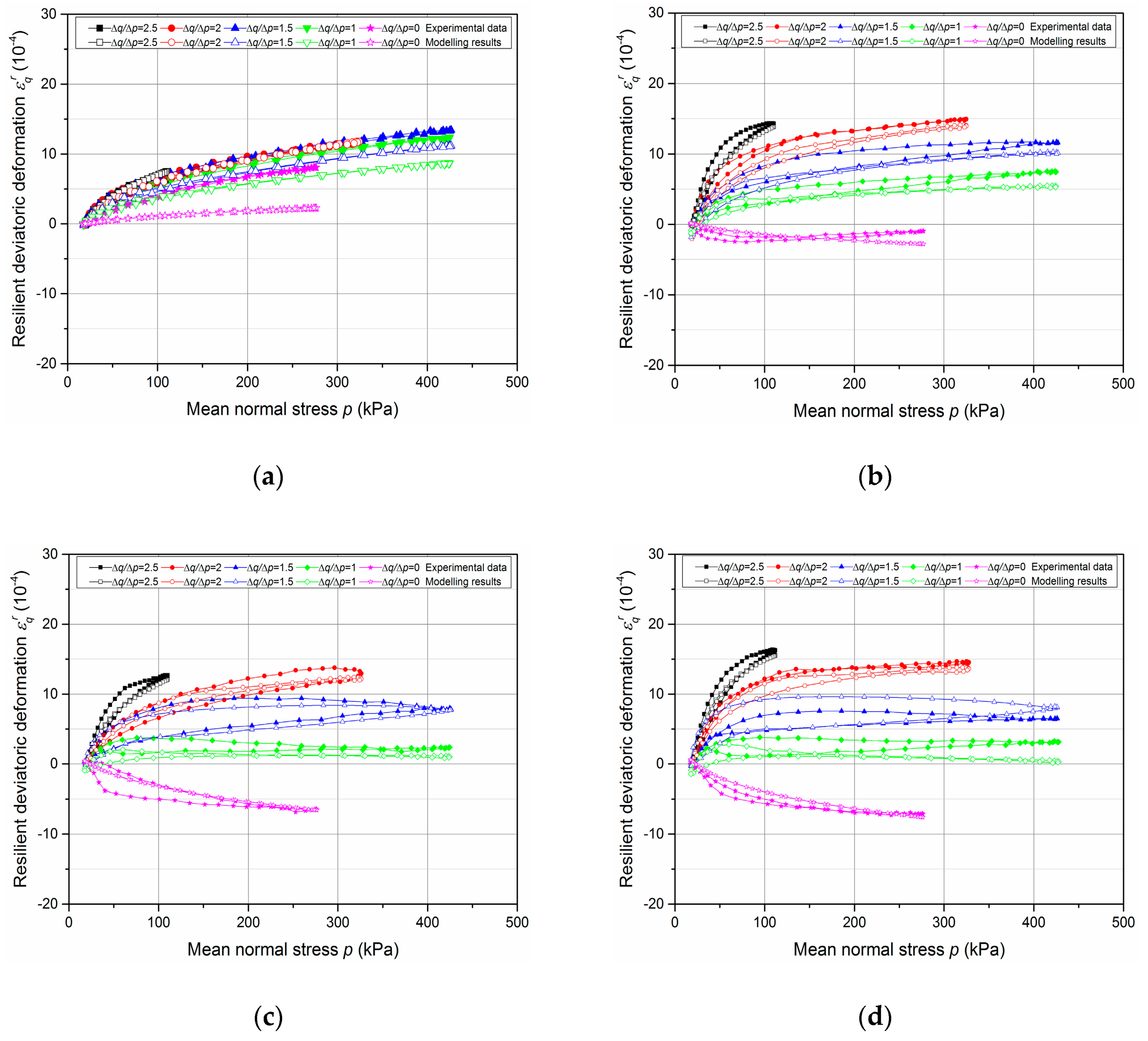
| UGM Bréfauchet Wetting path | Parameters of VG model | α | n | m | ws (%) | wr(%) |
| 0.199 | 1.932 | 0.482 | 5.4 | 2.9 |
| Materials | Δq/Δp | Δp (kPa) | Δq (kPa) | Confining Pressure (kPa) |
|---|---|---|---|---|
| UGM Bréfauchet | 3(Conditioning) | 166.67 | 500 | 70–CCP |
| 0 | 250 | 0 | 270–VCP | |
| 1 | 400 | 400 | 286.67–VCP | |
| 1.5 | 400 | 600 | 220–VCP | |
| 2 | 300 | 600 | 120–VCP | |
| 2.5 | 90 | 225 | 35–VCP |
| UGM Bréfauchet | a | o | R2 | ||
| 69.644 | 1.277 | 6.246 | −0.0003 | 0.937 |
| UGM Bréfauchet | S*(kPa) | b | d | e | f | R2 |
| 1.5 | 351.627 | −0.733 | −1.393 | −9.642 | 0.891 | |
| 2.5 | 267.284 | −0.800 | −0.464 | −3.218 | 0.896 | |
| 3.5 | 219.425 | −0.867 | −0.677 | −4.687 | 0.898 |
| w (%) | Δq/Δp | Parameters (UGM Bréfauchet) | Ccorrel | |||
|---|---|---|---|---|---|---|
| Ka | Ga | n | γ1 | |||
| 3.5 | 0; 1; 1.5; 2; 2.5 | 152.63 | 118.54 | 0.02 | 29.07 | 0.636 |
| 4.2 | 0; 1; 1.5; 2; 2.5 | 16.77 | 38.47 | 0.27 | 0.80 | 0.799 |
| 4.3 | 0; 1; 1.5; 2; 2.5 | 14.15 | 32.06 | 0.33 | 0.64 | 0.835 |
| 4.6 | 0; 1; 1.5; 2; 2.5 | 9.04 | 23.42 | 0.20 | 0.56 | 0.827 |
| Average values | 48.15 | 53.12 | 0.21 | 7.77 | / | |
| w (%) | Δq/Δp | Parameters (UGM Bréfauchet) | Ccorrel | |||
|---|---|---|---|---|---|---|
| Ka | Ga | n | γ3 | |||
| 3.5 | 0; 1; 1.5; 2; 2.5 | 87.02 | 70.90 | 0.45 | 0.20 | 0.573 |
| 4.2 | 0; 1; 1.5; 2; 2.5 | 23.55 | 54.18 | 0.29 | 1.43 | 0.821 |
| 4.3 | 0; 1; 1.5; 2; 2.5 | 25.80 | 65.39 | 0.33 | 1.96 | 0.853 |
| 4.6 | 0; 1; 1.5; 2; 2.5 | 18.62 | 55.91 | 0.22 | 2.18 | 0.865 |
| Average values | 38.75 | 61.60 | 0.32 | 1.44 | / | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, P.; Chazallon, C. Hydro-Mechanical Behaviour of an Unbound Granular Base Course Material Used in Low Traffic Pavements. Materials 2020, 13, 852. https://doi.org/10.3390/ma13040852
Jing P, Chazallon C. Hydro-Mechanical Behaviour of an Unbound Granular Base Course Material Used in Low Traffic Pavements. Materials. 2020; 13(4):852. https://doi.org/10.3390/ma13040852
Chicago/Turabian StyleJing, Peng, and Cyrille Chazallon. 2020. "Hydro-Mechanical Behaviour of an Unbound Granular Base Course Material Used in Low Traffic Pavements" Materials 13, no. 4: 852. https://doi.org/10.3390/ma13040852
APA StyleJing, P., & Chazallon, C. (2020). Hydro-Mechanical Behaviour of an Unbound Granular Base Course Material Used in Low Traffic Pavements. Materials, 13(4), 852. https://doi.org/10.3390/ma13040852





