Uniaxial Compressive Behavior of Concrete Columns Confined with Superelastic Shape Memory Alloy Wires
Abstract
:1. Introduction
2. Materials
2.1. Superelastic SMA Wires
2.2. Mechanical Properties of Fiber Reinforced Polymer (FRP)
2.3. Mechanical Properties of Concrete
3. Experiments Test Setup and Procedure
4. Experimental Phenomena and Test Results Analysis
4.1. Experimental Phenomena
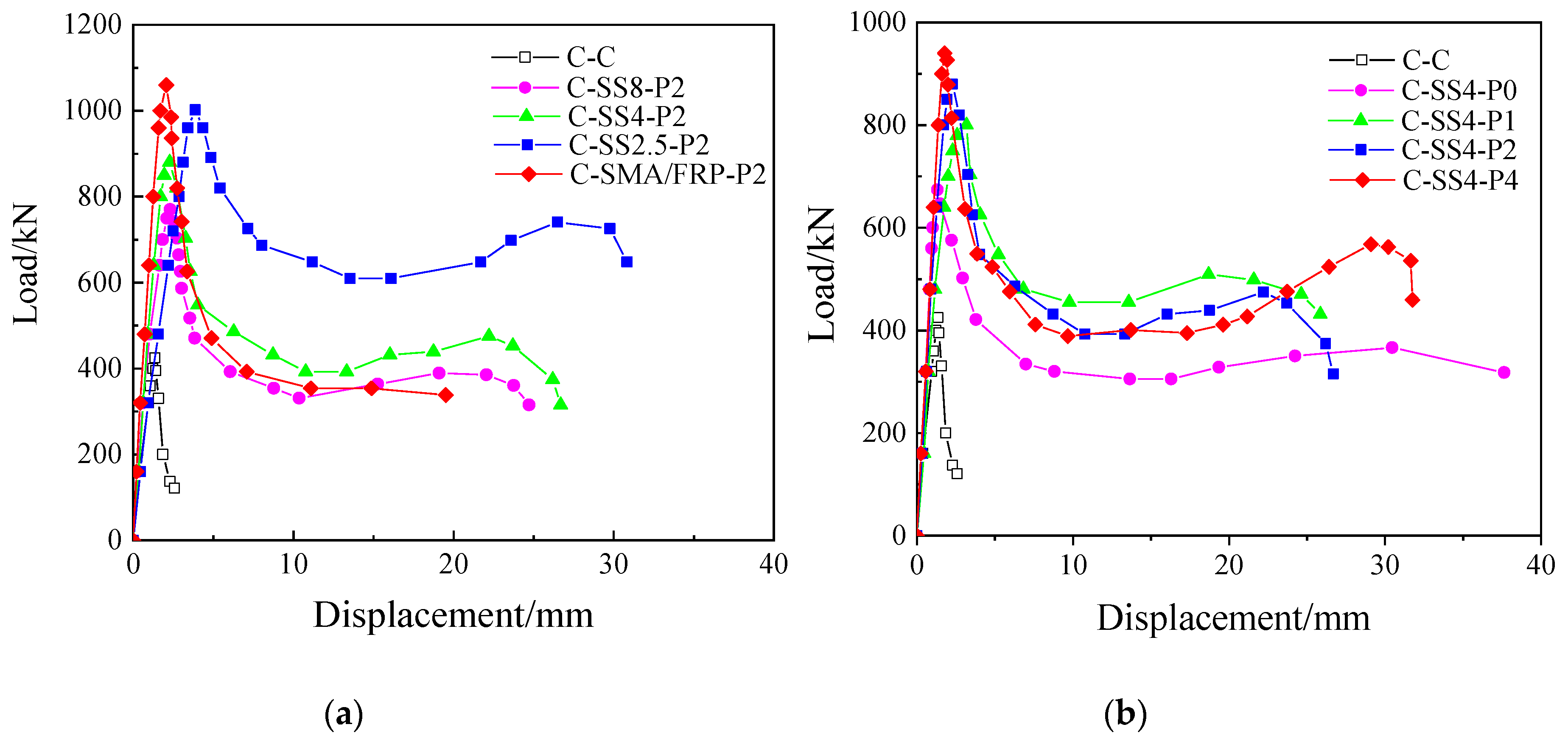
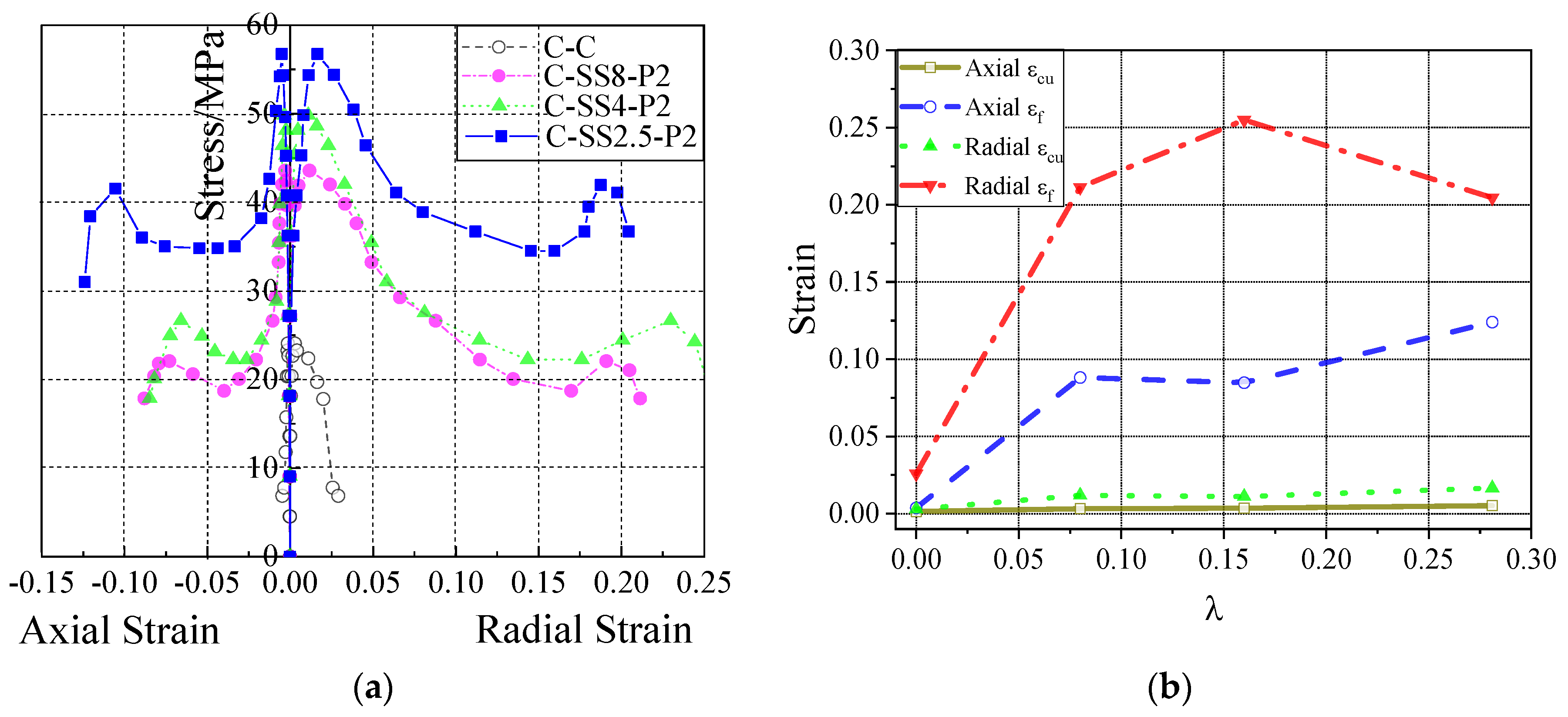
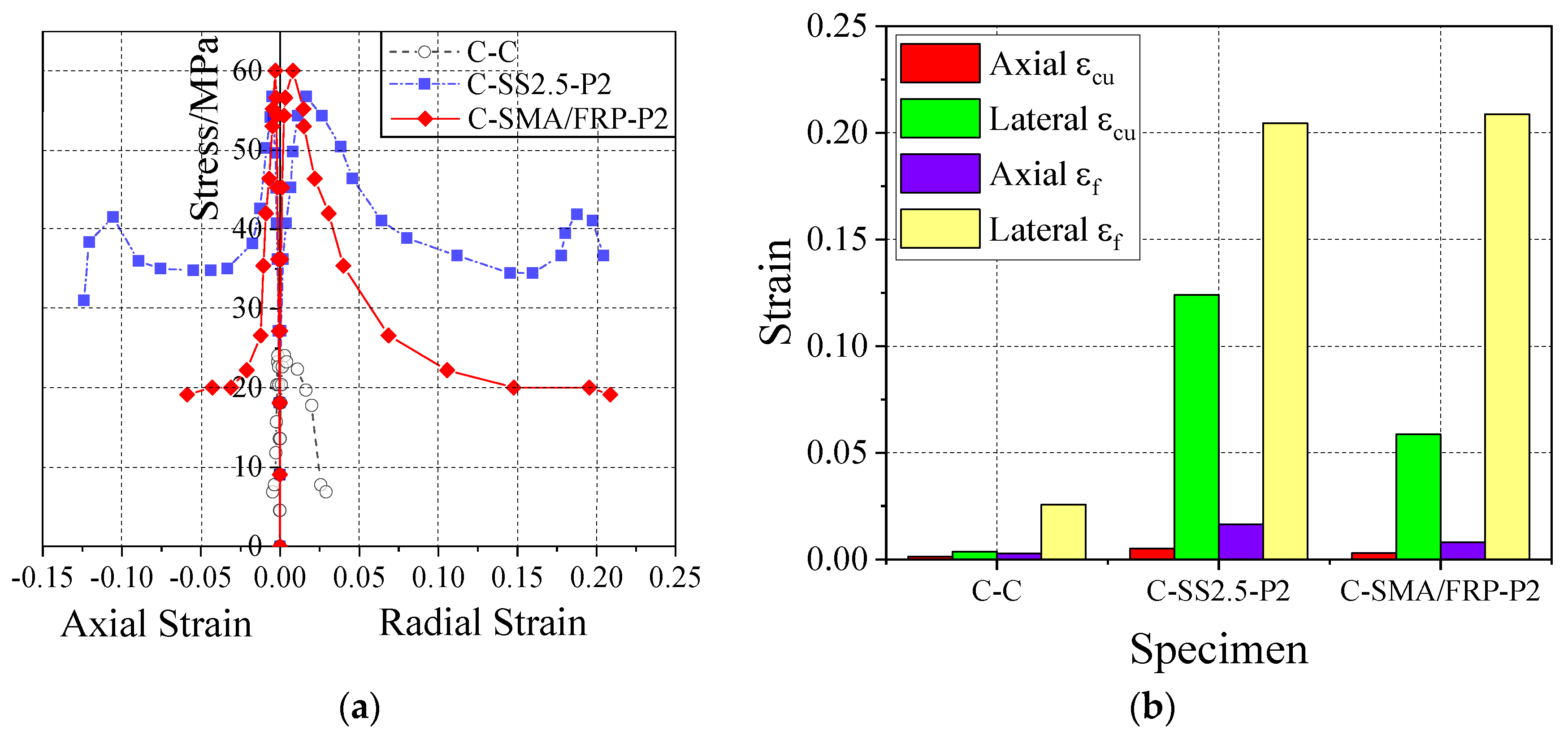
4.2. Test Results Analysis
4.3. Axial and Lateral Strain Relationship of Concrete Column
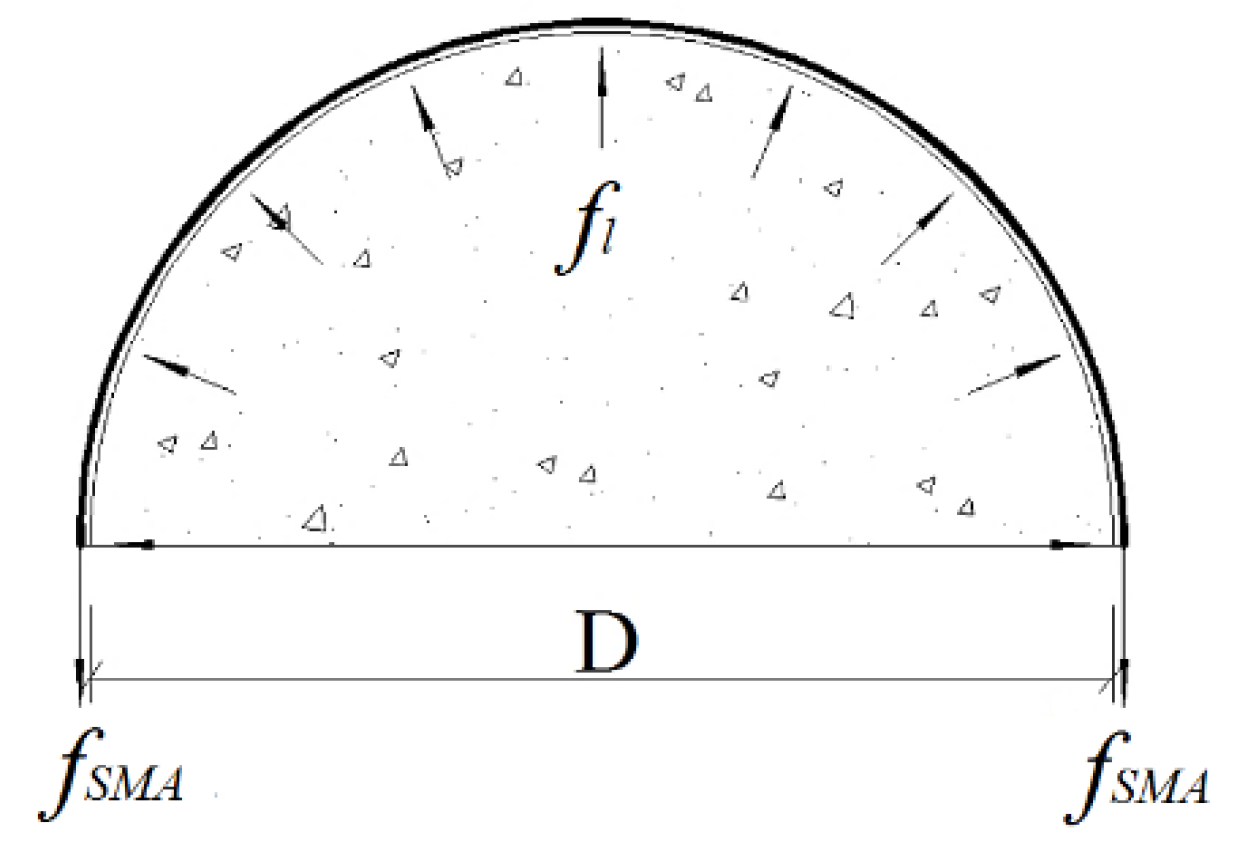
5. Design and Calculation of Ultimate Axial Bearing Capacity of Superelastic SMA RC Columns
- (1)
- During the prestraining process, the superelastic SMA wire changes uniformly under tension, and the constraint effect on the cylinder surface is also uniform. The differences in the prestrain level on the cylinder surface due to the friction between the concrete and the SMA wires can be neglected;
- (2)
- The axial compressive strength of concrete cylinders constrained by prestrained superelastic SMA wires is composed of the axial compressive strength of the unconstrained concrete cylinders and the increased axial compressive strength of the concrete cylinders enhanced by the lateral restraint effect of the superelastic SMA wires. The axial compressive strength of SMA constrained concrete cylinders can be obtained by linearly superposing the axial compressive strength of unconstrained concrete cylinder and the increased axial compressive strength of the concrete cylinders enhanced by the lateral restraint effect of the superelastic SMA wires;
- (3)
- The axial load on the cylinder is fully borne by the concrete, and the superelastic SMA wire does not bear the axial load;
- (4)
- The SMA wires are always in a tensioned state, and in reliable contact with the concrete columns. The two items work together and deform together, which is also proved by experimental phenomena. Hence there is no relative slippage during the loading process.
5.1. Calculation of Compressive Strength of Concrete Columns Confieded by Prestressed Superelastic SMA Wires
5.2. Comparison of Calculated and Recorded Ultimate Axial Bearing Capacities
6. Conclusions
- (1)
- This paper proposes an effective method of using superelastic SMA wires to achieve active restraint and strengthen the bearing capacity of concrete columns.
- (2)
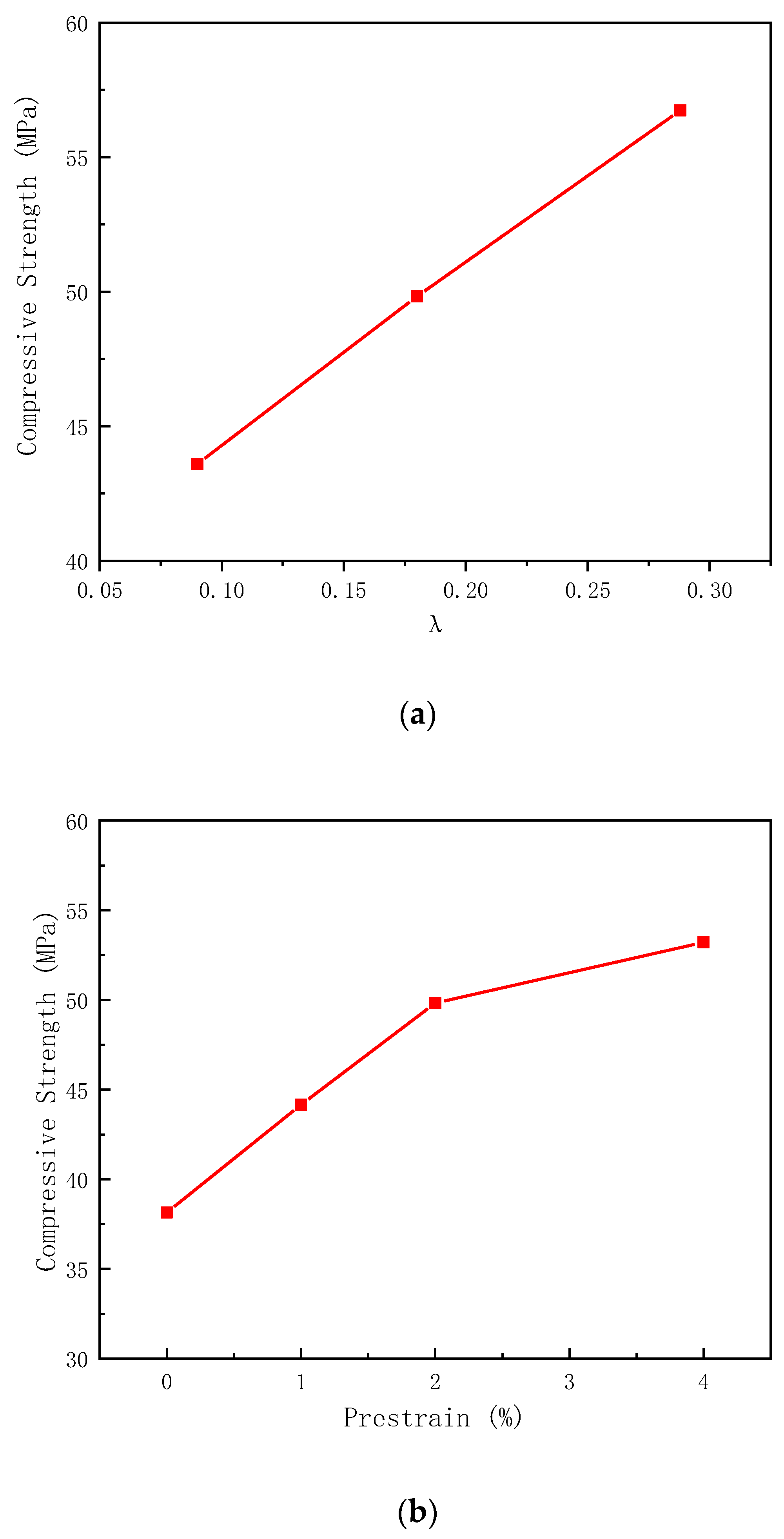
- With the same prestrain level (α = 2%), an increase in reinforced amounts (λ) of superelastic SMA from 0.09 to 0.288 leads to an approximately linear increase of ultimate bearing capacity of SMA RC columns from 80% to 135%, compared with the plain concrete column.
- (3)
- With the same reinforced amounts (λ = 0.180), an increase in prestrain level from 0% to 4% results in an remarkable increase of ultimate bearing capacity of SMA RC columns from 60% to 120%. However with prestrain level increasing, the enhancing trend weakened.
- (4)
- Though both SMA and SMA/FRP have similar effects on strengthening the ultimate bearing capacity of concrete columns, SMA reinforced columns have better ductility.
- (5)
- In the main deformation area of the concrete columns, the enhancing effect of SMA wires on the lateral strain is better than that in the axial strain.
- (6)
- A practical calculation method and formula for the ultimate axial compression bearing capacity of concrete columns restrained by prestrained SMA wires is proposed.
- (7)
- The number of test samples in this study is limited, so further research is needed on the bearing performance of superelastic SMA reinforced concrete columns. In particular, the calculation method for the bearing capacity of super-elastic SMA-constrained concrete columns will be further developed in future research.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiao, L.; Peng, J.; Zhang, J.; Ma, Y.; Cai, C.S. Comparative assessment of mechanical properties of HPS between electrochemical corrosion and spray corrosion. Constr. Build. Mater. 2020, 237, 117735. [Google Scholar] [CrossRef]
- Peng, J.; Xiao, L.; Zhang, J.; Cai, C.S.; Wang, L. Flexural behavior of corroded HPS beams. Eng. Struct. 2019, 195, 274–287. [Google Scholar] [CrossRef]
- Yin, X.; Song, G.; Liu, Y. Vibration suppression of wind/traffic/bridge coupled system using multiple pounding tuned mass dampers (MPTMD). Sensors 2019, 19, 1133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, N.; Wang, F.; Song, G. New entropy-based vibro-acoustic modulation method for metal fatigue crack detection: An exploratory study. Measurement 2020, 150, 107075. [Google Scholar] [CrossRef]
- Huo, L.; Li, X.; Chen, D.; Li, H.; Song, G. Identification of the impact direction using the beat signals detected by piezoceramic sensors. Smart Mater. Struct. 2017, 26, 085020. [Google Scholar] [CrossRef]
- Zhang, C.; Gholipour, G.; Mousavi, A.A. Nonlinear dynamic behavior of simply-supported RC beams subjected to combined impact-blast loading. Eng. Struct. 2019, 181, 124–142. [Google Scholar] [CrossRef]
- Qi, B.X.; Kong, Q.Z.; Qian, H.; Patil, D.; Lim, L.; Li, M.; Liu, D.; Song, G. Study of impact damage in PVA-ECC beam under low-velocity impact loading using piezoceramic transducers and PVDF thin-film transducers. Sensors 2018, 18, 671. [Google Scholar] [CrossRef] [Green Version]
- Gholipour, G.; Zhang, C.; Mousavi, A.A. Effects of axial load on nonlinear response of RC columns subjected to lateral impact load: Ship-pier collision. Eng. Fail. Anal. 2018, 91, 397–418. [Google Scholar] [CrossRef]
- Liu, C.; Yang, W.; Yan, Z.; Lu, Z.; Luo, N. Base pounding model and response analysis of base-isolated structures under earthquake excitation. Appl. Sci. 2017, 7, 1238. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.J.; Duan, P.H.; Qian, H. Dynamic response analysis of long-span continuous bridge considering the effect of train speeds and earthquakes. Int. J. Struct. Stab. Dyn. 2020, in press. [Google Scholar]
- Qian, H.; Li, H.N.; Song, G.B. Experimental investigations of building structure with a superelastic shape memory alloy friction damper subject to seismic loads. Smart Mater. Struct. 2016, 25, 1–8. [Google Scholar] [CrossRef]
- Zhang, C. Control force characteristics of different control strategies for the wind-excited 76-story benchmark building structure. Adv. Struct. Eng. 2014, 17, 543–560. [Google Scholar] [CrossRef]
- Perera, R.; Torres, L.; Ruiz, A.; Barris, C.; Baena, M. An EMI-Based Clustering for Structural Health Monitoring of NSM FRP Strengthening Systems. Sensors 2019, 19, 3775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, L.; Li, C.; Zhang, C.; Liang, T.; Zhao, Z. The Strain Transfer Mechanism of Fiber Bragg Grating Sensor for Extra Large Strain Monitoring. Sensors 2019, 19, 1851. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Li, L.; Ou, J. Swinging motion control of suspended structures: Principles and applications. Struct. Control Health Monit. 2010, 17, 549–562. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, M.; Yin, X.; Huang, Z.; Wang, L. Debonding detection of reinforced concrete (RC) beam with near-surface mounted (NSM) pre-stressed carbon fiber reinforced polymer (CFRP) plates using embedded piezoceramic smart aggregates (SAs). Appl. Sci. 2020, 10, 50. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Jiang, J.; Deng, X.; Deng, Z. Detecting Debonding between Steel Beam and Reinforcing CFRP Plate Using Active Sensing with Removable PZT-Based Transducers. Sensors 2020, 20, 41. [Google Scholar] [CrossRef] [Green Version]
- Xia, L.; Zheng, Y. Deep embedment (DE) FRP shear strengthening of concrete bridge slabs under loads close to supports. Appl. Sci. 2018, 8, 721. [Google Scholar] [CrossRef] [Green Version]
- Di, B.; Wang, J.; Li, H.; Zheng, J.; Zheng, Y.; Song, G. Investigation of bonding behavior of FRP and steel bars in self-compacting concrete structures using acoustic emission method. Sensors 2019, 19, 159. [Google Scholar] [CrossRef] [Green Version]
- Andrawes, B.; Shin, M. Seismic retrofitting of bridge columns using shape memory alloys. Proceedings of SPIE—The International Society for Optical Engineering. Act. Passiv. Smart Struct. Integr. Syst. 2008, 6928. [Google Scholar] [CrossRef]
- Choi, E.; Chung, Y.S.; Cho, B.S.; Nam, T.H. Confining concrete cylinders using shape memory alloy wires. Eur. Phys. J. Spec. Top. 2008, 158, 255–259. [Google Scholar] [CrossRef]
- Karabinis, A.I. Rousakis TC. Concrete confined by FRP material: A plasticity approach. Eng. Struct. 2002, 24, 923–932. [Google Scholar] [CrossRef]
- Li, J.; Zu, L.; Zhong, G.; He, M.; Yin, H.; Tan, Y. Stiffness characteristics of soft finger with embedded SMA fibers. Compos. Struct. 2017, 160, 758–764. [Google Scholar] [CrossRef]
- Choi, E.; Nam, T.H.; Cho, S.C.; Chung, Y.S.; Park, T. The behavior of concrete cylinders confined by shape memory alloy wires. Smart Mater. Struct. 2008, 17, 32–42. [Google Scholar] [CrossRef]
- Chen, Q.; Andrawes, B. Cyclic stress–strain behavior of concrete confined with NiTiNb-shape memory alloy spirals. J. Struct. Eng. 2017, 143, 1943–1954. [Google Scholar] [CrossRef]
- Ilki, A.; Peker, O.; Karamuk, E.; Demir, C.; Kumbasar, N. FRP retrofit of low and medium strength circular and rectangular reinforced concrete columns. J. Mater. Civ. Eng. 2008, 20, 169–188. [Google Scholar] [CrossRef]
- Wu, Y.F.; Zhou, Y.W. Unified Strength Model Based on Hoek-Brown Failure Criterion for Circular and Square Concrete Columns Confined by FRP. J. Compos. Constr. 2010, 14, 175–184. [Google Scholar] [CrossRef]
- Dundar, C.; Erturkmen, D.; Tokgoz, S. Studies on carbon fiber polymer confined slender plain and steel fiber reinforced concrete columns. Eng. Struct. 2015, 102, 31–39. [Google Scholar] [CrossRef]
- Kilicarslan, A.; Song, G.; Grigoriadis, K.M. Modeling and hysteresis compensation in a thin SMA wire using ANFIS methods. J. Intell. Mater. Syst. Struct. 2011, 22, 45–57. [Google Scholar] [CrossRef]
- Qian, H.; Li, H.; Song, G. Theoretical and Experimental Investigations on the Application of Superelastic Shape Memory Alloys in Seismic Engineering. In Earth and Space 2010: Engineering, Science, Construction, and Operations in Challenging Environments; ASCE: Reston, VA, USA, 2010; pp. 3406–3415. [Google Scholar]
- Patil, D.; Song, G. A review of shape memory material’s applications in the offshore oil and gas industry. Smart Mater. Struct. 2017, 26, 093002. [Google Scholar] [CrossRef]
- Li, H.; Cui, D.; Song, G. Experimental investigation on self-rehabilitation of intelligent concrete beams reinforced with shape memory alloys. In Earth and Space, Proceedings of the 10th Biennial International Conference on Engineering, Construction, and Operations in Challenging Environments and Second NASA/ARO/ASCE Workshop on Granular Materials in Lunar and Martian Exploration, Houston, TX, USA, 5–8 March 2006; ASCE: Reston, VA, USA, 2006. [Google Scholar]
- Song, G.; Mo, Y.L.; Otero, K.; Gu, H. Health monitoring and rehabilitation of a concrete structure using intelligent materials. Smart Mater. Struct. 2006, 15, 309–314. [Google Scholar] [CrossRef] [Green Version]
- Andrawes, B.; ASCE, A.M.; Shina, M.; Wierschem, N. Active Confinement of Reinforced Concrete Bridge Columns Using Shape Memory Alloys. J. Bridge Eng. 2010, 15, 38–46. [Google Scholar] [CrossRef]
- Song, D.; Kang, G.; Kan, Q.; Yu, C.; Zhang, C. The effect of martensite plasticity on the cyclic deformation of super-elastic NiTi shape memory alloy. Smart Mater. Struct. 2014, 23, 5008. [Google Scholar] [CrossRef]
- Qian, H.; Li, H.; Song, G.; Guo, W. Recentering Shape Memory Alloy Passive Damper for Structural Vibration Control. Math. Probl. Eng. 2013, 2013, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Andrawes, B.; Shin, M. Experimental Investigation of Concrete Columns Wrapped with Shape Memory Alloy Spirals. In Proceedings of the Atc & Sei Conference on Improving the Seismic Performance of Existing Buildings & Other Structures, San Francisco, CA, USA, 9–11 December 2009; pp. 835–840. [Google Scholar]
- Choi, E.; Chung, Y.S.; Choi, J.H.; Kim, H.T.; Lee, H. The confining effectiveness of NiTiNb and NiTi SMA wire jackets for concrete. Smart Mater. Struct. 2010, 19, 24–32. [Google Scholar] [CrossRef]
- Chen, Q.; Andrawes, B. Experimentally validated modeling of concrete actively confined using SMA reinforcement. In Proceedings of the NCEE 2014-10th US National Conference on Earthquake Engineering: Frontiers of Earthquake Engineering, Anchorage, AK, USA, 21–25 July 2014. [Google Scholar] [CrossRef]
- Chen, Q.; Andrawes, B. Monotonic and cyclic experimental testing of concrete confined with shape memory alloy spirals. In Proceedings of the 10th US National Conference on Earthquake Engineering, Anchorage, AK, USA, 21–25 July 2014. [Google Scholar]
- Shin, M.; Andrawes, B. Experimental investigation of actively confined concrete using shape memory alloys. Eng. Struct. 2010, 32, 656–664. [Google Scholar] [CrossRef]
- Shin, M.; Andrawes, B. Lateral cyclic behavior of reinforced concrete columns retrofitted with shape memory spirals and FRP wraps. J. Struct. Eng. 2011, 137, 1282–1290. [Google Scholar] [CrossRef]
- Chen, Q.; Andrawes, B. Testing of concrete elements with internal shape memory alloy spirals. Mag. Concr. Res. 2017, 69, 1751–1763. [Google Scholar] [CrossRef]
- Park, J.; Choi, E.; Park, K.; Kim, H.T. Comparing the cyclic behavior of concrete cylinders confined by shape memory alloy wire or steel jackets. Smart Mater. Struct. 2011, 20, 8–19. [Google Scholar] [CrossRef] [Green Version]
- Pratik, S.D.; Andrawes, B. Hybrid confinement of high strength concrete using shape memory alloys and fiber-reinforced polymers. J. Struct. Integr. Maint. 2018, 3, 22–32. [Google Scholar]
- Aliakbar, G.; Togay, O. Understanding the compressive behavior of shape memory alloy (SMA)-confined normal- and high-strength concrete. Compos. Struct. 2018, 202, 943–953. [Google Scholar]
- Saiidi, M.S.; Sadrossadat-Zadeh, M.; Ayoub, C.; Itani, A. Pilot Study of Behavior of Concrete Beams Reinforced with Shape Memory Alloys. J. Mater. Civ. Eng. 2007, 19, 454–461. [Google Scholar] [CrossRef]
- Abdulridha, A.; Palermo, D.; Foo, S.; Vecchio, F.J. Behavior and modeling of superelastic shape memory alloy reinforced concrete beams. Eng. Struct. 2013, 49, 893–904. [Google Scholar] [CrossRef]
- Rojob, H.; El-Hacha, R. Self-prestressing using iron-based shape memory alloy for flexural strengthening of reinforced concrete beams. Aci Struct. J. 2017, 114, 523–532. [Google Scholar]
- Michels, J.; Shahverdi, M.; Czaderski, C.; El-Hacha, R. Mechanical performance of iron-based shape-memory alloy ribbed bars for concrete prestressing. Aci Mater. J. 2018, 115, 877–886. [Google Scholar]
- Alam, M.S.; Youssef, M.A.; Nehdi, M. Analytical prediction of the seismic behavior of superelastic shape memory alloy reinforced concrete elements. Eng. Struct. 2008, 30, 3399–3411. [Google Scholar] [CrossRef]
- Youssef, M.A.; Alam, M.S.; Nehdi, M. Experimental investigation on the seismic behavior of beam-column joints reinforced with superelastic shape memory alloys. J. Earthq. Eng. 2008, 12, 1205–1222. [Google Scholar] [CrossRef]
- Shajil, N.; Srinivasan, S.M.; Santhanam, M. Self-centering of shape memory alloy fiber reinforced cement mortar members subjected to strong cyclic loading. Mater. Struct. 2013, 46, 651–661. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, D.J.; Chung, Y.S.; Choi, E. Direct tensile behavior of shape-memory-alloy fiber-reinforced cement. Constr. Build. Mater. 2016, 102, 462–470. [Google Scholar] [CrossRef]
- Nehdi, M.L.; Ali, M. Experimental and numerical study of engineered cementitious composite with strain recovery under impact loading. Appl. Sci. 2019, 9, 994. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Jiang, H.; Wang, J. Numerical simulation and behavior insights of steel columns with SMA bolts towards earthquake resilience. J. Constr. Steel Res. 2019, 161, 285–295. [Google Scholar] [CrossRef]
- Hollaway, L.C.; Head, P.R. Composite materials and structures in civil engineering. Compr. Compos. Mater. 2000, 6, 489–527. [Google Scholar]
- Uemura, M. Reinforcement of Concrete Columns with CFRP. Compr. Compos. Mater. 2000, 6, 529–539. [Google Scholar]
- Zhu, J.; Wang, X. Experimental Study on the Axial Compression Performance of Damaged Concrete Column Reinforced by CFRP Sheets. Earthq. Resist. Eng. Retrofit. 2015, 37, 100–105. [Google Scholar]
- Code of China. Code for Design of Concrete Structures; (GB 50010-2010); Code of China: Beijing, China, 2010. [Google Scholar]
- Code of China. Standards for Testing Methods of Concrete Structures; (GB 50152-2012); Code of China: Beijing, China, 2012. [Google Scholar]
- Mander, J.; Priestley, M.; Park, R. Observed stress-strain behavior of confined concrete. Asce Struct. J. 1988, 100, 215–221. [Google Scholar] [CrossRef]
- Mander, J.; Priestley, M.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]

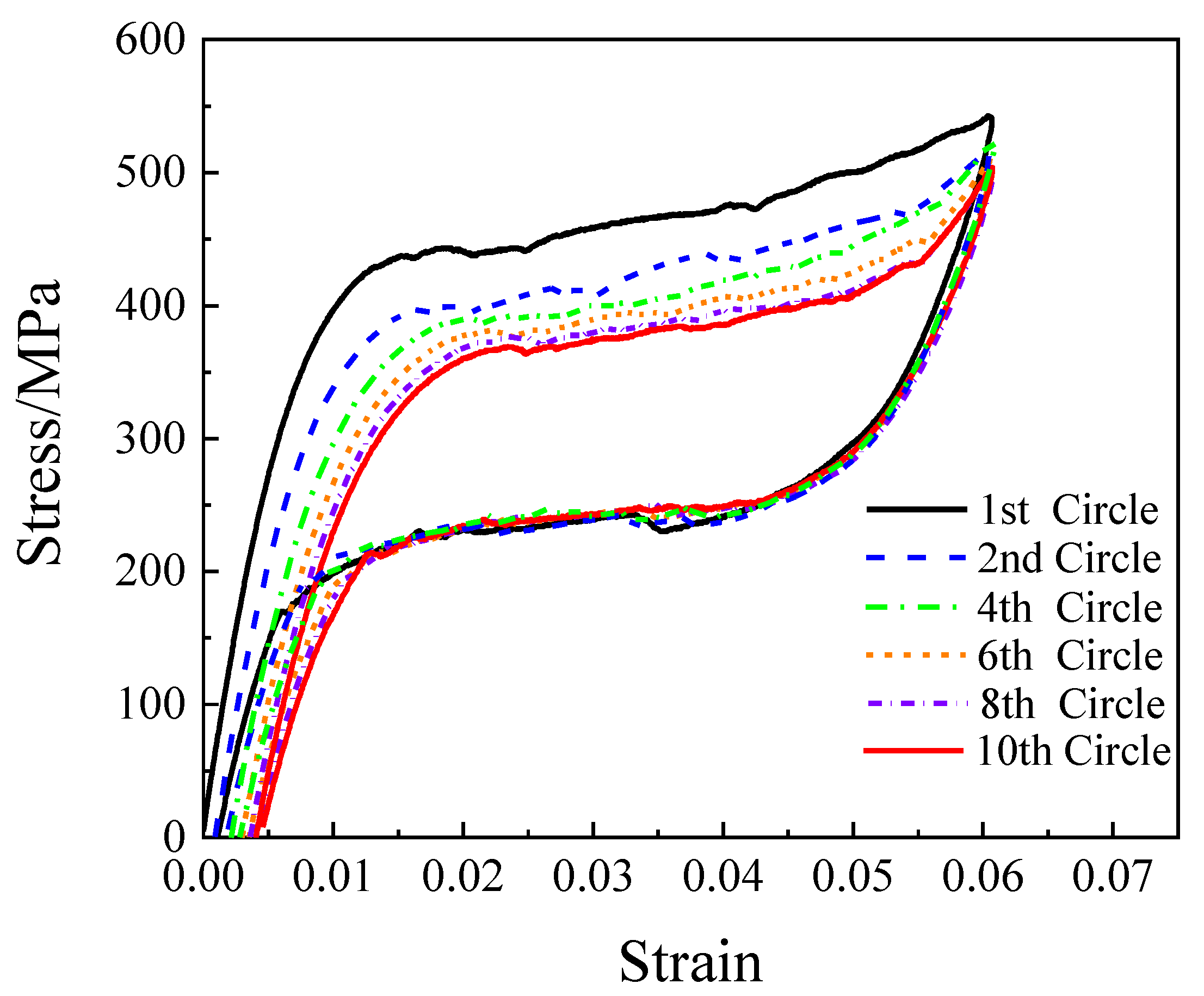

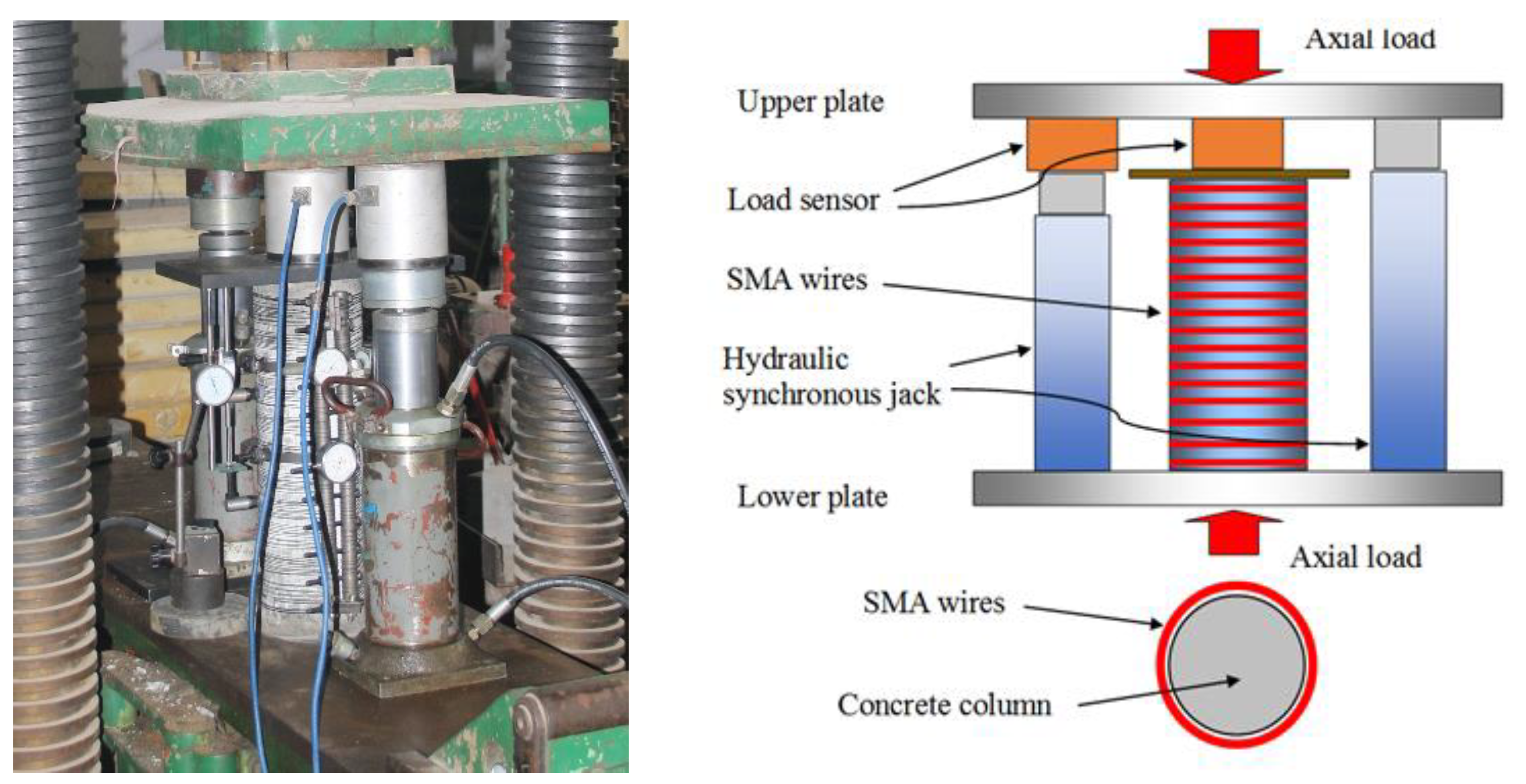
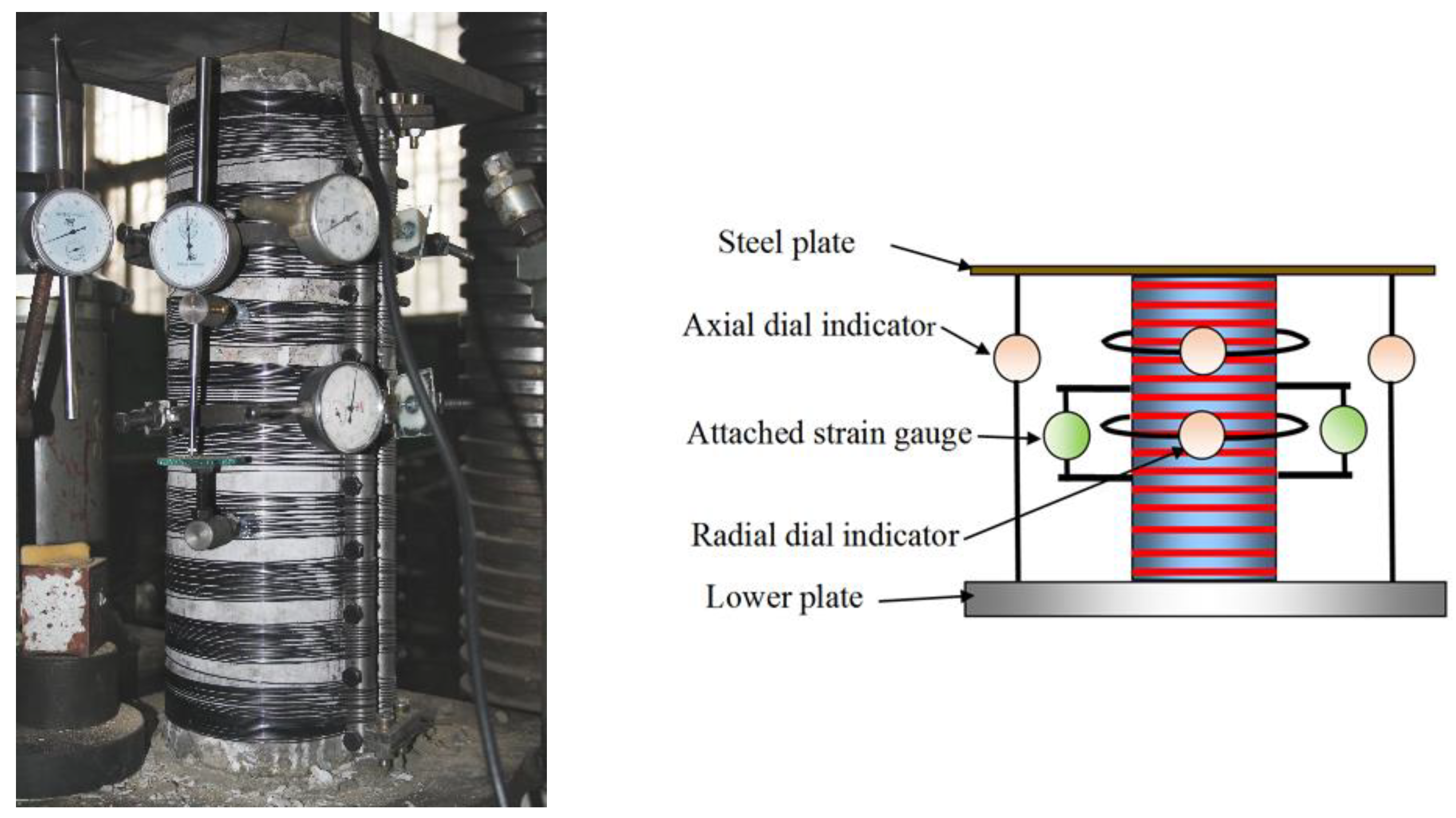


| Diameter (mm) | Nominal Cross-sectional Area (mm2) | Young’s Modulus (GPa) | Yield Strength (MPa) | 6% Strain Strength (MPa) |
|---|---|---|---|---|
| 1.20 | 1.13 | 247.94 | 442.32 | 542.10 |
| Nominal Thickness (mm) | Young’s Modulus (GPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|
| 0.11 | 290 | 3200 | 0.1062 |
| Specimen | Reinforcement Spacing s (mm) | Configuring Feature Values λ | Prestrain Level α |
|---|---|---|---|
| C-C | - | - | - |
| C-SS8-P2 | 8.0 | 0.090 | 2% |
| C-SS4-P0 C-SS4-P1 C-SS4-P2 C-SS4-P4 | 4.0 | 0.180 | 0% 1% 2% 4% |
| C-SS2.5-P2 | 2.5 | 0.288 | 2% |
| C-SMA/FRP-P2 | SMA@6.25+3FRP@125 | 0.288 | 2% |
| Specimen | Ncu/kN | γcu | Axial cu | Lateral cu | Nf/kN | γf | Axial f | Lateral f |
|---|---|---|---|---|---|---|---|---|
| C-C | 425 | 1.000 | 0.0014 | 0.0028 | 200 | 1.000 | 0.0036 | 0.0257 |
| C-SS48P2 | 770 | 1.812 | 0.0031 | 0.0117 | 360 | 1.800 | 0.0881 | 0.2114 |
| C-SS4-P0 | 674 | 1.586 | 0.0033 | 0.0115 | 318 | 1.590 | 0.0821 | 0.3669 |
| C-SS4-P1 | 800 | 1.882 | 0.0039 | 0.0274 | 432 | 2.160 | 0.0886 | 0.2563 |
| C-SS4-P2 | 880 | 2.071 | 0.0035 | 0.0109 | 373 | 1.865 | 0.0847 | 0.2549 |
| C-SS4-P4 | 940 | 2.212 | 0.0034 | 0.0076 | 459 | 2.295 | 0.1328 | 0.2138 |
| C-SS2.5-P2 | 1002 | 2.358 | 0.0051 | 0.0165 | 648 | 3.240 | 0.1240 | 0.2045 |
| C-SMA/FRP-P2 | 1060 | 2.494 | 0.0030 | 0.0081 | 338 | 1.690 | 0.0586 | 0.2087 |
| Specimen Number | λ | α | σcu/MPa | (fcc − fc) | (fcc − fc)1 | (fcc − fc)1/(fcc − fc) |
|---|---|---|---|---|---|---|
| C-C | - | - | 24.06 | - | - | - |
| C-SS8-P2 | 0.090 | 2% | 43.59 | 19.53 | 19. 62 | 1.004 |
| C-SS4-P0 | 0.180 | 0% | 38.15 | 14.09 | 13.99 | 0.993 |
| C-SS4-P1 | 0.180 | 1% | 44.16 | 20.10 | 20.78 | 1.034 |
| C-SS4-P2 | 0.180 | 2% | 49.82 | 25.76 | 25.61 | 0.994 |
| C-SS4-P4 | 0.180 | 4% | 53.22 | 29.16 | 29.40 | 1.008 |
| C-SS2.5-P2 | 0.288 | 2% | 56.74 | 32.68 | 32.80 | 1.004 |
| Literature Tests | Specimen Number | λ | α | fcc1/MPa | fcc/MPa | fcc1/fcc |
|---|---|---|---|---|---|---|
| Literature [21] | Ma1 | 0.097 | 2.9% | 28.06 | 27.79 | 1.010 |
| Ma2 | 0.097 | 2.9% | 28.06 | 27.41 | 1.024 | |
| Ma3 | 0.048 | 2.9% | 27.72 | 26.02 | 1.065 | |
| Ma4 | 0.048 | 2.9% | 27.72 | 27.12 | 1.022 | |
| Au1 | 0.097 | 0% | 26.66 | 25.48 | 1.046 | |
| Au2 | 0.048 | 0% | 26.55 | 26.51 | 1.001 | |
| Literature [24] | Ma2-I | 0.097 | 2.9% | 28.06 | 27.31 | 1.027 |
| Ma2-II | 0.097 | 2.9% | 28.06 | 27.41 | 1.024 | |
| Ma4-I | 0.048 | 2.9% | 27.72 | 26.61 | 1.042 | |
| Ma4-II | 0.048 | 2.9% | 27.72 | 26.12 | 1.061 | |
| Au4 | 0.097 | 0% | 26.66 | 27.02 | 0.987 | |
| Au2 | 0.048 | 0% | 26.55 | 26.19 | 1.014 | |
| Literature [38] | NiTiNb-1 | 0.211 | 4.2% | 45.31 | 45.38 | 0.998 |
| NiTiNb-2 | 0.211 | 4.2% | 45.31 | 43.97 | 1.030 | |
| NiTi-1 | 0.155 | 6.2% | 38.19 | 38.48 | 0.992 | |
| NiTi-2 | 0.155 | 6.2% | 38.19 | 40.63 | 0.940 | |
| Literature [44] | NiTiNb-1 | 0.081 | 4.8% | 43.10 | 43.50 | 0.991 |
| NiTiNb-2 | 0.040 | 4.8% | 41.43 | 38.00 | 1.090 | |
| This Paper | C-SS8-P2 | 0.090 | 2.0% | 43.54 | 43.60 | 0.999 |
| C-SS4-P0 | 0.180 | 0.0% | 37.94 | 38.15 | 0.995 | |
| C-SS4-P1 | 0.180 | 1.0% | 44.71 | 44.16 | 1.012 | |
| C-SS4-P2 | 0.180 | 2.0% | 49.52 | 49.82 | 0.994 | |
| C-SS4-P4 | 0.180 | 4.0% | 53.29 | 53.22 | 1.001 | |
| C-SS2.5-P2 | 0.288 | 2.0% | 56.69 | 56.74 | 0.999 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, C.; Qian, H.; Song, G. Uniaxial Compressive Behavior of Concrete Columns Confined with Superelastic Shape Memory Alloy Wires. Materials 2020, 13, 1227. https://doi.org/10.3390/ma13051227
Hong C, Qian H, Song G. Uniaxial Compressive Behavior of Concrete Columns Confined with Superelastic Shape Memory Alloy Wires. Materials. 2020; 13(5):1227. https://doi.org/10.3390/ma13051227
Chicago/Turabian StyleHong, Chenkai, Hui Qian, and Gangbing Song. 2020. "Uniaxial Compressive Behavior of Concrete Columns Confined with Superelastic Shape Memory Alloy Wires" Materials 13, no. 5: 1227. https://doi.org/10.3390/ma13051227
APA StyleHong, C., Qian, H., & Song, G. (2020). Uniaxial Compressive Behavior of Concrete Columns Confined with Superelastic Shape Memory Alloy Wires. Materials, 13(5), 1227. https://doi.org/10.3390/ma13051227







