Determination, Modeling and Evaluation of Kinetics of 223Ra Sorption on Hydroxyapatite and Titanium Dioxide Nanoparticles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of 223Ra Stock Solution
2.2. Britton–Robinson Buffer Solution
2.3. Sorbent Material Preparation
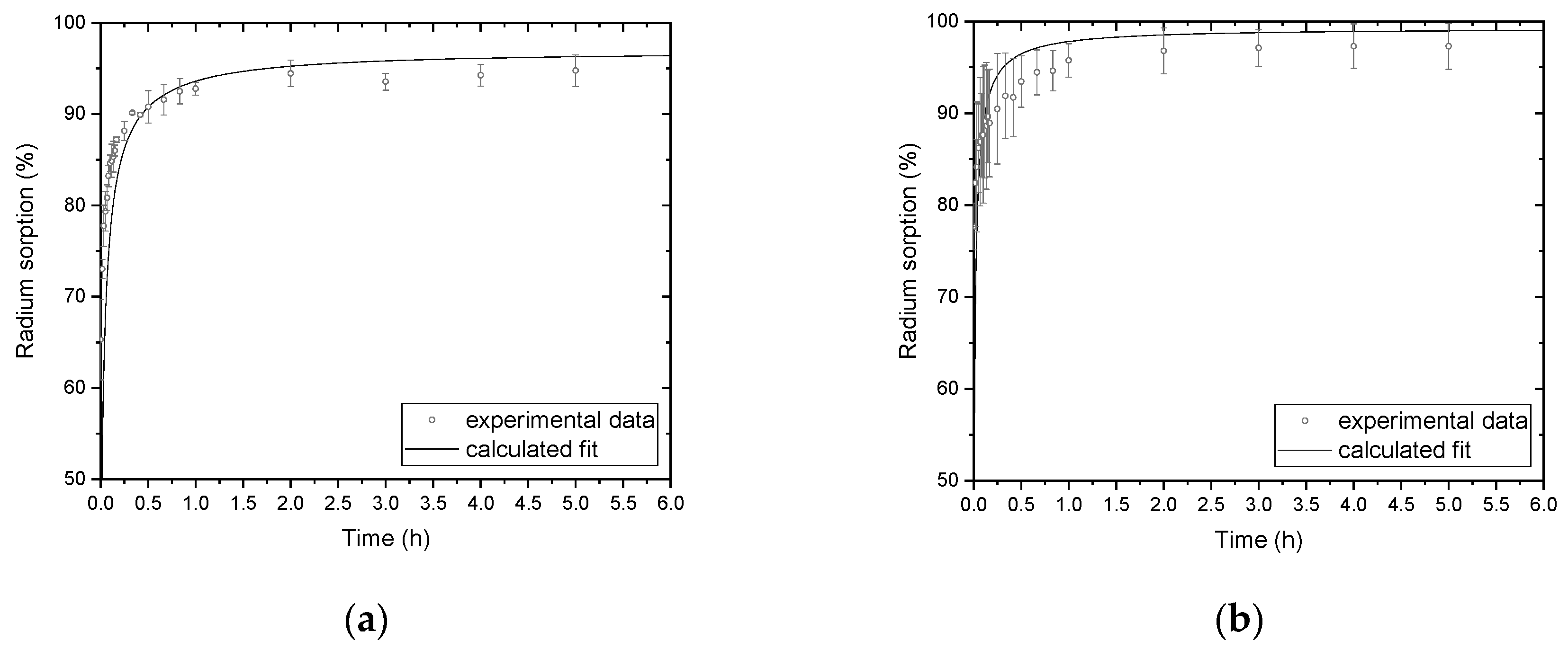
2.4. Determination of Kinetic Dependences
2.5. Kinetic Models for Two-Phase Systems
2.6. Procedure of the Experimental Data Evaluation
3. Results and Discussion
3.1. Parameters of nHAp and nTiO2
3.2. Evaluation of Kinetic Dependence
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- RES3T/Rossendorf Expert System for Surface and Sorption Thermodynamics. Available online: https://www.hzdr.de/db/res3t.login (accessed on 16 January 2019).
- Yasukawa, A.; Yokoyama, T.; Kandori, K.; Ishikawa, T. Reaction of calcium hydroxyapatite with Cd2+ and Pb2+ ions. Colloids Surf. A Physicochem. Eng. Asp. 2007, 299, 203–208. [Google Scholar] [CrossRef]
- Sandrine, B.; Ange, N.; Didier, B.A.; Eric, C.; Patrick, S. Removal of aqueous lead ions by hydroxyapatites: Equilibria and kinetic processes. J. Hazard. Mater. 2007, 139, 443–446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maruszewska, A.; Podsiadly, R. Dyes based on the azo-1H-pyrrole moiety—Synthesis, spectroscopic and electrochemical properties, and adsorption on TiO2. Colora. Technol. 2016, 132, 92–97. [Google Scholar] [CrossRef]
- Li, W.; Pan, G.; Zhang, M.; Zhao, D.; Yang, Y.; Chen, H.; He, G. EXAFS studies on adsorption irreversibility of Zn(II) on TiO2: Temperature dependence. J. Colloid Interface Sci. 2008, 319, 385–391. [Google Scholar] [CrossRef] [PubMed]
- Kukleva, E.; Suchankova, P.; Stamberg, K.; Vlk, M.; Slouf, M.; Kozempel, J. Surface protolytic property characterization of hydroxyapatite and titanium dioxide nanoparticles. RSC Adv. 2019, 9, 21989–21995. [Google Scholar] [CrossRef] [Green Version]
- Dzombak, D.A.; Morel, F.M.N. Surface Complexation Modeling: Hydrous Ferric Oxide; Wiley-Interscience: New York, NY, USA, 1990. [Google Scholar]
- Luetzenkirchen, J. Surface Complexation Modelling; Academic Press: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Filipská, H.; Štamberg, K. Mathematical Modeling of a Cs(I)-Sr(II)-Bentonite—Magnetite Sorption System, Simulating the Processes Taking Place in a Deep Geological Repository. Acta Polytech. J. Adv. Eng. 2005, 45, 11–18. [Google Scholar]
- Suchánková, P.; Kukleva, E.; Štamberg, K.; Nykl, P.; Vlk, M.; Kozempel, J. Study of 223Ra uptake mechanism on hydroxyapatite and titanium dioxide nanoparticles as a function of pH. RSC Adv. 2020, 10, 3659–3666. [Google Scholar] [CrossRef] [Green Version]
- Kroupová, H.; Štamberg, K. Experimental study and mathematical modelling of Cs(I) and Sr(II) sorption on bentonite as barrier material in deep geological repository. Acta Geodynam. Mater. 2005, 2, 79–86. [Google Scholar]
- Liu, M.; Jing, H.; Bai, R.; Wang, Y. Adsorption of icariin on nano-hydroxyapatite: Isotherm, kinetics, pH, ionic strength and construction. Nanomed. Nanotechnol. Biol. Med. 2016, 12, 478–479. [Google Scholar] [CrossRef]
- Valizadeh, S.; Rasoulifard, M.H.; Dorraji, M.S.S. Adsorption and photocatalytic degradation of organic dyes onto crystalline and amorphous hydroxyapatite: Optimization, kinetic and isotherm studies. Korean J. Chem. Eng. 2016, 33, 481–489. [Google Scholar] [CrossRef]
- Hammari, L.E.; Laghzizil, A.; Saoiabi, A.; Barboux, P.; Meyer, M.; Brandès, S.; Guilard, R. Some Factors Affecting the Removal of Lead(II) Ions from Aqueous Solution by Porous Calcium Hydroxyapatite: Relationships between Surface and Adsorption Properties. Adsorpt. Sci. Technol. 2006, 24, 507–516. [Google Scholar] [CrossRef]
- Gómez del Río, J.; Sanchez, P.; Morando, P.J.; Cicerone, D.S. Retention of Cd, Zn and Co on hydroxyapatite filters. Chemosphere 2006, 64, 1015–1020. [Google Scholar] [CrossRef] [PubMed]
- Summary of Product Characteristic: GalliaPharm—Radionuclide Generator. Available online: http://mri.medagencies.org/download/DK_H_2294_001_FinalPI.pdf (accessed on 17 January 2019).
- Alvarez-Corena, J.R.; Bergendahl, J.A.; Hart, F.L. Advanced oxidation of five contaminants in water by UV/TiO2: Reaction kinetics and byproducts identification. J. Environ. Manag. 2016, 181, 544–551. [Google Scholar] [CrossRef]
- Roncaroli, F.; Blesa, M.A. Kinetics of adsorption of oxalic acid on different titanium dioxide samples. J. Colloid Interface Sci. 2011, 356, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Pena, M.E.; Korfiatis, G.P.; Patel, M.; Lippincott, L.; Meng, X. Adsorption of As(V) and As(III) by nanocrystalline titanium dioxide. Water Res. 2005, 39, 2327–2337. [Google Scholar] [CrossRef] [PubMed]
- Jegadeesan, G.; Al-Abed, S.R.; Sundaram, V.; Choi, H.; Scheckel, K.G.; Dionysiou, D.D. Arsenic sorption on TiO2 nanoparticles: Size and crystallinity effects. Water Res. 2010, 44, 965–973. [Google Scholar] [CrossRef]
- Nano, G.V.; Strathmann, T.J. Ferrous iron sorption by hydrous metal oxides. J. Colloid Interface Sci. 2006, 297, 443–454. [Google Scholar] [CrossRef]
- Vasileva, E.; Proinova, I.; Hadjiivanov, K. Solid-phase extraction of heavy metal ions on a high surface area titanium dioxide (anatase). Analyst 1996, 121, 607–612. [Google Scholar] [CrossRef]
- Kozempel, J.; Vlk, M. Nanoconstructs in Targeted Alpha-Therapy. Recent Pat. Nanomed. 2014, 4, 71–76. [Google Scholar] [CrossRef]
- Parker, C.; Nilsson, S.; Heinrich, D.; Helle, S.I.; O’sullivan, J.M.; Fosså, S.D.; Chodacki, A.; Wiechno, P.; Logue, J.; Widmark, A.; et al. Alpha Emitter Radium-223 and Survival in Metastatic Prostate Cancer. N. Eng. J. Med. 2013, 369, 213–223. [Google Scholar] [CrossRef] [Green Version]
- EMA: Xofigo. 2013. Available online: https://www.ema.europa.eu/en/medicines/human/EPAR/xofigo (accessed on 20 November 2019).
- EMA: PRAC Recommendation. 2018. Available online: https://www.ema.europa.eu/en/documents/referral/xofigo-article-20-procedure-prac-recommends-restricting-use-prostate-cancer-medicine-xofigo_en.pdf (accessed on 20 December 2019).
- Guseva, L.I.; Tikhomirova, G.S.; Dogadkin, N.N. Anion-Exchange Separation of Radium from Alkaline-Earth Metals and Actinides in Aqueous-Methanol Solutions of HNO3. 227Ac-223Ra Generator. Radiochemistry 2004, 46, 58–62. [Google Scholar] [CrossRef]
- Beneš, P.; Štamberg, K.; Štegman, R. Study of the Kinetics of the Interaction of Cs-137 and Sr-85 with Soils Using a Batch Method: Methodological Problems. Radiochim. Acta 1994, 66, 315–321. [Google Scholar]
- Herbelin, A.L.; Westall, J.C. FITEQL-A Computer Programm for Determination of Chemical Equilibrium Constants from Experimental Data, 1996, Version 3.2. Report 96-01; Department of Chemistry, Oregon State University: Corvallis, OR, USA, 1996. [Google Scholar]
- Mokhodoeva, O.; Vlk, M.; Málková, E.; Kukleva, E.; Mičolová, P.; Štamberg, K.; Šlouf, M.; Dzhenloda, R.; Kozempel, J. Study of 223Ra uptake mechanism by Fe3O4 nanoparticles: Towards new prospective theranostic SPIONs. J. Nanopart. Res. 2016, 18, 301. [Google Scholar] [CrossRef]
| Control Process | Model Abbreviation | Differential Equation | Equation # |
|---|---|---|---|
| Mass transfer | DM | dq/dt = KDM × (q* − q) | (3) |
| Film diffusion | FD | dq/dt = KFD × (c − c*) | (4) |
| KFD = 3 × D/(δ × R × hs) | (5) | ||
| Diffusion | ID | dq/dt = KID × (c − c*)/{[1 − (q/q*)]−1/3 − 1} | (6) |
| in an inert layer | KID = 3 × D/(R2 × hs) | (7) | |
| Diffusion | RLD | dq/dt = KRLD × (q* − q)/{[1 − (q/q*)]−1/3 − 1} | (8) |
| in a reacted layer | KRLD = 3 × D/(R2 × hs) | (9) | |
| Chemical reaction | CR | dq/dt = KCR × rCR × [1 − (q/q*)]2/3 | (10) |
| in the reaction zone, | KCR = 3/(R × hs) | (11) | |
| e.g., 1st order reversible reaction | RCR = KCR × (c − c*) | (12) | |
| Gel diffusion | GD | dq/dt = KGD × [(q* − q0)2 − (q − q0)2]/(q − q0) | (13) |
| KGD = D × π2/(2 × R2) | (14) | ||
| Following balance equations hold: | |||
| dq/dt = −r × dc/dt | (15) | ||
| if c is the integration variable: q = r × (c0 − c) + q0 | (16) | ||
| if q is the integration variable: c = c0 − (q − q0)/r | (17) | ||
| Equilibrium equations used: q* = Kd × c, and c* = q/Kd | (18) | ||
| Parameter | Unit | nHAp | nTiO2 |
|---|---|---|---|
| Specific surface area | (m2·kg−1) | 117 ± 8 | 330 ± 10 |
| Crystallite size | (nm) | 5.18 | 2.64 |
| Equivalent diameter | (nm) | 21.7 ± 6.9 | 5.3 ± 1.7 |
| Surface edge sites | (mol·kg−1) | 5.10 ± 1.20 | 0.20 ± 0.01 |
| Surface layer sites | (mol·kg−1) | 0.15 ± 0.01 | 0.67 ± 0.01 |
| pH applicability | pH | 5–10 | 2–10 |
| Specific mass | (g·cm−3) | 3.14–3.21 | 3.90–4.30 |
| Experiment No. | nHAp | nTiO2 | ||||
|---|---|---|---|---|---|---|
| c0 | Kd | r | c0 | Kd | r | |
| (mol·Laq−1) | (Laq∙kg−1) | (Laq∙kg−1) | (mol·Laq−1) | (Laq∙kg−1) | (Laq∙kg−1) | |
| 1 | 9.92 × 10−12 | 3.03 × 104 | 1000 | 1.01 × 10−11 | 5.90 × 104 | 1000 |
| 2 | 9.46 × 10−12 | 1.55 × 104 | 1000 | 1.05 × 10−11 | 1.25 × 105 | 1000 |
| 3 | 1.12 × 10−11 | 1.54 × 104 | 1000 | 9.86 × 10−12 | 1.52 × 105 | 1000 |
| Mean value ± σes * | 1.02 × 10−11 ± 0.07 × 10−11 | 2.04 × 104 ± 0.70 × 104 | 1000 | 1.01 × 10−11 ± 0.03 × 10−11 | 1.12 × 105 ± 0.39 × 105 | 1000 |
| Sorbent | Experiment No. | WSOS/DF | |||||
|---|---|---|---|---|---|---|---|
| DM | FD | ID | RLD | CR | GD | ||
| nHAp | 1 | 59.70 | 1860 | 5.35 | 5.47 | 1320 | 40.30 |
| 2 | 8.28 | 186 | 7.45 | 7.25 | 92.60 | 10.10 | |
| 3 | 8.06 | 461 | 2.60 | 2.71 | 250 | 27.60 | |
| Mean value ± σes * | 25.34 ± 24.29 | 835.67 ± 732.96 | 5.13 ± 1.99 | 5.14 ± 1.87 | 554.20 ± 545.30 | 26.00 ± 12.38 | |
| nTiO2 | 1 | 48.70 | 54.70 | 6.72 | 7.63 | 52.80 | 9.99 |
| 2 | 5.76 | 757 | 1.23 | 3.18 | 36.30 | 9.42 | |
| 3 | 33.40 | 258 | 8.09 | 16.10 | 239 | 5.43 | |
| Mean value ± σes * | 29.29 ± 17.77 | 356.57 ± 295.06 | 5.35 ± 2.97 | 8.96 ± 5.36 | 109.37 ± 91.91 | 8.27 ± 2.04 | |
| Sorbent | Experiment No.: | KRLD ± σ (cm3·g−1·min−1) | Mean * KRLD ± σes (cm3·g−1·min−1) | Mean * D ± σes (cm2·min−1) | Mean * t1/2 ± σes (min) |
|---|---|---|---|---|---|
| nHAp | 1 | 1.24 × 10−1 | 5.03 × 10−1 ± 2.72 × 10−1 | 2.50 × 10−12 ± 1.80 × 10−12 | 0.75 ± 0.18 |
| 2 | 7.53 × 10−1 | ||||
| 3 | 6.31 × 10−1 | ||||
| nTiO2 | 1 | 2.82 × 10−2 | 4.01 × 10−2 ± 2.44 × 10−2 | 1.60 × 10−14 ± 0.96 × 10−14 | 0.51 ± 0.32 |
| 2 | 1.80 × 10−2 | ||||
| 3 | 0.74 × 10−2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suchánková, P.; Kukleva, E.; Štamberg, K.; Nykl, P.; Sakmár, M.; Vlk, M.; Kozempel, J. Determination, Modeling and Evaluation of Kinetics of 223Ra Sorption on Hydroxyapatite and Titanium Dioxide Nanoparticles. Materials 2020, 13, 1915. https://doi.org/10.3390/ma13081915
Suchánková P, Kukleva E, Štamberg K, Nykl P, Sakmár M, Vlk M, Kozempel J. Determination, Modeling and Evaluation of Kinetics of 223Ra Sorption on Hydroxyapatite and Titanium Dioxide Nanoparticles. Materials. 2020; 13(8):1915. https://doi.org/10.3390/ma13081915
Chicago/Turabian StyleSuchánková, Petra, Ekaterina Kukleva, Karel Štamberg, Pavel Nykl, Michal Sakmár, Martin Vlk, and Ján Kozempel. 2020. "Determination, Modeling and Evaluation of Kinetics of 223Ra Sorption on Hydroxyapatite and Titanium Dioxide Nanoparticles" Materials 13, no. 8: 1915. https://doi.org/10.3390/ma13081915
APA StyleSuchánková, P., Kukleva, E., Štamberg, K., Nykl, P., Sakmár, M., Vlk, M., & Kozempel, J. (2020). Determination, Modeling and Evaluation of Kinetics of 223Ra Sorption on Hydroxyapatite and Titanium Dioxide Nanoparticles. Materials, 13(8), 1915. https://doi.org/10.3390/ma13081915







