Nickel Porous Compacts Obtained by Medium-Frequency Electrical Resistance Sintering
Abstract
:1. Introduction
2. Experimental Procedure and Materials
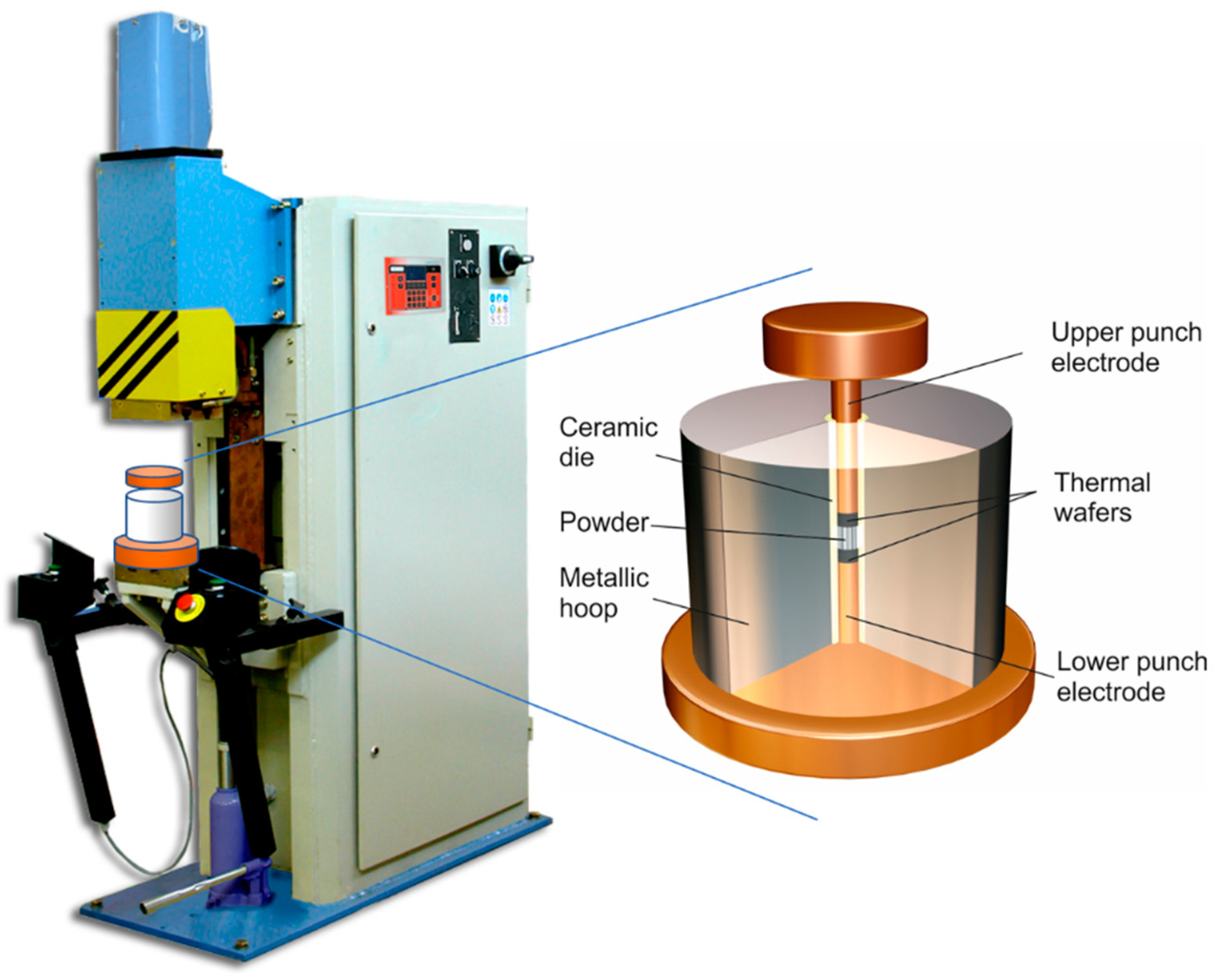
2.1. MF-ERS Equipment
2.2. Experimental Procedure
2.2.1. Powder Characterization
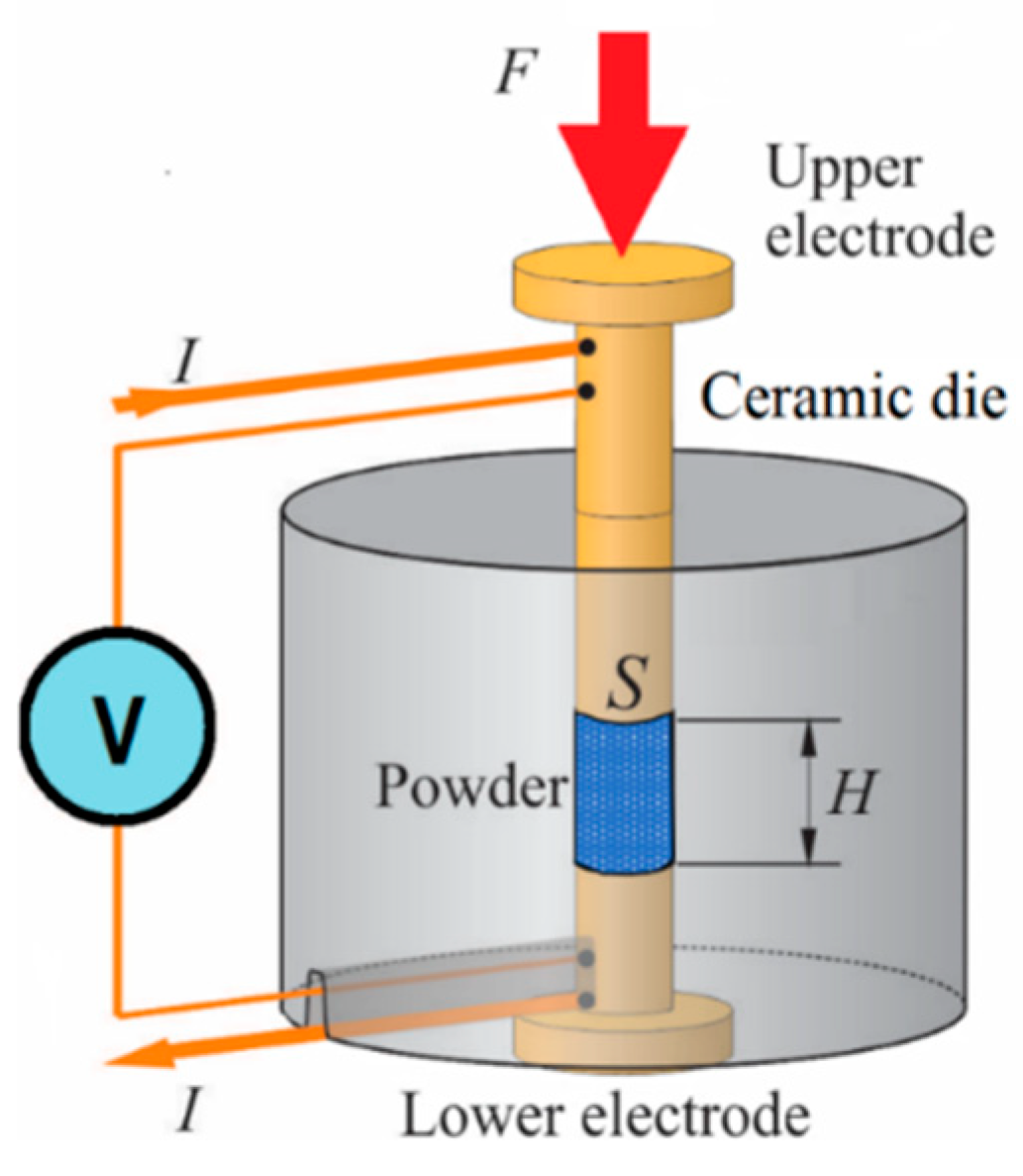
2.2.2. MF-ERS Process
2.2.3. Compacts Characterisation
2.3. Material
3. Results and Discussion
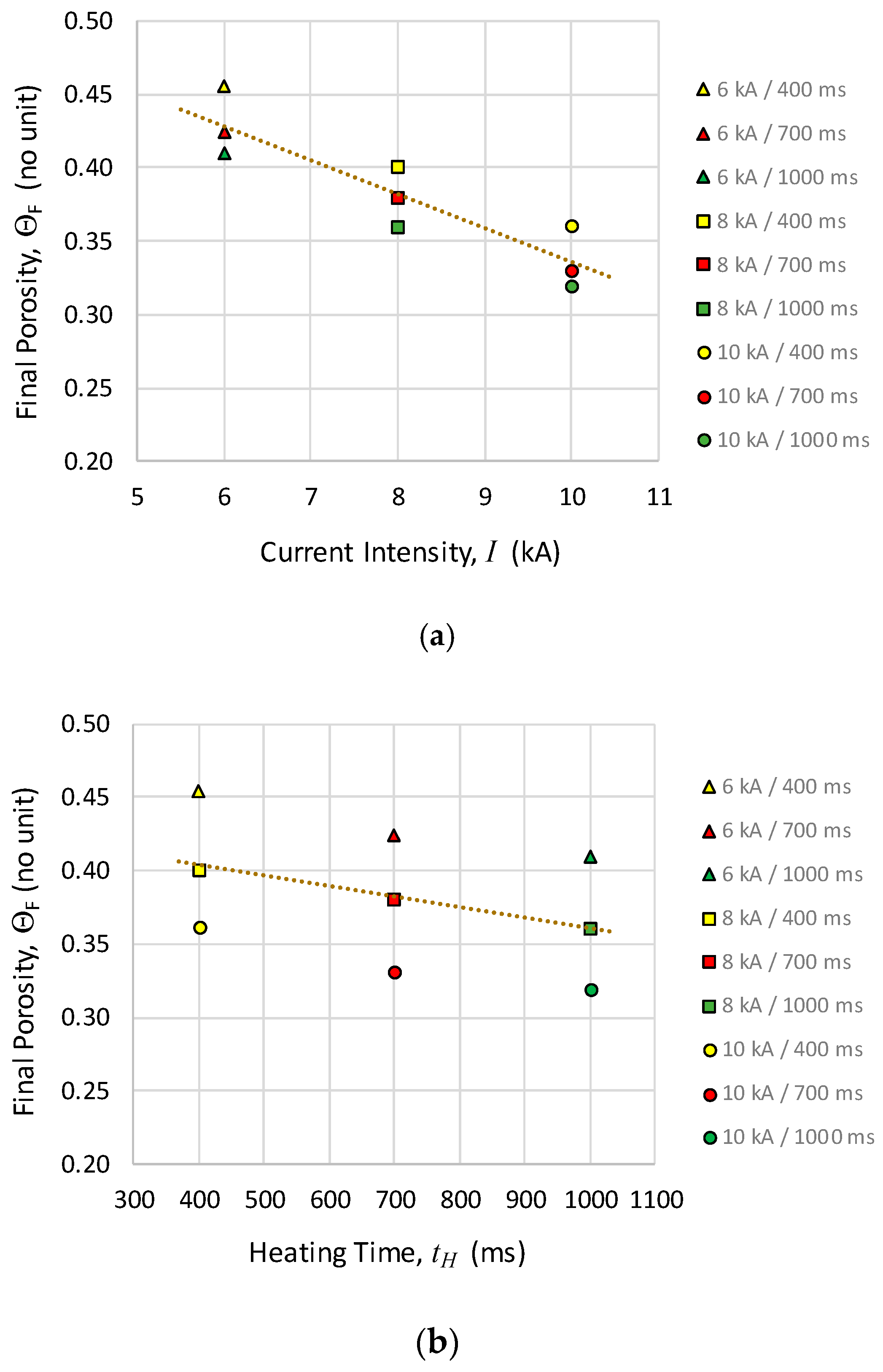
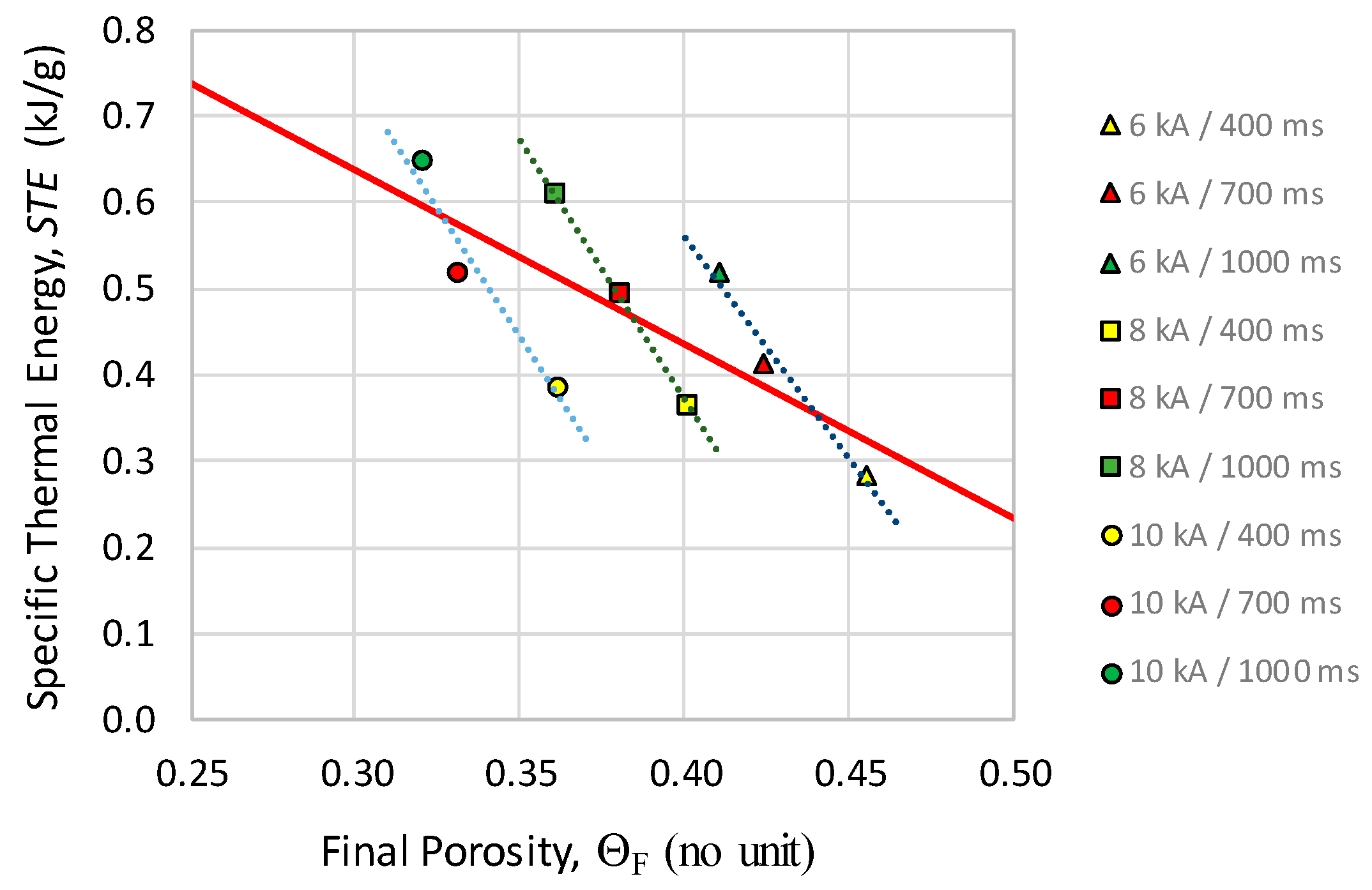
3.1. Final Porosity and Specific Thermal Energy
3.2. Porosity Distribution
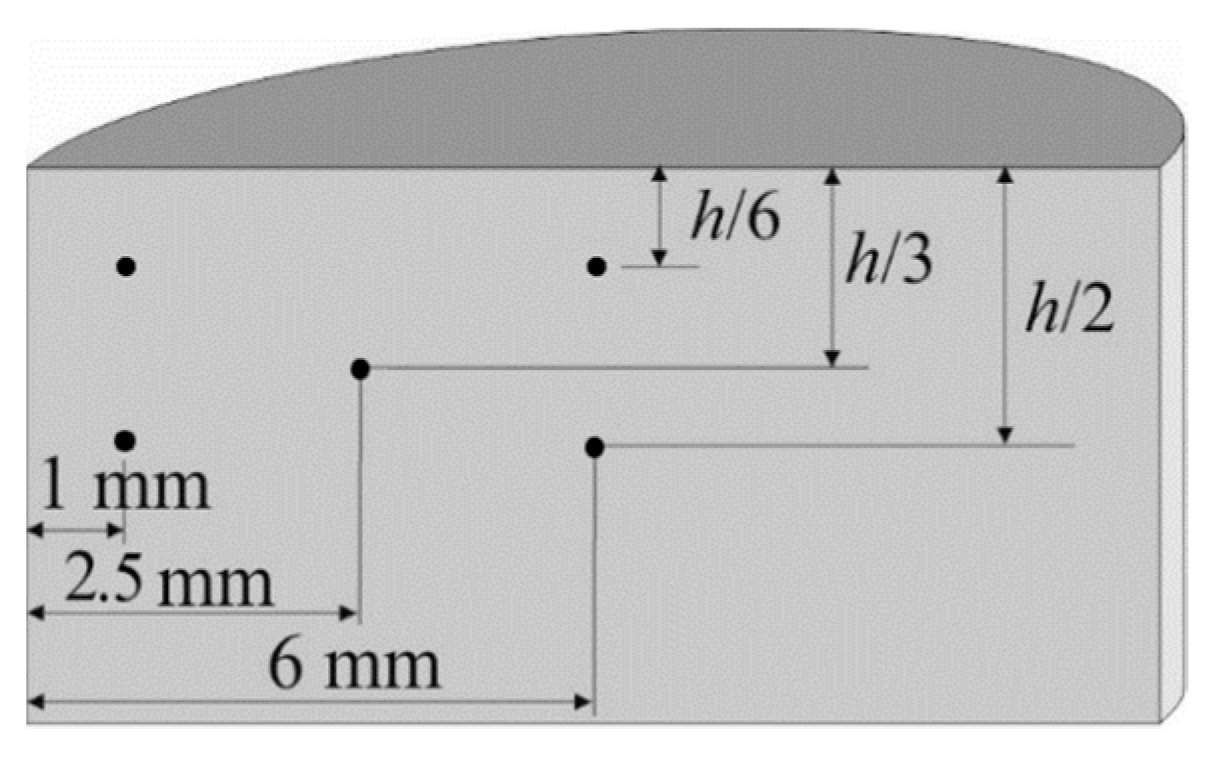
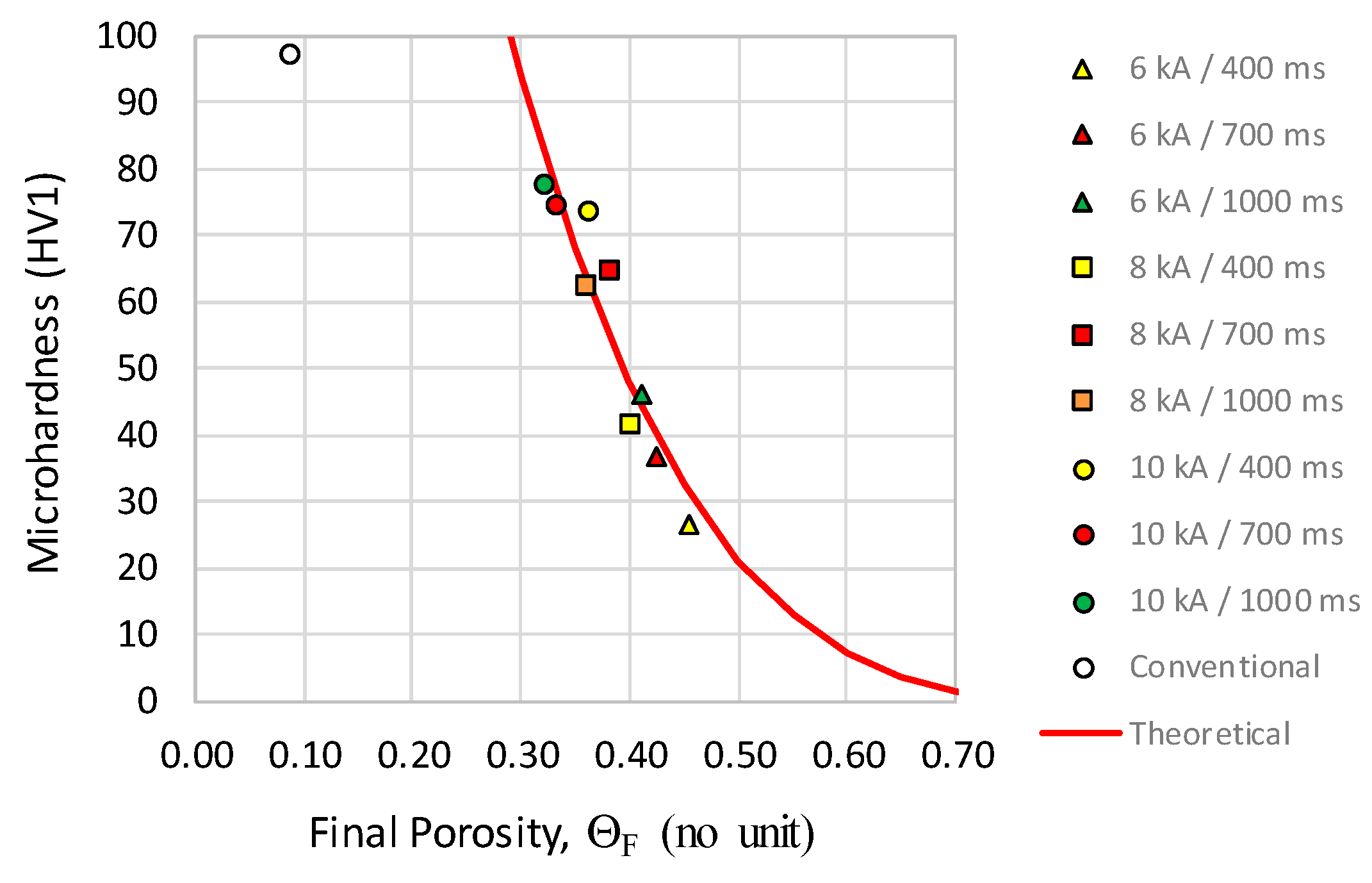
3.3. Microhardness Distribution
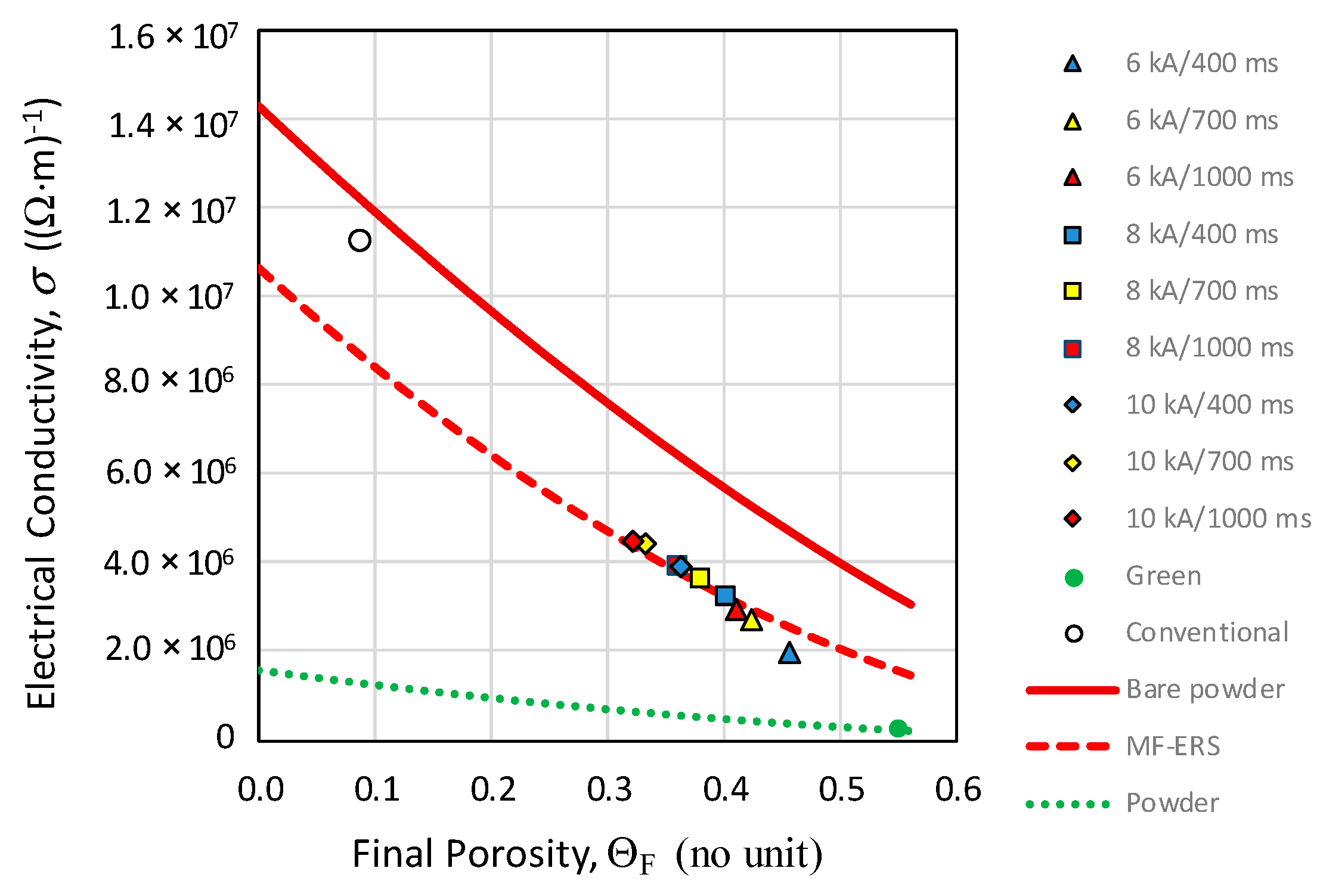
3.4. Electrical Resistivity
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lux, J. Improved Manufacture of Electric Incandescence Lamp Filaments from Tungsten or Molybdenum or an Alloy thereof. GB Patent 27,002, 1906. [Google Scholar]
- Grasso, S.; Sakka, Y.; Maizza, G. Electric current activated/assisted sintering (ECAS): A review of patents 1906–2008. Sci. Technol. Adv. Mater. 2009, 10, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Grasso, S.; Biesuz, M.; Zoli, L.; Taveri, G.; Duff, A.I.; Ke, D.; Jiang, A.; Reece, M.J. A review of cold sintering processes. J. Adv. Appl. Ceram. Struct. Funct. Bio. 2020, 119, 115–142. [Google Scholar] [CrossRef] [Green Version]
- Orrù, R.; Licheri, R.; Locci, A.M.; Cincotti, A.; Cao, G. Consolidation/synthesis of materials by electric current activated/assisted sintering. Mat. Sci. Eng. R Rep. 2009, 63, 127–287. [Google Scholar] [CrossRef]
- Olevsky, E.A.; Dudina, D.V. Field-Assisted Sintering Science and Applications, 1st ed.; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Taylor, G.F. Apparatus for Making Hard Metal Compositions. U.S. Patent 1,896,854, 7 February 1933. [Google Scholar]
- Lenel, F.V. Resistance Sintering Under Pressure. JOM. 1955, 7, 158–167. [Google Scholar] [CrossRef]
- Montes, J.M.; Cuevas, F.G.; Ternero, F.; Astacio, R.; Caballero, E.S.; Cintas, J. Medium-Frequency Electrical Resistance Sintering of Oxidized, C.P. Iron Powder. Metals 2018, 8, 426. [Google Scholar] [CrossRef] [Green Version]
- Fais, A. A Faster FAST: Electro-Sinter-Forging. Met. Powder Rep. 2018, 73, 80–86. [Google Scholar] [CrossRef]
- Cannella, E.; Nielsen, C.V.; Bay, N. Process Investigation and Mechanical Properties of Electro Sinter Forged (ESF) Titanium Discs. Int. J. Adv. Manuf. Technol. 2019, 104, 1985–1998. [Google Scholar] [CrossRef]
- Brisson, E.; Carre, P.; Desplats, H.; Rogeon, P.; Keryvin, V.; Bonhomme, A. Effective Thermal and Electrical Conductivities of AgSnO2 During Sintering. Part I: Experimental Characterization and Mechanisms. Met. Mater. Trans. A 2016, 47, 6304–6318. [Google Scholar] [CrossRef]
- Cuevas, F.G.; Andreouli, D.; Gallardo, J.M.; Oikonomou, V.; Cintas, J.; Torres, Y.; Montes, J.M. Ceramic dies selection for electrical resistance sintering of metallic materials. Ceram. Int. 2019, 45, 14555–14561. [Google Scholar] [CrossRef]
- Montes, J.M.; Cuevas, F.G.; Cintas, J.; Urban, P. A One-Dimensional Model of the Electrical Resistance Sintering Process. Met. Mater. Trans. A 2015, 46, 963–980. [Google Scholar] [CrossRef]
- Montes, J.M.; Cuevas, F.G.; Reina, F.J.V.; Ternero, F.; Astacio, R.; Caballero, E.S.; Cintas, J. Modelling and Simulation of the Electrical Resistance Sintering Process of Iron Powders. Met. Mater. Int. 2019, in press. [Google Scholar] [CrossRef]
- Davis, J.R. ASM Specialty Handbook: Nickel, Cobalt and Their Alloys; ASM International: New York, NY, USA, 2001. [Google Scholar]
- Weissler, G.A. Resistance Sintering with Alumina Dies. Int. J. Powder Met. Powder Technol. 1981, 17, 107–118. [Google Scholar]
- Suzuki, T. Study on spark sintering method with nickel powder. S. J. Japan Soc. Powders Powder Met. 1971, 18, 28–32. [Google Scholar] [CrossRef]
- Montes, J.M.; Cuevas, F.G.; Cintas, J. Porosity effect on the electrical conductivity of sintered powder compacts. Appl. Phys. A 2008, 92, 375–380. [Google Scholar] [CrossRef]
- Montes, J.M.; Cuevas, F.G.; Cintas, J.; Ternero, F.; Caballero, E.S. Electrical Resistivity of Powdered Porous Compacts. In Electrical and Electronic Properties of Materials; IntechOpen: Rijeka, Croatia, 2018. [Google Scholar] [CrossRef] [Green Version]
- McLachlan, D.S. Equation for the Conductivity of Metal-Insulator Mixtures. J. Phys. C: Solid State Phys. 1986, 19, 1339–1345. [Google Scholar] [CrossRef]
- MPIF. Standard 4, Determination of Apparent Density of Free-Flowing Metal Powders Using the Hall Apparatus. In Standard Test Methods for Metal Powders and Powder Metallurgy Products; Metal Powder Industries Federation (MPIF): Princeton, NJ, USA, 2016. [Google Scholar]
- MPIF. Standard 46, Determination of tap density of metal powders. In Standard Test Methods for Metal Powders and Powder Metallurgy Products; Metal Powder Industries Federation (MPIF): Princeton, NJ, USA, 2016. [Google Scholar]
- MPIF. Standard 45, Method for Determination of Compressibility of Metal Powders. In Standard Test Methods for Metal Powders and Powder Metallurgy Products; Metal Powder Industries Federation (MPIF): Princeton, NJ, USA, 2016. [Google Scholar]
- Montes, J.M.; Cuevas, F.G.; Ternero, F.; Astacio, R.; Caballero, E.S.; Cintas, J. A method to determine the electrical resistance of a metallic powder mass under compression. Metals 2017, 7, 479. [Google Scholar] [CrossRef] [Green Version]
- ISO. Test method. In Standard ISO 6507-1:2018, Metallic Materials—Vickers Hardness Test—Part 1; European Committee for Standardization (CEN): Brussels, Belgium, 2018. [Google Scholar]
- Webster, G.J. The Measurement Instrumentation and Sensors Handbook; CRC Press: Boca Raton, FL, USA; Springer: Heidelberg, Germany, 1999. [Google Scholar]
- Brandes, E.A. Smithells Metals Reference Book, 6th ed.; Butterworths: Oxford, UK, 1983. [Google Scholar]
- Garino, T.J. Electrical Behavior of Oxidized Metal Powders During and After Compaction. J. Mater. Res. 2002, 17, 2691–2697. [Google Scholar] [CrossRef]
- Lefebvre, L.P.; Pleizier, G.; Deslandes, Y. Electrical Resistivity of Green Powder Compacts. Powder Metall 2001, 44, 259–266. [Google Scholar] [CrossRef]
- Evans, U.R. The Corrosion and Oxidation of Metals: First Supplementary Volume; Edward Arnold Publishers Ltd: London, UK, 1968. [Google Scholar]
- German, R.M. Sintering Theory and Practice, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- ASM International. Powder Metallurgy. In Metals Handbook; ASM International: Novelty, OH, USA, 2015; Volume 7. [Google Scholar]






| Heating Time (ms) | ||||
|---|---|---|---|---|
| 400 | 700 | 1000 | ||
| Intensity (kA) | 6 | 0.45 | 0.42 | 0.41 |
| 8 | 0.40 | 0.38 | 0.36 | |
| 10 | 0.36 | 0.33 | 0.32 | |
| Heating Time (ms) | ||||
|---|---|---|---|---|
| 400 | 700 | 1000 | ||
| Intensity (kA) | 6 | 0.29 | 0.42 | 0.52 |
| 8 | 0.37 | 0.50 | 0.61 | |
| 10 | 0.39 | 0.52 | 0.65 | |
| Heating Time (ms) | ||||
|---|---|---|---|---|
| 400 | 700 | 1000 | ||
| Intensity (kA) | 6 | 27 ± 9 | 37 ± 7 | 46 ± 9 |
| 8 | 42 ± 14 | 65 ± 5 | 68 ± 9 | |
| 10 | 74 ± 8 | 75 ± 6 | 78 ± 6 | |
| Heating Time (ms) | ||||
|---|---|---|---|---|
| 400 | 700 | 1000 | ||
| Intensity (kA) | 6 | 1.97 × 106 | 2.73 × 106 | 2.94 × 106 |
| 8 | 3.23 × 106 | 3.62 × 106 | 3.88 × 106 | |
| 10 | 3.91 × 106 | 4.44 × 106 | 4.50 × 106 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ternero, F.; Caballero, E.S.; Astacio, R.; Cintas, J.; Montes, J.M. Nickel Porous Compacts Obtained by Medium-Frequency Electrical Resistance Sintering. Materials 2020, 13, 2131. https://doi.org/10.3390/ma13092131
Ternero F, Caballero ES, Astacio R, Cintas J, Montes JM. Nickel Porous Compacts Obtained by Medium-Frequency Electrical Resistance Sintering. Materials. 2020; 13(9):2131. https://doi.org/10.3390/ma13092131
Chicago/Turabian StyleTernero, Fátima, Eduardo S. Caballero, Raquel Astacio, Jesús Cintas, and Juan M. Montes. 2020. "Nickel Porous Compacts Obtained by Medium-Frequency Electrical Resistance Sintering" Materials 13, no. 9: 2131. https://doi.org/10.3390/ma13092131





