Abstract
The removal of the hazardous Hg2+ from aqueous solutions was studied by ion exchange using titanosilicate in sodium form (Na-ETS-4). Isothermal batch experiments at fixed pH were performed to measure equilibrium and kinetic data, considering two very distinct situations to assess the influence of competition effects: (i) the counter ions initially in solution are Na+ and Hg2+ (both are exchangeable); (ii) the initial counter ions in solution are tetrapropylammonium (TPA+) and Hg2+ (only Hg2+ is exchangeable, since TPA+ is larger than the ETS-4 micropores). The results confirmed that ETS-4 is highly selective for Hg2+, with more than 90% of the mercury being exchanged from the fluid phase. The final equilibrium attained under the presence of TPA+ or Na+ in solution was very similar, however, the Hg2+/Na+/ETS-4 system in the presence of Na+ required more 100 h to reach equilibrium than in the presence of TPA+. The Hg2+/Na+/ETS-4 system was modelled and analyzed in terms of equilibrium (mass action law) and mass transfer (Maxwell–Stefan (MS) formalism). Concerning equilibrium, no major deviations from ideality were found in the range of studied concentrations. On the other hand, the MS based model described successfully (average deviation of 5.81%) all kinetic curves of mercury removal.
1. Introduction
Water pollution is one of the main concerns the World is currently facing. The continuous increase of the world population, the need for high quality drinking water, and water scarcity in many regions of our planet make water treatment processes a hot subject among researchers.
Heavy metals are considered traditional water contaminants. As a result of many applications in industrial, construction and agricultural sectors, there is inevitably some loss and dispersion of metals back into the environment [1]. In addition to the so-called anthropogenic sources, metal releases can also be of natural origin, like rocks and soil erosion, emissions from volcanoes, and atmospheric deposition [1]. Mercury is one of the most hazardous metal contaminants, since its presence in water, even at very low concentrations, causes severe harmful effects to biota. This happens because of bioaccumulation and biomagnification [2], which means that the concentration of Hg2+ in the biota is much higher than in water. For these reasons mercury was classified as a priority pollutant by the European Union [3] and is in the Top 3 of the priority list of hazardous substances established by the Agency for Toxic Substances and Disease Registry [4].
Nowadays, with the legal restrictions imposed in the so-called developed countries, mercury contamination cannot be solely linked to localized individual emissions of the metal being more associated to the widespread air pollution instead [5]. Consequently, in remote areas free of anthropogenic pressure the mercury levels found in fish are very high despite its extraordinarily low levels in air and surface water [5]. This fact raises a new question regarding water treatment. Conventional and widely used processes like precipitation, that is very effective for high metals concentrations, may not be efficient to remove the current levels of mercury found in water. In this context, the use of high capacity and selective sorbent materials (e.g., ion exchangers and adsorbents) can be the right solution for the removal of low levels of contamination. Materials like zeolites, clays, carbons, polymers, and biosorbents from agricultural and agro-forest residues, have been extensively studied in the literature [1,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24].
Synthetic microporous materials like titanosilicates and zirconosilicates have been successfully studied as ion exchangers for divalent metals uptake [1,6,7,8,9,10,11,12,13,14,15,16]. These materials have attracted considerable attention during the last decades since they are stable, possess a narrow pore size distribution, consist of a variety of framework structures, exhibit high capacity and frequently a remarkable selectivity for target species. The selectivity of these materials is attributed to the geometric matching of their channels and/or cavities with the size of the counter ions, which promotes interatomic/ionic interaction and coordination [25]. Moreover, it is well-known that these materials have a negatively-charged skeleton balanced by the presence of exchangeable cations held electrostatically within the micropores. These cations (frequently Na+ or K+) may play an important role on the extension and kinetics of the process, since their size and/or coordination forces can enhance or hinder the ion exchange [26].
ETS-4 (Engelhard Titanium Silicates No. 4) presents one of the highest ion exchange capacity among all reported titanosilicate materials (theoretical capacity of 6.39 eq kg−1), which makes it an excellent ion exchanger within a limited temperature range (<200 °C) [27,28]. However, few studies exist in the literature involving this solid: Al-Attar and Dyer [29] studied the sorption of uranium onto titanosilicate materials, among them ETS-4; Popa et al. [30] applied ETS-4 for the purification of waste waters containing radioactive ions (60Co2+, 115mCd2+, and 203Hg2+), and later published a review on titanosilicates materials for radioactive wastewaters purification [31]; Lopes et al. [32,33] and Ferreira et al. [11] used ETS-4 for Hg2+ and Cd2+ removal from water, respectively, and later Cardoso et al. [12] studied the competitive removal of these cations (Cd2+ and Hg2+) from water ; Figueiredo et al. [15] investigated the removal of Cs+ from aqueous solutions carrying out both batch and fixed-bed experiments with ETS-4.
Lopes et al. [34] studied the impact of pH and temperature on the ETS-4 uptake efficiency of Hg2+ from solution and concluded that its removal increases with increasing pH, until a maximum value around pH 4–6, and with decreasing temperature. These conditions are very attractive from the industrial point of view since the pH of domestic, medical, and industrial effluents is generally in this interval and, hence, no significant pH adjustments are necessary [13,35,36,37]. To test the capacity of ETS-4 in these conditions, NaOH is commonly added to adjust the system’s pH. One may anticipate that the addition of Na+ cations to the solution can influence the mercury removal efficiency, since they enter in the porous structure of ETS-4 and compete with Hg2+ ions for the active site. In this essay, in order to analyze this competition rigorously, a tetrapropylammonium hydroxide solution (TPAOH) is chosen as pH adjuster because its cation (tetrapropylammonium cation, TPA+) is larger than the pores of ETS-4 and thus cannot penetrate the solid.
The present work focuses the experimental and modelling study of the equilibrium and kinetics of the Hg2+/Na+/ETS-4 system, using a TPAOH solution as pH adjuster. In this way, the stringent competition between the large concentration of Na+ in solution (when NaOH is used) and the target Hg2+ cations is rigorously analyzed in terms of equilibrium and mass transfer. The mass action law, expressed in terms of activities, is used to model the equilibrium, and the Ioannidis et al. method [38,39] is adopted to optimize noncorrelated parameters. With respect to kinetics, the Maxwell–Stefan (MS) formalism is chosen and compared with semi-empirical pseudo-first and pseudo-second order equations.
2. Materials and Methods
2.1. Chemicals
All reagents used in this work were of analytical grade and used without further purification. Sodium hydroxide (NaOH) 0.1 M, potassium chloride (KCl), nitric acid (25 vol%) and tetrapropylammonium hydroxide solution (TPAOH, mol m−3) were purchased from Merck (New York, NY, USA). The certified standard solution of Hg(NO3)2 (1000 ± 1 kg m−3) was purchased from Spectrosol® BDH. All working solutions, including standards for the calibration curves, were obtained by diluting the corresponding stock solutions in ultra-pure water (Millipore, Integral 10 system, Molsheim, France).
The TPAOH solution was analyzed by cold vapor-atomic fluorescence spectrometry (hydride/vapor generator PS Analytical Model 10.003 (PS Analytical, Kent, UK), coupled to a PS Analytical Model 10.023 Merlin atomic fluorescence spectrometer (PS Analytical, Kent, UK) in order to quantify its original amount of mercury.
2.2. Engelhard Titanium Silicate No. 4 (ETS-4)
ETS-4 is the synthetic analogue of the mineral zorite [38] with chemical composition [Na9Ti5Si12O38(OH)·4H2O]. It is one of the main members of a class of heteropolyhedra transition metal silicates with pore size of m and particle size of m [10]. Briefly, the synthesis [33] started with the preparation of an alkaline solution, by dissolving metasilicate (BDH), NaOH and KCl in H2O. Then, TiCl3 (15 wt % TiCl3 and 10 wt % HCl, Merck) was added to this solution and stirred thoroughly. The gel, with molar composition 5.9 Na2O:0.7 K2O:5.0 SiO2:1.0 TiO2:114 H2O, was then transferred to a Teflon-lined autoclave and treated at 230 °C for 17 h under autogenous pressure without agitation. The product was filtered off, washed at room temperature with distilled water, and dried at 70 °C overnight.
The framework of this microporous material comprises corner-sharing SiO4 tetrahedra, TiO5 pentahedra and TiO6 octahedra, and each titanium ion has an associated (−2) charge, which is neutralized by extra-framework cations, usually Na+ [33]. The possibility of replacement of those cations by others like Hg2+ makes ETS-4 a good ion exchange material.
2.3. Ion Exchange Studies and Analytical Procedures
Prior to use, all glassware necessary for the ion exchange studies was acid washed with HNO3 (25 vol%), during 24 h, to inactivate the glass surface and then rinsed abundantly with ultra-pure water.
The ion exchange experiments were carried out under isothermal batch conditions (295 ± 1 K) in 2 m3 volumetric flasks, closed to avoid losses of mercury. The starting time of each experiment was the instant of ETS-4 addition to the solution. The suspensions were magnetically stirred (1400 rpm) and aliquots were collected at increasing times, using a m3 syringe coupled to a Teflon tube, filtered through a Millipore membrane with pore size of m (previously washed with nitric acid solution (2 vol%)), adjusted to pH < 2 with concentrated HNO3, and then analyzed by cold vapor-atomic fluorescence (as described in Section 2.1) to ascertain the mercury concentration.
2.3.1. Ion Exchange of TPA+ Solution (without Hg2+) Using Na-ETS-4
Rigorous masses of ETS-4 (pristine and washed with ultra-pure water to remove any vestigial amounts of Na+ from its synthesis) were added to ultra-pure water containing m3 of TPAOH mol m−3 (doses of 7.71 and 8.33 g m−3). Triplicate aliquots were collected (i) before the addition of TPAOH and ETS-4, (ii) immediately after the addition of TPAOH, just before the addition of ETS-4, (iii) immediately after the addition of ETS-4, and (iv) after three and seven days of contact. The Na+ concentration of the aliquots was measured by flame atomic absorption spectroscopy (Perkin Elmer, Überlingen, Germany), after filtering.
2.3.2. Ion Exchange of Hg2+ Solution Using Na-ETS-4
The initial Hg2+ concentration was fixed in all assays (ca. mol m−3; see Table 1) and the solutions were prepared by diluting the mercury stock solution in ultra-pure water (18.2 MΩ cm). The solution pH was adjusted to 6 [34] using NaOH or TPAOH solutions. For the kinetic studies, rigorous masses of pre-washed ETS-4 (doses of 13.64, 15.63 and 15.09 g m−3, denoted by Expression (6), Expression (9), and Expression (14), respectively) were added to the mercury solution. In Expressions (6) and (9) the pH was adjusted with TPAOH while in Expression (14) it was adjusted with NaOH. For quality control, a blank experiment (i.e., without ETS-4) was always run in parallel under the same operating conditions. Duplicate aliquots were collected at 0, 15, 30, and 45 min, and at 1, 1.5, 2, 4, 8, 20, 30, 45, 70, 100, and 200 h. The horizontal branch of each curve was used to determine the equilibrium isotherm. Additional experiments were carried out by changing the dose of ETS-4 (7.15–25.85 g m−3; see Table 1) to obtain new isotherm data points, for which only the initial and equilibrium concentrations were measured (0, 24, 48, 72, and 80 h). After solid-solution separation, the Hg2+ was quantified by cold vapour-atomic fluorescence (as mentioned in Section 2.1) with a range of standards for calibration between g m−3, a limit of detection of g m−3 and a precision and accuracy < 5%. Several blanks and standards were always analyzed with the sample batch.

Table 1.
Features and initial conditions of each experiment.
The average Hg2+ concentration in the solid at time , (mol m−3) was calculated by material balance according to:
where subscript denotes Hg2+, (mol m−3) is the initial mercury concentration in solution, is the mercury concentration in solution at time , (m3) is the volume of solution, and (kg) and kg m−3 are the mass and the density of ETS-4, respectively. The percentage of Hg2+ removed was calculated by:
where is the mercury concentration in solution at equilibrium.
3. Modelling
The ion exchange process was accurately modelled and analyzed in terms of equilibrium and kinetics. Concerning equilibrium, the mass action law was combined with Debye–Hückel equation and Wilson model to obtain the activity coefficients in the fluid and exchanger phases, respectively (see Supplementary Material) [13,39,40]. The Maxwell–Stefan (MS) phenomenological model was adopted to describe the ion exchange mass transfer [41,42]. The MS formalism, the material balances, the initial and the boundary conditions, and the numerical solution approach are described in the Supplementary Material. For comparison, the pseudo-first and pseudo-second order rate equations (see Supplemental Material) were also adopted.
The MS diffusivities, the convective mass transfer coefficient and the sorption rate constants of the semi-empirical equations were optimized by fitting the appropriate models to the experimental data. The MS model was solved numerically using the Method of Lines and a finite-difference approach. The Nelder–Mead algorithm was used to optimize the parameters, minimizing the average absolute relative deviation (AARD) defined by:
where NDP is the number of data points, and superscripts calc and exp refer to the calculated and experimental mercury concentration in the solution. Matlab R2014a® software was used for all calculations.
4. Results and Discussion
4.1. Check that Tetrapropylammonium Cation (TPA+) Cannot Penetrate ETS-4 Pores
In this study a TPAOH solution was selected for pH adjustments. Since the mercury concentration in this TPAOH solution was only mol m−3, which represents less than 0.8% of the initial mercury concentration (), this contribution was considered irrelevant. The values of were determined analytically for all the assays.
The possibility of exchanging the Na+ initially present in the ETS-4 by the TPA+ used to adjust the solution pH was investigated. Results showed that the ultra-pure water before and after the addition of the TPAOH solution was free of sodium (<0.01 g m−3). Nonetheless, immediately after the addition of ETS-4 the sodium concentration increased and remained constant after three and seven days, with an increment of g of Na+ per gram of ETS-4 and liter of solution. The same approach was carried out with ETS-4 previously washed with ultra-pure water, aiming to remove possible trace amounts of Na+ coming from its synthesis. Results showed that when pre-washed ETS-4 was used the solution was free of sodium (<0.01 g m−3), even seven days after the ETS-4 addition to the TPAOH solution. This confirms that TPAOH solution is not a source of Na+ to the working solution and that the TPA+ is large enough to penetrate into the crystal’s pores and exchange with the Na+ of the sorbent. In conclusion, the presence of the Na+ cation in solution in the first assay came from the ETS-4 surface and not from the pores of its framework.
4.2. Isotherm of the Hg2+/Na+/ETS-4 System
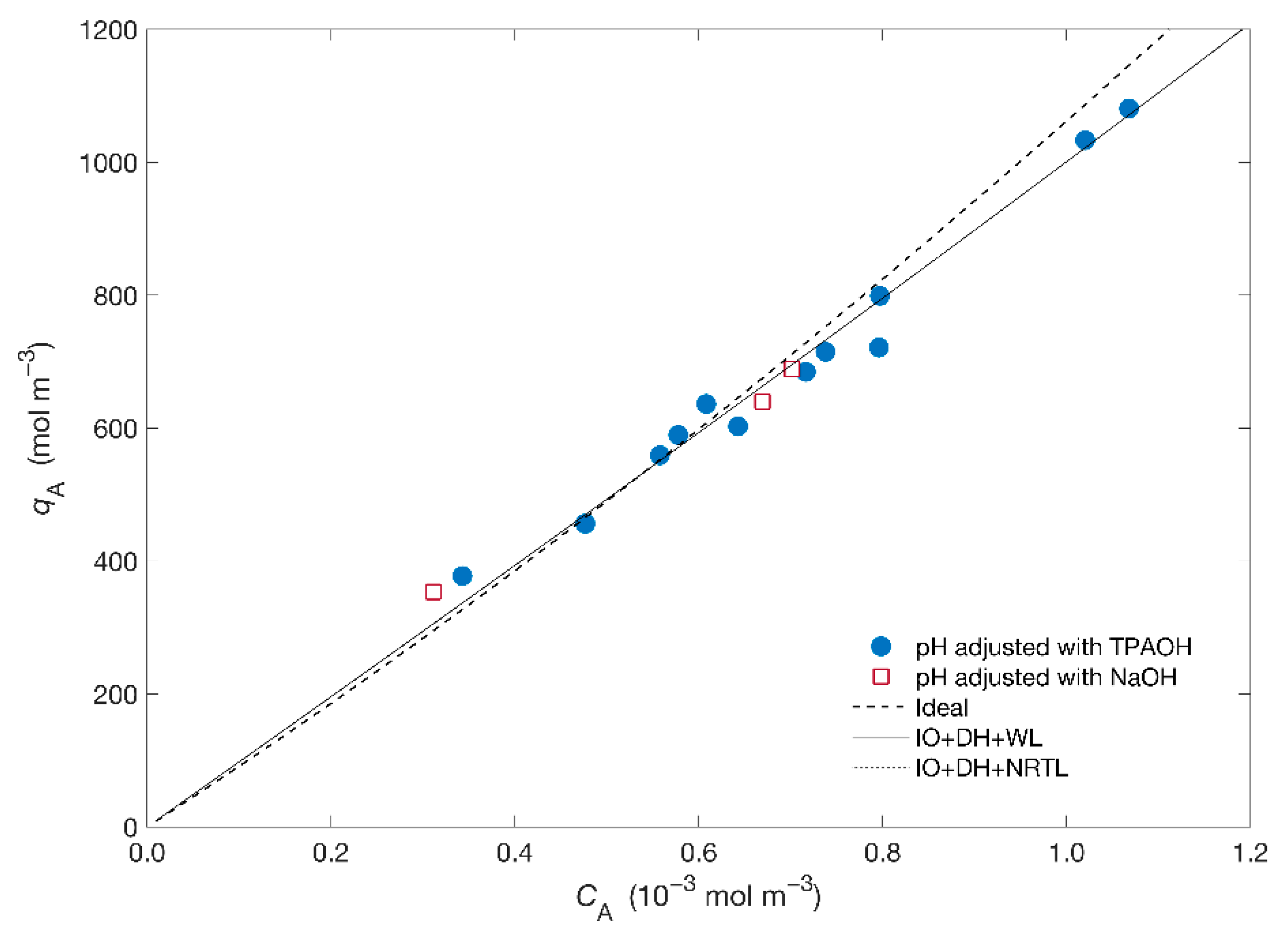
Figure 1 displays the isotherm of the Hg2+/Na+/ETS-4 system expressed as molar concentration of mercury in the solid () as a function of the equilibrium concentration in solution (). The isotherm is apparently linear in all range of studied concentrations.
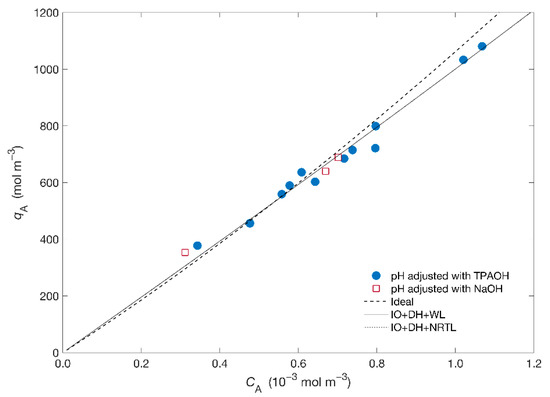
Figure 1.
Equilibrium data (symbols) and isotherm modelling (lines) results for the system Hg2+/Na+/ETS-4. Acronyms: IO = Ioannidis et al. approach, DH = Debye–Hückel, WL = Wilson.
Concerning modelling, the Ioannidis et al. [39,43] approach was adopted to obtain the equilibrium constant, , (where A is Hg2+ and B is Na+—see Supplementary Material) for two combinations of the solid activity coefficient ()—specifically, the Wilson and NRTL models—and Debye–Hückel for the fluid phase activity model (). The adjusted , the Wilson parameters ( and ) and the NRTL parameters ( and ) are listed in Table 2 together with the calculated AARD. From Figure 1 and Table 2 it is possible to observe the goodness of fit using the activity coefficient models (AARD = 0.89%) comparatively to the ideal situation (AARD = 0.93%) with the ideal isotherm overpredicting the results. Figure 1 also shows that the equilibrium curves obtained using the activity coefficient models are essentially overlapped, regardless of the chosen model for the solid phase, resulting in similar for both models. On other hand, the small ionic strength of the solutions, molal, contributes for the small deviations from ideality, allowing a reasonable adjustment of the ideal model to the results.

Table 2.
Equilibrium parameters obtained for the Hg2+/Na+/ETS-4 system. The range of ionic strength (I) in the liquid solution is molal.
4.3. Kinetics Modelling of the Hg2+/Na+/ETS-4 System
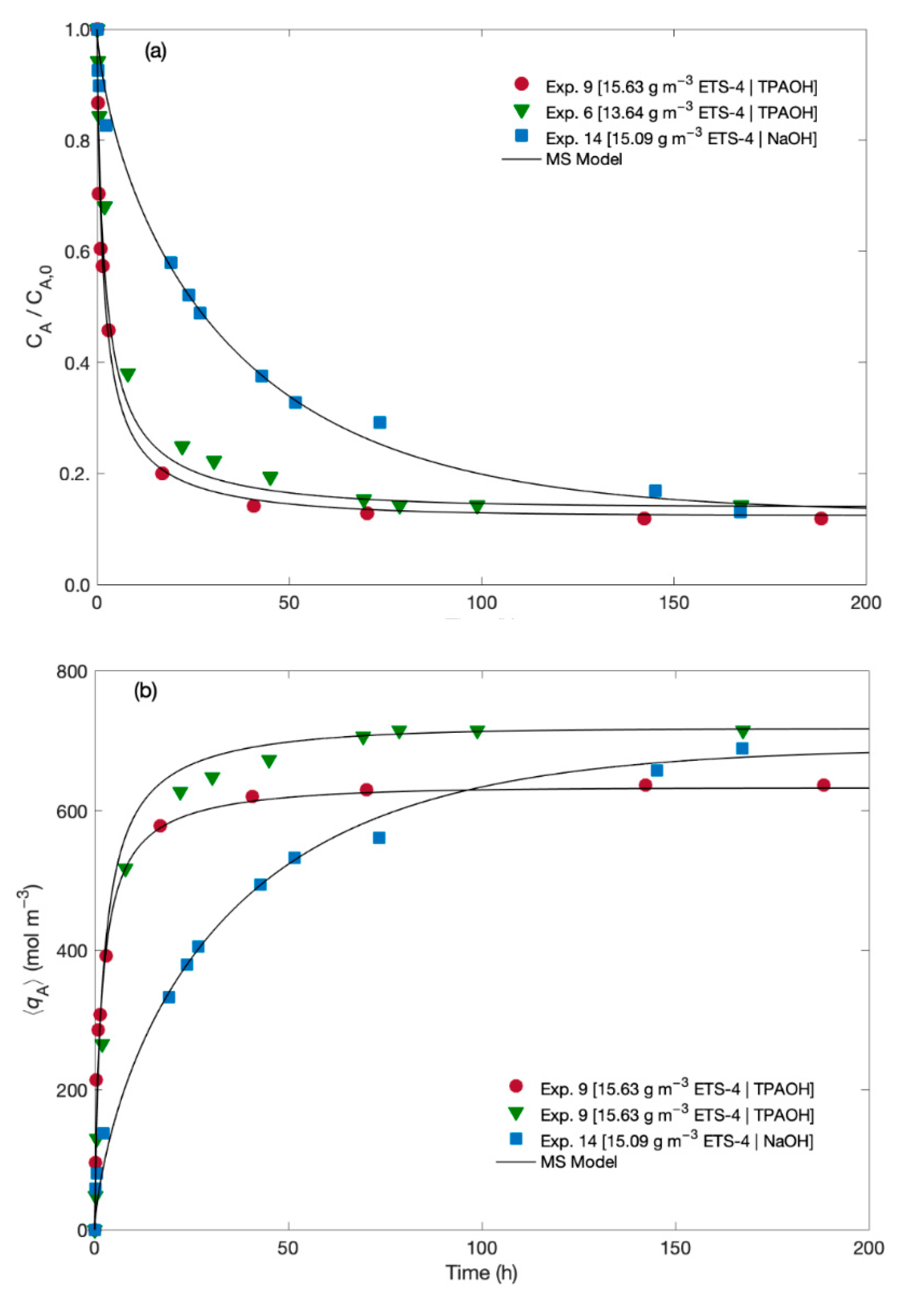
The experimental data for the normalized Hg2+ concentration in the fluid and in the solid along time are plotted in Figure 2 together with the MS modelling results. The experiments differ in the solution used for pH adjustment (namely, TPAOH solution and NaOH solution), and in the ETS-4 load (namely, 13.64 and 15.09/15.63 g m−3).
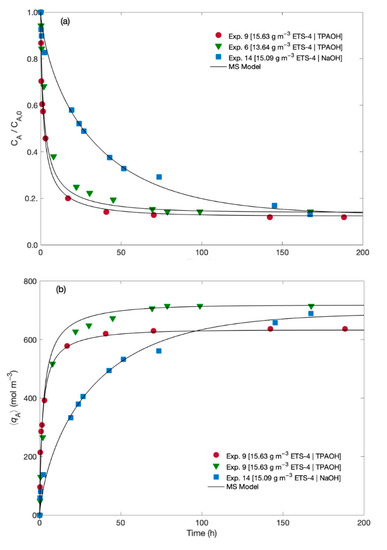
Figure 2.
Experimental (symbols) and MS model (lines) results along time for (a) normalized Hg2+ concentration in the fluid, and (b) in the solid.
The results suggest that independently of the pH adjusting solution, the addition of a few milligrams per litre of ETS-4 significantly decreases the Hg2+ concentration in solution (Figure 2a). As expected, the ion exchange of Hg2+ is faster at the beginning, slowing down until equilibrium attainment. Such kinetic pattern is due to the large mass transport driving forces that prevail at the beginning of the ion exchange process, since ETS-4 particles are initially free of metal ions. However, depending of the pH adjusting solution (TPAOH or NaOH) relevant differences were observed on the kinetics of Hg2+ uptake, as the final equilibrium is attained much faster when using TPAOH than when using NaOH solution. In fact, the Hg2+/Na+/ETS-4 system in the presence of NaOH solution needed more 100 h to reach equilibrium than in the presence of TPAOH solution, since the NaOH solution reduces significantly the driving force for mass transport of sodium and hence the ion exchange process is slower than when using the TPAOH solution. This statement is corroborated mathematically by the initial uptake rates, which were estimated from the first derivative of at . The evolution of the solid loading, , in Figure 2b complements and confirms these interpretations, since and are linearly related by Equation (1).
The initial uptake rates of Hg2+ when using TPAOH solution were and mol m−3 h−1 for 13.6 and 15.6 g m−3 of ETS-4, respectively. When the pH was adjusted with a NaOH solution the initial uptake rate of Hg2+ was mol m−3 h−1, (with 15.1 g m−3 of ETS-4). The kinetic selectivity (i.e., the ratio between the removal rates when using TPAOH and NaOH solutions, for ca. 15 g m−3 of ETS-4) was 1.7, confirming that the kinetics of Hg2+ exchange is slower when Na+ is added to the working solution. These results can be explained by the competition effect between Na+ and Hg2+ in the ion exchange phenomenon, with the concentration of Na+ being much higher than the concentration of Hg2+ (when the pH is adjusted with the NaOH solution). In fact, comparing Exps. 9 and 14 (which use TPAOH and NaOH, respectively), the initial concentration of Na+ in solution was 0 and mol m−3, respectively, whereas the initial Hg2+ concentration was and mol m−3, respectively.
As equilibrium is approached, the normalized Hg2+ concentration in the fluid converges to the same value ( 0.13 ± 0.01) regardless of the pH adjusting solution At equilibrium, and depending on the amount of ETS-4, 86 to 88% of Hg2+ was exchanged by the Na+ initially present in the solid. These results clearly demonstrate that ETS-4 is highly selective for Hg2+ cation and at equilibrium the ion exchange process is not affected by the presence of high amounts of Na+ in solution (which is the case when a NaOH solution is used for pH adjustment).
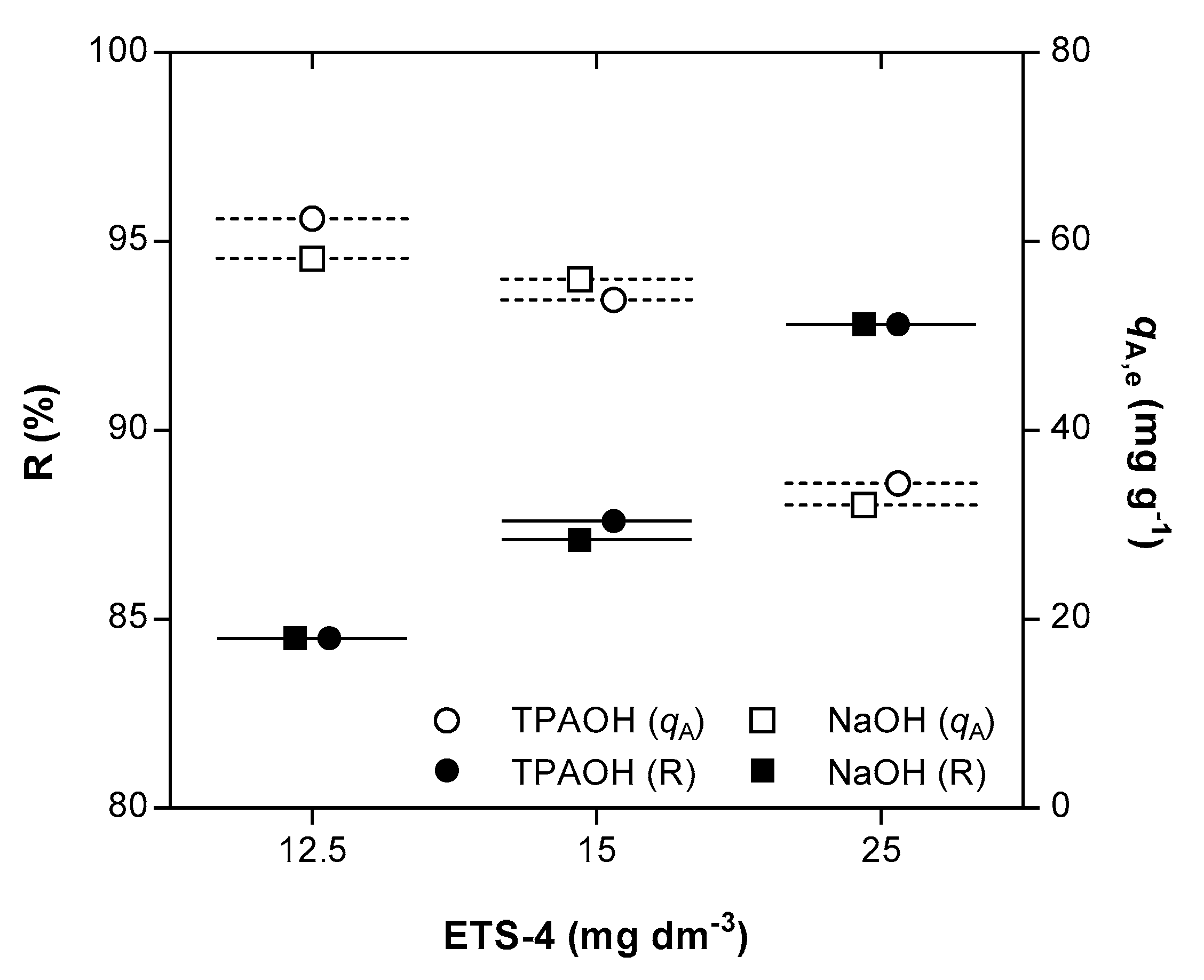
A considerable improvement on the ion exchange results of Hg2+ was achieved by increasing the amount of ETS-4. For example, independently of the pH adjusting solution, duplicating the ETS-4 dose increased Hg2+ removal from 84.5% (ca. 12.56 g m−3 of ETS-4, Exps. 4 and 13) to 92.5% (ca. 25.52 g m−3, Exp. 12 and 15) (Figure 3). The extensive ion exchange capacity is proportional to the solid mass since the initial mercury concentration in solution was fixed around 1 g m−3 in all assays. The equilibrium selectivity () was calculated by the ratio between the distribution coefficients of Hg2+ at equilibrium, when using TPAOH and NaOH solutions (). The value found for the equilibrium selectivity was 1.02 ± 0.04, confirming that the presence of Na+ cation in solution does not mitigate the extension of the ion exchange process.
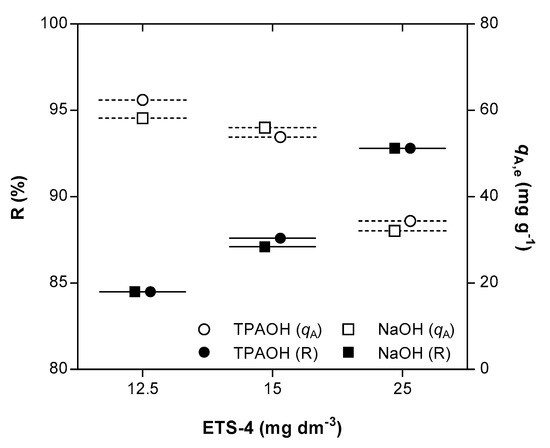
Figure 3.
Removal (R) of Hg2+ (black symbols) and equilibrium concentrations of Hg2+ in the solid phase ( (white symbols) as function of ETS-4 dose, when using TPAOH (circle) or NaOH (square) as pH adjusting solution. All data refers to the final equilibrium conditions attained.
With respect to the results obtained with the MS model (lines in Figure 2) the good agreement between modelling and measurements is noteworthy, corresponding to AARD = 5.81% (see Table 3). A trustworthy correlation is accomplished even in the transition region from the steep descent to the horizontal branch, where the kinetic curves are usually very difficult to fit.

Table 3.
Optimized parameters of Maxwell–Stefan, pseudo-first and pseudo-second order models, and respective calculated deviations (AARD).
The MS diffusion coefficients (Table 3) are in the order of 10−16–10−21 m2 s−1, being consistent with the small pore diameters of ETS-4 ((30–40) × 10−9 m) [44] and similar to literature values for other systems (Table 4). For instance, similar values can be found in the following articles: (i) Barrer and Rees [45] reported self-diffusion coefficients of , , and m2 s−1 for Na+, K+, and Rb+ in analcite, respectively; (ii) Coker and Rees [46] obtained apparent diffusion coefficients of and m2 s−1 for Ca2+ and Mg2+ in semi-crystalline Zeolite Na-A, respectively; and (iii) Lopes et al. [47] obtained diffusion coefficients of and m2 s−1 for Hg2+ and Na+ in Hg2+/Na+/ETS-4 system, respectively, using the Nerst-Plank model.

Table 4.
Comparison between MS diffusivities and convective mass transfer coefficient optimized in this work and published in the literature.
Concerning the convective mass transfer coefficient, the fitted value ( m s−1) differs from that predicted by the Armanante and Kirwan correlation [48] ( m s−1). However, this method is not entirely appropriate for this case since ETS-4 particles ( m) are one order of magnitude lower than the inferior limit studied by the authors (range of m) [48].
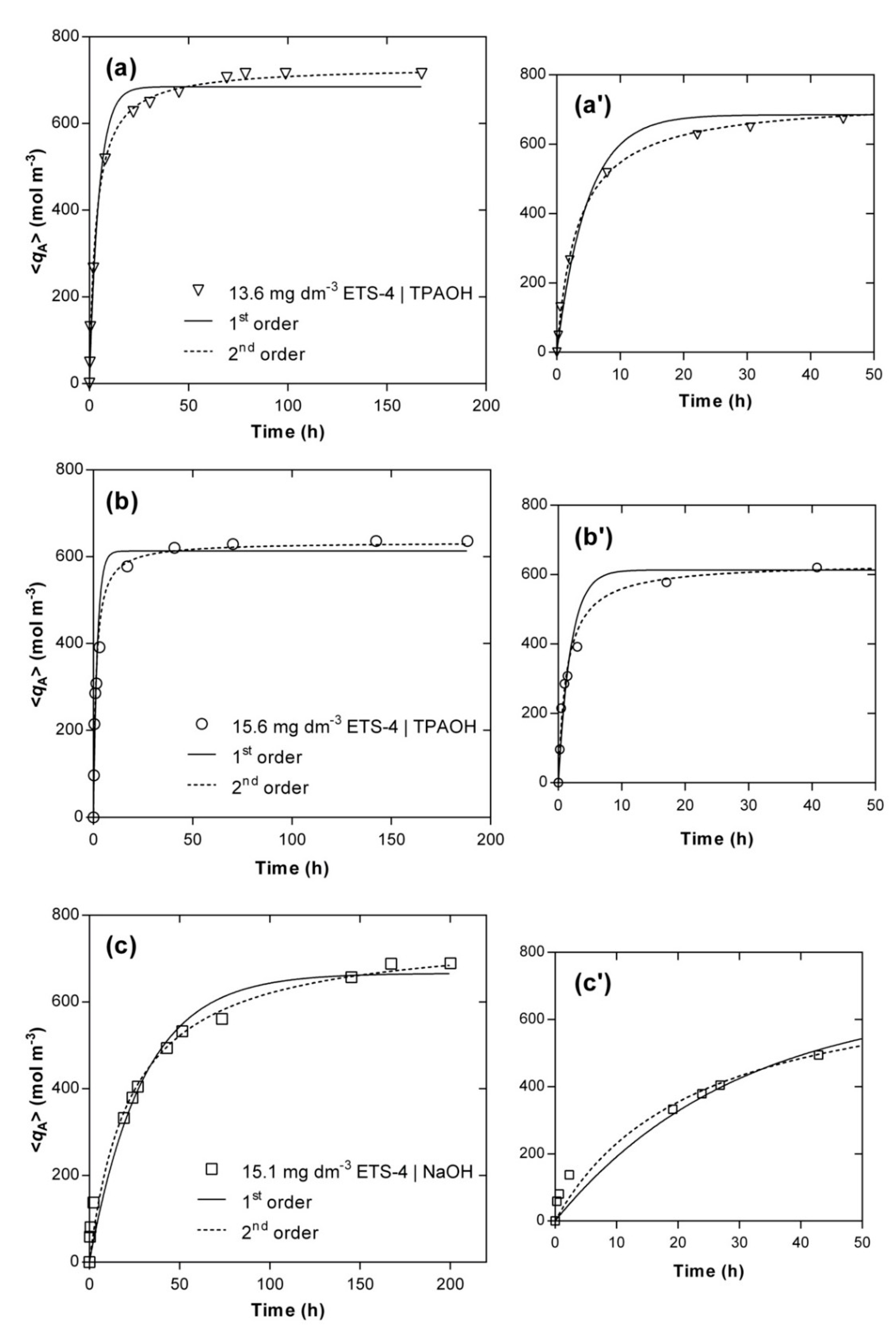
For comparison, the fittings accomplished by the pseudo-first and pseudo-second order models are also presented, since they are two of the most adopted expressions in the literature for a huge variety of materials [12,50,51,52,53,54]. Figure 4 displays the evolution of the experimental (symbols) and calculated (lines) concentrations of Hg2+ in the solid phase along time, , and Table 3 contains the parameters fitted for each kinetic experiment, namely and (see Equations (S24) and (S25), in Supplementary Material). A good agreement between experimental data and model fitting was achieved, especially by the pseudo-second order model (AARD = 8.30%) being poorer for the pseudo-first order model (AARD = 14.50%). Nonetheless, in all cases the simple empirical models performed worse than the MS model (AARD = 5.81%).
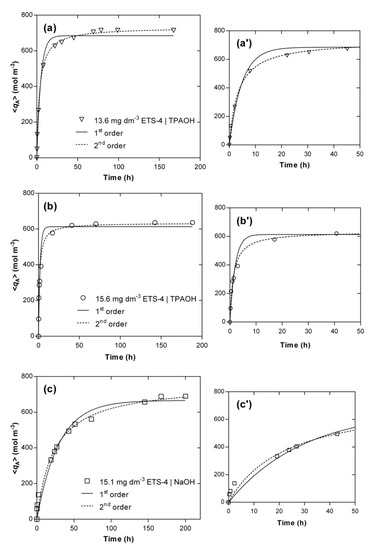
Figure 4.
Experimental (symbols) and modelling (lines) results of Hg2+ concentration in the solid phase versus time. Experimental conditions: (a) TPAOH solution, 15.6 g m−3 of ETS-4 (Ο); (b) TPAOH solution, 13.6 g m−3 of ETS-4 (▽); (c) NaOH solution, 15.1 g m−3 of ETS-4 (☐). On the right side (a’–c’), the zoom-in for the first 50 h of each system is shown.
For the systems using TPAOH solution to adjust the pH, the main deviations occurred in the transition between the steep ascendant part of each curve and the horizontal branch (Figure 4a’,b’), in particular for the first-order model, whereas the equilibrium values calculated by the pseudo-second order model matched accurately the experimental points (relative errors of 2.9% and 3.3%, respectively, for 13.6 and 15.6 g m−3 of ETS-4). For the system using NaOH, the major deviations occurred for the initial times ( h) (Figure 4c’) and the model overestimated the equilibrium concentration of Hg2+ in the solid (relative error of 10.8%). Additionally, the pseudo-second order model kinetic constants, , also confirmed that the ion exchange of Hg2+ is much faster in the presence of the TPA+ than Na+ ( versus m3 mol−1 h−1) when using the same amount of ETS-4 (ca. 15 g m−3) and initial concentration of mercury ( mol m−3).
5. Conclusions
The ion exchange of a hazardous metal ion, Hg2+, using the well-known titanosilicate no. 4 in sodium form (Na-ETS-4) as a cation exchanger was studied carrying out isothermal batch experiments and using two pH adjusting solutions with cations of different size (tetrapropylammonium and sodium cations). The results reveal that ETS-4 is highly effective and selective for Hg2+ uptake independently of the counter ions in solution. Moreover, the presence of Na+ in the fluid phase does not affect the equilibrium Hg2+ removal while it imparts a strong effect on the ion exchange kinetics (and thus on the equilibration time), since the addition of Na+ in the liquid phase decreases the driving force for sodium mass transfer.
In terms of modelling, equilibrium was accurately modeled by the mass action law and rigorously expressed in term of activities (Debye–Hückel model for solution and Wilson and NRTL models for the solid exchanger phase). Comparing to the ideal model, no major deviations from ideality were found in the range of concentrations studied, despite a noticeable biased increase at higher concentrations. Concerning kinetic modelling, the Maxwell–Stefan (MS) approach was adopted and the MS diffusivities of each pair of species and the film mass transfer coefficient were obtained. With an average deviation of 5.81%, the MS model described successfully the kinetic curves of mercury removal being notoriously better than the semi-empirical models frequently used in the literature, namely the pseudo-first (AARD = 15.08%) and pseudo-second (AARD = 10.78%) order equations. Nevertheless, the pseudo-second order model was able to describe the ion exchange of Hg2+ by the ETS-4 from the fluid phase.
Supplementary Materials
The following are available online at https://www.mdpi.com/1996-1944/14/1/11/s1, Modelling Ion Exchange Equilibrium and Kinetics. Table S1: Models adopted for the estimation of activity coefficients of counter ions in the liquid and exchange phase.
Author Contributions
Conceptualization: C.B.L., E.P., I.P. and C.M.S.; methodology: S.P.C. and T.L.F.; formal analysis: C.B.L., I.P. and C.M.S.; investigation: S.P.C. and T.L.F.; resources: E.P. and C.M.S.; writing—original draft preparation: S.P.C.; writing—review and editing: C.B.L., I.P. and C.M.S.; supervision: C.B.L., E.P. and C.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was developed within the scope of the project CICECO-Aveiro Institute of Materials, FCT Ref. UID/CTM/50011/2019, financed by national funds through the FCT/MCTES. Cláudia B. Lopes acknowledges hirings funded by national funds (OE), through FCT–Fundação para a Ciência e a Tecnologia, I.P., in the scope of the framework contract foreseen in the numbers 4, 5, and 6 of the article 23, of the Decree-Law 57/2016, of August 29, changed by Law 57/2017, of July 19.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lopes, C.B.; Lito, P.F.; Cardoso, S.P.; Pereira, E.; Duarte, A.C.; Silva, C.M. Metal Recovery, Separation and/or Pre-concentration. In Ion Exchange Technology II—Applications; Inamuddin, D., Luqman, M., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 237–322. [Google Scholar]
- Coelho, J.P.; Santos, H.; Reis, A.T.; Falcão, J.; Rodrigues, E.T.; Pereira, M.E.; Duarte, A.C.; Pardal, M.A. Mercury bioaccumulation in the spotted dogfish (Scyliorhinus canicula) from the Atlantic Ocean. Mar. Pollut. Bull. 2010, 60, 1372–1375. [Google Scholar] [CrossRef] [PubMed]
- European Union. Directive 2013/39/EU of the European Parliament and of the Council of 12 August 2013 amending Directives 2000/60/EC and 2008/105/EC as regards priority substances in the field of water policy. Off. J. Eur. Union. 2013, 226, 1–17. [Google Scholar]
- ATSDR. ATSDR 2015 Subst. Prior. List. (n.d.). Available online: http://www.atsdr.cdc.gov/spl/index.html (accessed on 20 January 2019).
- Krabbenhoft, D.P.; Rickert, D.A. Mercury Contamination of Aquatic Ecosystems. Available online: http://pubs.usgs.gov/fs/1995/fs216-95/ (accessed on 1 April 2020).
- Sylvester, P.; Behrens, E.A.; Graziano, G.M.; Clearfield, A. An Assessment of Inorganic Ion-Exchange Materials for the Removal of Strontium from Simulated Hanford Tank Wastes. Sep. Sci. Technol. 1999, 34, 1981–1992. [Google Scholar] [CrossRef]
- Zhao, G.X.S.; Lee, J.L.; Chia, P.A. Unusual Adsorption Properties of Microporous Titanosilicate ETS-10 toward Heavy Metal Lead. Langmuir 2003, 19, 1977–1979. [Google Scholar] [CrossRef]
- Lopes, C.B.; Coimbra, J.; Otero, M.; Pereira, E.; Duarte, A.C.; Lin, Z.; Rocha, J. Uptake of Hg2+ from aqueous solutions by microporous titano- and zircono-silicates. Quim. Nova 2008, 31, 321–325. [Google Scholar] [CrossRef]
- Camarinha, E.D.; Lito, P.F.; Antunes, B.M.; Otero, M.; Lin, Z.; Rocha, J.; Pereira, E.; Duarte, A.C.; Silva, C.M. Cadmium(II) removal from aqueous solution using microporous titanosilicate ETS-10. Chem. Eng. J. 2009, 155, 108–114. [Google Scholar] [CrossRef]
- Barreira, L.D.; Lito, P.F.; Antunes, B.M.; Otero, M.; Lin, Z.; Rocha, J.; Pereira, E.; Duarte, A.C.; Silva, C.M. Effect of pH on cadmium (II) removal from aqueous solution using titanosilicate ETS-4. Chem. Eng. J. 2009, 155, 728–735. [Google Scholar] [CrossRef]
- Ferreira, T.R.; Lopes, C.B.; Lito, P.F.; Otero, M.; Lin, Z.; Rocha, J.; Pereira, E.; Duarte, A.C.; Silva, C.M. Cadmium(II) removal from aqueous solution using microporous titanosilicate ETS-4. Chem. Eng. J. 2009, 147, 173–179. [Google Scholar] [CrossRef]
- Cardoso, S.P.; Lopes, C.B.; Pereira, E.; Duarte, A.C.; Silva, C.M. Competitive removal of Cd2+ and Hg2+ ions from water using titanosilicate ETS-4: Kinetic behaviour and selectivity. Water. Air. Soil Pollut. 2013, 224, 1535. [Google Scholar] [CrossRef]
- Cardoso, S.P.; Azenha, I.S.; Lin, Z.; Portugal, I.; Rodrigues, A.E.; Silva, C.M. Experimental measurement and modeling of ion exchange equilibrium and kinetics of cadmium(II) solutions over microporous stannosilicate AV-6. Chem. Eng. J. 2016, 295, 139–151. [Google Scholar] [CrossRef]
- Figueiredo, B.R.; Ananias, D.; Portugal, I.; Rocha, J.; Silva, C.M. Tb/Eu-AV-9: A lanthanide silicate for the sensing and removal of cesium ions from aqueous solutions. Chem. Eng. J. 2016, 286, 679–688. [Google Scholar] [CrossRef]
- Figueiredo, B.R.; Portugal, I.; Rocha, J.; Silva, C.M. Fixed-bed removal of Cs+ from aqueous solutions by microporous silicate ETS-4: Measurement and modeling of loading-regeneration cycles. Chem. Eng. J. 2016, 301, 276–284. [Google Scholar] [CrossRef]
- Figueiredo, B.R.; Ananias, D.; Rocha, J.; Silva, C.M. Cs+ ion exchange over lanthanide silicate Eu-AV-20: Experimental measurement and modelling. Chem. Eng. J. 2015, 268, 208–218. [Google Scholar] [CrossRef]
- Duan, C.; Ma, T.; Wang, J.; Zhou, Y. Removaal of heavy metals from aqueous solution using carbon-based adsorbents: A review. J. Water Process. Eng. 2020, 37, 101339. [Google Scholar] [CrossRef]
- Filice, S.; Mazurkiewicz-Pawlicka, M.; Malolepszy, A.; Stobinski, L.; Kwiatkowski, R.; Boczkowska, A.; Gradon, L.; Scalese, S. Sulfonated Pentablock Copolymer Membranes and Graphene Oxide Addition for Efficient Removal of Metal Ions from Water. Nanomaterials 2020, 10, 1157. [Google Scholar] [CrossRef]
- Wadhawan, S.; Jain, A.; Nayyar, J.; Mehta, S.K. Role of nanomaterials as adsorbents in heavy metal ion removal from waste water: A review. J. Water. Process Eng. 2020, 33, 101038. [Google Scholar] [CrossRef]
- Upadhyay, U.; Sreedhar, I.; Singh, S.A.; Patel, C.M.; Anitha, K.L. Recent advances in heavy metal removal by chitosan based adsorbents. Carbohydr. Polym. 2021, 251, 117000. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, W.; Zhao, Y.; Bai, H.; Wen, T.; Kang, S.; Song, G.; Song, S.; Komarneni, S. Removal of heavy metals and dyes by clay-based adsorbents: From natural clays to 1D and 2D nano-composites. Chem. Eng. J. 2021, in press. [Google Scholar] [CrossRef]
- Fabre, E.; Dias, M.; Costa, M.; Henriques, B.; Vale, C.; Lopes, C.B.; Pinheiro-Torres, J.; Silva, C.M.; Pereira, E. Negligible effect of potentially toxic elements and rare earth elements on mercury removal from contaminated waters by green, brown and red living marine macroalgae. Sci. Total Environ. 2020, 724, 138133. [Google Scholar] [CrossRef]
- Fabre, E.; Rocha, A.; Cardoso, S.P.; Brandão, P.; Vale, C.; Lopes, C.B.; Pereira, E.; Silva, C.M. Purification of mercury-contaminated water using new AM-11 and AM-14 microporous silicates. Sep. Purif. Technol. 2020, 239, 116438. [Google Scholar] [CrossRef]
- Fabre, E.; Lopes, C.B.; Vale, C.; Pereira, E.; Silva, C.M. Valuation of banana peels as an effective biosorbent for mercury removal under low environmental concentrations. Sci. Total Environ 2020, 709, 135883. [Google Scholar] [CrossRef]
- Clearfield, A.; Poojary, D.M.; Behrens, E.A.; Cahill, R.A.; Bortun, A.I.; Bortun, L.N. Structural Basis of Selectivity in Tunnel Type Inorganic Ion Exchangers. In Metal-Ion Separation and Preconcentration; Bond, A.H., Dietz, M.L., Rogers, R.D., Eds.; American Chemical Society: Washington, DC, USA, 1999; pp. 168–182. [Google Scholar]
- Helfferich, F.G. Ion Exchange; Dover Publications: New York, NY, USA, 1962. [Google Scholar]
- Nair, S.; Jeong, H.-K.; Chandrasekaran, A.; Braunbarth, C.M.; Tsapatsis, M.; Kuznicki, S.M. Synthesis and Structure Determination of ETS-4 Single Crystals. Chem. Mater. 2001, 13, 4247–4254. [Google Scholar] [CrossRef]
- Oleksiienko, O.; Wolkersdorfer, C.; Sillanpää, M. Titanosilicates in cation adsorption and cation exchange—A review. Chem. Eng. J. 2017, 317, 570–585. [Google Scholar] [CrossRef]
- Al Attar, L.; Dyer, A. Sorption of uranium onto titanosilicate materials. J. Radioanal. Nucl. Chem. 2001, 247, 121–128. [Google Scholar]
- Popa, K.; Pavel, C.C.; Bilba, N.; Cecal, A. Purification of waste waters containing 60Co2+, 115mCd2+ and 203Hg2+ radioactive ions by ETS-4 titanosilicate. J. Radioanal. Nucl. Chem. 2006, 269, 155–160. [Google Scholar] [CrossRef]
- Popa, K.; Pavel, C.C.; Bilba, N.; Cecal, A. Radioactive wastewaters purification using titanosilicates materials: State of the art and perspectives. Desalination 2012, 293, 78–86. [Google Scholar] [CrossRef]
- Lopes, C.B.; Otero, M.; Lin, Z.; Pereira, E.; Silva, C.M.; Rocha, J.; Duarte, A.C. Removal of Mercury From Aqueous Solutions by ETS-4 Microporous Titanosilicate: Effect of Contact Time, Titanosilicate Mass and Initial Metal Concentration. In Proceedings of the 11th International Conference on Environmental Remediation and Radioactive Waste Management (ICEM2007), Bruges, Belgium, 2–6 September 2007. [Google Scholar]
- Lopes, C.B.; Otero, M.; Lin, Z.; Silva, C.M.; Rocha, J.; Pereira, E.; Duarte, A.C. Removal of Hg2+ ions from aqueous solution by ETS-4 microporous titanosilicate—Kinetic and equilibrium studies. Chem. Eng. J. 2009, 151, 247–254. [Google Scholar] [CrossRef]
- Lopes, C.B.; Otero, M.; Lin, Z.; Silva, C.M.; Pereira, E.; Rocha, J.; Duarte, A.C. Effect of pH and temperature on Hg2+ water decontamination using ETS-4 titanosilicate. J. Hazard. Mater. 2010, 175, 439–444. [Google Scholar] [CrossRef]
- Tolosana, S.; Ehrlich, R. Composition of liquid effluent discharged by medical institutions in Cape Town. S. Afr. J. Sci. 2000, 96, 417–420. [Google Scholar]
- Chojnacki, A.; Chojnacka, K.; Hoffmann, J.; Górecki, H. The application of natural zeolites for mercury removal: From laboratory tests to industrial scale. Miner. Eng. 2004, 17, 933–937. [Google Scholar] [CrossRef]
- Álvarez-Ayuso, E.; García-Sánchez, A.; Querol, X. Purification of metal electroplating waste waters using zeolites. Water Res. 2003, 37, 4855–4862. [Google Scholar] [CrossRef] [PubMed]
- Philippou, A.; Anderson, M.W. Structural investigation of ETS-4. Zeolites 1996, 16, 98–107. [Google Scholar] [CrossRef]
- Lito, P.F.; Cardoso, S.P.; Loureiro, J.M.; Silva, C.M. Ion Exchange Equilibria and Kinetics. In Ion Exchange Technology I—Theory and Materials; Inamuddin, D., Luqman, M., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 51–120. [Google Scholar]
- Zemaitis, J.F.; Clark, D.M.; Rafal, M.; Scricvner, N.C. Handbook of Aqueous Electrolyte Thermodynamics: Theory & Application; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Lito, P.F.; Aniceto, J.P.S.; Silva, C.M. Maxwell–Stefan based modelling of ion exchange systems containing common species (Cd2+, Na+) and distinct sorbents (ETS-4, ETS-10). Int. J. Environ. Sci. Technol. 2013, 12, 183–192. [Google Scholar] [CrossRef][Green Version]
- Lito, P.F.; Aniceto, J.P.S.; Silva, C.M. Modelling ion exchange kinetics in zeolyte-type materials using Maxwell–Stefan approach. Desalin. Water Treat. 2013, 52, 5333–5342. [Google Scholar] [CrossRef]
- Ioannidis, S.; Anderko, A.; Sanders, S.J. Internally consistent representation of binary ion exchange equilibria. Chem. Eng. Sci. 2000, 55, 2687–2698. [Google Scholar] [CrossRef]
- Kuznicki, S.M.; Bell, V.A.; Nair, S.; Hillhouse, H.W.; Jacubinas, R.M.; Braunbarth, C.M.; Toby, B.H.; Tsapatsis, M. A titanosilicate molecular sieve with adjustable pores for size-selective adsorption of molecules. Nature 2001, 412, 720–724. [Google Scholar] [CrossRef]
- Barrer, R.M.; Rees, L.V.C. Energies of Activation for Self-diffusion of Alkali Metal Ions in Analcite. Nature 1960, 187, 768–769. [Google Scholar] [CrossRef]
- Coker, E.N.; Rees, L.V.C. Kinetics of ion exchange in quasi-crystalline aluminosilicate zeolite precursors. Microporous Mesoporous Mater. 2005, 84, 171–178. [Google Scholar] [CrossRef]
- Lopes, C.B.; Lito, P.F.; Otero, M.; Lin, Z.; Rocha, J.; Silva, C.M.; Pereira, E.; Duarte, A.C. Mercury removal with titanosilicate ETS-4: Batch experiments and modelling. Microporous Mesoporous Mater. 2008, 115, 98–105. [Google Scholar] [CrossRef]
- Armenante, P.M.; Kirwan, D.J. Mass transfer to microparticles in agitated systems. Chem. Eng. Sci. 1989, 44, 2781–2796. [Google Scholar] [CrossRef]
- Silva, C.M.; Lito, P.F. Application of the Maxwell–Stefan approach to ion exchange in microporous materials. Batch process modelling. Chem. Eng. Sci. 2007, 62, 6939–6946. [Google Scholar] [CrossRef]
- Lopes, C.B.; Oliveira, J.R.; Rocha, L.S.; Tavares, D.S.; Silva, C.M.; Silva, S.P.; Hartog, N.; Duarte, A.C.; Pereira, E. Cork stoppers as an effective sorbent for water treatment: The removal of mercury at environmentally relevant concentrations and conditions. Environ. Sci. Pollut. Res. 2014, 21, 2108–2121. [Google Scholar] [CrossRef] [PubMed]
- Tavares, D.S.; Lopes, C.B.; Daniel-da-Silva, A.L.; Duarte, A.C.; Trindade, T.; Pereira, E. The role of operational parameters on the uptake of mercury by dithiocarbamate functionalized particles. Chem. Eng. J. 2014, 254, 559–570. [Google Scholar] [CrossRef]
- Rocha, L.S.; Almeida, Â.; Nunes, C.; Henriques, B.; Coimbra, M.A.; Lopes, C.B.; Silva, C.M.; Duarte, A.C.; Pereira, E. Simple and effective chitosan based films for the removal of Hg from waters: Equilibrium, kinetic and ionic competition. Chem. Eng. J. 2016, 300, 217–229. [Google Scholar] [CrossRef]
- Rocha, L.S.; Lopes, C.B.; Borges, J.A.; Duarte, A.C.; Pereira, E. Valuation of Unmodified Rice Husk Waste as an Eco-Friendly Sorbent to Remove Mercury: A Study Using Environmental Realistic Concentrations. Water, Air, Soil Pollut. 2013, 224, 1599. [Google Scholar] [CrossRef]
- Henriques, B.; Rocha, L.S.; Lopes, C.B.; Figueira, P.; Monteiro, R.J.R.; Duarte, A.C.; Pardal, M.A.; Pereira, E. Study on bioaccumulation and biosorption of mercury by living marine macroalgae: Prospecting for a new remediation biotechnology applied to saline waters. Chem. Eng. J. 2015, 281, 759–770. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).