Analysis of Sn-Bi Solders: X-ray Micro Computed Tomography Imaging and Microstructure Characterization in Relation to Properties and Liquid Phase Healing Potential
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Imaging and Segmentation
2.3. Microstructural Parameter
2.4. RVE-FEM Model
3. Results
3.1. Tomographic Rendering
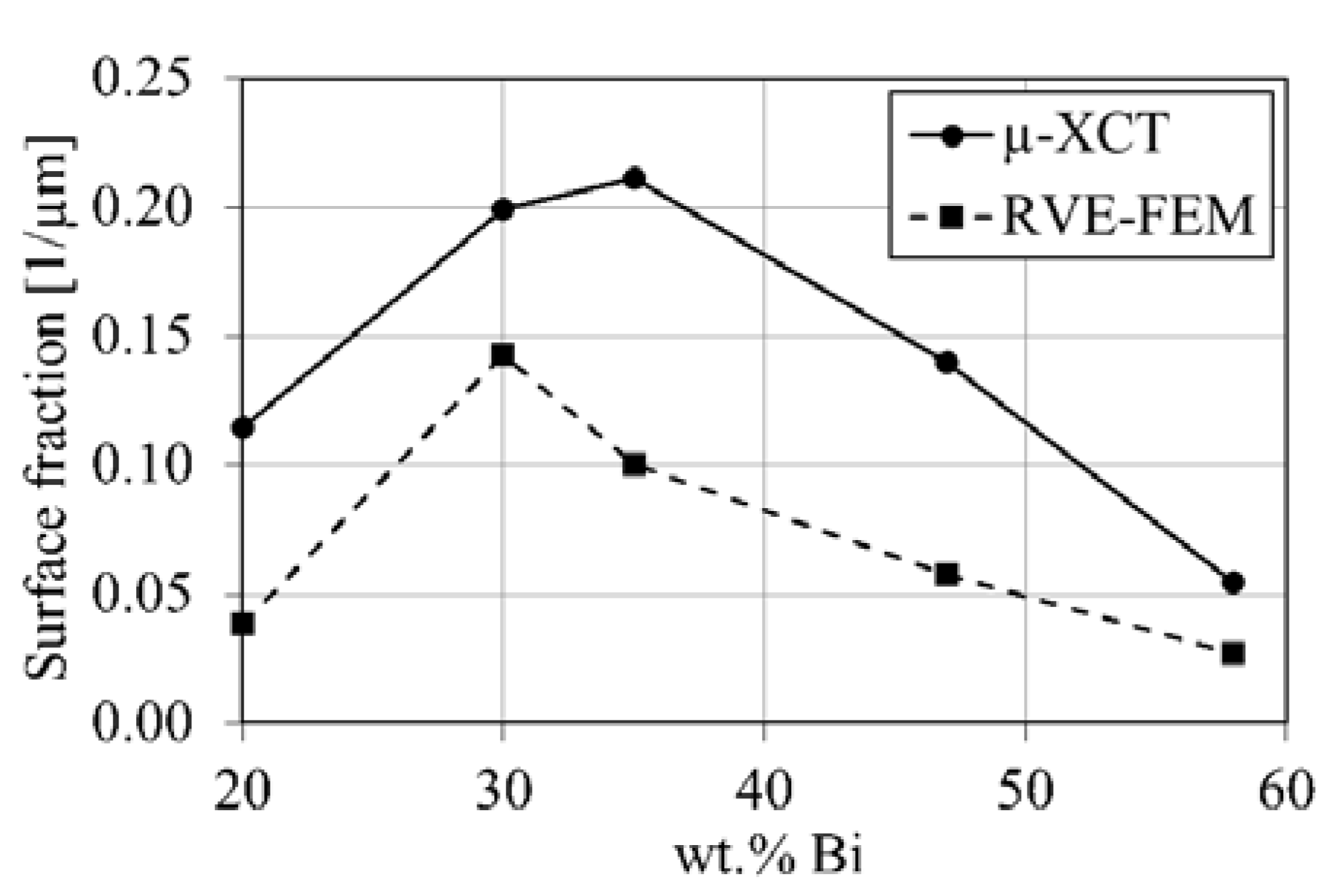
3.2. Volume Fractions
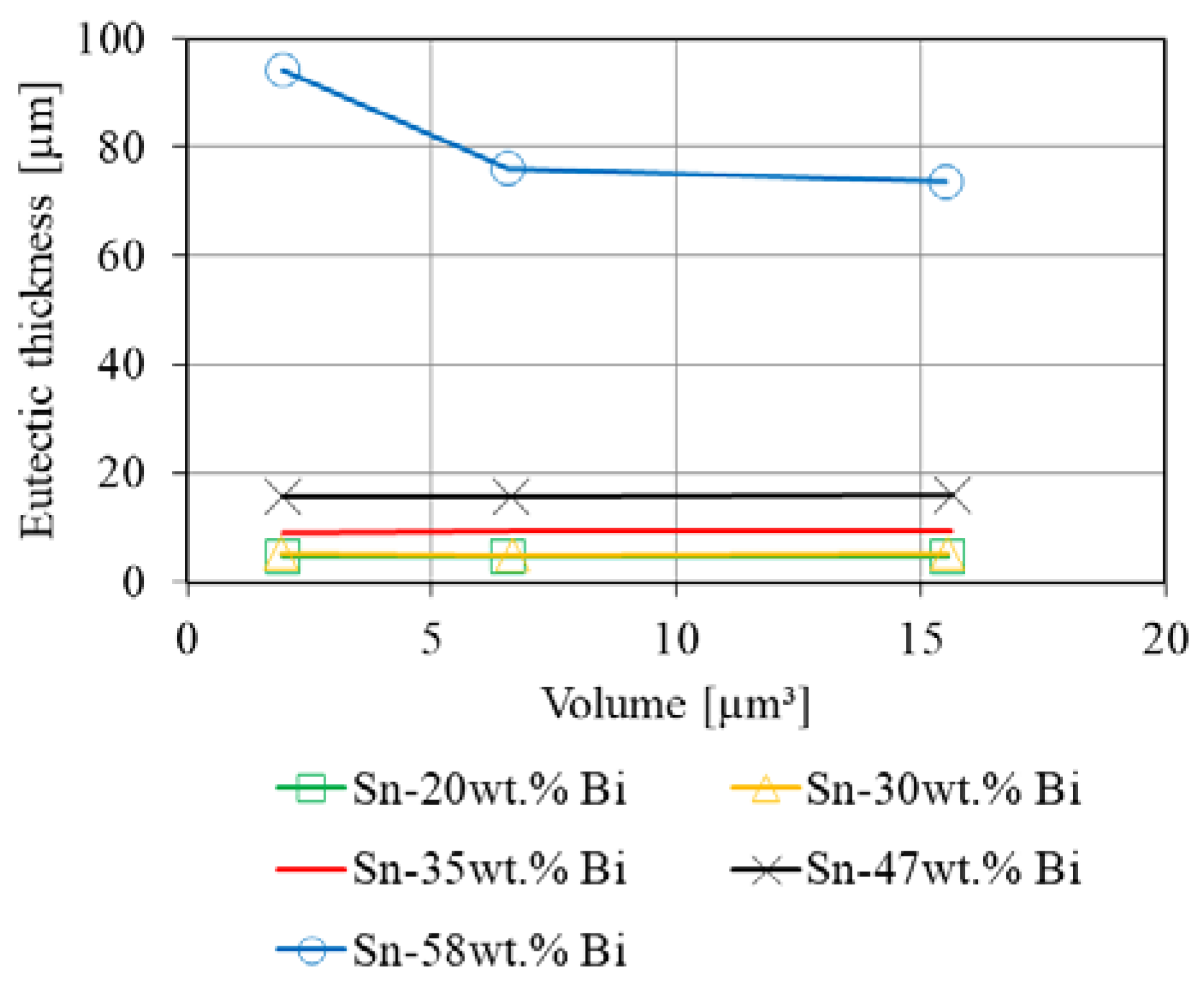
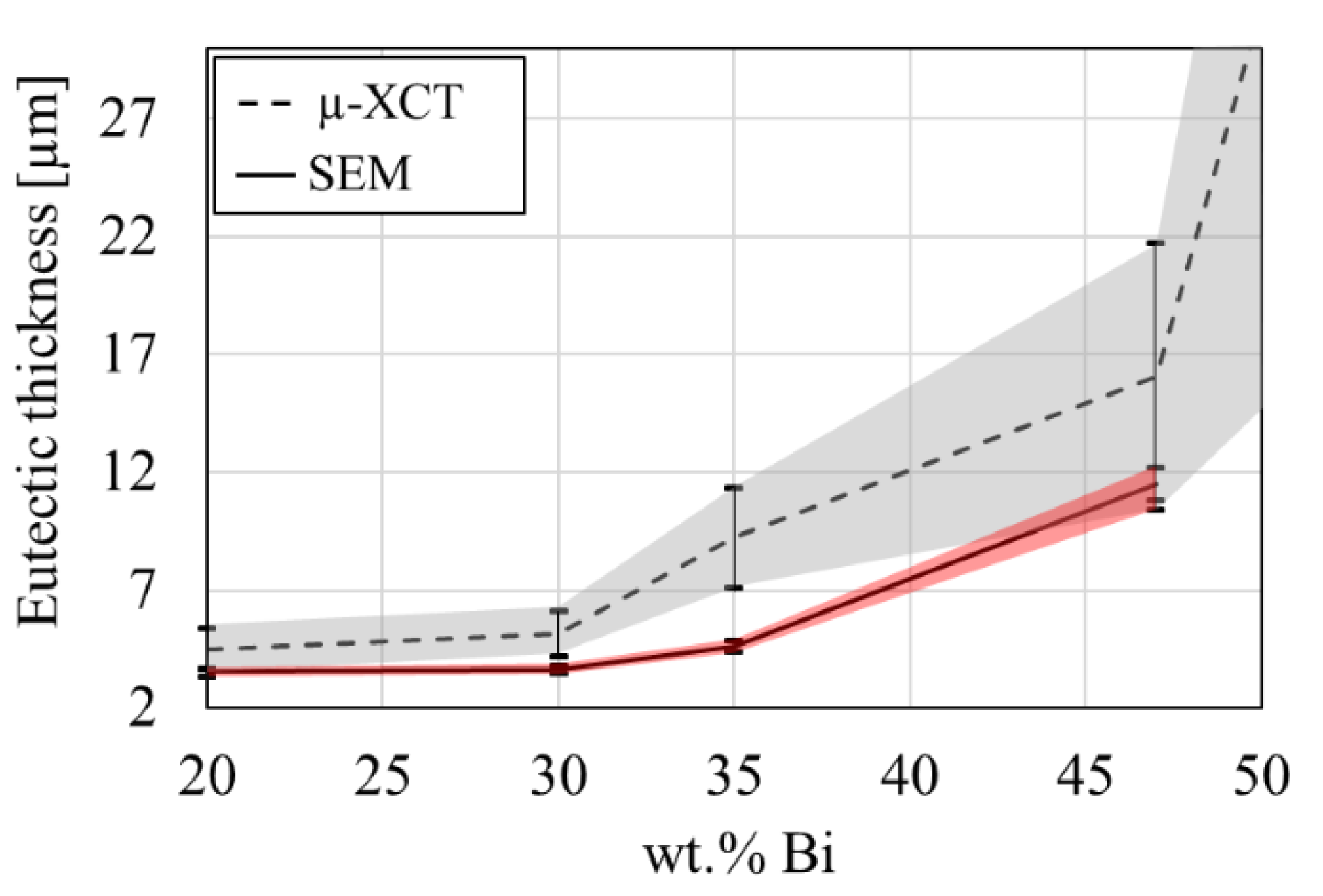
3.3. Eutectic Thickness
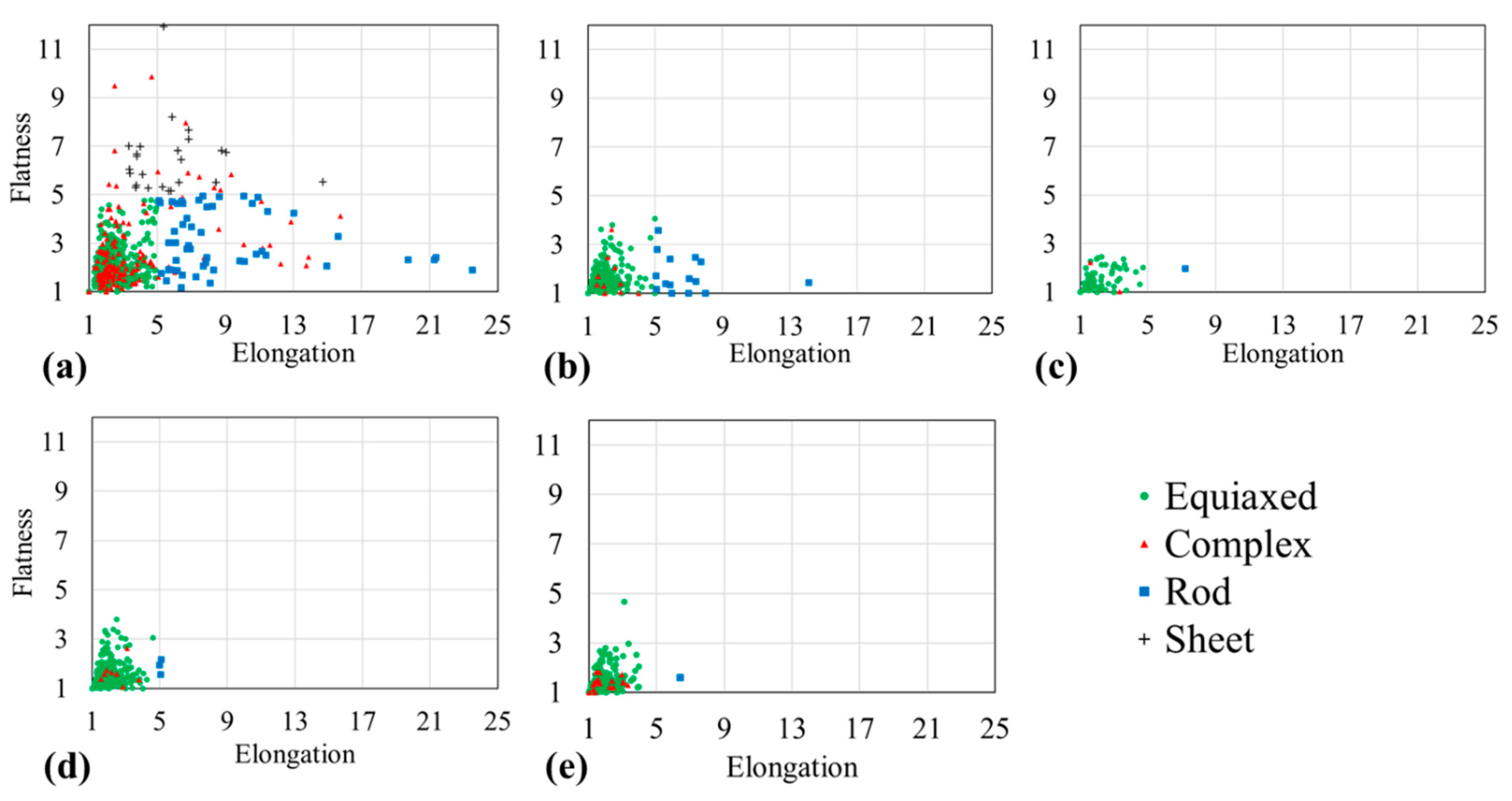
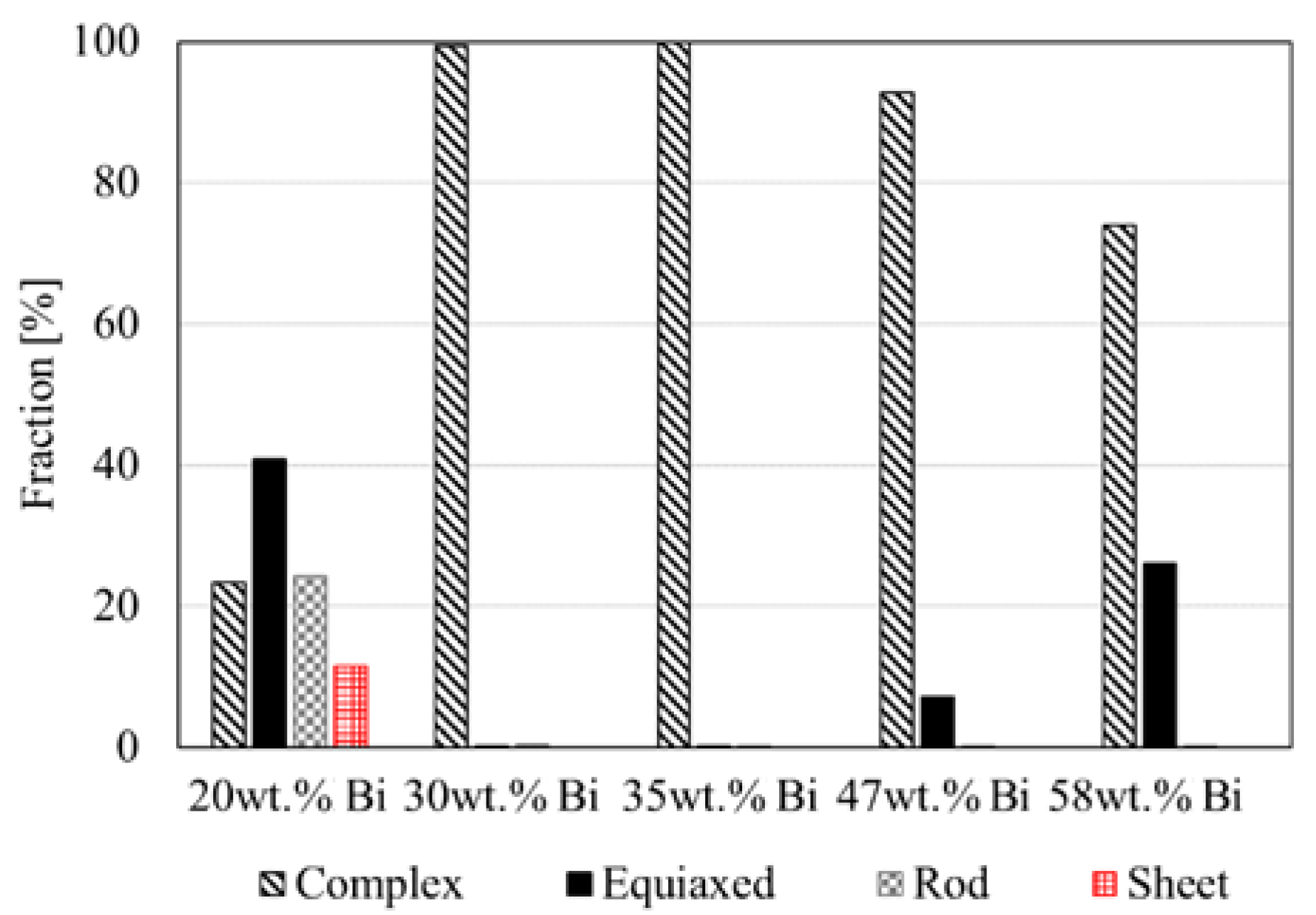
3.4. Morgphology Parameters
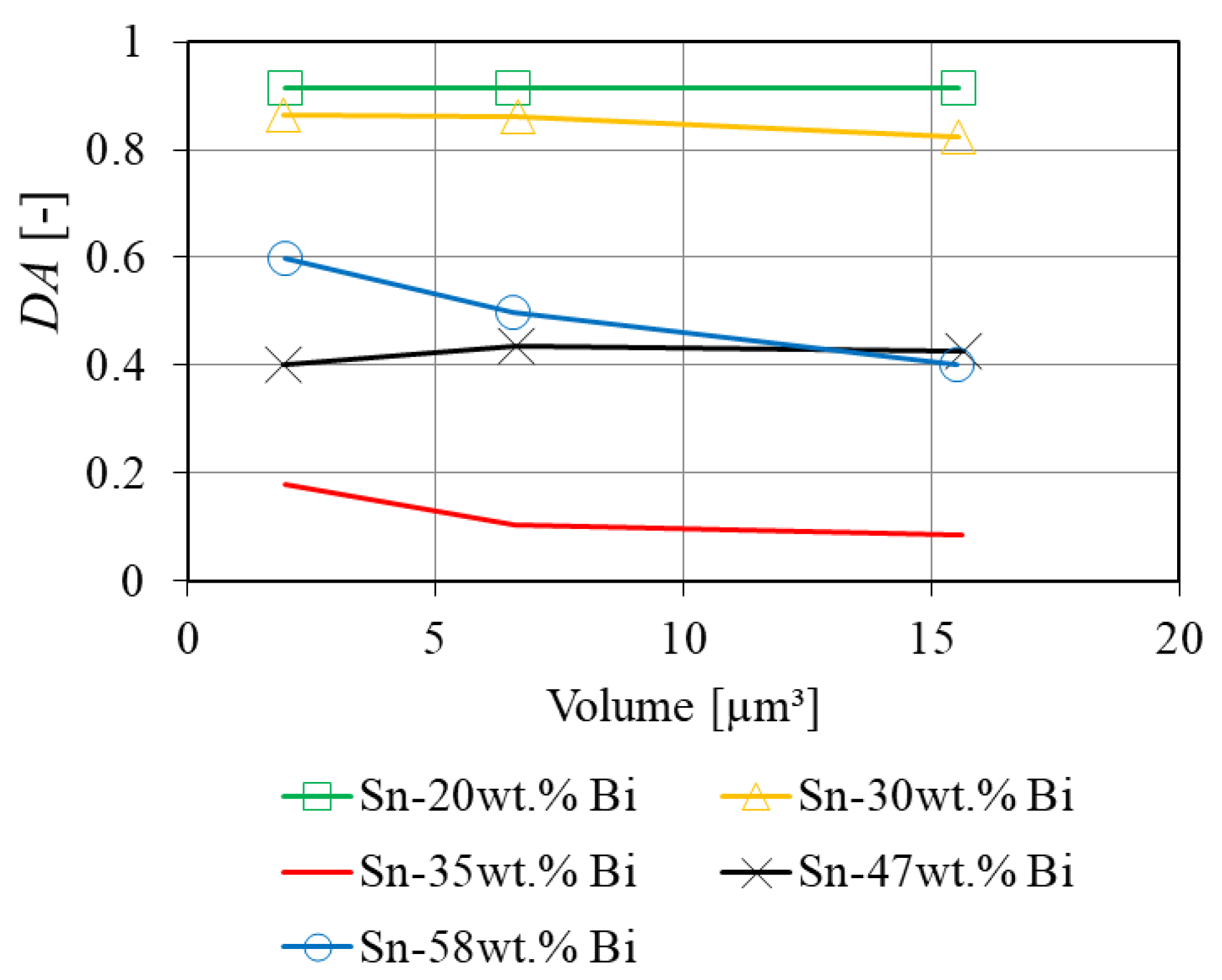
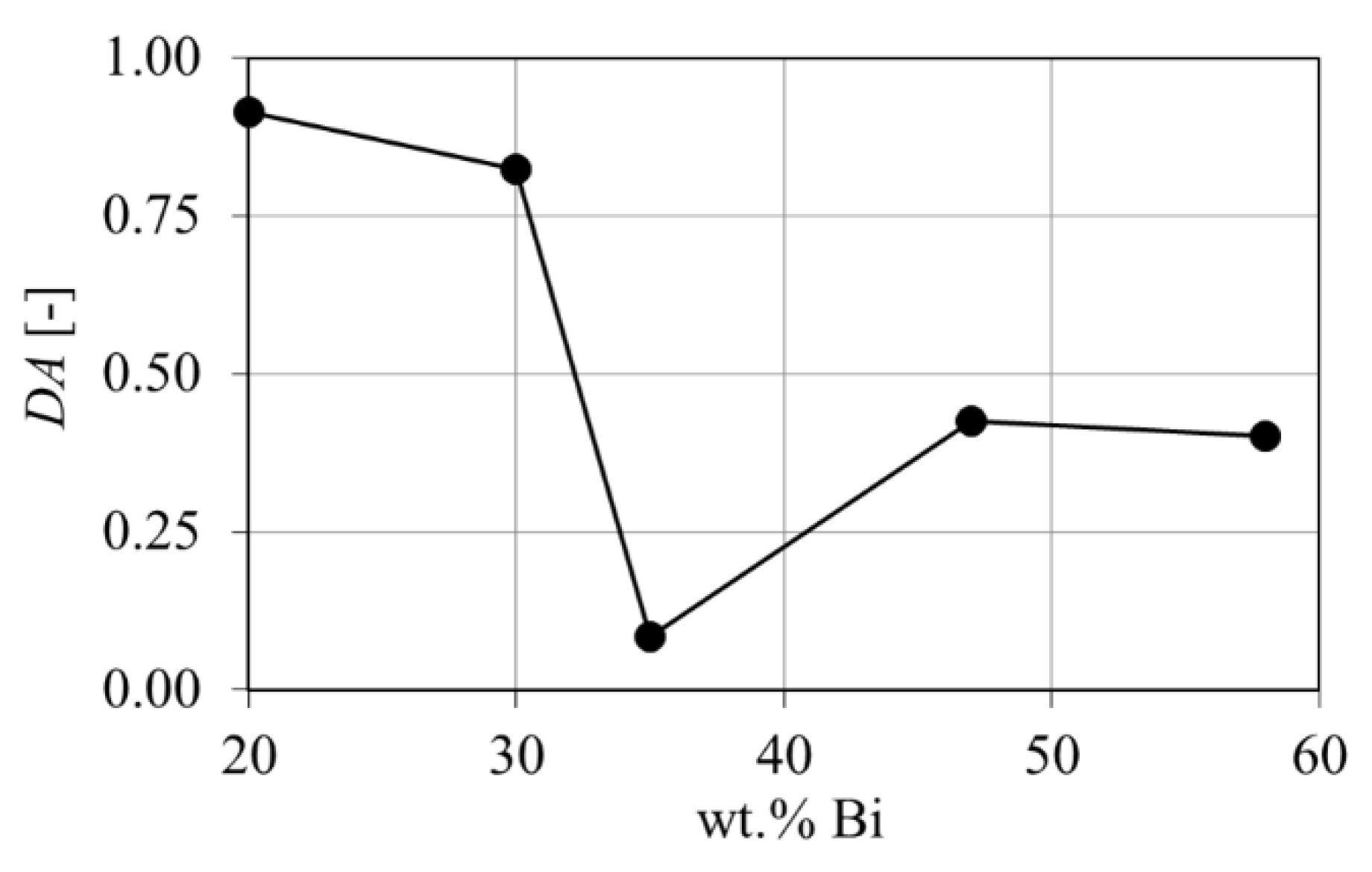
3.5. Geometric Anisotropy
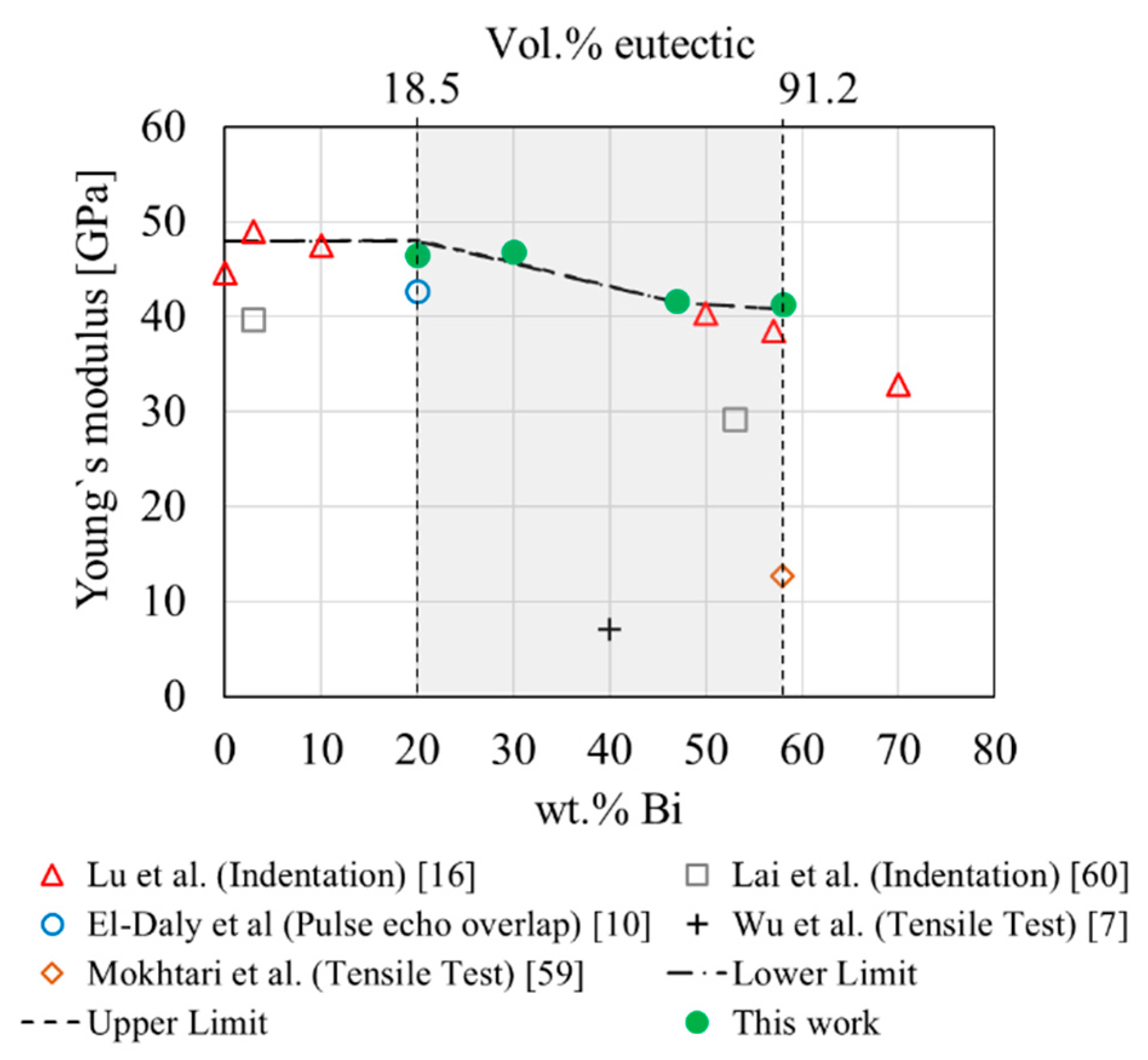
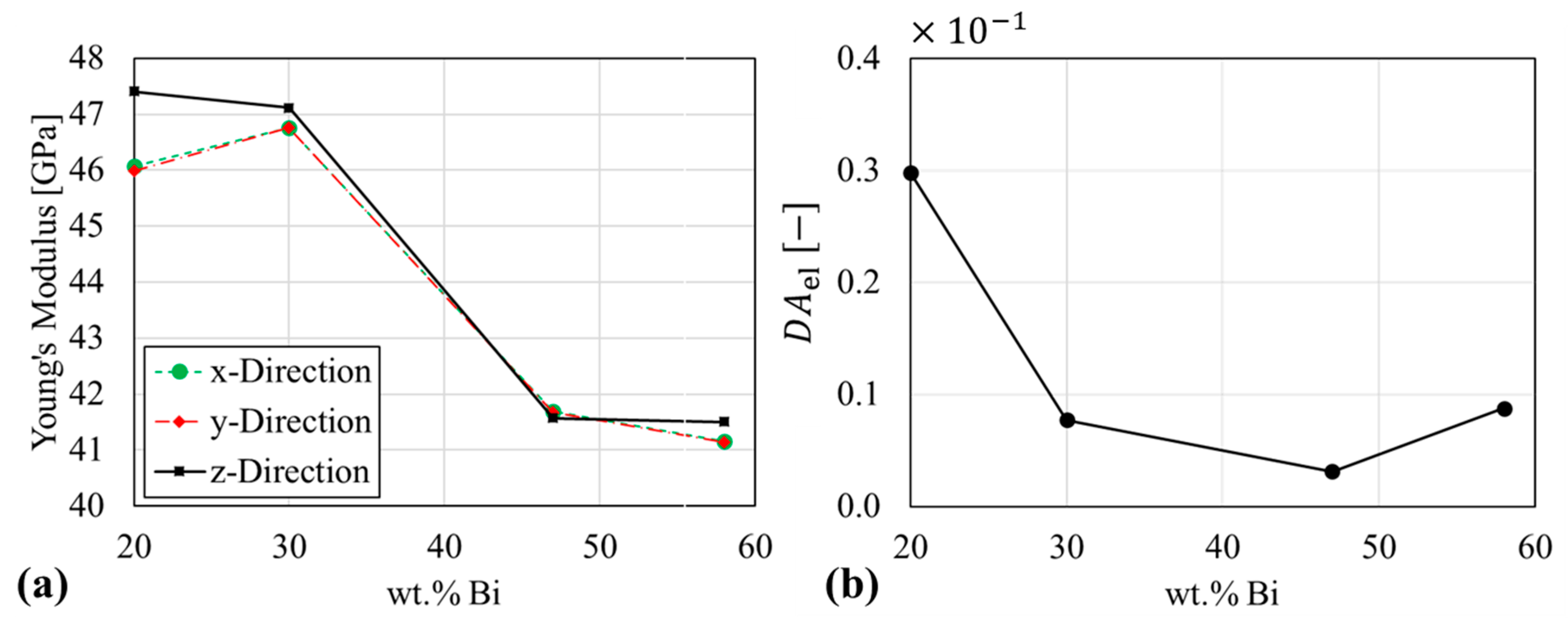
3.6. Computed Elastic Response
4. Discussion
4.1. Eutectic Surface Fraction
4.2. Eutectic Thickness: SEM & µ-XCT
4.3. Morphology Classification
4.4. Morphology and Elastic Anisotropy
4.5. Semi-Solid Shear Strength
4.6. Semi-Solid Uniaxial Compression
4.7. Semi-Solid Permeability
4.8. Implications for Liquid Phase Healing
5. Conclusions
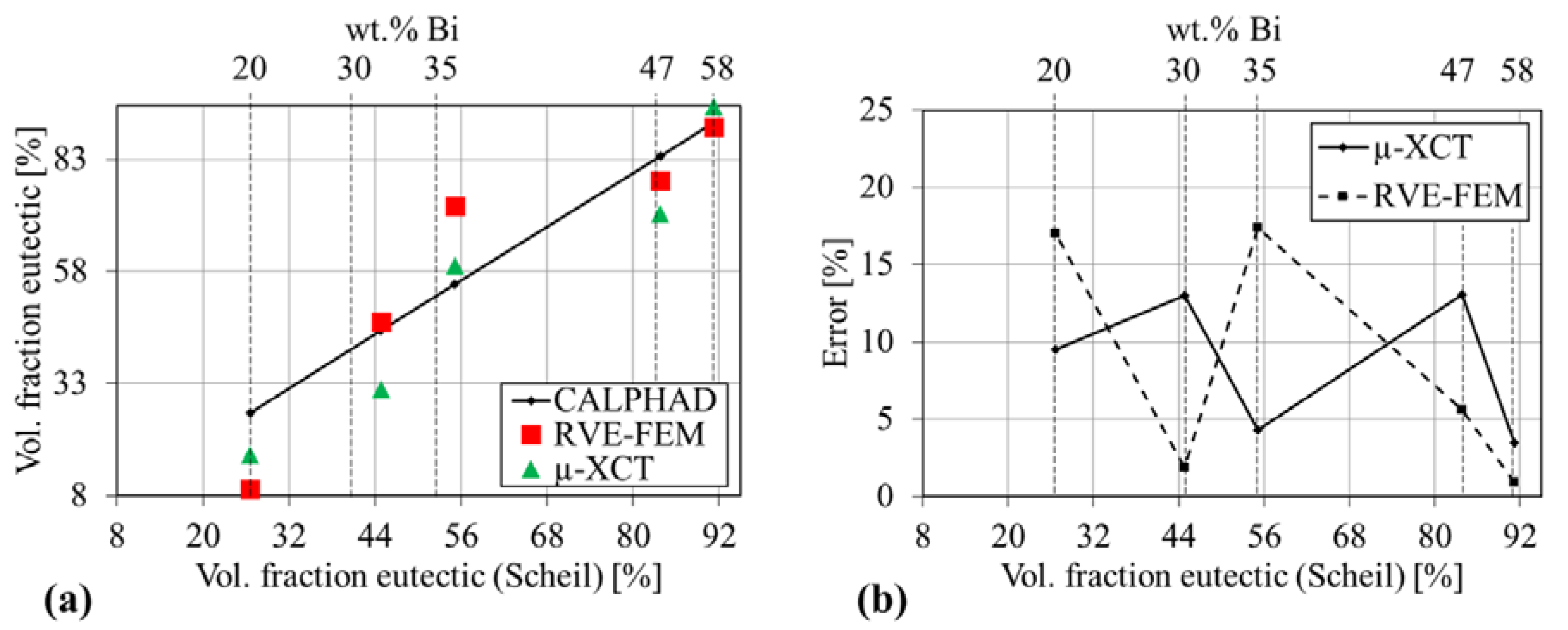
- Eutectic phase fractions measured with µ-XCT showed good correlation with expected values from CALPHAD calculations.
- The Sn-20 wt.% Bi alloy show fragmented domains of eutectic embedded in primary phase. The Sn-35 wt.% Bi alloy reveals interpenetrating primary and eutectic phase, which is reflected by the highest phase boundary area fraction. The Sn-58 wt.% Bi, despite its high eutectic phase fraction, showed a connected dendritic network of primary phase.
- The morphology analysis shows microstructural similarities of the investigated alloys. The Sn-20 wt.% Bi alloy is composed of four geometric features and its microstructure is categorized as “mixed”. The alloys with 30 wt.% and 35 wt.% Bi are composed of mainly “complex-shaped” areas. The alloys of near-eutectic composition, Sn- 47 wt.% Bi and 58 wt.% Bi, constitute from “complex” and “equiaxed” domains.
- The RVE-FE simulations showed an elastically isotropic response, despite significant spatial orientation of the microstructures. The similar elastic properties of primary and eutectic phase reduce the impact of geometric anisotropy. Results are in agreement with linear and inverse rule of mixture.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
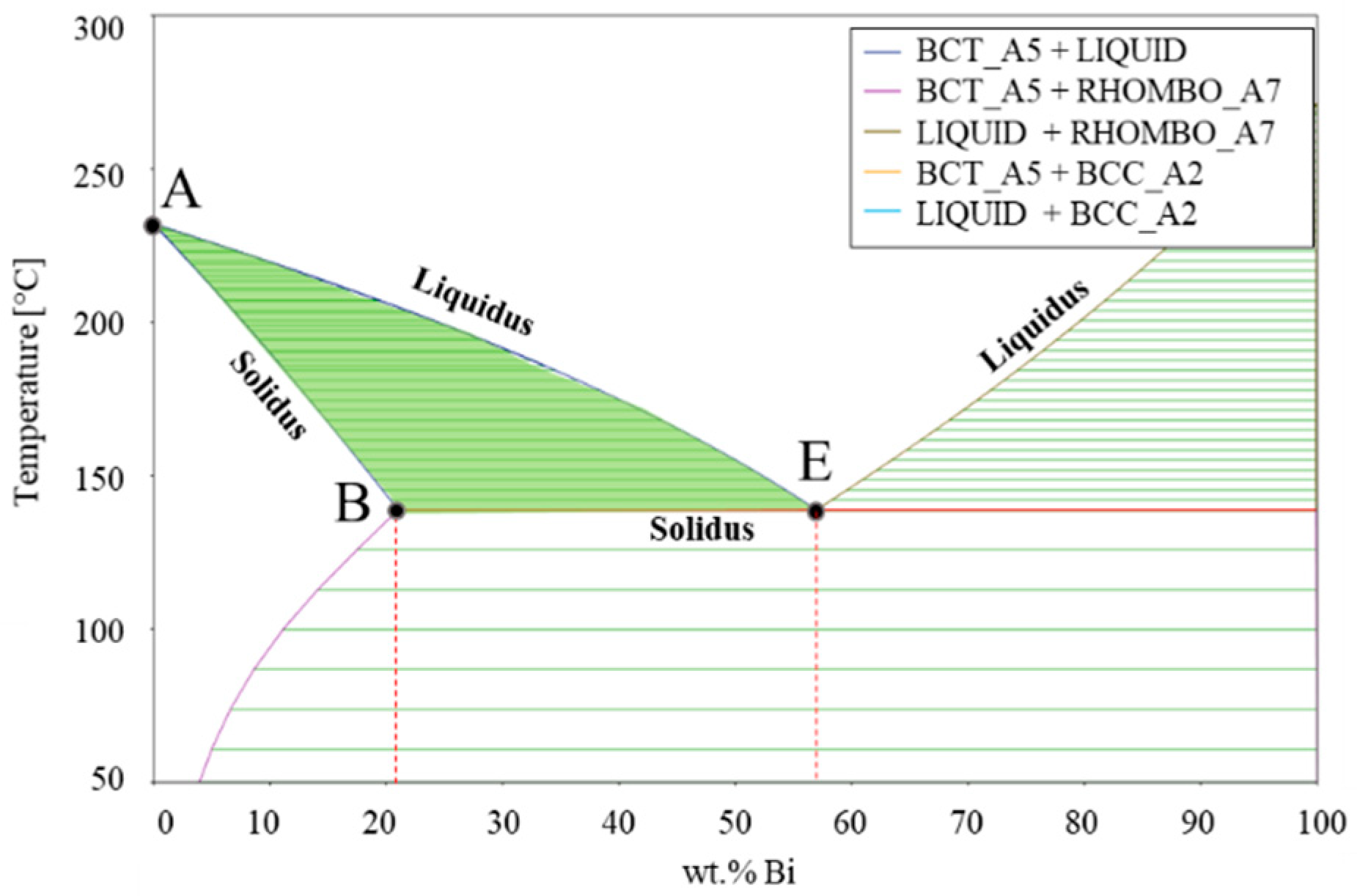
Appendix A. Phase Diagram & Scheil Analysis
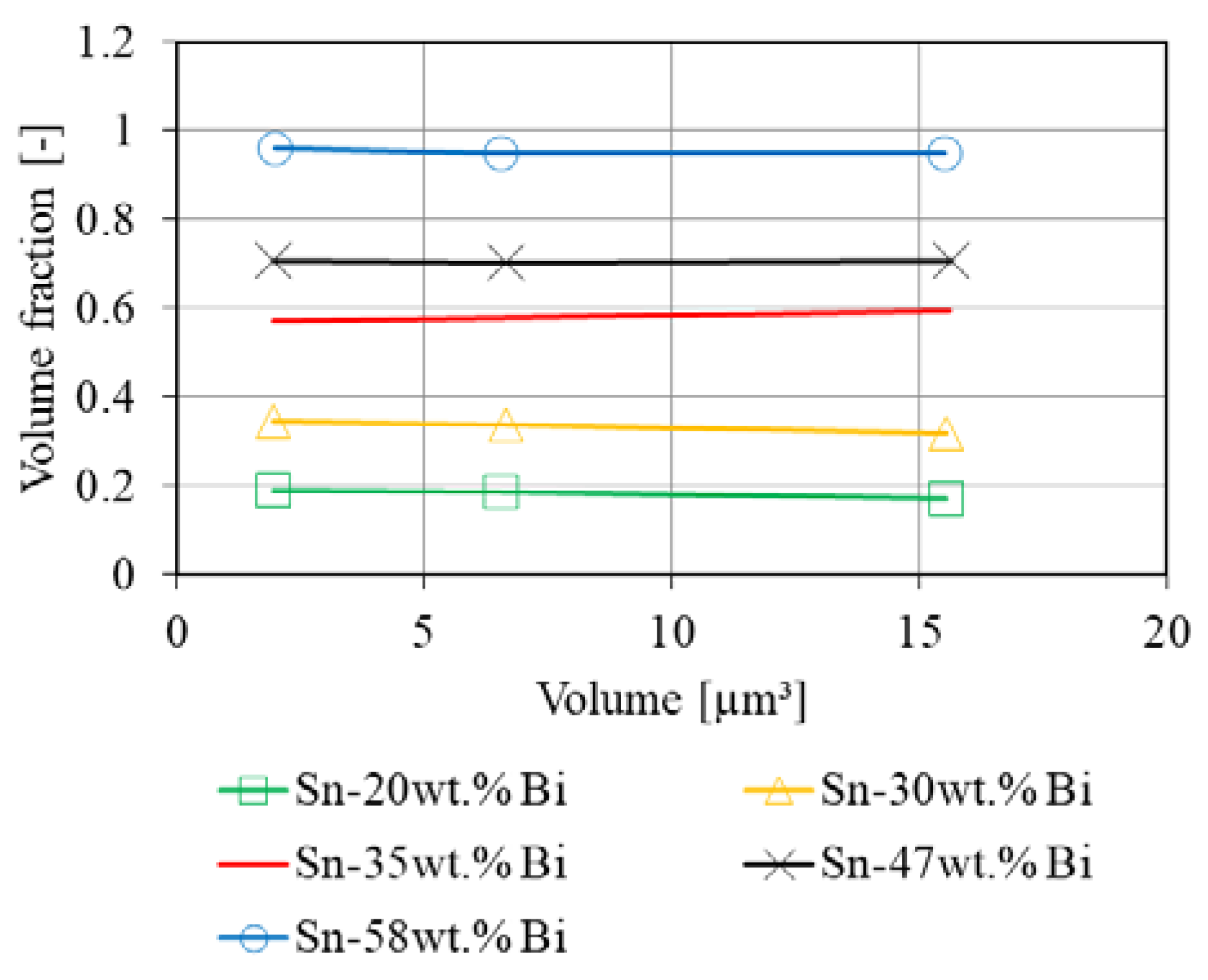
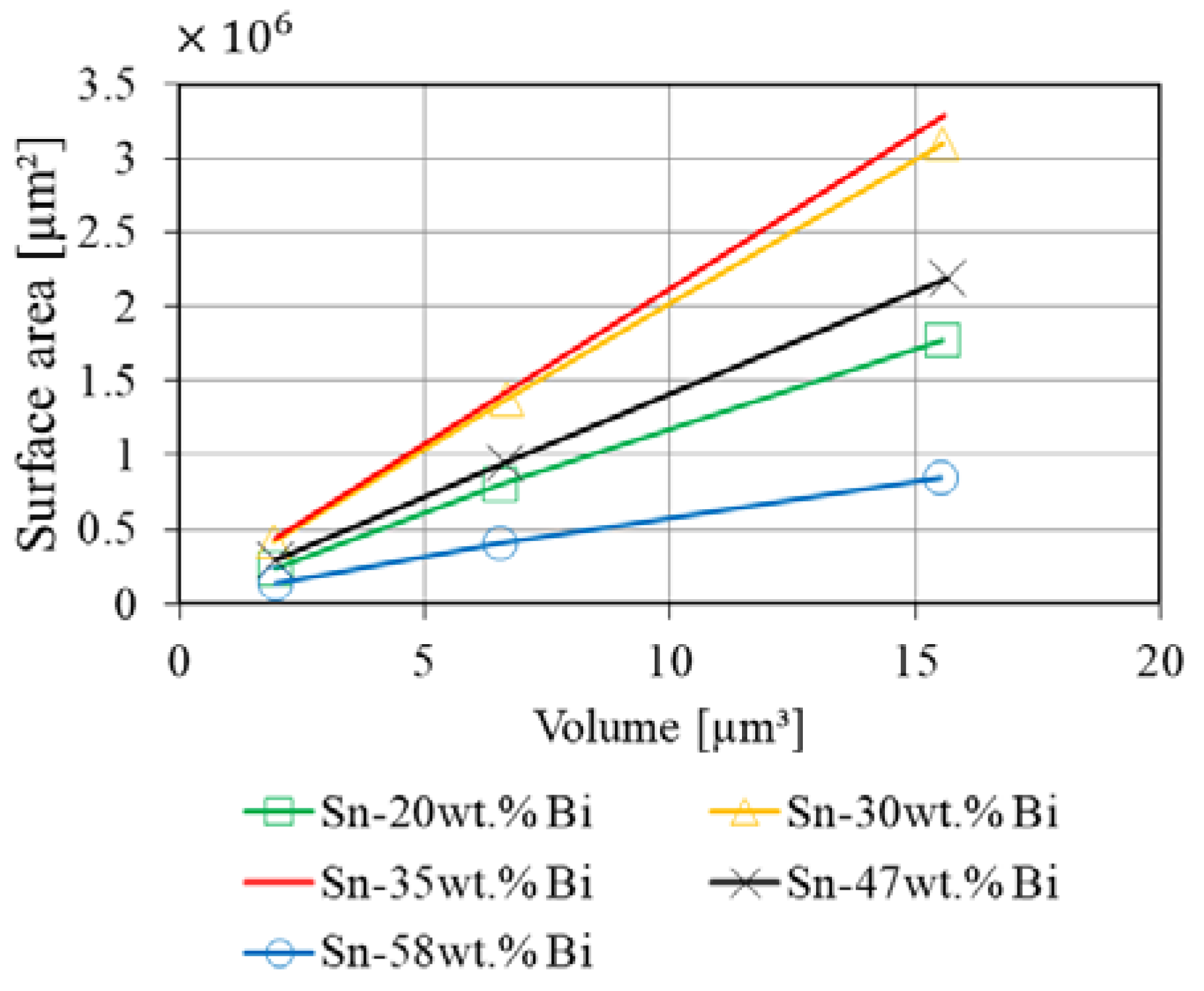
Appendix B. Volume of Interest Variations
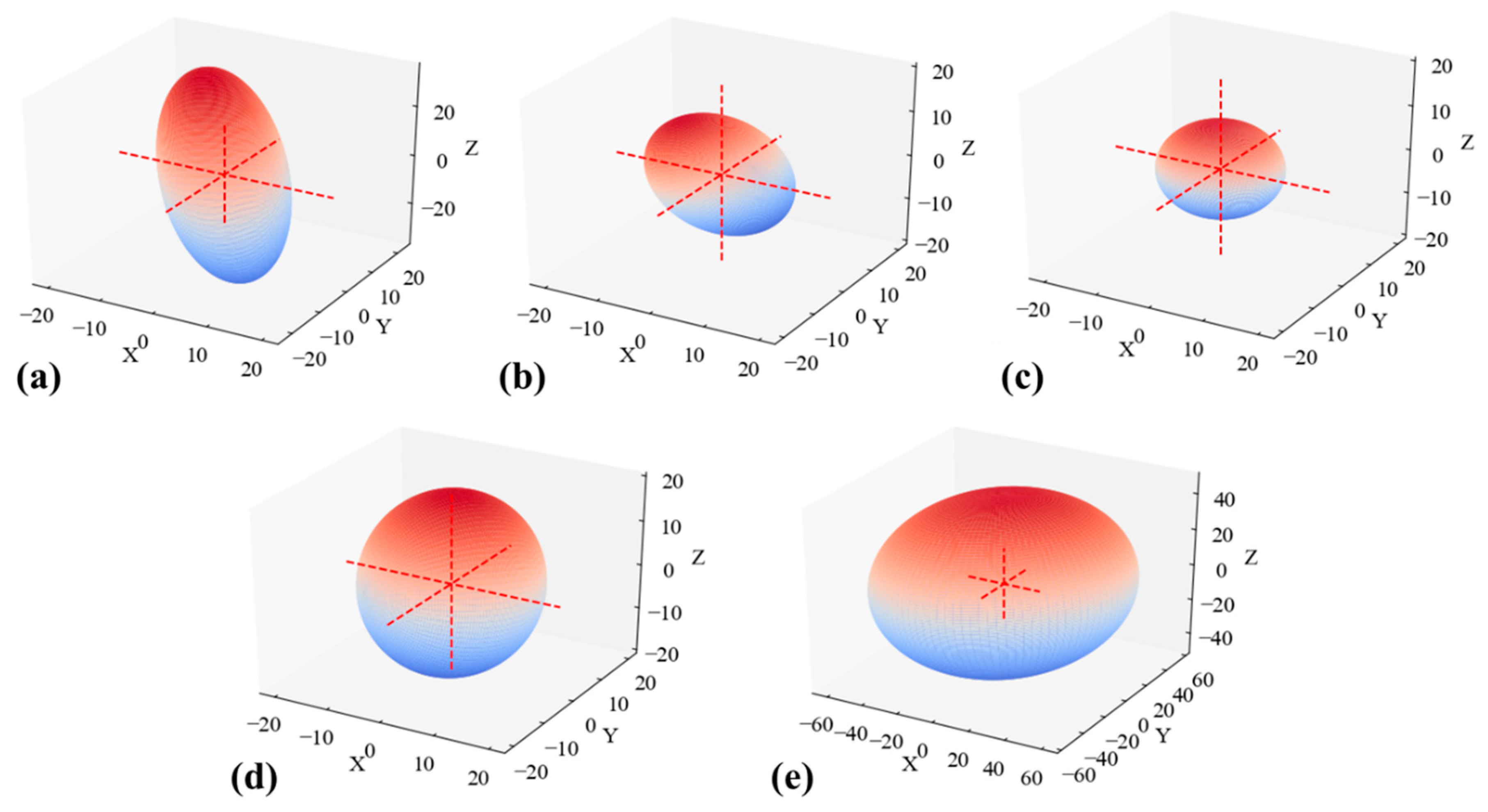
Appendix C. Ellipsoid Fit
| wt.% Bi | DA | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 0.914 | 0.159 | −0.119 | −0.980 | 0.415 | −0.893 | 0.176 | 0.896 | 0.434 | 0.093 | 0.0008 | 0.0018 | 0.0088 |
| 30 | 0.825 | −0.317 | −0.776 | 0.545 | −0.339 | 0.629 | 0.700 | 0.886 | −0.037 | 0.463 | 0.0036 | 0.0067 | 0.0208 |
| 35 | 0.085 | 0.690 | 0.676 | −0.259 | 0.660 | 0.734 | −0.160 | −0.299 | −0.061 | 0.952 | 0.0089 | 0.0090 | 0.0097 |
| 47 | 0.425 | 0.061 | 0.059 | 0.996 | 0.808 | 0.589 | −0.014 | 0.586 | 0.806 | 0.083 | 0.0025 | 0.0038 | 0.0044 |
| 58 | 0.401 | 0.824 | 0.565 | 0.050 | 0.564 | −0.825 | 0.032 | 0.059 | 0.002 | −0.998 | 0.0002 | 0.0004 | 0.0004 |
Appendix D. Volume Fractions of Morphologic Classes
| wt.% Bi | Equiaxed | Rod | Sheet | Complex |
|---|---|---|---|---|
| 58 | 26.034 | 0.033 | 0.0 | 74.0 |
| 47 | 7.076 | 0.108 | 0.0 | 92.8 |
| 35 | 0.065 | 0.002 | 0.0 | 99.9 |
| 30 | 0.244 | 0.271 | 0.0 | 99.5 |
| 20 | 40.859 | 24.171 | 11.5 | 23.4 |
References
- Cheng, F.; Gao, F.; Zhang, J.; Jin, W.; Xiao, X. Tensile properties and wettability of SAC0307 and SAC105 low Ag lead-free solder alloys. J. Mater. Sci. 2011, 46, 3424–3429. [Google Scholar] [CrossRef]
- Wang, F.; Chen, H.; Huang, Y.; Liu, L.; Zhang, Z. Recent progress on the development of Sn-Bi based low-temperature Pb-free solders. J. Mater. Sci. Mater. Electron. 2019, 30, 3222–3243. [Google Scholar] [CrossRef]
- Shalaby, R.M. Effect of silver and indium addition on mechanical properties and indentation creep behavior of rapidly solidified Bi-Sn based lead-free solder alloys. Mater. Sci. Eng. A 2013, 560, 86–95. [Google Scholar] [CrossRef]
- Shen, J.; Pu, Y.; Yin, H.; Luo, D.; Chen, J. Effects of minor Cu and Zn additions on the thermal, microstructure and tensile properties of Sn-Bi-based solder alloys. J. Alloys Compd. 2014, 614, 63–70. [Google Scholar] [CrossRef]
- Yang, C.H.; Zhou, S.; Lin, S.K.; Nishikawa, H. A computational thermodynamics-assisted development of Sn-Bi-In-Ga quaternary alloys as low-temperature Pb-free solders. Materials 2019, 12, 631. [Google Scholar] [CrossRef] [Green Version]
- Ren, G.; Wilding, I.J.; Collins, M.N. Alloying influences on low melt temperature SnZn and SnBi solder alloys for electronic interconnections. J. Alloys Compd. 2016, 665, 251–260. [Google Scholar] [CrossRef]
- Collins, M.N.; Punch, J.; Coyle, R.; Reid, M.; Popowich, R.; Read, P.; Fleming, D. Thermal Fatigue and Failure Analysis of SnAgCu Solder Alloys with Minor Pb Additions. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 1594–1600. [Google Scholar] [CrossRef]
- Wu, X.; Wu, J.; Wang, X.; Yang, J.; Xia, M.; Liu, B. Effect of in addition on microstructure and mechanical properties of Sn-40Bi alloys. J. Mater. Sci. 2020, 55, 3092–3106. [Google Scholar] [CrossRef]
- Silva, B.L.; Xavier, M.G.C.; Garcia, A.; Spinelli, J.E. Cu and Ag additions affecting the solidification microstructure and tensile properties of Sn-Bi lead-free solder alloys. Mater. Sci. Eng. A 2017, 705, 325–334. [Google Scholar] [CrossRef]
- Ren, G.; Collins, M.N. Improved reliability and mechanical performance of Ag microalloyed Sn58Bi solder alloys. Metals 2019, 9, 462. [Google Scholar] [CrossRef] [Green Version]
- Covre, T.O.R.; Da, E.; Silva, B.L.; Spinelli, E.; Garcia, A. Effects of Solidification Thermal Parameters on Microstructure and Mechanical Properties of Sn-Bi Solder Alloys. J. Electron. Mater. 2017, 46, 1754–1769. [Google Scholar] [CrossRef]
- El-Daly, A.A.; Ibrahiem, A.A.; Hammad, A.E. Impact of permanent magnet stirring on dendrite growth and elastic properties of Sn-Bi alloys revealed by pulse echo overlap method. J. Alloys Compd. 2018, 767, 464–473. [Google Scholar] [CrossRef]
- Silva, B.L.; Reinhart, G.; Nguyen-Thi, H.; Mangelinck-Noël, N.; Garcia, A.; Spinelli, J.E. Microstructural development and mechanical properties of a near-eutectic directionally solidified Sn-Bi solder alloy. Mater. Charact. 2015, 107, 43–53. [Google Scholar] [CrossRef]
- Silva, B.L.; Garcia, A.; Spinelli, J.E. Complex eutectic growth and Bi precipitation in ternary Sn-Bi-Cu and Sn-Bi-Ag alloys. J. Alloys Compd. 2017, 691, 600–605. [Google Scholar] [CrossRef]
- Kamioka, H. Temperature variations of elastic moduli up to eutectic temperature in tin-bismuth alloys. Jpn. J. Appl. Phys. 1983, 22, 1805–1809. [Google Scholar] [CrossRef]
- Kamioka, H. Behavior of Tin-Bismuth Alloys near Melting Point Found by Measurement of Sound Velocity. J. Phys. Soc. Jpn. 1984, 53, 1349–1355. [Google Scholar] [CrossRef]
- Shen, L.; Septiwerdani, P.; Chen, Z. Elastic modulus, hardness and creep performance of SnBi alloys using nanoindentation. Mater. Sci. Eng. A 2012, 558, 253–258. [Google Scholar] [CrossRef]
- Maire, E.; Withers, P.J. Quantitative X-ray tomography. Int. Mater. Rev. 2014, 59, 1–43. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Chawla, N.; Pacheco, M.; Noveski, V. Three-dimensional (3D) microstructural characterization and quantification of reflow porosity in Sn-rich alloy/copper joints by X-ray tomography. Mater. Charact. 2011, 62, 970–975. [Google Scholar] [CrossRef]
- Rauer, M.; Volkert, A.; Schreck, T.; Härter, S.; Kaloudis, M. Computed-tomography-based analysis of voids in SnBi57Ag1 solder joints and their influence on the reliability. J. Fail. Anal. Prev. 2014, 14, 272–281. [Google Scholar] [CrossRef] [Green Version]
- Shi, L.; Mei, Y.; Chen, G.; Chen, X. In situ X-ray observation and simulation of ratcheting-fatigue interactions in solder joints. Electron. Mater. Lett. 2017, 13, 97–106. [Google Scholar] [CrossRef]
- Yazzie, K.E.; Williams, J.J.; Phillips, N.C.; De Carlo, F.; Chawla, N. Multiscale microstructural characterization of Sn-rich alloys by three dimensional (3D) X-ray synchrotron tomography and focused ion beam (FIB) tomography. Mater. Charact. 2012, 70, 33–41. [Google Scholar] [CrossRef]
- Kirubanandham, A.; Lujan-Regalado, I.; Vallabhaneni, R.; Chawla, N. Three Dimensional Characterization of Tin Crystallography and Cu6Sn5 Intermetallics in Solder Joints by Multiscale Tomography. JOM 2016, 68, 2879–2887. [Google Scholar] [CrossRef]
- Kaira, C.S.; Mayer, C.R.; De Andrade, V.; De Carlo, F.; Chawla, N. Nanoscale three-dimensional microstructural characterization of an Sn-rich solder alloy using high-resolution transmission X-ray microscopy (TXM). Microsc. Microanal. 2016, 22, 808–813. [Google Scholar] [CrossRef]
- Mertens, J.C.E.; Williams, J.J.; Chawla, N. A Study of Pb-Rich Dendrites in a Near-Eutectic 63Sn-37Pb Solder Microstructure via Laboratory-Scale Micro X-ray Computed Tomography (l XCT). J. Electron. Mater. 2014, 43, 4442–4456. [Google Scholar] [CrossRef]
- Maleki, M.; Cugnoni, J.; Botsis, J. Isothermal ageing of SnAgCu solder alloys: Three-dimensional morphometry analysis of microstructural evolution and its effects on mechanical response. J. Electron. Mater. 2014, 43, 1026–1042. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.; Cheng, Y.; Xu, F.; Helfen, L.; Tian, T.; Di, M.; Chen, C.; Tu, K.; Baumbach, T. Study of electromigration-induced formation of discrete voids in flip-chip solder joints by in-situ 3D laminography observation and fi nite-element modeling. Acta Mater. 2016, 117, 100–110. [Google Scholar] [CrossRef]
- Okereke, M.I.; Ling, Y. A computational investigation of the effect of three-dimensional void morphology on the thermal resistance of solder thermal interface materials. Appl. Therm. Eng. 2018, 142, 346–360. [Google Scholar] [CrossRef]
- Maleki, M.; Cugnoni, J.; Botsis, J. Multi-scale modeling of elasto-plastic response of SnAgCu lead-free solder alloys at different ageing conditions: Effect of microstructure evolution, particle size effects and interfacial failure. Mater. Sci. Eng. A 2016, 661, 132–144. [Google Scholar] [CrossRef]
- Sistaninia, M.; Phillion, A.B.; Drezet, J.M.; Rappaz, M. Three-dimensional granular model of semi-solid metallic alloys undergoing solidification: Fluid flow and localization of feeding. Acta Mater. 2012, 60, 3902–3911. [Google Scholar] [CrossRef] [Green Version]
- Kopp, R.; Choi, J.; Neudenberger, D. Simple compression test and simulation of an Sn-15% Pb alloy in the semi-solid state. J. Mater. Process. Technol. 2003, 135, 317–323. [Google Scholar] [CrossRef]
- Sheykh-jaberi, F.; Cockcroft, S.L.; Maijer, D.M.; Phillion, A.B. Meso-scale modelling of semi-solid deformation in aluminum foundry alloys: Effects of feeding and microstructure on hot tearing susceptibility. J. Mater. Process. Technol. 2020, 279, 116551. [Google Scholar] [CrossRef]
- Sistaninia, M.; Terzi, S.; Phillion, A.B.; Drezet, J.M.; Rappaz, M. 3-D granular modeling and in situ X-ray tomographic imaging: A comparative study of hot tearing formation and semi-solid deformation in Al-Cu alloys. Acta Mater. 2013, 61, 3831–3841. [Google Scholar] [CrossRef] [Green Version]
- Eskin, D.G.; Suyitno; Katgerman, L. Mechanical properties in the semi-solid state and hot tearing of aluminium alloys. Prog. Mater. Sci. 2004, 49, 629–711. [Google Scholar] [CrossRef]
- Siroky, G.; Kraker, E.; Kieslinger, D.; Kozeschnik, E.; Ecker, W. Micromechanics-based damage model for liquid-assisted healing. Int. J. Damage Mech. 2020, 0, 1–22. [Google Scholar] [CrossRef]
- Siroky, G.; Melinc, D.; Magnien, J.; Kozeschnik, E.; Kieslinger, D.; Kraker, E.; Ecker, W. Healing solders: A numerical investigation of damage-healing experimentse. In Proceedings of the 2020 21st International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Cracow, Poland, 5–8 July 2020; pp. 1–7. [Google Scholar]
- Chawla, N.; Sidhu, R.S. Microstructure-based modeling of deformation in Sn-rich (Pb-free) solder alloys. J. Mater. Sci. Mater. Electron. 2007, 18, 175–189. [Google Scholar] [CrossRef]
- Harrigan, T.P.; Mann, R.W. Characterization of microstructural anisotropy in cancellous bone using a second rank tensor. J. Mater. Sci. 1985, 19, 761–767. [Google Scholar] [CrossRef]
- Fang, H.; Versteylen, C.D.; Zhang, S.; Yang, Y.; Cloetens, P.; Ngan-tillard, D. Autonomous filling of creep cavities in Fe-Au alloys studied by synchrotron X-ray nano-tomography. Acta Mater. 2016, 121, 352–364. [Google Scholar] [CrossRef]
- Wadell, H. Volume, Shape, and Roundness of Quartz Particles. J. Geol. 1935, 43. [Google Scholar] [CrossRef]
- Garb, C.; Leitner, M.; Tauscher, M.; Weidt, M.; Brunner, R. Statistical analysis of micropore size distributions in Al-Si castings evaluated by X-ray computed tomography. Int. J. Mater. Res. 2018, 109, 889–899. [Google Scholar] [CrossRef]
- Borbély, A.; Csikor, F.F.; Zabler, S.; Cloetens, P.; Biermann, H. Three-dimensional characterization of the microstructure of a metal-matrix composite by holotomography. Mater. Sci. Eng. A 2004, 367, 40–50. [Google Scholar] [CrossRef]
- Isaac, A.; Sket, F.; Reimers, W.; Camin, B.; Sauthoff, G.; Pyzalla, A.R. In situ 3D quantification of the evolution of creep cavity size, shape, and spatial orientation using synchrotron X-ray tomography. Mater. Sci. Eng. A 2008, 478, 108–118. [Google Scholar] [CrossRef]
- Kroupa, A.; Dinsdale, A.T.; Watson, A.; Vrestal, J.; Vízdal, J.; Zemanova, A. The development of the COST 531 lead-free solders thermodynamic database. J. Miner. Met. Mater. Soc. 2007, 59, 20–25. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doube, M.; Klosowski, M.M.; Arganda-Carreras, I.; Cordelières, F.P.; Dougherty, R.P.; Jackson, J.S.; Schmid, B.; Hutchinson, J.R.; Shefelbine, S.J. BoneJ: Free and extensible bone image analysis in ImageJ. Bone 2010, 47, 1076–1079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hildebrand, T.; Rüegsegger, P. A new method for the model-independent assessment of thickness in three-dimensional images. J. Microsc. 1997, 185, 67–75. [Google Scholar] [CrossRef]
- Chawla, N.; Sidhu, R.S.; Ganesh, V.V. Three-dimensional visualization and microstructure-based modeling of deformation in particle-reinforced composites. Acta Mater. 2006, 54, 1541–1548. [Google Scholar] [CrossRef]
- Mokhtari, O.; Nishikawa, H. Correlation between microstructure and mechanical properties of Sn-Bi-X solders. Mater. Sci. Eng. A 2016, 651, 831–839. [Google Scholar] [CrossRef]
- Lai, Z.; Ye, D. Microstructure and fracture behavior of non eutectic Sn-Bi solder alloys. J. Mater. Sci. Mater. Electron. 2016, 27, 3182–3192. [Google Scholar] [CrossRef]
- Wijaya, A.; Eichinger, B.; Chamasemani, F.F.; Sartory, B.; Hammer, R.; Maier-Kiener, V.; Kiener, D.; Mischitz, M.; Brunner, R. Multi-method characterization approach to facilitate a strategy to design mechanical and electrical properties of sintered copper. Mater. Des. 2020, 197, 109188. [Google Scholar] [CrossRef]
- Bieler, T.R.; Zhou, B.; Blair, L.; Zamiri, A.; Darbandi, P.; Pourboghrat, F.; Lee, T.K.; Liu, K.C. The role of elastic and plastic anisotropy of Sn in recrystallization and damage evolution during thermal cycling in SAC305 solder joints. J. Electron. Mater. 2012, 41, 283–301. [Google Scholar] [CrossRef]
- Martin, C.L.; Brown, S.B.; Favier, D.; Suéry, M. Shear deformation of high solid fraction (>0.60) semi-solid SnPb under various structures. Mater. Sci. Eng. A 1995, 202, 112–122. [Google Scholar] [CrossRef]
- Fuloria, D.; Lee, P.D. An X-ray microtomographic and finite element modeling approach for the prediction of semi-solid deformation behaviour in Al-Cu alloys. Acta Mater. 2009, 57, 5554–5562. [Google Scholar] [CrossRef]
- Kareh, K.M.; Lee, P.D.; Atwood, R.C.; Connolley, T.; Gourlay, C.M. Revealing the micromechanisms behind semi-solid metal deformation with time-resolved X-ray tomography. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef]
- Cai, B.; Karagadde, S.; Yuan, L.; Marrow, T.J.; Connolley, T.; Lee, P.D. In situ synchrotron tomographic quantification of granular and intragranular deformation during semi-solid compression of an equiaxed dendritic Al-Cu alloy. Acta Mater. 2014, 76, 371–380. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Chem. Eng. Res. Des. 1997, 75. [Google Scholar] [CrossRef]










| E | F | ||
|---|---|---|---|
| Sphere | - | - | ≤ 1.15 |
| Equiaxed | <5 | <5 | 1.15 < ≤ 2.5 |
| Rod | ≥5 | <5 | 1.15 < ≤ 2.5 |
| Sheet | - | ≥5 | 1.15 < ≤ 2.5 |
| Complex | - | - | ≥ 2.5 |
| Property | Value [Unit] |
|---|---|
| Young’s modulus primary phase | 50.0 [GPa] |
| Poisson number primary phase | 0.33 [-] |
| Young’s modulus eutectic phase | 40.0 [GPa] |
| Poisson number eutectic phase | 0.33 [-] |
| Composition | |
|---|---|
| Sn-20 wt.% Bi | 17.1% |
| Sn-30 wt.% Bi | 31.8% |
| Sn-35 wt.% Bi | 59.4% |
| Sn-47 wt.% Bi | 70.8% |
| Sn-58 wt.% Bi | 94.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siroky, G.; Kraker, E.; Rosc, J.; Kieslinger, D.; Brunner, R.; van der Zwaag, S.; Kozeschnik, E.; Ecker, W. Analysis of Sn-Bi Solders: X-ray Micro Computed Tomography Imaging and Microstructure Characterization in Relation to Properties and Liquid Phase Healing Potential. Materials 2021, 14, 153. https://doi.org/10.3390/ma14010153
Siroky G, Kraker E, Rosc J, Kieslinger D, Brunner R, van der Zwaag S, Kozeschnik E, Ecker W. Analysis of Sn-Bi Solders: X-ray Micro Computed Tomography Imaging and Microstructure Characterization in Relation to Properties and Liquid Phase Healing Potential. Materials. 2021; 14(1):153. https://doi.org/10.3390/ma14010153
Chicago/Turabian StyleSiroky, Georg, Elke Kraker, Jördis Rosc, Dietmar Kieslinger, Roland Brunner, Sybrand van der Zwaag, Ernst Kozeschnik, and Werner Ecker. 2021. "Analysis of Sn-Bi Solders: X-ray Micro Computed Tomography Imaging and Microstructure Characterization in Relation to Properties and Liquid Phase Healing Potential" Materials 14, no. 1: 153. https://doi.org/10.3390/ma14010153
APA StyleSiroky, G., Kraker, E., Rosc, J., Kieslinger, D., Brunner, R., van der Zwaag, S., Kozeschnik, E., & Ecker, W. (2021). Analysis of Sn-Bi Solders: X-ray Micro Computed Tomography Imaging and Microstructure Characterization in Relation to Properties and Liquid Phase Healing Potential. Materials, 14(1), 153. https://doi.org/10.3390/ma14010153









