Viscosity Model for Nanoparticulate Suspensions Based on Surface Interactions
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiments
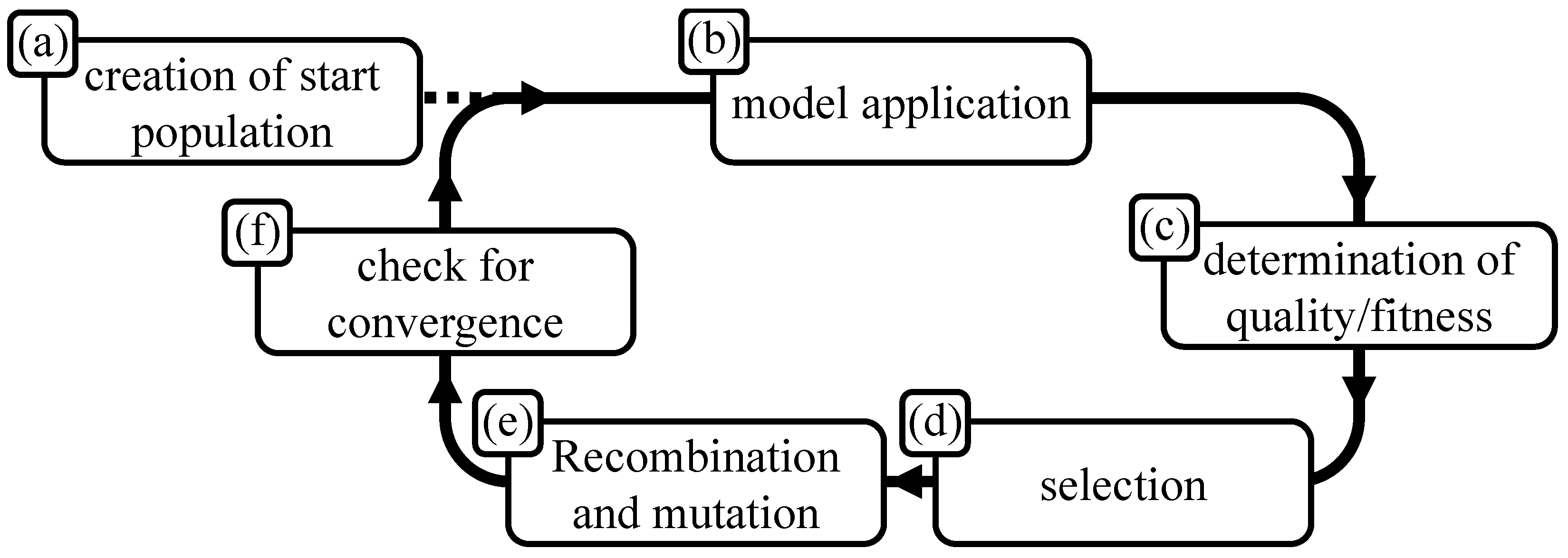
2.2. Genetic Algorithm
3. Model Development
3.1. Fundamental Considerations
3.2. Derivation of Model Equations
3.2.1. Model Framework and Adopted Sub-Models
3.2.2. Determination of Total Particle Interaction
3.2.3. Link between Surface Forces and Viscosity Increase
3.3. Identification of Best Model Variant
4. Results and Discussion
4.1. Convergence Studies
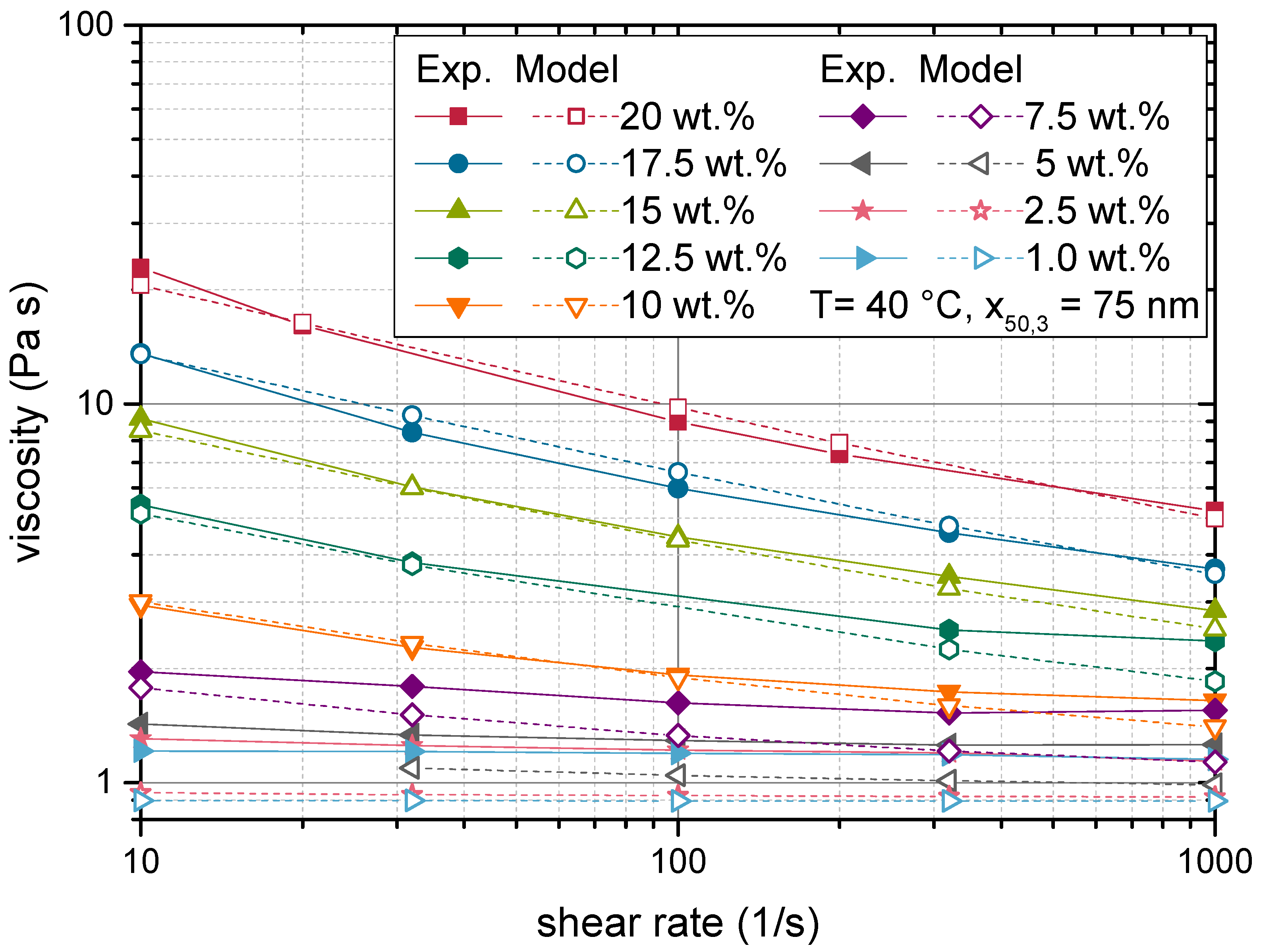
4.2. Model Calibration and Assessment of Descriptive Properties
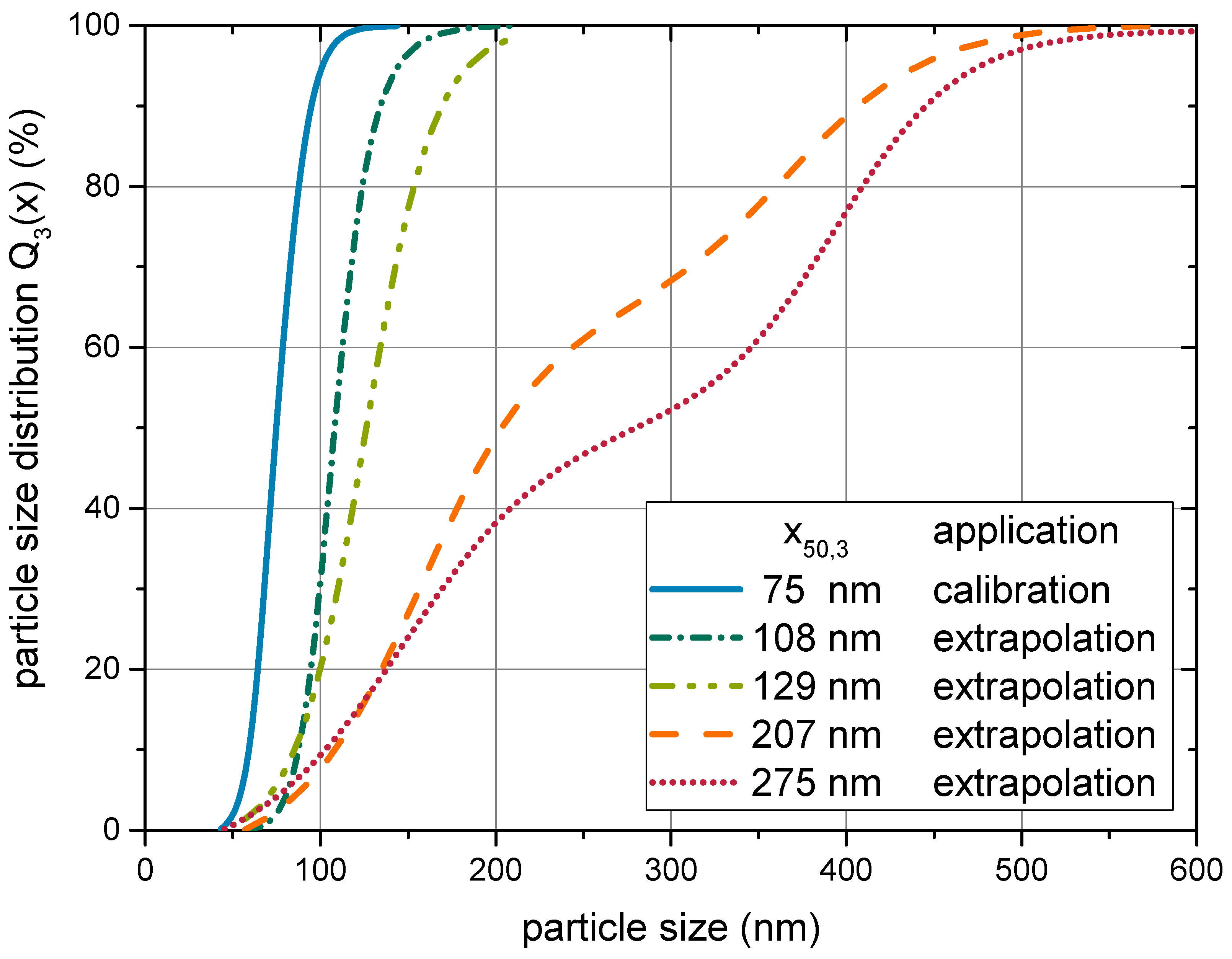
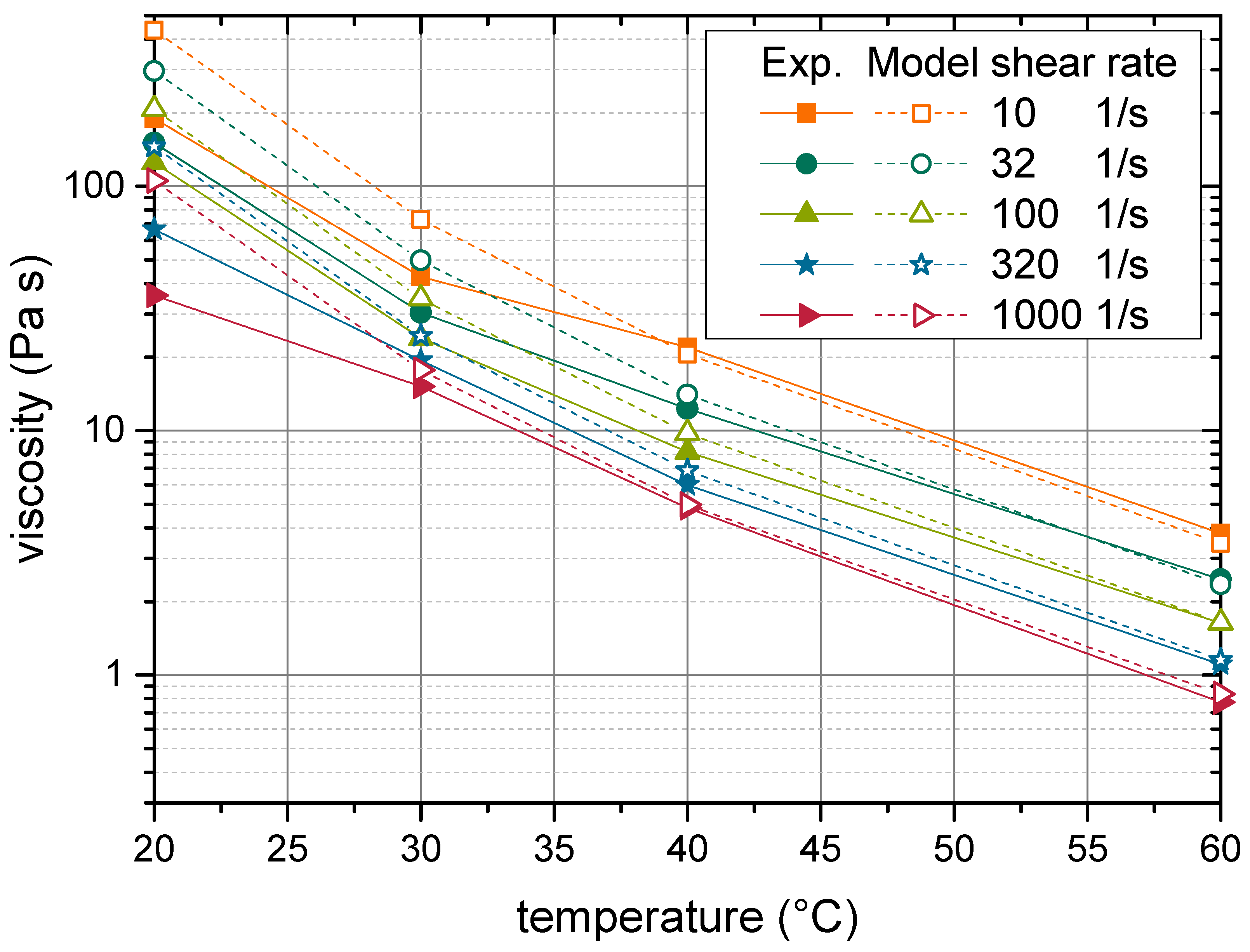
4.3. Predictive Properties
4.4. Comparison to Existing Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a | centre distance |
| A | Hamaker constant |
| b | surface distance |
| approximation parameter to Equation (31) | |
| approximation parameter to Equation (31) | |
| number fraction | |
| surface fraction | |
| volumetric solids content | |
| D | diffusion constant |
| F | force |
| h | Planck constant |
| hard sphere | |
| I | ion strength |
| k | constant |
| Boltzmann constant | |
| Faraday constant | |
| refractive index | |
| Baxter parameter [66] | |
| Péclet number | |
| r | radius |
| relative | |
| R | gas constant |
| Reynolds number | |
| suspension | |
| T | temperature |
| v | velocity |
| V | volumetric solids content |
| W | potential |
| x | particle size |
| z | z-parameter |
| resolution parameter | |
| dielectric constant | |
| -parameter | |
| shear rate | |
| viscosity | |
| Debye–Hückel parameter | |
| valence of ions | |
| main absorption frequency in the UV spectrum | |
| density | |
| shear stress |
Appendix A. Principles and Features of the Genetic Algorithm
References
- Einstein, A. Eine Neue Bestimmung der Moleküldimensionen. Ph.D. Thesis, Universität Zürich, Zurich, Switzerland, 1906. [Google Scholar] [CrossRef]
- Einstein, A. Berichtigung zu meiner Arbeit: “Eine neue Bestimmung der Moleküldimensionen”. Ann. Der Phys. 1911, 339, 591–592. [Google Scholar] [CrossRef]
- Murshed, S.S.; Estellé, P. A state of the art review on viscosity of nanofluids. Renew. Sustain. Energy Rev. 2017, 76, 1134–1152. [Google Scholar] [CrossRef]
- Sharma, A.K.; Tiwari, A.K.; Dixit, A.R. Rheological behaviour of nanofluids: A review. Renew. Sustain. Energy Rev. 2016, 53, 779–791. [Google Scholar] [CrossRef]
- Finke, B.; Nolte, H.; Schilde, C.; Kwade, A. Stress mechanisms acting during the dispersing in highly viscous media and their impact on the production of nanoparticle composites. Chem. Eng. Res. Des. 2019, 141, 56–65. [Google Scholar] [CrossRef]
- Rutgers, I.R. Relative viscosity and concentration. Rheol. Acta 1962, 2, 305–348. [Google Scholar] [CrossRef]
- Jeffrey, D.J.; Acrivos, A. The rheological properties of suspensions of rigid particles. AIChE J. 1976, 22, 417–432. [Google Scholar] [CrossRef]
- Stickel, J.J.; Powell, R.L. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 2005, 37, 129–149. [Google Scholar] [CrossRef]
- Mewis, J.; Wagner, N.J. Colloidal Suspension Rheology; Cambridge Series in Chemical Engineering; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Booth, F. The electroviscous effect for suspensions of solid spherical particles. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 203, 533–551. [Google Scholar] [CrossRef]
- Russel, W.B. The rheology of suspensions of charged rigid spheres. J. Fluid Mech. 1978, 85, 209. [Google Scholar] [CrossRef]
- Russel, W.B. Review of the Role of Colloidal Forces in the Rheology of Suspensions. J. Rheol. 1980, 24, 287–317. [Google Scholar] [CrossRef]
- Bossis, G.; Brady, J.F. Dynamic simulation of sheared suspensions. I. General method. J. Chem. Phys. 1984, 80, 5141–5154. [Google Scholar] [CrossRef]
- Brady, J.F.; Bossis, G. The rheology of concentrated suspensions of spheres in simple shear flow by numerical simulation. J. Fluid Mech. 1985, 155, 105. [Google Scholar] [CrossRef]
- Bossis, G.; Brady, J.F. The rheology of Brownian suspensions. J. Chem. Phys. 1989, 91, 1866–1874. [Google Scholar] [CrossRef]
- Brady, J.F.; Morris, J.F. Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 1997, 348, 103–139. [Google Scholar] [CrossRef]
- Batchelor, G.K. The stress system in a suspension of force-free particles. J. Fluid Mech. 1970, 41, 545. [Google Scholar] [CrossRef]
- Finke, B.; Kwade, A.; Schilde, C. Numerical Simulation of the Rheological Behavior of Nanoparticulate Suspensions. Materials 2020, 13, 4288. [Google Scholar] [CrossRef]
- Russel, W.B. The Huggins coefficient as a means for characterizing suspended particles. J. Chem. Soc. Faraday Trans. 2 1984, 80, 31. [Google Scholar] [CrossRef]
- Cichocki, B.; Felderhof, B.U. Diffusion coefficients and effective viscosity of suspensions of sticky hard spheres with hydrodynamic interactions. J. Chem. Phys. 1990, 93, 4427–4432. [Google Scholar] [CrossRef]
- Krishnamurthy, L.n.; Wagner, N.J. The influence of weak attractive forces on the microstructure and rheology of colloidal dispersions. J. Rheol. 2005, 49, 475–499. [Google Scholar] [CrossRef][Green Version]
- Buscall, R.; McGowan, J.I.; Morton-Jones, A.J. The rheology of concentrated dispersions of weakly attracting colloidal particles with and without wall slip. J. Rheol. 1993, 37, 621–641. [Google Scholar] [CrossRef]
- Masoud Hosseini, S.; Moghadassi, A.R.; Henneke, D.E. A new dimensionless group model for determining the viscosity of nanofluids. J. Therm. Anal. Calorim. 2010, 100, 873–877. [Google Scholar] [CrossRef]
- Masoumi, N.; Sohrabi, N.; Behzadmehr, A. A new model for calculating the effective viscosity of nanofluids. J. Phys. D Appl. Phys. 2009, 42, 055501. [Google Scholar] [CrossRef]
- Sharifpur, M.; Adio, S.A.; Meyer, J.P. Experimental investigation and model development for effective viscosity of Al2O3–glycerol nanofluids by using dimensional analysis and GMDH-NN methods. Int. Commun. Heat Mass Transf. 2015, 68, 208–219. [Google Scholar] [CrossRef]
- de Noni, A., Jr.; Garcia, D.E.; Hotza, D. A modified model for the viscosity of ceramic suspensions. Ceram. Int. 2002, 28, 731–735. [Google Scholar] [CrossRef]
- Mahbubul, I.M.; Saidur, R.; Amalina, M.A. Latest developments on the viscosity of nanofluids. Int. J. Heat Mass Transf. 2012, 55, 874–885. [Google Scholar] [CrossRef]
- Jux, M.; Finke, B.; Mahrholz, T.; Sinapius, M.; Kwade, A.; Schilde, C. Effects of Al(OH)O nanoparticle agglomerate size in epoxy resin on tension, bending, and fracture properties. J. Nanoparticle Res. 2017, 19, 241. [Google Scholar] [CrossRef]
- Nolte, H.; Schilde, C.; Kwade, A. Determination of particle size distributions and the degree of dispersion in nanocomposites. Compos. Sci. Technol. 2012, 72, 948–958. [Google Scholar] [CrossRef]
- Thon, C.; Finke, B.; Kwade, A.; Schilde, C. Artificial Intelligence in Process Engineering. Adv. Intell. Syst. 2021, 3, 2000261. [Google Scholar] [CrossRef]
- Doi, M.; Chen, D. Simulation of aggregating colloids in shear flow. J. Chem. Phys. 1989, 90, 5271–5279. [Google Scholar] [CrossRef]
- Chang, C.; Powell, R.L. Hydrodynamic transport properties of concentrated suspensions. AIChE J. 2002, 48, 2475–2480. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Elsevier Science: Saint Louis, MO, USA, 2015. [Google Scholar]
- Lagaly, G.; Schulz, O.; Zimehl, R. Dispersionen und Emulsionen; Steinkopff: Heidelberg, Germany, 1997. [Google Scholar] [CrossRef]
- Batchelor, G.K. Transport Properties of Two-Phase Materials with Random Structure. Annu. Rev. Fluid Mech. 1974, 6, 227–255. [Google Scholar] [CrossRef]
- Macdonald, J.R. Nearest-neighbor distribution functions and mean separation for impenetrable particles in one to three dimensions. Phys. Review. A Mol. Opt. Phys. 1992, 46, R2988–R2991. [Google Scholar] [CrossRef]
- Raasch, J. Beanspruchung und Verhalten suspendierter Feststoffteilchen in Scherströmungen hoher Zähigkeit. Ph.D. Thesis, Technische Hochschule Karlsruhe, Karlsruhe, Germany, 1961. [Google Scholar]
- Mueller, S.; Llewellin, E.W.; Mader, H.M. The rheology of suspensions of solid particles. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1201–1228. [Google Scholar] [CrossRef]
- Batchelor, G.K.; Green, J.T. The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 1972, 56, 375–400. [Google Scholar] [CrossRef]
- Wilson, H.J.; Davis, R.H. The viscosity of a dilute suspension of rough spheres. J. Fluid Mech. 2000, 421, 339–367. [Google Scholar] [CrossRef]
- Wilson, H.J.; Davis, R.H. Shear stress of a monolayer of rough spheres. J. Fluid Mech. 2002, 452. [Google Scholar] [CrossRef]
- Metzger, B.; Pham, P.; Butler, J.E. Irreversibility and chaos: Role of lubrication interactions in sheared suspensions. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 87, 052304. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, R.L. Discontinuous and Dilatant Viscosity Behavior in Concentrated Suspensions. I. Observation of a Flow Instability. Trans. Soc. Rheol. 1972, 16, 155–173. [Google Scholar] [CrossRef]
- Vand, V. Viscosity of Solutions and Suspensions. I. Theory. J. Phys. Chem. 1948, 52, 277–299. [Google Scholar] [CrossRef]
- Hoffman, R. Discontinuous and dilatant viscosity behavior in concentrated suspensions. II. Theory and experimental tests. J. Colloid Interface Sci. 1974, 46, 491–506. [Google Scholar] [CrossRef]
- Krieger, I.M. Flow Porperties of Latex and Concentrated Solutions. In Surfaces and Coatings Related to Paper and Wood; Marchessault, R.H., Skaar, C., Eds.; Syracuse University Press: New York, NY, USA, 1967; pp. 25–51. [Google Scholar]
- Krieger, I.M. Rheology of monodisperse latices. Adv. Colloid Interface Sci. 1972, 3, 111–136. [Google Scholar] [CrossRef]
- Wildemuth, C.R.; Williams, M.C. Viscosity of suspensions modeled with a shear-dependent maximum packing fraction. Rheol. Acta 1984, 23, 627–635. [Google Scholar] [CrossRef]
- Lionberger, R.A. Viscosity of bimodal and polydisperse colloidal suspensions. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2002, 65, 061408. [Google Scholar] [CrossRef] [PubMed]
- Koelman, J.M.V.A.; Hoogerbrugge, P.J. Dynamic Simulations of Hard-Sphere Suspensions Under Steady Shear. Europhys. Lett. 1993, 21, 363–368. [Google Scholar] [CrossRef]
- Batchelor, G.K.; Green, J.T. The determination of the bulk stress in a suspension of spherical particles to order c 2. J. Fluid Mech. 1972, 56, 401. [Google Scholar] [CrossRef]
- Batchelor, G.K. The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 1977, 83, 97. [Google Scholar] [CrossRef]
- Brady, J.F. The rheological behavior of concentrated colloidal dispersions. J. Chem. Phys. 1993, 99, 567–581. [Google Scholar] [CrossRef]
- Maranzano, B.J.; Wagner, N.J. The effects of particle size on reversible shear thickening of concentrated colloidal dispersions. J. Chem. Phys. 2001, 114, 10514–10527. [Google Scholar] [CrossRef]
- Boersma, W.H.; Laven, J.; Stein, H.N. Shear thickening (dilatancy) in concentrated dispersions. AIChE J. 1990, 36, 321–332. [Google Scholar] [CrossRef]
- Chen, H.; Ding, Y.; Tan, C. Rheological behaviour of nanofluids. New J. Phys. 2007, 9, 367. [Google Scholar] [CrossRef]
- Mooney, M. The viscosity of a concentrated suspension of spherical particles. J. Colloid Sci. 1951, 6, 162–170. [Google Scholar] [CrossRef]
- Maron, S.H.; Pierce, P.E. Application of ree-eyring generalized flow theory to suspensions of spherical particles. J. Colloid Sci. 1956, 11, 80–95. [Google Scholar] [CrossRef]
- Krieger, I.M.; Dougherty, T.J. A Mechanism for Non–Newtonian Flow in Suspensions of Rigid Spheres. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Rintoul, M.D.; Torquato, S. Computer simulations of dense hard–sphere systems. J. Chem. Phys. 1996, 105, 9258–9265. [Google Scholar] [CrossRef]
- Abliz, D.; Artys, T.; Ziegmann, G. Influence of model parameter estimation methods and regression algorithms on curing kinetics and rheological modelling. J. Appl. Polym. Sci. 2017, 134, 45137. [Google Scholar] [CrossRef]
- Chong, J.S.; Christiansen, E.B.; Baer, A.D. Rheology of concentrated suspensions. J. Appl. Polym. Sci. 1971, 15, 2007–2021. [Google Scholar] [CrossRef]
- Nolte, H.; Schilde, C.; Kwade, A. Production of Highly Loaded Nanocomposites by Dispersing Nanoparticles in Epoxy Resin. Chem. Eng. Technol. 2010, 33, 1447–1455. [Google Scholar] [CrossRef]
- Abliz, D.; Finke, B.; Berg, D.C.; Schilde, C.; Ziegmann, G. Flow of quasi-spherical nanoparticles in liquid composite molding processes. Part I: Influence of particle size and fiber distance distribution. Compos. Part A Appl. Sci. Manuf. 2019, 125, 105563. [Google Scholar] [CrossRef]
- Kole, M.; Dey, T.K. Viscosity of alumina nanoparticles dispersed in car engine coolant. Exp. Therm. Fluid Sci. 2010, 34, 677–683. [Google Scholar] [CrossRef]
- Baxter, R.J. Percus–Yevick Equation for Hard Spheres with Surface Adhesion. J. Chem. Phys. 1968, 49, 2770–2774. [Google Scholar] [CrossRef]
- Klingenberg, D.J.; Ulicny, J.C.; Golden, M.A. Mason numbers for magnetorheology. J. Rheol. 2007, 51, 883–893. [Google Scholar] [CrossRef]
- Liepins, G.E.; Hilliard, M.R. Genetic algorithms: Foundations and applications. Ann. Oper. Res. 1989, 21, 31–57. [Google Scholar] [CrossRef]
- Kramer, O. Genetic Algorithm Essentials; Springer International Publishing: Cham, Switzerland, 2017; Volume 679. [Google Scholar] [CrossRef]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic Algorithms: Concepts and Design; Springer Nature Switzerland AG: Cham, Switzerland, 1999; Available online: https://link.springer.com/book/10.1007/978-1-4471-0577-0 (accessed on 21 May 2021).
- Mitchell, M. An Introduction to Genetic Algorithms, 7th ed.; MIT press: Cambridge, MA, USA, 2001. [Google Scholar]
- Jansen, T. On Classifications of Fitness Functions. In Theoretical Aspects of Evolutionary Computing; Rozenberg, G., Bäck, T., Eiben, A.E., Kok, J.N., Spaink, H.P., Kallel, L., Naudts, B., Rogers, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 6, pp. 371–385. [Google Scholar] [CrossRef]
- Blickle, T.; Thiele, L. A Comparison of Selection Schemes Used in Evolutionary Algorithms. Evol. Comput. 1996, 4, 361–394. [Google Scholar] [CrossRef]
- Umbarkar, A.J.; Sheth, P.D. Crossover operators in genetic algorithms: A review. ICTACT J. Soft Comput. 2015, 06, 1083–1092. [Google Scholar] [CrossRef]
- Wright, A.H. Genetic Algorithms for Real Parameter Optimization. In Foundations of Genetic Algorithms 1991 (FOGA 1); Foundations of Genetic Algorithms; Rawlins, G.J.E., Ed.; Elsevier Science: Burlington, MA, USA, 1991; Volume 1, pp. 205–218. [Google Scholar] [CrossRef]
- Deb, K.; Deb, A. Analysing mutation schemes for real-parameter genetic algorithms. Int. J. Artif. Intell. Soft Comput. 2014, 4, 1. [Google Scholar] [CrossRef]


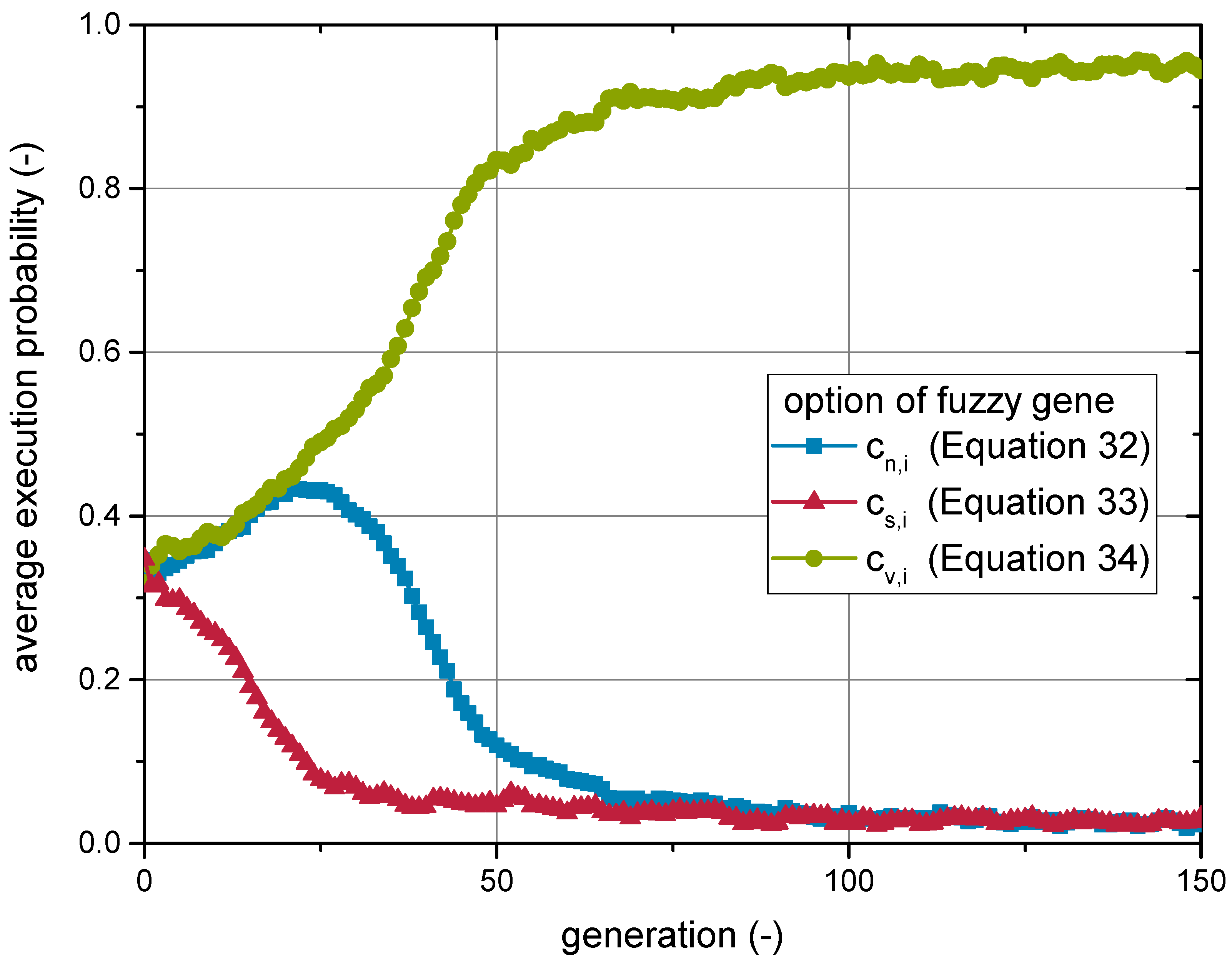
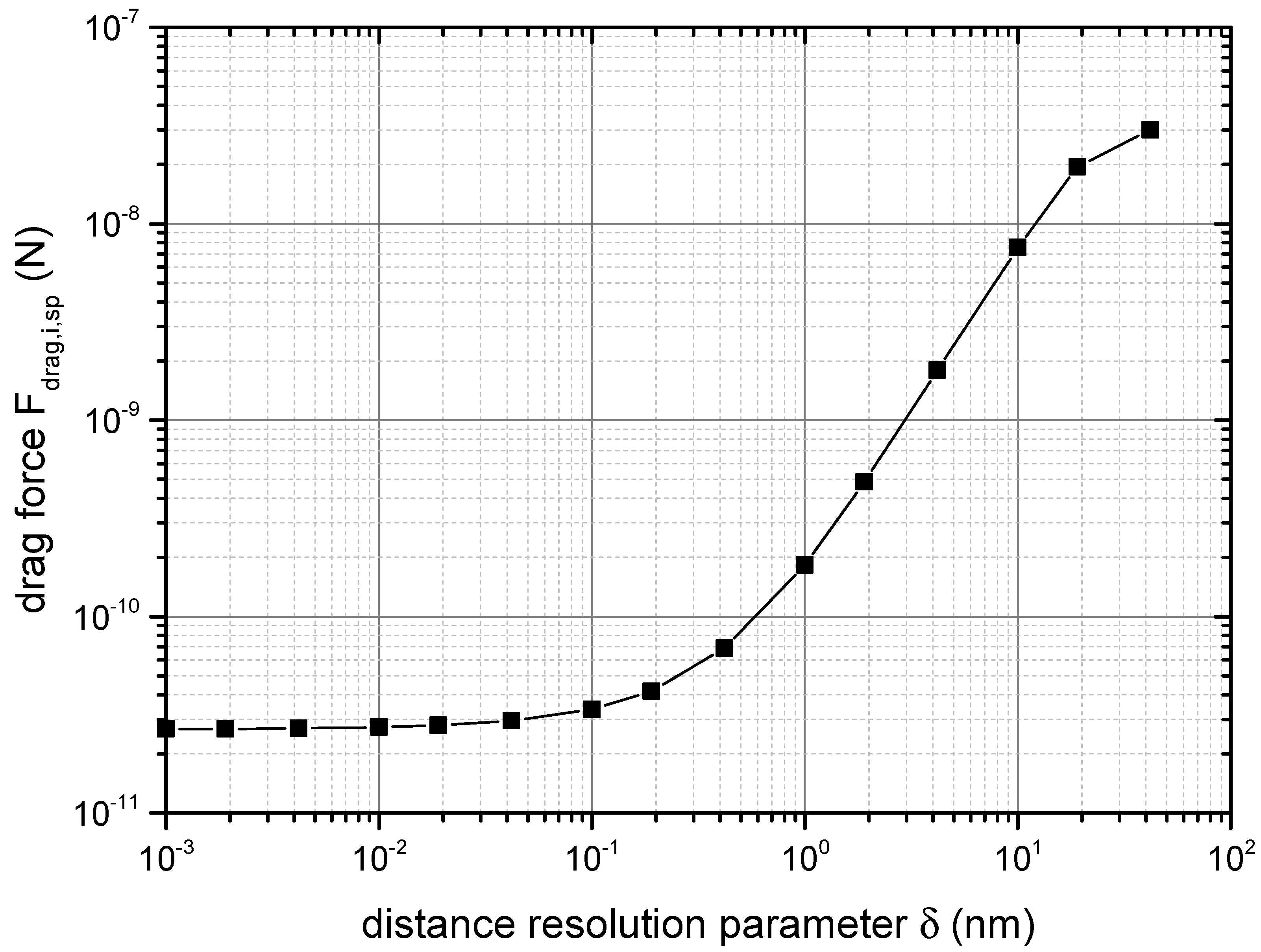
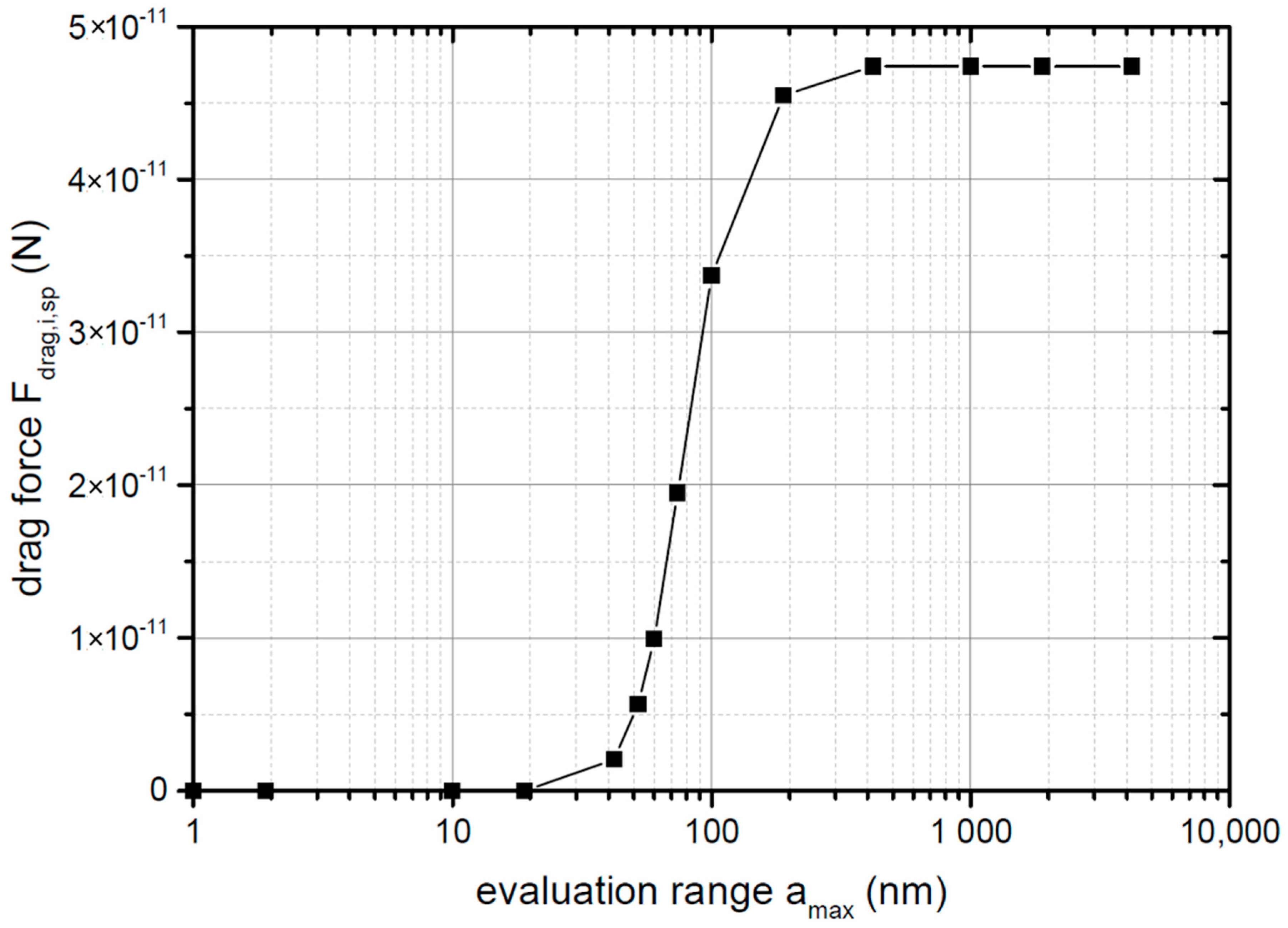




| Parameter | Development | Calibration |
|---|---|---|
| population size | 400 | 100 |
| mutation rate | ||
| mutation strength | − | |
| contrasting parameter c | none | |
| elite fraction |
| Parameter | Value | |
|---|---|---|
| proportionality factor | /kg | |
| proportionality coefficient |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Finke, B.; Sangrós Giménez, C.; Kwade, A.; Schilde, C. Viscosity Model for Nanoparticulate Suspensions Based on Surface Interactions. Materials 2021, 14, 2752. https://doi.org/10.3390/ma14112752
Finke B, Sangrós Giménez C, Kwade A, Schilde C. Viscosity Model for Nanoparticulate Suspensions Based on Surface Interactions. Materials. 2021; 14(11):2752. https://doi.org/10.3390/ma14112752
Chicago/Turabian StyleFinke, Benedikt, Clara Sangrós Giménez, Arno Kwade, and Carsten Schilde. 2021. "Viscosity Model for Nanoparticulate Suspensions Based on Surface Interactions" Materials 14, no. 11: 2752. https://doi.org/10.3390/ma14112752
APA StyleFinke, B., Sangrós Giménez, C., Kwade, A., & Schilde, C. (2021). Viscosity Model for Nanoparticulate Suspensions Based on Surface Interactions. Materials, 14(11), 2752. https://doi.org/10.3390/ma14112752








