Optimization of Residual Stress Measurement Conditions for a 2D Method Using X-ray Diffraction and Its Application for Stainless Steel Treated by Laser Cavitation Peening
Abstract
:1. Introduction
2. Experimental Apparatus and Procedures
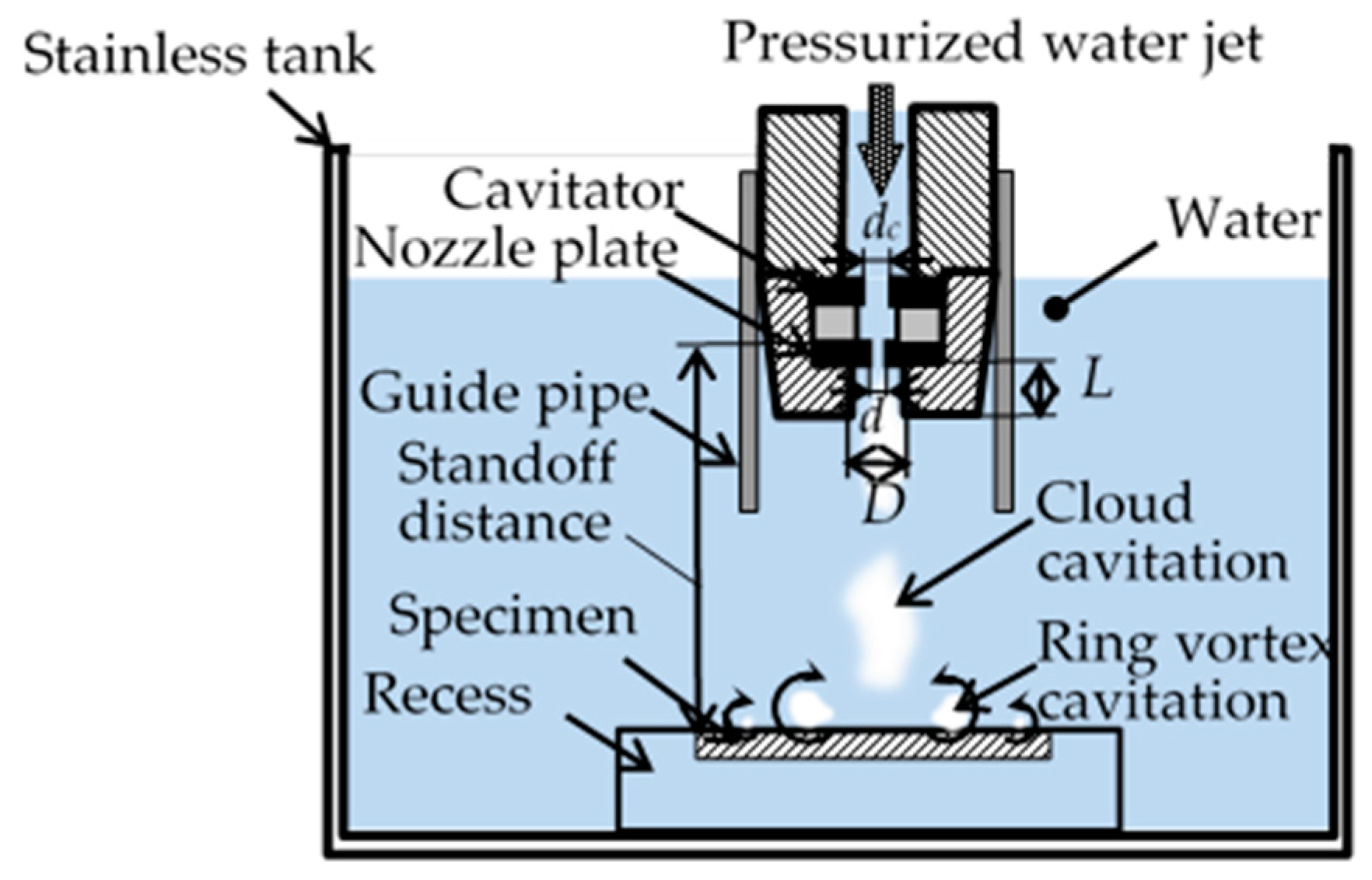
2.1. Peening Systems
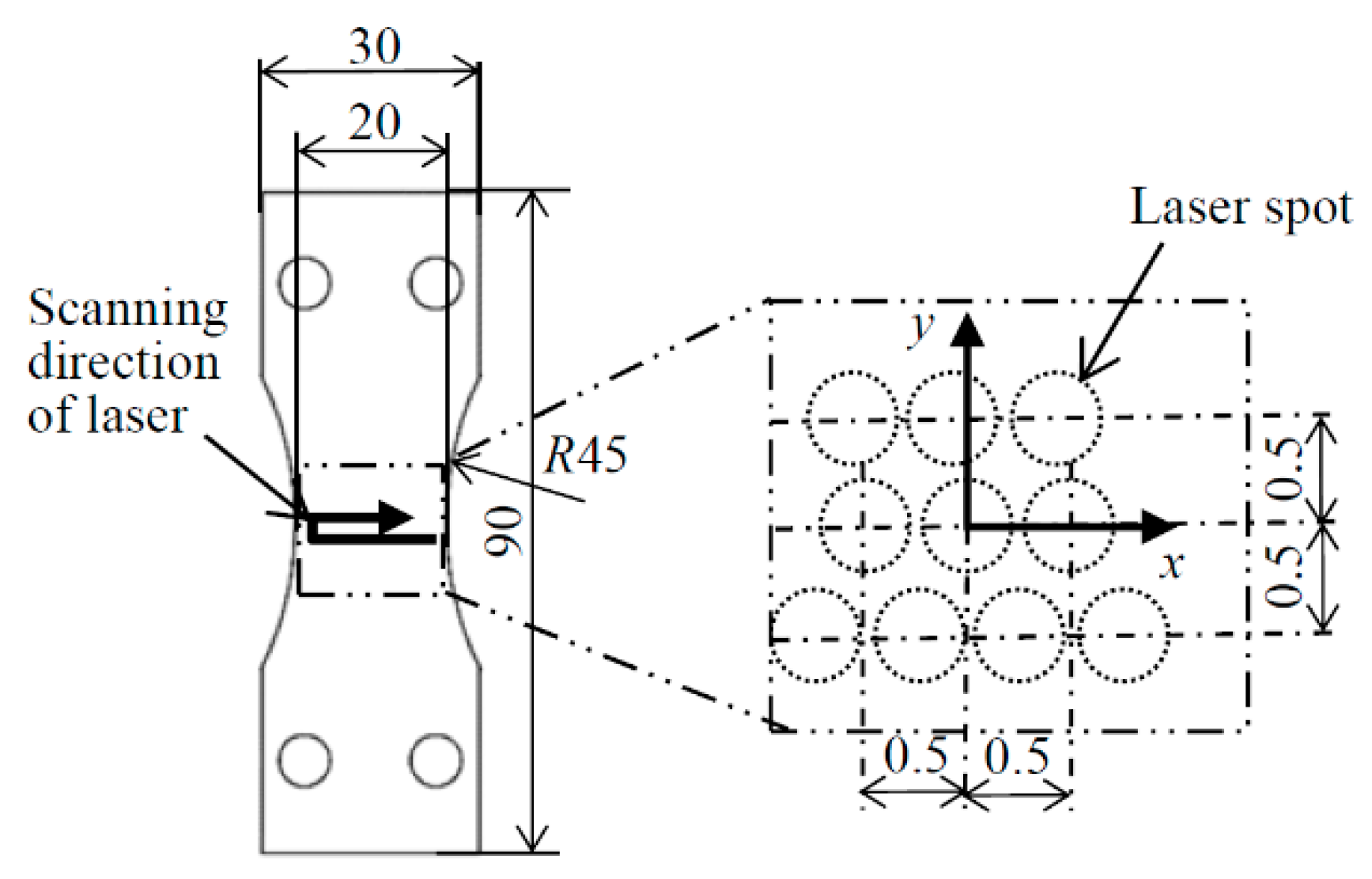
2.2. Material
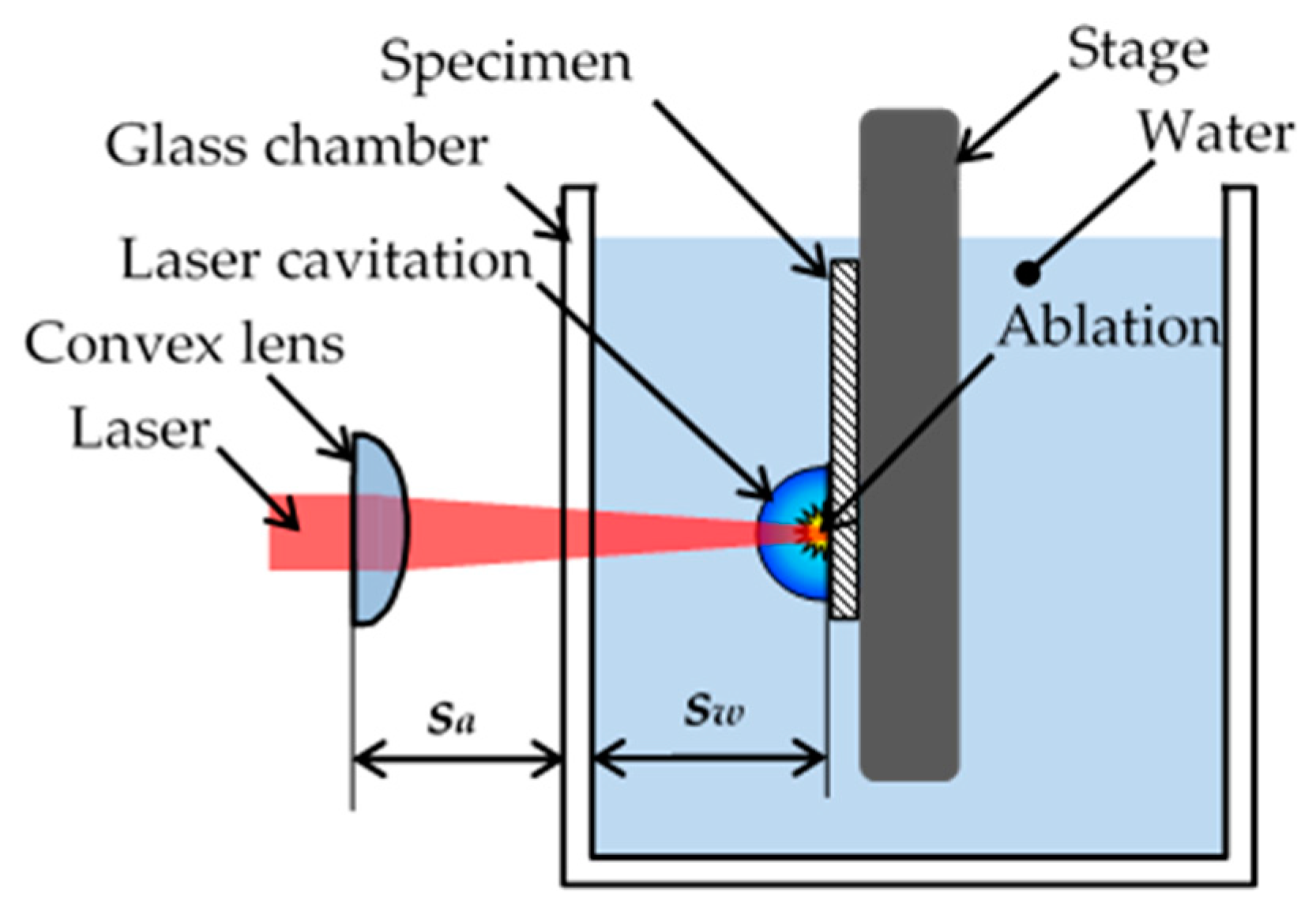
2.3. Residual Stress Measurement
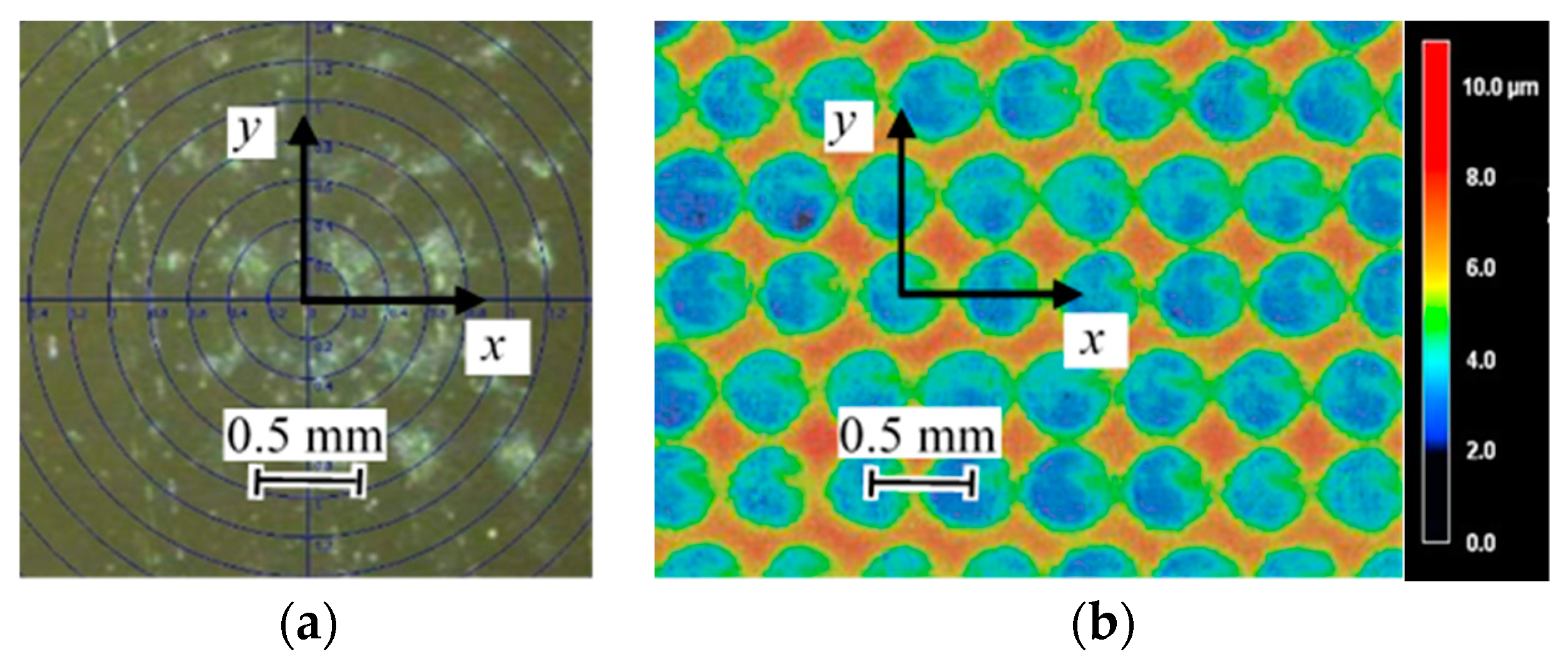
2.4. Observation of Specimen Surface
3. Results
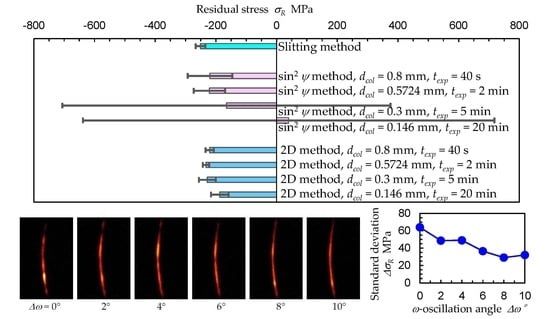
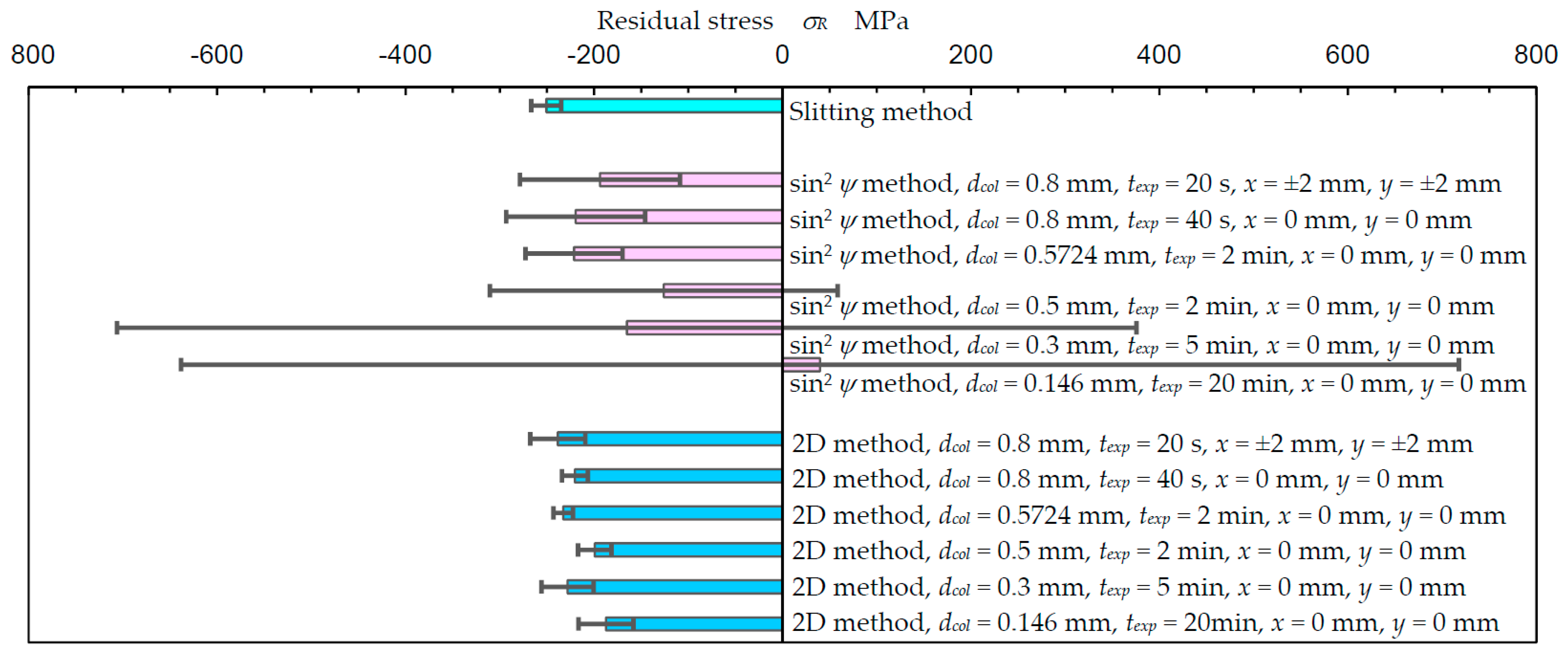
3.1. Comparison of Measured Residual Stress between the Slitting Method, sin2ψ Method and 2D Method
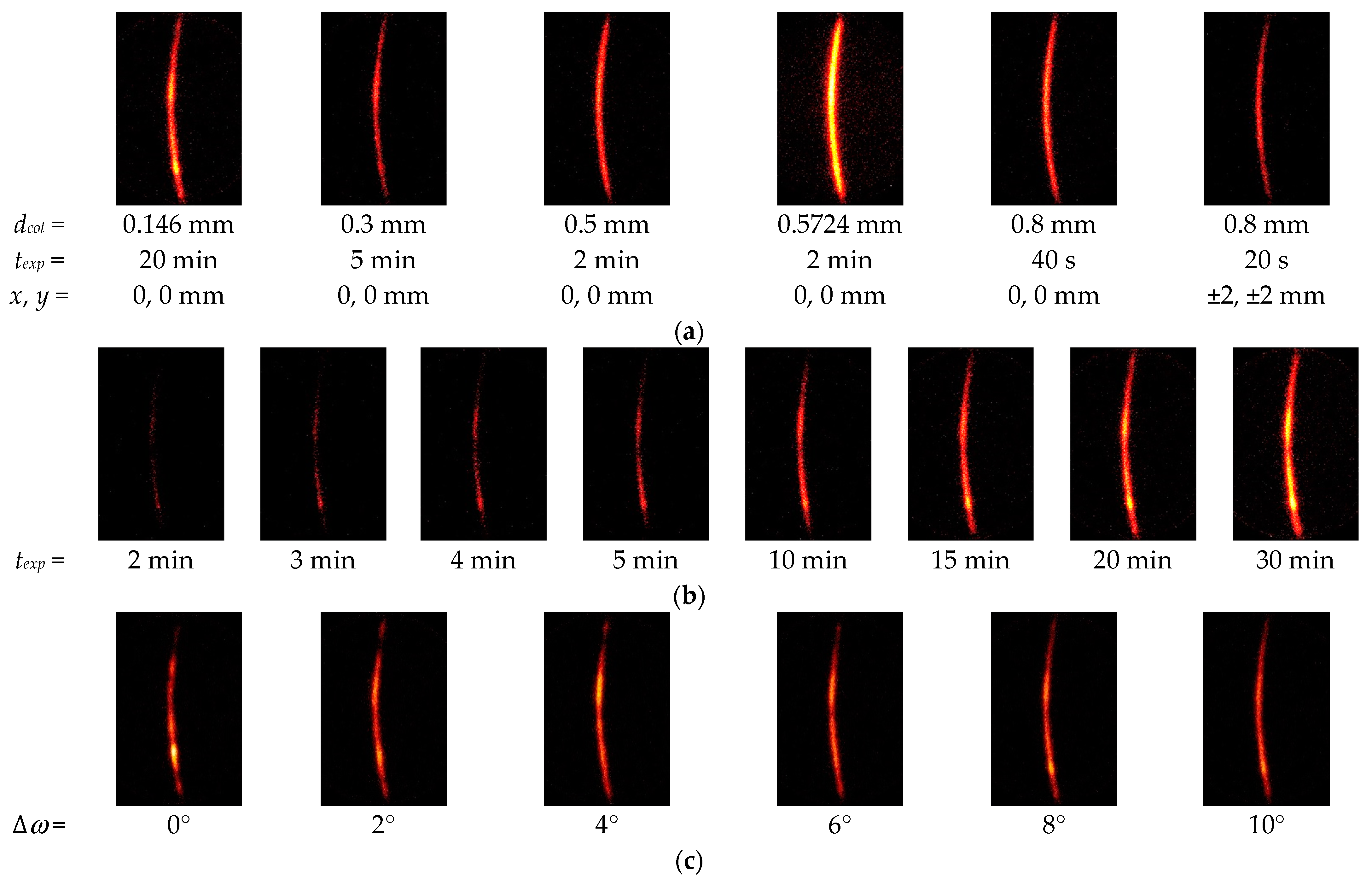
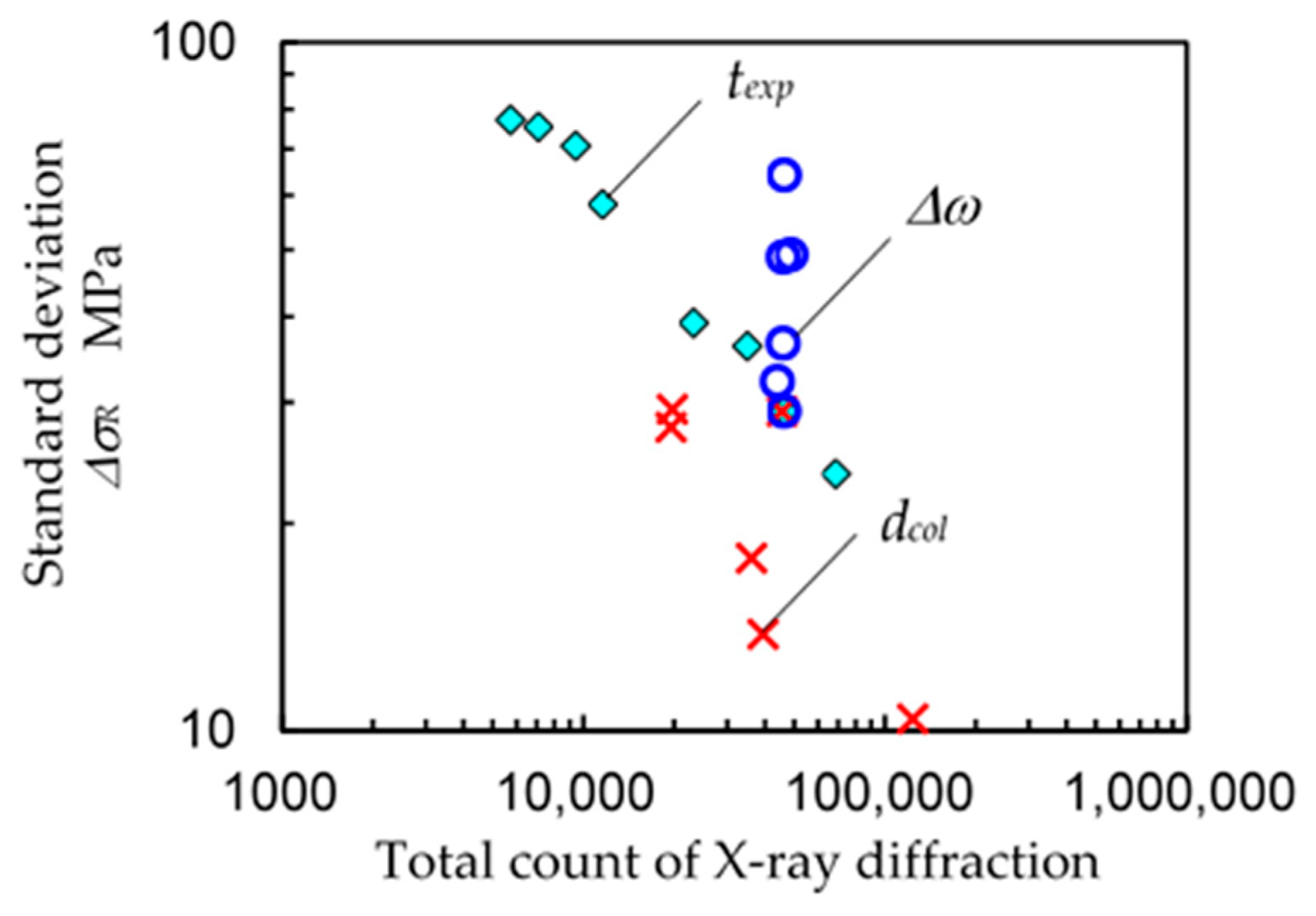
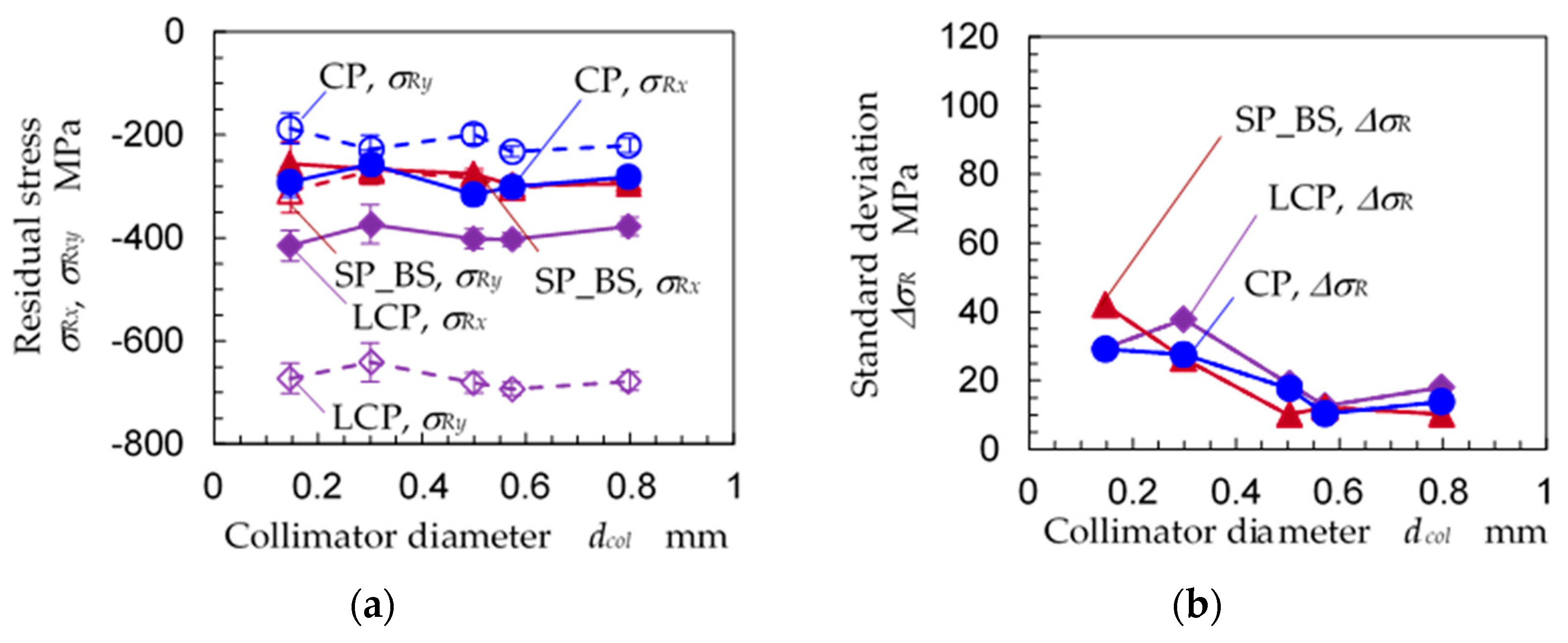
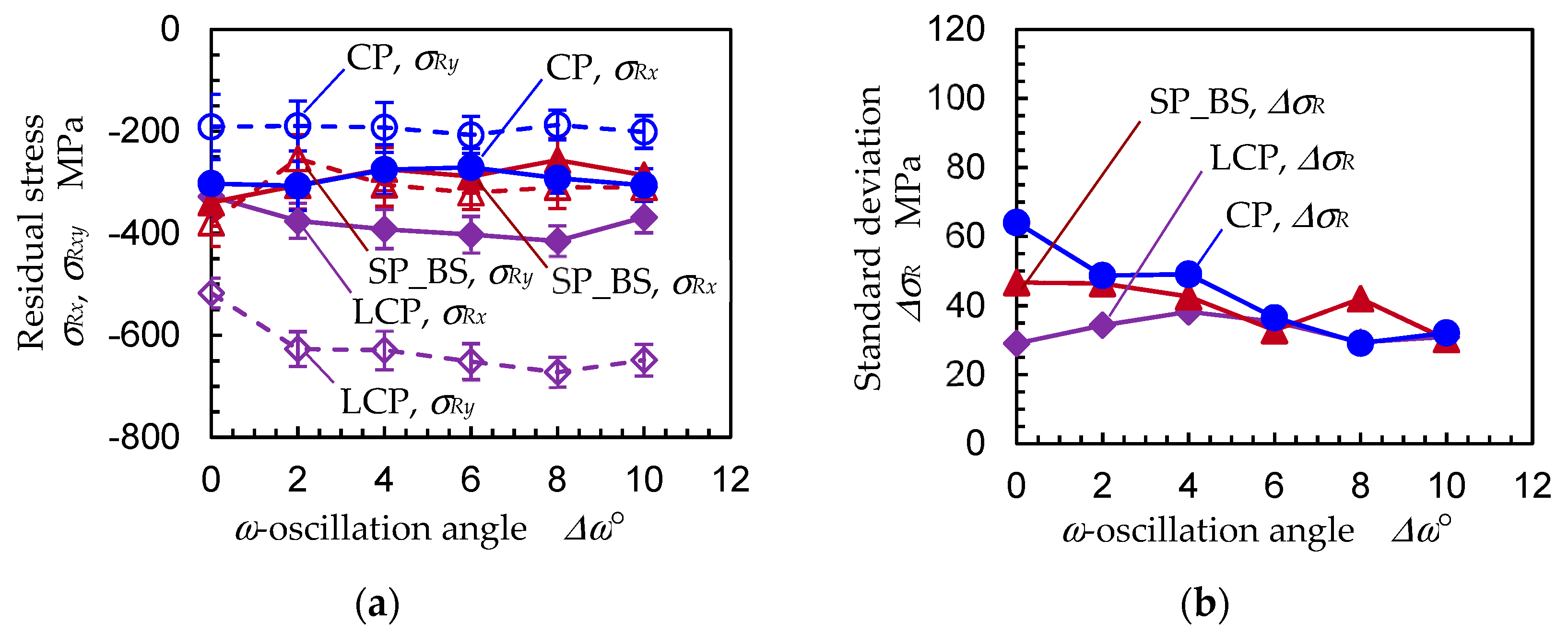
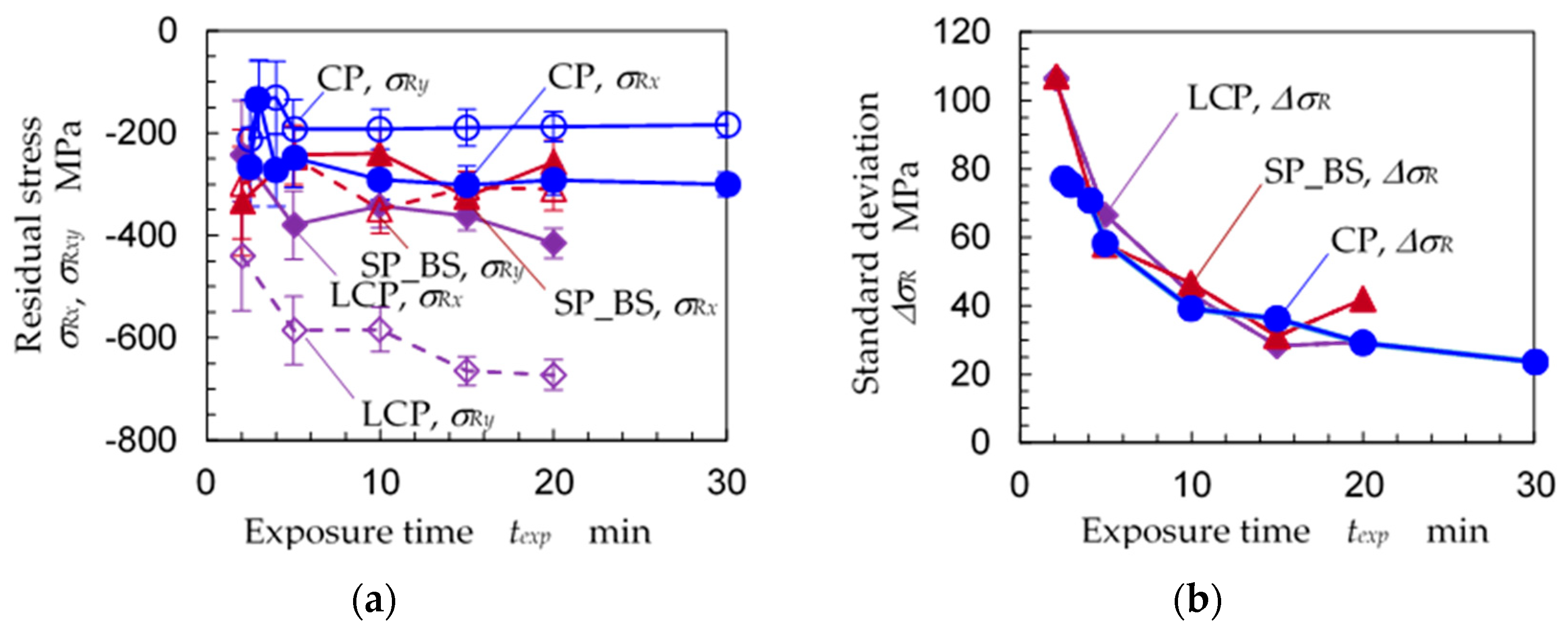
3.2. Optimum Condition for the 2D Method to Evaluate Residual Stress
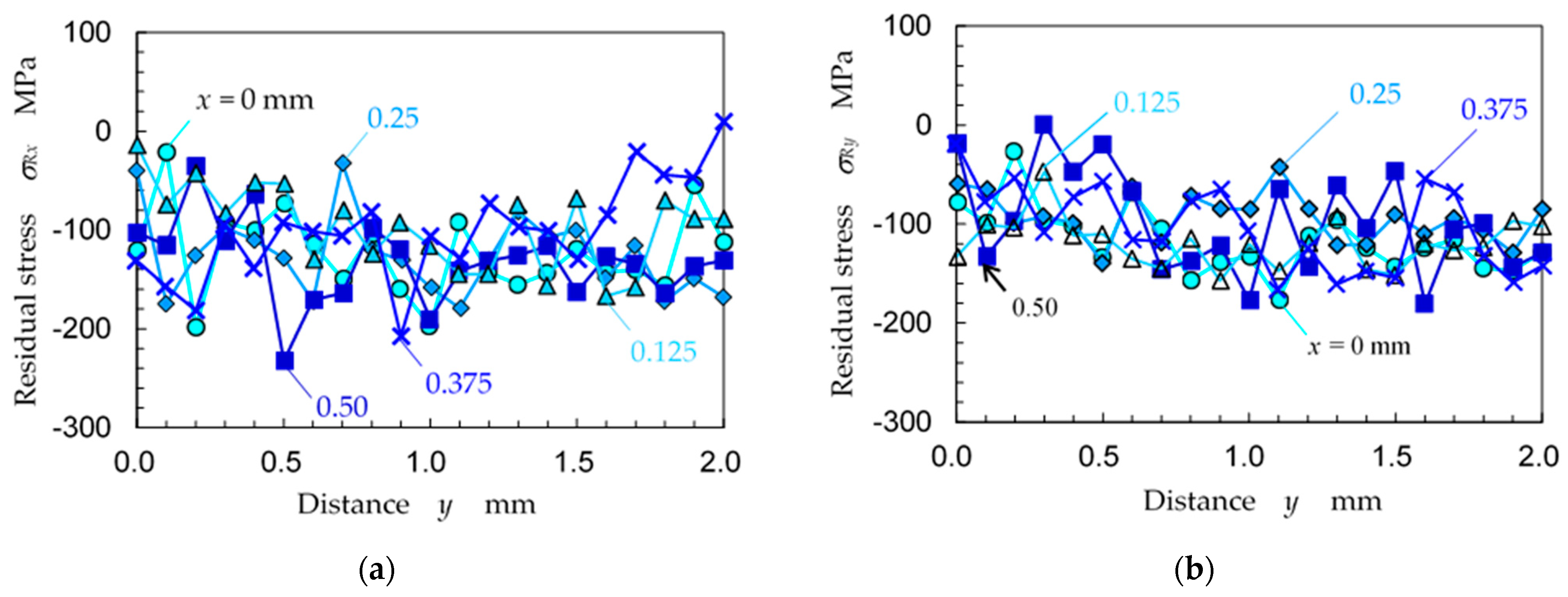
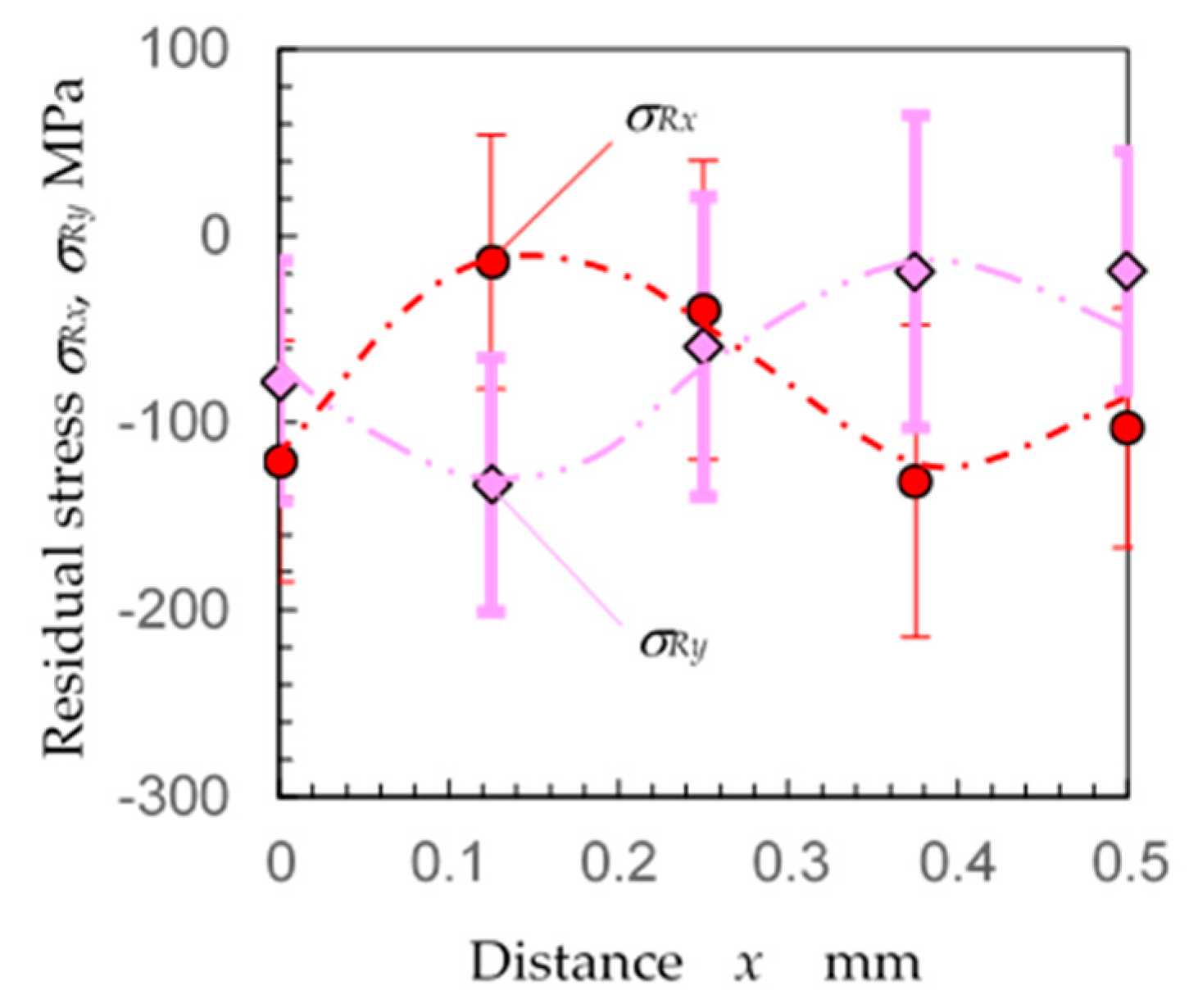
3.3. Residual Stress Distribution of Specimen Treated by Laser Cavitation Peening
4. Conclusions
- (1)
- Compared to the sin2ψ method, the 2D method can evaluate the residual stress in a small area, which is 1/15 of the area ratio of the sin2ψ method. In the present experiment, the measurable areas of the sin2ψ method and 2D method were 0.5724 mm in diameter and 0.146 mm in diameter, respectively.
- (2)
- The ω-oscillation of the specimen using the 2D method had the effect of reducing the measurement error to 1/2. This result is equivalent to the effect of reducing the measurement time to 1/5–1/4. The optimum ω-oscillation angle ∆ω was 8°.
- (3)
- The 2D method using optimized conditions can evaluate the residual stress distribution for a laser spot with a diameter of 0.5 mm.
- (4)
- The compressive residual stress under laser cavitation peening at 100 pulses/mm2 was larger in the stepwise direction than in the orthogonal direction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Nikitin, I.; Scholtes, B.; Maier, H.J.; Altenberger, I. High temperature fatigue behavior and residual stress stability of laser-shock peened and deep rolled austenitic steel aisi 304. Scr. Mater. 2004, 50, 1345–1350. [Google Scholar] [CrossRef]
- Withers, P.J. Residual stress and its role in failure. Rep. Prog. Phys. 2007, 70, 2211–2264. [Google Scholar] [CrossRef] [Green Version]
- Gujba, A.K.; Medraj, M. Laser peening process and its impact on materials properties in comparison with shot peening and ultrasonic impact peening. Materials 2014, 7, 7925–7974. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soyama, H. Comparison between shot peening, cavitation peening and laser peening by observation of crack initiation and crack growth in stainless steel. Metals 2020, 10, 63. [Google Scholar] [CrossRef] [Green Version]
- Arakawa, J.; Hanaki, T.; Hayashi, Y.; Akebono, H.; Sugeta, A. Evaluating the fatigue limit of metals having surface compressive residual stress and exhibiting shakedown. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 211–220. [Google Scholar] [CrossRef]
- Bikdeloo, R.; Farrahi, G.H.; Mehmanparast, A.; Mahdavi, S.M. Multiple laser shock peening effects on residual stress distribution and fatigue crack growth behaviour of 316L stainless steel. Theor. Appl. Fract. Mech. 2020, 105, 11. [Google Scholar] [CrossRef]
- Tang, L.Q.; Ince, A.; Zheng, J. Numerical modeling of residual stresses and fatigue damage assessment of ultrasonic impact treated 304L stainless steel welded joints. Eng. Fail. Anal. 2020, 108, 23. [Google Scholar] [CrossRef]
- Soyama, H.; Chighizola, C.R.; Hill, M.R. Effect of compressive residual stress introduced by cavitation peening and shot peening on the improvement of fatigue strength of stainless steel. J. Mater. Process. Technol. 2021, 288, 116877. [Google Scholar] [CrossRef]
- Edwards, L.; Bouchard, P.J.; Dutta, M.; Wang, D.Q.; Santisteban, J.R.; Hiller, S.; Fitzpatrick, M.E. Direct measurement of the residual stresses near a ‘boat-shaped’ repair in a 20 mm thick stainless steel tube butt weld. Int. J. Press. Vessels Pip. 2005, 82, 288–298. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Jiang, W.C.; Zhao, X.; Tu, S.T. Fatigue life of a dissimilar welded joint considering the weld residual stress: Experimental and finite element simulation. Int. J. Fatigue 2018, 109, 182–190. [Google Scholar] [CrossRef]
- Luo, Y.; Gu, W.B.; Peng, W.; Jin, Q.; Qin, Q.L.; Yi, C.M. A study on microstructure, residual stresses and stress corrosion cracking of repair welding on 304 stainless steel: Part i-effects of heat input. Materials 2020, 13, 2416. [Google Scholar] [CrossRef]
- Soyama, H. Laser cavitation peening and its application for improving the fatigue strength of welded parts. Metals 2021, 11, 531. [Google Scholar] [CrossRef]
- Webster, P.J.; Oosterkamp, L.D.; Browne, P.A.; Hughes, D.J.; Kang, W.P.; Withers, P.J.; Vaughan, G.B.M. Synchrotron X-ray residual strain scanning of a friction stir weld. J. Strain Anal. Eng. Des. 2001, 36, 61–70. [Google Scholar] [CrossRef]
- Peel, M.; Steuwer, A.; Preuss, M.; Withers, P.J. Microstructure, mechanical properties and residual stresses as a function of welding speed in aluminium AA5083 friction stir welds. Acta Mater. 2003, 51, 4791–4801. [Google Scholar] [CrossRef]
- Prime, M.B.; Gnaupel-Herold, T.; Baumann, J.A.; Lederich, R.J.; Bowden, D.M.; Sebring, R.J. Residual stress measurements in a thick, dissimilar aluminum alloy friction stir weld. Acta Mater. 2006, 54, 4013–4021. [Google Scholar] [CrossRef]
- Haghshenas, M.; Gharghouri, M.A.; Bhakhri, V.; Klassen, R.J.; Gerlich, A.P. Assessing residual stresses in friction stir welding: Neutron diffraction and nanoindentation methods. Int. J. Adv. Manuf. Technol. 2017, 93, 3733–3747. [Google Scholar] [CrossRef]
- Zhang, L.; Zhong, H.L.; Li, S.C.; Zhao, H.J.; Chen, J.Q.; Qi, L. Microstructure, mechanical properties and fatigue crack growth behavior of friction stir welded joint of 6061-T6 aluminum alloy. Int. J. Fatigue 2020, 135, 11. [Google Scholar] [CrossRef]
- Soyama, H.; Simoncini, M.; Cabibbo, M. Effect of cavitation peening on fatigue properties in friction stir welded aluminum alloy AA5754. Metals 2021, 11, 59. [Google Scholar] [CrossRef]
- Delosrios, E.R.; Walley, A.; Milan, M.T.; Hammersley, G. Fatigue-crack initiation and propagation on shot-peened surfaces in A316 stainless-steel. Int. J. Fatigue 1995, 17, 493–499. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R.; Merrien, P.; Lieurade, H.P. Laser shock processing of aluminium alloys. Application to high cycle fatigue behaviour. Mater. Sci. Eng. A 1996, 210, 102–113. [Google Scholar] [CrossRef]
- Sano, Y.; Obata, M.; Kubo, T.; Mukai, N.; Yoda, M.; Masaki, K.; Ochi, Y. Retardation of crack initiation and growth in austenitic stainless steels by laser peening without protective coating. Mater. Sci. Eng. A 2006, 417, 334–340. [Google Scholar] [CrossRef]
- Gill, A.; Telang, A.; Mannava, S.R.; Qian, D.; Pyoun, Y.-S.; Soyama, H.; Vasudevan, V.K. Comparison of mechanisms of advanced mechanical surface treatments in nickel-based superalloy. Mater. Sci. Eng. A 2013, 576, 346–355. [Google Scholar] [CrossRef]
- Soyama, H. Comparison between the improvements made to the fatigue strength of stainless steel by cavitation peening, water jet peening, shot peening and laser peening. J. Mater. Process. Technol. 2019, 269, 65–78. [Google Scholar] [CrossRef]
- SMS Committee on X-ray Study of Mechanical Behavior of Materials. Standard method for X-ray stress measurement. JSMS Stand. 2005, JSMS-SD-10-05, 1–21. [Google Scholar]
- He, B.B.; Preckwinkel, U.; Smith, K. Advantage of using 2D detectors for residual stress measurements. Adv. X-ray Anal. 2000, 42, 429–438. [Google Scholar]
- Takakuwa, O.; Soyama, H. Optimizing the conditions for residual stress measurement using a two-dimensional XRD method with specimen oscillation. Adv. Mater. Phys. Chem. 2013, 03, 8–18. [Google Scholar] [CrossRef] [Green Version]
- Hill, M. The slitting method. In Practical Residual Stress Measurement Methods; Schajer, G.S., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 89–108. [Google Scholar]
- ASTM E837-13a. Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method; ASTM: West Conshohocken, PA, USA, 2020. [Google Scholar]
- Chighizola, C.R.; D’Elia, C.R.; Weber, D.; Kirsch, B.; Aurich, J.C.; Linke, B.S.; Hill, M.R. Intermethod comparison and evaluation of measured near surface residual stress in milled aluminum. Exp. Mech. 2021, in press. [Google Scholar]
- Hatamleh, O.; Rivero, I.V.; Swain, S.E. An investigation of the residual stress characterization and relaxation in peened friction stir welded aluminum-lithium alloy joints. Mater. Des. 2009, 30, 3367–3373. [Google Scholar] [CrossRef]
- Correa, C.; de Lara, L.R.; Diaz, M.; Gil-Santos, A.; Porro, J.A.; Ocana, J.L. Effect of advancing direction on fatigue life of 316L stainless steel specimens treated by double-sided laser shock peening. Int. J. Fatigue 2015, 79, 1–9. [Google Scholar] [CrossRef]
- Kallien, Z.; Keller, S.; Ventzke, V.; Kashaev, N.; Klusemann, B. Effect of laser peening process parameters and sequences on residual stress profiles. Metals 2019, 9, 655. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.D.; Sun, G.F.; Lu, Y.; Chen, M.Z.; Bi, K.D.; Ni, Z.H. Microstructural characterization and mechanical behavior of ultrasonic impact peened and laser shock peened AISI 316L stainless steel. Surf. Coat. Technol. 2020, 385, 19. [Google Scholar] [CrossRef]
- Bhamare, S.; Ramakrishnan, G.; Mannava, S.R.; Langer, K.; Vasudevan, V.K.; Qian, D. Simulation-based optimization of laser shock peening process for improved bending fatigue life of Ti-6Al-2Sn-4Zr-2Mo alloy. Surf. Coat. Technol. 2013, 232, 464–474. [Google Scholar] [CrossRef]
- Correa, C.; de Lara, L.R.; Diaz, M.; Porro, J.A.; Garcia-Beltran, A.; Ocana, J.L. Influence of pulse sequence and edge material effect on fatigue life of Al2024-T351 specimens treated by laser shock processing. Int. J. Fatigue 2015, 70, 196–204. [Google Scholar] [CrossRef]
- Keller, S.; Chupakhin, S.; Staron, P.; Maawad, E.; Kashaev, N.; Klusemann, B. Experimental and numerical investigation of residual stresses in laser shock peened AA2198. J. Mater. Process. Technol. 2018, 255, 294–307. [Google Scholar] [CrossRef]
- Xu, G.; Luo, K.Y.; Dai, F.Z.; Lu, J.Z. Effects of scanning path and overlapping rate on residual stress of 316L stainless steel blade subjected to massive laser shock peening treatment with square spots. Appl. Surf. Sci. 2019, 481, 1053–1063. [Google Scholar] [CrossRef]
- Sano, Y.; Akita, K.; Sano, T. A mechanism for inducing compressive residual stresses on a surface by laser peening without coating. Metals 2020, 10, 816. [Google Scholar] [CrossRef]
- Pan, X.L.; Li, X.; Zhou, L.C.; Feng, X.T.; Luo, S.H.; He, W.F. Effect of residual stress on S-N curves and fracture morphology of Ti6Al4V titanium alloy after laser shock peening without protective coating. Materials 2019, 12, 3799. [Google Scholar] [CrossRef] [Green Version]
- Busse, D.; Ganguly, S.; Furfari, D.; Irving, P.E. Optimised laser peening strategies for damage tolerant aircraft structures. Int. J. Fatigue 2020, 141, 12. [Google Scholar] [CrossRef]
- Sun, R.J.; Keller, S.; Zhu, Y.; Guo, W.; Kashaev, N.; Klusemann, B. Experimental-numerical study of laser-shock-peening-induced retardation of fatigue crack propagation in Ti-17 titanium alloy. Int. J. Fatigue 2021, 145, 13. [Google Scholar] [CrossRef]
- Soyama, H. Enhancing the aggressive intensity of a cavitating jet by introducing a cavitator and a guide pipe. J. Fluid Sci. Technol. 2014, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Soyama, H. Enhancing the aggressive intensity of a cavitating jet by means of the nozzle outlet geometry. J. Fluids Eng. 2011, 133, 1–11. [Google Scholar] [CrossRef]
- Nishikawa, M.; Soyama, H. Two-step method to evaluate equibiaxial residual stress of metal surface based on micro-indentation tests. Mater. Des. 2011, 32, 3240–3247. [Google Scholar] [CrossRef]
- Naito, A.; Takakuwa, O.; Soyama, H. Development of peening technique using recirculating shot accelerated by water jet. Mater. Sci. Technol. 2012, 28, 234–239. [Google Scholar] [CrossRef]
- ASTM E112-13. Standard Test Methods for Determining Average Grain Size; ASTM: West Conshohocken, PA, USA, 2020. [Google Scholar]
- He, B.B. Two-Dimensional X-Ray Diffraction; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 249–328. [Google Scholar]
- Kumagai, M.; Curd, M.E.; Soyama, H.; Ungár, T.; Ribárik, G.; Withers, P.J. Depth-profiling of residual stress and microstructure for austenitic stainless steel surface treated by cavitation, shot and laser peening. Mater. Sci. Eng. A 2021, 813, 141037. [Google Scholar] [CrossRef]

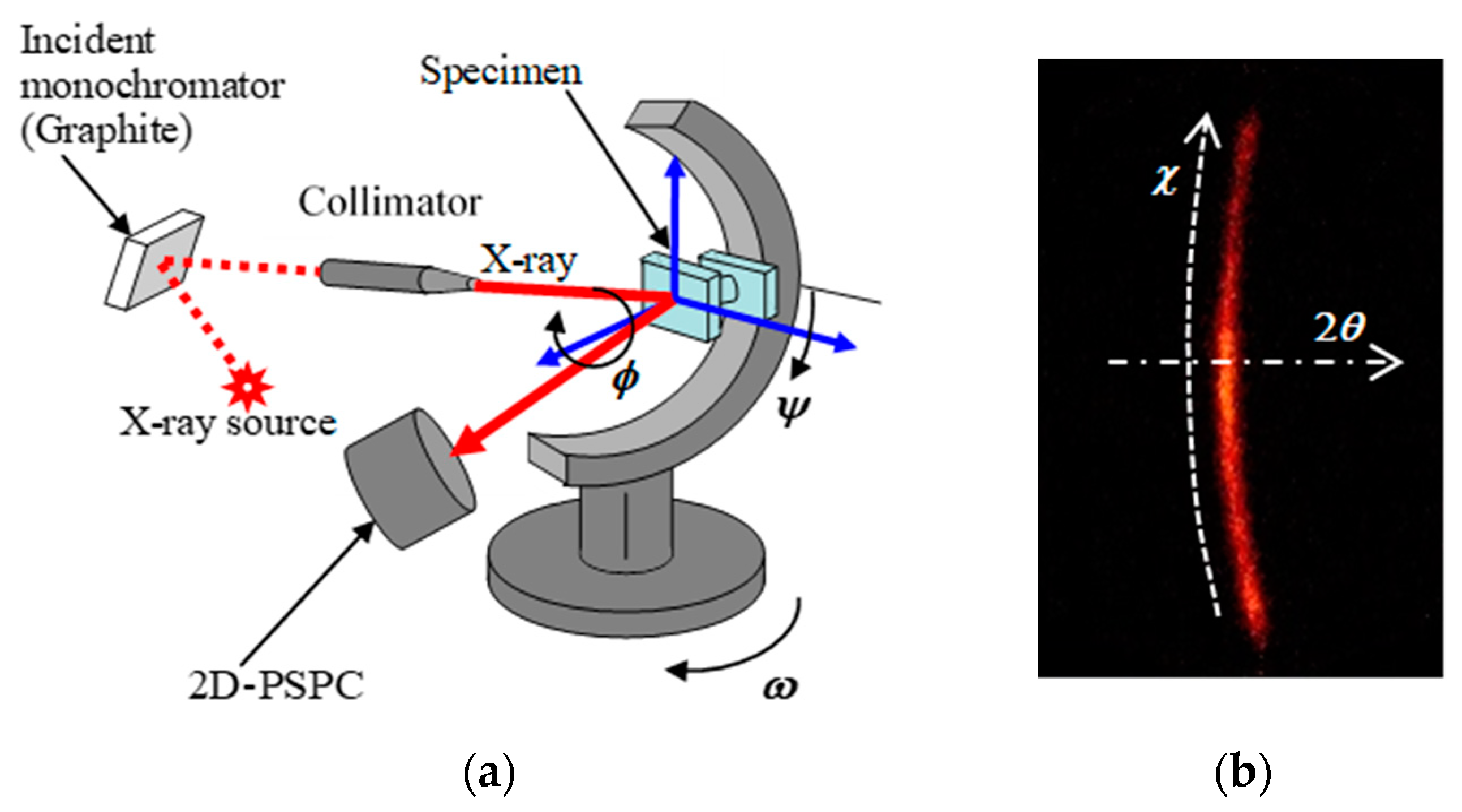


| Symbol | Peening Method | Peening Intensity | Thickness | Measured Side | Electrochemical Polishing |
|---|---|---|---|---|---|
| A | Cavitation peening CP | 8 s/mm | 2 mm | Peened side | None |
| B | Laser cavitation peening LCP | 100 pulses/mm2 | 6 mm | Peened side | 39 μm |
| C | Shot peening SP | 30 s | 3 mm | Back side | None |
| D | Laser cavitation peening LCP | 4 pulses/mm2 | 2 mm | Peened side | 33 μm |
| Method | ψ° | φ° |
|---|---|---|
| sin2ψ method | 0 | 0, 90, 180, 270 |
| 20.268 | 0, 90, 180, 270 | |
| 29.334 | 0, 90, 180, 270 | |
| 36.870 | 0, 90, 180, 270 | |
| 43.854 | 0, 90, 180, 270 | |
| 50.768 | 0, 90, 180, 270 | |
| 2D method | 0 | 0, 45, 90, 135, 180, 225, 270, 315 |
| 30 | 0, 45, 90, 135, 180, 225, 270, 315 | |
| 60 | 0, 45, 90, 135, 180, 225, 270, 315 |
| Method | 2θ° | χ° |
|---|---|---|
| sin2ψ method | 125–132 | 85–95 |
| 2D method | 125–132 | 70–110 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soyama, H.; Kuji, C.; Kuriyagawa, T.; Chighizola, C.R.; Hill, M.R. Optimization of Residual Stress Measurement Conditions for a 2D Method Using X-ray Diffraction and Its Application for Stainless Steel Treated by Laser Cavitation Peening. Materials 2021, 14, 2772. https://doi.org/10.3390/ma14112772
Soyama H, Kuji C, Kuriyagawa T, Chighizola CR, Hill MR. Optimization of Residual Stress Measurement Conditions for a 2D Method Using X-ray Diffraction and Its Application for Stainless Steel Treated by Laser Cavitation Peening. Materials. 2021; 14(11):2772. https://doi.org/10.3390/ma14112772
Chicago/Turabian StyleSoyama, Hitoshi, Chieko Kuji, Tsunemoto Kuriyagawa, Christopher R. Chighizola, and Michael R. Hill. 2021. "Optimization of Residual Stress Measurement Conditions for a 2D Method Using X-ray Diffraction and Its Application for Stainless Steel Treated by Laser Cavitation Peening" Materials 14, no. 11: 2772. https://doi.org/10.3390/ma14112772
APA StyleSoyama, H., Kuji, C., Kuriyagawa, T., Chighizola, C. R., & Hill, M. R. (2021). Optimization of Residual Stress Measurement Conditions for a 2D Method Using X-ray Diffraction and Its Application for Stainless Steel Treated by Laser Cavitation Peening. Materials, 14(11), 2772. https://doi.org/10.3390/ma14112772