Phase Diagram of Binary Alloy Nanoparticles under High Pressure
Abstract
1. Introduction
2. Theory and Model
2.1. Effect of Nanoparticle Size
2.2. Effect of Pressure on Thermodynamic Equations
2.3. Thermodynamic Equations of Nanoparticles under High Pressure
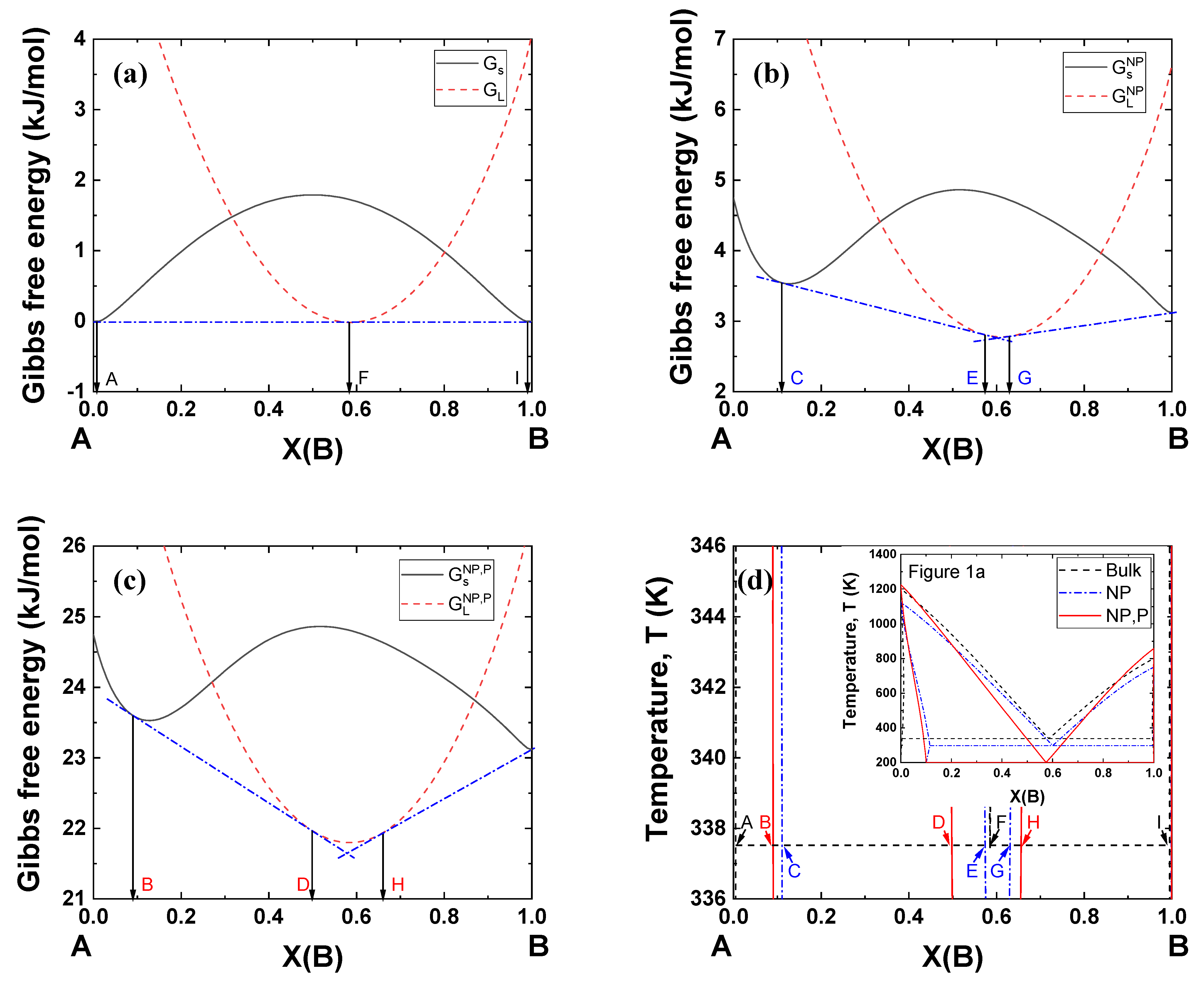
2.4. Phase Equilibria Model
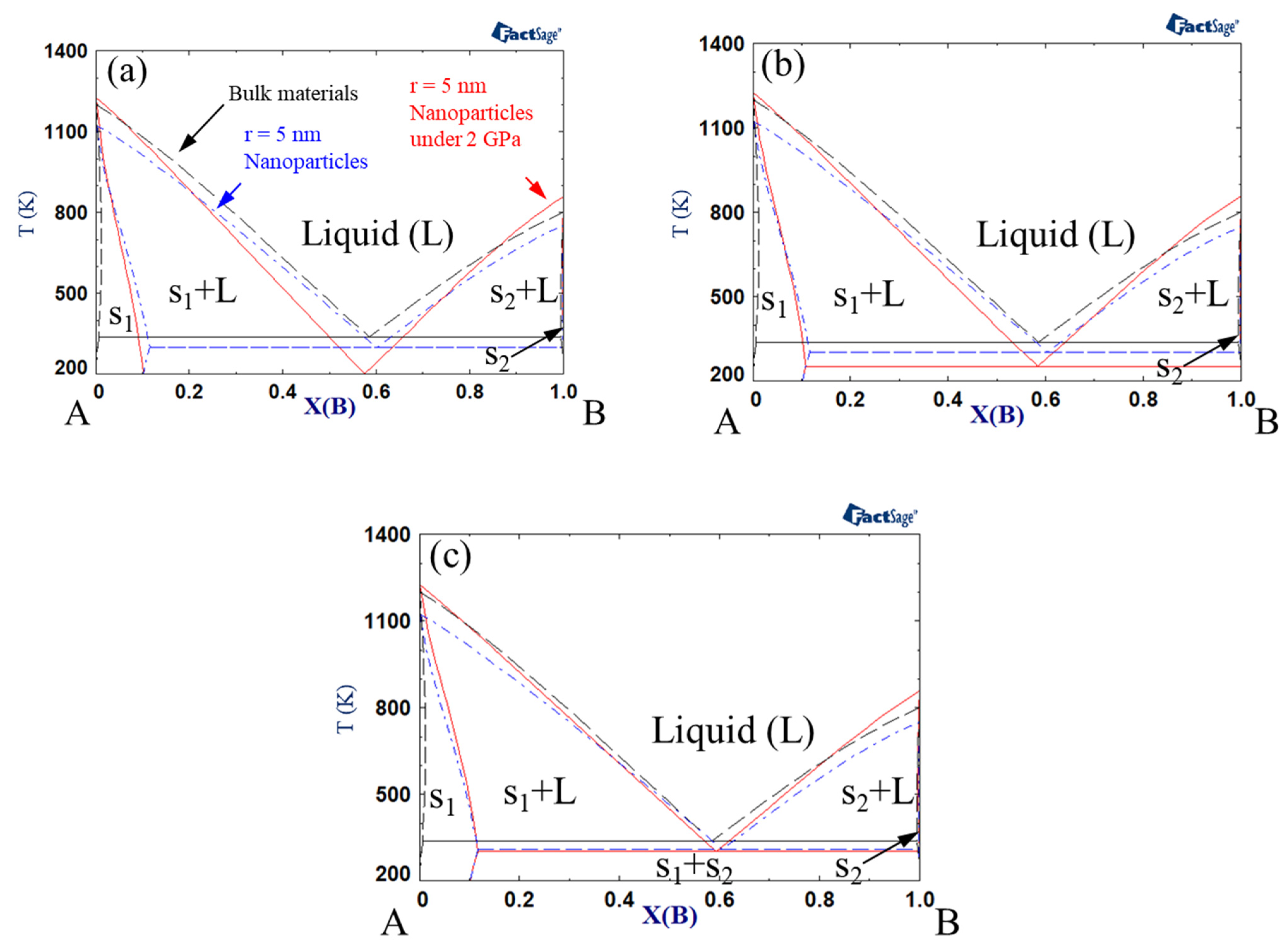
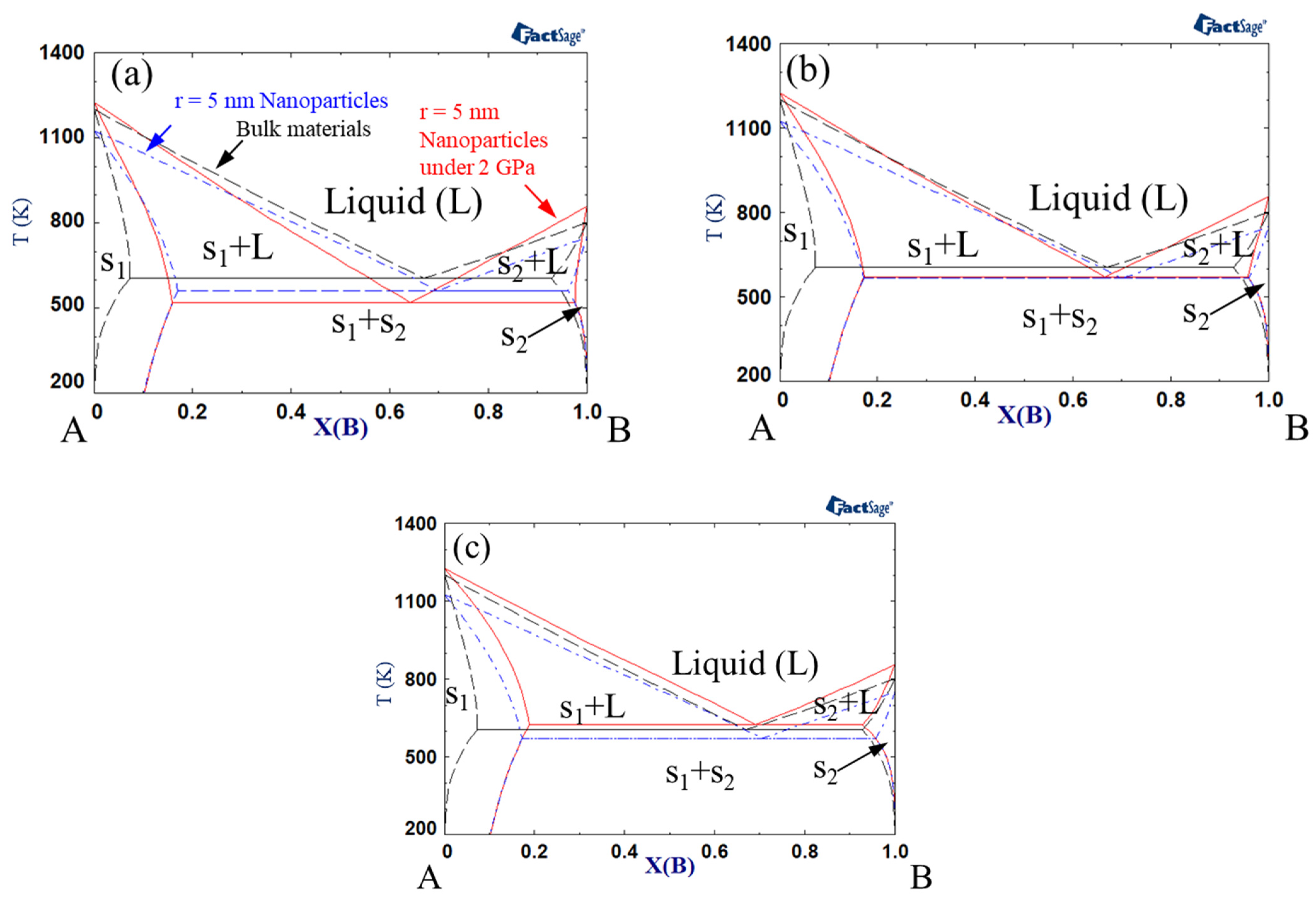
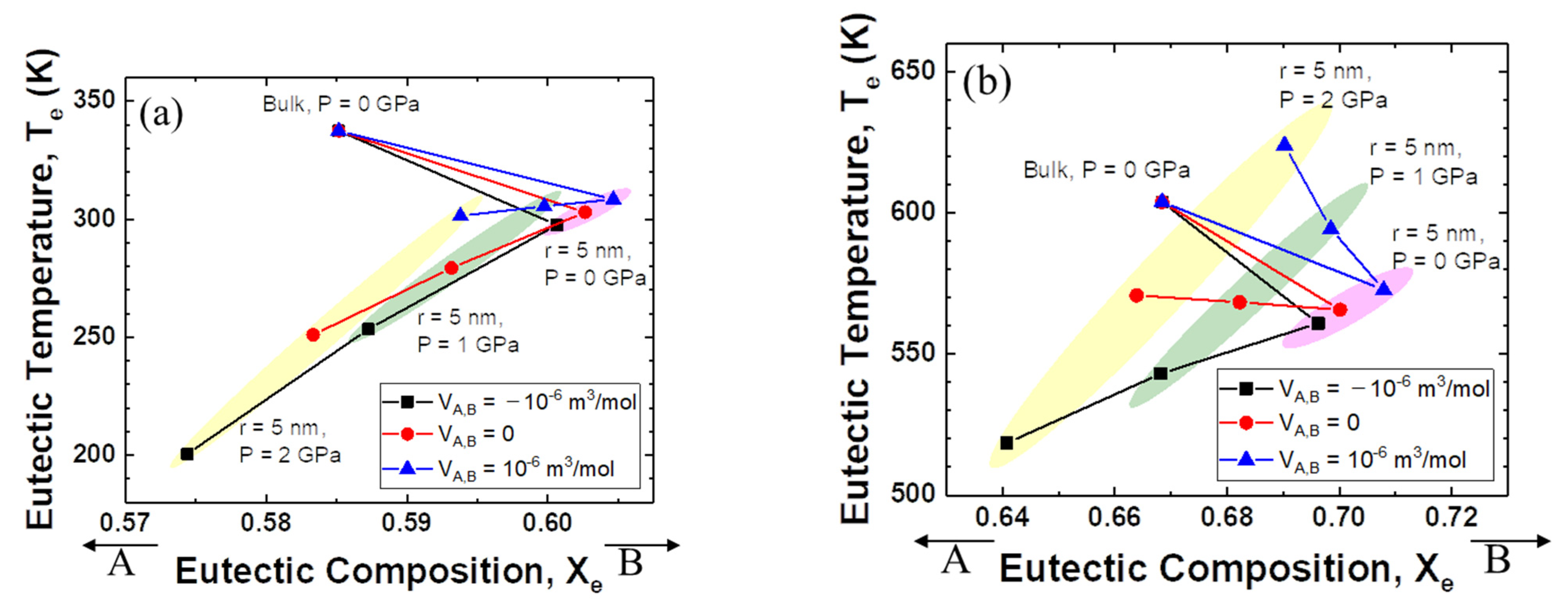
3. Results and Discussion
3.1. Variations in the Shape of the Phase Diagram
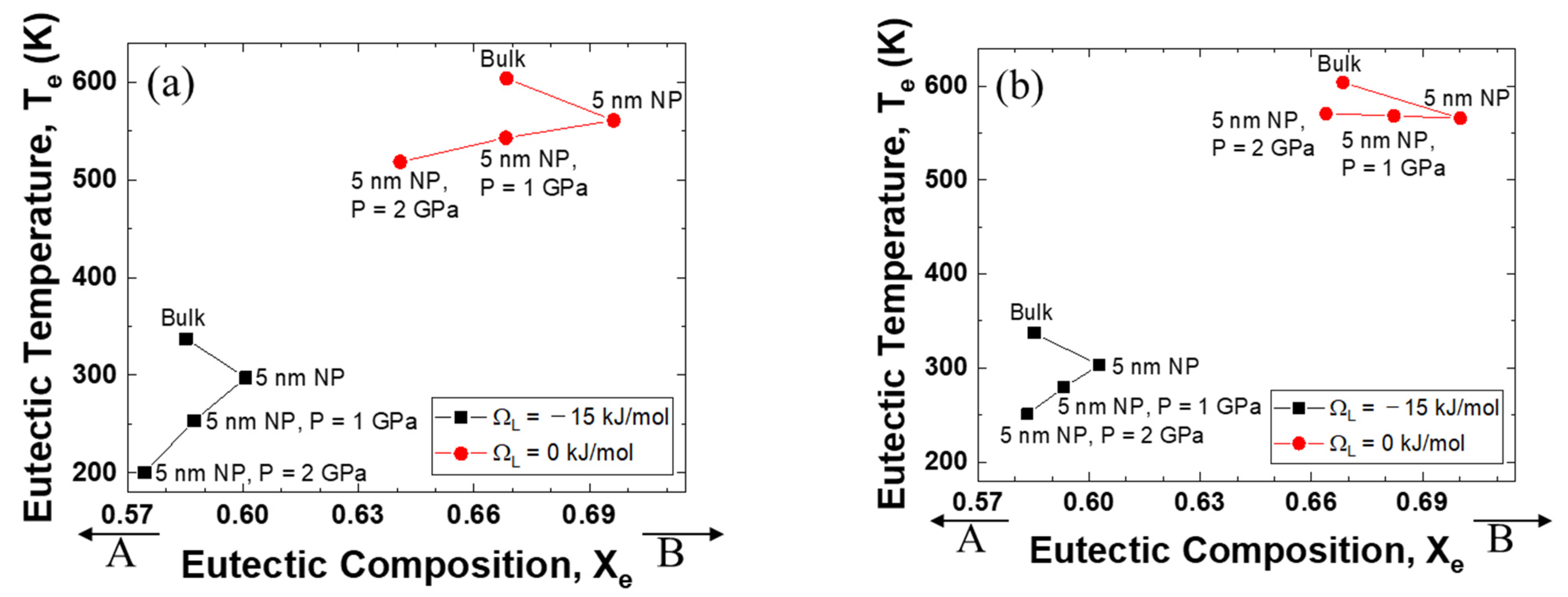
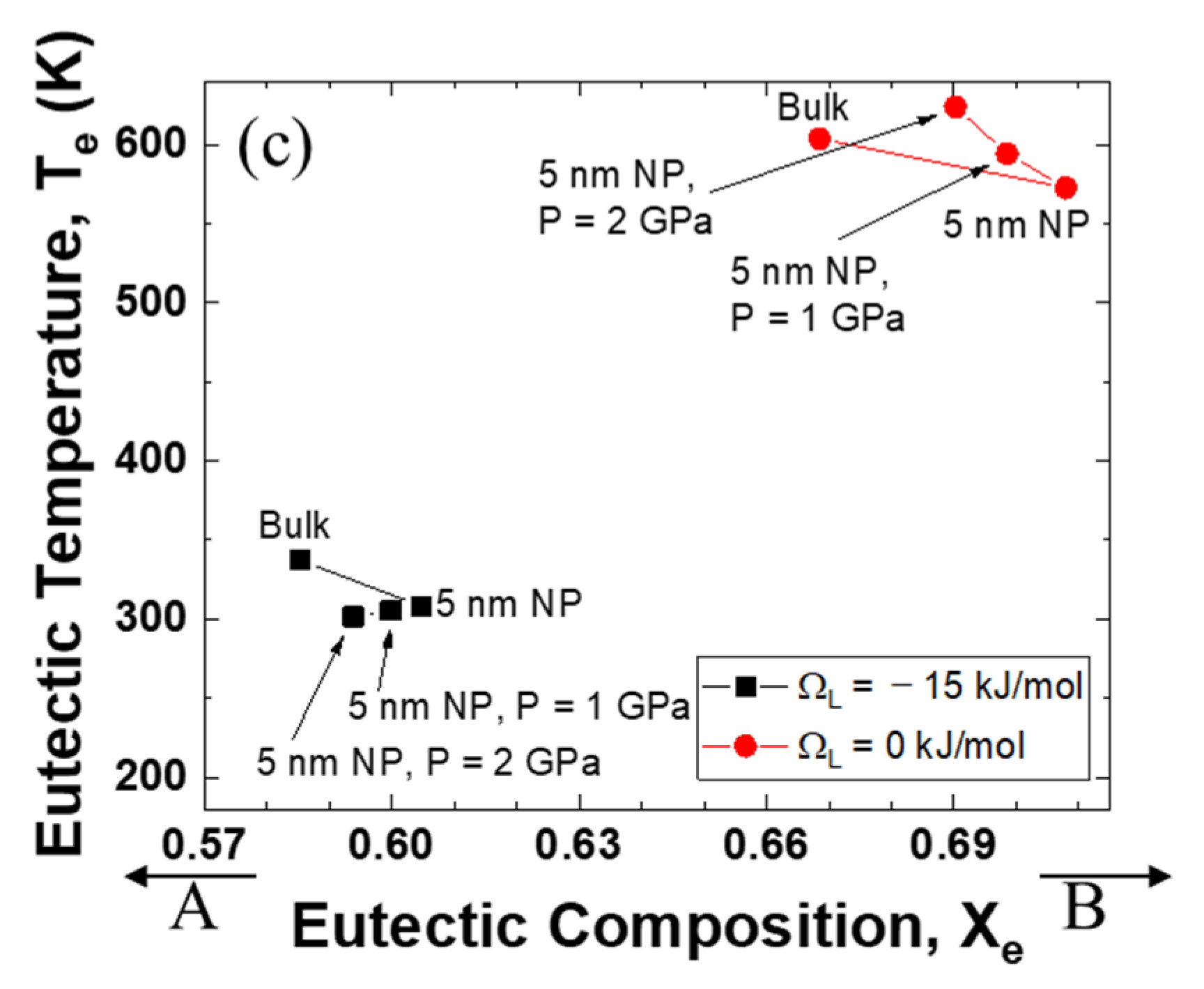
3.2. Variations in the Eutectic Points
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weissmüller, J. Alloy thermodynamics in nanostructures. J. Mater. Res. 1994, 9, 4–7. [Google Scholar] [CrossRef]
- Weissmüller, J.; Bunzel, P.; Wilde, G. Two-phase equilibrium in small alloy particles. Scr. Mater. 2004, 51, 813–818. [Google Scholar] [CrossRef]
- Tanaka, T.; Hara, S. Thermodynamic evaluation of binary phase diagrams in small particle systems. Z. Metallkd. 2001, 92, 467–472. [Google Scholar]
- Tanaka, T.; Hara, S. Thermodynamic evaluation of nano-particle binary alloy phase diagrams. Z. Metallkd. 2001, 92, 1236–1241. [Google Scholar]
- Lee, J.; Mori, H.; Lee, J.; Tanaka, T.; Penttilä, K. Phase diagrams of nanometer-sized particles in binary systems. JOM 2005, 57, 56–59. [Google Scholar] [CrossRef]
- Park, J.; Lee, J. Phase Diagram Reassessment of Ag-Au System Including Size Effect. Calphad 2008, 32, 135–141. [Google Scholar] [CrossRef]
- Lee, J.; Park, J.; Tanaka, T. Effects of interaction parameters and melting points of pure metals on the phase diagrams of the binary alloy nanoparticle systems: A classical approach based on the regular solution model. Calphad 2009, 33, 377–381. [Google Scholar] [CrossRef]
- Lee, J.; Sim, K.J. General Equations of Calphad-type Thermodynamic Description for Metallic Nanoparticle Systems. Calphad 2014, 44, 129–132. [Google Scholar] [CrossRef]
- Sim, K.; Lee, J.J. Phase Stability of Ag-Sn Nanoparticles. J. Alloys Compd. 2014, 590, 140–146. [Google Scholar] [CrossRef]
- Hillert, M.; Agren, J. Effect of surface free energy and surface stress on phase equilibria. Acta Mater. 2002, 50, 2429–2441. [Google Scholar] [CrossRef]
- Shirinyan, A.S.; Gusak, A.M. Phase diagrams of decomposing nanoalloys. Phil. Mag. 2004, 84, 579–593. [Google Scholar] [CrossRef]
- Shirinyan, A.S.; Gusak, A.M.; Wautelet, M. Phase diagram versus diagram of solubility: What is the difference for nanosystems? Acta Mater. 2005, 53, 5025–5032. [Google Scholar] [CrossRef]
- Li, M.; Zhu, T.-S. Modeling the melting temperature of nanoscaled bimetallic alloys. Phys. Chem. Chem. Phys. 2016, 18, 16958–16963. [Google Scholar] [CrossRef] [PubMed]
- Kaptay, G. Nano-Calphad: Extension of the Calphad method to systems with nano-phases and complexions. J. Mater. Sci. 2012, 47, 8320–8335. [Google Scholar] [CrossRef]
- Lee, J.; Nakamoto, M.; Tanaka, T. Thermodynamic Study on the Melting of Nanometer-sized Gold Particles on Graphite Substrate. J. Mater. Sci. 2005, 40, 2167–2171. [Google Scholar] [CrossRef]
- Lee, J.; Tanaka, T.; Lee, J.; Mori, H. Effect of substrates on the melting temperature of gold nano particles. Calphad 2007, 31, 105–111. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.; Tanaka, T.; Mori, H. In-situ atomic scale observation of melting point suppression in nanometer-sized gold particles. Nanotechnology 2009, 20, 475706. [Google Scholar] [CrossRef] [PubMed]
- Guenther, G.; Guillon, O. Models of size-dependent nanoparticle melting tested on gold. J. Mater. Sci. 2014, 49, 7915–7932. [Google Scholar] [CrossRef]
- Tang, C.; Sung, Y.-M.; Lee, J. Nonlinear size-dependent melting of the silica-encapsulated silver nanoparticles. App. Phys. Lett. 2012, 100, 201903. [Google Scholar]
- Monji, F.; Jabbareh, M.A. Thermodynamic model for prediction of binary alloy nanoparticle phase diagram including size dependent surface tension effect. Calphad 2017, 58, 1–5. [Google Scholar] [CrossRef]
- Guisbiers, G.; Mendoza-Cruz, R.; Bazán-Díaz, L.; Velázquez-Salazar, J.J.; Mendoza-Perez, R.; Robledo-Torres, J.A.; Rodriguez-Lopez, J.-L.; Montejano-Carrizales, J.M.; Whetten, R.L.; José-Yacamán, M. Electrum, the Gold−Silver Alloy, from the Bulk Scale to the Nanoscale: Synthesis, Properties, and Segregation Rules. ACS Nano 2016, 10, 188–198. [Google Scholar] [CrossRef]
- Zhao, N.; He, Y.Q.; Yang, C.C. A new approach to construct bulk and size dependent continuous binary solution phase diagrams of alloys. RSC Adv. 2015, 5, 96323–96327. [Google Scholar] [CrossRef]
- Zhao, Z.; Fisher, A.; Cheng, D. Phase diagram and segregation of Ag–Co nanoalloys: Insights from theory and simulation. Nanotechnology 2016, 27, 115702. [Google Scholar] [CrossRef]
- Delsante, S.; Borzone, G.; Novakovic, R.; Piazza, D.; Pigozzi, G.; Janczak-Rusch, J.; Pilloni, M.; Ennas, G. Synthesis and thermodynamics of Ag–Cu nanoparticles. Phys. Chem. Chem. Phys. 2015, 17, 28387–28393. [Google Scholar] [CrossRef]
- Sopoušek, J.; Zobač, O.; Buršík, J.; Roupcová, P.; Vykoukal, V.; Brož, P.; Pinkas, J.; Vřešt’ál, J. Heat-induced spinodal decomposition of Ag–Cu nanoparticles. Phys. Chem. Chem. Phys. 2015, 17, 28277–28285. [Google Scholar] [CrossRef]
- Jabbareh, M.A.; Monji, F. Thermodynamic modeling of Ag-Cu nanoalloy phase diagram. Calphad 2018, 60, 208–213. [Google Scholar] [CrossRef]
- Delsante, S.; Novakovic, R.; Borzone, G. Synthesis, characterization and thermal stability of SnAg and SnAgCu nanoparticles. J. Alloys Compd. 2018, 747, 385–393. [Google Scholar] [CrossRef]
- Roshanghias, A.; Vrestal, J.; Yakymovych, A.; Richter, K.W.; Ipser, H. Sn–Ag–Cu nanosolders: Melting behavior and phase diagram prediction in the Sn-rich corner of the ternary system. Calphad 2015, 49, 101–109. [Google Scholar] [CrossRef]
- Sopousek, J.; Vrestal, J.; Zemanova, A.; Bursik, J. Phase diagram prediction and particle characterization of Sn-Ag nano alloy for low melting point lead-free solders. J. Min. Metall. Sect. B. 2012, 48, 419–425. [Google Scholar] [CrossRef]
- Bao, T.T.; Kim, Y.; Lee, J.; Lee, J.-G. Preparation and Thermal Analysis of Sn-Ag Nano Solders. Mater. Trans. 2010, 51, 2145–2149. [Google Scholar] [CrossRef]
- Guisbiers, G.; Mejia-Rosales, S.; Khanal, S.; Ruiz-Zepeda, F.; Whetten, R.L.; José-Yacaman, M. Gold−Copper Nano-Alloy, “Tumbaga”, in the Era of Nano: Phase Diagram and Segregation. Nano Lett. 2014, 14, 6718–6726. [Google Scholar] [CrossRef]
- Braidy, N.; Purdy, G.R.; Botton, G.A. Equilibrium and stability of phase-separating Au–Pt nanoparticles. Acta Mater. 2008, 56, 5972–5983. [Google Scholar] [CrossRef]
- Wilde, G.; Bunzel, P.; Rösner, H.; Weissmüller, J. Phase equilibria and phase diagrams of nanoscaled systems. J. Alloys Compd. 2007, 434–435, 286–289. [Google Scholar] [CrossRef]
- Dahan, Y.; Makov, G.; Shneck, R.Z. Nanometric size dependent phase diagram of Bi–Sn. Calphad 2016, 53, 136–145. [Google Scholar] [CrossRef]
- Jesser, W.A.; Shiflet, G.J.; Allen, G.L.; Crawford, J.L. Equilibrium phase diagrams of isolated nano-phases. Mater. Res. Innovat. 1999, 2, 211–216. [Google Scholar] [CrossRef]
- Shirinyan, A.; Wilde, G.; Bilogorodskyy, Y. Solidification loops in the phase diagram of nanoscale alloy particles: From a specific example towards a general vision. J. Mater. Sci. 2018, 53, 2859–2879. [Google Scholar] [CrossRef]
- Cui, M.; Lu, H.; Jiang, H.; Cao, Z.; Meng, X. Phase Diagram of Continuous Binary Nanoalloys: Size, Shape, and Segregation Effects. Sci. Rep. 2017, 7, 41990. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, F.-H.; Fisher, A.; Shen, Y.; Cheng, D. Phase stability and segregation behavior of nickel-based nanoalloys based on theory and simulation. J. Alloys Compd. 2017, 708, 1150–1160. [Google Scholar] [CrossRef]
- Guisbiers, G.; Khanal, S.; Ruiz-Zepeda, F.; Roque de la Puente, J.; José-Yacaman, M. Cu–Ni nano-alloy: Mixed, core–shell or Janus nano-particle? Nanoscale 2014, 6, 14630–14635. [Google Scholar] [CrossRef]
- Sopousek, J.; Vrestal, J.; Pinkas, J.; Broz, P.; Bursik, J.; Styskalik, A.; Skoda, D.; Zobac, O.; Lee, J. Cu–Ni nanoalloy phase diagram—Prediction and experiment. Calphad 2014, 45, 33–39. [Google Scholar] [CrossRef]
- Shirinyan, A.S. Two-phase equilibrium states in individual Cu–Ni nanoparticles: Size, depletion and hysteresis effects. Beilstein J. Nanotechnol. 2015, 6, 1811–1820. [Google Scholar] [CrossRef] [PubMed]
- Pavan, L.; Baletto, F.; Novakovic, R. Multiscale approach for studying melting transitions in CuPt nanoparticles. Phys. Chem. Chem. Phys. 2015, 17, 28364–28371. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zanolli, Z.; Stankovski, M.; Johansson, J. Size- and shape-dependent phase diagram of In–Sb nano-alloys. Nanoscale 2015, 7, 17387–17396. [Google Scholar] [CrossRef] [PubMed]
- Kroupa, A.; Káňa, T.; Buršík, J.; Zemanová, A.; Šob, M. Modelling of phase diagrams of nanoalloys with complex metallic phases: Application to Ni–Sn. Phys. Chem. Chem. Phys. 2015, 17, 28200–28210. [Google Scholar] [CrossRef]
- Bonham, B.; Guisbiers, G. Thermal stability and optical properties of Si–Ge nanoparticles. Nanotechnology 2017, 28, 245702. [Google Scholar] [CrossRef] [PubMed]
- Bajaj, S.; Haverty, M.G.; Arróyave, R.; Goddard III FRSC, W.A.; Shankar, S. Phase stability in nanoscale material systems: Extension from bulk phase diagrams. Nanoscale 2015, 7, 9868–9877. [Google Scholar] [CrossRef]
- Asadikiya, M.; Sabarou, H.; Chen, M.; Zhong, Y. Phase diagram for a nano-yttria-stabilized zirconia system. RSC Adv. 2016, 6, 17438–17445. [Google Scholar] [CrossRef]
- Drazin, J.W.; Castro, R.H.R. Phase Stability in Nanocrystals: A Predictive Diagram for Yttria–Zirconia. J. Am. Ceram. Soc. 2015, 98, 1377–1384. [Google Scholar] [CrossRef]
- Guenther, G.; Theissmann, R.; Guillon, O. Size-Dependent Phase Transformations in Bismuth Oxide Nanoparticles. II. Melting and Stability Diagram. J. Phys. Chem. C 2014, 118, 27020–27027. [Google Scholar] [CrossRef]
- Kim, S.S. Thermodynamic modeling of the CeO2–CoO nano-phase diagram. J. Alloys Compd. 2014, 588, 697–704. [Google Scholar] [CrossRef]
- Cheng, Y.; Su, H.; Koop, T.; Mikhailov, E.; Pöschl, U. Size dependence of phase transitions in aerosol nanoparticles. Nat. Commun. 2015, 6, 5923. [Google Scholar] [CrossRef]
- Lu, H.; Meng, X. Nanophase diagram of binary eutectic Au-Ge nanoalloys for vapor-liquid-solid semiconductor nanowires growth. Sci. Rep. 2015, 5, 11263. [Google Scholar] [CrossRef]
- Koto, M. Thermodynamics and kinetics of the growth mechanism of vapor–liquid–solid grown nanowires. J. Cryst. Growth 2015, 424, 49–54. [Google Scholar] [CrossRef]
- Schwalbach, E.J.; Voorhees, P.W. Phase Equilibrium and Nucleation in VLS-Grown Nanowires. Nano Lett. 2008, 8, 3739–3745. [Google Scholar] [CrossRef]
- Adhikari, H.; Marshall, A.F.; Goldthorpe, I.A.; Chidsey, C.E.D.; McIntyre, P.C. Metastability of Au–Ge Liquid Nanocatalysts: Ge Vapor–Liquid–Solid Nanowire Growth Far below the Bulk Eutectic Temperature. ACS Nano 2007, 1, 415–422. [Google Scholar] [CrossRef] [PubMed]
- Ben Shalom, S.; Kim, H.G.; Emuna, M.; Argaman, U.; Greenberg, Y.; Lee, J.; Yahel, E.; Makov, G. Anomalous pressure dependent phase diagram of liquid Ga–In alloys. J. Alloys Compd. 2020, 822, 153537. [Google Scholar] [CrossRef]
- Kim, H.G.; Lee, J.; Makov, G. Thermodynamic Calculation of Bi–Sn Alloy Phase Diagram Under Pressure with Advanced Density Measurements. Met. Mater. Int. 2020, 26, 586–590. [Google Scholar] [CrossRef]
- Emuna, M.; Greenberg, Y.; Hevroni, R.; Korover, I.; Yahel, E.; Makov, G. Phase diagrams of binary alloys under pressure. J. Alloys Compd. 2016, 687, 360–369. [Google Scholar] [CrossRef]
- Kirshon, Y.; Ben Shalom, S.; Emuna, M.; Greenberg, Y.; Lee, J.; Makov, G.; Yahel, E. Thermophysical Measurements in Liquid Alloys and Phase Diagram Studies. Materials 2019, 12, 3999. [Google Scholar] [CrossRef]
- Lee, J.; Schuh, C.A.; Luo, J.; Zhong, Y. Forword: Thermodynamics of nanomaterials. Calphad 2019, 65, 402. [Google Scholar] [CrossRef]
- Tolbert, S.H.; Alivisatos, A.P. Size Dependence of a First Order Solid-Solid Phase Transition: The Wurtzite to Rock Salt Transformation in CdSe Nanocrystals. Science 1994, 265, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Qadri, S.B.; Yang, J.; Ratna, B.R.; Skelton, E.F.; Hu, J.Z. Pressure Induced Structural Transitions in Nanometer Size Particles of PbS. Appl. Phys. Lett. 1996, 69, 2205–2207. [Google Scholar] [CrossRef]
- Wang, Z.; Saxena, S.K.; Pischedda, V.; Liermann, H.P.; Zha, C.S. X-Ray Diffraction Study on Pressure-Induced Phase Transformations in Nanocrystalline Anatase/rutile (TiO2). J. Phys. Condens. Matter. 2001, 13, 8317–8323. [Google Scholar] [CrossRef]
- Daou, T.J.; Pourroy, G.; Bégin-Colin, S.; Grenèche, J.M.; Ulhaq-Bouillet, C.; Legaré, P.; Bernhardt, P.; Leuvrey, C.; Rogez, G. Hydrothermal Synthesis of Monodisperse Magnetite Nanoparticles. Chem. Mater. 2006, 18, 4399–4404. [Google Scholar] [CrossRef]
- Hsu, Y.-J.; Gordeeva, A.; Antlauf, M.; Häussermann, U.; Andersson, O. Development of a high pressure stirring cell up to 2 GPa: A new window for chemical reactions and material synthesis. High Press. Res. 2020, 40, 358–368. [Google Scholar] [CrossRef]
- Makov, G.; Emuna, M.; Yahel, E.; Kim, H.G.; Lee, J. Effect of pressure on the interactions and phase diagrams of binary alloys. Comp. Mat. Sci. 2019, 169, 109103. [Google Scholar] [CrossRef]
- Iida, T.; Guthrie, R.I.L. The Physical Properties of Liquid Metals; Oxford University Press Inc.: New York, NY, USA, 1993; pp. 10–11. [Google Scholar]
- Hack, K. The SGTE Casebook, 2nd ed.; Woodhead Publishing Limited: Cambridge, UK, 2008; pp. 50–55. [Google Scholar]
- Pelton, A.D. Phase Diagrams and Thermodynamic Modeling of Solutions; Elsevier: Amsterdam, The Netherlands, 2019; pp. 108–110. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.G.; Lee, J.; Makov, G. Phase Diagram of Binary Alloy Nanoparticles under High Pressure. Materials 2021, 14, 2929. https://doi.org/10.3390/ma14112929
Kim HG, Lee J, Makov G. Phase Diagram of Binary Alloy Nanoparticles under High Pressure. Materials. 2021; 14(11):2929. https://doi.org/10.3390/ma14112929
Chicago/Turabian StyleKim, Han Gyeol, Joonho Lee, and Guy Makov. 2021. "Phase Diagram of Binary Alloy Nanoparticles under High Pressure" Materials 14, no. 11: 2929. https://doi.org/10.3390/ma14112929
APA StyleKim, H. G., Lee, J., & Makov, G. (2021). Phase Diagram of Binary Alloy Nanoparticles under High Pressure. Materials, 14(11), 2929. https://doi.org/10.3390/ma14112929