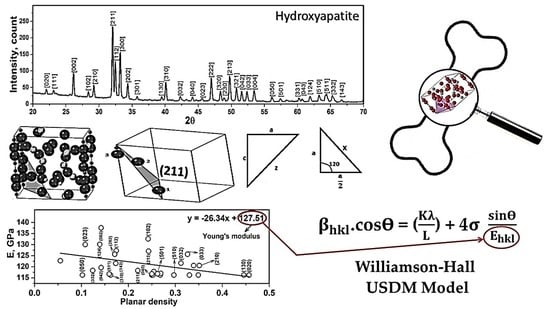
X-ray Diffraction Analysis and Williamson-Hall Method in USDM Model for Estimating More Accurate Values of Stress-Strain of Unit Cell and Super Cells (2 × 2 × 2) of Hydroxyapatite, Confirmed by Ultrasonic Pulse-Echo Test
Abstract
:1. Introduction
2. Methods
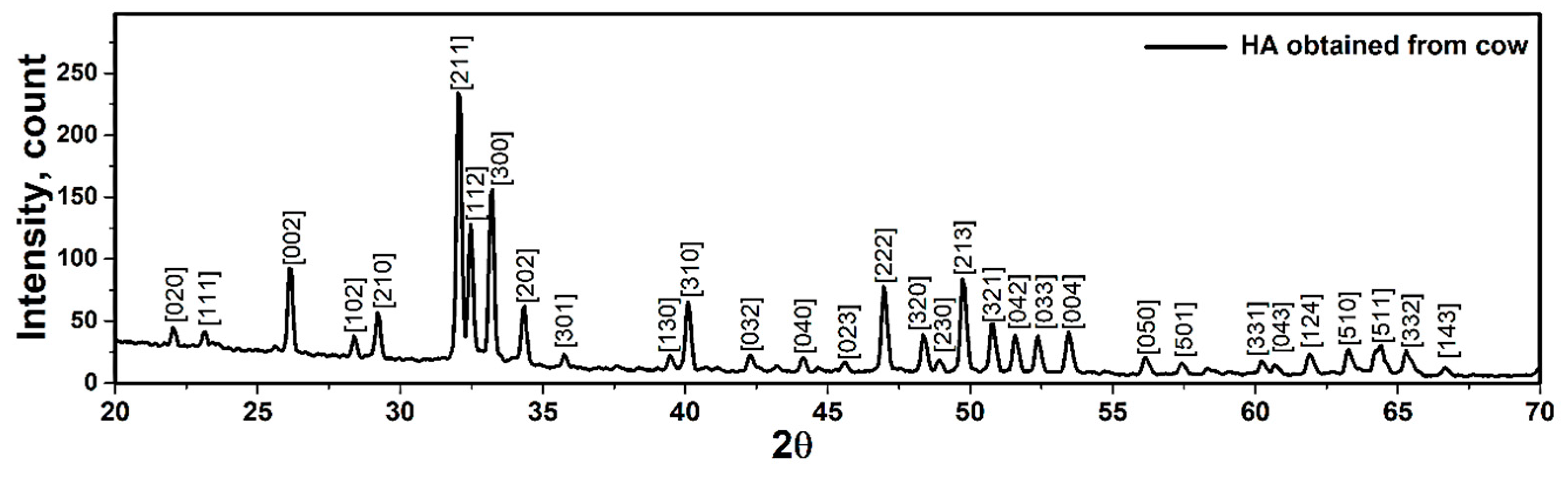
2.1. Structural Analyses of Synthesized Hydroxyapatite
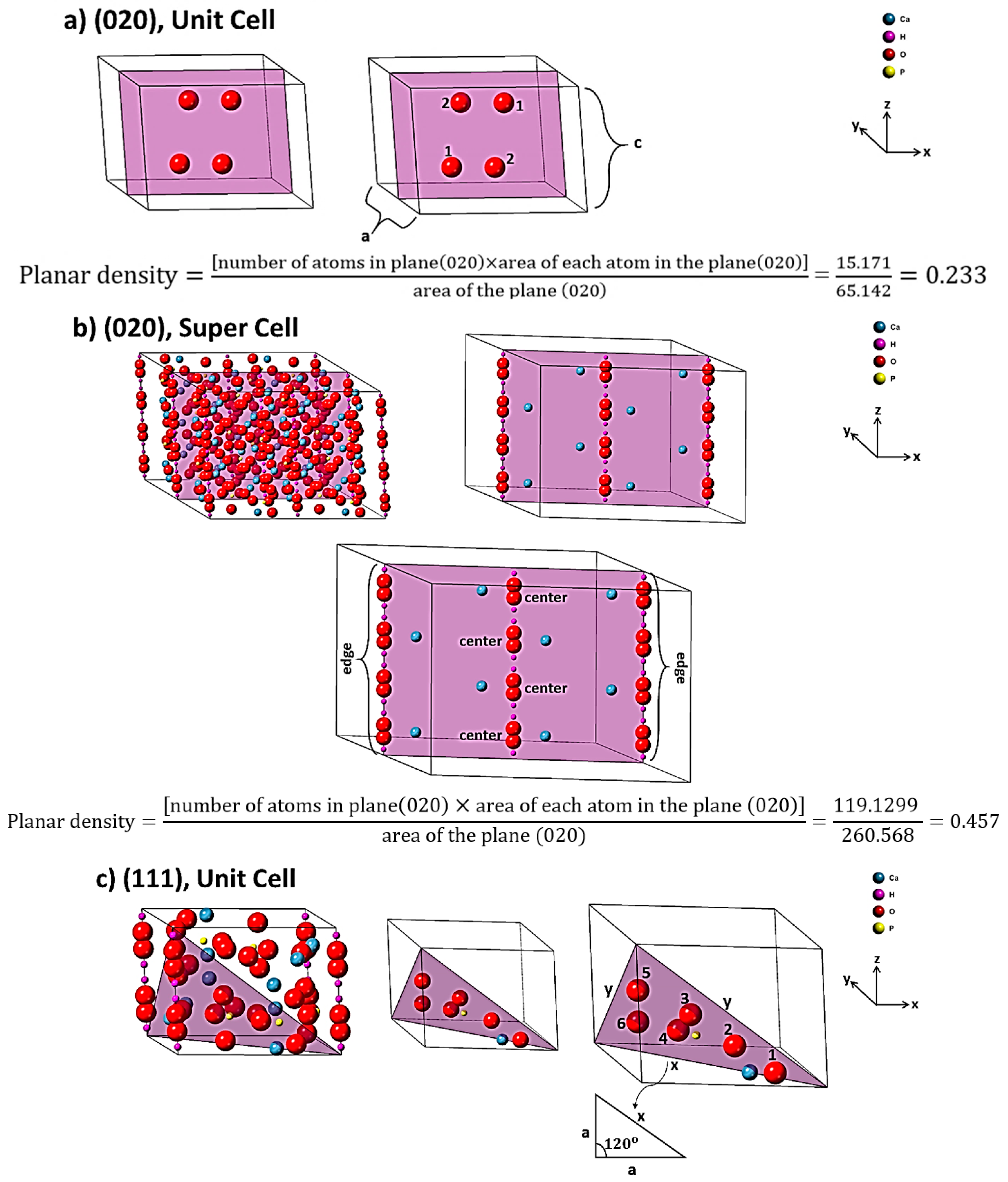
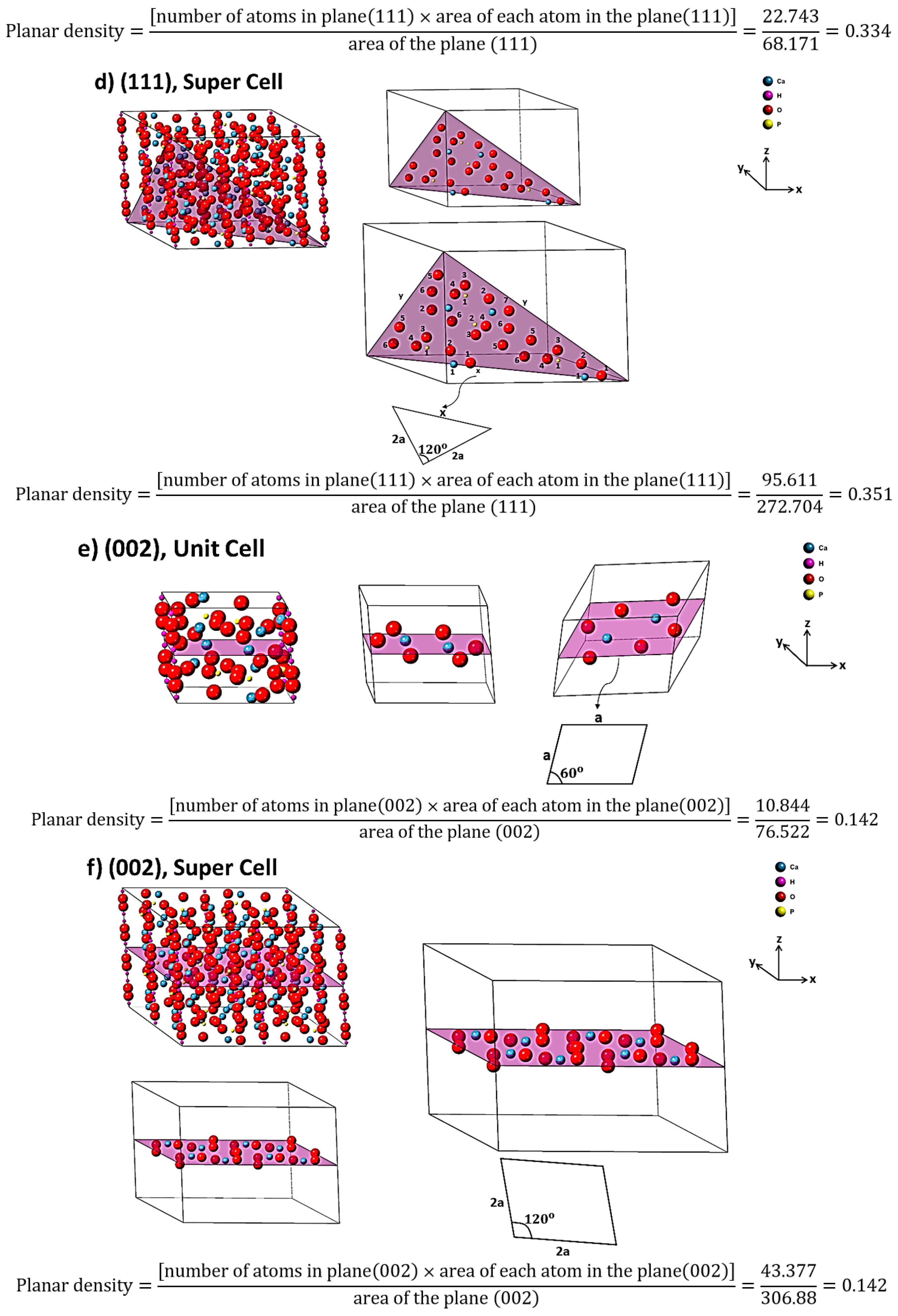
2.2. Planar Density of Unit Cell and Super Cells (2 × 2 × 2) of Hydroxyapatite
2.3. Elastic Stiffness Constant and Elastic Compliance of Hydroxyapatite
2.4. The Young’s Modulus versus Planar Density of Unit Cell and Super Cells (2 × 2 × 2) of Hydroxyapatite
3. Result and Discussion
3.1. Positive and Negative Slope Values of Unit Cell and Super Cells (2 × 2 × 2)
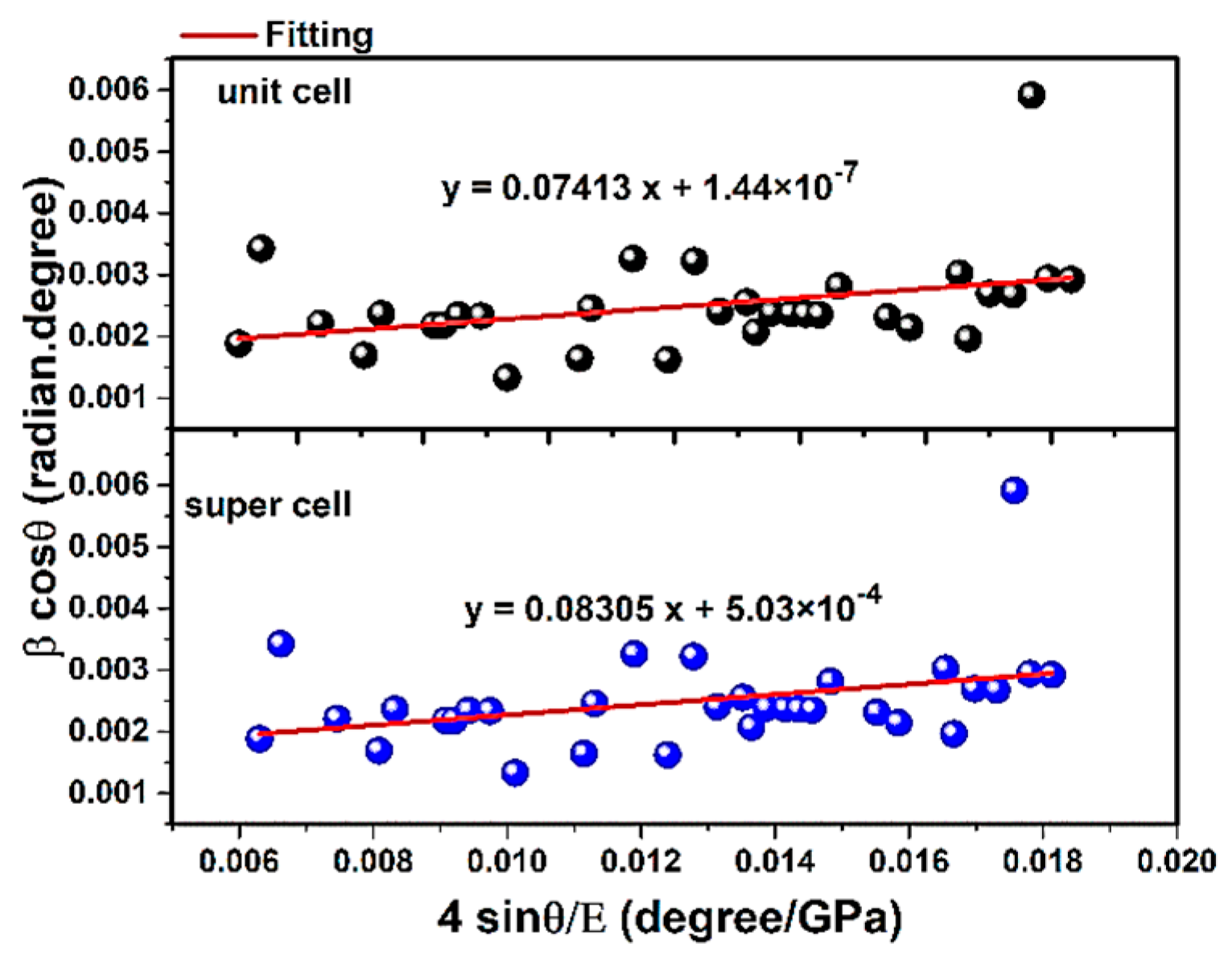
3.2. Williamson-Hall Method in USDM Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sasmita, F.; Wibisono, G.; Judawisastra, H.; Priambodo, T.A. Determination of elastic modulus of ceramics using ultrasonic testing. AIP Conf. Proc. 2018, 1945, 020017. [Google Scholar] [CrossRef]
- Shimada, M.; Matsushita, K.; Kuratani, S.; Okamoto, T.; Koizumi, M.; Tsukuma, K.; Tsukidate, T. Temperature dependence of young’s modulus and internal friction in alumina, silicon nitride, and partially stabilized zirconia ceramics. J. Am. Ceram. Soc. 1984, 67, C23–C24. [Google Scholar] [CrossRef]
- Vallet-Regí, M. Revisiting ceramics for medical applications. Dalton Trans. 2006, 5211–5220. [Google Scholar] [CrossRef] [PubMed]
- Marzieh, R.; Sohrab, N.; Arvydas, P.; Giedrius, J. Preparation and investigation of bioactive organic-inorganic nano-composite derived from PVB-co-VA-co-VAc/HA. In Proceedings of the 15th International Conference Mechatronic Systems and Materials, MSM 2020, Bialystok, Poland, 1–3 July 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020. [Google Scholar]
- Rabiei, M.; Palevicius, A.; Monshi, A.; Nasiri, S.; Vilkauskas, A.; Janusas, G. Comparing methods for calculating nano crystal size of natural hydroxyapatite using X-ray diffraction. Nanomaterials 2020, 10, 1627. [Google Scholar] [CrossRef] [PubMed]
- Shih, W.J.; Wang, M.C.; Hon, M.H. Morphology and crystallinity of the nanosized hydroxyapatite synthesized by hydrolysis using cetyltrimethylammonium bromide (CTAB) as a surfactant. J. Cryst. Growth 2005, 275, e2339–e2344. [Google Scholar] [CrossRef]
- Loganathan, T.M.; Sultan, M.T.H.; Gobalakrishnan, M.K. Ultrasonic inspection of natural fiber-reinforced composites. In Sustainable Composites for Aerospace Applications; Elsevier: Amsterdam, The Netherlands, 2018; pp. 227–251. ISBN 9780081021316. [Google Scholar]
- Nath, D.; Singh, F.; Das, R. X-ray diffraction analysis by Williamson-Hall, Halder-Wagner and size-strain plot methods of CdSe nanoparticles—A comparative study. Mater. Chem. Phys. 2020, 239, 122021. [Google Scholar] [CrossRef]
- Khorsand Zak, A.; Abd Majid, W.H.; Abrishami, M.E.; Yousefi, R. X-ray analysis of ZnO nanoparticles by Williamson-Hall and size-strain plot methods. Solid State Sci. 2011, 13, 251–256. [Google Scholar] [CrossRef]
- Venkateswarlu, K.; Chandra Bose, A.; Rameshbabu, N. X-ray peak broadening studies of nanocrystalline hydroxyapatite by WilliamsonHall analysis. Phys. B Condens. Matter 2010, 405, 4256–4261. [Google Scholar] [CrossRef]
- Bahrololoom, M.; Javidi, M.; Javadpour, S. Characterisation of natural hydroxyapatite extracted from bovine cortical bone ash. J. Ceram. Process. Res. 2009, 10, 129–138. [Google Scholar]
- Shahabi, S.; Najafi, F.; Majdabadi, A.; Hooshmand, T.; Haghbin Nazarpak, M.; Karimi, B.; Fatemi, S.M. Effect of gamma irradiation on structural and biological properties of a PLGA-PEG-hydroxyapatite composite. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef]
- Pasero, M.; Kampf, A.R.; Ferraris, C.; Pekov, I.V.; Rakovan, J.; White, T.J. Nomenclature of the apatite supergroup minerals. Eur. J. Mineral. 2010, 22, 163–179. [Google Scholar] [CrossRef]
- Hench, L.L. An Introduction to Bioceramics, 2nd ed.; Imperial College Press: London, UK, 2013; ISBN 9781908977168. [Google Scholar]
- Lin, K.; Chang, J. Structure and properties of hydroxyapatite for biomedical applications. In Hydroxyapatite (Hap) for Biomedical Applications; Elsevier: Amsterdam, The Netherlands, 2015; pp. 3–19. [Google Scholar]
- Bystrov, V.S.; Coutinho, J.; Bystrova, A.V.; Dekhtyar, Y.D.; Pullar, R.C.; Poronin, A.; Palcevskis, E.; Dindune, A.; Alkan, B.; Durucan, C.; et al. Computational study of hydroxyapatite structures, properties and defects. J. Phys. D Appl. Phys. 2015, 48, 195302. [Google Scholar] [CrossRef]
- Rajkumar, M.; Sundaram, N.; Rajendran, V. Preparation of size controlled, stoichiometric and bioresorbable hydroxyapatite nanorod by varying initial pH, Ca/P ratio and sintering temperature. Digest J. Nanomater. Biostruct. 2011, 6, 169–179. [Google Scholar]
- Landi, E.; Riccobelli, S.; Sangiorgi, N.; Sanson, A.; Doghieri, F.; Miccio, F. Porous apatites as novel high temperature sorbents for carbon dioxide. Chem. Eng. J. 2014, 254, 586–596. [Google Scholar] [CrossRef]
- Rabiei, M.; Palevicius, A.; Dashti, A.; Nasiri, S.; Monshi, A.; Vilkauskas, A.; Janusas, G. Measurement Modulus of elasticity related to the atomic density of planes in unit cell of crystal lattices. Materials 2020, 13, 4380. [Google Scholar] [CrossRef] [PubMed]
- Rajabi, K.; Hosseini-Hashemi, S. Application of the generalized Hooke’s law for viscoelastic materials (GHVMs) in nanoscale mass sensing applications of viscoelastic nanoplates: A theoretical study. Eur. J. Mech. A Solids 2018, 67, 71–83. [Google Scholar] [CrossRef]
- Kanoun, M.B.; Goumri-Said, S.; Abdullah, K. Theoretical study of physical properties and oxygen incorporation effect in nanolaminated ternary carbides 211-MAX phases. In Advances in Science and Technology of Mn+1AXn Phases; Elsevier: Amsterdam, The Netherlands, 2012; pp. 177–196. [Google Scholar]
- Li, Y.; Thompson, R.B. Relations between elastic constants Cij and texture parameters for hexagonal materials. J. Appl. Phys. 1990, 67, 2663–2665. [Google Scholar] [CrossRef] [Green Version]
- Huntington, H.B. The elastic constants of crystals. Solid State Phys. Adv. Res. Appl. 1958, 7, 213–351. [Google Scholar] [CrossRef]
- Mah, M.; Schmitt, D.R. Determination of the complete elastic stiffnesses from ultrasonic phase velocity measurements. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Neighbours, J.R.; Schacher, G.E. Determination of elastic constants from sound-velocity measurements in crystals of general symmetry. J. Appl. Phys. 1967, 38, 5366–5375. [Google Scholar] [CrossRef]
- ASTM E797/E797M-15. Standard Practice for Measuring Thickness by Manual Ultrasonic Pulse-Echo Contact Method. Available online: https://www.astm.org/Standards/E797.htm (accessed on 19 November 2020).
- Van Buskirk, W.C.; Cowin, S.C.; Ward, R.N. Ultrasonic measurement of orthotropic elastic constants of bovine femoral bone. J. Biomech. Eng. 1981, 103, 67–72. [Google Scholar] [CrossRef]
- ASTM E214-05. Standard Practice for Immersed Ultrasonic Testing by the Reflection Method Using Pulsed Longitudinal Waves (Withdrawn 2007). Available online: https://www.astm.org/Standards/E214.htm (accessed on 19 November 2020).
- ASTM E1001-16. Standard Practice for Detection and Evaluation of Discontinuities by the Immersed Pulse-Echo Ultrasonic Method Using Longitudinal Waves. Available online: https://www.astm.org/Standards/E1001.htm (accessed on 19 November 2020).
- Elliot, S. The Physics and Chemistry of Solids; Wiley: Hoboken, NJ, USA, 1998; Available online: https://www.wiley.com/en-us/The+Physics+and+Chemistry+of+Solids-p-9780471981954 (accessed on 19 November 2020).
- McHugh, P.E. Introduction to crystal plasticity theory. In Mechanics of Microstructured Materials; Springer: Cham, Switzerland, 2004; pp. 125–171. [Google Scholar]
- Pandech, N.; Sarasamak, K.; Limpijumnong, S. Elastic properties of perovskite A TiO3 (A = Be, Mg, Ca, Sr, and Ba) and PbBO3 (B = Ti, Zr, and Hf): First principles calculations. J. Appl. Phys. 2015, 117, 174108. [Google Scholar] [CrossRef]
- Wang, H.; Prendiville, P.L.; McDonnell, P.J.; Chang, W.V. An ultrasonic technique for the measurement of the elastic moduli of human cornea. J. Biomech. 1996, 29, 1633–1636. [Google Scholar] [CrossRef]
- Bray, D.E.; Stanley, R.K. Nondestructive Evaluation: A Tool in Design, Manufacturing and Service; CRC Press: Boca Raton, FL, USA, 1996; Available online: https://books.google.com.et/books?id=5WtmjwEACAAJ&printsec=copyright#v=onepage&q&f=false (accessed on 19 November 2020).
- Rabiei, M.; Palevicius, A.; Nasiri, S.; Dashti, A.; Vilkauskas, A.; Janusas, G. Relationship between young’s modulus and planar density of unit cell, super cells (2 × 2 × 2), symmetry cells of perovskite (CaTiO3) LATTICE. Materials 2021, 14, 1258. [Google Scholar] [CrossRef]
- Bodke, M.; Gawai, U.; Patil, A.; Dole, B. Estimation of accurate size, lattice strain using Williamson-Hall models, SSP and TEM of Al doped ZnO nanocrystals. Mater. Tech. 2018, 106. [Google Scholar] [CrossRef] [Green Version]
- Figliola, R.S.; Beasley, D.E. Theory and Design for Mechanical Measurements, 7th ed.; Wiley: Hoboken, NJ, USA, 2014; Available online: https://www.wiley.com/en-us/Theory+and+Design+for+Mechanical+Measurements%2C+7th+Edition-p-9781119475651 (accessed on 19 November 2020).
- Moradi, K.; Sabbagh Alvani, A.A. First-Principles study on Sr-doped hydroxyapatite as a biocompatible filler for photo-cured dental composites. J. Aust. Ceram. Soc. 2020, 56, 591–598. [Google Scholar] [CrossRef]
- Bhat, S.S.; Waghmare, U.V.; Ramamurty, U. First-Principles study of structure, vibrational, and elastic properties of stoichiometric and calcium-deficient hydroxyapatite. Cryst. Growth Des. 2014, 14, 3131–3141. [Google Scholar] [CrossRef]
- Ching, W.Y.; Rulis, P.; Misra, A. Ab initio elastic properties and tensile strength of crystalline hydroxyapatite. Acta Biomater. 2009, 5, 3067–3075. [Google Scholar] [CrossRef] [Green Version]
- De Leeuw, N.H.; Bowe, J.R.; Rabone, J.A.L. A computational investigation of stoichiometric and calcium-deficient oxy- and hydroxy-apatites. Faraday Discuss. 2007, 134, 195–214. [Google Scholar] [CrossRef]
- Katz, J.L.; Ukraincik, K. On the anisotropic elastic properties of hydroxyapatite. J. Biomech. 1971, 4, 221–227. [Google Scholar] [CrossRef]
- Zhang, J.M.; Zhang, Y.; Xu, K.W.; Ji, V. Anisotropic elasticity in hexagonal crystals. Thin Solid Films 2007, 515, 7020–7024. [Google Scholar] [CrossRef]
- Berdichevsky, V. Energy of dislocation networks. Int. J. Eng. Sci. 2016, 103, 35–44. [Google Scholar] [CrossRef]
- Reed-Hill, R.E.; Abbaschian, R. Physical Metallurgy Principles; Cengage: Boston, MA, USA, 1992. [Google Scholar]
- Shi, D.; Jiang, G.; Bauer, J. The effect of structural characteristics on the in vitro bioactivity of hydroxyapatite. J. Biomed. Mater. Res. 2002, 63, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Ragel, C.V.; Vallet-Regí, M.; Rodríguez-Lorenzo, L.M. Preparation and in vitro bioactivity of hydroxyapatite/solgel glass biphasic material. Biomaterials 2002, 23, 1865–1872. [Google Scholar] [CrossRef]
- Dasgupta, S.; Banerjee, S.S.; Bandyopadhyay, A.; Bose, S. Zn- and Mg-doped hydroxyapatite nanoparticles for controlled release of protein. Langmuir 2010, 26, 4958–4964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uysal, I.; Severcan, F.; Tezcaner, A.; Evis, Z. Co-Doping of hydroxyapatite with zinc and fluoride improves mechanical and biological properties of hydroxyapatite. Prog. Nat. Sci. Mater. Int. 2014, 24, 340–349. [Google Scholar] [CrossRef] [Green Version]
- Ptáček, P. Apatites and Their Synthetic Analogues—Synthesis, Structure, Properties and Applications; InTech: London, UK, 2016. [Google Scholar]
- Suryanarayana, C.; Norton, M.G.; Suryanarayana, C.; Norton, M.G. Practical aspects of X-ray diffraction. In X-ray Diffraction; Springer: New York, NY, USA, 1998; pp. 63–94. [Google Scholar]
- Itatani, K.; Tsuchiya, K.; Sakka, Y.; Davies, I.J.; Koda, S. Superplastic deformation of hydroxyapatite ceramics with B2O3 or Na2O addition fabricated by pulse current pressure sintering. J. Eur. Ceram. Soc. 2011, 31, 2641–2648. [Google Scholar] [CrossRef]

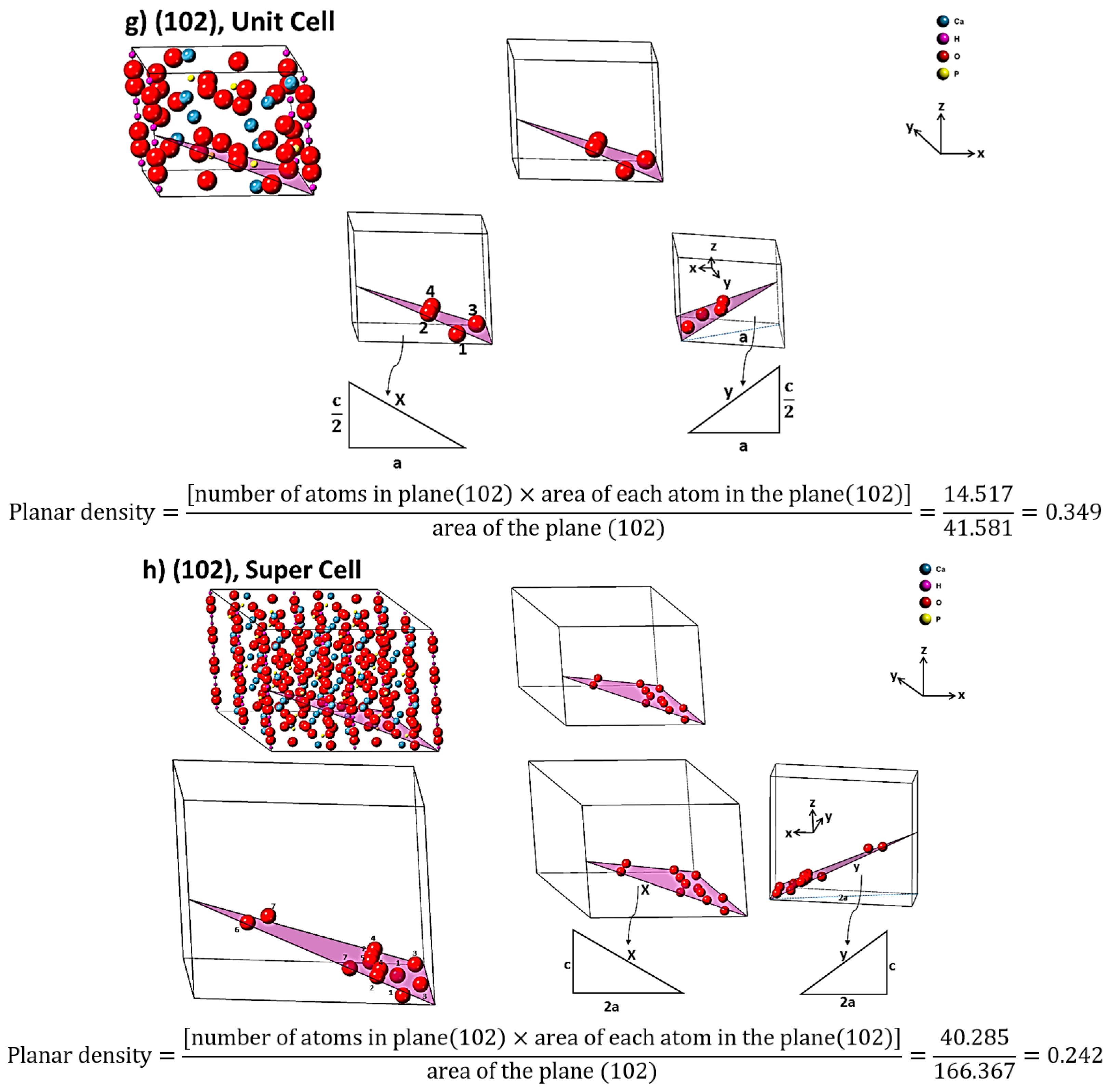

| Crystal System | a | c | Cell | Crystal Density (g/cm3) | Space Group |
|---|---|---|---|---|---|
| HCP | 9.400 | 6.930 | 530.301 | 3.140 | P63/m |
| Stiffness Constant (C), (Gpa) | Theory. from Ref [40] (Ching et al.) | Theory. from Ref [41] (Leeuw et al.) | Experiment. from Ref [42] (Katz et al.) | Theory. This Study | Experiment. This Study |
|---|---|---|---|---|---|
| 140.00 | 134.40 | 137.00 | 139.58 | 135.78 | |
| 42.40 | 48.90 | 42.50 | 48.03 | 49.21 | |
| 58.30 | 68.50 | 54.90 | 61.22 | 56.62 | |
| 174.80 | 184.70 | 172.00 | 181.08 | 179.22 | |
| 47.50 | 51.40 | 39.60 | 50.93 | 41.73 |
| Compliance Constant (S), (Gpa) | Theory. (Ching et al.) | Theory. (Leeuw et al.) | Experiment. (Katz et al.) | Theory. This Study | Experiment. This Study |
|---|---|---|---|---|---|
| 0.008607002 | 0.009621806 | 0.008752330 | 0.008881114 | 0.009126549 | |
| −0.001638900 | −0.002074100 | −0.001829681 | −0.002041879 | −0.002424797 | |
| −0.002324030 | −0.002799231 | −0.002209613 | −0.002312227 | −0.002117248 | |
| 0.007271063 | 0.007490496 | 0.007224509 | 0.007085868 | 0.006917516 | |
| 0.021052632 | 0.019455253 | 0.025252525 | 0.019634793 | 0.023963575 |
| Number of Measurement | L (mm) | ||
|---|---|---|---|
| 1 | 6.26 | 2.52 | 11.59 |
| 2 | 6.27 | 2.50 | 11.61 |
| 3 | 6.26 | 2.51 | 11.59 |
| 4 | 6.25 | 2.53 | 11.57 |
| 5 | 6.24 | 2.54 | 11.55 |
| Study | Young Modulus (E), (Gpa) in This Method (Intercept Value) | |
|---|---|---|
| Unit Cell | Super Cells (2 × 2 × 2) | |
| Theory. (Ching et al.) | 118.43 | 127.51 |
| Theory. (Leeuw et al.) | 113.94 | 128.91 |
| Experiment. (Katz et al.) | 109.54 | 117.52 |
| Theory. (This Study) | 118.62 | 131.74 |
| Experiment. (This Study) | 108.15 | 121.17 |
| Mechanical Properties | |||
|---|---|---|---|
| Structure | (GPa) | (GPa) | |
| Unit cell | 0.07413 | 0.00068 | 108.15 |
| Super cells (2 × 2 × 2) | 0.08305 | 0.00068 | 121.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabiei, M.; Palevicius, A.; Dashti, A.; Nasiri, S.; Monshi, A.; Doustmohammadi, A.; Vilkauskas, A.; Janusas, G. X-ray Diffraction Analysis and Williamson-Hall Method in USDM Model for Estimating More Accurate Values of Stress-Strain of Unit Cell and Super Cells (2 × 2 × 2) of Hydroxyapatite, Confirmed by Ultrasonic Pulse-Echo Test. Materials 2021, 14, 2949. https://doi.org/10.3390/ma14112949
Rabiei M, Palevicius A, Dashti A, Nasiri S, Monshi A, Doustmohammadi A, Vilkauskas A, Janusas G. X-ray Diffraction Analysis and Williamson-Hall Method in USDM Model for Estimating More Accurate Values of Stress-Strain of Unit Cell and Super Cells (2 × 2 × 2) of Hydroxyapatite, Confirmed by Ultrasonic Pulse-Echo Test. Materials. 2021; 14(11):2949. https://doi.org/10.3390/ma14112949
Chicago/Turabian StyleRabiei, Marzieh, Arvydas Palevicius, Amir Dashti, Sohrab Nasiri, Ahmad Monshi, Akram Doustmohammadi, Andrius Vilkauskas, and Giedrius Janusas. 2021. "X-ray Diffraction Analysis and Williamson-Hall Method in USDM Model for Estimating More Accurate Values of Stress-Strain of Unit Cell and Super Cells (2 × 2 × 2) of Hydroxyapatite, Confirmed by Ultrasonic Pulse-Echo Test" Materials 14, no. 11: 2949. https://doi.org/10.3390/ma14112949
APA StyleRabiei, M., Palevicius, A., Dashti, A., Nasiri, S., Monshi, A., Doustmohammadi, A., Vilkauskas, A., & Janusas, G. (2021). X-ray Diffraction Analysis and Williamson-Hall Method in USDM Model for Estimating More Accurate Values of Stress-Strain of Unit Cell and Super Cells (2 × 2 × 2) of Hydroxyapatite, Confirmed by Ultrasonic Pulse-Echo Test. Materials, 14(11), 2949. https://doi.org/10.3390/ma14112949