Theoretical Predictions of the Structural and Mechanical Properties of Tungsten–Rare Earth Element Alloys
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
3.1. Mechanical Properties of BCC Crystal of Tungsten (W)
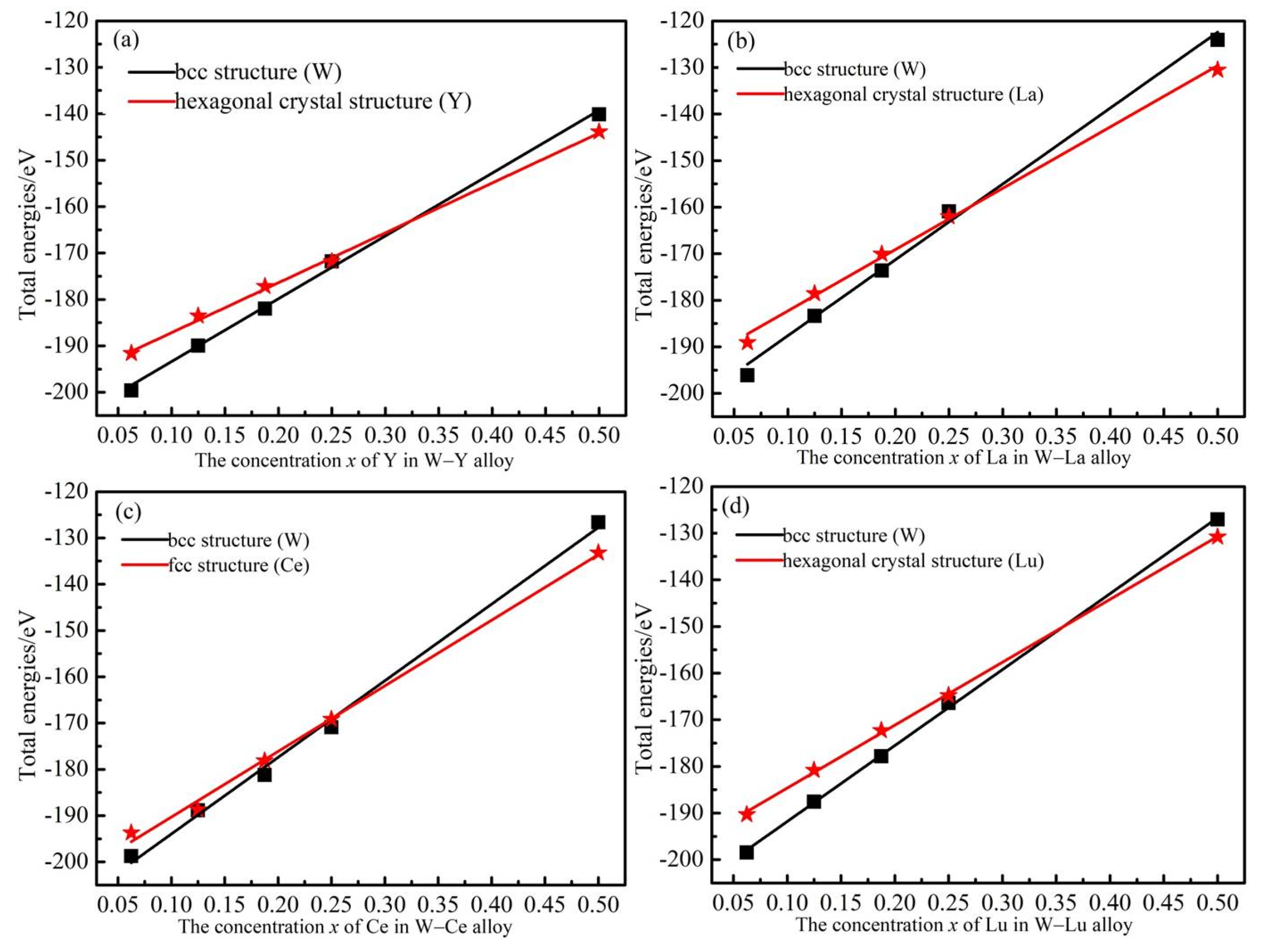
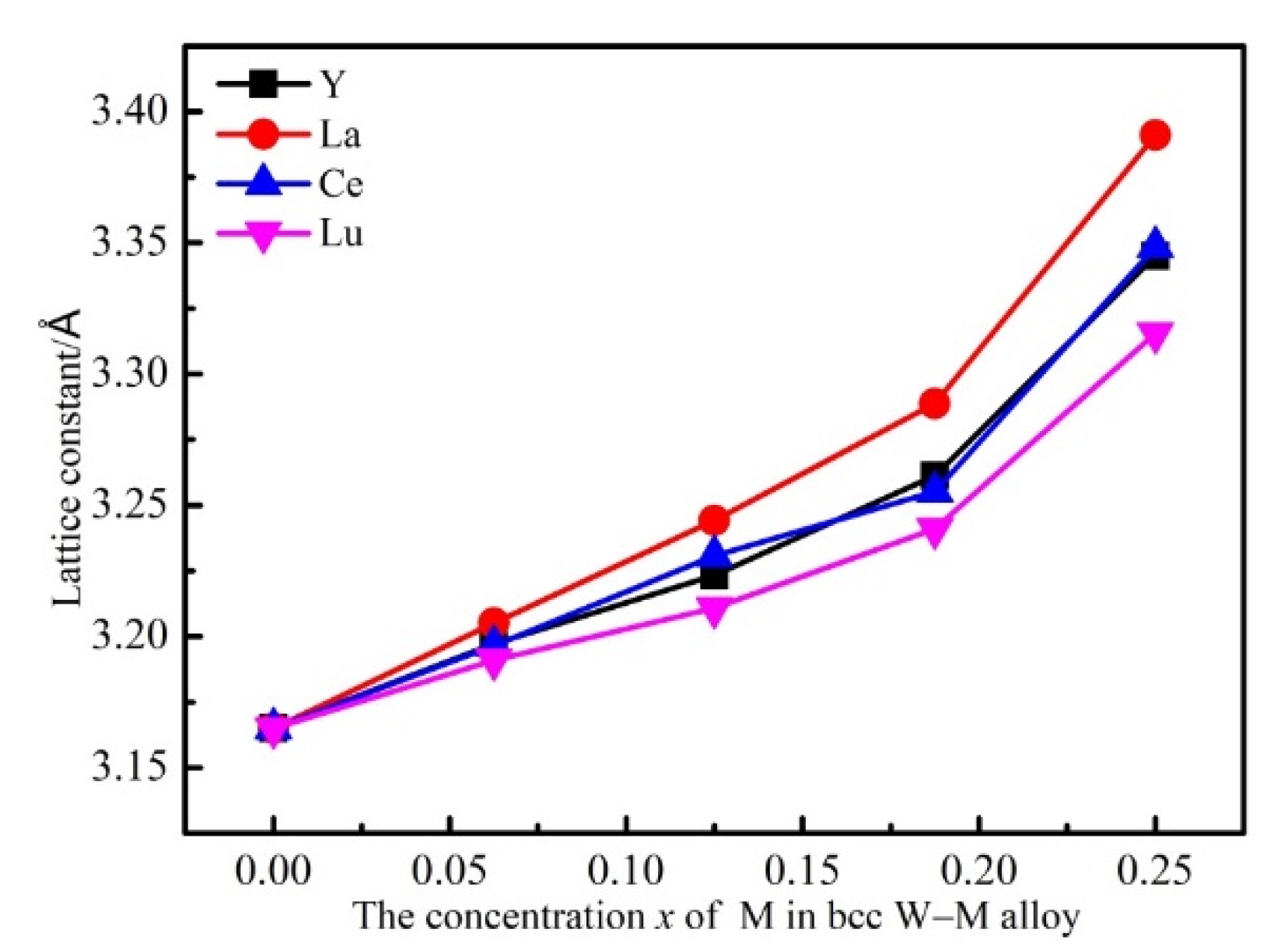
3.2. Phase Stability and Electronic Properties
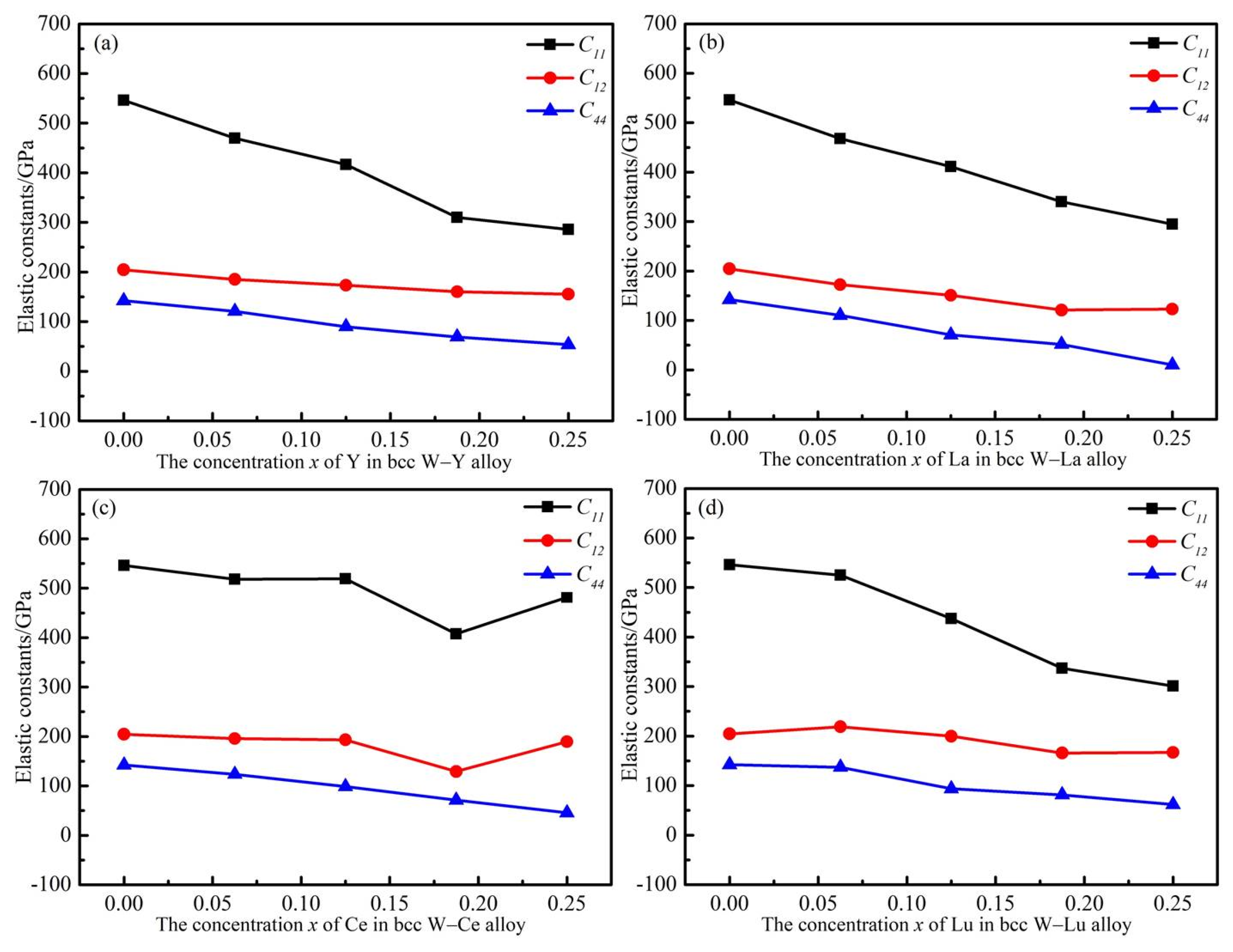
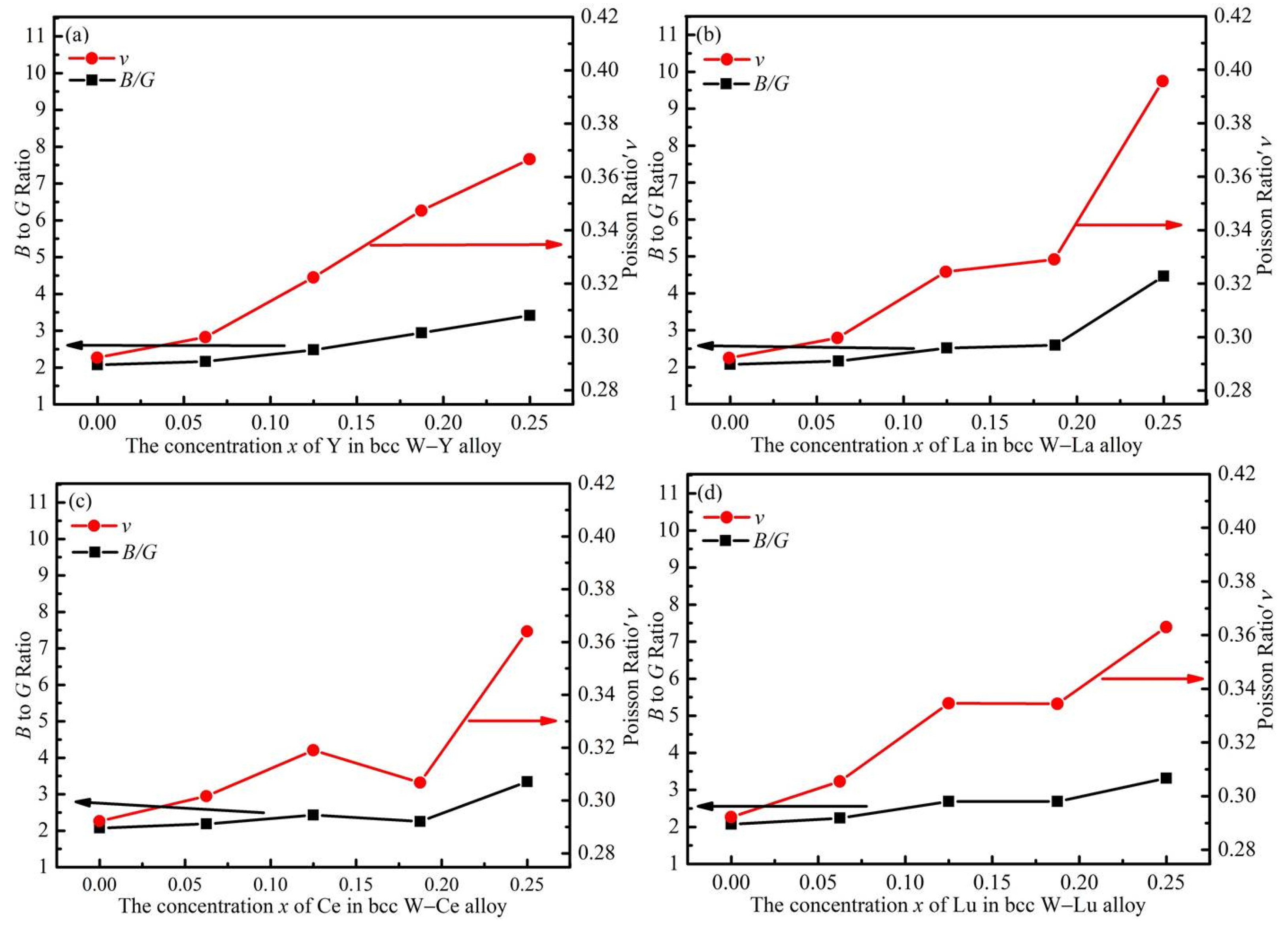
3.3. Mechanical Properties
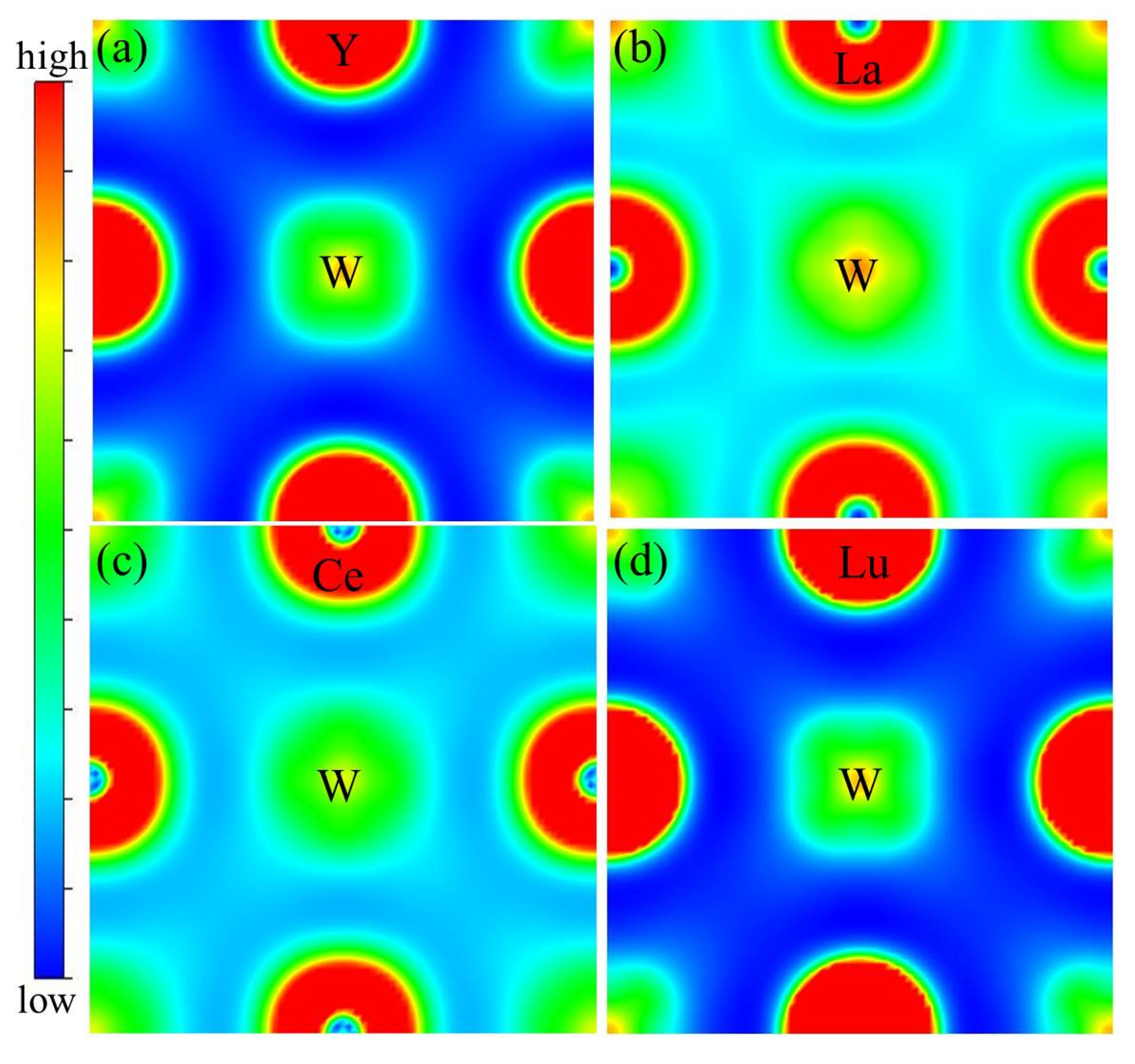
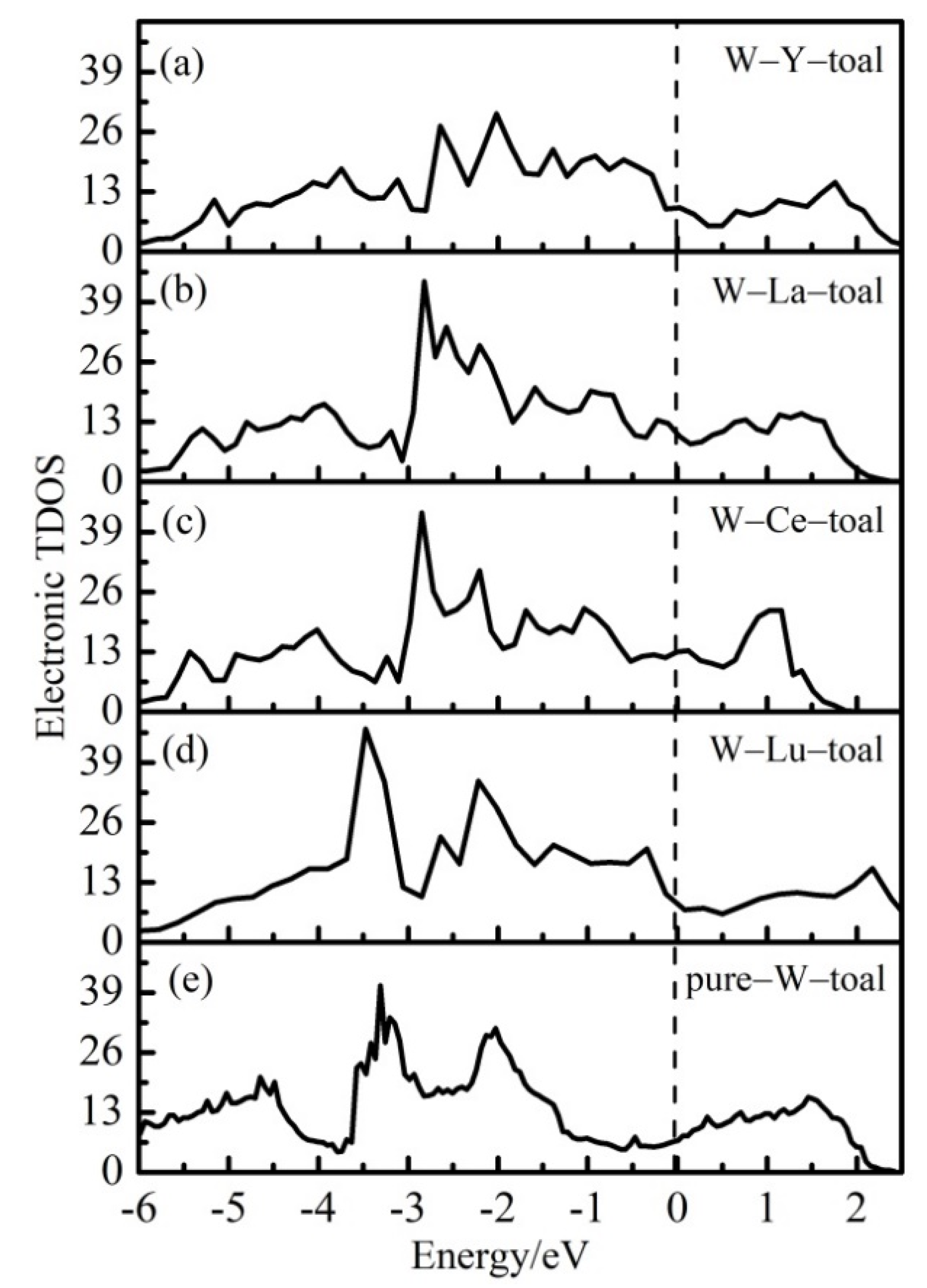
3.4. Electronic Structures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, K.M. Overview of the ITER test blanket module program. Nucl. Fusion Plasma Phys. 2006, 26, 161–169. [Google Scholar] [CrossRef]
- Pitts, R.A.; Carpentier, S.; Escourbiac, F.; Hirai, T.; Komarov, V.; Kukushkin, A.S.; Lisgo, S.; Loarte, A.; Merola, M.; Mitteau, R.; et al. Physics basis and design of the ITER plasma-facing components. J. Nucl. Mater. 2011, 415, S957–S964. [Google Scholar] [CrossRef]
- Wu, Y. Research Progress in Irradiation Damage Behavior of Tungsten and Its Alloys for Nuclear Fusion Reactor. Acta Metall. Sin. 2019, 55, 939–950. [Google Scholar] [CrossRef]
- Jiang, D.Y.; Ouyang, C.Y.; Liu, S.Q. Mechanical properties of W-Ti alloys from first-principles calculations. Fusion Eng. Des. 2016, 106, 34–39. [Google Scholar] [CrossRef]
- Terentyev, D.; Khvan, T.; You, J.H.; Van Steenberge, N. Development of chromium and chromium-tungsten alloy for the plasma facing components: Application of vacuum arc melting techniques. J. Nucl. Mater. 2020, 536, 152204. [Google Scholar] [CrossRef]
- Jiang, D.Y.; Zhou, Q.; Xue, L.; Wang, T.; Hu, J.F. First-principles study the phase stability and mechanical properties of binary W-Mo alloys. Fusion Eng. Des. 2018, 130, 56–61. [Google Scholar] [CrossRef]
- Jiang, D.; Liu, S. Mechanical Properties of W-Y Alloys by First-Principles Calculations. Rare Met. Mat. Eng. 2016, 45, 2895–2901. [Google Scholar]
- Hu, Y.J.; Fellinger, M.R.; Butler, B.G.; Wang, Y.; Darling, K.A.; Kecskes, L.J.; Trinkle, D.R.; Liu, Z.K. Solute-induced solid-solution softening and hardening in bcc tungsten. Acta Mater. 2017, 141, 304–316. [Google Scholar] [CrossRef]
- Jiang, D.Y.; Wang, T.; Huang, X.H.; Zou, X.H.; Hu, J.F. Effect of Hf additions on phase stability and mechanical properties of binary W-Hf alloys: A first-principles study. Fusion Eng. Des. 2018, 137, 295–302. [Google Scholar] [CrossRef]
- Jiang, D.Y.; Zhou, Q.; Liu, W.H.; Wang, T.; Hu, J.F. First-principles study the structures and mechanical properties of binary W-V alloys. Phys. B Condens. Matter 2019, 552, 165–169. [Google Scholar] [CrossRef]
- Xue, L.; Wang, X.; Xue, F.; Zhou, X.; Guo, F.; Jiang, D. Structural, mechanical, electronic properties and Debye temperature of tungsten-technetium alloy: A first-principles study. Fusion Eng. Des. 2021, 168, 112433. [Google Scholar] [CrossRef]
- Kim, Y.D.; Oh, N.L.; Oh, S.; Moon, I. Thermal conductivity of W-Cu composites at various temperatures. Mater. Lett. 2001, 51, 420–424. [Google Scholar] [CrossRef]
- Dosovitskiy, G.A.; Samoilenkov, S.V.; Kaul, A.R.; Rodionov, D.P. Thermal Expansion of Ni-W, Ni-Cr, and Ni-Cr-W Alloys between Room Temperature and 800 °C. Int. J. Thermophys. 2009, 30, 1931–1937. [Google Scholar] [CrossRef]
- Kong, X.; Wu, X.; You, Y.; Liu, C.S.; Fang, Q.F.; Chen, J.; Luo, G.N.; Wang, Z. First-principles calculations of transition metal-solute interactions with point defects in tungsten. Acta Mater. 2014, 66, 172–183. [Google Scholar] [CrossRef]
- Zhang, N.N.; Zhang, Y.J.; Yang, Y.; Zhang, P.; Ge, C.C. First-principles study of structural, mechanical, and electronic properties of W alloying with Zr. Chin. Phys. B 2019, 28, 46301. [Google Scholar] [CrossRef]
- Jiang, D.; Xiao, W.; Liu, D.; Liu, S. Structural stability, electronic structures, mechanical properties and debye temperature of W-Re alloys: A first-principles study. Fusion Eng. Des. 2021, 162, 112081. [Google Scholar] [CrossRef]
- Qiu, N.N.; Zhang, Y.; Zhang, C.; Tong, H.; Song, X.P. Tensile properties of tungsten-rhenium wires with nanofibrous structure. Int. J. Miner. Metall. Mater. 2018, 25, 1055–1059. [Google Scholar] [CrossRef]
- Xi, X.L.; Nie, Z.R.; Zou, J.X.; Yang, J.C.; Zuo, T.Y. Microstructure and emission properties of nanometer Ce-W material. J. Alloys Compd. 2007, 438, 202–206. [Google Scholar] [CrossRef]
- Xia, M.; Yan, Q.; Xu, L.; Guo, H.; Zhu, L.; Ge, C. Bulk tungsten with uniformly dispersed La2O3 nanoparticles sintered from co-precipitated La2O3/W nanoparticles. J. Nucl. Mater. 2013, 434, 85–89. [Google Scholar] [CrossRef]
- Zhang, X.X.; Yan, Q.Z. Morphology evolution of La2O3 and crack characteristic in W-La2O3 alloy under transient heat loading. J. Nucl. Mater. 2014, 451, 283–291. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B Condens. Matter 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Chevary, J.A.; Vosko, H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillonin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Zhao, J.; Winey, J.M.; Gupta, Y.M. First-principles calculations of second- and third-order elastic constants for single crystals of arbitrary symmetry. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 75, 94105. [Google Scholar] [CrossRef]
- Wallace, D.C. Thermoelastic theory of stressed crystals and higher-order elastic constants. Solid State Phys. 1970, 25, 301–404. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Wang, J.; Dang, W.; Liu, D.; Guo, Z. Size effect of He clusters on the interactions with self-interstitial tungsten atoms at different temperatures. Chin. Phys. B 2020, 29, 93101. [Google Scholar] [CrossRef]
- Jiang, D.Y.; Wu, M.S.; Liu, D.S.; Li, F.F.; Chai, M.G.; Liu, S.Q. Structural Stability, Electronic Structures, Mechanical Properties and Debye Temperature of Transition Metal Impurities in Tungsten: A First-Principles Study. Metals 2019, 9, 967. [Google Scholar] [CrossRef] [Green Version]
- Söderlind, P.; Eriksson, O.; Wills, J.M.; Boring, A.M. Theory of elastic constants of cubic transition metals and alloys. Phys. Rev. B Condens. Matter 1993, 48, 5844–5851. [Google Scholar] [CrossRef] [PubMed]
- Einarsdotter, K.; Sadigh, B.; Grimvall, G.; Ozoliņš, V. Phonon Instabilities in fcc and bcc Tungsten. Phys. Rev. Lett. 1997, 79, 2073–2076. [Google Scholar] [CrossRef] [Green Version]
- Seletskaia, T.; Osetsky, Y.; Stoller, R.E.; Stocks, G.M. First-principles theory of the energetics of He defects in bcc transition metals. Phys. Rev. B 2008, 78, 134103. [Google Scholar] [CrossRef]
- Zhang, N.N.; Zhang, Y.J.; Yang, Y.; Zhang, P.; Hu, Z.Y.; Ge, C.C. Trapping of helium atom by vacancy in tungsten: A density functional theory study. Eur. Phys. J. B 2017, 90, 1–5. [Google Scholar] [CrossRef]
- Li, C.M.; Luo, H.B.; Hu, Q.M.; Yang, R.; Johansson, B.; Levente, V. First-principles investigation of the composition dependent properties of Ni2+xMn1−xGa shape-memory alloys. Phys. Rev. B 2010, 82, 024201. [Google Scholar] [CrossRef]
- Meradji, H.; Drablia, S.; Ghemid, S.; Belkhir, H.; Bouhafs, B.; Tadjer, A. First-principles elastic constants and electronic structure of BP, BAs, and BSb. Phys. Status Solidi B 2004, 241, 2881–2885. [Google Scholar] [CrossRef]
- Pettifor, D.G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Tech. Lond. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Tang, B.Y.; Yu, W.Y.; Zeng, X.Q.; Ding, W.J.; Gray, M.F. First-principles study of the electronic structure and mechanical properties of CaMg2 Laves phase. Mater. Sci. Eng. A 2008, 489, 444–450. [Google Scholar] [CrossRef]
- Yan, M.F.; Chen, H.T. Structural, elastic and electronic properties of Cr2N: A first-principles study. Comp. Mater. Sci. 2014, 88, 81–85. [Google Scholar] [CrossRef]
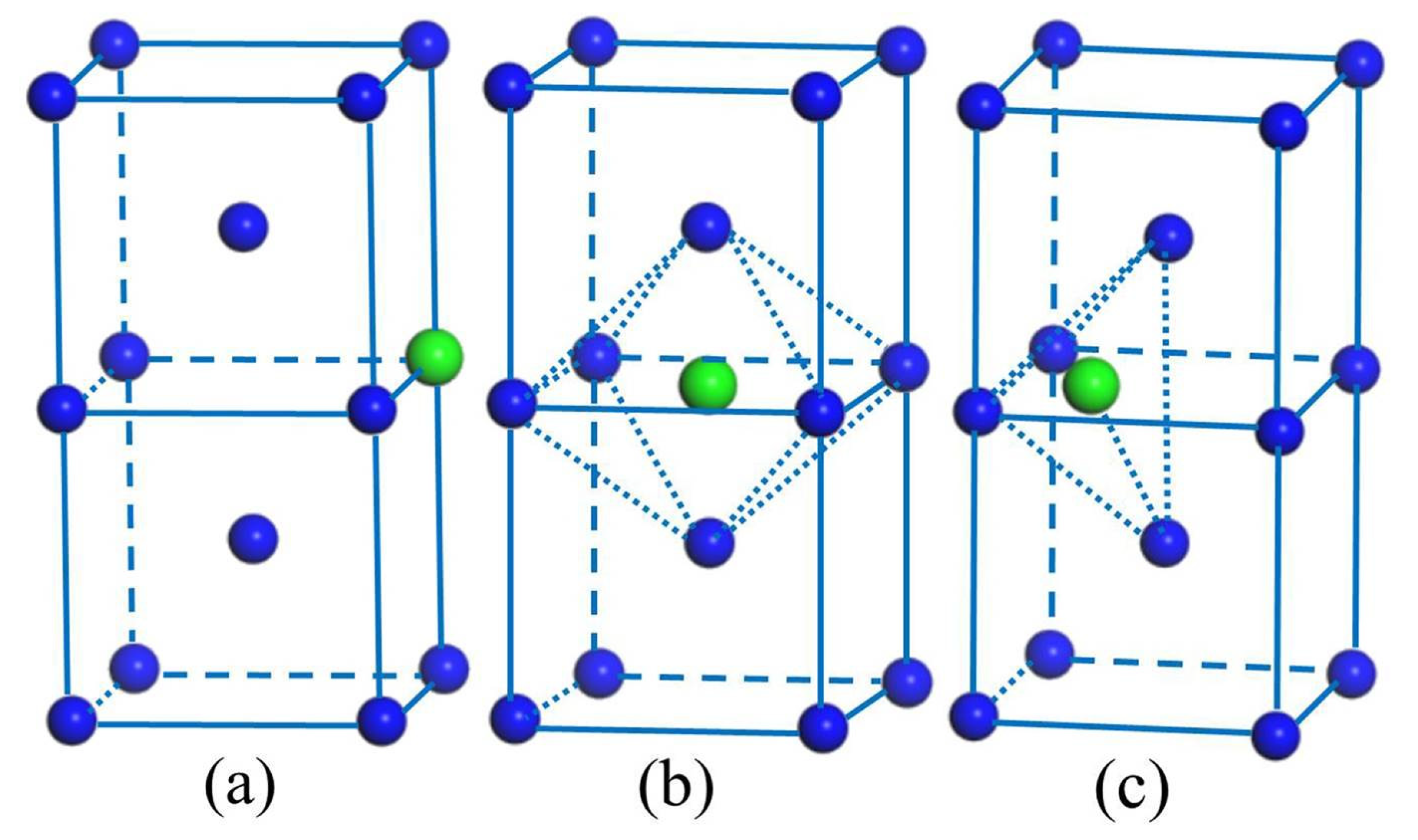



| Method | Configuration | C11/GPa | C12/GPa | C44/GPa |
|---|---|---|---|---|
| Present work | 16 atom cell | 546.05 | 204.59 | 142.22 |
| Present work | 54 atom cell | 545.50 | 210.96 | 143.69 |
| Present work | 128 atom cell | 558.42 | 205.48 | 143.58 |
| Theory [31] | 54 atom cell | 529.94 | 211.19 | 140.59 |
| Experiment [32] | - | 533.0 | 205.0 | 163.0 |
| Theory [32,33] | - | 533.0 | 207.0 | 163.0 |
| Method | B/GPa | G/GPa | E/GPa | B/G | ν | C′ |
|---|---|---|---|---|---|---|
| Present work | 318.41 | 153.62 | 397.02 | 2.07 | 0.29 | 31.19 |
| Theory [31] | 317.44 | 148.11 | 384.52 | 2.14 | 0.30 | 35.29 |
| Experiment [32] | 314.33 | 163.40 | 417.80 | 1.92 | 0.28 | 21.00 |
| Theory [32,33] | 322.33 | 173.00 | 440.24 | 1.86 | 0.27 | 22.00 |
| Elements | |||
| Y | −5.58 | 9.76 | 11.00 |
| La | −3.55 | 10.22 | 12.32 |
| Ce | −5.26 | 7.78 | 10.03 |
| Lu | −6.49 | 9.27 | 10.28 |
| Composition | Element | C11/GPa | C12/GPa | C44/GPa |
|---|---|---|---|---|
| Pure W | W | 546.05 | 204.59 | 142.22 |
| W0.9375M0.0625 | Y | 469.35 | 185.26 | 120.80 |
| La | 467.89 | 172.44 | 110.29 | |
| Ce | 518.31 | 195.78 | 123.57 | |
| Lu | 524.88 | 218.88 | 137.08 | |
| W0.875M0.125 | Y | 416.58 | 173.34 | 89.89 |
| La | 410.96 | 150.97 | 70.84 | |
| Ce | 519.02 | 193.33 | 98.54 | |
| Lu | 437.15 | 199.74 | 93.66 | |
| W0.8125M0.1875 | Y | 310.02 | 160.41 | 69.25 |
| La | 340.18 | 121.00 | 51.72 | |
| Ce | 407.71 | 129.16 | 71.29 | |
| Lu | 336.87 | 165.90 | 81.33 | |
| W0.75M0.25 | Y | 285.60 | 155.39 | 53.60 |
| La | 294.55 | 123.00 | 10.10 | |
| Ce | 481.70 | 189.46 | 45.56 | |
| Lu | 301.07 | 166.98 | 61.69 |
| Composition | Element | B/GPa | G/GPa | E/GPa | B/G | ν | C′/GPa |
|---|---|---|---|---|---|---|---|
| Pure W | W | 318.41 | 153.62 | 397.02 | 2.07 | 0.29 | 31.19 |
| W0.9375M0.0625 | Y | 279.96 | 129.30 | 336.14 | 2.17 | 0.30 | 32.23 |
| La | 270.92 | 125.26 | 325.61 | 2.16 | 0.30 | 31.07 | |
| Ce | 303.29 | 138.65 | 360.94 | 2.19 | 0.30 | 36.10 | |
| Lu | 320.88 | 143.45 | 374.53 | 2.24 | 0.31 | 40.90 | |
| W0.875M0.125 | Y | 254.42 | 102.58 | 271.29 | 2.48 | 0.32 | 41.73 |
| La | 237.63 | 94.50 | 250.32 | 2.51 | 0.32 | 40.07 | |
| Ce | 301.89 | 124.26 | 327.81 | 2.43 | 0.32 | 47.40 | |
| Lu | 278.88 | 103.68 | 276.74 | 2.69 | 0.33 | 53.04 | |
| W0.8125M0.1875 | Y | 210.28 | 71.47 | 192.60 | 2.94 | 0.34 | 45.58 |
| La | 194.06 | 74.87 | 199.01 | 2.59 | 0.33 | 34.64 | |
| Ce | 222.01 | 98.48 | 257.39 | 2.25 | 0.31 | 28.94 | |
| Lu | 222.89 | 82.99 | 221.49 | 2.69 | 0.33 | 42.29 | |
| W0.75M0.25 | Y | 198.79 | 58.21 | 159.08 | 3.42 | 0.37 | 50.90 |
| La | 180.18 | 40.37 | 112.69 | 4.46 | 0.40 | 56.45 | |
| Ce | 286.87 | 85.78 | 234.03 | 3.34 | 0.36 | 71.95 | |
| Lu | 211.68 | 63.83 | 174.00 | 3.32 | 0.36 | 52.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Wang, Z.; Zhang, N.; Ge, C.; Zhang, Y. Theoretical Predictions of the Structural and Mechanical Properties of Tungsten–Rare Earth Element Alloys. Materials 2021, 14, 3046. https://doi.org/10.3390/ma14113046
Wu M, Wang Z, Zhang N, Ge C, Zhang Y. Theoretical Predictions of the Structural and Mechanical Properties of Tungsten–Rare Earth Element Alloys. Materials. 2021; 14(11):3046. https://doi.org/10.3390/ma14113046
Chicago/Turabian StyleWu, Mingyu, Zhihang Wang, Ningning Zhang, Changchun Ge, and Yujuan Zhang. 2021. "Theoretical Predictions of the Structural and Mechanical Properties of Tungsten–Rare Earth Element Alloys" Materials 14, no. 11: 3046. https://doi.org/10.3390/ma14113046





