Elastic Restraint Effect of Concrete Circular Columns with Ultrahigh-Performance Concrete Jackets: An Analytical and Experimental Study
Abstract
:1. Introduction
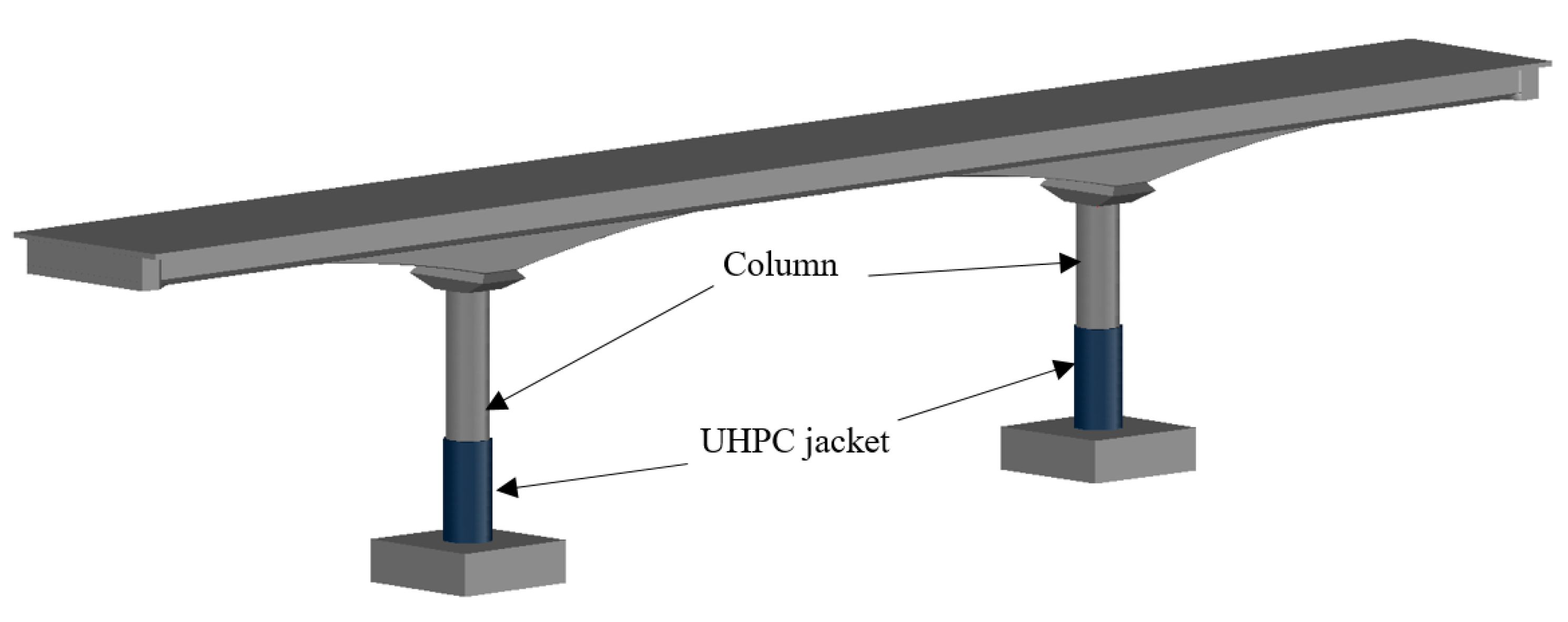
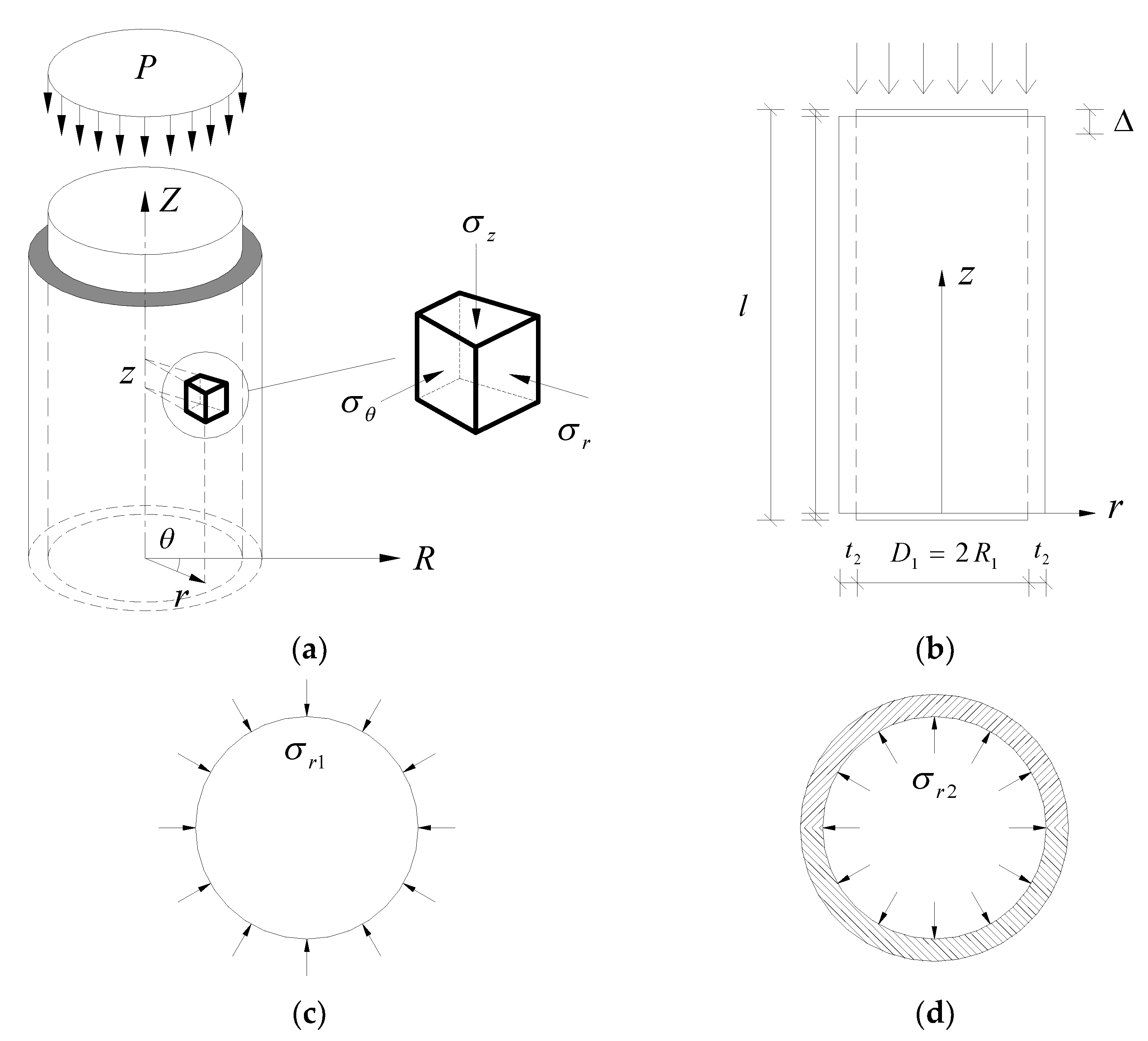
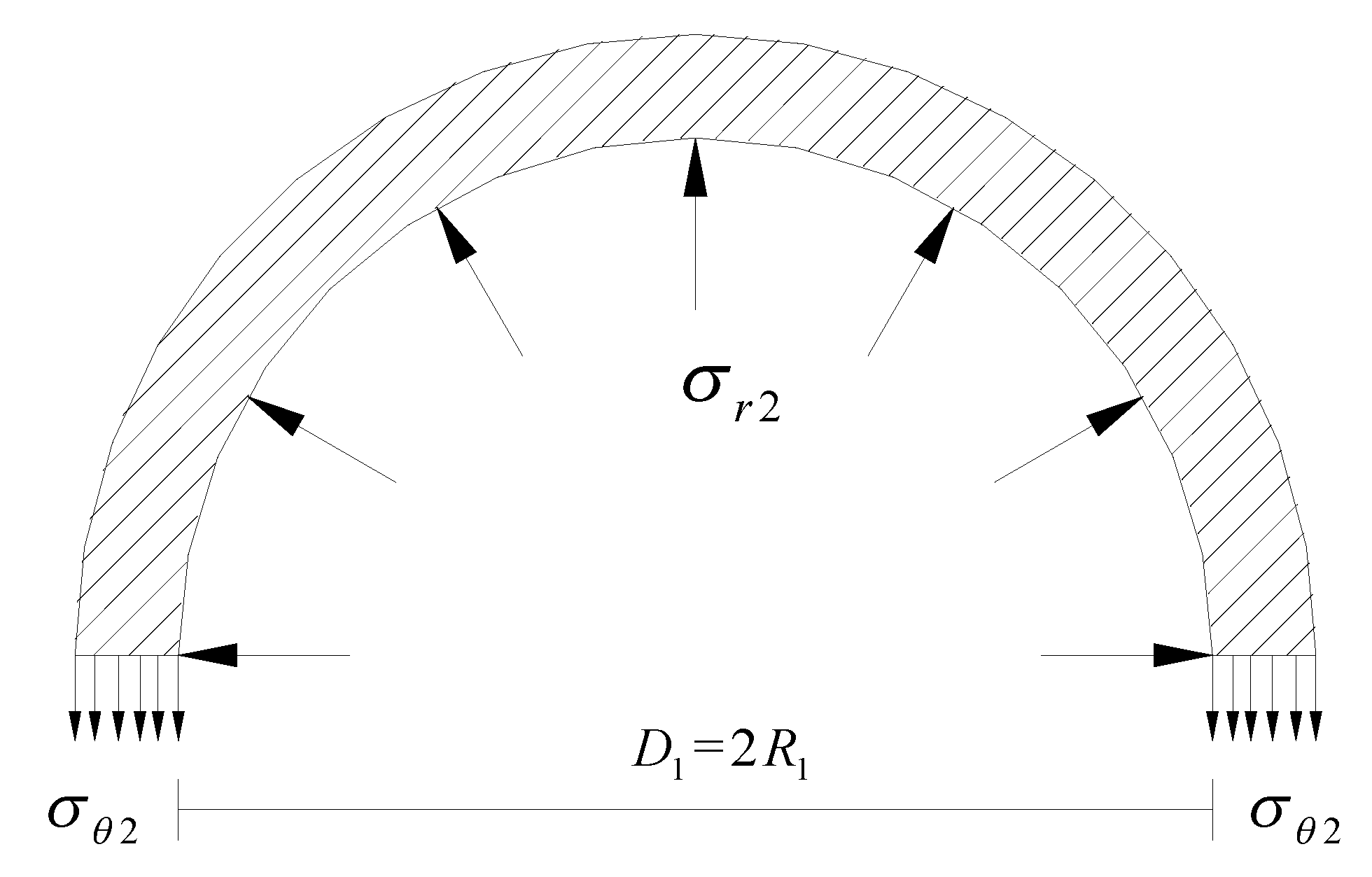
2. Analytical Solution for the Elastic Restraint Effect of Concrete Circular Columns with UHPC Jackets
3. Experimental Program
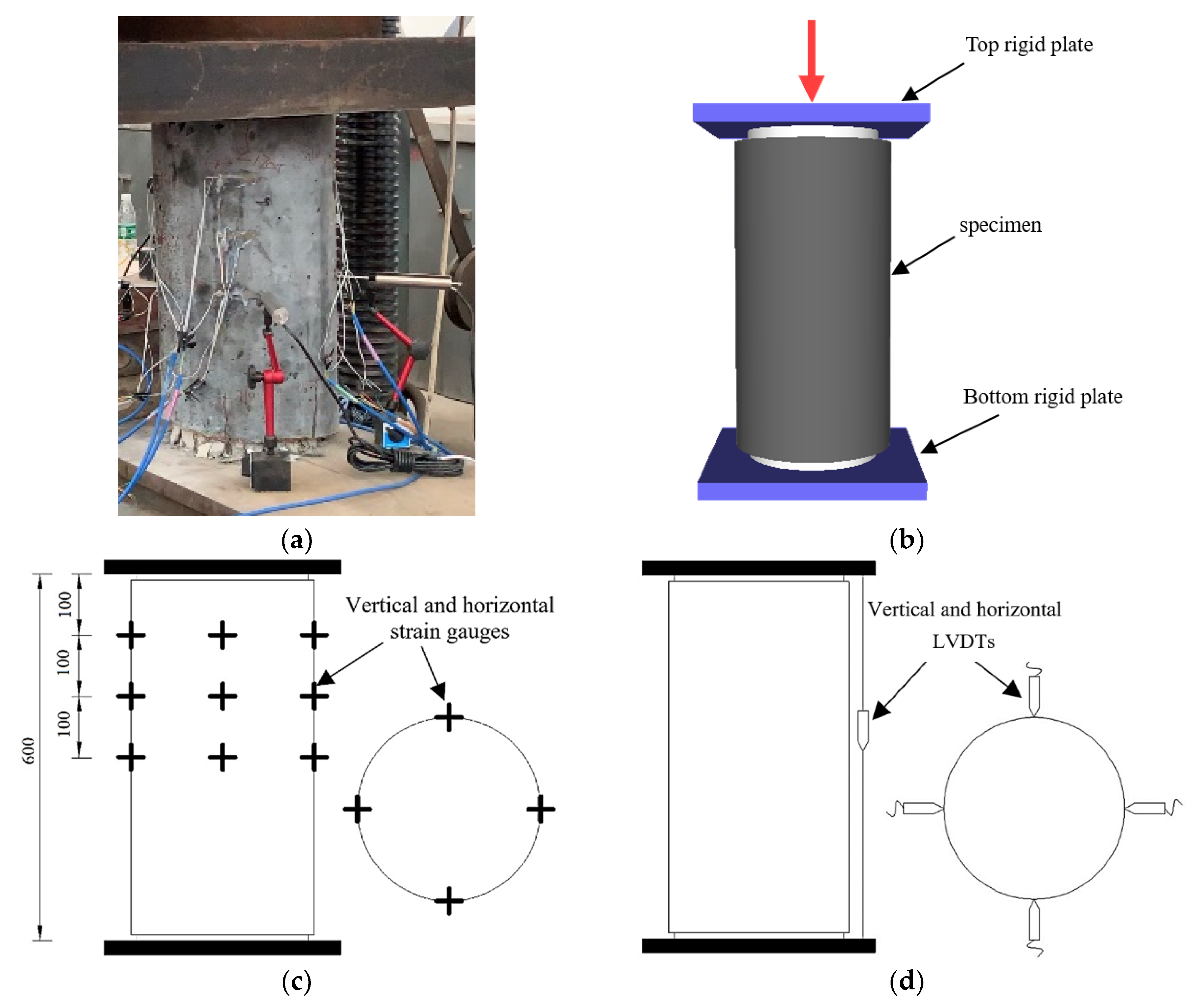
3.1. Specimens Fabrication
3.2. Specimens Loading
3.3. Test Results and Failure Modes
4. Verification of the Elastic Restraint Effect of Concrete Circular Columns with UHPC Jackets
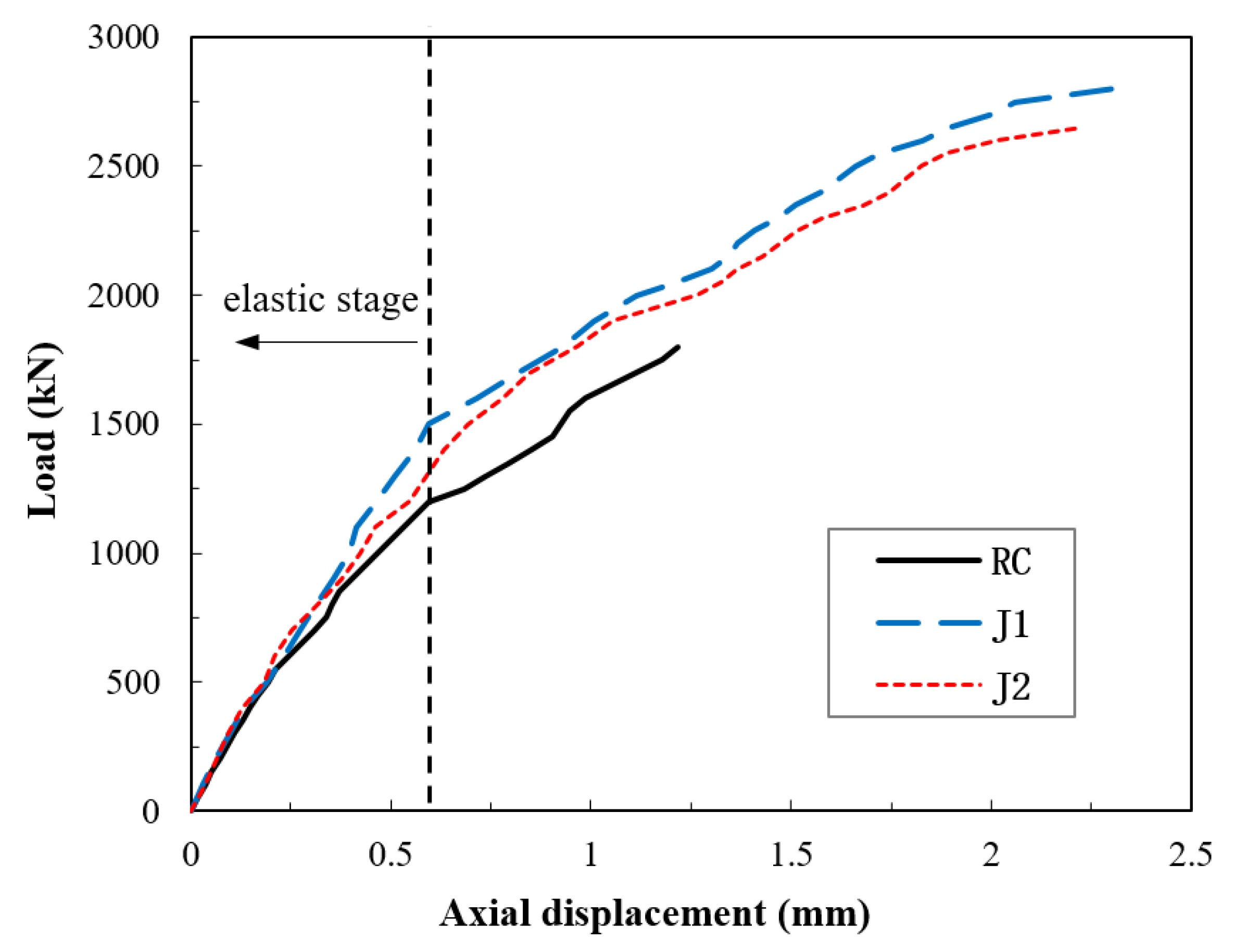
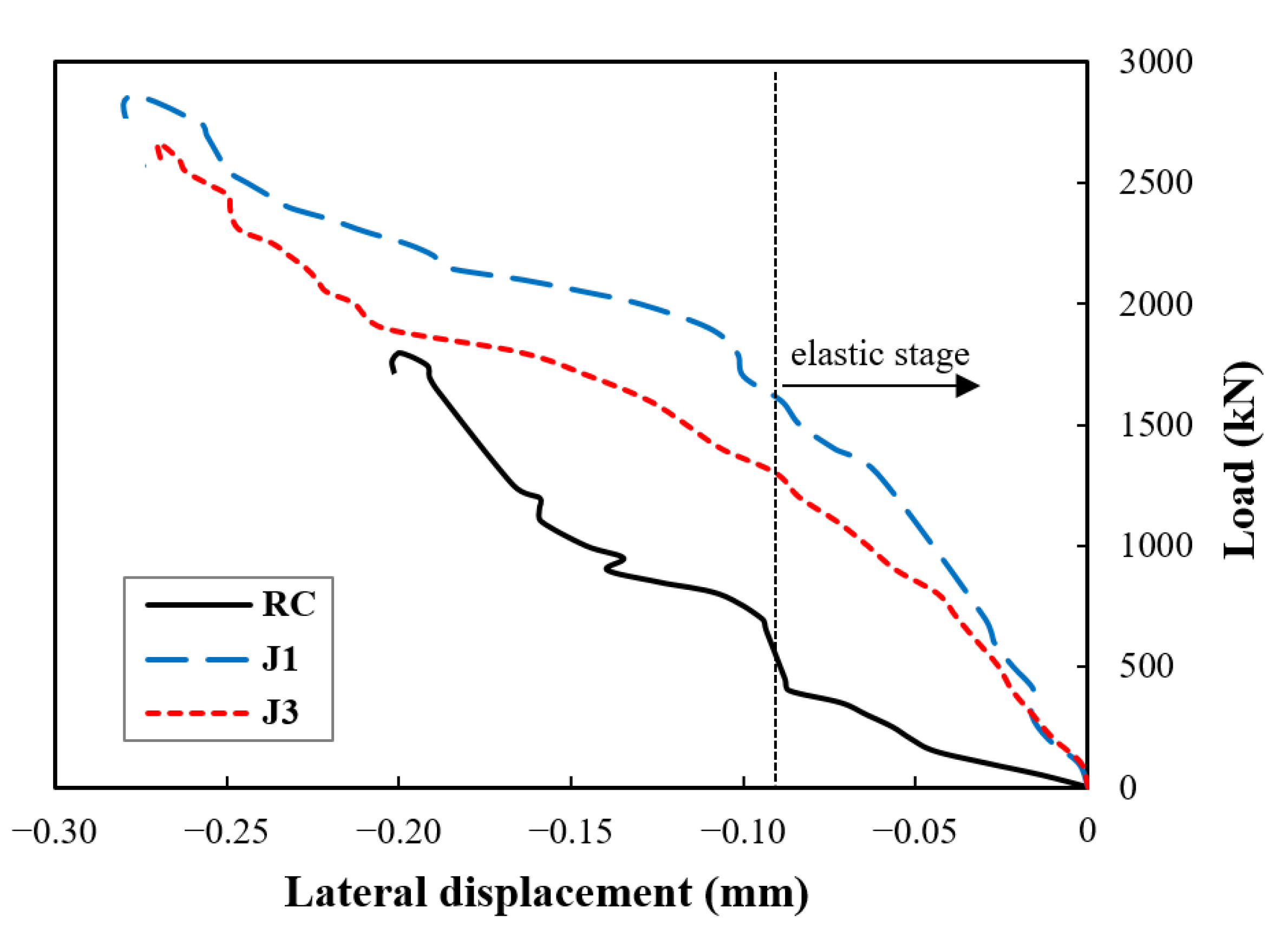
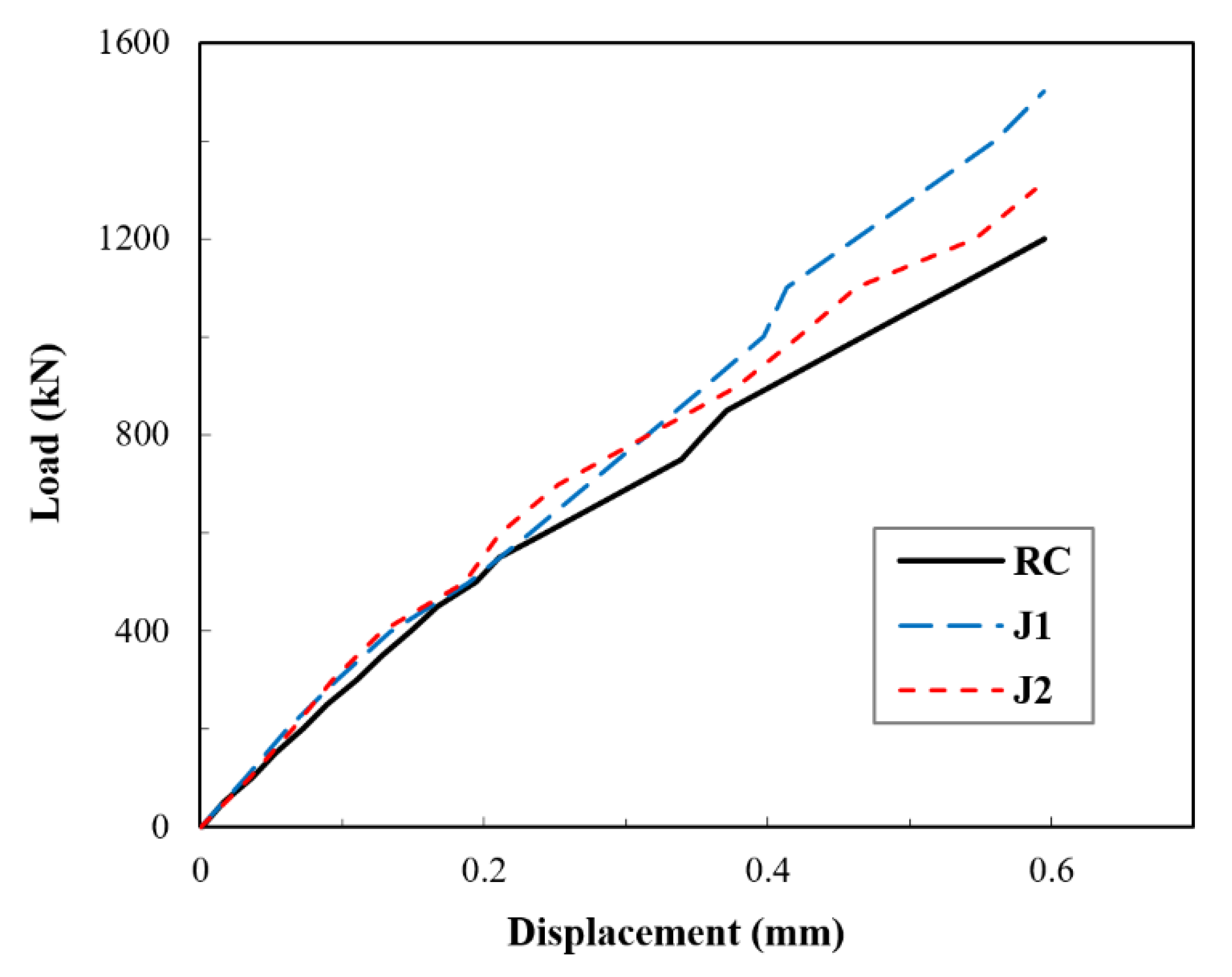
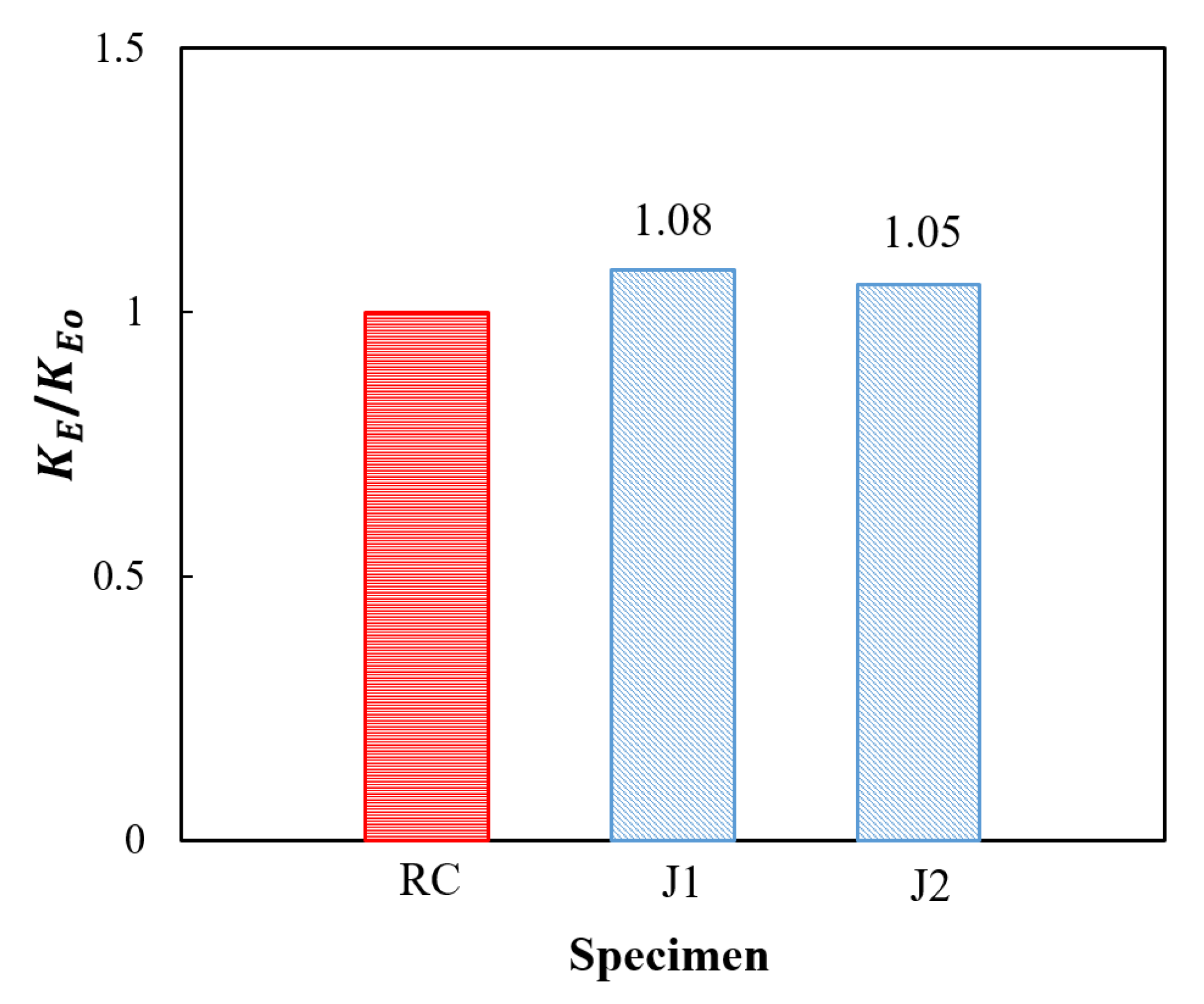
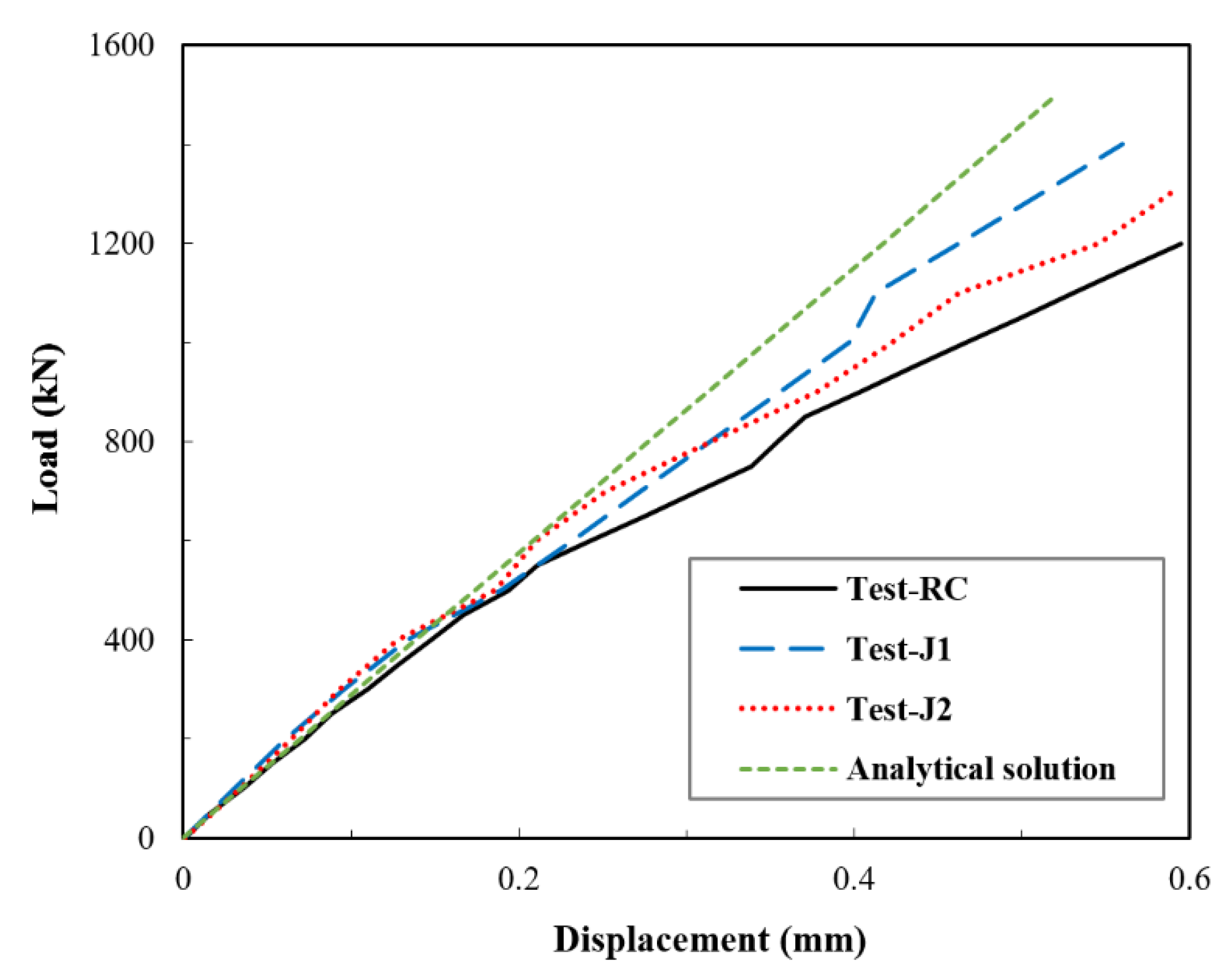
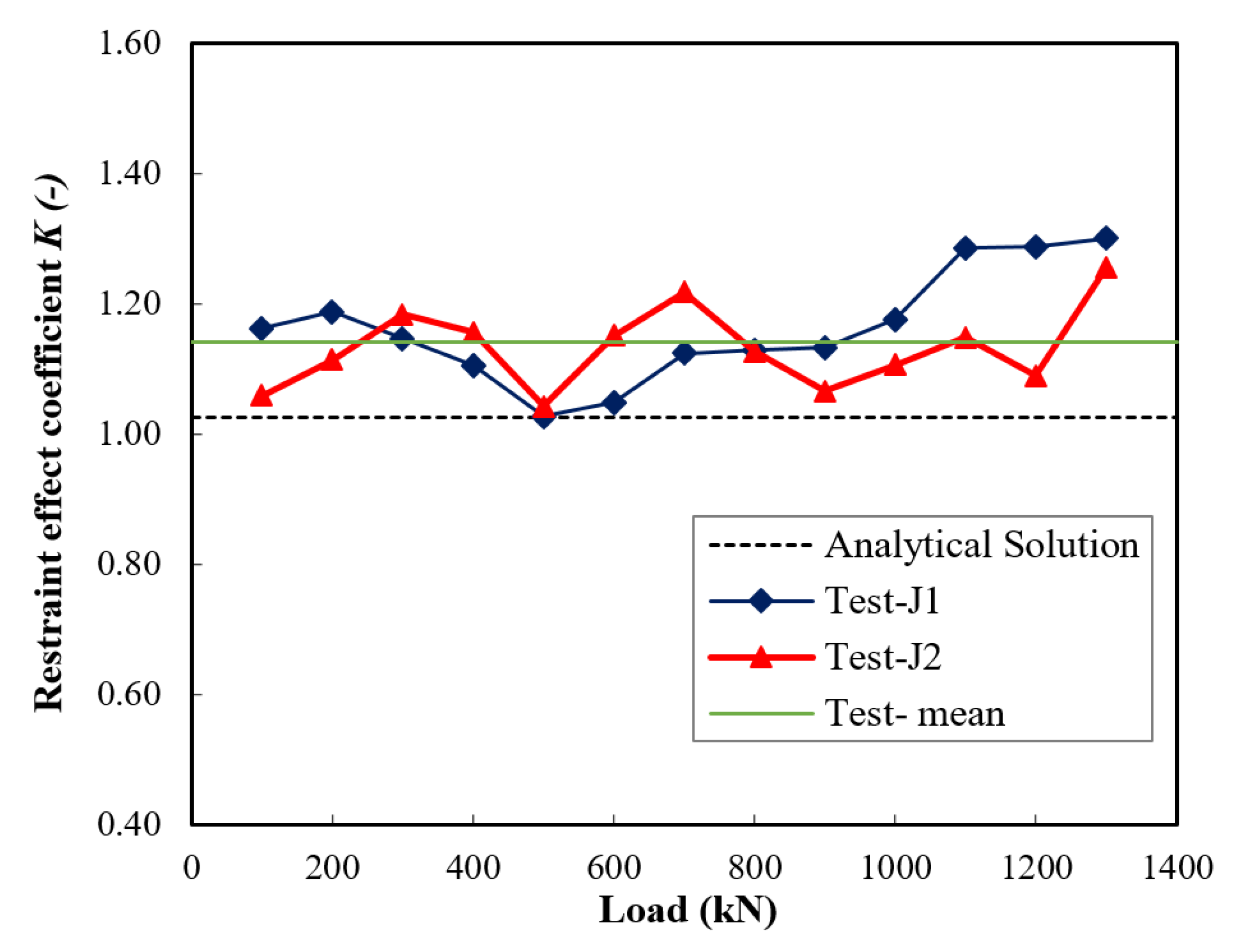
4.1. Vertical Load–Displacement Curve and Constraint Effect Analysis
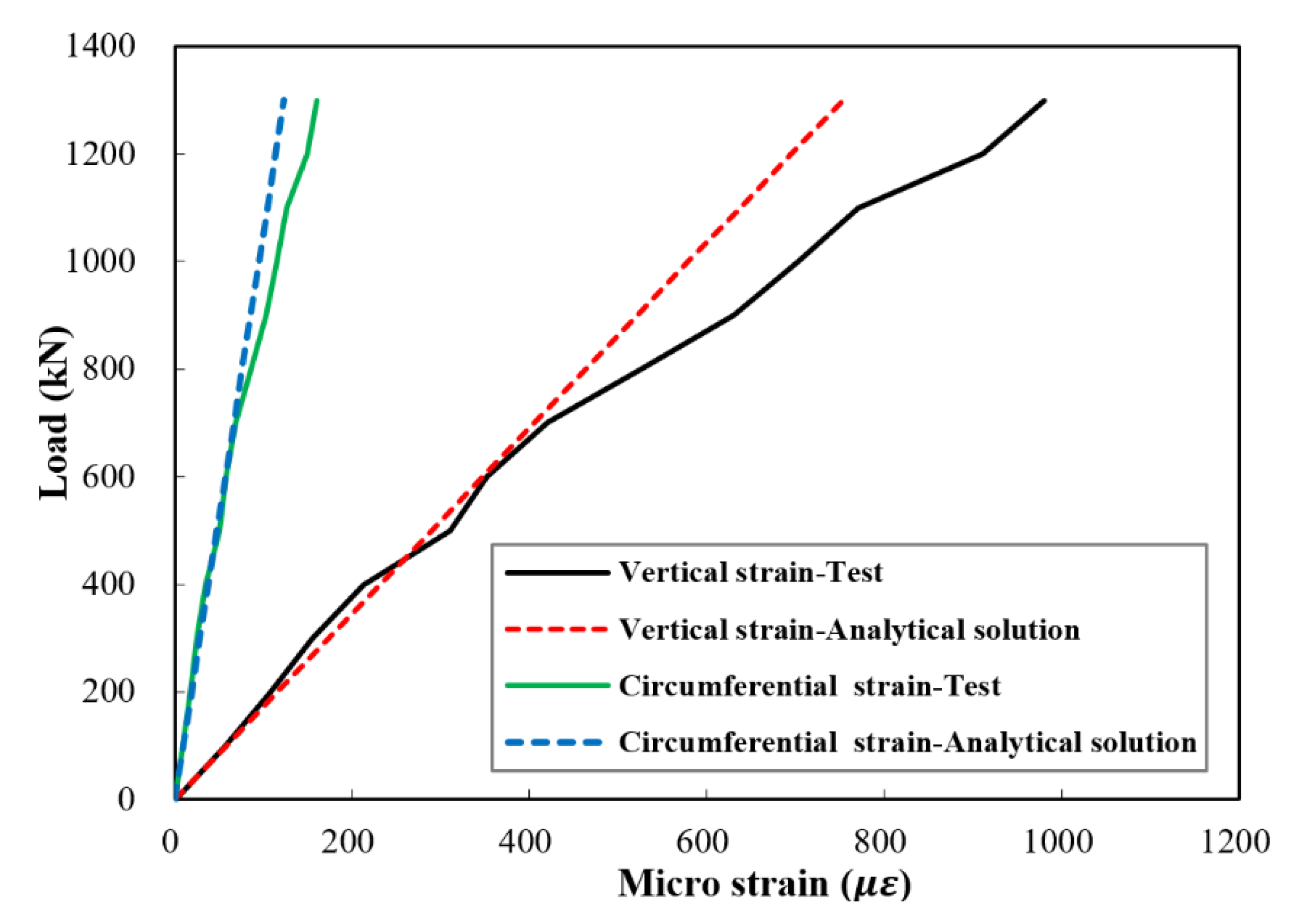
4.2. Circumferential (Hoop) Strain Analysis of UHPC Jackets
5. Conclusions
- UHPC jacketing was proven to be a viable retrofitting method that not only improves or restores the strength of concrete circular columns but also efficiently enhances the elastic behaviour, which is paramount when members are designed to maintain an elastic state under the increase in service loads.
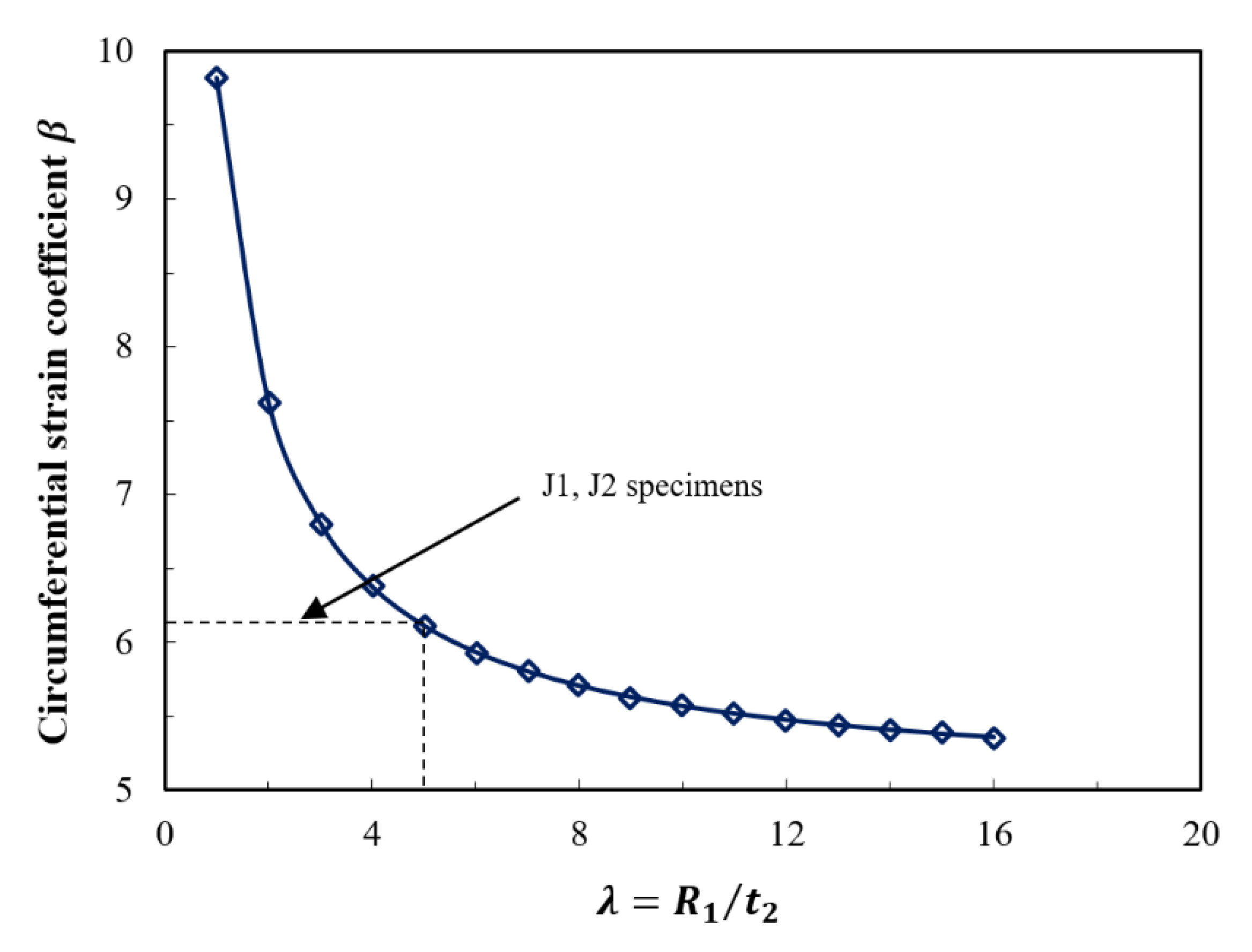
- The increase in the elastic enhancement was reflected by the restraint effect coefficient K, which increased with the increase in the UHPC jacket thickness. Based on the experimental data in this study, a value of 14% was achieved when a column diameter to jacket thickness ratio λ = 6 was used.
- UHPC jacketing was shown to be more significant in the nonlinear stage, where the load-bearing capacity increased by 50%, and the failure patterns tended to be gradually slow rather than abruptly brittle. Besides, the effectiveness of the UHPC jacket in the elastic stage was noticed to have a non-negligible improvement.
- Compared with the measured test data, the analytical solution derived herein gave good predictions of the stresses and strains in the elastic stage, and the value of β could be used as a theoretical basis for the design of the jacket.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, X.; Xie, N.; Fortune, K.; Gong, J. Durability of Steel Reinforced Concrete in Chloride Environments: An Overview. Constr. Build. Mater. 2012, 30, 125–138. [Google Scholar] [CrossRef]
- Li, Q.; Wang, C. Updating the Assessment of Resistance and Reliability of Existing Aging Bridges with Prior Service Loads. J. Struct. Eng. 2015, 141, 04015072. [Google Scholar] [CrossRef]
- Horszczaruk, E. Abrasion Resistance of High-Strength Concrete in Hydraulic Structures. Wear 2005, 259, 62–69. [Google Scholar] [CrossRef]
- Raza, S.; Khan, M.K.; Menegon, S.J.; Tsang, H.-H.; Wilson, J.L. Strengthening and Repair of Reinforced Concrete Columns by Jacketing: State-of-the-Art Review. Sustainability 2019, 11, 3208. [Google Scholar] [CrossRef] [Green Version]
- Ong, K.C.G.; Kog, Y.C.; Yu, C.H.; Sreekanth, A.P. V Jacketing of Reinforced Concrete Columns Subjected to Axial Load. Mag. Concr. Res. 2004, 56, 89–98. [Google Scholar] [CrossRef]
- Mohamed Sayed, A.; Mohamed Rashwan, M.; Emad Helmy, M. Experimental Behavior of Cracked Reinforced Concrete Columns Strengthened with Reinforced Concrete Jacketing. Materials 2020, 13, 2832. [Google Scholar] [CrossRef]
- Anand, P.; Sinha, A.K. Effect of Reinforced Concrete Jacketing on Axial Load Capacity of Reinforced Concrete Column. Civ. Eng. J. 2020, 6, 1266–1272. [Google Scholar] [CrossRef]
- Hollaway, L.C. A Review of the Present and Future Utilisation of FRP Composites in the Civil Infrastructure with Reference to Their Important In-Service Properties. Constr. Build. Mater. 2010, 24, 2419–2445. [Google Scholar] [CrossRef]
- Mancusi, G.; Feo, L.; Berardi, V.P. Concrete Open-Wall Systems Wrapped with FRP under Torsional Loads. Materials 2012, 5, 2055–2068. [Google Scholar] [CrossRef]
- Pham, T.M.; Hadi, M.N.; Youssef, J. Optimized FRP Wrapping Schemes for Circular Concrete Columns under Axial Compression. J. Compos. Constr. 2015, 19, 04015015. [Google Scholar] [CrossRef] [Green Version]
- Matthys, S.; Toutanji, H.; Taerwe, L. Stress–Strain Behavior of Large-Scale Circular Columns Confined with FRP Composites. J. Struct. Eng. 2006, 132, 123–133. [Google Scholar] [CrossRef]
- Mirmiran, A.; Shahawy, M. Behavior of Concrete Columns Confined by Fiber Composites. J. Struct. Eng. 1997, 123, 583–590. [Google Scholar] [CrossRef]
- George, J.; Sreekala, M.S.; Thomas, S. A Review on Interface Modification and Characterization of Natural Fiber Reinforced Plastic Composites. Polym. Eng. Sci. 2001, 41, 1471–1485. [Google Scholar] [CrossRef]
- Toutanji, H.; Ortiz, G. The Effect of Surface Preparation on the Bond Interface between FRP Sheets and Concrete Members. Compos. Struct. 2001, 53, 457–462. [Google Scholar] [CrossRef]
- Cabral-Fonseca, S.; Correia, J.R.; Custódio, J.; Silva, H.M.; Machado, A.M.; Sousa, J. Durability of FRP-Concrete Bonded Joints in Structural Rehabilitation: A Review. Int. J. Adhes. Adhes. 2018, 83, 153–167. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, Y.; Pang, Y.; Gao, D.; Xu, Q.; Zhang, S.; Sheikh, S.A. Experimental Study on the Interfacial Bond Behavior of FRP Plate-High-Strength Concrete under Seawater Immersion. Constr. Build. Mater. 2020, 259, 119799. [Google Scholar] [CrossRef]
- Wu, Y.-F.; Liu, T.; Oehlers, D.J. Fundamental Principles That Govern Retrofitting of Reinforced Concrete Columns by Steel and FRP Jacketing. Adv. Struct. Eng. 2006, 9, 507–533. [Google Scholar] [CrossRef]
- Choi, E.; Chung, Y.-S.; Park, J.; Cho, B.-S. Behavior of Reinforced Concrete Columns Confined by New Steel-Jacketing Method. ACI Struct. J. 2010, 107. [Google Scholar]
- Ghobarah, A.; Biddah, A.; Mahgoub, M. Rehabilitation of Reinforced Concrete Columns Using Corrugated Steel Jacketing. J. Earthq. Eng. 1997, 1, 651–673. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Garbatov, Y.; Zayed, A. Effect of Environmental Factors on Steel Plate Corrosion under Marine Immersion Conditions. Corros. Eng. Sci. Technol. 2011, 46, 524–541. [Google Scholar] [CrossRef]
- Bing, W.; Xiaoping, C.; Shujun, J.; Qingyou, L. Steel Plate with Corrosion Resistance to High Humid and Hot Marine Atmosphere and Manufacturing Method Thereof. CN 105132832 A, 9 December 2015. [Google Scholar]
- Trapko, T. Fibre Reinforced Cementitious Matrix Confined Concrete Elements. Mater. Des. 2013, 44, 382–391. [Google Scholar] [CrossRef]
- Ilki, A.; Demir, C.; Bedirhanoglu, I.; Kumbasar, N. Seismic Retrofit of Brittle and Low Strength RC Columns Using Fiber Reinforced Polymer and Cementitious Composites. Adv. Struct. Eng. 2009, 12, 325–347. [Google Scholar] [CrossRef]
- Rubino, F.; Nisticò, A.; Tucci, F.; Carlone, P. Marine Application of Fiber Reinforced Composites: A Review. J. Mar. Sci. Eng. 2020, 8, 26. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.S.; Lee, B.Y.; Seo, S.Y. A Seismic Strengthening Technique for Reinforced Concrete Columns Using Sprayed FRP. Polymers 2016, 8, 107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ates, A.O.; Khoshkholghi, S.; Tore, E.; Marasli, M.; Ilki, A. Sprayed Glass Fiber–Reinforced Mortar with or without Basalt Textile Reinforcement for Jacketing of Low-Strength Concrete Prisms. J. Compos. Constr. 2019, 23, 04019003. [Google Scholar] [CrossRef]
- Gong, T.; Heravi, A.; Alsous, G.; Curosu, I.; Mechtcherine, V. The Impact-Tensile Behavior of Cementitious Composites Reinforced with Carbon Textile and Short Polymer Fibers. Appl. Sci. 2019, 9, 4048. [Google Scholar] [CrossRef] [Green Version]
- Al-Gemeel, A.N.; Zhuge, Y. Using Textile Reinforced Engineered Cementitious Composite for Concrete Columns Confinement. Compos. Struct. 2019, 210, 695–706. [Google Scholar] [CrossRef]
- Shang, X.; Yu, J.; Li, L.; Lu, Z. Strengthening of RC Structures by Using Engineered Cementitious Composites: A Review. Sustainability 2019, 11, 3384. [Google Scholar] [CrossRef] [Green Version]
- Li, V.C.; Horii, H.; Kabele, P.; Kanda, T.; Lim, Y. Repair and Retrofit with Engineered Cementitious Composites. Eng. Fract. Mech. 2000, 65, 317–334. [Google Scholar] [CrossRef] [Green Version]
- Reggia, A.; Morbi, A.; Plizzari, G.A. Experimental Study of a Reinforced Concrete Bridge Pier Strengthened with HPFRC Jacketing. Eng. Struct. 2020, 210, 110355. [Google Scholar] [CrossRef]
- Cho, C.-G.; Han, B.-C.; Lim, S.-C.; Morii, N.; Kim, J.-W. Strengthening of Reinforced Concrete Columns by High-Performance Fiber-Reinforced Cementitious Composite (HPFRC) Sprayed Mortar with Strengthening Bars. Compos. Struct. 2018, 202, 1078–1086. [Google Scholar] [CrossRef]
- Mateckova, P.; Bilek, V.; Sucharda, O. Comparative Study of High-Performance Concrete Characteristics and Loading Test of Pretensioned Experimental Beams. Crystals 2021, 11, 427. [Google Scholar] [CrossRef]
- Shann, S.V. Application of Ultra High Performance Concrete (UHPC) as a Thin-Bonded Overlay for Concrete Bridge Decks. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2012. [Google Scholar]
- Zhou, M.; Lu, W.; Song, J.; Lee, G.C. Application of Ultra-High Performance Concrete in Bridge Engineering. Constr. Build. Mater. 2018, 186, 1256–1267. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Hao, H.; Liu, Z. Post-Blast Capacity of Ultra-High Performance Concrete Columns. Eng. Struct. 2017, 134, 289–302. [Google Scholar] [CrossRef]
- Abbas, S.; Nehdi, M.L. Mechanical Behavior of Ultrahigh-Performance Concrete Tunnel Lining Segments. Materials 2021, 14, 2378. [Google Scholar] [CrossRef]
- Graybeal, B.A. Characterization of the Behavior of Ultra-High Performance Concrete. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2005. [Google Scholar]
- Haber, Z.B.; De la Varga, I.; Graybeal, B.A.; Nakashoji, B.; El-Helou, R. Properties and Behavior of UHPC-Class Materials; United States, Federal Highway Administration, Office of Infrastructure Research and Development: McLean, VA, USA, 2018. [Google Scholar]
- Marani, A.; Jamali, A.; Nehdi, M.L. Predicting Ultra-High-Performance Concrete Compressive Strength Using Tabular Generative Adversarial Networks. Materials 2020, 13, 4757. [Google Scholar] [CrossRef] [PubMed]
- Ichikawa, S.; Matsuzaki, H.; Moustafa, A.; ElGawady, M.A.; Kawashima, K. Seismic-Resistant Bridge Columns with Ultrahigh-Performance Concrete Segments. J. Bridge Eng. 2016, 21, 04016049. [Google Scholar] [CrossRef]
- Tong, T.; Wang, J.; Lei, H.; Liu, Z. UHPC Jacket Retrofitting of Reinforced Concrete Bridge Piers with Low Flexural Reinforcement Ratios: Experimental Investigation and Three-Dimensional Finite Element Modeling. Struct. Infrastruct. Eng. 2020, 1–23. [Google Scholar] [CrossRef]
- Tong, T.; Lei, H.; Yuan, S.; Liu, Z. Experimental Investigation and Seismic Vulnerability Assessment of Low Flexural Strength Rectangular Bridge Piers Retrofitted with Ultrahigh-Performance Concrete Jackets. Eng. Struct. 2020, 206, 110132. [Google Scholar] [CrossRef]
- Aaleti, S.; Sritharan, S.; Abu-Hawash, A. Innovative UHPC-Normal Concrete Composite Bridge Deck. In Proceedings of the RILEM-fib-AFGC International Symposium on Ultra-High Performance Reinforced Concrete, Marseille, France, 1–3 October 2013; Toutlemonde, F., Resplendino, J., Eds.; Rilem Publications SARL: Bagneux, France, 2013; pp. 217–226. [Google Scholar]
- Graybeal, B.A.; Tanesi, J. Durability of an Ultrahigh-Performance Concrete. J. Mater. Civ. Eng. 2007, 19, 848–854. [Google Scholar] [CrossRef]
- Peter, R. Cost-Effectiveness and Sustainability of UHPC. In Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 13–15 September 2004; pp. 797–805. [Google Scholar]
- Sheheryar, M.; Rehan, R.; Nehdi, M.L. Estimating CO2 Emission Savings from Ultrahigh Performance Concrete: A System Dynamics Approach. Materials 2021, 14, 995. [Google Scholar] [CrossRef]
- Sedran, T.; Durand, C.; Larrard, F.D. An Example of UHPFRC Recycling. In Proceedings of the International Conference on Designing and Building with UHPFRC, State of the Art and Development, Marseille, France, 17–18 November 2009. [Google Scholar]
- Doiron, G. Pier Repair/Retrofit Using UHPC—Examples of Completed Projects in North America. In International Interactive Symposium on Ultra-High Performance Concrete; Iowa State University Digital Press: Ames, IA, USA, 2016; Volume 1. [Google Scholar]
- Farzad, M.; Shafieifar, M.; Azizinamini, A. Retrofitting of Bridge Columns Using UHPC. J. Bridge Eng. 2019, 24, 4019121. [Google Scholar] [CrossRef]
- Farzad, M.; Sadeghnejad, A.; Rastkar, S.; Moshkforoush, A.; Azizinamini, A. A Theoretical Analysis of Mechanical and Durability Enhancement of Circular Reinforced Concrete Columns Repaired with UHPC. Eng. Struct. 2020, 209, 109928. [Google Scholar] [CrossRef]
- Xie, J.; Fu, Q.; Yan, J.-B. Compressive Behaviour of Stub Concrete Column Strengthened with Ultra-High Performance Concrete Jacket. Constr. Build. Mater. 2019, 204, 643–658. [Google Scholar] [CrossRef]
- Dadvar, S.A.; Mostofinejad, D.; Bahmani, H. Strengthening of RC Columns by Ultra-High Performance Fiber Reinforced Concrete (UHPFRC) Jacketing. Constr. Build. Mater. 2020, 235, 117485. [Google Scholar] [CrossRef]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity; McGraw-Hill Book Co., Inc.: New York, NY, USA, 1951. [Google Scholar]
- GB/T 50152-2012. Standard for Test Method of Concrete Structures; Chinese Standard: Beijing, China, 2012. [Google Scholar]
- Association Française de Génie Civil (AFGC)/Service d’études techniques des routes et autoroutes (SETRA). Bétons Fibrés à Ultra-Hautes Performances, Recommandations Provisoires; Association Française de Génie Civil (AFGC): Paris, France, 2002. [Google Scholar]
- Attiogbe, E.K.; Darwin, D. Submicrocracking in Cement Paste and Mortar. Mater. J. 1987, 84, 491–500. [Google Scholar]





| Constituent | Proportion (kg) |
|---|---|
| Powder | 2095 |
| Steel fibres | 156 |
| Superplasticizer | 22.1 |
| Water | 182.4 |
| Property | Specimen Geometry | Test Results |
|---|---|---|
| Cubic compressive strength (MPa) | 150 × 150 × 150 | 44.2 |
| Modulus of Elasticity (MPa) | – | 34,500 |
| Tensile strength (MPa) | – | 2.79 |
| Passion’s ratio | – | 0.167 |
| Property | Specimen Geometry | Test Results |
|---|---|---|
| Cubic compressive strength (MPa) | 100 × 100 × 100 | 156.8 (MPa) |
| Modulus of Elasticity (MPa) | 100 × 100 × 300 | 55,468 (MPa) |
| Flexural strength (MPa) | 100 × 100 × 400 | 17.2 (MPa) |
| Poisson’s ratio a | – | 0.2 |
| Specimen | Ultimate Load (kN) | Ultimate Compressive Strength (MPa) | Ultimate Displacement (mm) | Ultimate Axial Strain (με) |
|---|---|---|---|---|
| RC | 1850 | 36.69 | 1.219 | 2031 |
| J1 | 2800 | 57.07 | 2.311 | 3852 |
| J2 | 2650 | 54.01 | 2.227 | 3712 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsomiri, M.; Jiang, X.; Liu, Z. Elastic Restraint Effect of Concrete Circular Columns with Ultrahigh-Performance Concrete Jackets: An Analytical and Experimental Study. Materials 2021, 14, 3278. https://doi.org/10.3390/ma14123278
Alsomiri M, Jiang X, Liu Z. Elastic Restraint Effect of Concrete Circular Columns with Ultrahigh-Performance Concrete Jackets: An Analytical and Experimental Study. Materials. 2021; 14(12):3278. https://doi.org/10.3390/ma14123278
Chicago/Turabian StyleAlsomiri, Mujahed, Xiaofang Jiang, and Zhao Liu. 2021. "Elastic Restraint Effect of Concrete Circular Columns with Ultrahigh-Performance Concrete Jackets: An Analytical and Experimental Study" Materials 14, no. 12: 3278. https://doi.org/10.3390/ma14123278
APA StyleAlsomiri, M., Jiang, X., & Liu, Z. (2021). Elastic Restraint Effect of Concrete Circular Columns with Ultrahigh-Performance Concrete Jackets: An Analytical and Experimental Study. Materials, 14(12), 3278. https://doi.org/10.3390/ma14123278







