Influence of the Printing Angle and Load Direction on Flexure Strength in 3D Printed Materials for Provisional Dental Restorations
Abstract
1. Introduction
2. Materials and Methods
3. Results and Statistical Analysis
- -
- The Df column displays the degrees of freedom for the independent variable (the number of levels in the variable minus 1), and the degrees of freedom for the residuals (the total number of observations minus one and minus the number of levels in the independent variables).
- -
- The Sum Sq column displays the sum of squares (a.k.a. the total variation between the group means and the overall mean).
- -
- The Mean Sq column is the mean of the sum of squares, calculated by dividing the sum of squares by the degrees of freedom for each parameter.
- -
- The F-value column is the test statistic from the F test. This is the mean square of each independent variable divided by the mean square of the residuals. The larger the F value, the more likely it is that the variation caused by the independent variable is real and not due to chance.
- -
- The Pr (>F) column is the p-value of the F-statistic. This shows how likely it is that the F-value calculated from the test would have occurred if the null hypothesis of no difference among group means were true.
- -
- Signif. Codes for asterixs or points that can be observed in the column Pr (>F) (i.e., p-values column) are the following: “***“ means that p-value is less than 0.001, “**” means that p-value is between 0.01 and 0.001, “*” means that p-value is between 0.01 and 0.05, “.” means that p-value is between 0.05 and 0.1.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, H.-J.; Park, H.-Y.; Kim, E.H.; Choi, H.H.; Jin, J.; Choi, J.; Yang, S.C.; Jung, Y.-G. Relationship between mechanical properties of ceramic green body and structures of photo-cured acrylate polymer for ceramic 3D printing based on photo polymerization. Ceram. Int. 2021, 47, 3867–3875. [Google Scholar] [CrossRef]
- Brighenti, R.; Cosma, M.P.; Marsavina, L.; Spagnoli, A.; Terzano, M. Laser-based additively manufactured polymers: A review on processes and mechanical models. J. Mater. Sci. 2021, 56, 961–998. [Google Scholar] [CrossRef]
- Stoia, D.I.; Linul, E.; Marsavina, L. Influence of manufacturing parameters on mechanical properties of porous materials by selective laser sintering. Materials 2019, 12, 871. [Google Scholar] [CrossRef] [PubMed]
- Stoia, D.I.; Linul, E.; Marsavina, L. Correlations between process parameters and outcome properties of laser-sintered polyamide. Polymers 2019, 11, 1850. [Google Scholar] [CrossRef] [PubMed]
- Della Bona, A.; Cantelli, V.; Britto, V.T.; Collares, K.F.; Stansbury, J.W. 3D printing restorative materials using a stereolithographic technique: A systematic review. Dent. Mater. 2021, 37, 336–350. [Google Scholar] [CrossRef]
- Tahayeri, A.; Morgan, M.; Fugolin, A.P.; Bompolaki, D.; Athirasala, A.; Pfeifer, C.S.; Ferracane, J.L.; Bertassoni, L.E. 3D printed versus conventionally cured provisional crown and bridge dental materials. Dent. Mater. 2018, 34, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Cha, H.S.; Park, J.M.; Kim, T.H.; Lee, J.H. Wear resistance of 3D-printed denture tooth resin opposing zirconia and metal antagonists. J. Prosthet. Dent. 2020, 124, 387–394. [Google Scholar] [CrossRef] [PubMed]
- Shim, J.S.; Kim, J.E.; Jeong, S.H.; Choi, Y.J.; Ryu, J.J. Printing accuracy, mechanical properties, surface characteristics, and microbial adhesion of 3D-printed resins with various printing orientations. J. Prosthet. Dent. 2020, 124, 468–475. [Google Scholar] [CrossRef] [PubMed]
- Digholkar, S.; Madhav, V.N.; Palaskar, J. Evaluation of the flexural strength and microhardness of provisional crown and bridge materials fabricated by different methods. J. Indian Prosthodont. Soc. 2016, 16, 328–334. [Google Scholar] [PubMed]
- Singh, A.; Garg, S. Comparative evaluation of flexural strength of provisional crown and bridge materials—An invitro study. J. Clin. Diagn. Res. 2016, 10, ZC72–ZC77. [Google Scholar] [CrossRef] [PubMed]
- Moraru, A.M.O.; Preoteasa, C.T.; Preoteasa, E. Masticatory function parameters in patients with removable dental prosthesis. J. Med. Life 2019, 12, 43–48. [Google Scholar] [CrossRef] [PubMed]
- Lobbezoo, F.; Ahlberg, J.; Glaros, A.G.; Kato, T.; Koyano, K.; Lavigne, G.J.; de Leeuw, R.; Manfredini, D.; Svensson, P.; Winocur, E. Bruxism defined and graded: An international consensus. J. Oral Rehabil. 2013, 40, 2–4. [Google Scholar] [CrossRef] [PubMed]
- Kessler, A.; Reymus, M.; Hickel, R.; Kunzelmann, K.H. Three-body wear of 3D printed temporary materials. Dent. Mater. 2019, 35, 1805–1812. [Google Scholar] [CrossRef] [PubMed]
- Next Dent. Available online: https://nextdent.com (accessed on 14 April 2021).
- DETAX Highend Medical Matetials. Available online: https://www.detax.de/en/shop/produkte/Freeprint-temp.php (accessed on 14 April 2021).
- American National Standard/American Dental Association Standard. Polymer-Based Restorative Materials; No. 27; American National Standard: Washington, DC, USA, 2016. [Google Scholar]
- ASTM D790. Standard Test Method for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials; ASTM: Boca Raton, FL, USA, 2014. [Google Scholar]
- Verzani, J. Using R for Introductory Statistics, 2nd ed.; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2014; pp. 1–413. [Google Scholar]
- R Documentation for the “Aov” Function. Available online: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/aov (accessed on 5 November 2020).
- R Documentation for the “Bartlett Test” Function. Available online: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/bartlett.test (accessed on 6 November 2020).
- R Documentation for the “Shapiro Test” Function. Available online: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/shapiro.test (accessed on 6 November 2020).
- Samaradasa, W. ANOVA under unequal error variances. Biometrics 1995, 51, 589–599. [Google Scholar]
- Wilcox, R.R. Adjusting for unequal variances when comparing means in one-way and two-way fixed effects ANOVA models. J. Educ. Stat. 1989, 14, 269–278. [Google Scholar] [CrossRef]
- Lachenbruch, P.A.; Clements, P.J. ANOVA, Kruskal-Wallis, normal scores and unequal variance. Commun. Stat. Theory Methods 1991, 20, 107–126. [Google Scholar] [CrossRef]
- Richter, S.J.; Payton, M.E. Performing two-way analysis of variance under variance heterogeneity. J. Mod. Appl. Stat. Methods 2003, 2, 13. [Google Scholar] [CrossRef]
- R Documentation for the “Oneway” Function. Available online: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/oneway.test (accessed on 7 November 2020).
- R Documentation for the “Kruskal Test” Function. Available online: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/kruskal.test (accessed on 7 November 2020).
- Unkovskiy, A.; Bui, P.H.; Schille, C.; Geis-Gerstorfer, J.; Huettig, F.; Spintzyk, S. Objects build orientation, positioning, andcuring influence dimensional accuracy and flexuralproperties of stereolithographically printed resin. Dent. Mater. 2018, 34, 324–333. [Google Scholar] [CrossRef] [PubMed]
- Alharbi, N.; Osman, R.; Wismeijer, D. Effects of build direction on the mechanical properties of 3D-printed complete coverage interim dental restorations. J. Prosthet. Dent. 2016, 115, 760–767. [Google Scholar] [CrossRef] [PubMed]

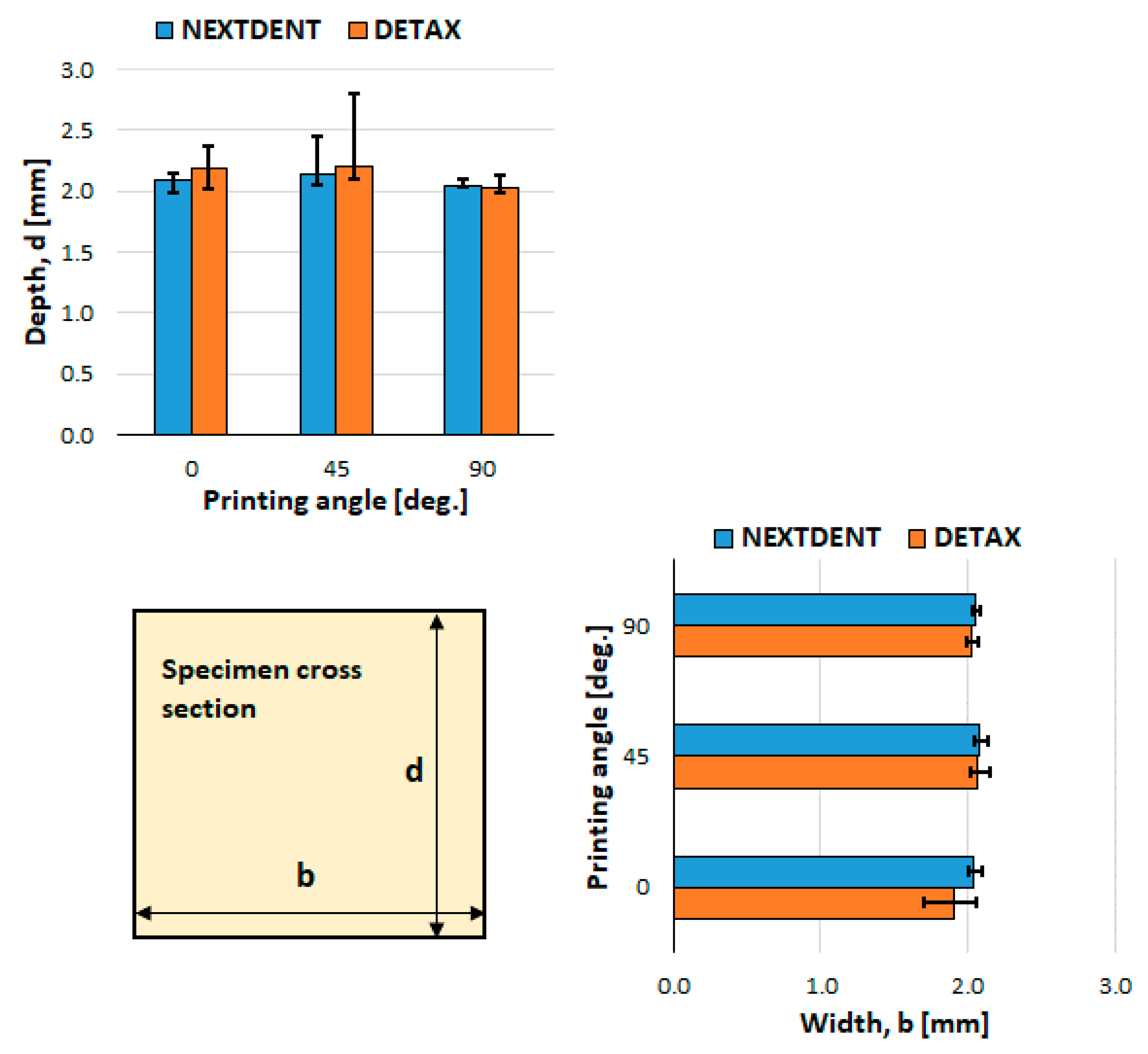
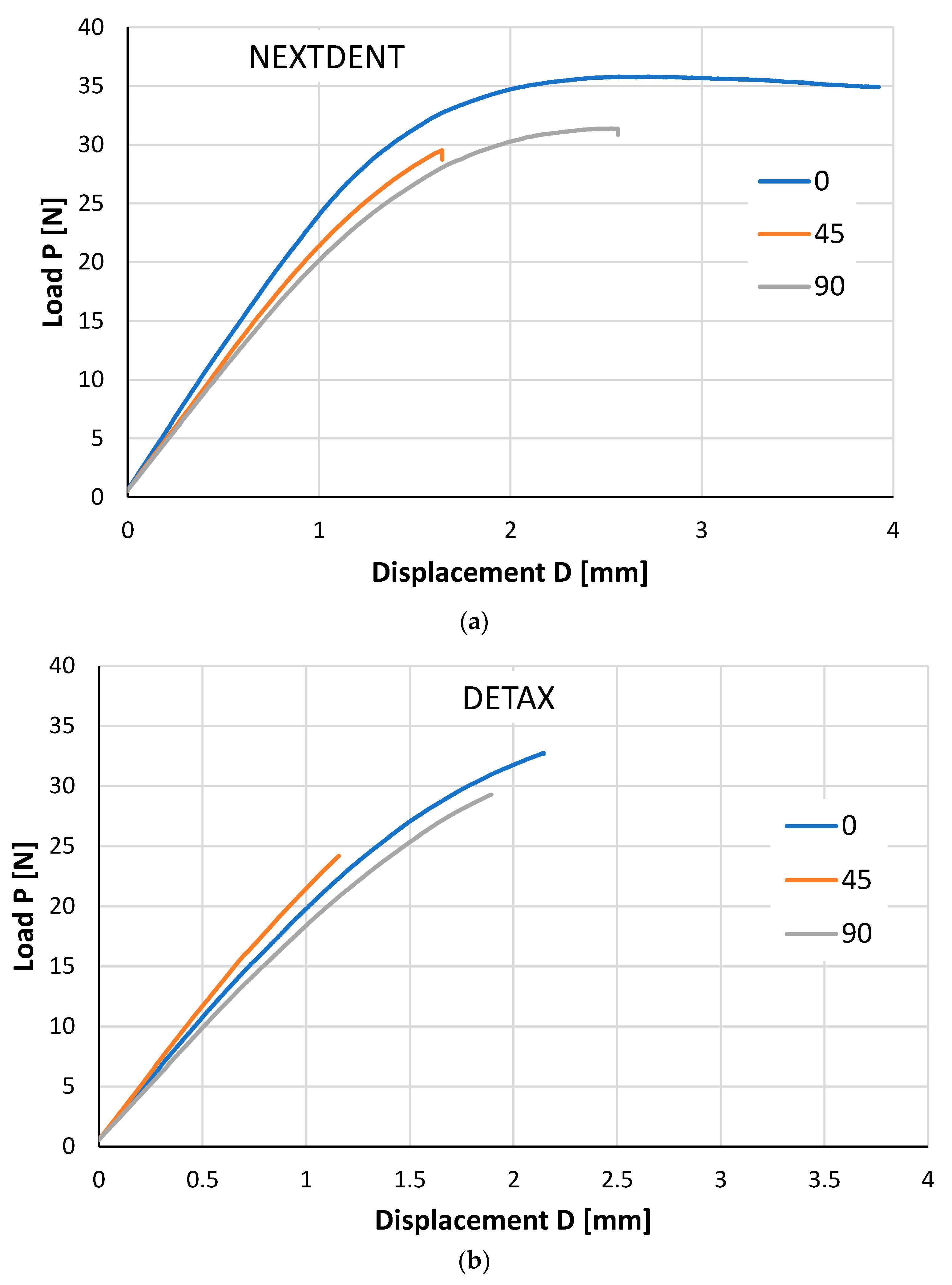
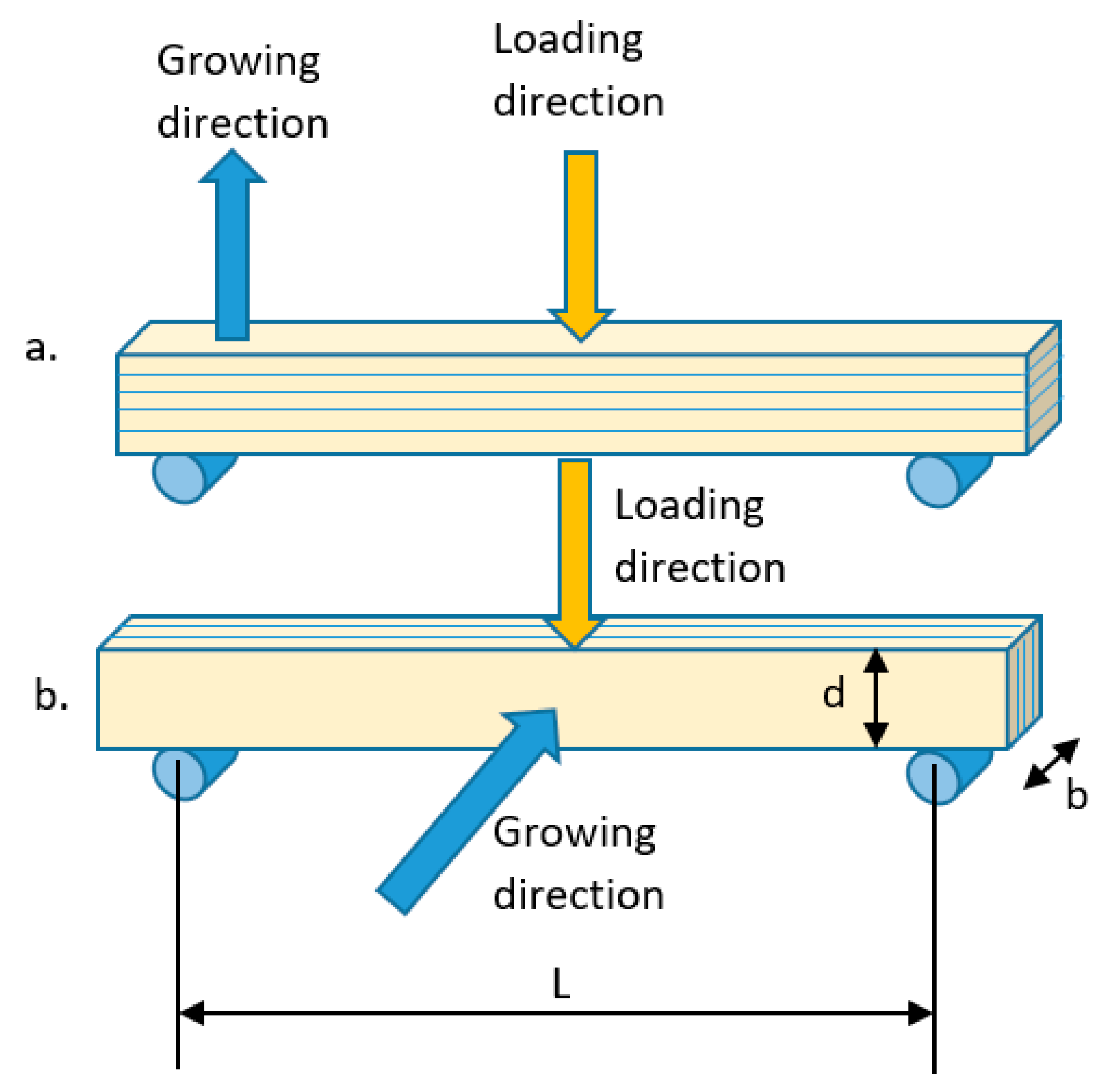
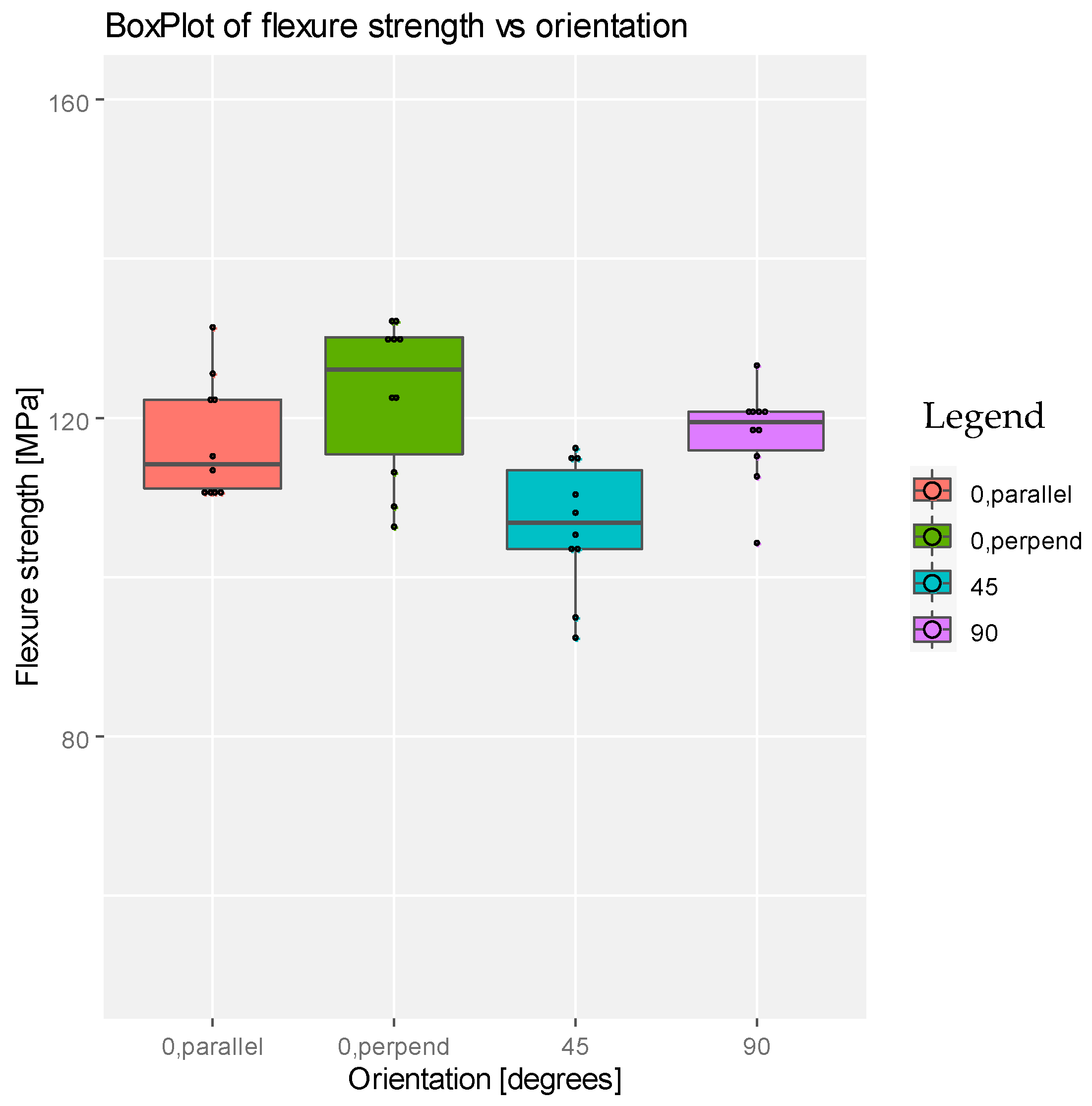
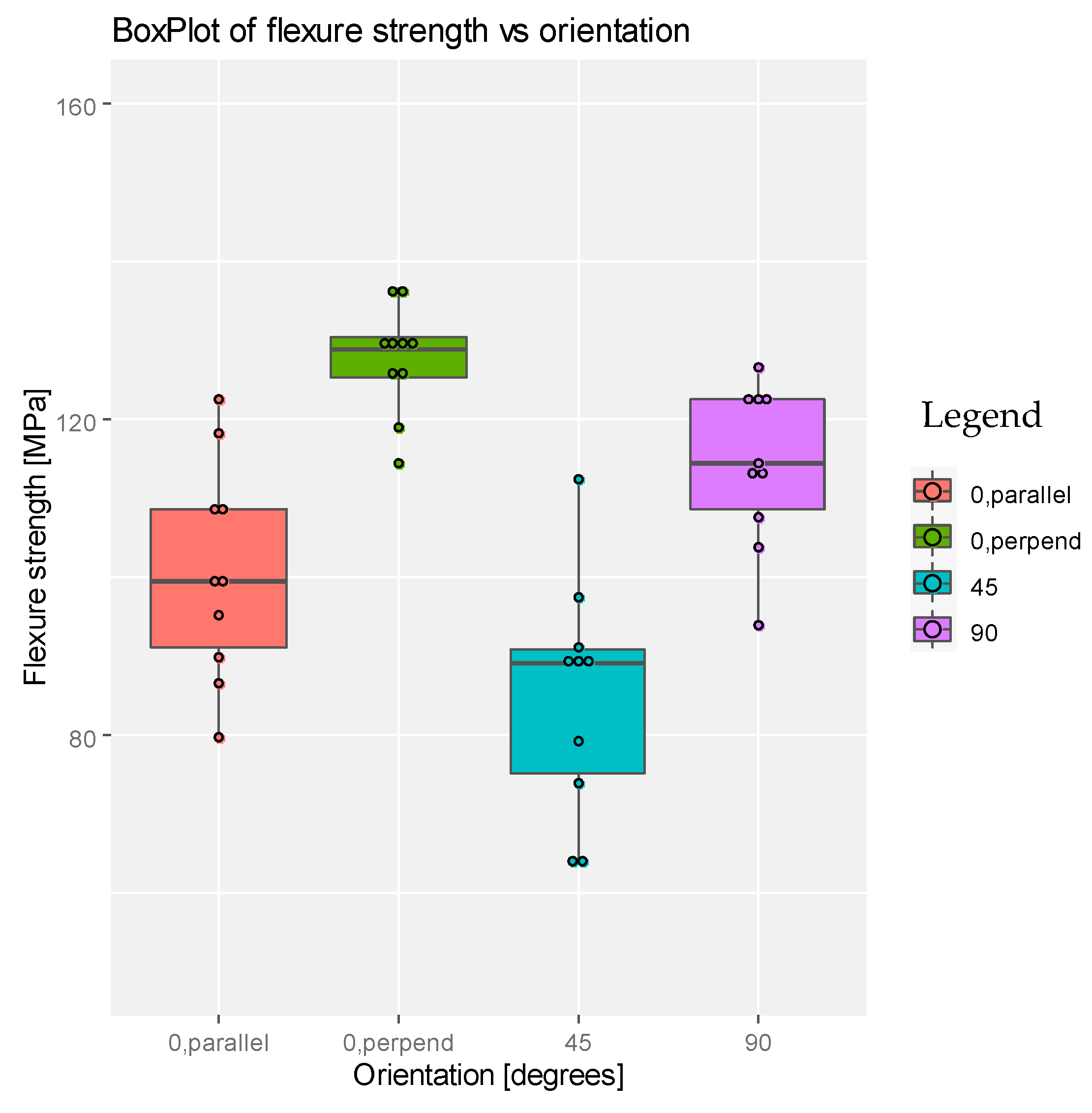
| Specimen Orientation (Degrees) | Loading Direction | Young Modulus (MPa) | Flexure Strength (MPa) | Strain at Break (%) |
|---|---|---|---|---|
| 0 | parallel | 3284.79 | 122.61 | 6.19 |
| 0 | perpendicular | 2765.42 | 117.24 | 8.83 |
| 45 | – | 2610.48 | 106.35 | 5.46 |
| 90 | – | 2766.83 | 117.84 | 8.07 |
| Specimen Orientation (Degrees) | Loading Direction | Young Modulus (MPa) | Flexure Strength (MPa) | Strain at Break (%) |
|---|---|---|---|---|
| 0 | parallel | 2703.69 | 127.54 | 7.62 |
| 0 | perpendicular | 2253.38 | 100.76 | 6.45 |
| 45 | – | 2453.25 | 85.05 | 3.81 |
| 90 | – | 2542.17 | 113.98 | 5.55 |
| Statistical Parameter | 0 Degree Parallel | 0 Degree Perpendicular | 45 Degrees | 90 Degrees |
|---|---|---|---|---|
| Mean value | 117.236 | 122.608 | 106.348 | 117.843 |
| Variance | 55.83274 | 97.75551 | 67.40968 | 36.41227 |
| Statistical Parameter | 0 Degree Parallel | 0 Degree Perpendicular | 45 Degrees | 90 Degrees |
|---|---|---|---|---|
| Mean value | 100.754 | 127.539 | 85.058 | 113.980 |
| Variance | 188.49760 | 46.21454 | 226.84195 | 103.64136 |
| Material | Df | Sum Sq | Mean Sq | F Value | Pr (>F) |
|---|---|---|---|---|---|
| NEXTDENT | 3 | 1418 | 472.5 | 7.342 | 0.000581 *** |
| Residuals | 36 | 2317 | 64.4 | ||
| Significance codes: | 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | ||||
| Material | Df | Sum Sq | Mean Sq | F Value | Pr (>F) |
|---|---|---|---|---|---|
| DETAX | 3 | 9909 | 3303 | 23.38 | 0.000001.42 *** |
| Residuals | 36 | 5087 | 141 | – | – |
| Significance codes: | 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | ||||
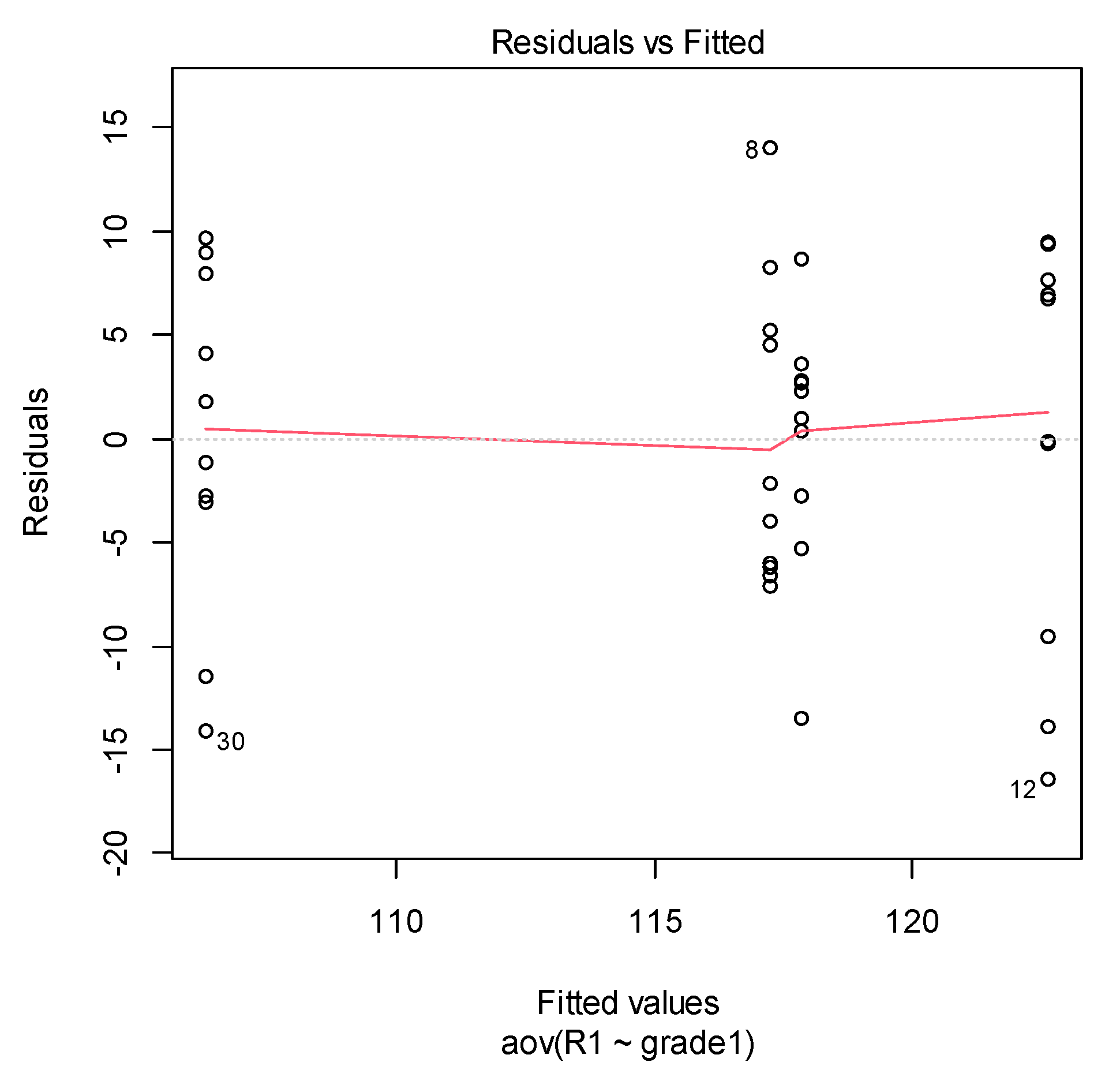
| Bartlett’s test of homogeneity of variances | ||
| data: R1 by grade1 | ||
| Bartlett’s K-squared = 2.1245, | df = 3, | p-value = 0.547 |
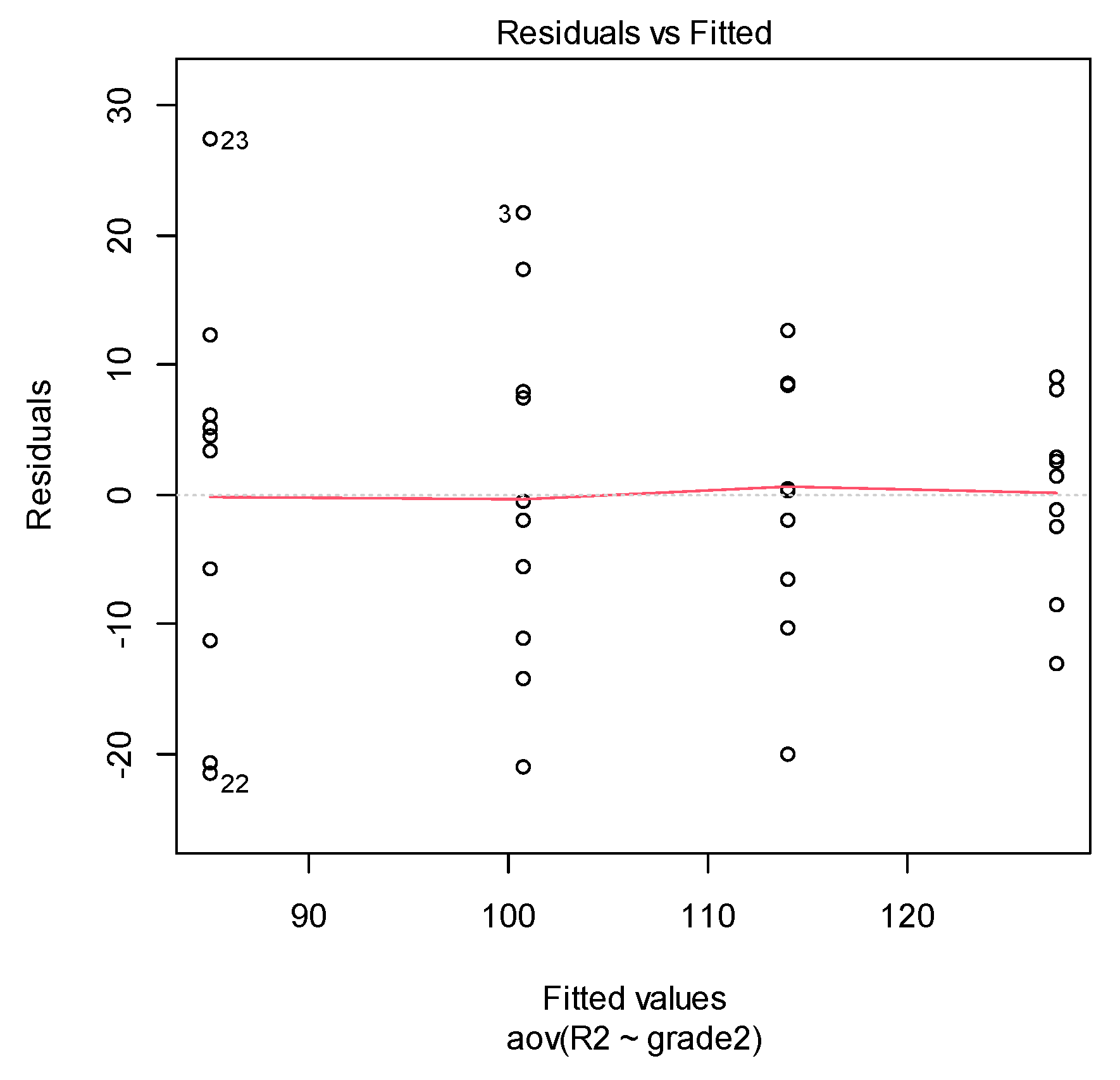
| Bartlett’s test of homogeneity of variances | ||
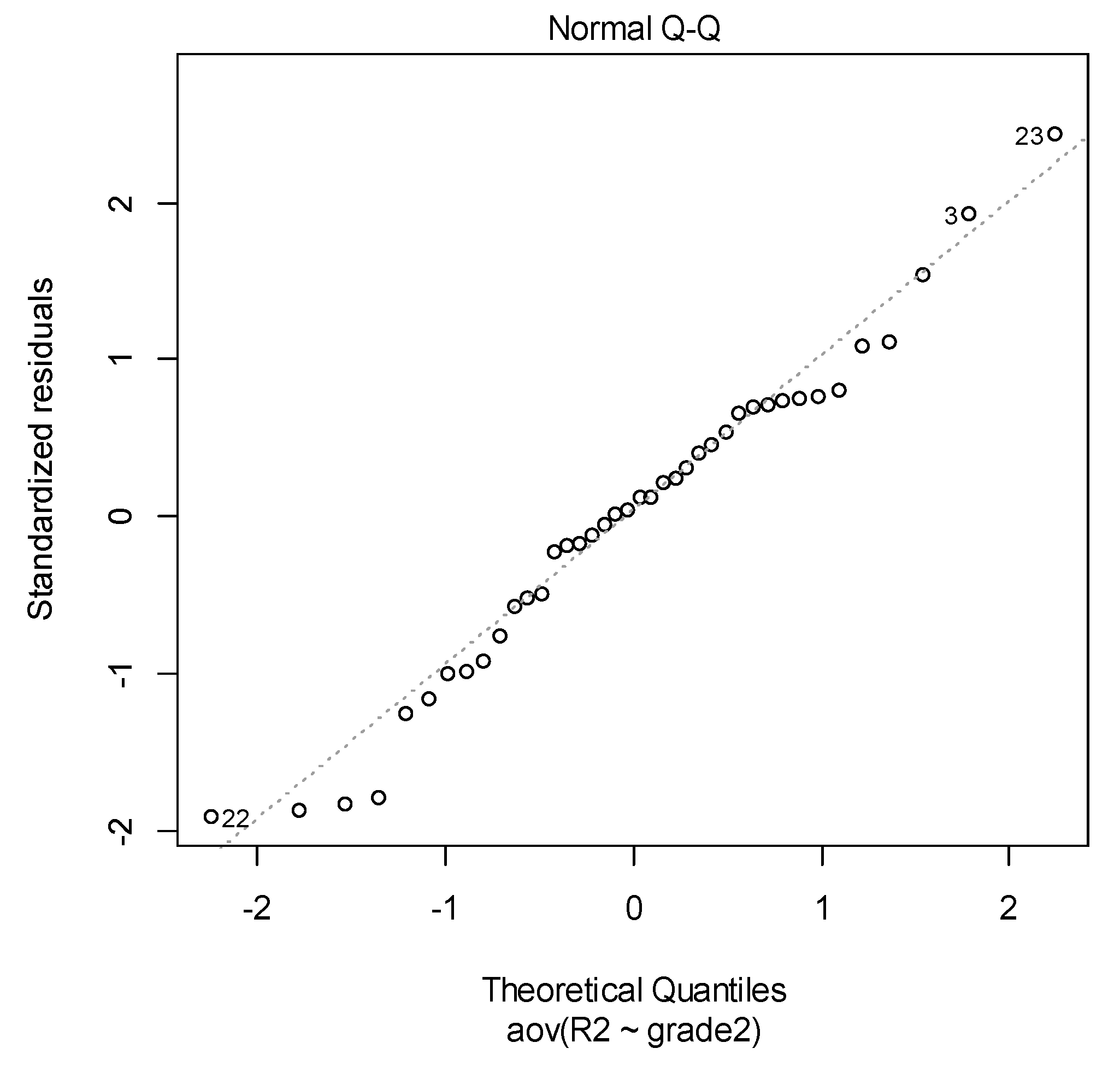
| data: R2 by grade2 | ||
| Bartlett’s K-squared = 5.7283, | df = 3, | p-value = 0.1256 |
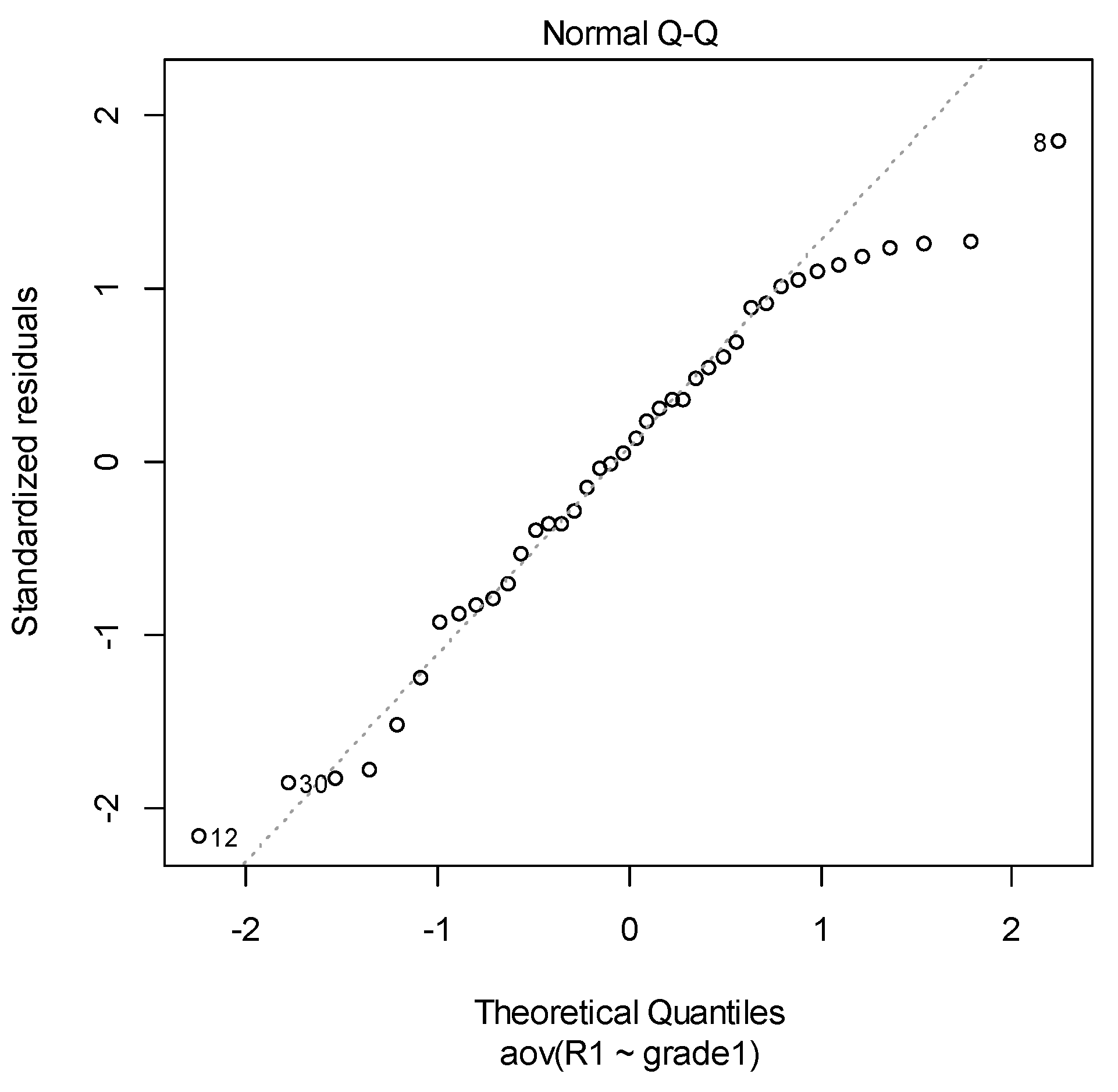
| Shapiro–Wilk normality test | |
| data: aov_residuals1 | |
| W = 0.96326 | p-value = 0.2161 |
| Shapiro–Wilk normality test | |
| data: aov_residuals2 | |
| W = 0.97589 | p-value = 0.5405 |
| Pairwise comparisons using t-tests with pooled SD | |||
| data: df1$R1 and df1$grade1 | |||
| – | 0, parallel | 0, perpend | 45 |
| 0, perpend | 0.21451 | – | – |
| 45 | 0.00890 | 0.00037 | – |
| 90 | 0.86659 | 0.23096 | 0.00851 |
| Pairwise comparisons using t-tests with pooled SD | |||
| data: df2$R2 and df2$grade2 | |||
| 0, parallel | 0, perpend | 45 | |
| 0, perpend | 0.00027 | – | – |
| 45 | 0.0083 | 0.00000001 | – |
| 90 | 0.0176 | 0.0176 | 0.000012 |
| One-way analysis of means (not assuming equal variances) | |||
| data: R1 and grade1 | |||
| F = 6.0859 | num df = 3.000 | denom df = 19.719 | p-value = 0.004171 |
| One-way analysis of means (not assuming equal variances) | |||
| data: R2 and grade2 | |||
| F = 26.075 | num df = 3.000 | denom df = 19.05 | p-value = 0.0000005906 |
| Kruskal-Wallis rank sum test | ||
| data: R1 by grade1 | ||
| Kruskal–Wallis chi-squared = 13.348 | df = 3 | p-value = 0.003942 |
| Kruskal–Wallis rank sum test | ||
| data: R2 by grade2 | ||
| Kruskal–Wallis chi-squared = 27.101 | df = 3 | p-value = 0.000005607 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derban, P.; Negrea, R.; Rominu, M.; Marsavina, L. Influence of the Printing Angle and Load Direction on Flexure Strength in 3D Printed Materials for Provisional Dental Restorations. Materials 2021, 14, 3376. https://doi.org/10.3390/ma14123376
Derban P, Negrea R, Rominu M, Marsavina L. Influence of the Printing Angle and Load Direction on Flexure Strength in 3D Printed Materials for Provisional Dental Restorations. Materials. 2021; 14(12):3376. https://doi.org/10.3390/ma14123376
Chicago/Turabian StyleDerban, Paula, Romeo Negrea, Mihai Rominu, and Liviu Marsavina. 2021. "Influence of the Printing Angle and Load Direction on Flexure Strength in 3D Printed Materials for Provisional Dental Restorations" Materials 14, no. 12: 3376. https://doi.org/10.3390/ma14123376
APA StyleDerban, P., Negrea, R., Rominu, M., & Marsavina, L. (2021). Influence of the Printing Angle and Load Direction on Flexure Strength in 3D Printed Materials for Provisional Dental Restorations. Materials, 14(12), 3376. https://doi.org/10.3390/ma14123376








