Bonding of Al6061 by Hot Compression Forming: A Computational and Experimental Study of Interface Conditions at Bonded Surfaces
Abstract
:1. Introduction
2. Materials and Methods
2.1. Bonding and Debonding Experimental Setup and Metallurgical Charcterization
2.2. Computational Modeling
3. Results
3.1. Determination of Al6061 Flow Stress
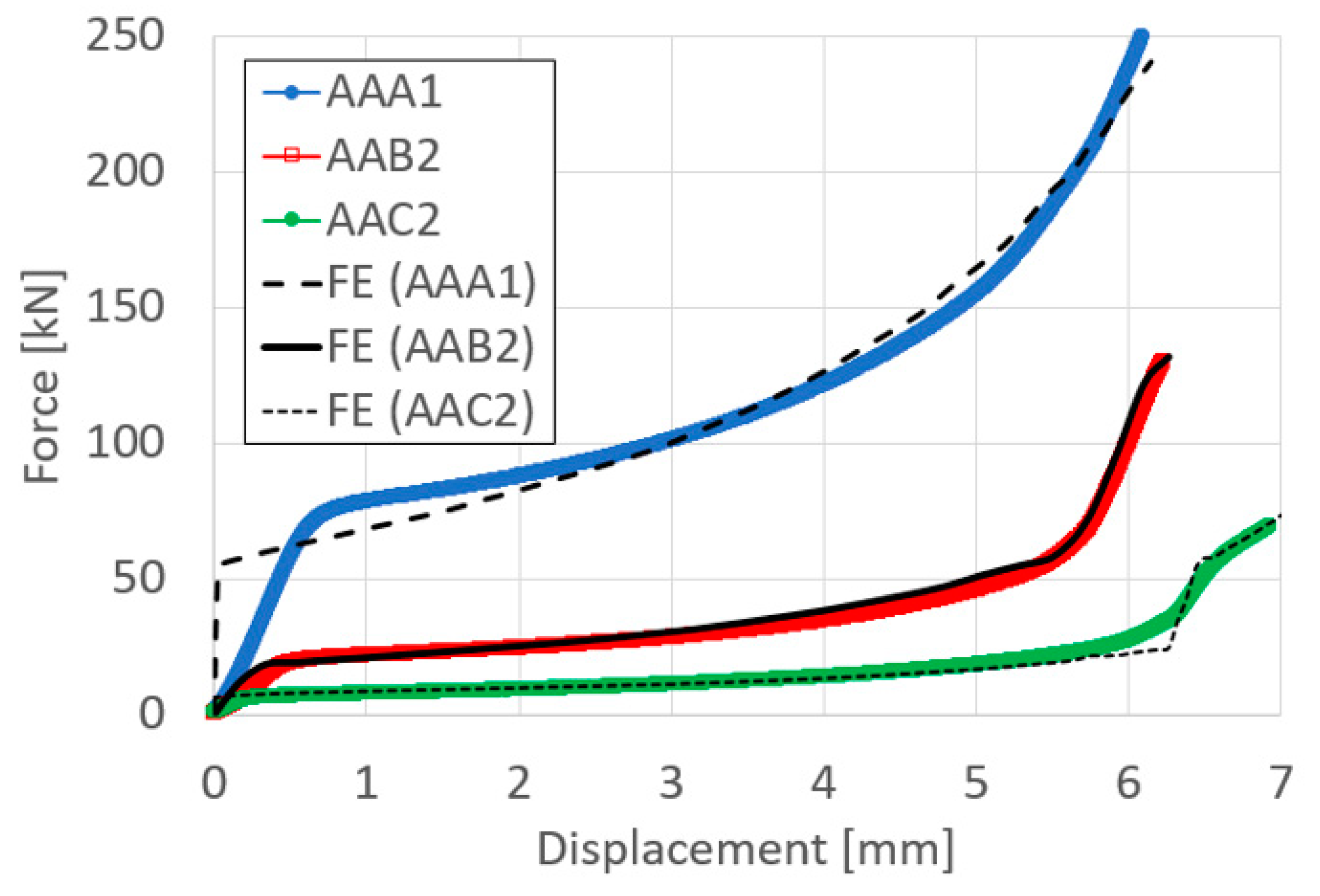
3.2. Compression Bonding Tests
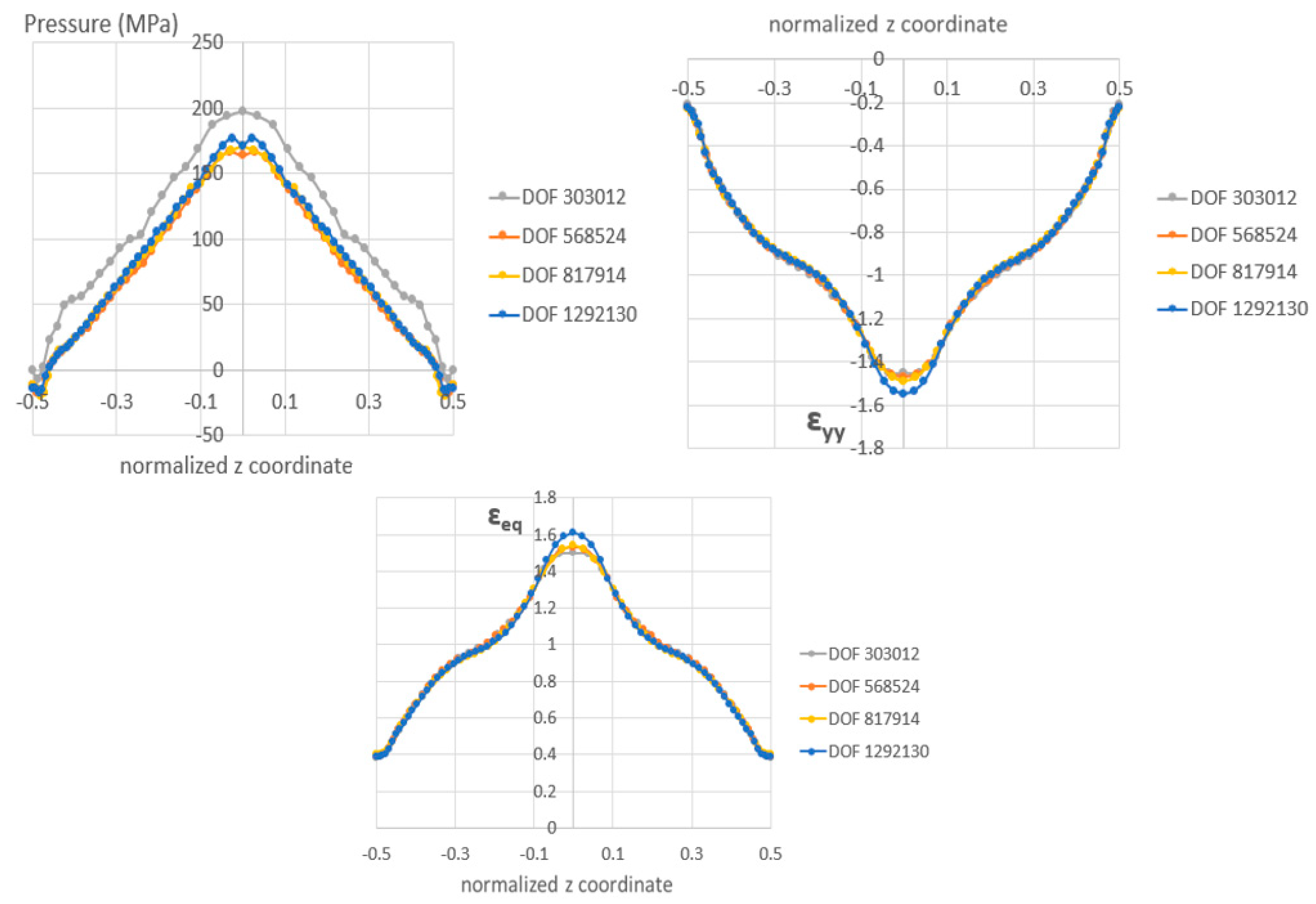
3.3. Validation of the Finite Element Models
3.4. Debonding Experiments
3.5. Macroscopic Charcterization Following Debonding Tests
3.6. Microscopic Charcterization Following Debonding
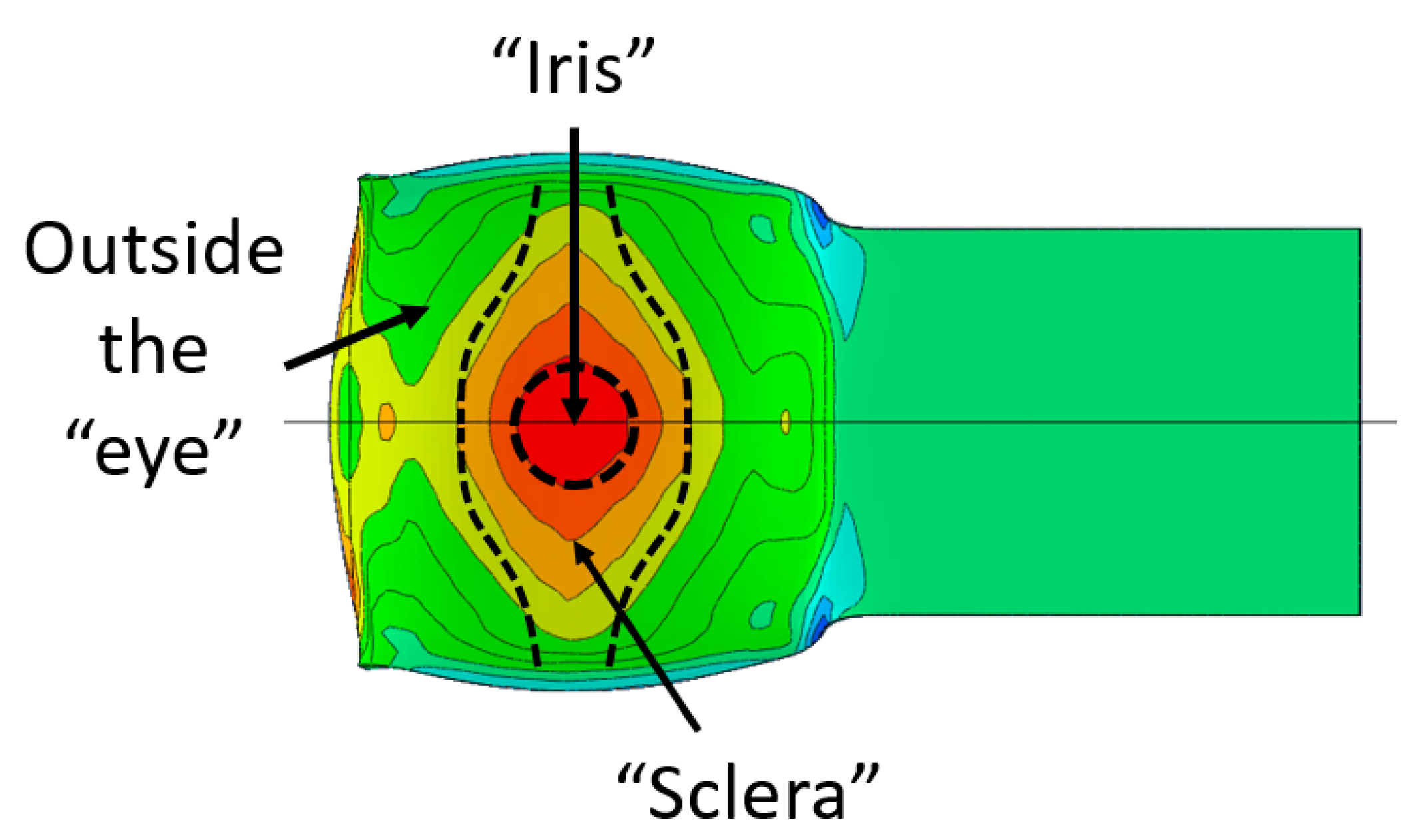
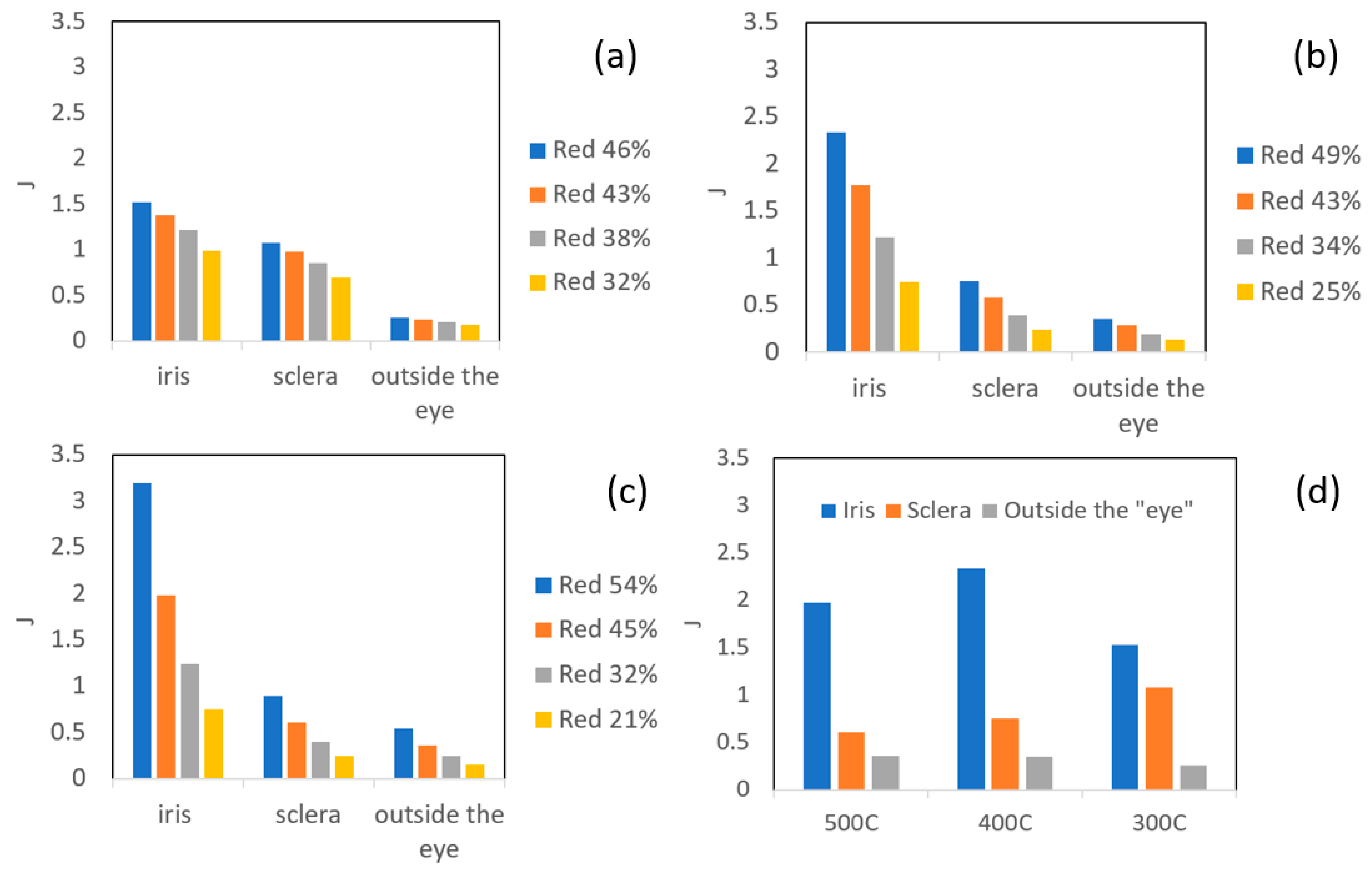
4. Correlation between Computed Thermo-Mechanical Fields and Microscopic Observations
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Verification of the Computational Models

References
- Botelho, E.C.; Silva, R.A.; Pardini, L.C.; Renzende, M.C. A review on the development and properties of continuous Fiber/epoxy/aluminum hybrid composites for aircraft structures. Mater. Res. 2006, 9, 247–256. [Google Scholar] [CrossRef]
- Goushegir, S.M.; Scharnagl, N.; Dos Santos, J.F.; Amancio-Filho, S.T. Durability of Metal-Composite Friction Spot Joints under Environmental Conditions. Materials 2020, 13, 1144. [Google Scholar] [CrossRef] [Green Version]
- Samal, P.; Vundavilli, P.R.; Meher, A.; Mahapatra, M.M. Recent progress in aluminum metal matrix composites: A review on processing, mechanical and wear properties. J. Manuf. Process. 2020, 59, 131–152. [Google Scholar] [CrossRef]
- Danesh Manesh, H.; Shahabi, H.S. Effective parameters on bonding strength of roll bonded Al/St/Al multilayer strips. J. Alloys Compd. 2009, 476, 292–299. [Google Scholar] [CrossRef]
- Zhang, X.P.; Yang, T.H.; Castagne, S.; Wang, J.T. Microstructure bonding strength and thickness ratio of Al/Mg/Al alloy laminated composites prepared by hot rolling. Mater. Sci. Eng. A 2011, 528, 1954–1960. [Google Scholar] [CrossRef]
- Hassan, M.; Ali, A.; Ilyas, M.; Hussain, G.; Ul Haq, I. Experimental and numerical simulation of steel/steel (St/St) interface in bi-layer sheet metal. Int. J. Lightweight Mater. Manuf. 2019, 2, 89–96. [Google Scholar] [CrossRef]
- Lumley, R. Fundamentals of Aluminum Metallurgy, Production Processing and Applications, 1st ed.; Woodhead Publishing: Cambridge, UK, 2011. [Google Scholar]
- Chunlei, G.; Yongdong, X.; Mengjun, W. Prediction of the flow stress of Al6061 at hot deformation conditions. Mater. Sci. Eng. A 2011, 528, 4199–4203. [Google Scholar] [CrossRef]
- Helmut, M. Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 127–147. [Google Scholar]
- Mori, K.I.; Bay, N.; Fratini, L.; Micari, F.; Tekkaya, A.E. Joining by plastic deformation. CIRP Ann. Manuf. Technol. 2013, 62, 673–694. [Google Scholar] [CrossRef]
- Zinong, T.; Bing, Z.; Jun, J.; Zhiqiang, L.; Jianguo, L. A study on the hot roll bonding of aluminum alloys. Procedia Manuf. 2020, 50, 56–62. [Google Scholar] [CrossRef]
- Ghalehbandi, S.M.; Malaki, M.; Gupta, M. Accumulative roll bonding—A review. Appl. Sci. 2019, 9, 3627. [Google Scholar] [CrossRef] [Green Version]
- Clerico, P.; Mininger, X.; Prevond, L.; Baudin, T.; Helbert, A.L. Compromise between magnetic shielding and mechanical strength of thin Al/Steel/Al sandwiches produced by cold roll bonding: Experimental and numerical approaches. J. Alloys Compd. 2019, 798, 67–81. [Google Scholar] [CrossRef]
- Kazanowski, P.; Epler, M.E.; Misiolek, W.Z. Bi-Metal rod extrusion-process and product optimization. Mater. Sci. Eng. A 2004, 369, 170–180. [Google Scholar] [CrossRef]
- Priel, E.; Ungarish, Z.; Navi, N.U. Co-extrusion of a Mg/Al Composite Billet: A Computational Study Validated by Experiments. J. Mater. Process. Technol. 2016, 236, 103–113. [Google Scholar] [CrossRef]
- Qing, T.; Xiu, L.; Qingsong, W. Diffusion bonding of Al6061 and Cu by hot isostatic pressing. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2020, 35, 183–191. [Google Scholar]
- Xie, B.; Sun, M.; Xu, B.; Wang, C.; Zhang, J.; Zhao, L.; Li, D.; Li, Y. Evolution of interfacial characteristics and mechanical properties for 316LN stainless steel joints manufactured by hot-compression bonding. J. Mater. Process. Technol. 2020, 283, 116733. [Google Scholar] [CrossRef]
- Xu, X.; Ma, X.; Yu, S.; Zhao, G.; Wang, Y.; Chen, X. Bonding mechanism and mechanical properties of 2196 Al-Cu-Li alloy joined by hot compression deformation. Mater. Charact. 2020, 167, 110486. [Google Scholar] [CrossRef]
- Lesuer, D.R.; Syn, C.K.; Sherby, O.D.; Wadsworth, J.; Lewandowski, J.J.; Hunt, W.H. Mechanical behavior of laminated metal composites. Int. Mater. Rev. 1996, 41, 169–197. [Google Scholar] [CrossRef]
- Alkramifard, H.R.; Mirzadeh, H.; Parsa, M.H. Estimating interface bonding strength in clad sheets based on tensile test results. Mater. Des. 2014, 64, 307–309. [Google Scholar] [CrossRef]
- Mittleman, B.; Guttmann, G.M.; Priel, E. A computational analysis of thermo-mechanical fields in hot roll bonding of aluminum validated by experiments. J. Miner. Met. Mater. Soc. 2019, 72, 718–728. [Google Scholar] [CrossRef]
- Mittelman, B.; Priel, E.; Navi, N.U. A finite element study of thermo-mechanical fields and their relation to friction conditions in Al1050 ring compression tests. J. Manuf. Mater. Process. 2018, 2, 83. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, T.; Obikawa, T.; Yukutake, E.; Ueda, S.; Nishizaki, I. Tool temperature and process modeling of friction stir welding. Mod. Mech. Eng. 2018, 8, 78–94. [Google Scholar] [CrossRef] [Green Version]
- Jeurgens, L.P.H.; Sloof, W.G.; Tichelaar, F.D.; Mittemeijer, J. Growth kinetics and mechanisms of aluminum-oxide films formed by thermal oxidation of aluminum. J. Appl. Phys. 2002, 92, 1649–1656. [Google Scholar] [CrossRef]
- Bay, N. Cold pressure welding-The mechanisms governing bonding. J. Eng. Ind. 1979, 101, 121–127. [Google Scholar] [CrossRef]






| Specimen Temp. [°C] | 25 | 300 | 400 | 500 |
|---|---|---|---|---|
| Flow stress [MPa] |
| Temperature [°C] | Specimen No. | Reduction [%] | Wavg [mm] | Lavg [mm] |
|---|---|---|---|---|
| 300 | AAA1 | 46.48 | 34.2 | 28.2 |
| AAA2 | 43.54 | 31.47 | 27.95 | |
| AAA3 | 38.33 | 29.65 | 23.2 | |
| AAA4 | 32.39 | 26.75 | 22.52 | |
| 400 | AAB2 | 49.45 | 34.5 | 26.50 |
| AAB3 | 43.39 | 31.50 | 25.56 | |
| AAB4 | 34.29 | 28.98 | 23.70 | |
| AAB5 | 25.02 | 25.60 | 21.50 | |
| 500 | AAC2 | 53.45 | 37.50 | 28.75 |
| AAC3 | 44.84 | 32.80 | 23.4 | |
| AAC4 | - | - | - | |
| AAC5 | - | - | - |
| Temperature [°C] | Specimen No. | Actual Reduction [%] | Notes | |
|---|---|---|---|---|
| 300 | AAA1 | 46.48 | 12.16 | |
| AAA2 | 43.54 | 11.19 | ||
| AAA3 | 38.33 | 5.08 | ||
| AAA4 | 32.39 | 4.26 | ||
| 400 | AAB2 | 49.45 | 10.89 | |
| AAB3 | 43.39 | 11.73 | ||
| AAB4 | 34.29 | 8.28 | ||
| AAB5 | 25.02 | 7.22 | ||
| 500 | AAC2 | 53.45 | 7.29 | |
| AAC3 | 44.84 | 7.50 | ||
| AAC4 | - | - | No bonding | |
| AAC5 | - | - | No bonding |
| “iris” | “sclera” | Outside the “eye” | |
|---|---|---|---|
| AAA1 (Bonded at 300 °C, 46.5% reduction) |  |  |  |
| AAB2 (Bonded at 400 °C, 49.5% reduction) |  |  |  |
| AAC3 (Bonded at 500 °C, 45% reduction) |  |  |  |
| Spec. | AAA1 (Bonded at 300 °C, 46.5% Reduction) | AAB2 (Bonded at 400 °C, 49.5% Reduction) |
|---|---|---|
| Macro image |  |  |
| ɛ11 (Max. principal strain) | 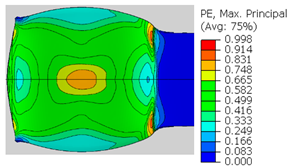 | 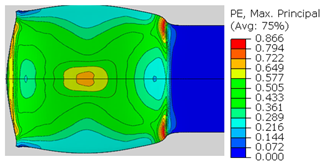 |
| ɛ22 (Mid principal strain) | 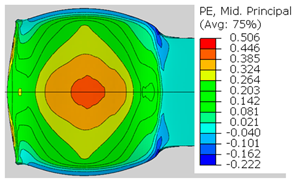 | 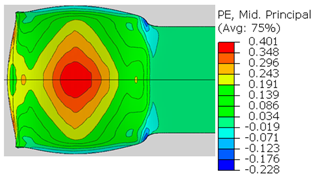 |
| ɛ33 (Min. principal strain) | 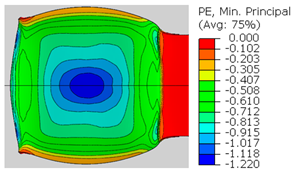 | 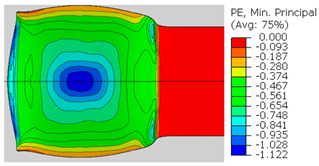 |
| Spec. | AAC3 (Bonded at 500 °C, 45% reduction) | AAC4 (Bonded at 500 °C, 32% reduction) |
| Macro image |  |  |
| ɛ11 (Max. principal strain) |  |  |
| ɛ22 (Mid principal strain) | 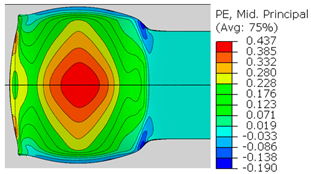 | 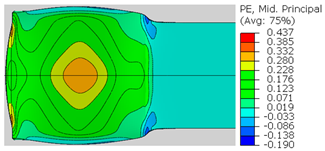 |
| ɛ33 (Min. principal strain) | 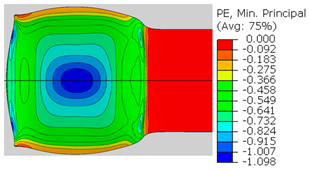 | 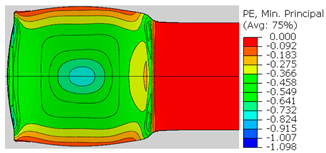 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mittelman, B.; Ben-Haroush, M.; Aloush, I.; Mordechay, L.; Priel, E. Bonding of Al6061 by Hot Compression Forming: A Computational and Experimental Study of Interface Conditions at Bonded Surfaces. Materials 2021, 14, 3598. https://doi.org/10.3390/ma14133598
Mittelman B, Ben-Haroush M, Aloush I, Mordechay L, Priel E. Bonding of Al6061 by Hot Compression Forming: A Computational and Experimental Study of Interface Conditions at Bonded Surfaces. Materials. 2021; 14(13):3598. https://doi.org/10.3390/ma14133598
Chicago/Turabian StyleMittelman, Brigit, Michael Ben-Haroush, Ira Aloush, Linoy Mordechay, and Elad Priel. 2021. "Bonding of Al6061 by Hot Compression Forming: A Computational and Experimental Study of Interface Conditions at Bonded Surfaces" Materials 14, no. 13: 3598. https://doi.org/10.3390/ma14133598
APA StyleMittelman, B., Ben-Haroush, M., Aloush, I., Mordechay, L., & Priel, E. (2021). Bonding of Al6061 by Hot Compression Forming: A Computational and Experimental Study of Interface Conditions at Bonded Surfaces. Materials, 14(13), 3598. https://doi.org/10.3390/ma14133598






