Investigation of the Relationship between Morphology and Thermal Conductivity of Powder Metallurgically Prepared Aluminium Foams
Abstract
:1. Introduction
2. Methodology
2.1. Preparation of Samples
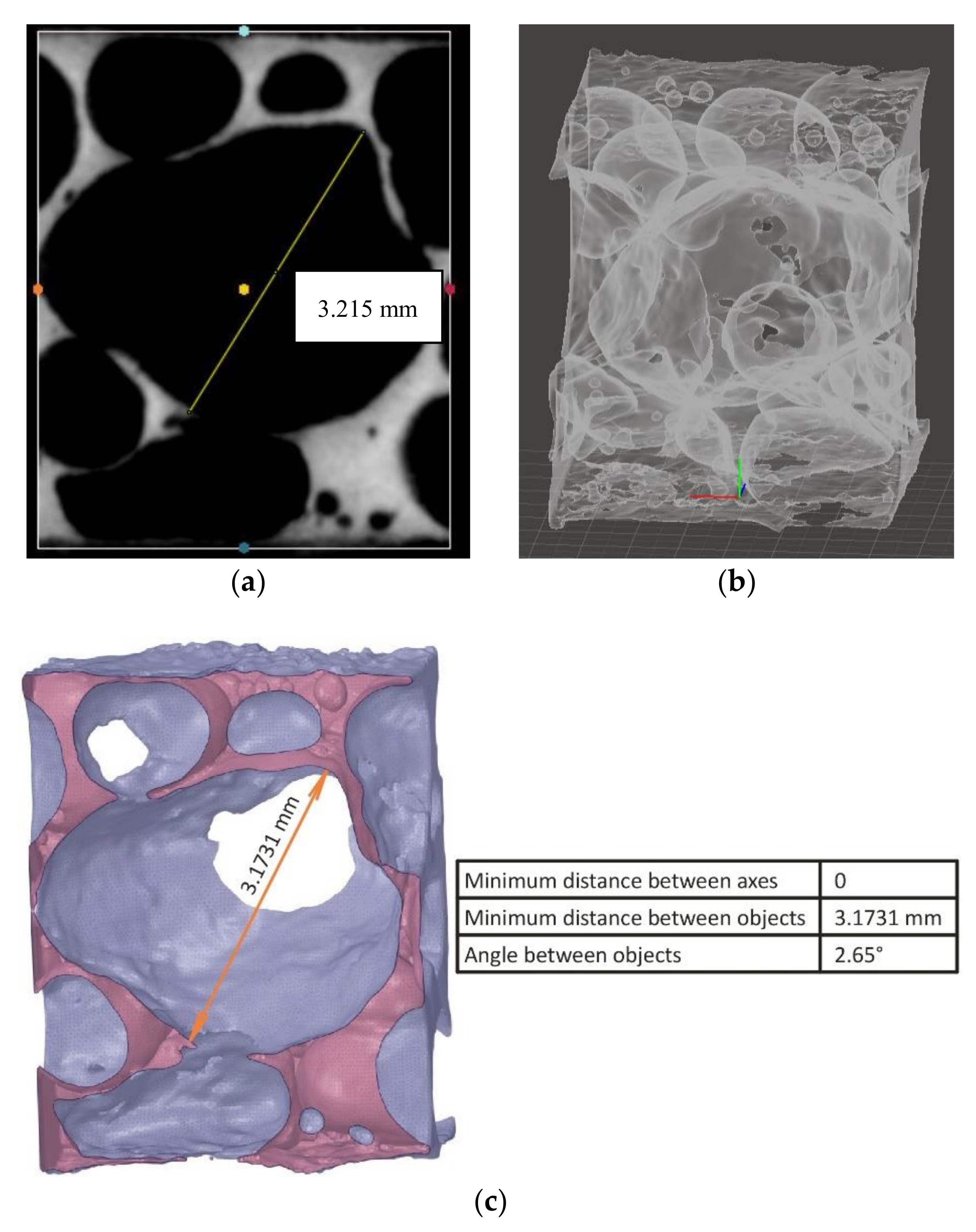
2.2. X-ray Tomography of Aluminium Foam
3. Modelling and Analysis
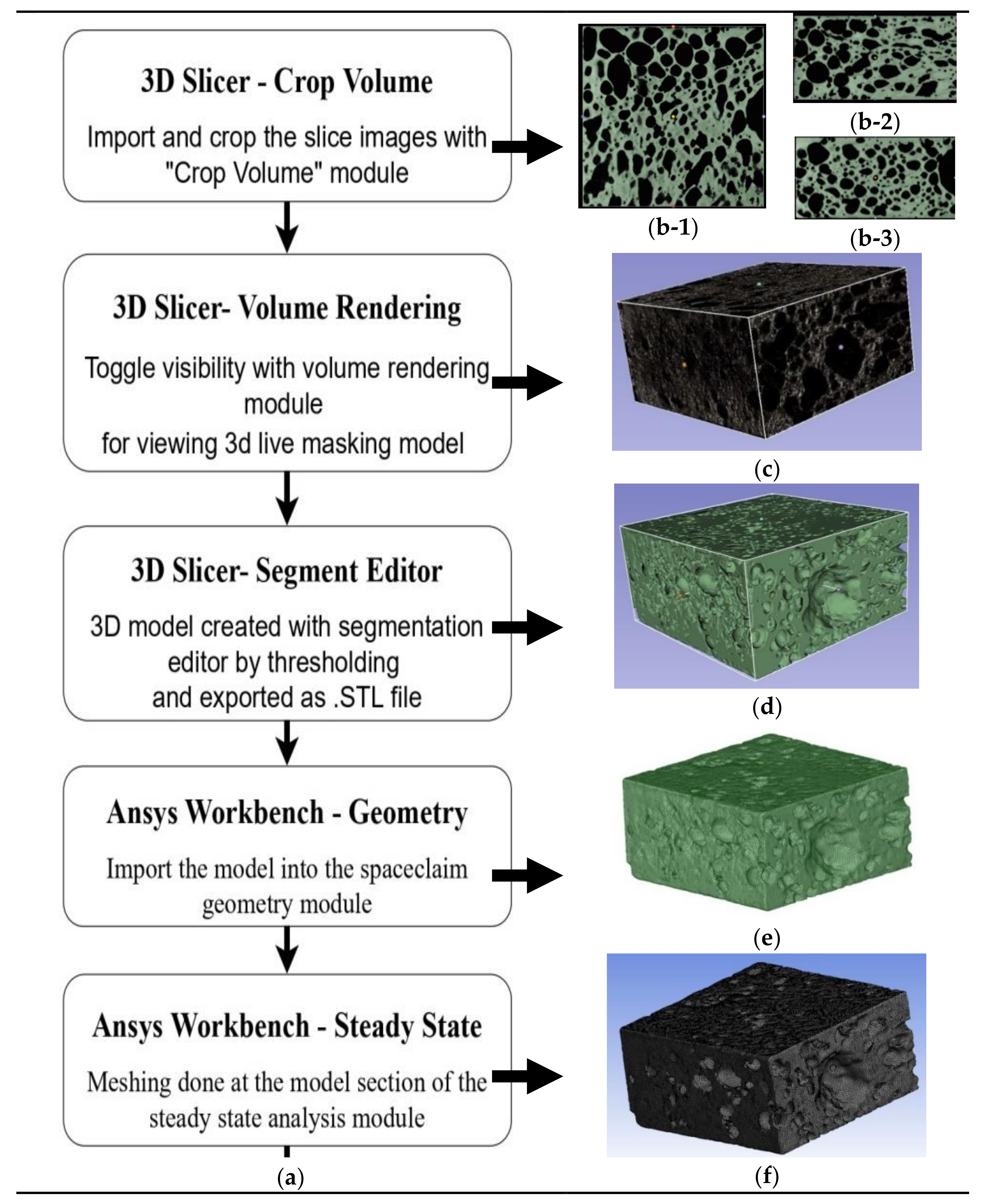
3.1. Creation of Model
3.2. Recreation of the Model
3.3. Boundary Conditions and Simulations
4. Analytical Approach and Validation
5. Results
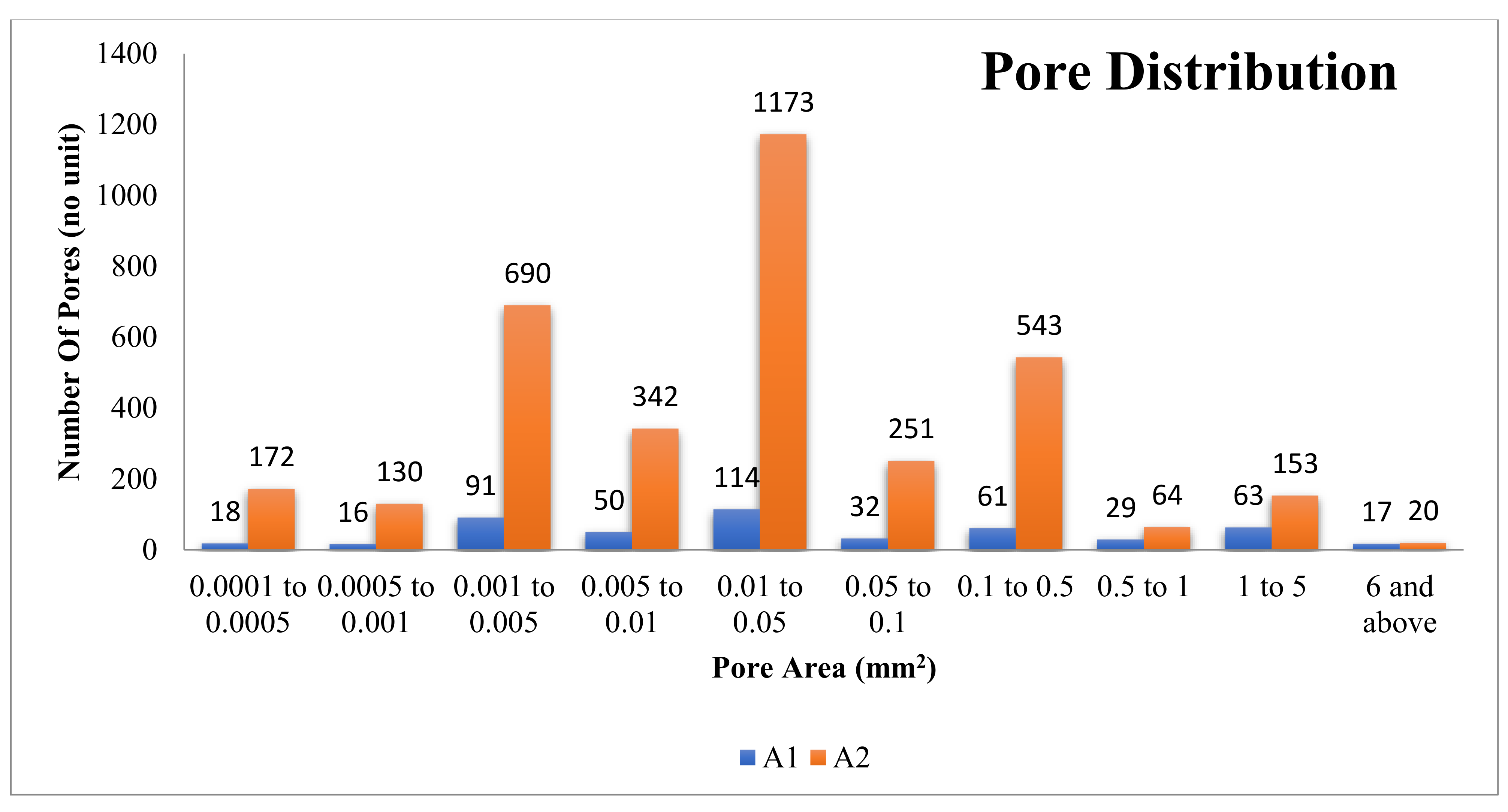
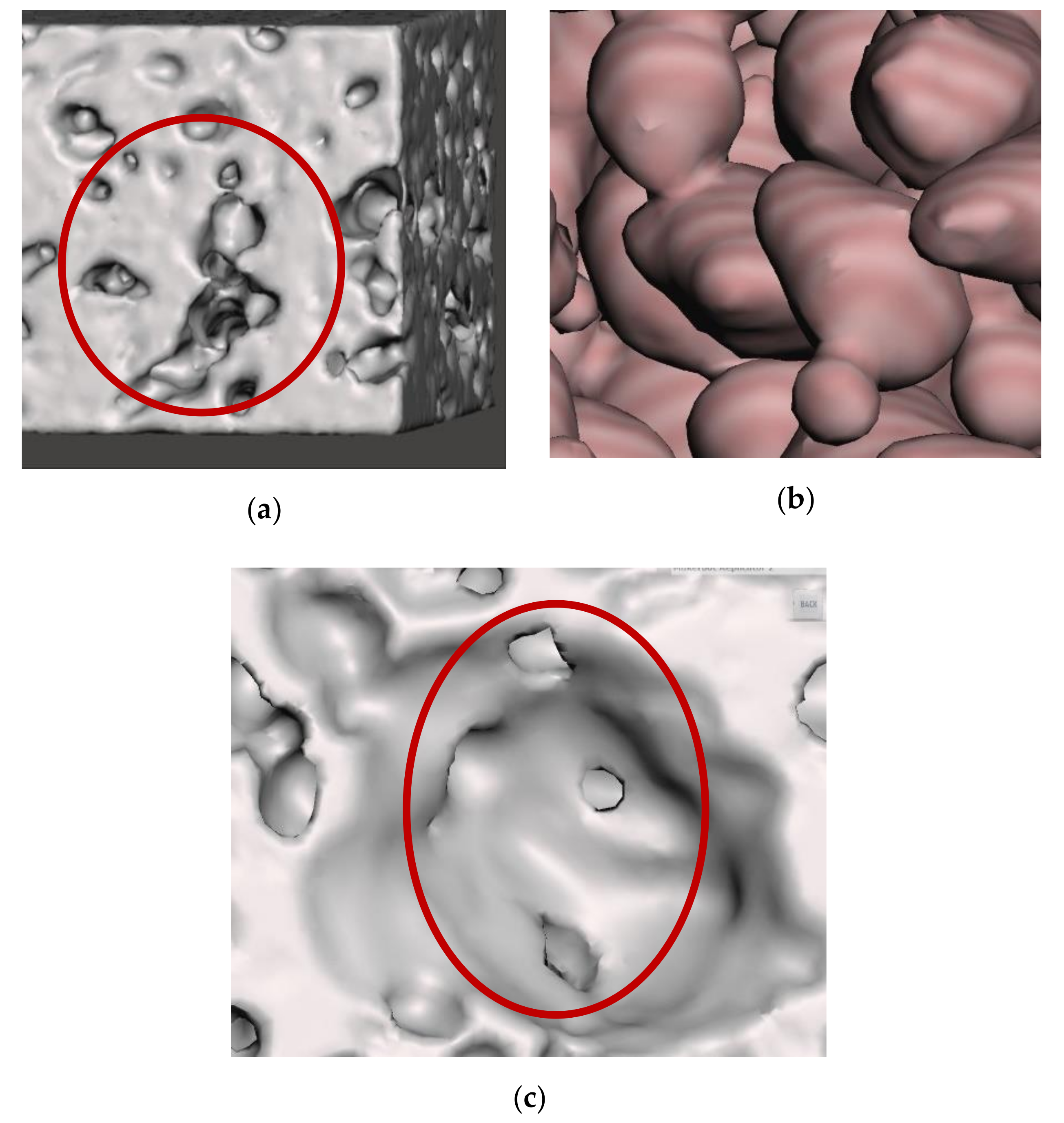
5.1. Pore Size and Morphology
5.2. Numerical Study
6. Discussion
6.1. Reconstruction of Actual Foam and Defects
6.2. Influence of Struts and Pore Wall Thickness
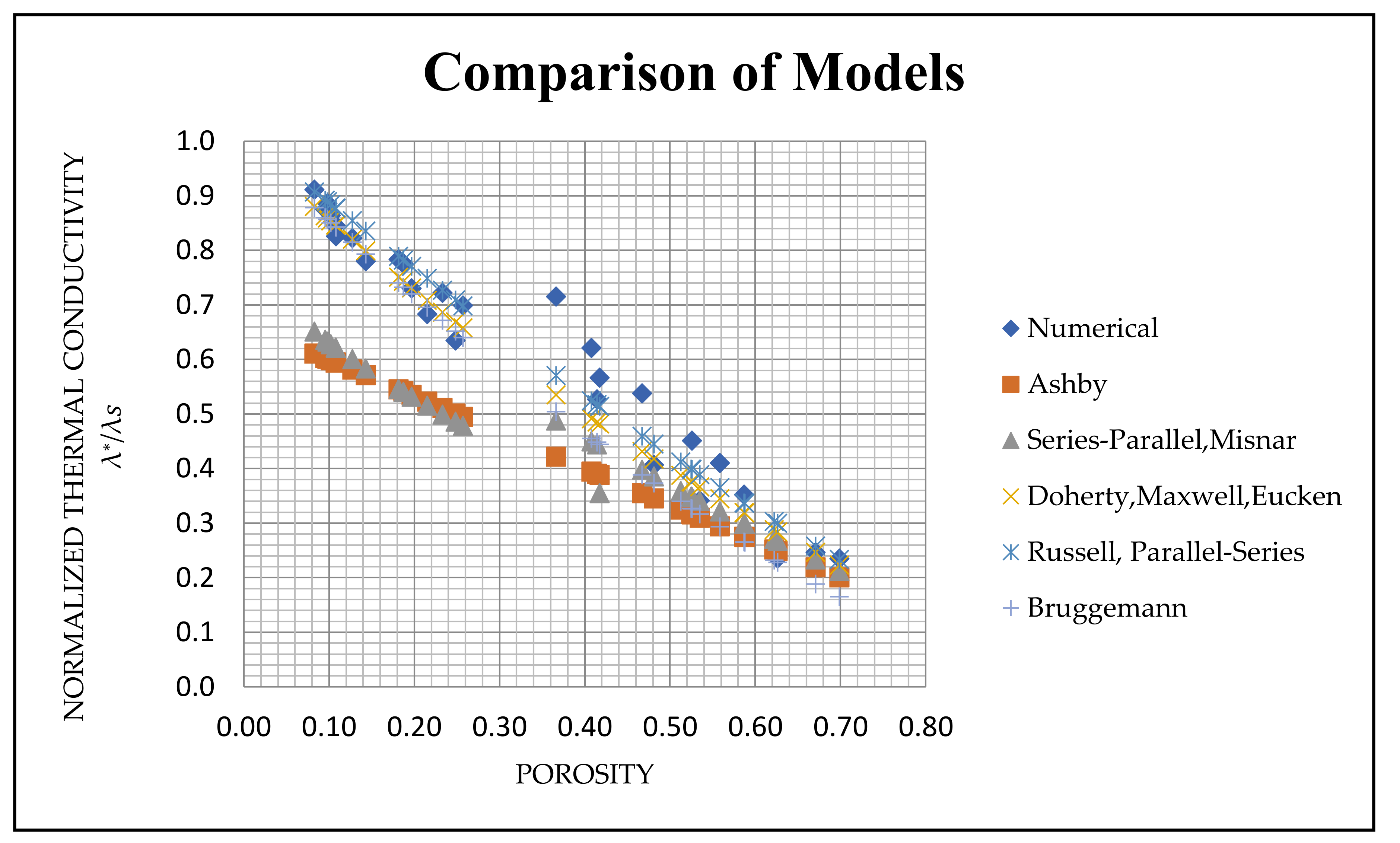
6.3. Comparison with Analytical Models
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PM | Powder Metallurgy |
| PCMs | Phase Change Materials |
| TES | Thermal Energy Storage |
| Apparent density, g/cm3 | |
| Bulk density, g/cm3 | |
| Relative density | |
| Pore Volume, mm3 | |
| Bulk Volume, mm3 | |
| q | Heat flux density, W/m2 |
| Q | Amount of heat transfer flow rate, W |
| ∇T | Temperature gradient, K |
| Thermal conductivity, W/(m·K) | |
| Thermal conductivity of foam, W/(m·K) | |
| Effective thermal conductivity of foam, W/(m·K) | |
| Thermal conductivity of the solid phase, W/(m·K) | |
| Thermal conductivity of the solid material, W/(m·K) | |
| , | Thermal conductivity of the gas phase of foam, W/(m·K) |
| Convective heat transfer, W/(m·K) | |
| Radiative heat transfer, W/(m·K) | |
| Surface area perpendicular to the direction of heat flux, m2 | |
| Total Surface area, m2 | |
| Pore area, m2 | |
| L | Thickness of the sample, m |
| Vf | Volume Fraction |
| μ | Dynamic viscosity, N·s/m2 |
| Extinction coefficient |
References
- Jerz, J.; Šebek, J.; Simančík, F.; Španielka, J. Aluminum foam heat exchangers for future zero-energy buildings. Symp. Energ. Graz Austria 2018, 2, 14–16. [Google Scholar] [CrossRef]
- Solórzano, E.; Reglero, J.A.; Rodríguez-Pérez, M.A.; Lehmhus, D.; Wichmann, M.; de Saja, J.A. An experimental study on the thermal conductivity of aluminium foams by using the transient plane source method. Int. J. Heat Mass Transf. 2008, 51, 6259–6267. [Google Scholar] [CrossRef]
- Duschlbauer, D.; Böhm, H.J.; Pettermann, H.E. Numerical Simulation of Thermal Conductivity of MMCs: Effect of Thermal Interface Resistance. Mater. Sci. Technol. 2003, 19, 1107–1114. [Google Scholar] [CrossRef]
- Kumar, P.; Topin, F. Different arrangements of simplifed models to predict effective thermal conductivity of open-cell foams. Heat Mass Transf. 2017, 53, 2473–2486. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Zhang, J.; Triantafillou, T.C. Failure surfaces for cellular materials under multiaxial loads—I. Modelling. Int. J. Mech. Sci. 1989, 31, 635–663. [Google Scholar] [CrossRef]
- Ashby, M.F. The mechanical properties of cellular solids. Metall. Trans. A 1983, 14, 1755–1769. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, J. Thermal conductivity prediction of closed-cell aluminium alloy considering micropore effect. Adv. Mech. Eng. 2015, 7, 1–8. [Google Scholar]
- Bracconi, M.; Ambrosetti, M.; Maestri, M.; Groppi, G.; Tronconi, E. A fundamental analysis of the influence of the geometrical properties on the effective thermal conductivity of open-cell foams. Chem. Eng. Process. Process. Intensif. 2018, 129, 181–189. [Google Scholar] [CrossRef]
- Ghosh, I. Heat transfer correlation for high-porosity open-cell foam. Int. J. Heat Mass Transf. 2009, 52, 1488–1494. [Google Scholar] [CrossRef]
- Boomsma, K.; Poulikakos, D. On the effective thermal conductivity of a three-dimensionally structured fluid-saturated metal foam. Int. J. Heat Mass Transf. 2001, 44, 827–836. [Google Scholar] [CrossRef]
- Wang, H.; Guo, L. Experimental investigation on pressure drop and heat transfer in metal foam-filled tubes under convective boundary condition. Chem. Eng. Sci. 2016, 155, 438–448. [Google Scholar] [CrossRef]
- Baillis, D.; Coquard, R. Radiative and conductive thermal properties of foams. In Cellular and Porous Materials: Thermal Properties Simulation and Prediction; Öchsner, A., Murch, G.E., de Lemos, M.J.S., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 343–384. ISBN 9783527319381. [Google Scholar]
- Nammi, S.K.; Myler, P.; Edwards, G. Finite element analysis of closed-cell aluminium foam under quasi-static loading. Mater. Des. 2010, 31, 712–722. [Google Scholar] [CrossRef]
- Sertkaya, A.A.; Ateş, A.; Altinişik, K.; Dinçer, K. Experimental and numerical analysis of one-dimensional heat transfer on open-cell aluminium foams. Gazi Univ. J. Sci. 2015, 28, 149–159. [Google Scholar]
- Lu, G.Y.; Su, B.Y.; Li, Z.Q.; Wang, Z.H.; Song, W.D.; Tang, H.P. Thermal properties of closed-cell aluminium foam with circular pores. Therm. Sci. 2014, 18, 1619–1624. [Google Scholar] [CrossRef]
- Kim, S.; Chung, H.J.; Rhee, K.Y. Application of image processing to predict compressive behaviour of aluminium foam. Arch. Metall. Mater. 2016, 61, 635–640. [Google Scholar] [CrossRef] [Green Version]
- Di Giorgio, P.; Iasiello, M.; Viglione, A.; Mameli, M.; Filippeschi, S.; Di Marco, P.; Andreozzi, A.; Bianco, N. Numerical analysis of a paraffin/metal foam composite for thermal Storage. In 34th UIT Heat Transfer Conference 2016, IOP Conference Series: Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 796, p. 012032. [Google Scholar] [CrossRef]
- Michailidis, N.; Stergioudi, F.; Omar, H.; Papadopoulos, D.; Tsipas, D.N. Experimental and FEM analysis of the material response of porous metals imposed to mechanical loading. Colloids Surf. A Physicochem. Eng. Asp. 2011, 382, 124–131. [Google Scholar] [CrossRef]
- Simančík, F.; Jerz, J.; Kováčik, J. Aluminium foam—A new light-weight structural material. Kov. Mater. 1997, 35, 265–277. [Google Scholar]
- Kim, C.W.; Cho, J.I.; Choi, S.W.; Kim, Y.C. The effect of alloying elements on thermal conductivity of aluminium alloys in high pressure die casting. Adv. Mater. Res. 2013, 813, 175–178. [Google Scholar] [CrossRef]
- Garcia-Moreno, F.; Banhart, J. Influence of gas pressure and blowing agent content on the formation of aluminium alloy foam. Adv. Eng. Mater. 2021. [Google Scholar] [CrossRef]
- Wikihow. Available online: http://www.wikihow.com/Calculate-Porosity (accessed on 4 December 2020).
- Rajak, D.K.; Kumaraswamidhas, L.A.; Das, S. Technical overview of aluminium alloy foam. Rev. Adv. Mater. Sci. 2017, 48, 68–86. [Google Scholar]
- Petit, C.; Meille, S.; Maire, E. Cellular solids studied by x-ray tomography and finite element modelling—A review. J. Mater. Res. 2013, 28, 2191–2201. [Google Scholar] [CrossRef]
- Mankovits, T.; Varga, T.A.; Manó, S.; Kocsis, I. Compressive response determination of closed-cell aluminium foam and linear-elastic finite element simulation of µCT-based directly reconstructed geometrical models. J. Mech. Eng. 2018, 64, 105–113. [Google Scholar]
- Sutygina, A.; Betke, U.; Scheffler, M. Open-Cell Aluminum Foams by the Sponge Replication Technique. Materials (Basel) 2019, 12, 3840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Solar Electricity Handbook. Available online: http://www.solarelectricityhandbook.com/solar-irradiance.html (accessed on 5 May 2020).
- Powell, R.L.; Childs, G.E. Aip-Handbook-Section4g Thermal Conductivity, pp 143–161. Available online: http://web.mit.edu/8.13/8.13c/references-fall/aip/aip-handbook-section4g.pdf (accessed on 5 May 2020).
- Cole, I.S.; Paterson, D.A. Mathematical models of the dependence of surface temperatures of exposed metal plates on environmental parameters. Corros. Eng. Sci. Technol. 2006, 41, 67–76. [Google Scholar] [CrossRef]
- Shimizu, T.; Matsuura, K.; Furue, H.; Matsuzak, K. Thermal conductivity of high porosity alumina refractory bricks made by slurry gelation and foaming method. J. Eur. Ceram. Soc. 2013, 33, 3429–3435. [Google Scholar] [CrossRef] [Green Version]
- Ordóñez-Miranda, J.; Alvarado-Gil, J.J.; Medina-Ezquivel, R. Generalized Bruggeman formula for the effective thermal conductivity of particulate composites with an interface layer. Int. J. Thermophys. 2010, 31, 975–986. [Google Scholar] [CrossRef]
- Lu, T.J.; Chen, C. Thermal transport and fire retardance properties of cellular aluminum alloys. Acta Mater. 1999, 47, 1469–1485. [Google Scholar] [CrossRef]








| Sample (Al 99.7%) | Porosity (%) | ||
|---|---|---|---|
| A1 | 0.7413 | 0.2745 | 72.5 |
| A2 | 1.62375 | 0.6014 | 39.9 |
| CT Slice Images | Plane | ||
|---|---|---|---|
| XY | YZ | XZ | |
| Sample A1-images | 1828 | 275 | 1846 |
| Resolution (mm) | 207 × 575 | 551 × 575 | 551 × 207 |
| Sample A2-images | 1846 | 257 | 1830 |
| Resolution (mm) | 169 × 553 | 526 × 553 | 526 × 169 |
| Literature Model | Original Equation |
|---|---|
| Series | |
| Parallel | |
| Ashby | |
| Series–Parallel | |
| Parallel–Series | |
| Maxwell | |
| Doherty | |
| Eucken | |
| Russell | |
| Bruggemann | |
| Misnar | |
| Effective Medium Theory |
| Sectional Model | Total Surface Area, AT (mm2) | Volume, Vs (mm3) | Porosity, (−) | Amount of Heat Transferred, Q(W) | |
|---|---|---|---|---|---|
| A1 × 11 | 746.279 | 281.363 | 0.4141 | 82.386 | 118.7901 |
| A1 × 12 | 829.780 | 223.401 | 0.5348 | 55.770 | 76.9624 |
| A1 × 13 | 911.695 | 179.458 | 0.6263 | 38.101 | 53.1681 |
| A1 × 14 | 983.216 | 144.769 | 0.6985 | 33.079 | 52.9591 |
| A1 × 21 | 735.981 | 284.441 | 0.4077 | 82.632 | 140.0198 |
| A1 × 22 | 605.721 | 304.306 | 0.3663 | 102.06 | 161.3040 |
| A1 × 23 | 895.662 | 158.188 | 0.6706 | 34.423 | 55.6175 |
| A1 × 24 | 707.148 | 234.158 | 0.5124 | 50.337 | 76.5937 |
| A1 × 31 | 806.345 | 198.646 | 0.5867 | 50.624 | 79.3599 |
| A1 × 32 | 859.840 | 228.164 | 0.5249 | 54.934 | 74.7945 |
| A1 × 33 | 863.694 | 255.886 | 0.4671 | 78.903 | 121.2035 |
| A1 × 34 | 797.629 | 249.219 | 0.4810 | 69.839 | 91.7156 |
| A1 × 41 | 816.204 | 198.064 | 0.5875 | 47.265 | 64.5991 |
| A1 × 42 | 777.008 | 227.724 | 0.5258 | 60.863 | 101.7067 |
| A1 × 43 | 765.947 | 181.521 | 0.6220 | 39.695 | 57.0227 |
| A1 × 44 | 762.215 | 212.093 | 0.5583 | 58.670 | 92.4256 |
| A2 × 11 | 981.644 | 356.867 | 0.2568 | 119.09 | 157.4956 |
| A2 × 12 | 711.010 | 393.237 | 0.1811 | 136.08 | 176.6529 |
| A2 × 13 | 785.134 | 411.559 | 0.1429 | 138.40 | 175.8803 |
| A2 × 14 | 683.321 | 434.460 | 0.0953 | 147.79 | 197.1705 |
| A2 × 21 | 833.184 | 390.388 | 0.1870 | 134.57 | 174.8835 |
| A2 × 22 | 1176.810 | 279.846 | 0.4172 | 82.143 | 127.7012 |
| A2 × 23 | 713.388 | 428.457 | 0.1078 | 139.33 | 186.1727 |
| A2 × 24 | 916.761 | 377.033 | 0.2148 | 114.07 | 154.0352 |
| A2 × 31 | 752.608 | 419.181 | 0.1271 | 142.89 | 185.4161 |
| A2 × 32 | 653.556 | 440.510 | 0.0827 | 157.01 | 205.3113 |
| A2 × 33 | 828.518 | 385.874 | 0.1964 | 124.79 | 164.6494 |
| A2 × 34 | 697.840 | 428.582 | 0.1075 | 148.94 | 190.5596 |
| A2 × 41 | 693.305 | 431.242 | 0.1020 | 145.28 | 194.7236 |
| A2 × 42 | 985.347 | 361.126 | 0.2480 | 107.52 | 143.0932 |
| A2 × 43 | 656.713 | 433.204 | 0.0979 | 149.36 | 199.7562 |
| A2 × 44 | 869.328 | 368.362 | 0.2329 | 119.83 | 162.7146 |
| Solid model | 388.08 | 480.2 | 0 | 181.11 | 225.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gopinathan, A.; Jerz, J.; Kováčik, J.; Dvorák, T. Investigation of the Relationship between Morphology and Thermal Conductivity of Powder Metallurgically Prepared Aluminium Foams. Materials 2021, 14, 3623. https://doi.org/10.3390/ma14133623
Gopinathan A, Jerz J, Kováčik J, Dvorák T. Investigation of the Relationship between Morphology and Thermal Conductivity of Powder Metallurgically Prepared Aluminium Foams. Materials. 2021; 14(13):3623. https://doi.org/10.3390/ma14133623
Chicago/Turabian StyleGopinathan, Arun, Jaroslav Jerz, Jaroslav Kováčik, and Tomáš Dvorák. 2021. "Investigation of the Relationship between Morphology and Thermal Conductivity of Powder Metallurgically Prepared Aluminium Foams" Materials 14, no. 13: 3623. https://doi.org/10.3390/ma14133623
APA StyleGopinathan, A., Jerz, J., Kováčik, J., & Dvorák, T. (2021). Investigation of the Relationship between Morphology and Thermal Conductivity of Powder Metallurgically Prepared Aluminium Foams. Materials, 14(13), 3623. https://doi.org/10.3390/ma14133623








