InSe/Te van der Waals Heterostructure as a High-Efficiency Solar Cell from Computational Screening
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Geometry and Stability
3.2. Electronic Properties
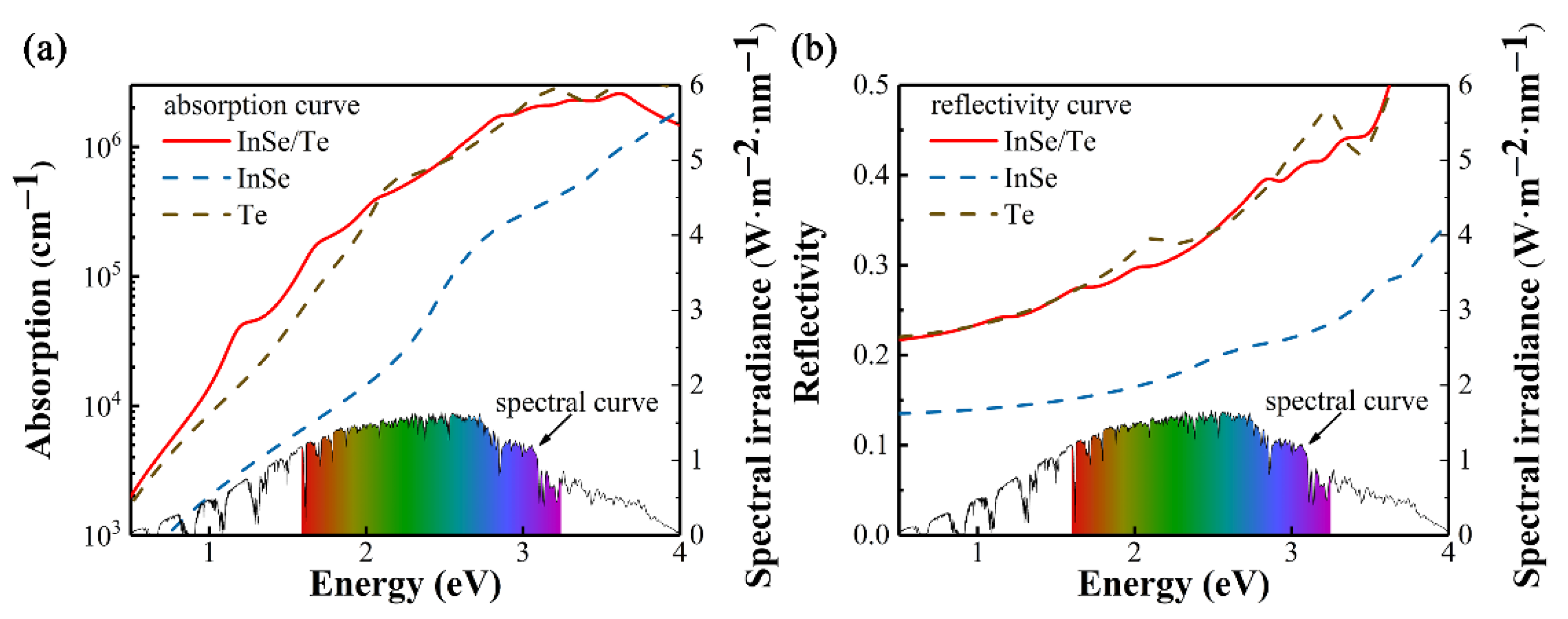
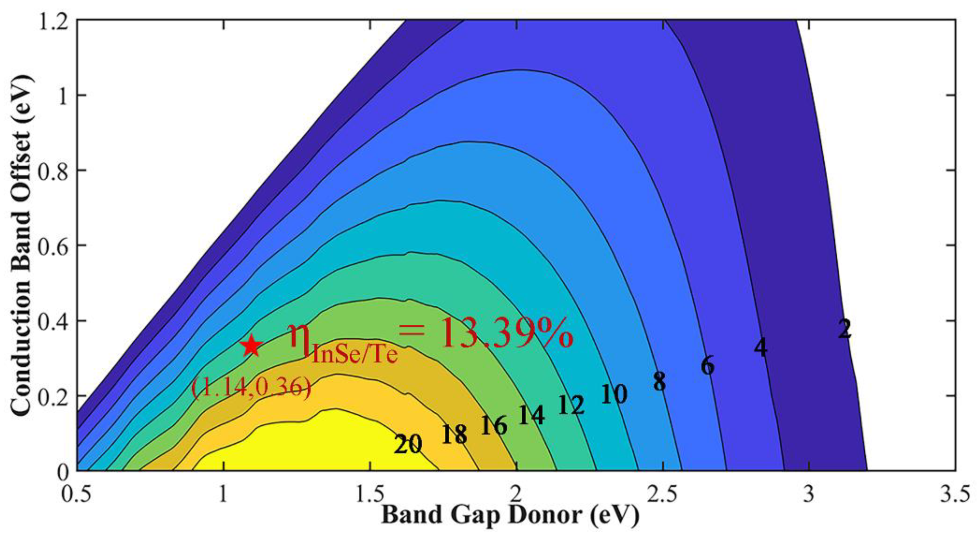
3.3. Solar Cell Applications
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef]
- Liu, Y.; Weiss, N.O.; Duan, X.; Cheng, H.-C.; Huang, Y.; Duan, X. Van der Waals heterostructures and devices. Nat. Rev. Mater. 2016. [Google Scholar] [CrossRef]
- Cheng, W.; Zhou, Z.; Pan, M.; Yang, H.; Xie, Y.; Wang, B.; Zhan, Q.; Li, R.-W. Stretchable spin valve with strain-engineered wrinkles grown on elastomeric polydimethylsiloxane. J. Phys. D Appl. Phys. 2019, 52. [Google Scholar] [CrossRef]
- Wang, X.; Xia, F. Van der Waals heterostructures: Stacked 2D materials shed light. Nat. Mater. 2015, 14, 264–265. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Zhang, S.; Wu, Z.; Wang, P.; Xu, Z.; Chen, H.; Yin, W.; Zhong, H.; Lin, S. 18.5% efficient graphene/GaAs van der Waals heterostructure solar cell. Nano Energy 2015, 16, 310–319. [Google Scholar] [CrossRef] [Green Version]
- Bernardi, M.; Palummo, M.; Grossman, J.C. Semiconducting Monolayer Materials as a Tunable Platform for Excitonic Solar Cells. ACS Nano 2012, 6, 10082–10089. [Google Scholar] [CrossRef] [Green Version]
- Eren, I.; Ozen, S.; Sozen, Y.; Yagmurcukardes, M.; Sahin, H. Vertical van der Waals Heterostructure of Single Layer InSe and SiGe. J. Phys. Chem. C 2019, 123, 31232–31237. [Google Scholar] [CrossRef]
- Withers, F.; Pozo-Zamudio, O.D.; Mishchenko, A.; Rooney, A.P.; Gholinia, A.; Watanabe, K.; Taniguchi, T.; Haigh, S.J.; Geim, A.K.; Tartakovskii, A.I. Light-emitting diodes by band-structure engineering in van der Waals heterostructures. Nat. Mater. 2015, 14, 301–306. [Google Scholar] [CrossRef] [PubMed]
- Koma, A. Van der Waals epitaxy—A new epitaxial growth method for a highly lattice-mismatched system. Thin Solid Films 1992, 216, 72–76. [Google Scholar] [CrossRef]
- Pierucci, D.; Henck, H.; Avila, J.; Balan, A.; Naylor, C.H.; Patriarche, G.; Dappe, Y.J.; Silly, M.G.; Sirotti, F.; Johnson, A.T.; et al. Band alignment and minigaps in monolayer MoS2-graphene van der Waals heterostructures. Nano Lett. 2016, 16, 4054–4061. [Google Scholar] [CrossRef]
- Jin, C.; Ma, E.Y.; Karni, O.; Regan, E.C.; Wang, F.; Heinz, T.F. Ultrafast dynamics in van der Waals heterostructures. Nat. Nanotechnol. 2018, 13, 994–1003. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhang, L.; Cao, T.; Jin, C.; Qiu, D.; Zhou, Q.; Zettl, A.; Yang, P.; Louie, S.G.; Wang, F. Evolution of interlayer coupling in twisted molybdenum disulfide bilayers. Nat. Commun. 2014, 5, 4966. [Google Scholar] [CrossRef]
- Duong, D.L.; Yun, S.J.; Lee, Y.H. Van der Waals Layered Materials: Opportunities and Challenges. ACS Nano 2017, 11, 11803–11830. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; Sa, B.; Zhou, J.; Sun, Z. MXenes: Promising donor and acceptor materials for high-efficiency heterostructure solar cells. Sustain. Energy Fuels 2021, 5, 135–143. [Google Scholar] [CrossRef]
- Chen, J.; He, X.; Sa, B.; Zhou, J.; Xu, C.; Wen, C.; Sun, Z. III–VI van der Waals heterostructures for sustainable energy related applications. Nanoscale 2019, 11, 6431–6444. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Das, S.; Pandey, D.; Thomas, J.; Roy, T. The role of graphene and other 2D materials in solar photovoltaics. Adv. Mater. 2019, 31, e1802722. [Google Scholar] [CrossRef] [Green Version]
- Fonash, S.J. Solar Cell Device Physics; Academic Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Tsai, M.L.; Li, M.Y.; Retamal, J.R.D.; Lam, K.T.; Lin, Y.C.; Suenaga, K.; Chen, L.J.; Liang, G.; Li, L.J.; He, J.H. Single atomically sharp lateral monolayer p-n heterojunction solar cells with extraordinarily high power conversion efficiency. Adv. Mater. 2017, 29. [Google Scholar] [CrossRef]
- Tan, C.; Cao, X.; Wu, X.J.; He, Q.; Yang, J.; Zhang, X.; Chen, J.; Zhao, W.; Han, S.; Nam, G.H.; et al. Recent advances in ultrathin two-dimensional nanomaterials. Chem. Rev. 2017, 117, 6225–6331. [Google Scholar] [CrossRef]
- Kuhn, A.; Chevy, A.; Chevalier, R. Crystal structure and interatomic distances in GaSe. Phys. Status Solidi 1975, 31, 469–475. [Google Scholar] [CrossRef]
- Gouskov, A.; Camassel, J.; Gouskov, L. Growth and characterization of III–VI layered crystals like GaSe, GaTe, InSe, GaSe1−xTex and GaxIn1−xSe. Prog. Cryst. Growth Charact. 1982, 5, 323–413. [Google Scholar] [CrossRef]
- Bandurin, D.A.; Tyurnina, A.V.; Yu, G.L.; Mishchenko, A.; Zolyomi, V.; Morozov, S.V.; Kumar, R.K.; Gorbachev, R.V.; Kudrynskyi, Z.R.; Pezzini, S.; et al. High electron mobility, quantum Hall effect and anomalous optical response in atomically thin InSe. Nat. Nanotechnol. 2017, 12, 223–227. [Google Scholar] [CrossRef]
- Mudd, G.W.; Svatek, S.A.; Hague, L.; Makarovsky, O.; Kudrynskyi, Z.R.; Mellor, C.J.; Beton, P.H.; Eaves, L.; Novoselov, K.S.; Kovalyuk, Z.D.; et al. High broad-band photoresponsivity of mechanically formed InSe-graphene van der Waals heterostructures. Adv. Mater. 2015, 27, 3760–3766. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Wu, J.; Jin, K.; Ding, H.; Li, T.; Wu, C.; Pan, N.; Wang, X. Highly polarized and fast photoresponse of black phosphorus-InSe vertical p-n heterojunctions. Adv. Funct. Mater. 2018, 28. [Google Scholar] [CrossRef]
- He, C.; Zhang, J.H.; Zhang, W.X.; Li, T.T. Type-II InSe/g-C3N4 heterostructure as a high-efficiency oxygen evolution reaction catalyst for photoelectrochemical water splitting. J. Phys. Chem. Lett. 2019, 10, 3122–3128. [Google Scholar] [CrossRef]
- Yan, F.; Zhao, L.; Patane, A.; Hu, P.; Wei, X.; Luo, W.; Zhang, D.; Lv, Q.; Feng, Q.; Shen, C.; et al. Fast, multicolor photodetection with graphene-contacted p-GaSe/n-InSe van der Waals heterostructures. Nanotechnology 2017, 28, 27LT01. [Google Scholar] [CrossRef] [Green Version]
- Apte, A.; Bianco, E.; Krishnamoorthy, A.; Yazdi, S.; Rao, R.; Glavin, N.; Kumazoe, H.; Varshney, V.; Roy, A.; Shimojo, F.; et al. Polytypism in ultrathin tellurium. 2D Mater. 2018, 6. [Google Scholar] [CrossRef] [Green Version]
- Xing, C.; Xie, Z.; Liang, Z.; Liang, W.; Fan, T.; Ponraj, J.S.; Dhanabalan, S.C.; Fan, D.; Zhang, H. 2D nonlayered selenium nanosheets: Facile synthesis, photoluminescence, and ultrafast photonics. Adv. Opt. Mater. 2017, 5. [Google Scholar] [CrossRef]
- Singh, J.; Jamdagni, P.; Jakhar, M.; Kumar, A. Stability, electronic and mechanical properties of chalcogen (Se and Te) monolayers. Phys. Chem. Chem. Phys. 2020, 22, 5749–5755. [Google Scholar] [CrossRef]
- Peng, Q.; Guo, Z.; Sa, B.; Zhou, J.; Sun, Z. New gallium chalcogenides/arsenene van der Waals heterostructures promising for photocatalytic water splitting. Int. J. Hydrogen Energy 2018, 43, 15995–16004. [Google Scholar] [CrossRef]
- Kresse, G.G.; Furthmüller, J.J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B Condens. Matter 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B Condens. Matter 1994, 49, 14251–14269. [Google Scholar] [CrossRef] [PubMed]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, G.; Peng, L.; Li, K.; Zhu, L.; Zhou, J.; Miao, N.; Sun, Z. ALKEMIE: An intelligent computational platform for accelerating materials discovery and design. Comput. Mater. Sci. 2021, 186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B Condens. Matter 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1998, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Sa, B.; Zhan, H.; Sun, Z. Electric field-modulated data storage in bilayer InSe. J. Mater. Chem. C 2017, 5, 12228–12234. [Google Scholar] [CrossRef]
- Klimes, J.; Bowler, D.R.; Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 2010, 22, 022201. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Peng, Q.; Xiong, R.; Sa, B.; Zhou, J.; Wen, C.; Wu, B.; Anpo, M.; Sun, Z. Computational mining of photocatalysts for water splitting hydrogen production: Two-dimensional InSe-family monolayers. Catal. Sci. Technol. 2017, 7, 2744–2752. [Google Scholar] [CrossRef]
- Demirci, S.; Avazlı, N.; Durgun, E.; Cahangirov, S. Structural and electronic properties of monolayer group III monochalcogenides. Phys. Rev. B 2017, 95. [Google Scholar] [CrossRef]
- Zhuang, H.L.; Hennig, R.G. Single-layer group-III monochalcogenide photocatalysts for water splitting. Chem. Mater. 2013, 25, 3232–3238. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, Z.; Sa, B.; Wu, B.; Sun, Z. Blue phosphorene/MS2 (M = Nb, Ta) heterostructures as promising flexible anodes for lithium-Ion batteries. ACS Appl. Mater. Interfaces 2016, 8, 21. [Google Scholar] [CrossRef]
- Yang, X.; Sa, B.; Lin, P.; Xu, C.; Zhu, Q.; Zhan, H.; Sun, Z. Tunable contacts in graphene/InSe van der Waals heterostructures. J. Phys. Chem. C 2020, 124, 23699–23706. [Google Scholar] [CrossRef]
- Chiu, M.H.; Zhang, C.; Shiu, H.W.; Chuu, C.P.; Chen, C.H.; Chang, C.Y.; Chen, C.H.; Chou, M.Y.; Shih, C.K.; Li, L.J. Determination of band alignment in the single-layer MoS2/WSe2 heterojunction. Nat. Commun. 2015, 6, 7666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liao, J.; Sa, B.; Zhou, J.; Ahuja, R.; Sun, Z. Design of high-efficiency visible-light photocatalysts for water splitting: MoS2/AlN(GaN) heterostructures. J. Phys. Chem. C 2014, 118, 17594–17599. [Google Scholar] [CrossRef]
- Bjoerkman, T.; Gulans, A.; Krasheninnikov, A.V.; Nieminen, R.M. van der Waals bonding in layered compounds from advanced density-functional first-principles calculations. Phys. Rev. Lett. 2012, 108, 235502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scharber, M.C.; Mühlbacher, D.; Koppe, M.; Denk, P.; Waldauf, C.; Heeger, A.J.; Brabec, C.J. Design rules for donors in bulk-heterojunction solar cells—Towards 10 % energy-conversion efficiency. Adv. Mater. 2006, 18, 789–794. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, Z.; Sa, B.; Wu, B.; Sun, Z. Electronic structures and enhanced optical properties of blue phosphorene/transition metal dichalcogenides van der Waals heterostructures. Sci. Rep. 2016, 6, 31994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chaurasiya, R.; Gupta, G.K.; Dixit, A. Ultrathin Janus WSSe buffer layer for W(S/Se)2 absorber based solar cells: A hybrid, DFT and macroscopic, simulation studies. Sol. Energy Mater. Sol. Cells 2019, 201. [Google Scholar] [CrossRef]
- Chaurasiya, R.; Gupta, G.K.; Dixit, A. Heterostructure AZO/WSeTe/W(S/Se)2 as an efficient single junction solar cell with ultrathin janus WSeTe buffer layer. J. Phys. Chem. C 2021, 125, 4355–4362. [Google Scholar] [CrossRef]
- A. G173-03, A.I. West Conshohocken, PA. 2012. Available online: www.astm.org (accessed on 17 May 2021).
- Dai, J.; Zeng, X.C. Bilayer phosphorene: Effect of stacking order on bandgap and its potential applications in thin-film solar cells. J. Phys. Chem. Lett. 2014, 5, 1289–1293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qin, F.; Gao, F.; Dai, M.; Hu, Y.; Yu, M.; Wang, L.; Feng, W.; Li, B.; Hu, P. Multilayer InSe-Te van der Waals Heterostructures with an Ultrahigh Rectification Ratio and Ultrasensitive Photoresponse. ACS Appl. Mater. Interfaces 2020, 12, 37313–37319. [Google Scholar] [CrossRef] [PubMed]

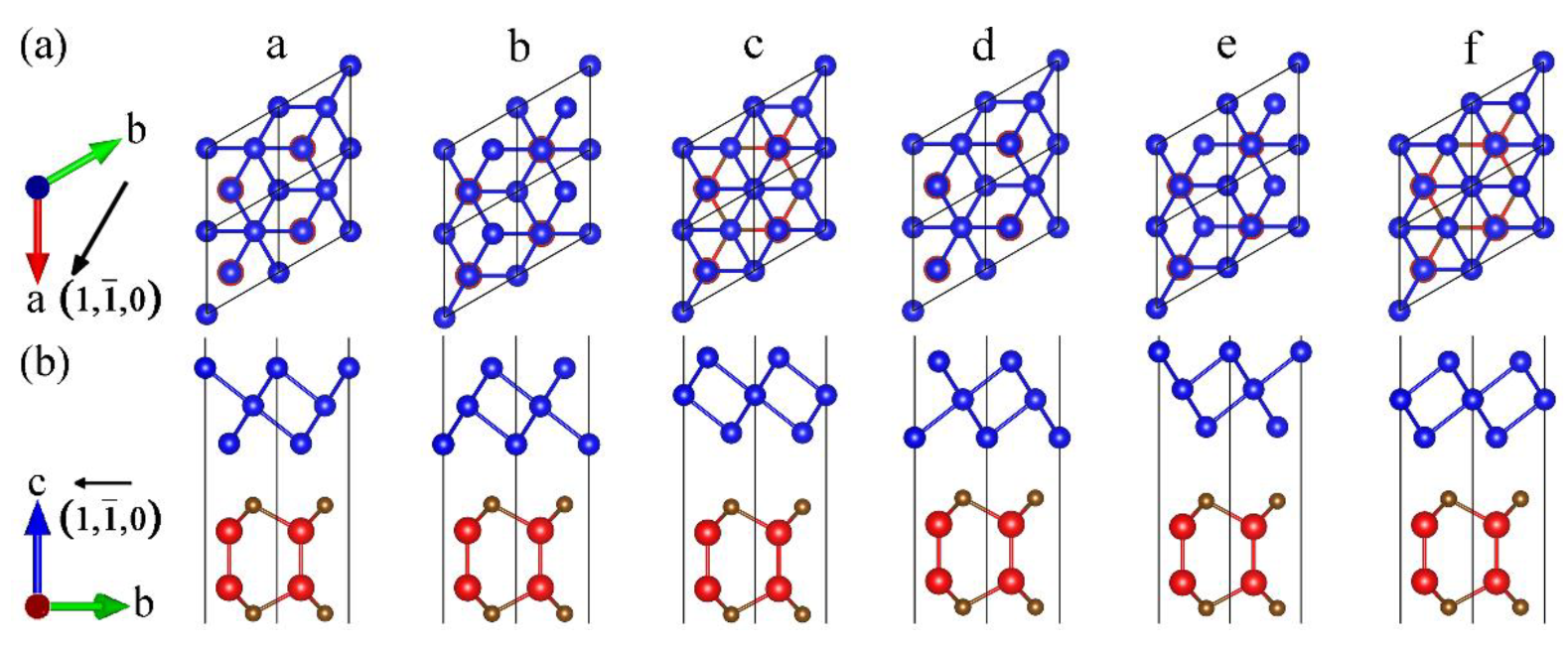
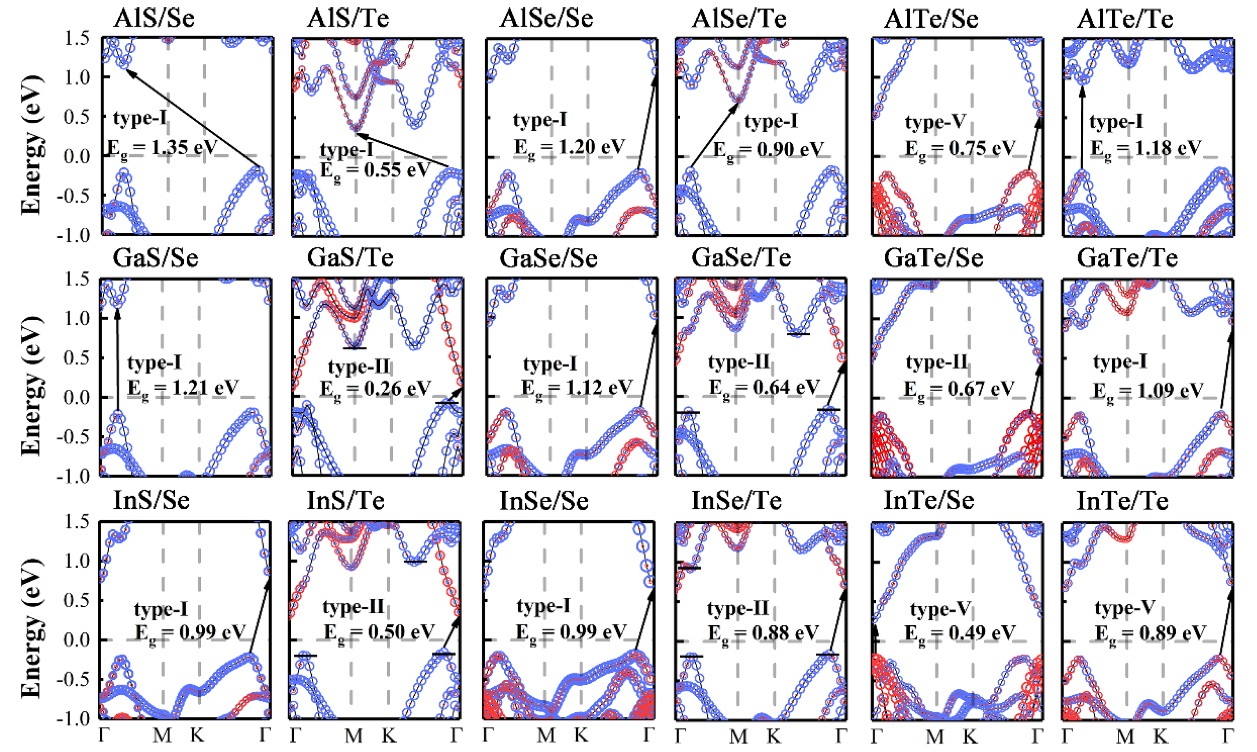

| System | Configuration | a | Ef | Eb | Type | ||
|---|---|---|---|---|---|---|---|
| AlS-Se | d | 3.627 | −174.0 | 20.7 | 1.00 | 1.35 | Ι |
| AlS-Te | d | 3.822 | 492.3 | 20.4 | 0.15 | 0.55 | Ι |
| AlSe-Se | d | 3.744 | −246.9 | 20.9 | 0.76 | 1.20 | Ι |
| AlSe-Te | d | 3.935 | 58.5 | 20.4 | 0.52 | 0.90 | Ι |
| AlTe-Se | b | 3.965 | −67.9 | 24.1 | 0.43 | 0.75 | V |
| AlTe-Te | d | 4.129 | −280.3 | 20.5 | 0.83 | 1.18 | Ι |
| GaS-Se | d | 3.660 | −213.7 | 21.2 | 0.76 | 1.21 | Ι |
| GaS-Te | d | 3.863 | 328.0 | 22.4 | 0.00 | 0.26 | II |
| GaSe-Se | d | 3.764 | −250.0 | 21.5 | 0.60 | 1.12 | Ι |
| GaSe-Te | d | 3.963 | −24.3 | 21.8 | 0.20 | 0.64 | II |
| GaTe-Se | b | 3.980 | −74.8 | 25.6 | 0.36 | 0.67 | II |
| GaTe-Te | d | 4.141 | −300.8 | 21.4 | 0.58 | 1.09 | Ι |
| InS-Se | b | 3.829 | −206.7 | 21.4 | 0.60 | 0.99 | Ι |
| InS-Te | d | 4.024 | −164.8 | 21.7 | 0.16 | 0.50 | II |
| InSe-Se | b | 3.921 | −107.9 | 22.7 | 0.44 | 0.99 | Ι |
| InSe-Te | d | 4.112 | −278.7 | 21.5 | 0.39 | 0.88 | II |
| InTe-Se | b | 4.124 | 178.0 | 29.0 | 0.20 | 0.49 | V |
| InTe-Te | b | 4.290 | −309.5 | 21.7 | 0.44 | 0.89 | V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Li, R.; Xiong, R.; Zhang, Y.; Xu, C.; Wen, C.; Sa, B. InSe/Te van der Waals Heterostructure as a High-Efficiency Solar Cell from Computational Screening. Materials 2021, 14, 3768. https://doi.org/10.3390/ma14143768
Ma Z, Li R, Xiong R, Zhang Y, Xu C, Wen C, Sa B. InSe/Te van der Waals Heterostructure as a High-Efficiency Solar Cell from Computational Screening. Materials. 2021; 14(14):3768. https://doi.org/10.3390/ma14143768
Chicago/Turabian StyleMa, Zechen, Ruifeng Li, Rui Xiong, Yinggan Zhang, Chao Xu, Cuilian Wen, and Baisheng Sa. 2021. "InSe/Te van der Waals Heterostructure as a High-Efficiency Solar Cell from Computational Screening" Materials 14, no. 14: 3768. https://doi.org/10.3390/ma14143768
APA StyleMa, Z., Li, R., Xiong, R., Zhang, Y., Xu, C., Wen, C., & Sa, B. (2021). InSe/Te van der Waals Heterostructure as a High-Efficiency Solar Cell from Computational Screening. Materials, 14(14), 3768. https://doi.org/10.3390/ma14143768






