Low-Computational-Cost Technique for Modeling Macro Fiber Composite Piezoelectric Actuators Using Finite Element Method
Abstract
:1. Introduction
2. Mechanical and Electric Properties of MFC
2.1. MFC Homogenization Model
2.2. Nonlinearity Effect and Free Strain
3. Methodology of the Proposed Technique for Modeling MFC
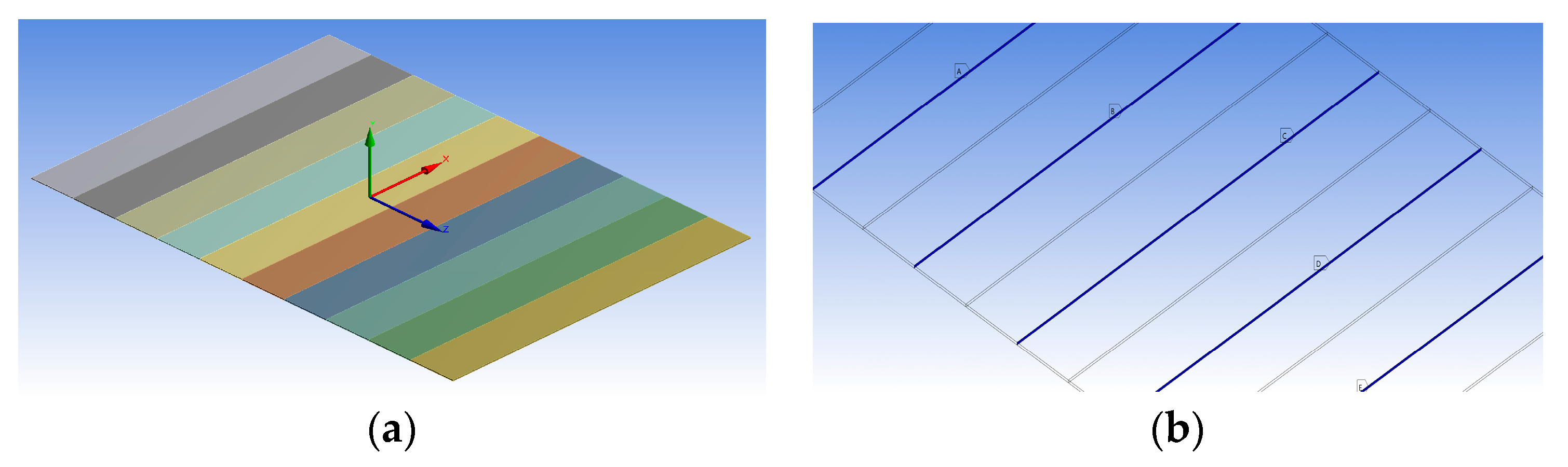
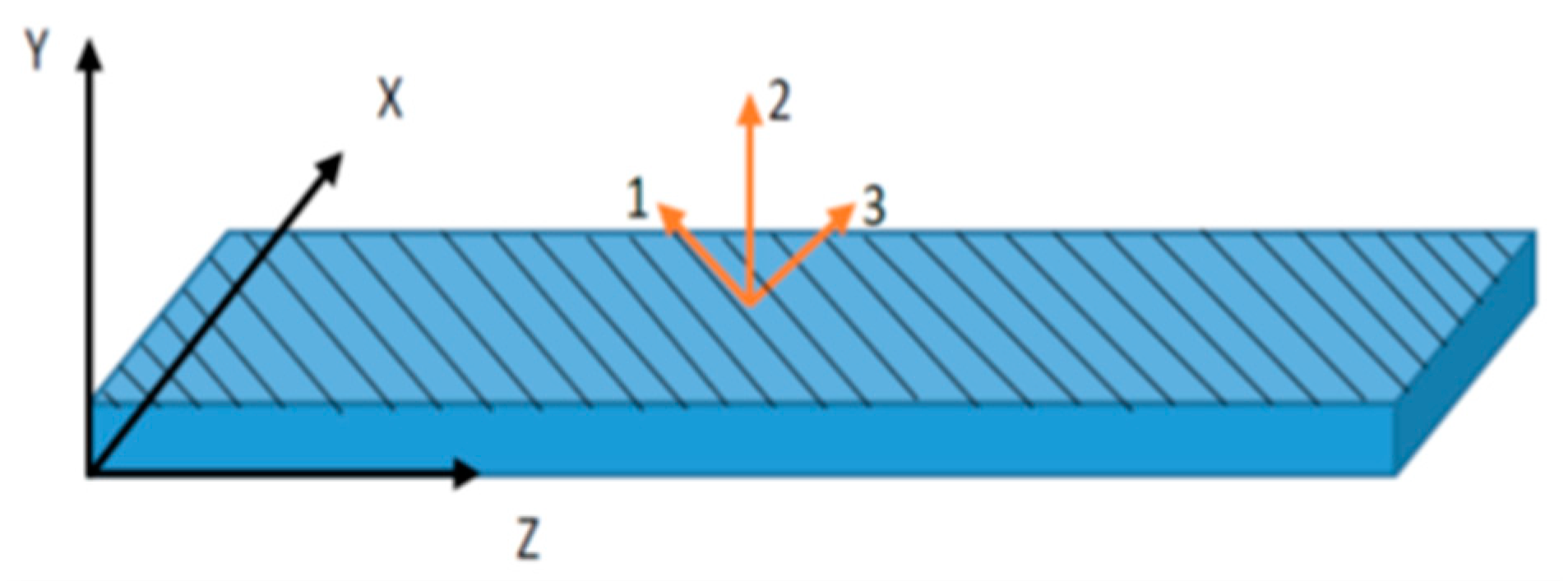
3.1. Description of the FE Model of MFC
3.2. Hypothesis of the New Technique for Modeling MFC
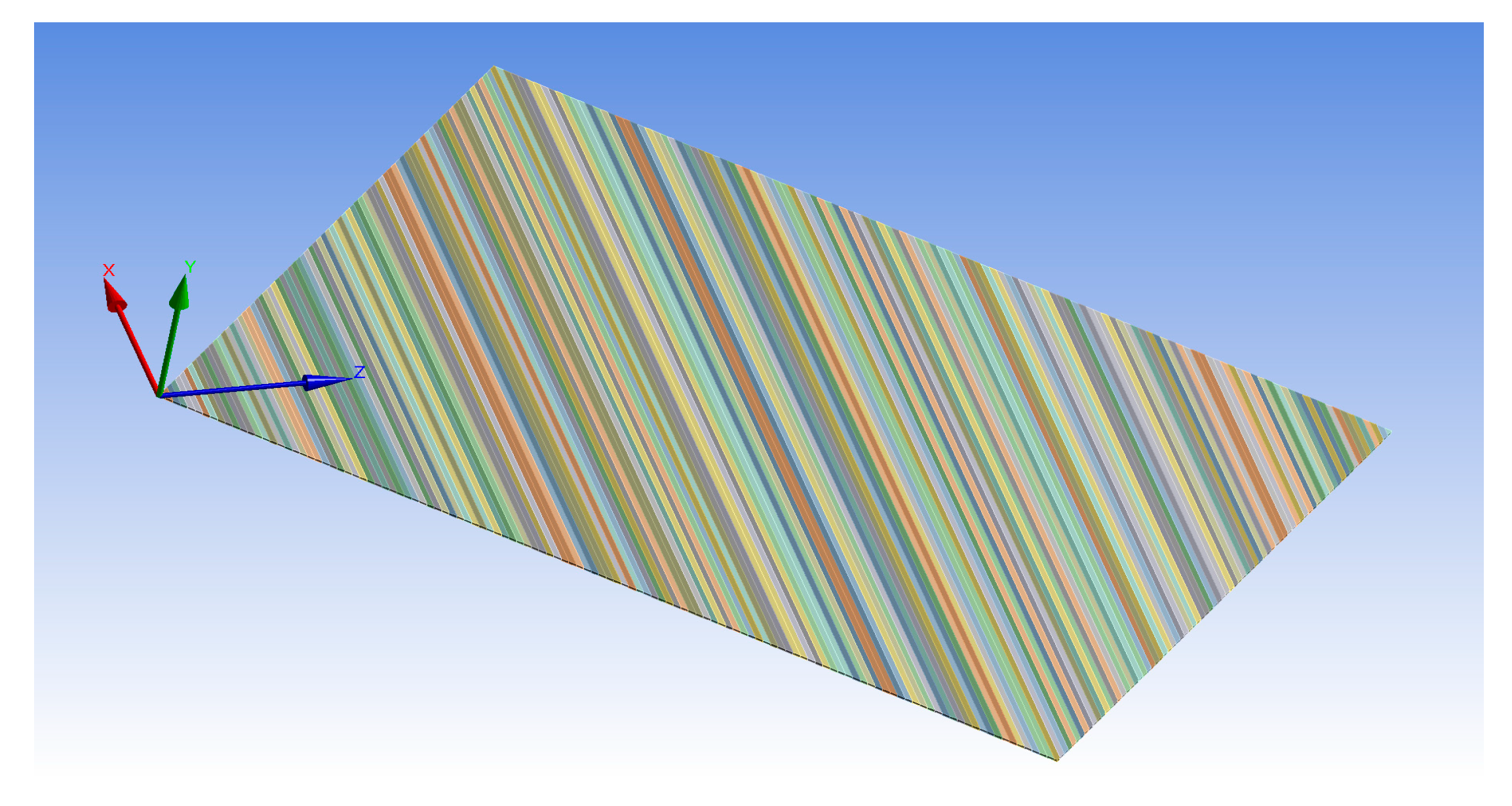
3.3. Modeling of MFC with 45° Fiber Orientation
4. Simulation Validation of the Proposed Technique
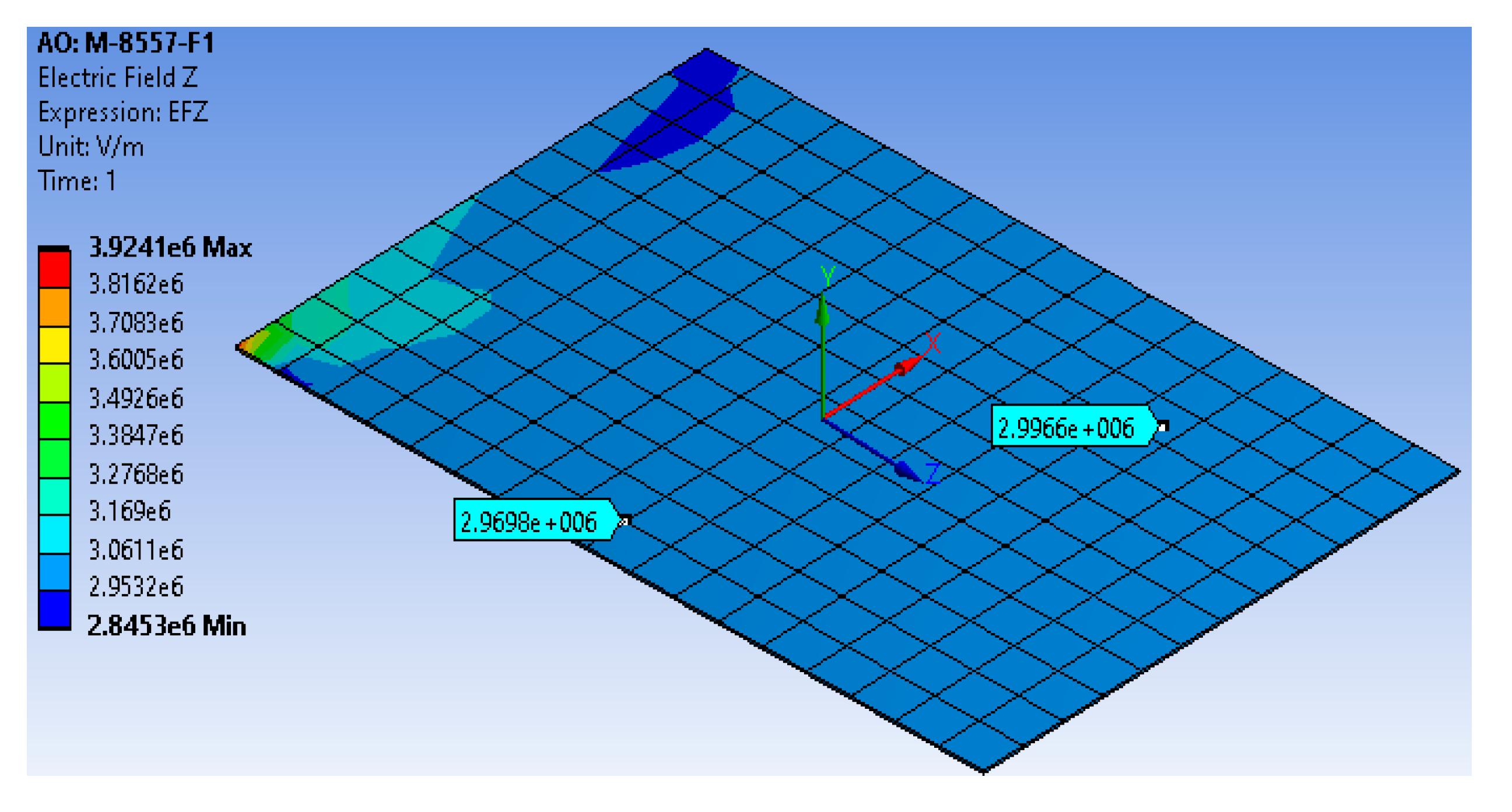
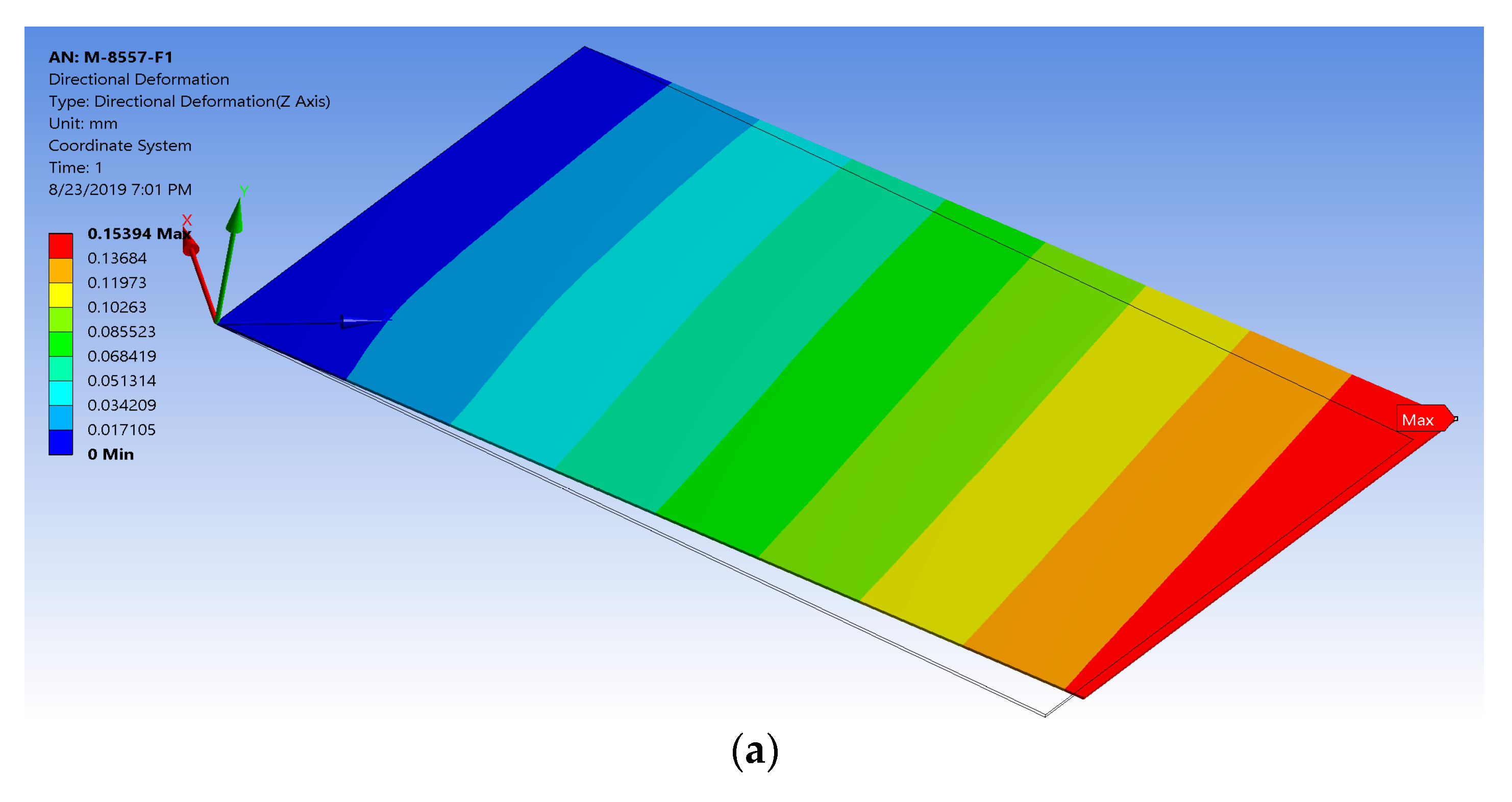
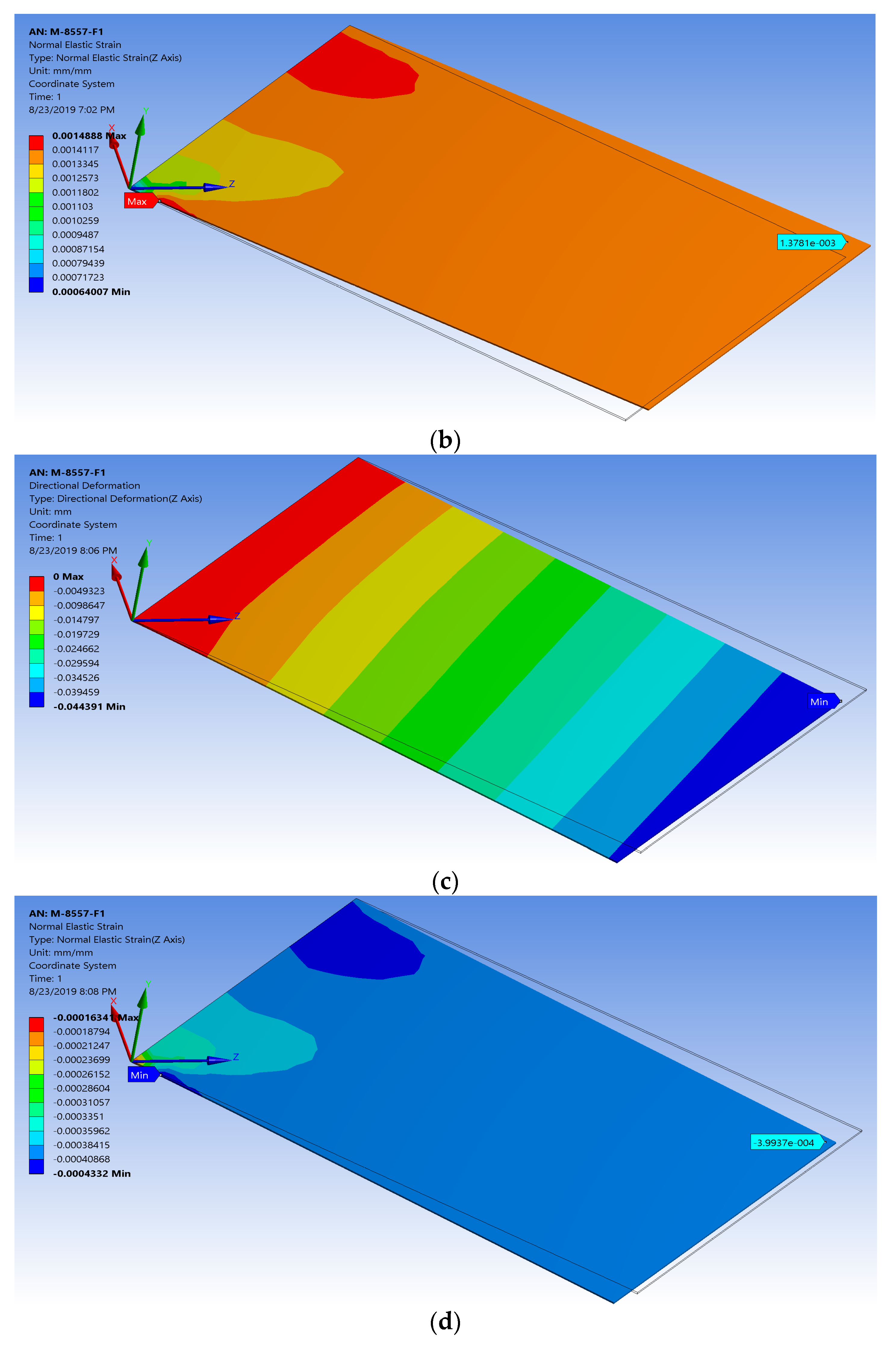
4.1. Validation of the Proposed Technique with the Detailed FE Model of MFC with 45° Fiber Orientation
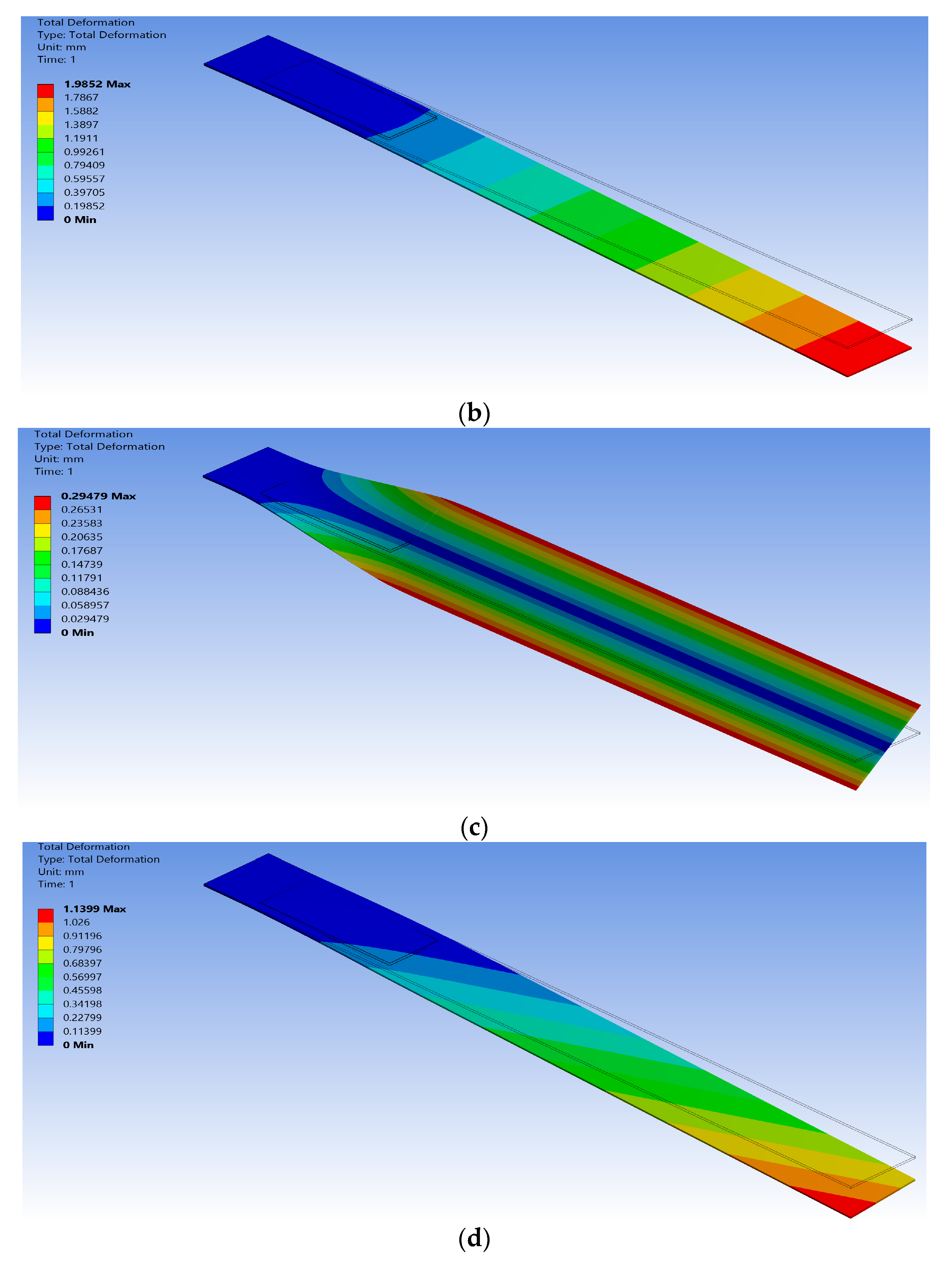
4.2. Validation of the Proposed Technique for Bimorph Wing
5. Experimental Verification of the Proposed Technique
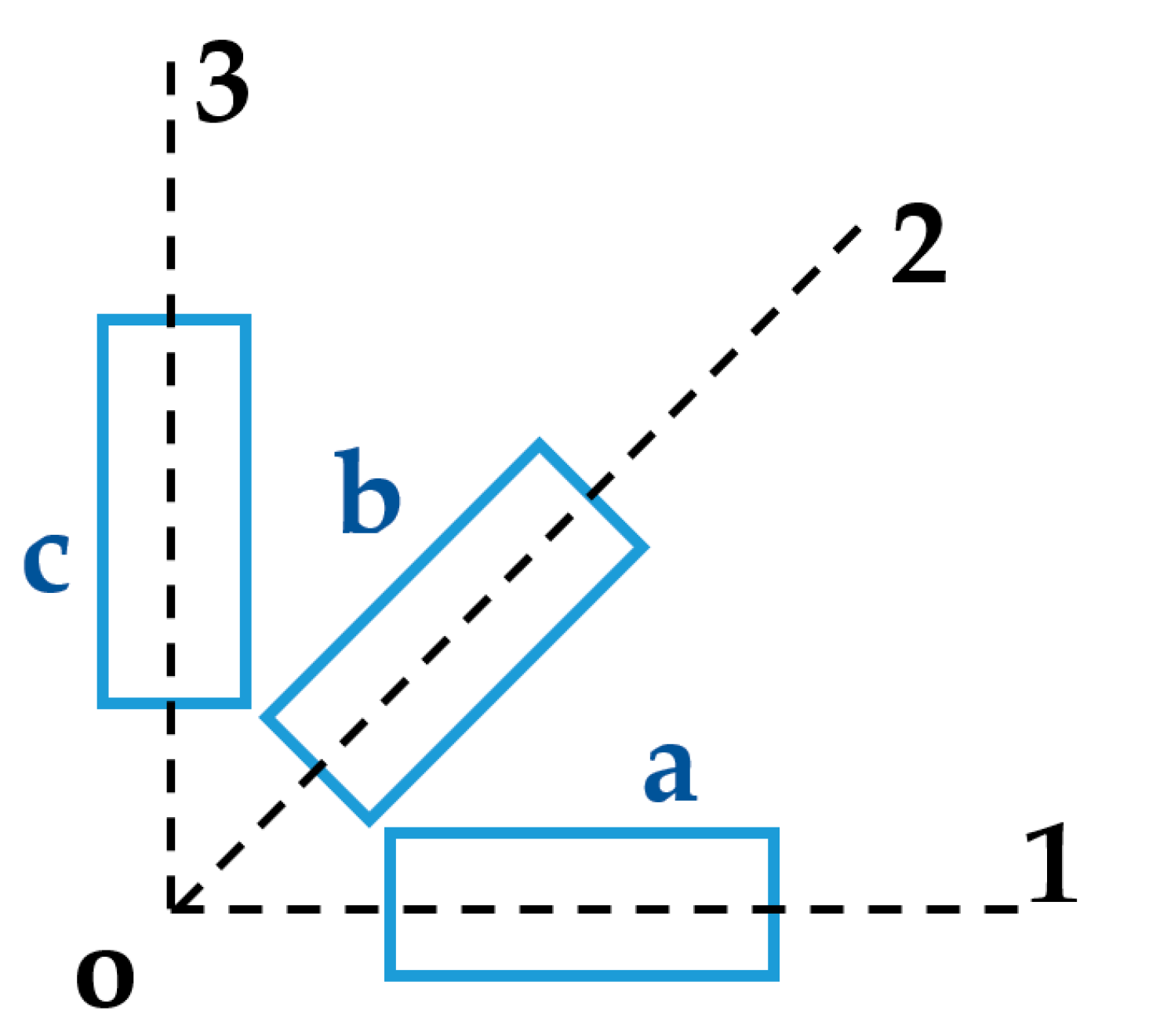
5.1. Mathematical Equations of Rectangular Rosette
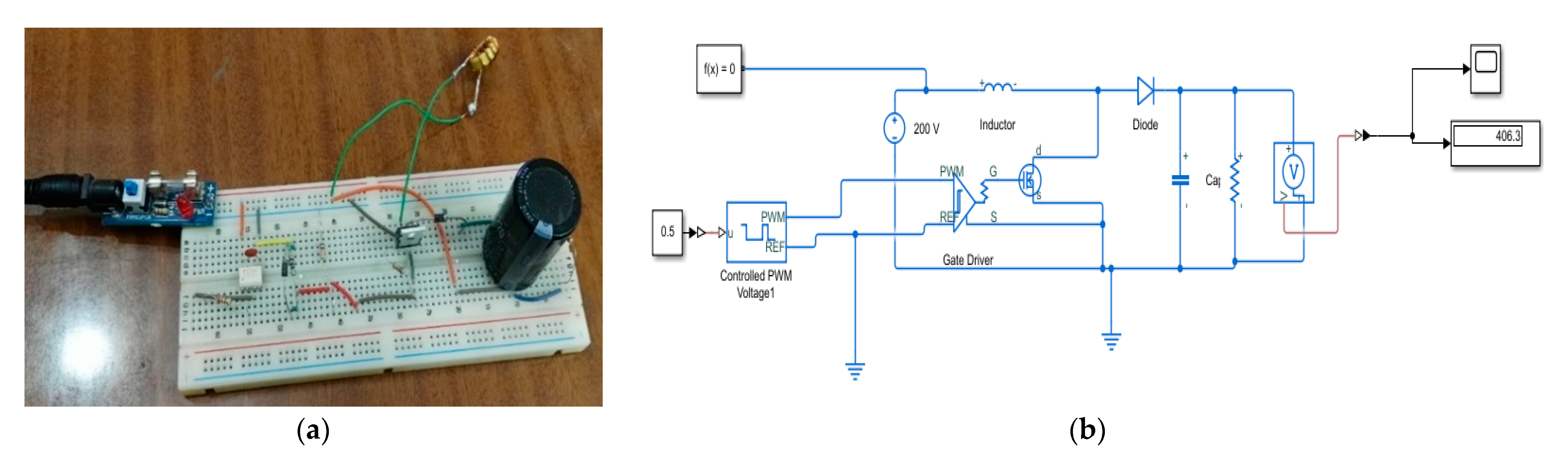
5.2. Power Amplifier and Boost Converter Circuit
5.3. Experimental Procedures
- Firstly, the FE model was verified with applied displacements at the tip of the cantilever beam without activating MFC, as illustrated in Figure 12. The measurements were acquired from the rosette strain gauges and compared with their equivalent strains in the FE simulation.
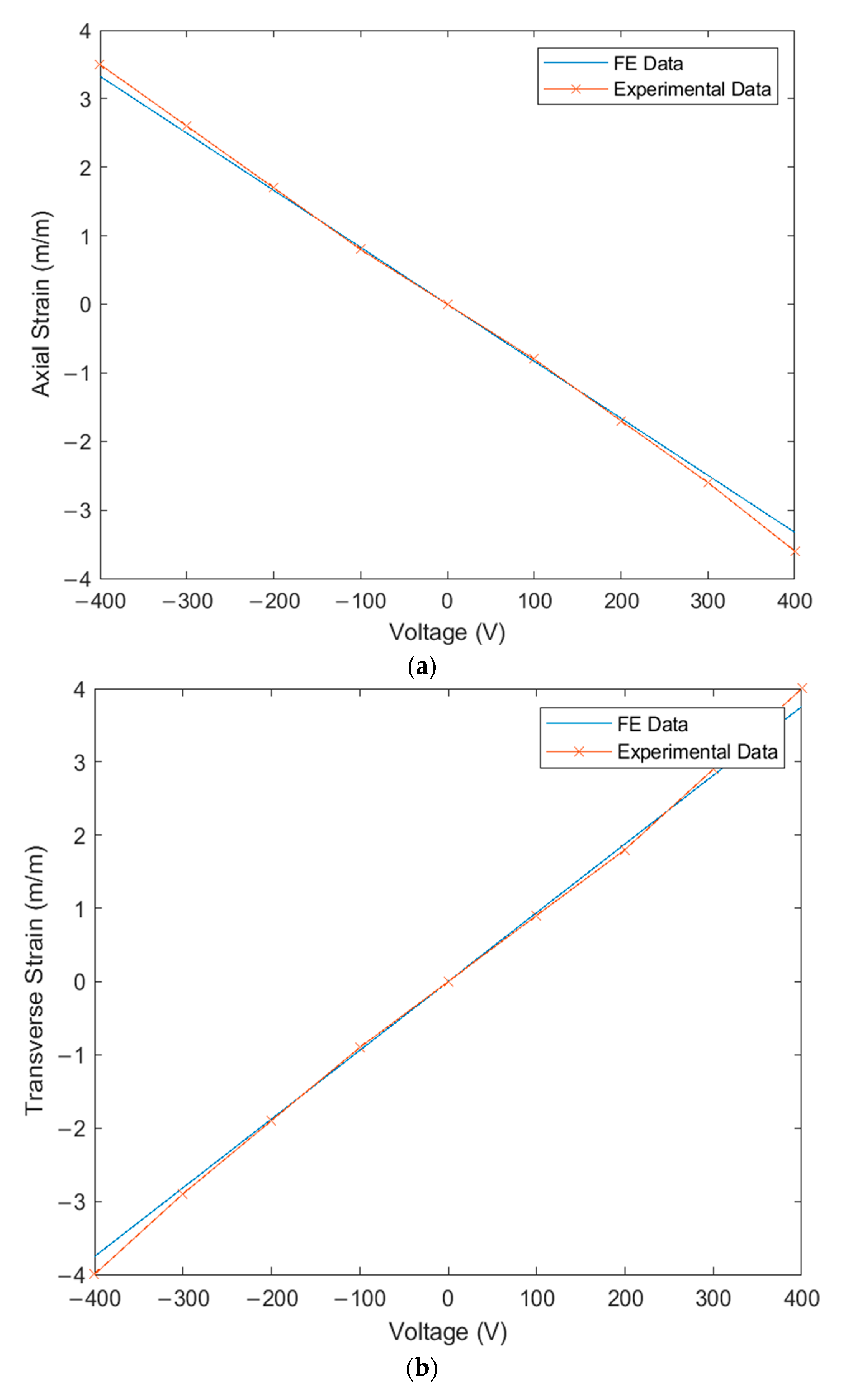
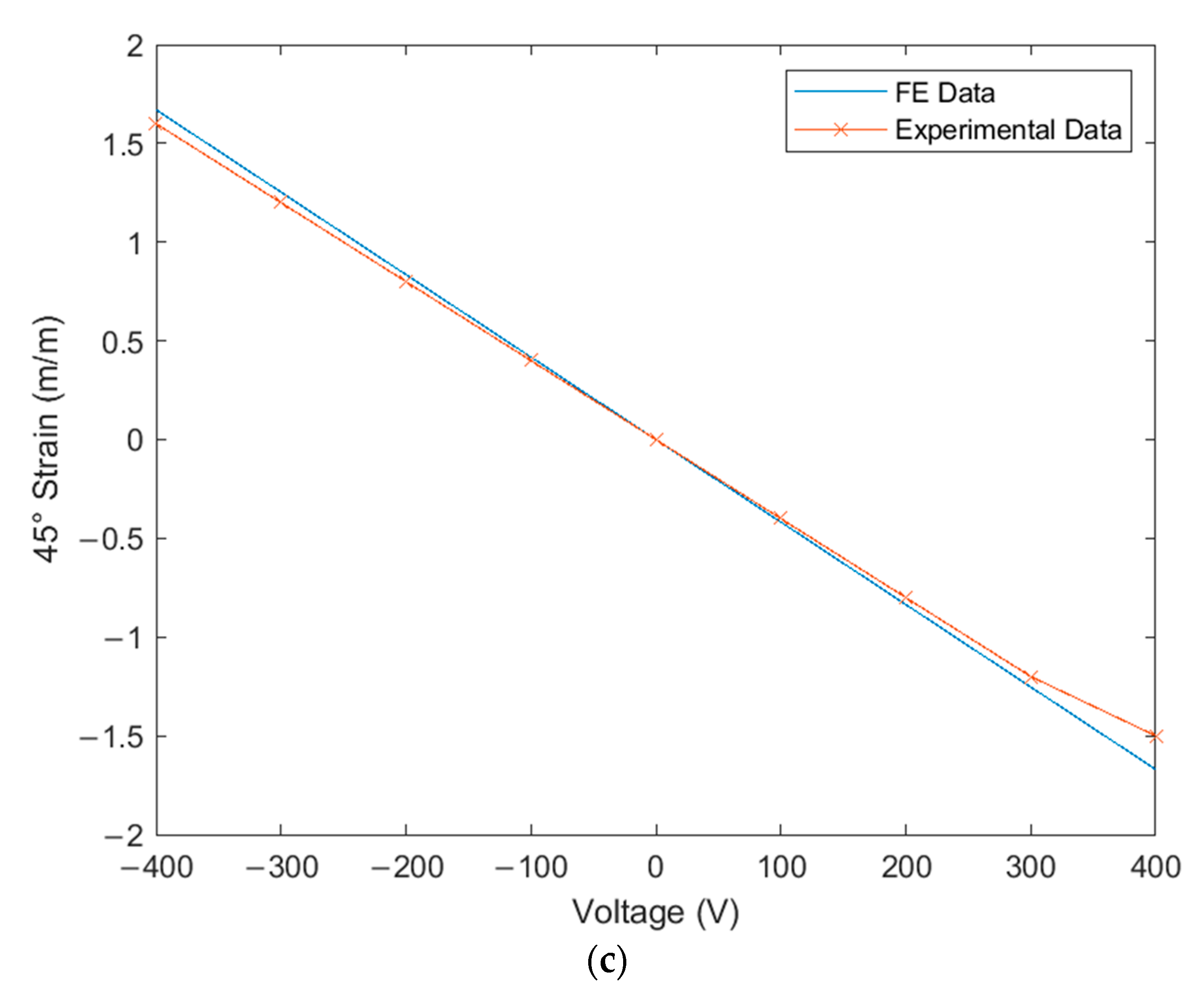
- Secondly, the FE simulation was verified with the physical MFC placed on the beam, as illustrated in Figure 13. The MFC actuator was statically energized from 0 to 400 V with a step of 100 V. The measurements were acquired from the three strain gauges and compared with their equivalent strains in the FE simulation.
- It is worth mentioning that each reading needed some time to settle for every measurement. Moreover, there was a non-zero initial offset in the measurements which was compensated for by the readings. This offset was produced from the HX711 circuit, bridge circuit, and the extra weight on the beam due to wires. Additionally, the offset may vary for each set of measurements, whereas, if the wires are slightly moved, the readings will also change. Thus, the non-zero offset was checked frequently for every set of measurements.
6. Experimental Results and Discussion
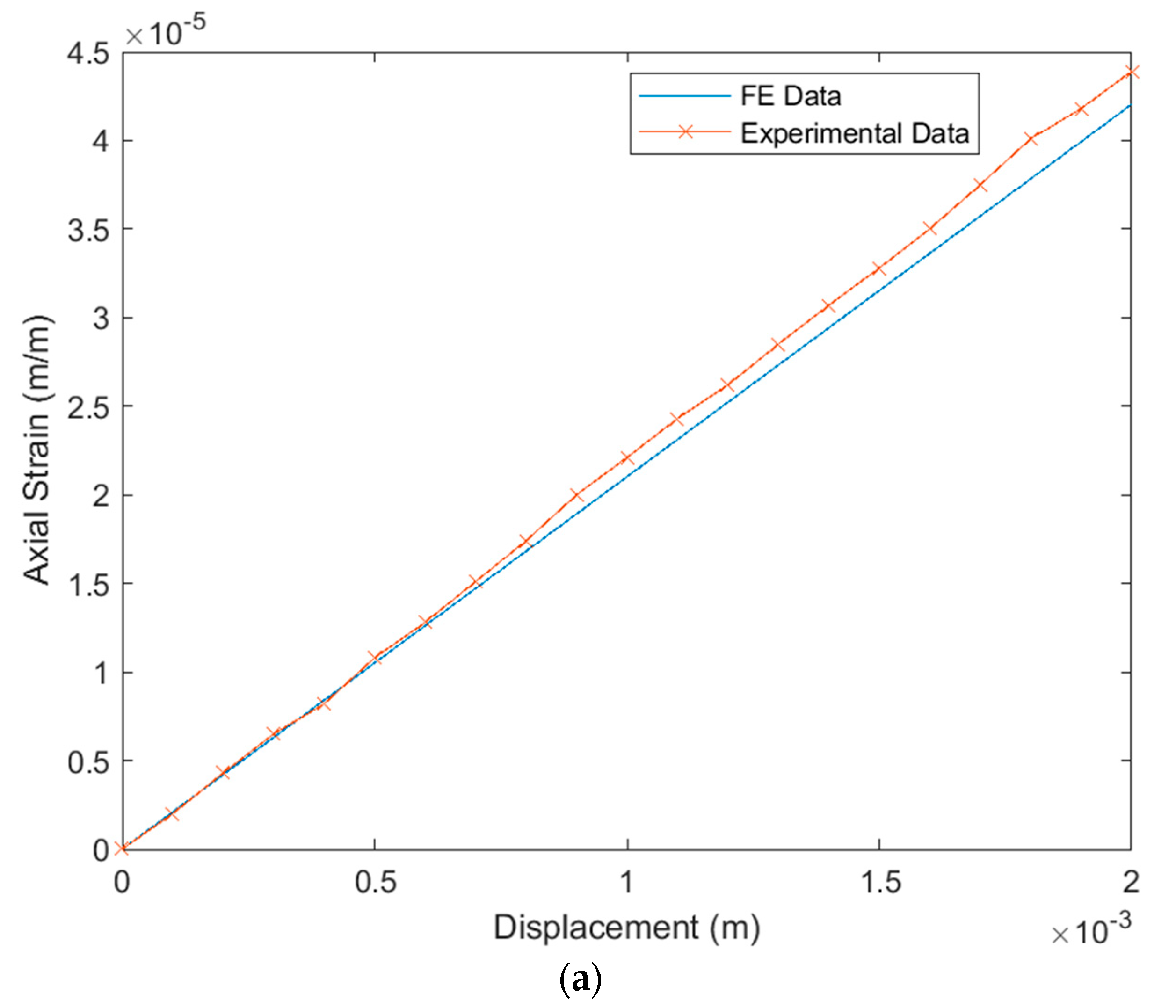
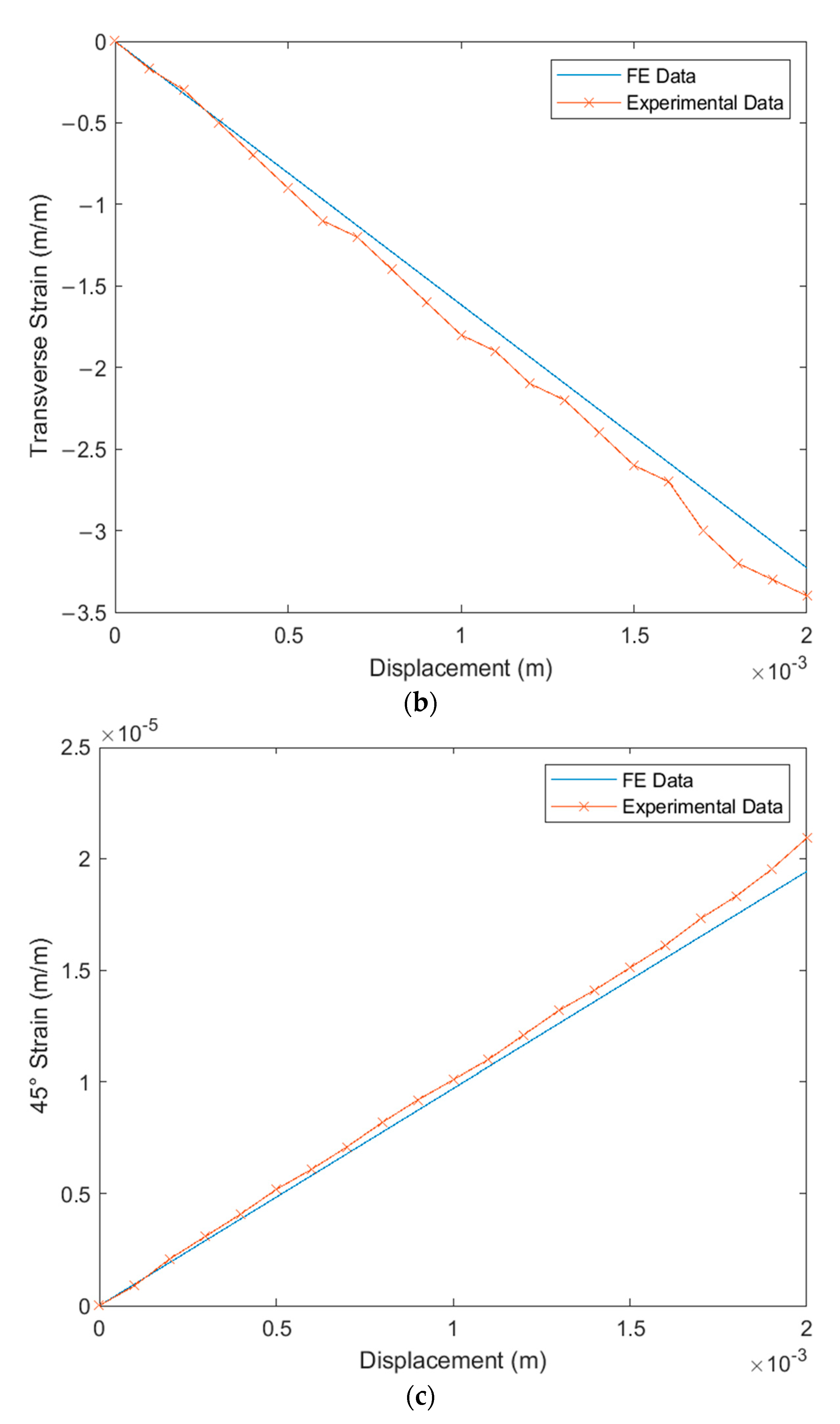
6.1. Verification of the FE Simulation under Tip Displacements
6.2. Verification of FE Simulation under MFC Actuation
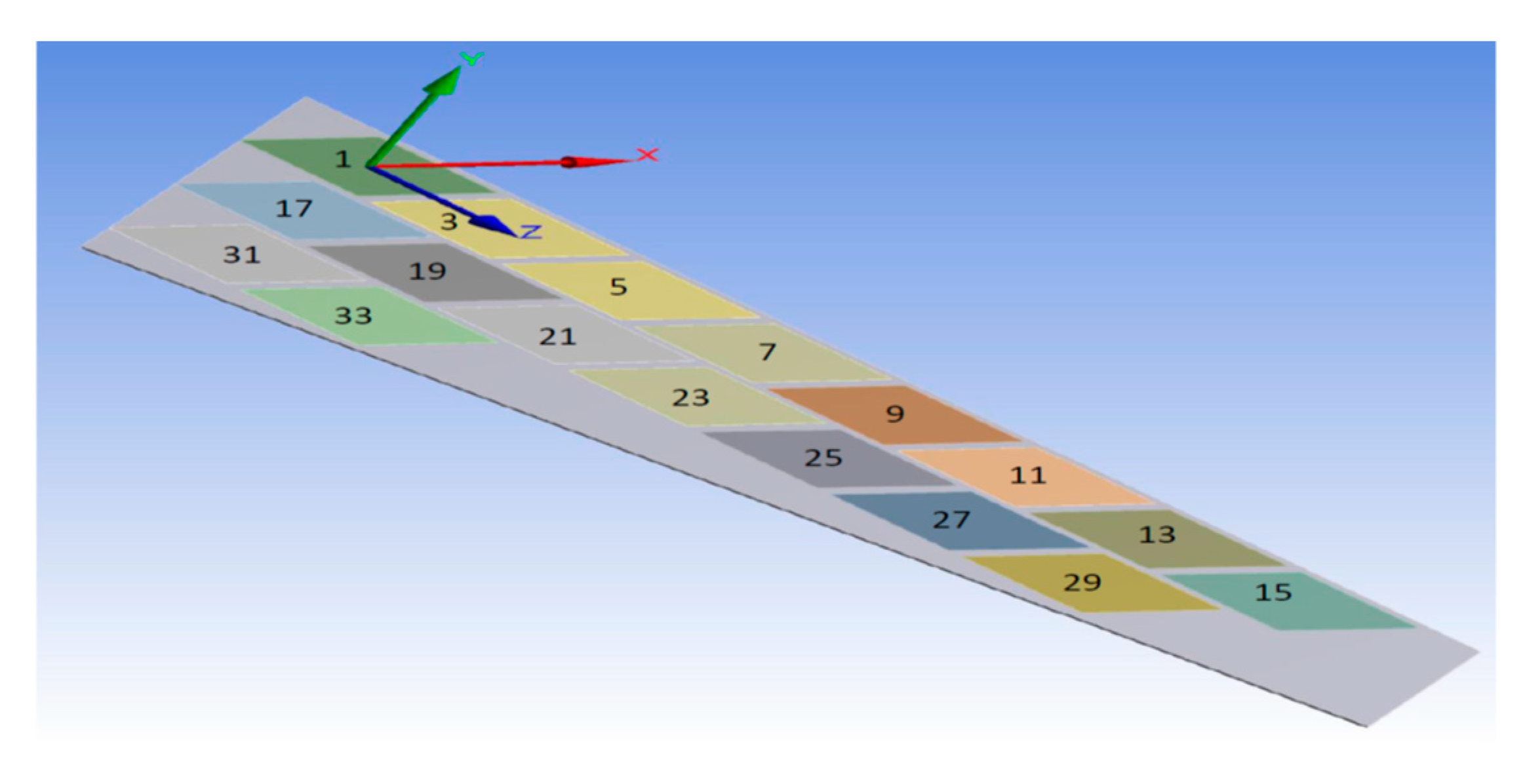
7. Modeling of Morphing Wing Actuated by Multiple MFCs Using the Newly Proposed Technique
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sodano, H.; Park, G.; Inman, D. An Investigation into the Performance of Macro-Fiber Composites for Sensing and Structural Vibration Applications. Mech. Syst. Signal Process. 2004, 18, 683–697. [Google Scholar] [CrossRef]
- Williams, R.B.; Grimsley, B.; Inman, D.; Wilkie, W. Manufacturing and Mechanics-Based Characterization of Macro Fiber Composite Actuators. In Proceedings of the ASME 2020 International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 17–22 November 2002; pp. 79–89. [Google Scholar]
- Wilkie, W.; Inman, D.; High, J.; Williams, R.B. Recent Developments in NASA Piezocomposite Actuator Technology. In Proceedings of the 9th International Conference on New Actuators Bremen, Bremen, Germany, 14–16 June 2004. [Google Scholar]
- ©Smart-Materials Corp. Macro Fiber Composite—Datasheet. [online]. 2013. Available online: https://www.smart-material.com/media/Datasheets/MFC_V2.4-datasheet-web.pdf (accessed on 31 July 2021).
- Wilkie, W.K.; Bryant, R.G.; Fox, R.L.; Hellbaum, R.F.; High, J.W.; Jalink, A., Jr.; Little, B.D.; Mirick, P.H. Method of Fabricating a Piezoelectric Composite Apparatus. U.S. Patent US6629341B2, 7 October 2003. [Google Scholar]
- Williams, R.; Park, G.; Inman, D.; Wilkie, W.K. An Overview of Composite Actuators with Piezoceramic Fibers. Proc. SPIE Int. Soc. Opt. Eng. 2002, 4753, 421–427. [Google Scholar]
- Bent, A.A.; Hagood, N.W.; Rodgers, J.P. Anisotropic Actuation with Piezoelectric Fiber Composites. J. Intell. Mater. Syst. Struct. 1995, 6, 338–349. [Google Scholar] [CrossRef]
- Wilkie, W. NASA MFC Piezocomposites: A Development History. In Proceedings of the International Symposium on Macro Fiber Composite Applications ISMA, Volkswagen “Transparent Factory”, Dresden, Germany, 27–28 September 2005. [Google Scholar]
- Du, C.; Liu, P.; Yang, H.; Jiang, G.; Wang, L.; Oeser, M. Finite Element Modeling and Performance Evaluation of Piezoelectric Energy Harvesters with Various Piezoelectric Unit Distributions. Materials 2021, 14, 1405. [Google Scholar] [CrossRef] [PubMed]
- del Castillo, M.; Pérez, N. Machine Learning Identification of Piezoelectric Properties. Materials 2021, 14, 2405. [Google Scholar] [CrossRef] [PubMed]
- Min, H.; Zhang, J.; Fan, M. Size Effect of a Piezoelectric Patch on a Rectangular Plate with the Neural Network Model. Materials 2021, 14, 3240. [Google Scholar] [CrossRef]
- de Medeiros, R.; Moreno, M.E.; Marques, F.D.; Tita, V. Effective Properties Evaluation for Smart Composite Materials. J. Braz. Soc. Mech. Sci. Eng. 2012, 34, 362–370. [Google Scholar] [CrossRef] [Green Version]
- Botta, F.; Toccaceli, F. Piezoelectric Plates Distribution for Active Control of Torsional Vibrations. Actuators 2018, 7, 23. [Google Scholar] [CrossRef] [Green Version]
- Grzybek, D.; Kata, D.; Sikora, W.; Sapiński, B.; Micek, P.; Pamuła, H.; Huebner, J.; Rutkowski, P. Piezoelectric Particulate Composite for Energy Harvesting from Mechanical Vibration. Materials 2020, 13, 4925. [Google Scholar] [CrossRef]
- Zhang, J. A Direct Jacobian Total Lagrangian Explicit Dynamics Finite Element Algorithm for Real-Time Simulation of Hyperelastic Materials. Int. J. Numer. Methods Eng. 2021. [Google Scholar] [CrossRef]
- Zhang, W.; Zhong, Z.; Peng, C.; Yuan, W.; Wu, W. GPU-Accelerated Smoothed Particle Finite Element Method for Large Deformation Analysis in Geomechanics. Comput. Geotech. 2021, 129, 103856. [Google Scholar] [CrossRef]
- Oliver, J.; Caicedo, M.; Huespe, A.E.; Hernández, J.A.; Roubin, E. Reduced Order Modeling Strategies for Computational Multiscale Fracture. Comput. Methods Appl. Mech. Eng. 2017, 313, 560–595. [Google Scholar] [CrossRef] [Green Version]
- Caicedo, M.; Mroginski, J.L.; Toro, S.; Raschi, M.; Huespe, A.; Oliver, J. High Performance Reduced Order Modeling Techniques Based on Optimal Energy Quadrature: Application to Geometrically Non-Linear Multiscale Inelastic Material Modeling. Arch. Comput. Methods Eng. 2019, 26, 771–792. [Google Scholar] [CrossRef]
- Raschi, M.; Lloberas-Valls, O.; Huespe, A.; Oliver, J. High Performance Reduction Technique for Multiscale Finite Element Modeling (HPR-FE2): Towards Industrial Multiscale FE Software. Comput. Methods Appl. Mech. Eng. 2021, 375, 113580. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Shen, Y.; Salles, L.; Blahoš, J.; Touzé, C. Direct Computation of Nonlinear Mapping via Normal Form for Reduced-Order Models of Finite Element Nonlinear Structures. Comput. Methods Appl. Mech. Eng. 2021, 384, 113957. [Google Scholar] [CrossRef]
- Li, H.; Wang, D.; Song, Z.; Zhang, F. Numerical Analysis of an Unconditionally Energy-Stable Reduced-Order Finite Element Method for the Allen-Cahn Phase Field Model. Comput. Math. Appl. 2021, 96, 67–76. [Google Scholar] [CrossRef]
- Mou, C.; Wang, Z.; Wells, D.R.; Xie, X.; Iliescu, T. Reduced Order Models for the Quasi-Geostrophic Equations: A Brief Survey. Fluids 2021, 6, 16. [Google Scholar] [CrossRef]
- Shen, Y.; Vizzaccaro, A.; Kesmia, N.; Yu, T.; Salles, L.; Thomas, O.; Touzé, C. Comparison of Reduction Methods for Finite Element Geometrically Nonlinear Beam Structures. Vibration 2021, 4, 14. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, W.; Xun, G.; Wu, Z. Dynamic Shape Control of Piezocomposite-Actuated Morphing Wings with Vibration Suppression. J. Intell. Mater. Syst. Struct. 2018, 29, 358–370. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, W.; Wu, Z. Feedback Tracking Control for Dynamic Morphing of Piezocomposite Actuated Flexible Wings. J. Sound Vib. 2018, 416, 17–28. [Google Scholar] [CrossRef]
- Giddings, P.; Bowen, C.; Kim, H.A. A Coupled Field Finite Element Model to Predict Actuation Properties of Piezoelectrically Actuated Bistable Composites. In Proceedings of the ICCM-17: 17th International Conference on Composite Materials, Citeseer, Edinburgh, UK, 27–31 July 2009. [Google Scholar]
- Bowen, C.R.; Giddings, P.F.; Salo, A.I.; Kim, H.A. Modeling and Characterization of Piezoelectrically Actuated Bistable Composites. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011, 58, 1737–1750. [Google Scholar] [CrossRef] [PubMed]
- Wilkie, W.K.; Bryant, R.G.; High, J.W.; Fox, R.L.; Hellbaum, R.F.; Jalink, A., Jr.; Little, B.D.; Mirick, P.H. Low-Cost Piezocomposite Actuator for Structural Control Applications. In SPIE Proceedings; Smart Structures and Materials 2000: Industrial and Commercial Applications of Smart Structures Technologies; SPIE: Bellingham, WA, USA, 2000; Volume 3991, pp. 323–334. [Google Scholar]
- Williams, R.B.; Inman, D.J.; Schultz, M.R.; Hyer, M.W.; Wilkie, W.K. Nonlinear Tensile and Shear Behavior of Macro Fiber Composite Actuators. J. Compos. Mater. 2004, 38, 855–869. [Google Scholar] [CrossRef]
- Nielsen, B.B.; Nielsen, M.S.; Santos, I.F. A Layered Shell Containing Patches of Piezoelectric Fibers and Interdigitated Electrodes: Finite Element Modeling and Experimental Validation. J. Intell. Mater. Syst. Struct. 2017, 28, 78–96. [Google Scholar] [CrossRef]
- Steiger, K.; Mokrỳ, P. Finite Element Analysis of the Macro Fiber Composite Actuator: Macroscopic Elastic and Piezoelectric Properties and Active Control Thereof by Means of Negative Capacitance Shunt Circuit. Smart Mater. Struct. 2015, 24, 025026. [Google Scholar] [CrossRef]
- Na, Y.; Kim, J. Smart Wing Using Piezoelectric Actuators. In Proceedings of the IMAC-XXIV: Conference & Exposition on Structural Dynamics, St. Louis, MO, USA, 30 January–2 February 2006. [Google Scholar]
- Huang, D. Finite Element Modelling of Macro Fiber Composite with Interdigitated Electrode for Engineering Applications. In Proceedings of the 2017 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Chengdu, China, 27–30 October 2017; pp. 463–470. [Google Scholar]
- Kochersberger, K.B.; Ohanian III, O.J.; Probst, T.; Gelhausen, P.A. Design and Flight Test of the Generic Micro-Aerial Vehicle (GenMAV) Utilizing Piezoelectric Conformal Flight Control Actuation. J. Intell. Mater. Syst. Struct. 2017, 28, 2793–2809. [Google Scholar] [CrossRef]
- Gustafson, E.A. Design, Simulation, and Wind Tunnel Verication of a Morphing Airfoil. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2011. [Google Scholar]
- Emad, D.; Fanni, M.A.; Mohamed, A.M. New Efficient Technique for Finite Element Modeling of Macro Fiber Composite Piezoelectric Materials. Mater. Sci. Forum 2020, 998, 221–226. [Google Scholar] [CrossRef]
- Moheimani, S.R.; Fleming, A.J. Piezoelectric Transducers for Vibration Control and Damping; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hyer, M.W.; White, S.R. Stress Analysis of Fiber-Reinforced Composite Materials; DEStech Publications, Inc.: Lancaster, PA, USA, 2009. [Google Scholar]
- Wilkie, W.; High, J.; Bockman, J. Reliability Testing of NASA Piezocomposite Actuators; U.S. Army Research Laboratory and NASA Langley Research Center: Hampton, VA, USA, 2002. [Google Scholar]
- Williams, R.B.; Inman, D.J.; Wilkie, W.K. Nonlinear Response of the Macro Fiber Composite Actuator to Monotonically Increasing Excitation Voltage. J. Intell. Mater. Syst. Struct. 2006, 17, 601–608. [Google Scholar] [CrossRef]
- Xue, Z.; Li, L.; Ichchou, M.N.; Li, C. Hysteresis and the Nonlinear Equivalent Piezoelectric Coefficient of MFCs for Actuation. Chin. J. Aeronaut. 2017, 30, 88–98. [Google Scholar] [CrossRef] [Green Version]
- Kuhnen, K.; Krejci, P. Compensation of Complex Hysteresis and Creep Effects in Piezoelectrically Actuated Systems—A New Preisach Modeling Approach. IEEE Trans. Autom. Control. 2009, 54, 537–550. [Google Scholar] [CrossRef]
- Kugi, A.; Thull, D.; Kuhnen, K. An Infinite-Dimensional Control Concept for Piezoelectric Structures with Complex Hysteresis. Struct. Control. Health Monit. 2006, 13, 1099–1119. [Google Scholar] [CrossRef]
- Ruderman, M.; Hoffmann, F.; Bertram, T. Modeling and Identification of Elastic Robot Joints with Hysteresis and Backlash. IEEE Trans. Ind. Electron. 2009, 56, 3840–3847. [Google Scholar] [CrossRef]
- Su, C.-Y.; Feng, Y.; Hong, H.; Chen, X. Adaptive Control of System Involving Complex Hysteretic Nonlinearities: A Generalised Prandtl–Ishlinskii Modelling Approach. Int. J. Control. 2009, 82, 1786–1793. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J. Modeling and Inverse Compensation for Coupled Hysteresis in Piezo-Actuated Fabry–Perot Spectrometer. IEEE/ASME Trans. Mechatron. 2017, 22, 1903–1913. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, D. Non-Symmetrical Bouc–Wen Model for Piezoelectric Ceramic Actuators. Sens. Actuators A Phys. 2012, 181, 51–60. [Google Scholar] [CrossRef]
- Aadnoy, B.; Looyeh, R. Chapter 2—Stress and Strain Transformation, in Petroleum Rock Mechanics, 1st ed.; Gulf Professional Publishing: Houston, TX, USA, 2011. [Google Scholar]
- Jones, R.M. Mechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Reuter, R.C., Jr. Concise Property Transformation Relations for an Anisotropic Lamina. J. Compos. Mater. 1971, 5, 270–272. [Google Scholar] [CrossRef]








| Williams’s Experimental Work [29] | Manufacturer Datasheet [4] | |
|---|---|---|
| E3 (GPa) | 29.4 | 30.336 |
| E1 (GPa) | 15.2 | 15.3857 |
| 0.312 | 0.31 | |
| 0.161 | 0.16 | |
| G13 (GPa) | 6.06 | 5.515 |
| High field | 460 | −210 | ~0.9 |
| Low Field | 400 | −170 | ~0.75 |
| Simulation Parameters | Simple FE Model | Detailed FE Model | % Difference |
|---|---|---|---|
| Number of mesh elements | 204 elements | 66,323 elements | 99.7% |
| Computational time | 3 s | 209 s | 98.6% |
| Memory usage | 262 MB | 1 GB | 74.4% |
| Result file size | 407 KB | 63 MB | 99.4% |
| Voltage (V) | % Difference in Shear Strain | % Difference in Maximum Principal Strain | % Difference in Minimum Principal Strain | % Difference in Principal Angle |
|---|---|---|---|---|
| −400 | 1.86% | −3.38% | −4.80% | 6.31% |
| −300 | 4.51% | −2.15% | −1.33% | 6.71% |
| −200 | 4.51% | −0.58% | 0.09% | 5.22% |
| −100 | 4.51% | 4.10% | 4.29% | 0.46% |
| 0 | 0.00% | 0.00% | 0.00% | 0.00% |
| 100 | 4.51% | 4.29% | 4.10% | 0.46% |
| 200 | 9.82% | 5.62% | 0.32% | 7.57% |
| 300 | 4.51% | −1.33% | −2.15% | 6.71% |
| 400 | 9.81% | −3.18% | −4.21% | 14.00% |
| Voltage Applied to MFC | Maximum Deflection in x-, y-, and z-Axes | Comments on the Deformation | Total Deformation | |
|---|---|---|---|---|
| 1 | 17 → 30 = −500 V | Δx = −25.6 µm Δy = −2.75 mm Δz = −6.16 µm | All MFCs-F1 type are actuated to generate a clockwise twisting moment | 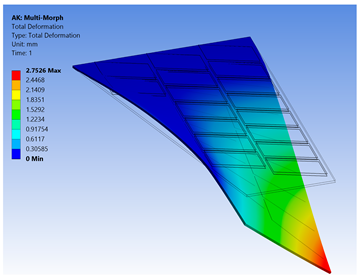 |
| 2 | 17 → 30 = +500 V | Δx = 25.6 µm Δy = 2.75 mm Δz = 6.16 µm | All MFCs-F1 type are actuated to generate a counterclockwise twisting moment |  |
| 3 | 1 → 16 = +1500 V 31 → 34 = +1500 V | Δx = −0.24 mm Δy = −70 µm Δz = 89.8 µm | All MFCs-P1 type are actuated to generate a bending moment |  |
| 4 | 17, 19, 21, 23, 25, 27, 29 = +500 V 18, 20, 22, 24, 26, 28, 30 = −500 V | Δx = −12.5 µm Δy = −3.97 mm Δz = 9.9 µm | All MFCs-F1 type are actuated to generate a clockwise bending moment |  |
| 5 | 17, 19, 21, 23, 25, 27, 29 = −500 V 18, 20, 22, 24, 26, 28, 30 = +500 V | Δx = 12.5 µm Δy = 3.97 mm Δz = 9.9 µm | All MFCs-F1 type are actuated to generate a counterclockwise bending moment |  |
| 6 | 17 → 30 = −500 V 1 → 16 = +1500 V 31 → 34 = +1500 V | Δx = −0.27 mm Δy = −2.8 mm Δz = 91 µm | Applying configuration 1 with configuration 3 |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emad, D.; Fanni, M.A.; Mohamed, A.M.; Yoshida, S. Low-Computational-Cost Technique for Modeling Macro Fiber Composite Piezoelectric Actuators Using Finite Element Method. Materials 2021, 14, 4316. https://doi.org/10.3390/ma14154316
Emad D, Fanni MA, Mohamed AM, Yoshida S. Low-Computational-Cost Technique for Modeling Macro Fiber Composite Piezoelectric Actuators Using Finite Element Method. Materials. 2021; 14(15):4316. https://doi.org/10.3390/ma14154316
Chicago/Turabian StyleEmad, Diaa, Mohamed A. Fanni, Abdelfatah M. Mohamed, and Shigeo Yoshida. 2021. "Low-Computational-Cost Technique for Modeling Macro Fiber Composite Piezoelectric Actuators Using Finite Element Method" Materials 14, no. 15: 4316. https://doi.org/10.3390/ma14154316
APA StyleEmad, D., Fanni, M. A., Mohamed, A. M., & Yoshida, S. (2021). Low-Computational-Cost Technique for Modeling Macro Fiber Composite Piezoelectric Actuators Using Finite Element Method. Materials, 14(15), 4316. https://doi.org/10.3390/ma14154316







