Comparison of J Integral Assessments for Cracked Plates and Pipes
Abstract
:1. Introduction
2. Background of the GSM and FC Methods
2.1. The GSM Method
- is the strain energy density
- Γ is any contour encircling the tip of the crack in a counterclockwise direction
- Ti are the components of the traction vector
- ui are the displacement vector components
- ds is a length increment along the contour Γ
2.2. The FC Method
3. Use of the GSM and FC Methods for Cracked Plates
3.1. Description of Procedure
3.2. Results of Calculations
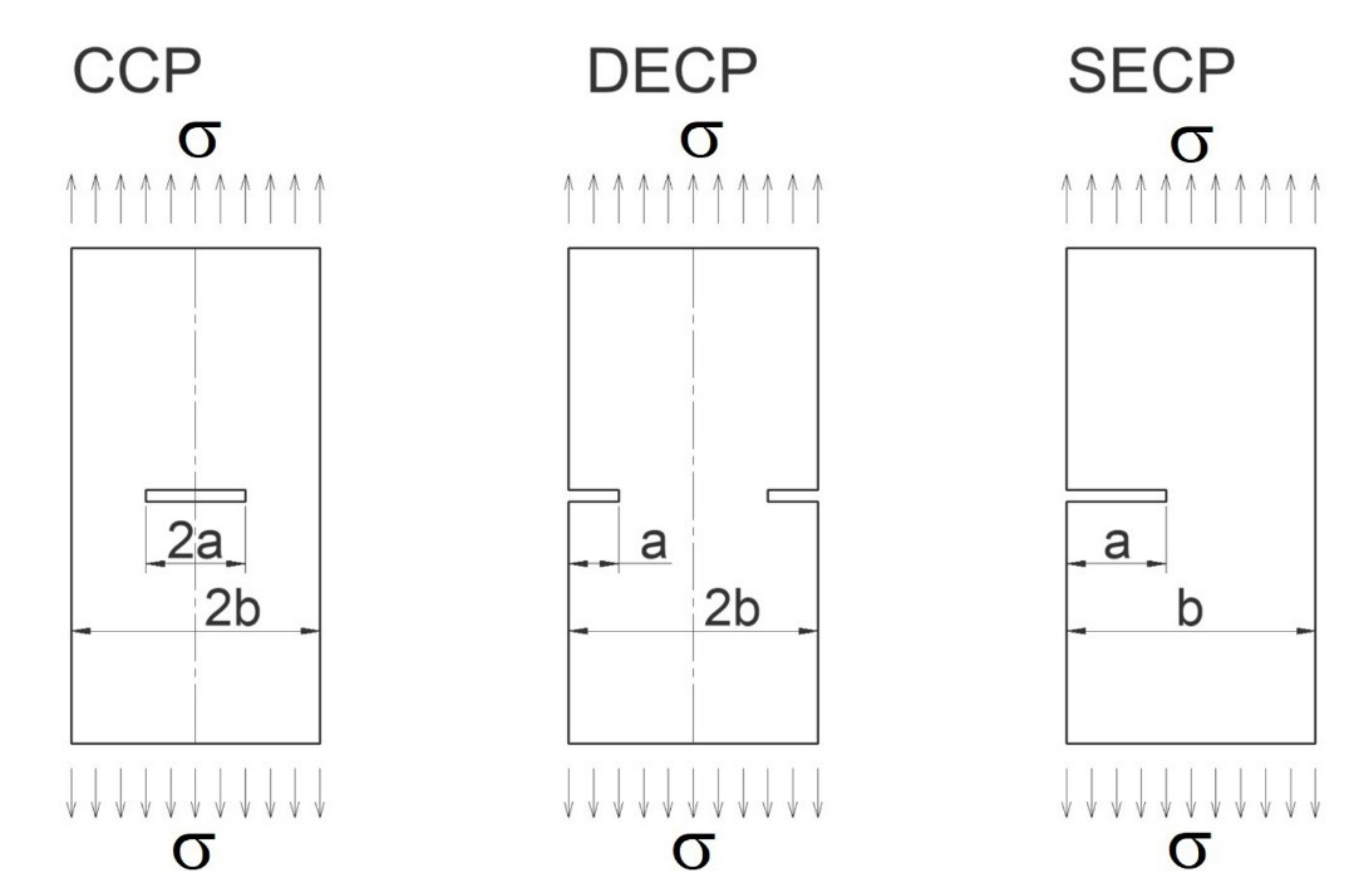
3.2.1. The Center-Cracked Panel (CCP)
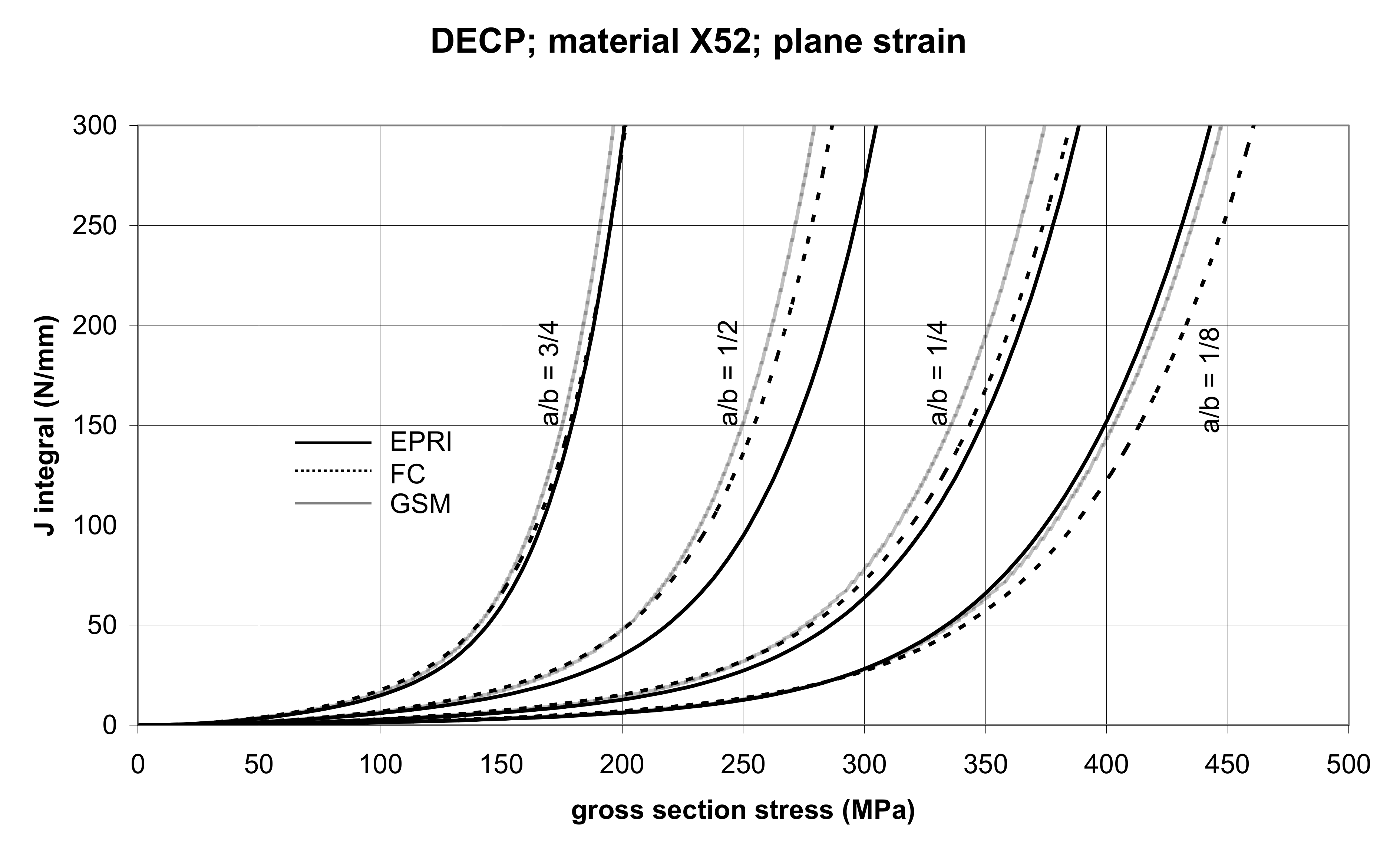
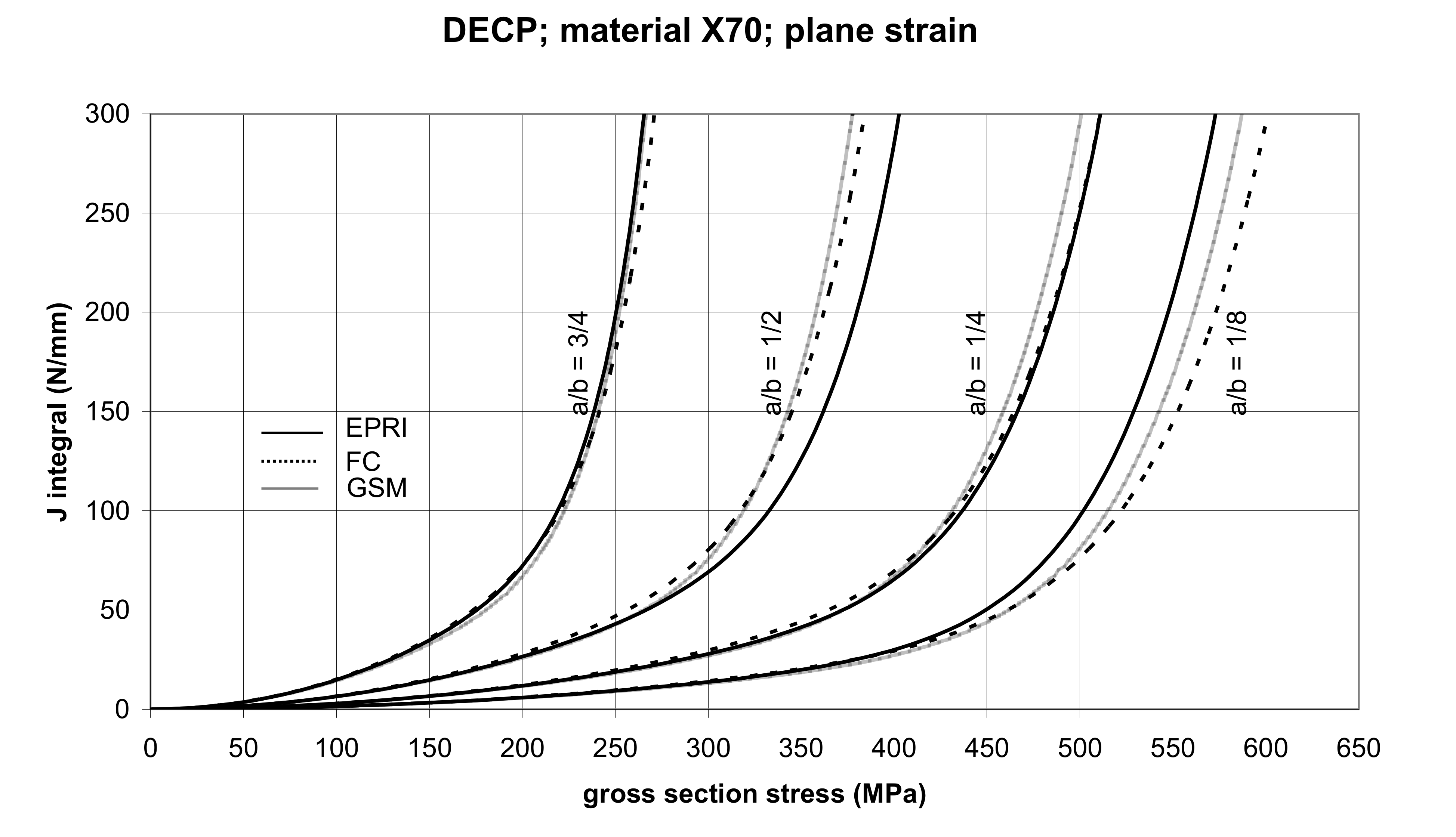
3.2.2. The Double-Edge Cracked Panel (DECP)
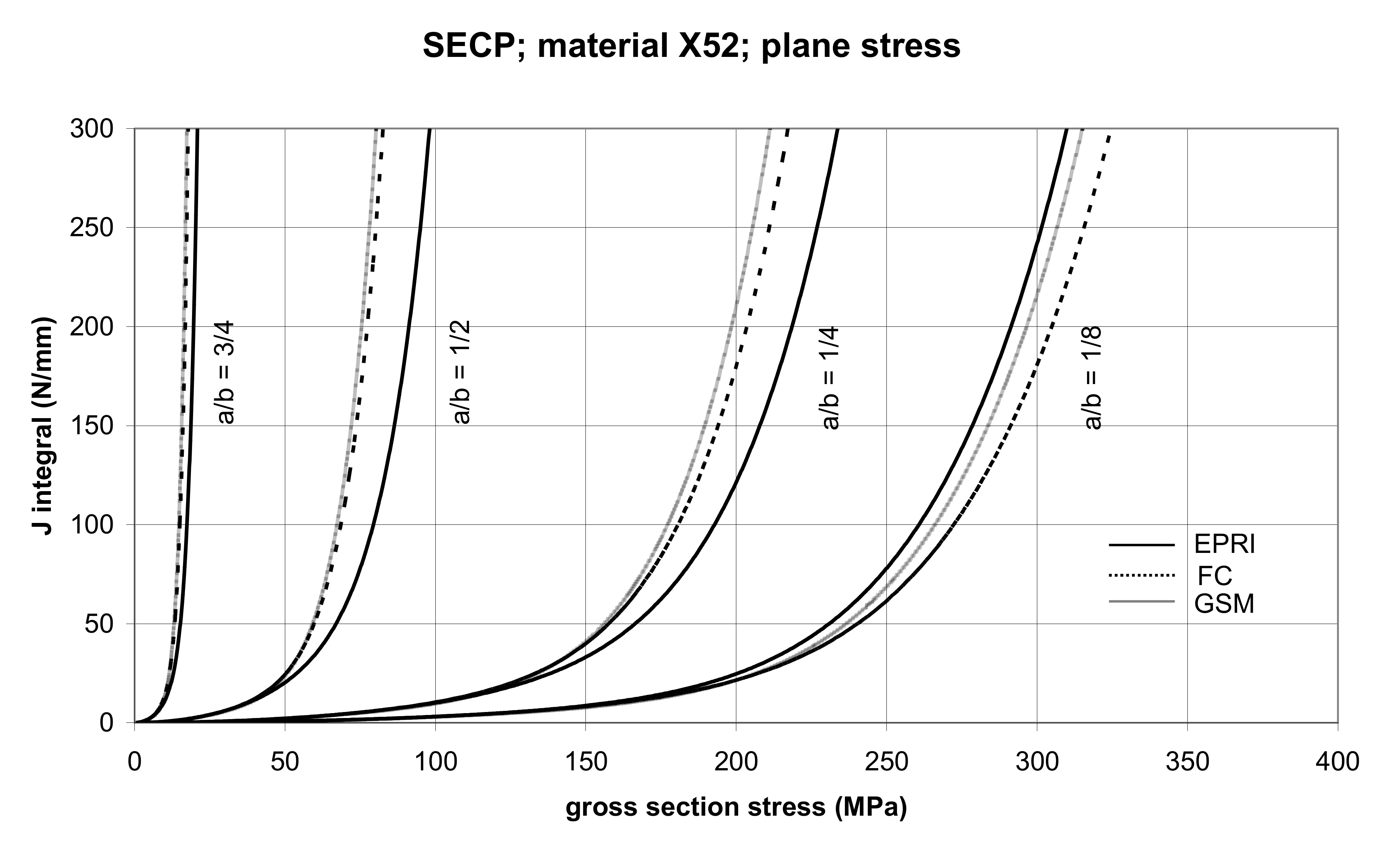
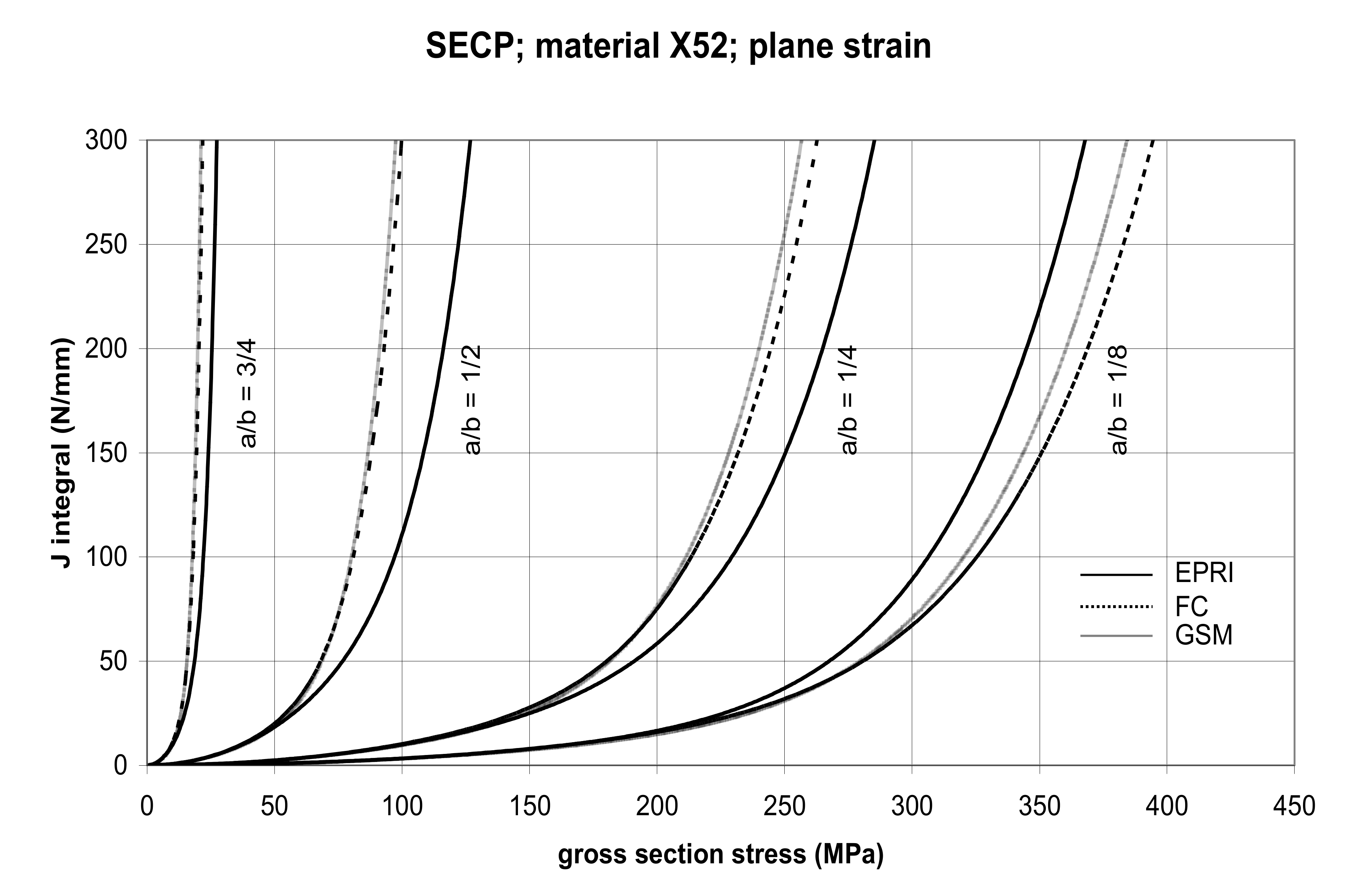
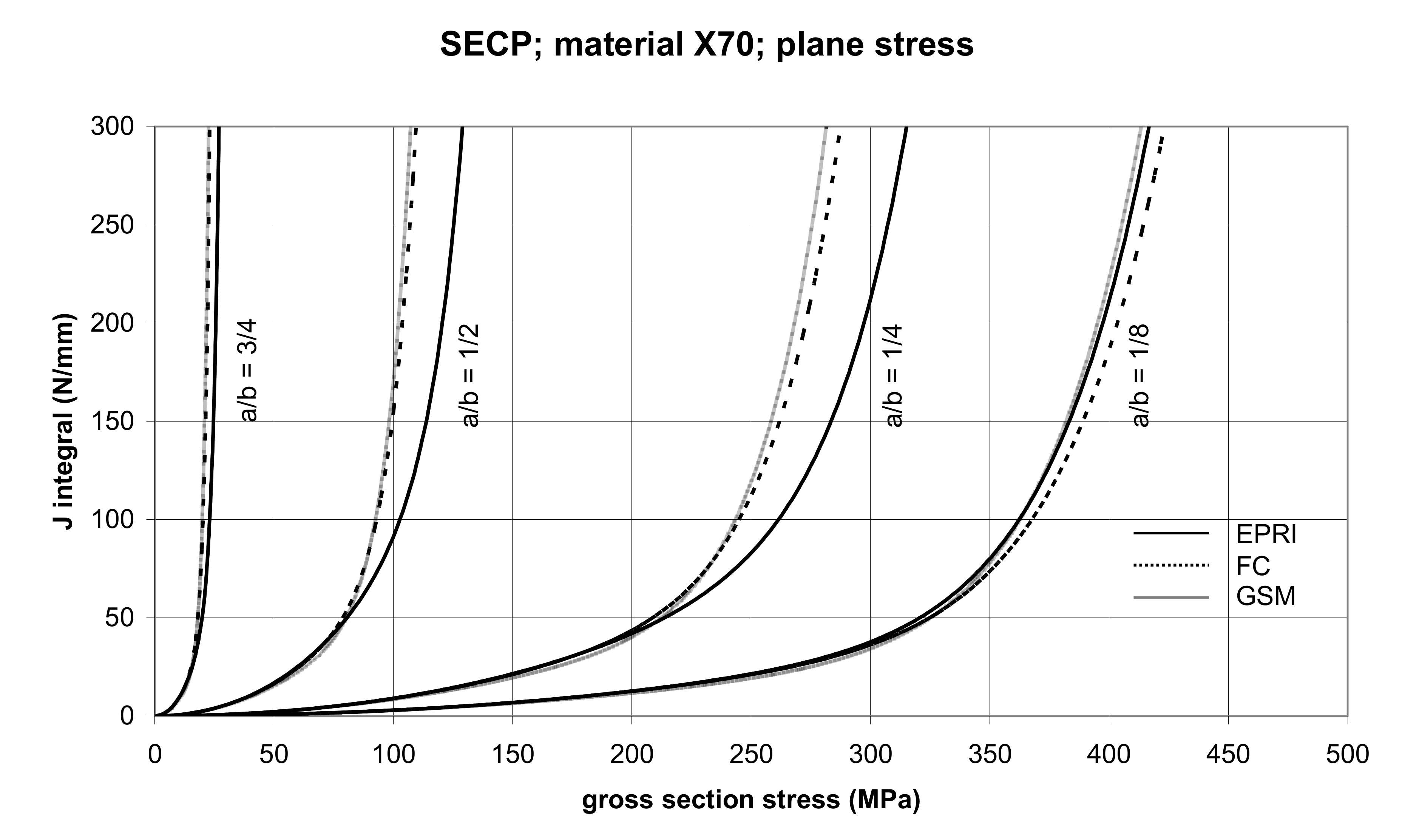
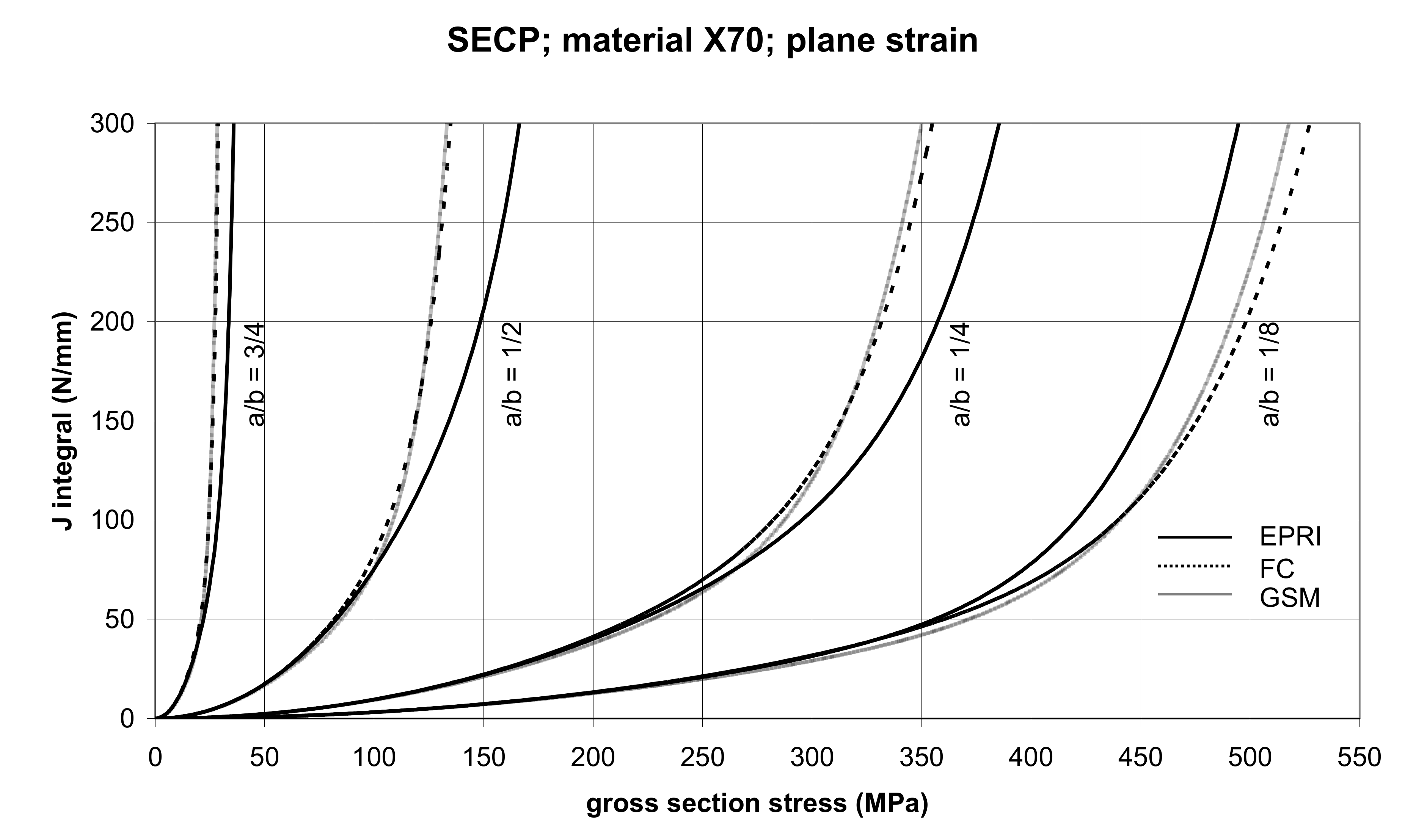
3.2.3. The Single-Edge Cracked Panel (SECP)
4. Use of the FC and GSM Methods for Cracked Pipes
4.1. Preparation of Pipe Segment
4.2. Procedure of the Tests and Experimental Results
4.3. Verification of Applicability of FC and GSM Method for Pipes
5. Discussion of Results
5.1. Cracked Panels
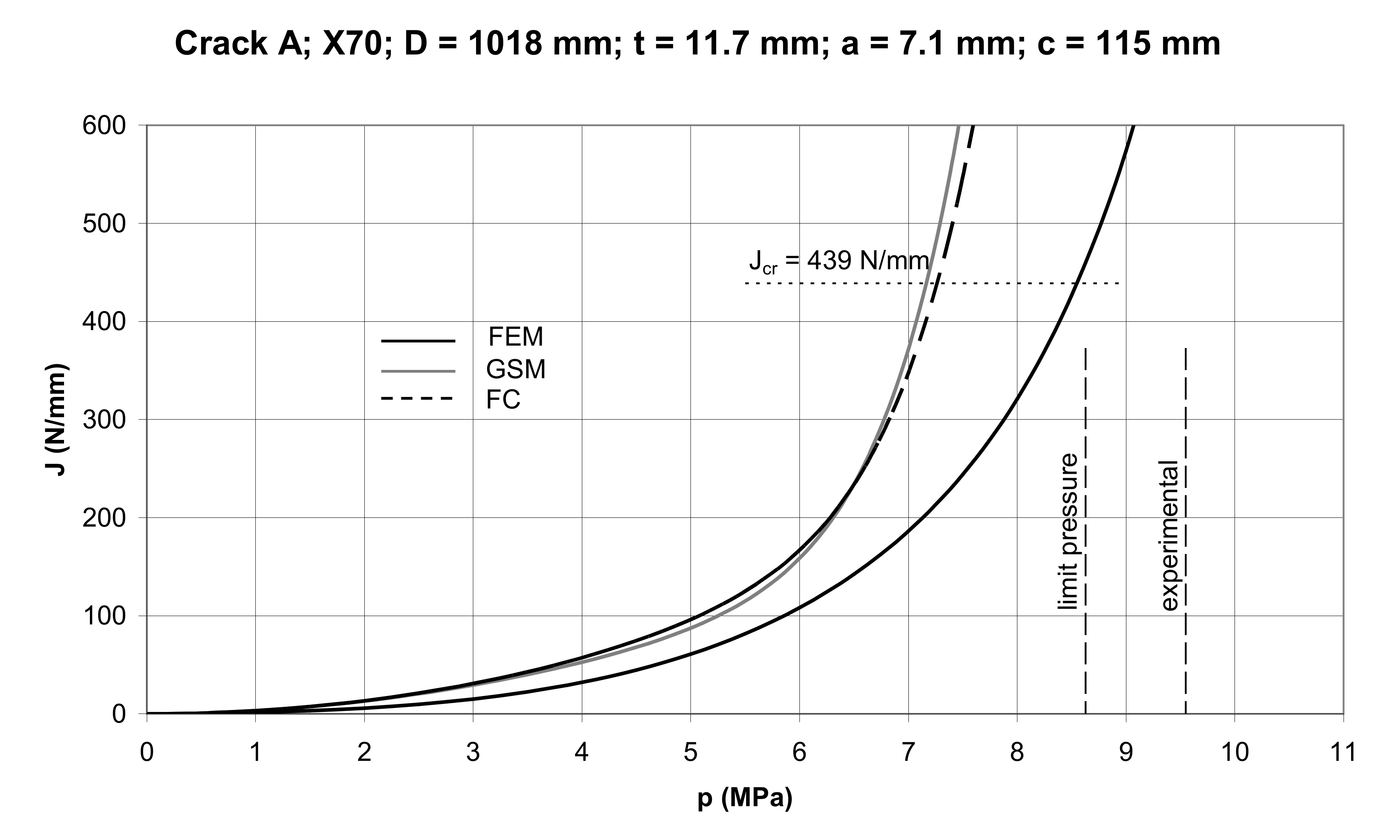
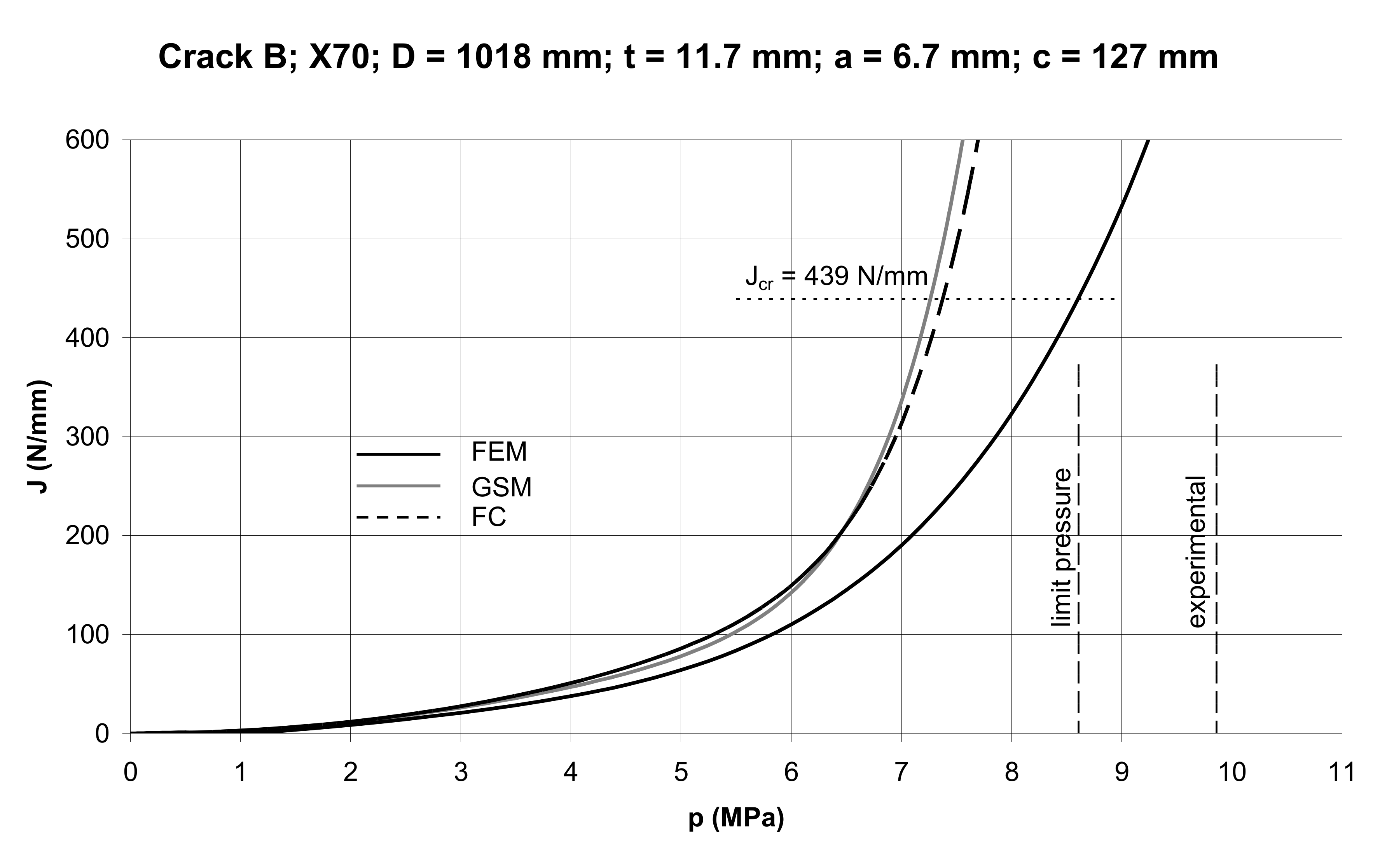
5.2. Cracked Pipes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| a | = crack length (depth); |
| b | = specimen width; |
| c | = half crack length; |
| C | = limit load parameter; |
| D | = outside diameter of a pipe; |
| E | = Young’s modulus; |
| f | = specific function of the ratio a/b for cracked specimens; |
| J, Jcr | = J integral, critical J integral; |
| Je | = elastic component of J integral; |
| Jm | = J integral corresponding to the maximum load in testing CT specimens; |
| Jpl | = plastic component of J integral; |
| kt | = theoretical stress concentration factor; |
| KI, KI p | = stress intensity factor for mode I, provisional KI; |
| n | = Ramberg–Osgood exponent; |
| p | = internal pressure in a pipe; |
| pL | = limit internal pressure; |
| pY | = yield internal pressure; |
| P | = acting load; |
| P0 | = reference load; |
| PL | = limit load; |
| R, Ri | = mean radius, internal radius of a pipe; |
| Rm | = ultimate tensile strength; |
| t | = wall thickness of a pipe; |
| w | = strain energy density; |
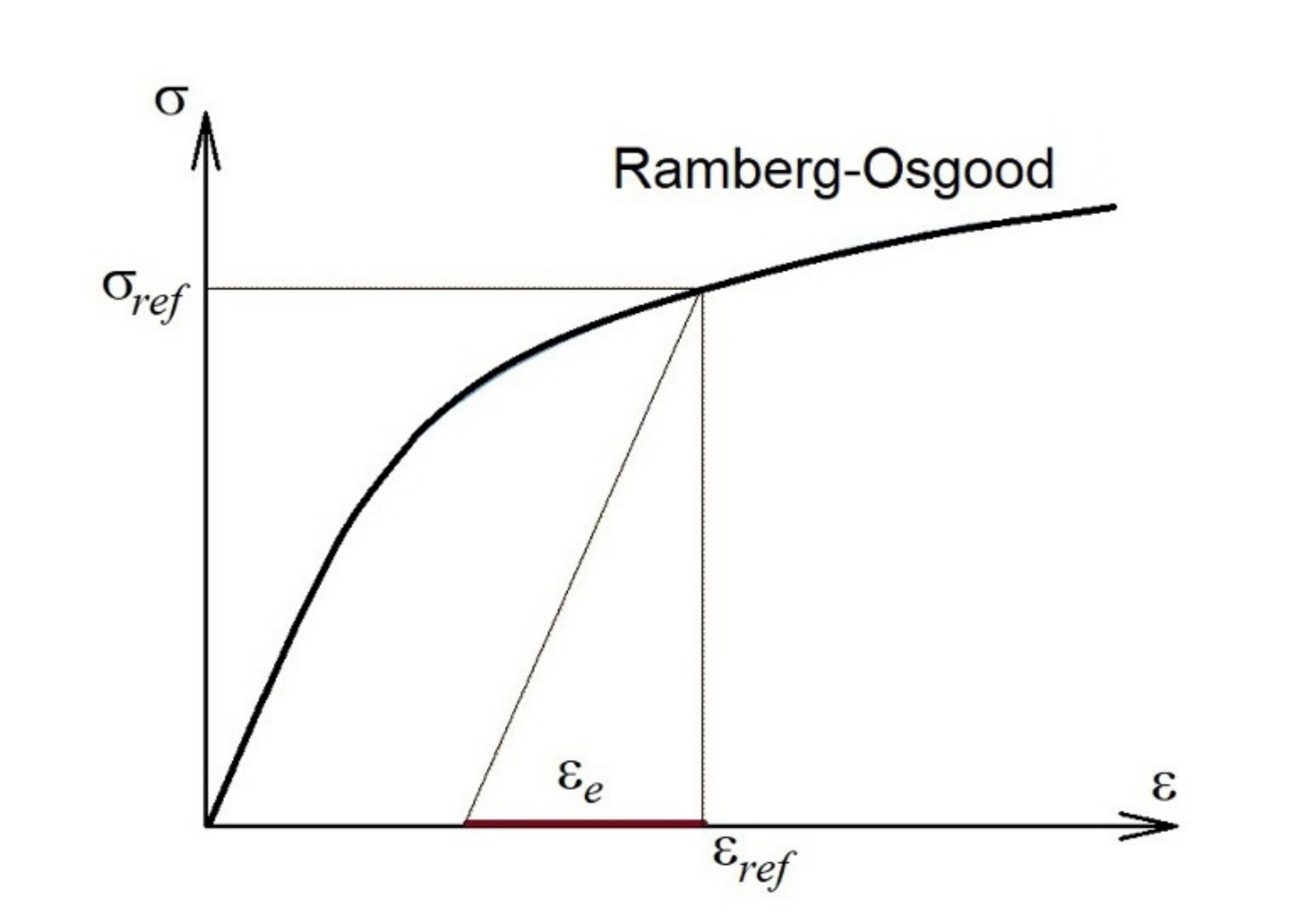
| α | = Ramberg–Osgood constant; |
| εo | = elastic strain at the yield stress; |
| εe | = elastic strain at the reference stress; |
| εref | = reference strain; |
| η, ξ | = geometric parameters for a surface semi-elliptical crack in a pipe wall; |
| σn | = net section stress or hoop stress in the ligament surrounding a longitudinal surface crack in a pipe wall; |
| σo | = yield stress; |
| σref | = reference stress; |
| σfs | = flow stress; |
| σφ | = hoop stress; |
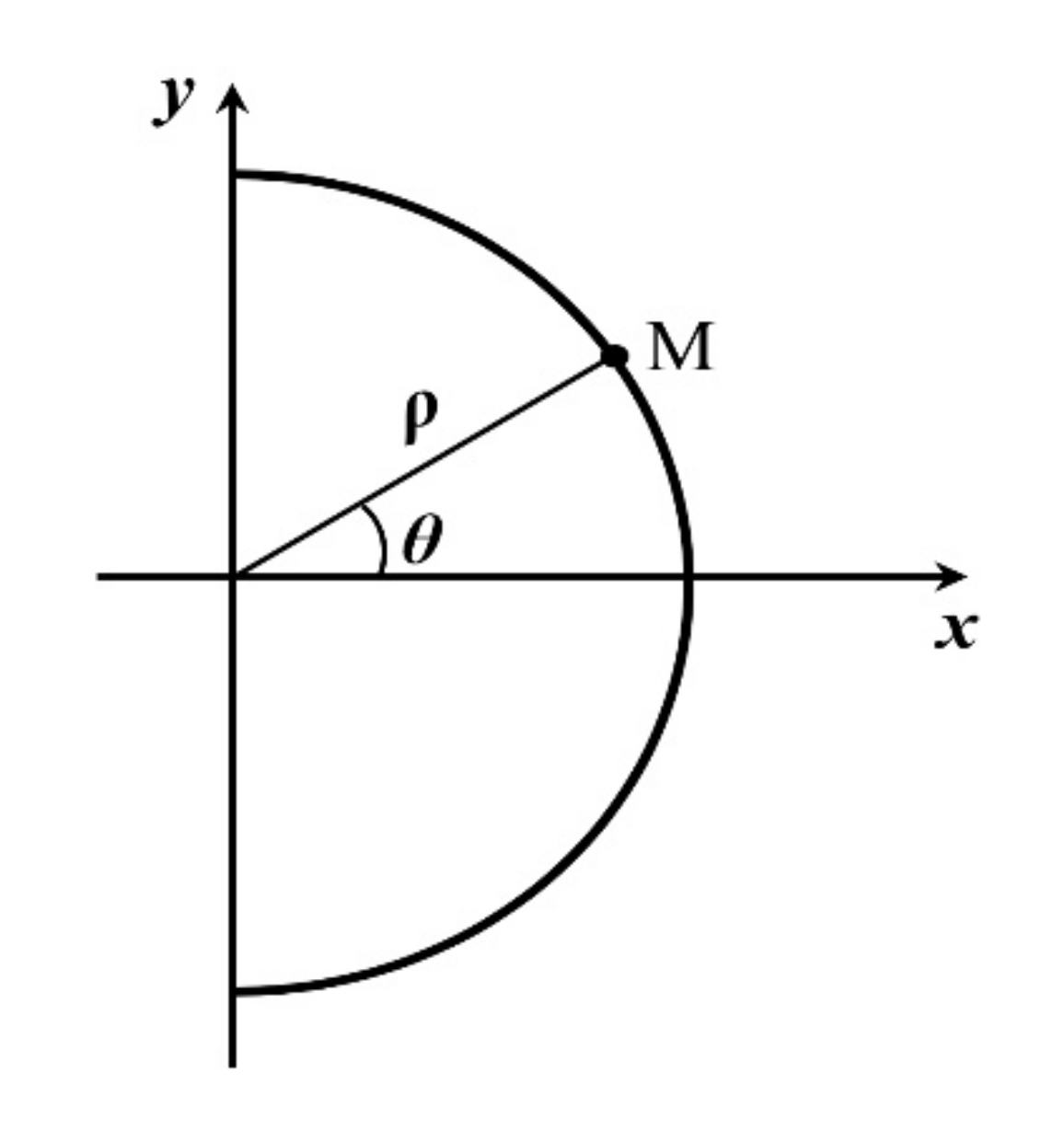
| (ρ, θ) | = polar coordinates of a point on the periphery of the notch root; |
| φ | = correction function for small plastic zone; |
| ψ | = geometric parameter for SECP specimens; |
References
- Gajdoš, Ľ.; Srnec, M. An approximate method for J integral determination. Acta Tech. CSAV 1994, 39, 151–171. [Google Scholar]
- RCC-MR. Design and Construction Rules for Mechanical Components of FBR Nuclear Island, 1st ed.; French Association for the Design, Construction and Operating Supervision of the Equipment for Electronuclear Boilers (AFCEN): Paris, France, 1985; Volume 18. [Google Scholar]
- Rice, J.R. A path independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef] [Green Version]
- Funari, M.F.; Lonetti, P.; Spadea, S. A crack growth strategy based on moving mesh method and fracture mechanics. Theor. Appl. Fract. Mech. 2019, 102, 103–115. [Google Scholar] [CrossRef]
- Tankasala, H.C.; Li, T.; Seiler, P.E.; Deshpande, V.S.; Fleck, N.A. An assessment of the J-integral test for a metallic foam. J. Mech. Phys. Solids 2020, 141, 103958. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, F.; Liu, Y.; Wang, L. J-integral evaluation of a mode I crack in gradient nanocrystalline metals. Mater. Today Comm. 2020, 25, 101328. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.C.; Irwin, R. The Stress Analysis of Cracks Handbook; Del Research Corporation: Hellertown, PA, USA, 1973. [Google Scholar]
- Rooke, D.P.; Cartwright, D.J. Compendium of Stress Intensity Factors; Her Majesty’s Stationery Office: London, UK, 1974. [Google Scholar]
- Murakami, Y. Stress Intensity Factors Handbook; The Society of Materials Science, Pergamon Press: Tokyo, Japan, 1987. [Google Scholar]
- Marie, S.; Chapuliot, S.; Kayser, Y.; Lacire, M.H.; Drubay, B.; Barthelet, B.; Triay, M. French RSE-M and RCC-MR code appendices for flaw analysis. Presentation of the fracture parameters calculation- Part I, General overview. Int. J. Pres. Ves. Pip. 2007, 84, 590–600. [Google Scholar] [CrossRef]
- Muñoz Garcia, J.E.; Petesch, C.; Lebarbé, T.; Bonne, D.; Gelineau, O.; Pascal, C.; Blat, M. Design and construction rules for mechanical components of high-temperature, experimental and fusion nuclear installations. The RCC-MRx Code last edition. Bull. JSME Mech. Eng. J. 2020, 7, 1–12. [Google Scholar]
- Ainsworth, R.A. The assessment of defects in structures of strain hardening material. Eng. Fract. Mech. 1984, 9, 633–642. [Google Scholar] [CrossRef]
- Matvienko, Y.G.; Morozov, E.M. Inter-relationship of non-linear fracture mechanics criteria. Phys. Chem. Mech. Mater. 1989, 25, 3–10. (In Russian) [Google Scholar]
- Matvienko, Y.G.; Morozov, E.M. Calculation of the energy J-integral for bodies with notches and cracks. Int. J. Fract. 2004, 125, 249–261. [Google Scholar] [CrossRef]
- Matvienko, Y.G. J-estimation formulas for non-linear crack problems. Int. J. Fract. 1994, 68, R15–R18. [Google Scholar] [CrossRef]
- Norio, H.; Yasuhiro, K. Calculation of stress intensity factor from stress concentration factor. Eng. Fract. Mech. 1978, 10, 215–221. [Google Scholar] [CrossRef]
- Glinka, G. Energy density approach to calculation of inelastic strain- stress near notches and cracks. Eng. Fract. Mech. 1985, 22, 485–508. [Google Scholar] [CrossRef]
- Kumar, V.; German, M.D.; Shih, C.F. An engineering approach for elastic- plastic fracture analysis. In Prepared for Electric Power Research Institute (EPRI); General Electric Co.: Schenectady, NY, USA, 1981. [Google Scholar]
- Milne, I.; Ainsworth, R.A.; Dowling, A.R.; Stewart, A.T. Assessment of the integrity of structures containing defects. Int. J. Press. Vessel. Pip. 1988, 32, 3–104. [Google Scholar] [CrossRef]
- Gajdoš, Ľ.; Šperl, M. Application of a fracture-mechanics approach to gas pipelines. Int. J. Mech. Mechatron. Eng. 2011, 5, 67–74. [Google Scholar]
- Gajdoš, Ľ.; Šperl, M. Evaluating the integrity of pressure pipelines by fracture mechanics. In Applied Fracture Mechanics; Belov, A., Ed.; InTech: Rijeka, Croatia, 2012; pp. 283–310. [Google Scholar]
- Gajdoš, Ľ.; Šperl, M. Critical conditions of pressurized pipes. Eng. Mech. 2013, 20, 401–412. [Google Scholar]
- Miller, A.G. Review of limit loads of structures containing defects. Int. J. Pres. Ves. Pip. 1988, 32, 197–327. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics, Fundamentals and Applications. Part V: Reference Material–Compilation of K, J, Compliance and Limit Load Solutions, 2nd ed.; CRC Press: Boca Raton, IL, USA, 1995; pp. 601–654. [Google Scholar]
- Witek, M. Structural integrity of steel pipeline with clusters of corrosion defects. Materials 2021, 14, 852. [Google Scholar] [CrossRef] [PubMed]
- Nykyforchyn, H.; Zvirko, O.; Dzioba, I.; Krechkovska, H.; Hredil, M.; Tsyrulnyk, O.; Student, O.; Lipiec, S. Assessment of operational degradation of pipeline steels. Materials 2021, 14, 3247. [Google Scholar] [CrossRef]
- Harrison, R.P.; Loosemore, K.; Milne, I.; Dowling, A.R. Assessment of the Integrity of Structures Containing Defects; CEGB Report R/H/R6–Rev. 2; Central Electricity Generating Board, Research Division: London, UK, 1980. [Google Scholar]
- Newman, J.C. Fracture analysis of surface and through-cracked sheets and plates. Eng. Fract. Mech. 1973, 5, 667–689. [Google Scholar] [CrossRef]
- Rahman, S.; Brust, F.W. Approximate methods for predicting J- integral of a circumferentially surface-cracked pipe subject to bending. Int. J. Fract. 1997, 85, 111–130. [Google Scholar] [CrossRef]
- Sharma, R.K.; Shrivastava, S.K.; Dixit, P.M.; Basu, S. On the problem of an axial semi-elliptical crack in a hollow ductile cylinder. Int. J. Fract. 2006, 140, 269–275. [Google Scholar] [CrossRef]

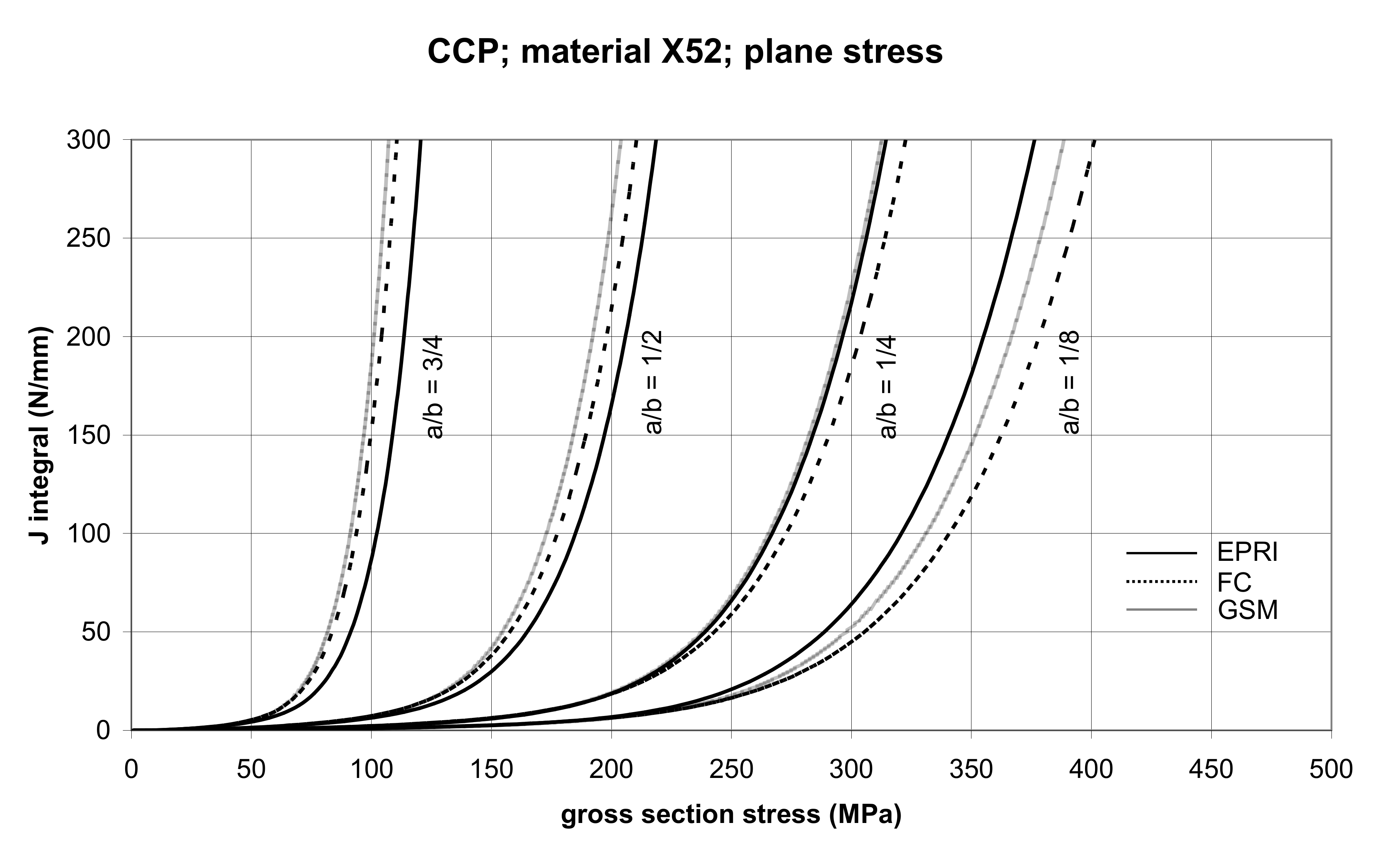

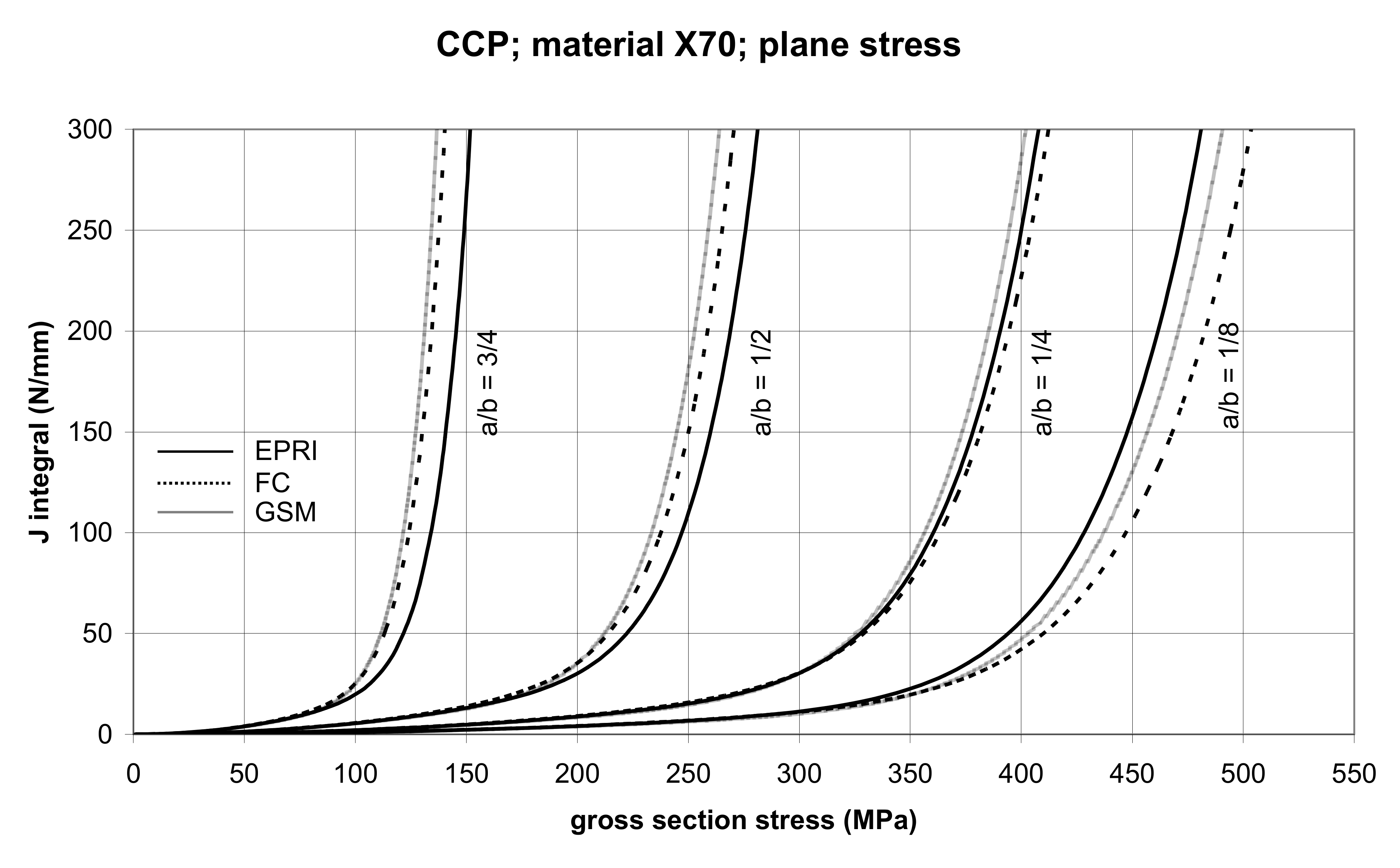
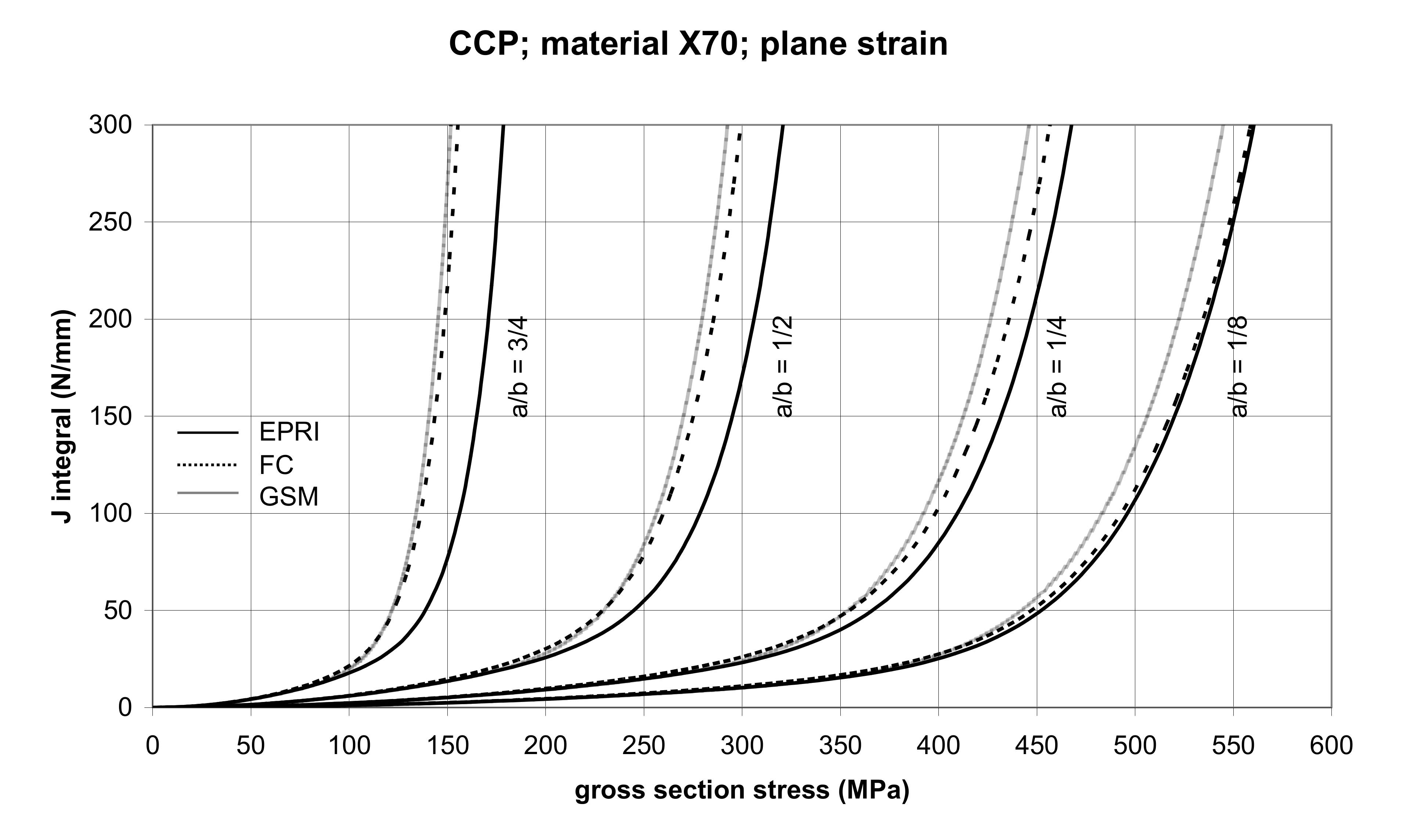
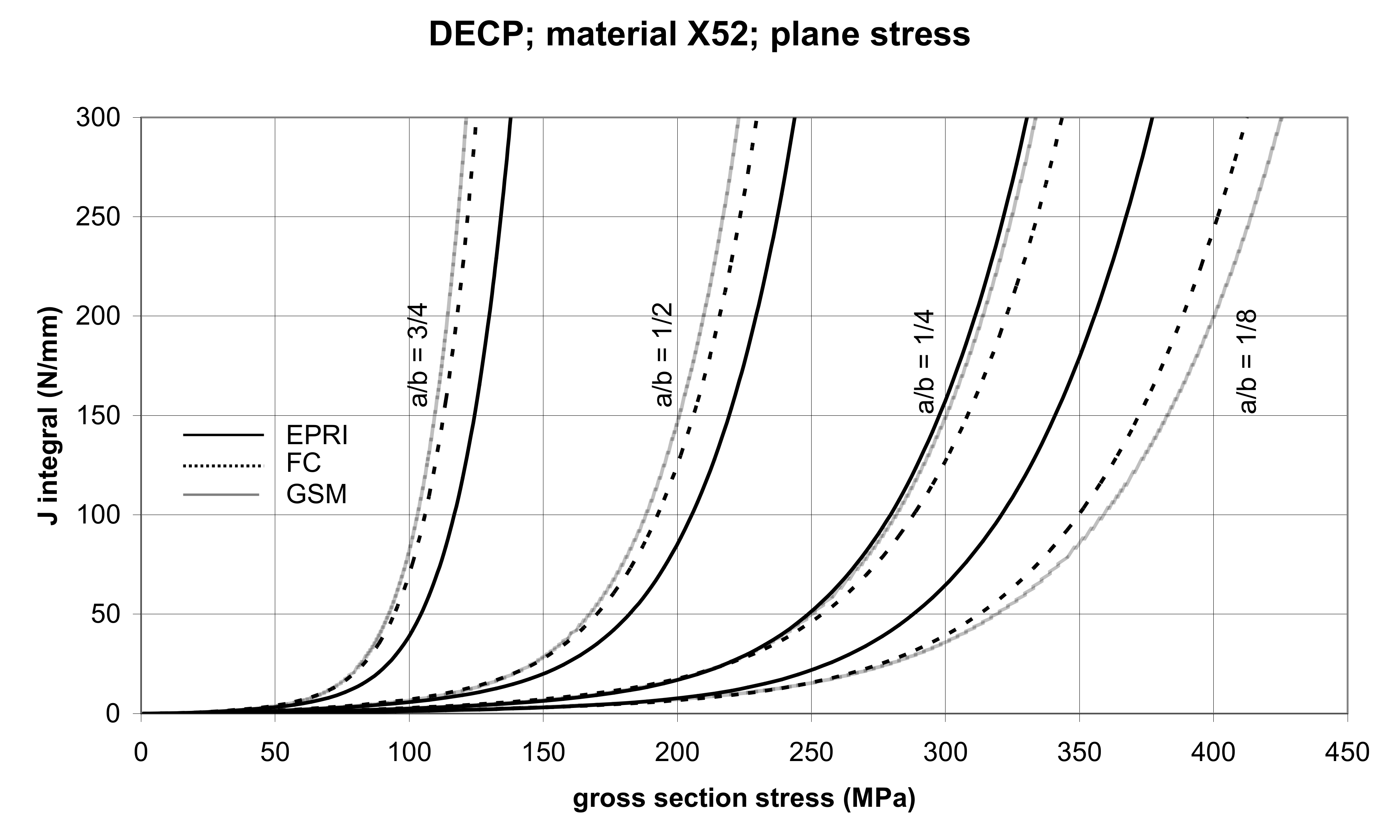




| Material | Characteristics | |||
|---|---|---|---|---|
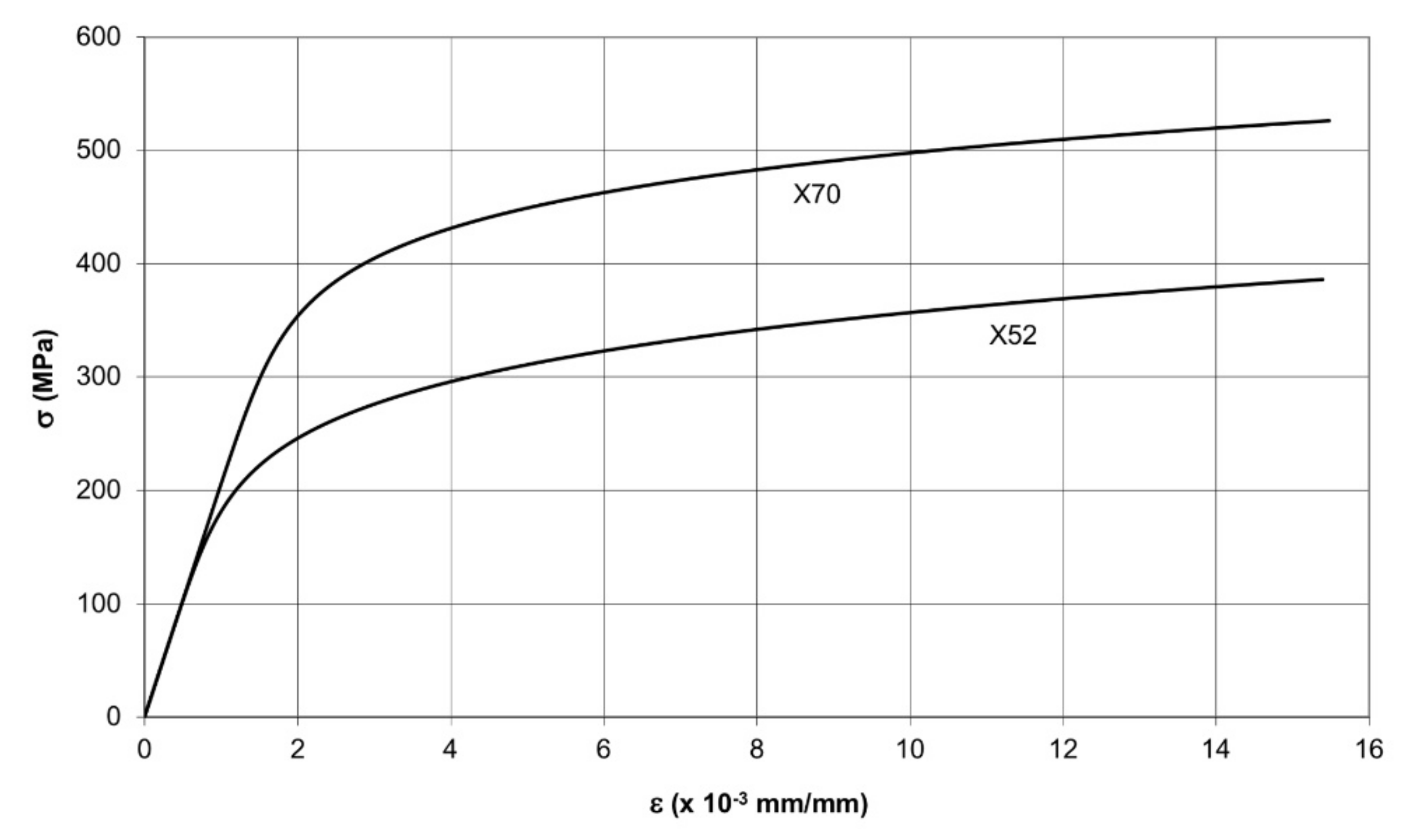
| α (1) | n (1) | σ0 (MPa) | Rm (MPa) | |
| X52 | 2.40 | 6.25 | 313 | 493 |
| X70 | 5.92 | 9.62 | 536 | 644 |
| Specimen | C | |
|---|---|---|
| Plane Stress | Plane Strain | |
| CCP | 1 | 2/√3 |
| DECP | 2/√3 | 0.91 + 0.36/(1 − a/b) |
| SECP | 1.072 ψ | 1.455 ψ |
| Characteristics | Crack A | Crack B |
|---|---|---|
| Crack dimensions | ||
| half-length, c (mm) | 115 | 127 |
| depth in fracture, af (mm) | 7.1 | 6.7 |
| Ramberg–Osgood parameters | ||
| α/n/σ0 (MPa) | 5.92/9.62/536 | 5.92/9.62/536 |
| Flow stress | ||
| σfs (MPa) | 590 | 590 |
| Fracture toughness | ||
| Jcr = Jm (N/mm) | 439 | 439 |
| Fracture pressure | ||
| pf (MPa) | 9.55 | 9.86 |
| Quantity | Ri (mm) | t (mm) | c (mm) | af (mm) | pf (MPa) |
|---|---|---|---|---|---|
| Crack A | 497.8 | 11.7 | 115 | 7.1 | 9.55 |
| Crack B | 497.8 | 11.7 | 127 | 6.7 | 9.86 |
| Quantity | pGS (MPa) | pFC (MPa) | pFEM (MPa) | pL (MPa) | pexp = pf (MPa) |
|---|---|---|---|---|---|
| Crack A | 7.16 | 7.26 | 8.56 | 8.63 | 9.55 |
| Crack B | 7.26 | 7.38 | 8.60 | 8.61 | 9.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajdoš, Ľ.; Šperl, M.; Bayer, J.; Kuželka, J. Comparison of J Integral Assessments for Cracked Plates and Pipes. Materials 2021, 14, 4324. https://doi.org/10.3390/ma14154324
Gajdoš Ľ, Šperl M, Bayer J, Kuželka J. Comparison of J Integral Assessments for Cracked Plates and Pipes. Materials. 2021; 14(15):4324. https://doi.org/10.3390/ma14154324
Chicago/Turabian StyleGajdoš, Ľubomír, Martin Šperl, Jan Bayer, and Jiří Kuželka. 2021. "Comparison of J Integral Assessments for Cracked Plates and Pipes" Materials 14, no. 15: 4324. https://doi.org/10.3390/ma14154324
APA StyleGajdoš, Ľ., Šperl, M., Bayer, J., & Kuželka, J. (2021). Comparison of J Integral Assessments for Cracked Plates and Pipes. Materials, 14(15), 4324. https://doi.org/10.3390/ma14154324





