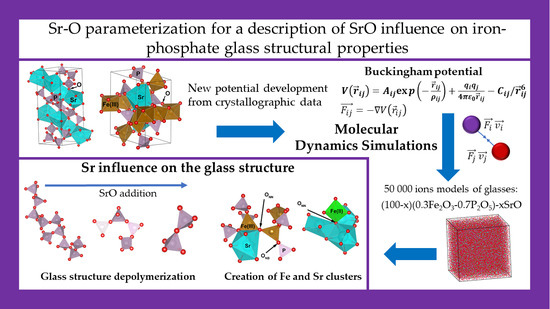
Development of a New Sr-O Parameterization to Describe the Influence of SrO on Iron-Phosphate Glass Structural Properties Using Molecular Dynamics Simulations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulation Methods
2.2. Development of Sr-O Interatomic Potential Parameters
2.3. Glass Synthesis
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sales, B.C. Phosphate Glasses. MRS Bull. 1987, 12, 32–35. [Google Scholar] [CrossRef]
- Hench, L.L. Bioceramics: From concept to clinic. Am. Ceram. Soc. Bull. 1993, 72, 93–98. [Google Scholar] [CrossRef]
- Knowles, J.C. Phosphate based glasses for biomedical applications. J. Mater. Chem. 2003, 13, 2395–2401. [Google Scholar] [CrossRef]
- Carini, G.; D’Angelo, G.; Tripodo, G.; Fontana, A.; Rossi, F.; Saunders, G.A. Low-energy magnetic excitations in the Pr metaphosphate glass. Europhys. Lett. 1997, 40, 435–440. [Google Scholar] [CrossRef]
- Durville, F.M.; Behrens, E.G.; Powell, R.C. Laser-induced refractive-index gratings in Eu-doped glasses. Phys. Rev. B 1986, 34, 4213–4220. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Zhu, C.; Yang, Y.; Yuan, S.; Chen, G. Luminescent properties of Dy3+-doped and Dy3+-Tm3+ co-doped phosphate glasses. J. Lumin. 2008, 128, 1162–1164. [Google Scholar] [CrossRef]
- Wacławska, I.; Szumera, M. Thermal behaviour of Fe-doped silicate–phosphate glasses. J. Therm. Anal. Calorim. 2010, 101, 423–427. [Google Scholar] [CrossRef]
- Szumera, M.; Waclawska, I.; Olejniczak, Z. Influence of B2O3 on the structure and crystallization of soil active glasses. J. Therm. Anal. Calorim. 2010, 99, 879–886. [Google Scholar] [CrossRef]
- Kuczek, J.; Jeleń, P.; Stoch, P.; Błachowski, A.; Wacławska, I.; Szumera, M. Raman and Mössbauer studies of iron phosphate-silicate glasses. J. Mol. Struct. 2018, 1170, 82–89. [Google Scholar] [CrossRef]
- Bunker, B.C.; Arnold, G.W.; Wilder, J.A. Phosphate glass dissolution in aqueous solutions. J. Non. Cryst. Solids 1984, 64, 291–316. [Google Scholar] [CrossRef]
- Ma, L.; Brow, R.K.; Schlesinger, M.E. Dissolution behavior of Na2O–FeO–Fe2O3–P2O5 glasses. J. Non. Cryst. Solids 2017, 463, 90–101. [Google Scholar] [CrossRef] [Green Version]
- Ojovan, M.I.; Lee, W.E. An Introduction to Nuclear Waste Immobilisation, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 978-0-08-102702-8. [Google Scholar]
- Donald, I.W. Waste Immobilization in Glass and Ceramic Based Hosts: Radioactive, Toxic and Hazardous Wastes; Wiley: Hoboken, NJ, USA, 2010; ISBN 978-1-444-31936-1. [Google Scholar]
- Stefanovsky, S.V.; Stefanovsky, O.I.; Remizov, M.B.; Belanova, E.A.; Kozlov, P.V.; Glazkova, Y.S.; Sobolev, A.V.; Presniakov, I.A.; Kalmykov, S.N.; Myasoedov, B.F. FTIR and Mössbauer spectroscopic study of sodium-aluminum-iron phosphate glassy materials for high level waste immobilization. J. Nucl. Mater. 2015, 466, 142–149. [Google Scholar] [CrossRef]
- Moghanian, A.; Firoozi, S.; Tahriri, M.; Sedghi, A. A comparative study on the in vitro formation of hydroxyapatite, cytotoxicity and antibacterial activity of 58S bioactive glass substituted by Li and Sr. Mater. Sci. Eng. C. Mater. Biol. Appl. 2018, 91, 349–360. [Google Scholar] [CrossRef]
- Varshneya, A.K. Fundamentals of Inorganic Glasses; Academic Press: Cambridge, MA, USA, 1994; ISBN 978-0-08-057150-8. [Google Scholar]
- Brow, R.K. Review: The structure of simple phosphate glasses. J. Non-Cryst. Solids 2000, 263–264, 1–28. [Google Scholar] [CrossRef]
- Hoppe, U. A structural model for phosphate glasses. J. Non-Cryst. Solids 1996, 195, 138–147. [Google Scholar] [CrossRef]
- Al-Hasni, B.; Mountjoy, G. Structural investigation of iron phosphate glasses using molecular dynamics simulation. J. Non-Cryst. Solids 2011, 357, 2775–2779. [Google Scholar] [CrossRef]
- Goj, P.; Stoch, P. Influence of CaO on structural features of polyphosphate P2O5-Fe2O3-FeO glasses by molecular dynamics simulations. J. Non-Cryst. Solids 2020, 537, 120014. [Google Scholar] [CrossRef]
- Goj, P.; Stoch, P. Molecular dynamics simulations of P2O5-Fe2O3-FeO-Na2O glasses. J. Non-Cryst. Solids 2018, 500, 70–77. [Google Scholar] [CrossRef]
- Stoch, P.; Goj, P.; Ciecińska, M.; Stoch, A. Structural features of 19Al2O3-19Fe2O3-62P2O5 glass from a theoretical and experimental point of view. J. Non-Cryst. Solids 2019, 521, 119499. [Google Scholar] [CrossRef]
- Rao, K.J. Structural Chemistry of Glasses; Elsevier: Amsterdam, The Netherlands, 2002; ISBN 9780080518039. [Google Scholar]
- Shelby, J.E. Introduction to Glass Science and Technology; RSC Paperbacks Series; Royal Society of Chemistry: London, UK, 2005; ISBN 978-0854046393. [Google Scholar]
- Wedgwood, F.A.; Wright, A.C. Short range antiferromagnetic ordering in vitreous Fe2O3-P2O5. J. Non-Cryst. Solids 1976, 21, 95–105. [Google Scholar] [CrossRef]
- Marasinghe, G.K.; Karabulut, M.; Ray, C.S.; Day, D.E.; Shumsky, M.G.; Yelon, W.B.; Booth, C.H.; Allen, P.G.; Shuh, D.K. Structural features of iron phosphate glasses. J. Non-Cryst. Solids 1997, 222, 144–152. [Google Scholar] [CrossRef]
- Wright, A.C.; Sinclair, R.N.; Shaw, J.L.; Haworth, R.; Marasinghe, G.K.; Day, D.E. A neutron diffraction study of the structure of iron phosphate glasses. Phys. Chem. Glas. Eur. J. Glas. Sci. Technol. Part B 2008, 49, 1–7. [Google Scholar]
- Stoch, P.; Goj, P.; Ciecińska, M.; Jeleń, P.; Błachowski, A.; Stoch, A.; Krakowiak, I. Influence of aluminum on structural properties of iron-polyphosphate glasses. Ceram. Int. 2020, 46, 19146–19157. [Google Scholar] [CrossRef]
- Stoch, P.; Szczerba, W.; Bodnar, W.; Ciecinska, M.; Stoch, A.; Burkel, E. Structural properties of iron-phosphate glasses: Spectroscopic studies and ab initio simulations. Phys. Chem. Chem. Phys. 2014, 16, 19917–19927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goj, P.; Stoch, P. Molecular dynamics simulations of P2O5-Fe2O3-FeO glass system. Ceram. Mater. 2018, 70, 102–115. [Google Scholar]
- Joseph, K.; Premila, M.; Amarendra, G.; Kutty, K.V.G.; Sundar, C.S.; Rao, P.R.V. Structure of cesium loaded iron phosphate glasses: An infrared and Raman spectroscopy study. J. Nucl. Mater. 2012, 420, 49–53. [Google Scholar] [CrossRef]
- Joseph, K.; Kutty, K.V.G.; Chandramohan, P.; Rao, P.R.V. Studies on the synthesis and characterization of cesium-containing iron phosphate glasses. J. Nucl. Mater. 2009, 384, 262–267. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short—Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Cormack, A.N.; Du, J. Molecular dynamics simulations of soda–lime–silicate glasses. J. Non-Cryst. Solids 2001, 293–295, 283–289. [Google Scholar] [CrossRef]
- Plimpton, S.; Pollock, R.; Stevens, M.J. Particle Mesh Ewald and rRESPA for Parallel Molecular Dynamics Simulations. In Proceedings of the Eighth SIAM Conference on Parallel Processing for Scientific Computing, Minneapolis, MN, USA, 14–17 March 1997; pp. 1–13. [Google Scholar]
- Jolley, K.; Smith, R. Iron phosphate glasses: Structure determination and radiation tolerance. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2016, 374, 8–13. [Google Scholar] [CrossRef] [Green Version]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Li, X.; Xiao, Z.; He, Y.; Wang, Y.; Luo, J.; Shi, J.; Huang, Q.; Kong, L. Crystallization behavior, structure and properties of glasses in SrO–Fe2O3–P2O5 system. J. Non-Cryst. Solids 2019, 523, 119588. [Google Scholar] [CrossRef]
- Ciecińska, M.; Goj, P.; Stoch, A.; Stoch, P. Thermal properties of 60P2O5–(40−x)Al2O3–xNa2O glasses. J. Therm. Anal. Calorim. 2019, 139, 1763–1769. [Google Scholar] [CrossRef] [Green Version]
- Stoch, P.; Goj, P.; Wajda, A.; Stoch, A. Alternative insight into aluminium-phosphate glass network from ab initio molecular dynamics simulations. Ceram. Int. 2020, 47, 1891–1902. [Google Scholar] [CrossRef]
- Hoppe, U.; Walter, G.; Kranold, R.; Stachel, D. Structural specifics of phosphate glasses probed by diffraction methods: A review. J. Non-Cryst. Solids 2000, 263–264, 29–47. [Google Scholar] [CrossRef]
- Hoppe, U.; Ebendorff-Heidepriem, H.; Neuefeind, J.; Bowron, D.T. A Neutron and X-ray Diffraction Study of the Structure of Nd Phosphate Glasses. Z. Naturforsch. A 2001, 56, 237–243. [Google Scholar] [CrossRef] [Green Version]
- Hoppe, U.; Karabulut, M.; Metwalli, E.; Brow, R.K.; Jóvári, P. The Fe–O coordination in iron phosphate glasses by X-ray diffraction with high energy photons. J. Phys. Condens. Matter 2003, 15, 6143–6153. [Google Scholar] [CrossRef]
- Stoch, P.; Stoch, A.; Ciecinska, M.; Krakowiak, I.; Sitarz, M. Structure of phosphate and iron-phosphate glasses by DFT calculations and FTIR/Raman spectroscopy. J. Non-Cryst. Solids 2016, 450, 48–60. [Google Scholar] [CrossRef]
- Hoppe, U.; Kranold, R.; Stachel, D.; Barz, A.; Hannon, A.C. Variation in P-O Bonding in Phosphate Glasses—A Neutron Diffraction Study. Z. Nat. A 2000, 55, 369–380. [Google Scholar] [CrossRef]
- Hoppe, U.; Walter, G.; Kranold, R.; Stachel, D. An X-ray Diffraction Study of the Structure of Vitreous P2O5. Z. Nat. A 1998, 53, 93–104. [Google Scholar] [CrossRef]
- Wright, A.C.; Sinclair, R.N.; Shaw, J.L.; Haworth, R.; Marasinghe, G.K.; Day, D.E.; Bingham, P.A.; Forder, S.D.; Cuello, G.J.; Fischer, H.E.; et al. The atomic and magnetic structure and dynamics of iron phosphate glasses. Phys. Chem. Glasses Eur. J. Glass Sci. Technol. Part B 2012, 53, 227–244. [Google Scholar]
- Joseph, K.; Jolley, K.; Smith, R. Iron phosphate glasses: Structure determination and displacement energy thresholds, using a fixed charge potential model. J. Non-Cryst. Solids 2015, 411, 137–144. [Google Scholar] [CrossRef] [Green Version]
- Christie, J.K.; Malik, J.; Tilocca, A. Bioactive glasses as potential radioisotope vectors for in situ cancer therapy: Investigating the structural effects of yttrium. Phys. Chem. Chem. Phys. 2011, 13, 17749. [Google Scholar] [CrossRef] [PubMed]
- Christie, J.K.; Ainsworth, R.I.; de Leeuw, N.H. Investigating structural features which control the dissolution of bioactive phosphate glasses: Beyond the network connectivity. J. Non-Cryst. Solids 2016, 432, 31–34. [Google Scholar] [CrossRef] [Green Version]
- Mead, R.N.; Mountjoy, G. A molecular dynamics study of the atomic structure of (CaO)x(SiO2)1−x glasses. J. Phys. Chem. B 2006, 110, 14273–14278. [Google Scholar] [CrossRef] [PubMed]
- Görlich, E. The structure of SiO2—Current views. Ceram. Int. 1982, 8, 3–16. [Google Scholar] [CrossRef]
- Mozgawa, W.; Sitarz, M.; Król, M. Spectroscopic Characterization of Silicate Amorphous Materials. In Molecular Spectroscopy—Experiment and Theory: From Molecules to Functional Materials; Springer: Cham, Switzerland, 2019; pp. 457–481. [Google Scholar]















| Pair (i-j) | qi (e) | Aij (eV) | qij (Å) | |
|---|---|---|---|---|
| Fe(II)-O | 1.2 | 11,777 | 0.2071 | 21.642 |
| Fe(III)-O | 1.8 | 19,952 | 0.1825 | 4.6583 |
| O-O | −1.2 | 1844 | 0.3436 | 192.58 |
| P-O | 3.0 | 27,722 | 0.1819 | 86.860 |
| Ca-O | 1.2 | 131,400 | 0.1875 | 60.0 |
| Sr-O | 1.2 | 433,269,870 | 0.120561 | 78.25863 |
| Cell Parameter | Simulation | Reference | Difference (%) |
|---|---|---|---|
| SrO (space group Fm-3; COD-1011328) | |||
| V (Å3) | 140.181 | 132.963 | 5.43 |
| a (Å) | 5.195 | 5.104 | 1.78 |
| b (Å) | 5.195 | 5.104 | 1.78 |
| c (Å) | 5.195 | 5.104 | 1.78 |
| α (o) | 90.000 | 90.000 | |
| β (o) | 90.000 | 90.000 | |
| γ (o) | 90.000 | 90.000 | |
| Sr2P2O7 (space group Pmmm; COD-1528537) | |||
| V (Å3) | 637.422 | 634.429 | 0.47 |
| a (Å) | 8.855 | 8.870 | −0.17 |
| b (Å) | 13.306 | 13.270 | 0.29 |
| c (Å) | 5.409 | 5.390 | 0.36 |
| α (o) | 90.000 | 90.000 | |
| β (o) | 90.000 | 90.000 | |
| γ (o) | 90.000 | 90.000 | |
| Sr(PO3)2 (space group P121/c1; COD-2008912) | |||
| V (Å3) | 960.913 | 998.300 | −3.75 |
| a (Å) | 7.073 | 7.209 | −1.89 |
| b (Å) | 7.808 | 7.953 | −1.82 |
| c (Å) | 17.399 | 17.414 | −0.09 |
| α (o) | 90.000 | 90.000 | |
| β (o) | 89.772 | 90.640 | −0.96 |
| γ (o) | 90.000 | 90.000 | |
| SrFe3(PO4)3O (space group P2/m; COD-1531869) | |||
| V (Å3) | 491.646 | 486.588 | 1.04 |
| a (Å) | 7.571 | 7.540 | 0.41 |
| b (Å) | 6.357 | 6.348 | 0.15 |
| c (Å) | 10.381 | 10.316 | 0.63 |
| α (o) | 90.000 | 90.000 | |
| β (o) | 100.261 | 99.740 | 0.52 |
| γ (o) | 90.000 | 90.000 | |
| SrFe3(PO4)3 (space group Imma; COD-1521446) | |||
| V (Å3) | 953.990 | 916.270 | 4.12 |
| a (Å) | 10.396 | 10.452 | −0.54 |
| b (Å) | 13.712 | 13.429 | 2.11 |
| c (Å) | 6.692 | 6.528 | 2.52 |
| α (o) | 90.000 | 90.000 | |
| β (o) | 90.000 | 90.000 | |
| γ (o) | 90.000 | 90.000 | |
| SrFe2(P2O7)2 (space group P-1; COD-2003248) | |||
| V (Å3) | 251.857 | 255.119 | −1.28 |
| a (Å) | 4.784 | 4.795 | −0.23 |
| b (Å) | 7.155 | 7.108 | 0.66 |
| c (Å) | 7.758 | 7.830 | −0.91 |
| α (o) | 88.072 | 89.830 | −1.96 |
| β (o) | 89.162 | 87.590 | 1.80 |
| γ (o) | 71.615 | 73.110 | −2.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goj, P.; Wajda, A.; Stoch, P. Development of a New Sr-O Parameterization to Describe the Influence of SrO on Iron-Phosphate Glass Structural Properties Using Molecular Dynamics Simulations. Materials 2021, 14, 4326. https://doi.org/10.3390/ma14154326
Goj P, Wajda A, Stoch P. Development of a New Sr-O Parameterization to Describe the Influence of SrO on Iron-Phosphate Glass Structural Properties Using Molecular Dynamics Simulations. Materials. 2021; 14(15):4326. https://doi.org/10.3390/ma14154326
Chicago/Turabian StyleGoj, Pawel, Aleksandra Wajda, and Pawel Stoch. 2021. "Development of a New Sr-O Parameterization to Describe the Influence of SrO on Iron-Phosphate Glass Structural Properties Using Molecular Dynamics Simulations" Materials 14, no. 15: 4326. https://doi.org/10.3390/ma14154326
APA StyleGoj, P., Wajda, A., & Stoch, P. (2021). Development of a New Sr-O Parameterization to Describe the Influence of SrO on Iron-Phosphate Glass Structural Properties Using Molecular Dynamics Simulations. Materials, 14(15), 4326. https://doi.org/10.3390/ma14154326