Structural Insights of Electrical Aging in PZT Thin Films as Revealed by In Situ Biasing X-ray Diffraction
Abstract
:1. Introduction
2. Materials and Methods
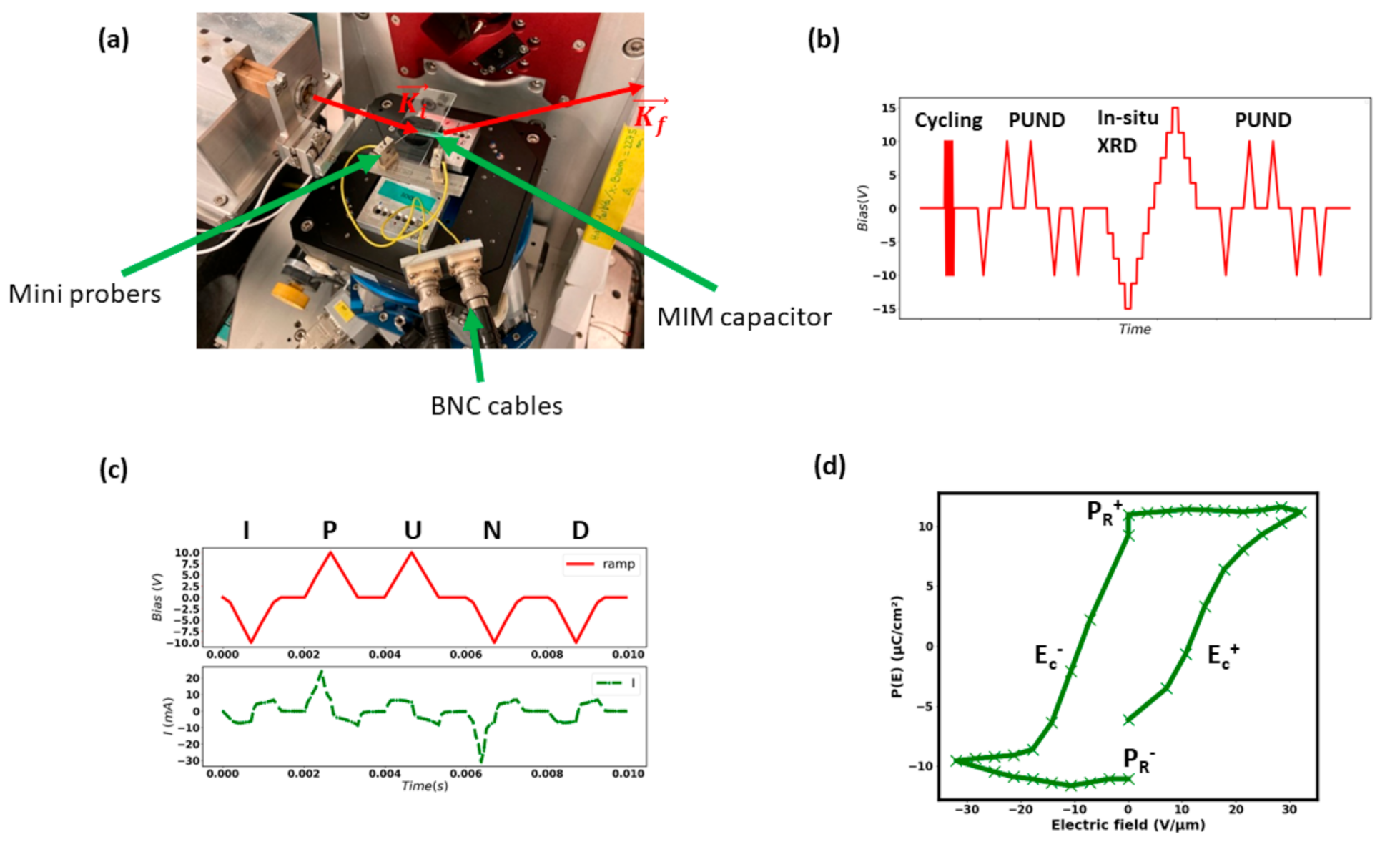
2.1. In Situ Biasing X-ray Diffraction Experiment
2.2. Aging and Polarization Measurement
3. Results and Discussions
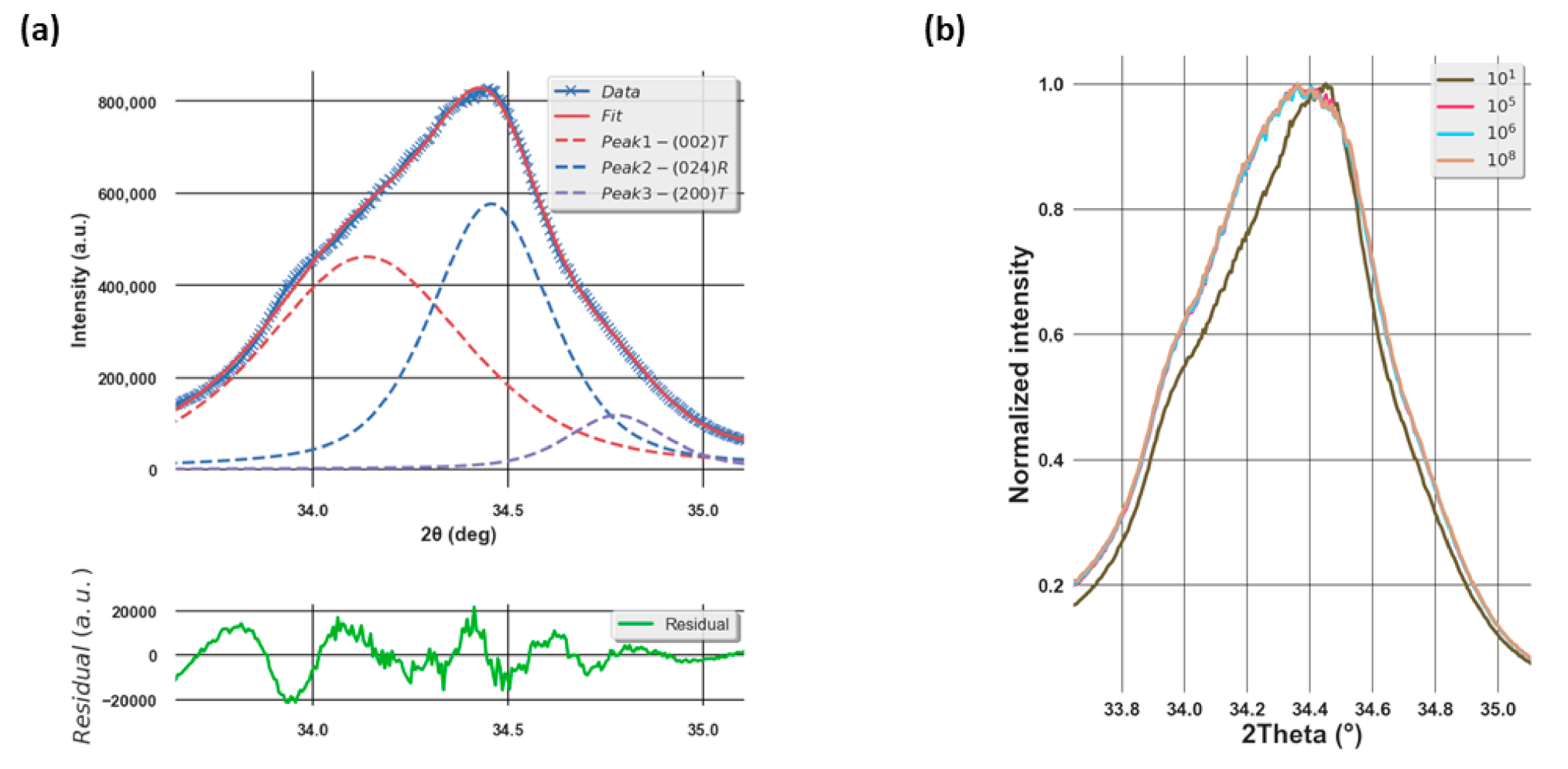
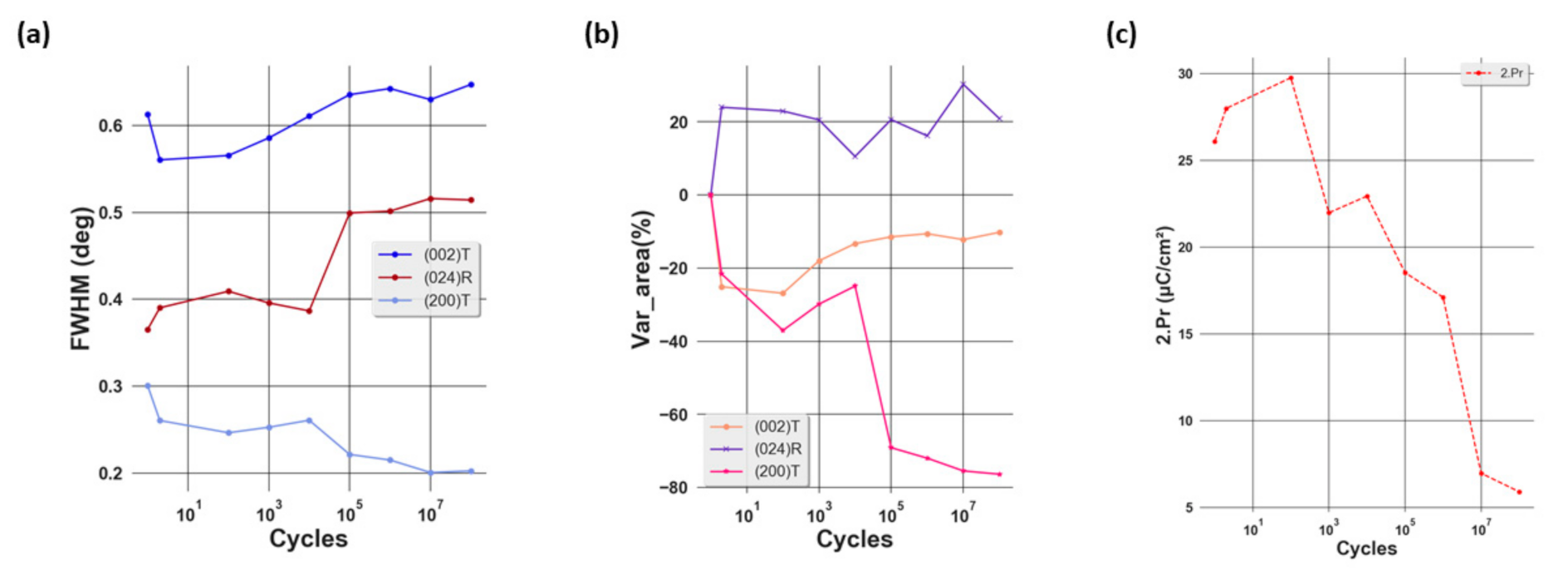
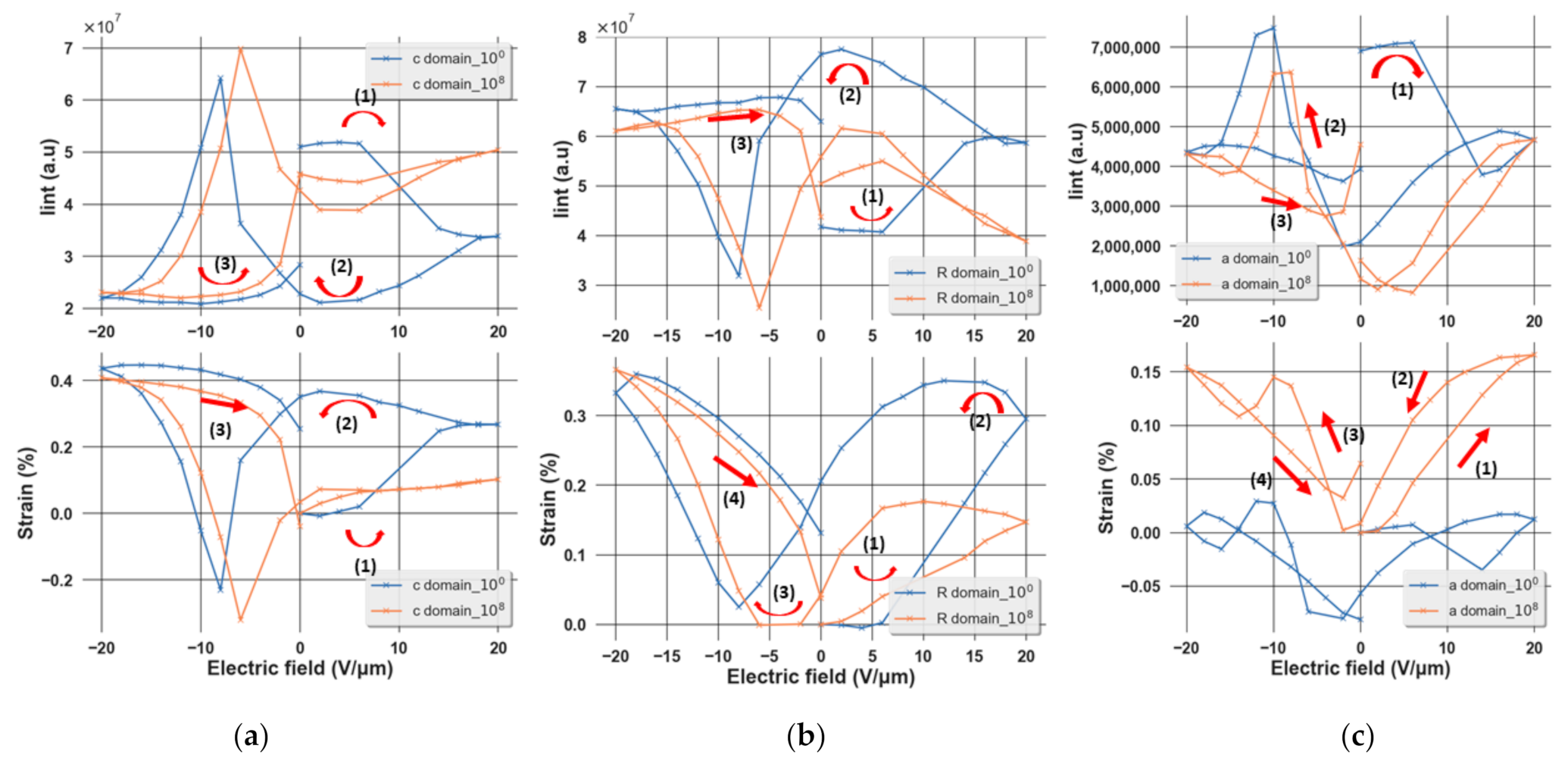
3.1. The Impact of Electric Field Cycling on the Structural Properties of PZT
3.2. Evolution of Piezoelectric Coefficient d33,eff during Aging
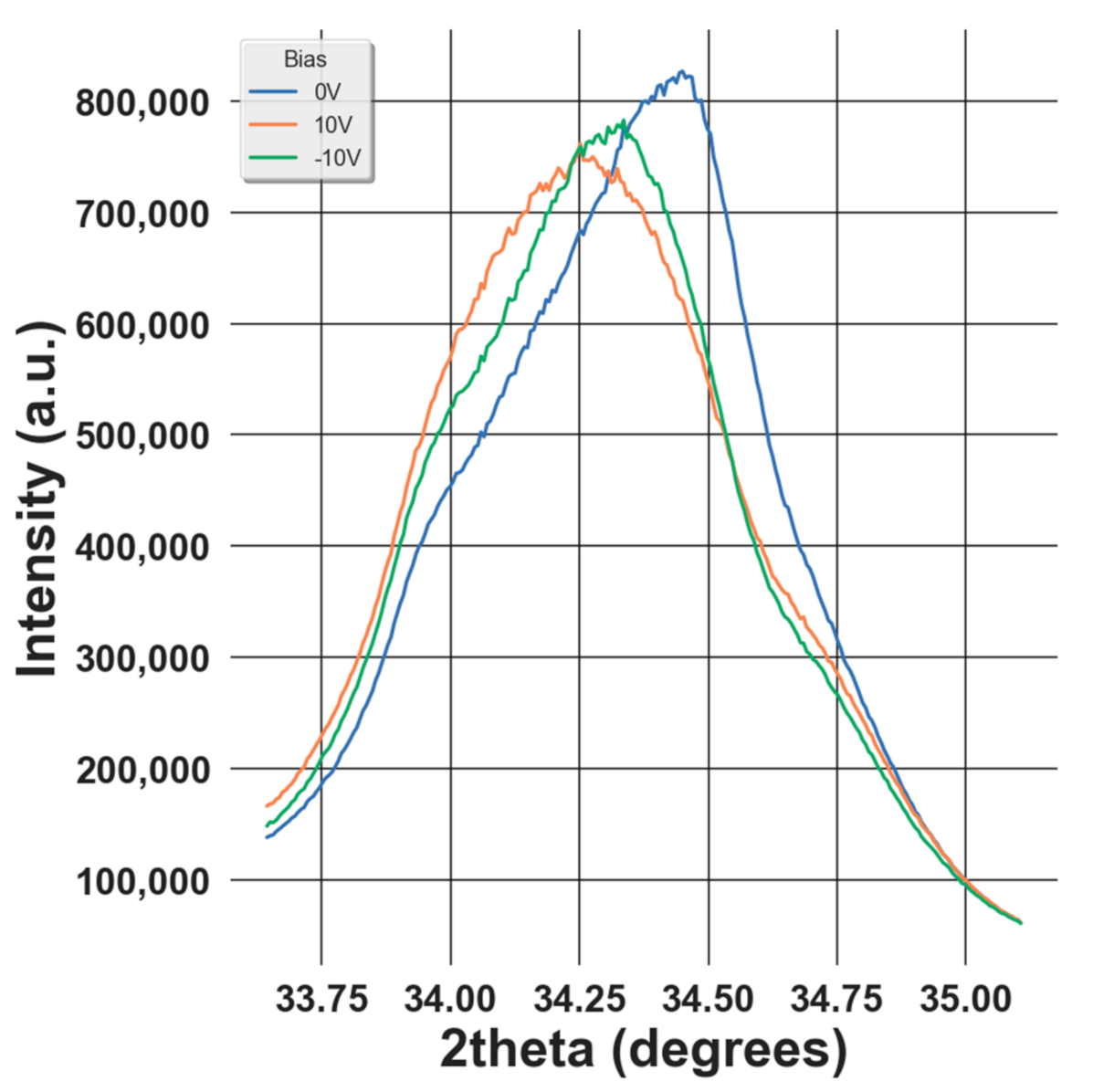
3.3. Evolution of Domain Behavior during Aging
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jaffe, H.; Berlincourt, D.A. Piezoelectric transducer materials. Proc. IEEE 1965, 53, 1372–1386. [Google Scholar] [CrossRef]
- Toprak, A.; Tigli, O. Piezoelectric energy harvesting: State-of-the-art and challenges. Appl. Phys. Rev. 2014, 1, 031104. [Google Scholar] [CrossRef]
- Tressler, J.F.; Alkoy, S.; Newnham, R.E. Piezoelectric Sensors and Sensor Materials. J. Electroceram. 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Lobl, H.P.; Klee, M.; Metzmacher, C.; Brand, W.; Milsom, R.; Lok, P.; Van Straten, F. Piezoelectric materials for BAW resonators and filters. In Proceedings of the 2001 IEEE Ultrasonics Symposium. Proceedings. An International Symposium (Cat. No.01CH37263), Atlanta, GA, USA, 7–10 October 2001; Volume 1, pp. 807–811. [Google Scholar] [CrossRef]
- Takasu, H. The Ferroelectric Memory and its Applications. J. Electroceram. 2000, 4, 327–338. [Google Scholar] [CrossRef]
- Randall, D.J.; Barber, R.W. Whatmore, Ferroelectric domain configurations in a modified-PZT ceramic. J. Mater. Sci. 1987, 22, 925–931. [Google Scholar] [CrossRef]
- Kim, Y.; Han, H.; Vrejoiu, I.; Lee, W.; Hesse, D.; Alexe, M. Origins of domain wall pinning in ferroelectric nanocapacitors. Nano Converg. 2014, 1, 24. [Google Scholar] [CrossRef] [Green Version]
- Hanzig, J.; Zschornak, M.; Hanzig, F.; Mehner, E.; Stöcker, H.; Abendroth, B.; Röder, C.; Talkenberger, A.; Schreiber, G.; Rafaja, D.; et al. Migration-induced field-stabilized polar phase in strontium titanate single crystals at room temperature. Phys. Rev. B 2013, 88, 024104. [Google Scholar] [CrossRef]
- Kholkin, L.; Tagantsev, A.K.; Colla, E.L.; Taylor, D.V.; Setter, N. Piezoelectric and dielectric aging in pb(zr,ti)o3 thin films and bulk ceramics. Integr. Ferroelectr. 1997, 15, 317–324. [Google Scholar] [CrossRef]
- Meng, X.J.; Sun, J.L.; Yu, J.; Wang, G.S.; Guo, S.L.; Chu, J.H. Enhanced fatigue property of PZT thin films using LaNiO3 thin layer as bottom electrode. Appl. Phys. A 2001, 73, 323–325. [Google Scholar] [CrossRef]
- Shepard, J.F.; Chu, F.; Kanno, I.; Trolier-McKinstry, S. Characterization and aging response of the d31 piezoelectric coefficient of lead zirconate titanate thin films. J. Appl. Phys. 1999, 85, 6711–6716. [Google Scholar] [CrossRef]
- Rhun, G.L.; Poullain, G.; Bouregba, R.; Leclerc, G. Fatigue properties of oriented PZT ferroelectric thin films. J. Eur. Ceram. Soc. 2005, 25, 2281–2284. [Google Scholar] [CrossRef]
- Shepard, J.F.; Chu, F.; Moses, P.J.; Trolier-McKinstry, S. The Influence of Film Thickness on the Magnitude and Aging Behavior of the Transverse Piezoelectric Coefficient (d31) of PZT Thin Films. MRS Online Proc. Libr. (OPL) 1997, 493. [Google Scholar] [CrossRef]
- Menou, N.; Muller, C.; Baturin, I.S.; Kuznetsov, D.K.; Shur, V.Y.; Hodeau, J.L.; Schneller, T. In Situ synchrotron X-ray diffraction study of electrical field induced fatigue in Pt/PbZr0.45Ti0.55O3/Pt ferroelectric capacitors. J. Phys. Condens. Matter. 2005, 17, 7681–7688. [Google Scholar] [CrossRef]
- Christman, J.A.; Woolcott, R.R.; Kingon, A.I.; Nemanich, R.J. Piezoelectric measurements with atomic force microscopy. MRS Online Proc. Libr. Arch. 1998, 541, 4. [Google Scholar]
- Kuffer, O.; Maggio-Aprile, I.; Triscone, J.-M.; Fischer, O.; Renner, C. Piezoelectric response of epitaxial Pb(Zr0.2Ti0.8)O3 films measured by scanning tunneling microscopy. Appl. Phys. Lett. 2000, 77, 1701–1703. [Google Scholar] [CrossRef] [Green Version]
- Kovacova, V.; Vaxelaire, N.; le Rhun, G.; Gergaud, P.; Schmitz-Kempen, T.; Defay, E. Correlation between electric-field-induced phase transition and piezoelectricity in lead zirconate titanate films. Phys. Rev. B 2014, 90, 140101. [Google Scholar] [CrossRef] [Green Version]
- Kholkin, L.; Wütchrich, C.; Taylor, D.V.; Setter, N. Interferometric measurements of electric field-induced displacements in piezoelectric thin films. Rev. Sci. Instrum. 1996, 67, 1935–1941. [Google Scholar] [CrossRef]
- Lefki, K.; Dormans, G.J.M. Measurement of piezoelectric coefficients of ferroelectric thin films. J. Appl. Phys. 1994, 76, 1764–1767. [Google Scholar] [CrossRef]
- Daniels, J.E.; Jo, W.; Rödel, J.; Jones, J.L. Electric-field-induced phase transformation at a lead-free morphotropic phase boundary: Case study in a 93%(Bi0.5Na0.5)TiO3–7% BaTiO3 piezoelectric ceramic. Appl. Phys. Lett. 2009, 95, 032904. [Google Scholar] [CrossRef] [Green Version]
- Hinterstein, M.; Rouquette, J.; Haines, J.; Papet, P.; Knapp, M.; Glaum, J.; Fuess, H. Structural Description of the Macroscopic Piezo- and Ferroelectric Properties of Lead Zirconate Titanate. Phys. Rev. Lett. 2011, 107, 077602. [Google Scholar] [CrossRef] [PubMed]
- Pramanick, A.; Damjanovic, D.; Daniels, J.E.; Nino, J.C.; Jones, J.L. Origins of Electro-Mechanical Coupling in Polycrystalline Ferroelectrics During Subcoercive Electrical Loading. J. Am. Ceram. Soc. 2011, 94, 293–309. [Google Scholar] [CrossRef]
- Allouche, B.; Gueye, I.; Rhun, G.L.; Gergaud, P.; Vaxelaire, N. In-Situ X-ray diffraction on functional thin films using a laboratory source during electrical biasing. Mater. Des. 2018, 154, 340–346. [Google Scholar] [CrossRef]
- Wallace, M.; Johnson-Wilke, R.L.; Esteves, G.; Fancher, C.M.; Wilke, R.H.; Jones, J.L.; Trolier-McKinstry, S. In Situ measurement of increased ferroelectric/ferroelastic domain wall motion in declamped tetragonal lead zirconate titanate thin films. J. Appl. Phys. 2015, 117, 054103. [Google Scholar] [CrossRef] [Green Version]
- Tan, G.; Kweon, S.H.; Shibata, K.; Yamada, T.; Kanno, I. In Situ XRD Observation of Crystal Deformation of Piezoelectric (K,Na)NbO 3 Thin Films. ACS Appl. Electron. Mater. 2020, 2, 2084–2089. [Google Scholar] [CrossRef]
- Vaxelaire, N.; Kovacova, V.; Bernasconi, A.; Le Rhun, G.; Alvarez-Murga, M.; Vaughan, G.B.; Defay, E.; Gergaud, P. Effect of structural in-depth heterogeneities on electrical properties of Pb(Zr0.52Ti0.48) O3 thin films as revealed by nano-beam X-ray diffraction. J. Appl. Phys. 2016, 120, 104101. [Google Scholar] [CrossRef]
- Martin, S.; Baboux, N.; Albertini, D.; Gautier, B. A new technique based on current measurement for nanoscale ferroelectricity assessment: Nano-positive up negative down. Rev. Sci. Instrum. 2017, 88, 023901. [Google Scholar] [CrossRef] [PubMed]
- Rojac, T.; Damjanovic, D. Domain walls and defects in ferroelectric materials. Jpn. J. Appl. Phys. 2017, 56, 10PA01. [Google Scholar] [CrossRef] [Green Version]
- Weitzing, H.; Schneider, G.A.; Steffens, J.; Hammer, M.; Hoffmann, M.J. Cyclic fatigue due to electric loading in ferroelectric ceramics. J. Eur. Ceram. Soc. 1999, 19, 1333–1337. [Google Scholar] [CrossRef]
- Herbiet, R.; Tenbrock, H.; Arlt, G. The aging behaviour of the complex material parameters ε, d s in ferroelectric PZT ceramics. Ferroelectrics 1987, 76, 319–326. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, K.; Bellec, E.; Zatterin, E.; Le Rhun, G.; Gergaud, P.; Vaxelaire, N. Structural Insights of Electrical Aging in PZT Thin Films as Revealed by In Situ Biasing X-ray Diffraction. Materials 2021, 14, 4500. https://doi.org/10.3390/ma14164500
Nguyen K, Bellec E, Zatterin E, Le Rhun G, Gergaud P, Vaxelaire N. Structural Insights of Electrical Aging in PZT Thin Films as Revealed by In Situ Biasing X-ray Diffraction. Materials. 2021; 14(16):4500. https://doi.org/10.3390/ma14164500
Chicago/Turabian StyleNguyen, Kien, Ewen Bellec, Edoardo Zatterin, Gwenael Le Rhun, Patrice Gergaud, and Nicolas Vaxelaire. 2021. "Structural Insights of Electrical Aging in PZT Thin Films as Revealed by In Situ Biasing X-ray Diffraction" Materials 14, no. 16: 4500. https://doi.org/10.3390/ma14164500
APA StyleNguyen, K., Bellec, E., Zatterin, E., Le Rhun, G., Gergaud, P., & Vaxelaire, N. (2021). Structural Insights of Electrical Aging in PZT Thin Films as Revealed by In Situ Biasing X-ray Diffraction. Materials, 14(16), 4500. https://doi.org/10.3390/ma14164500




