A FEM-Based Optimization Method for Driving Frequency of Contactless Magnetoelastic Torque Sensors in Steel Shafts
Abstract
1. Introduction
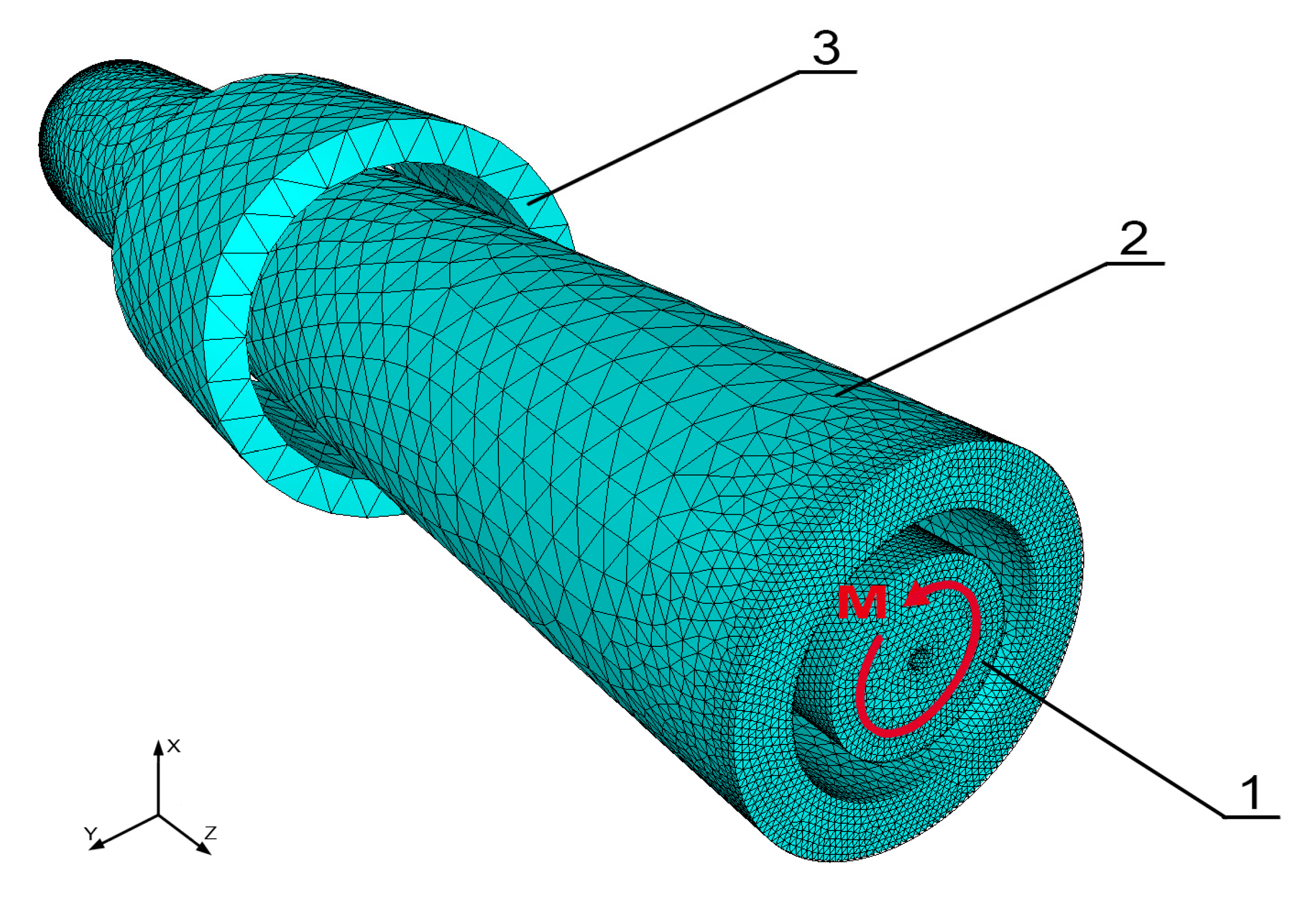
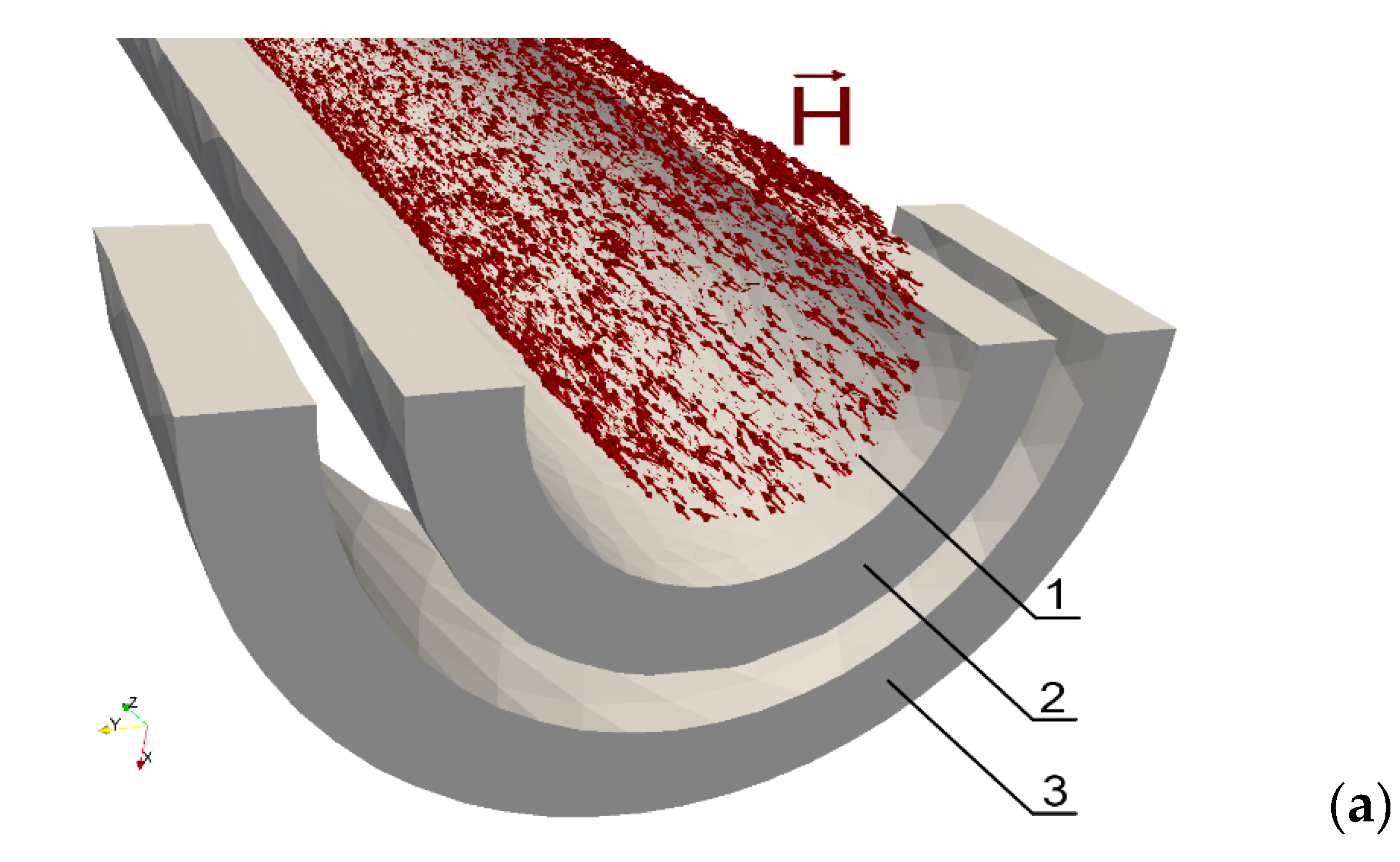
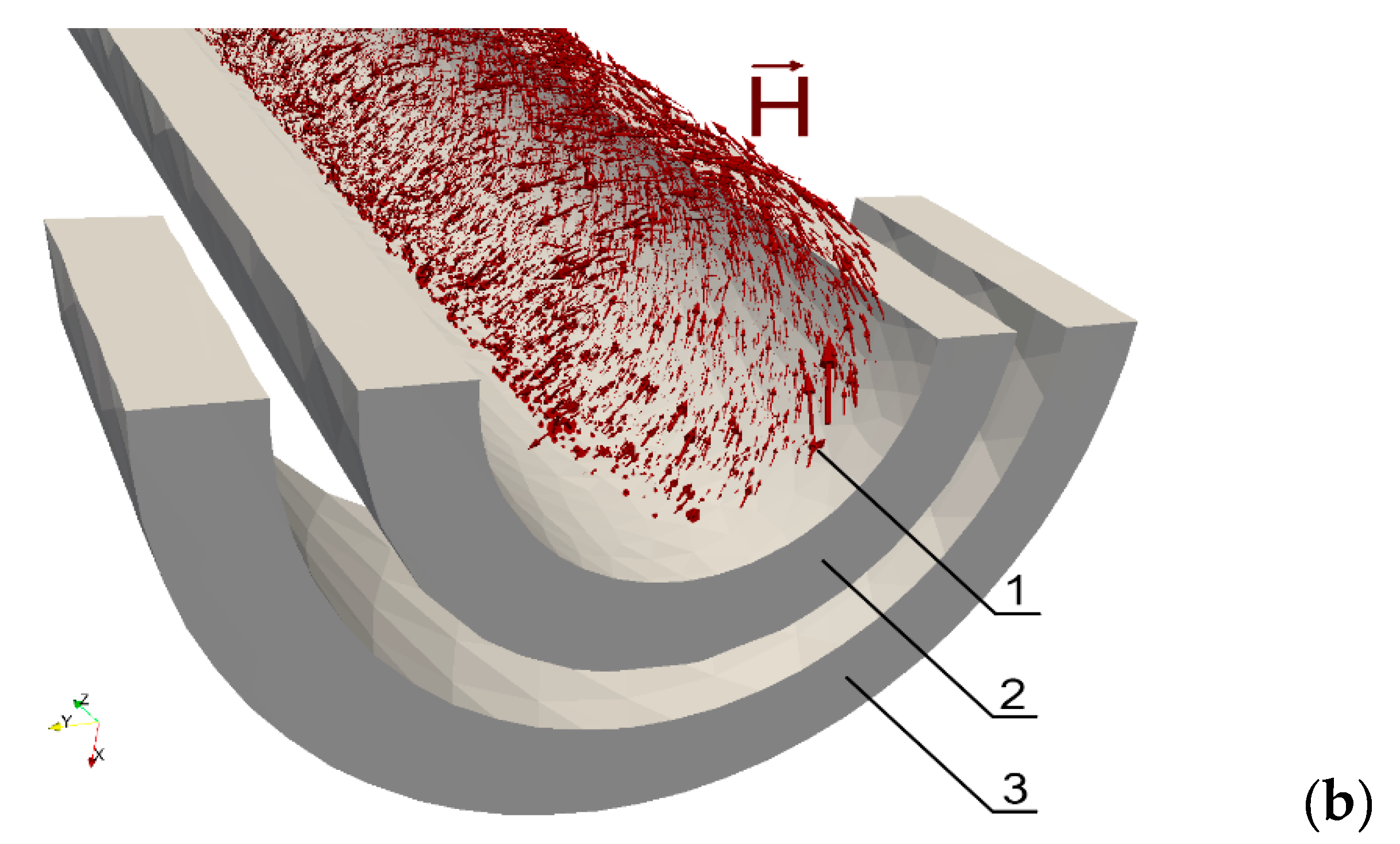
2. Finite Element Model for Development of Contactless Torque Sensors Utilizing Ferromagnetic Construction Steels
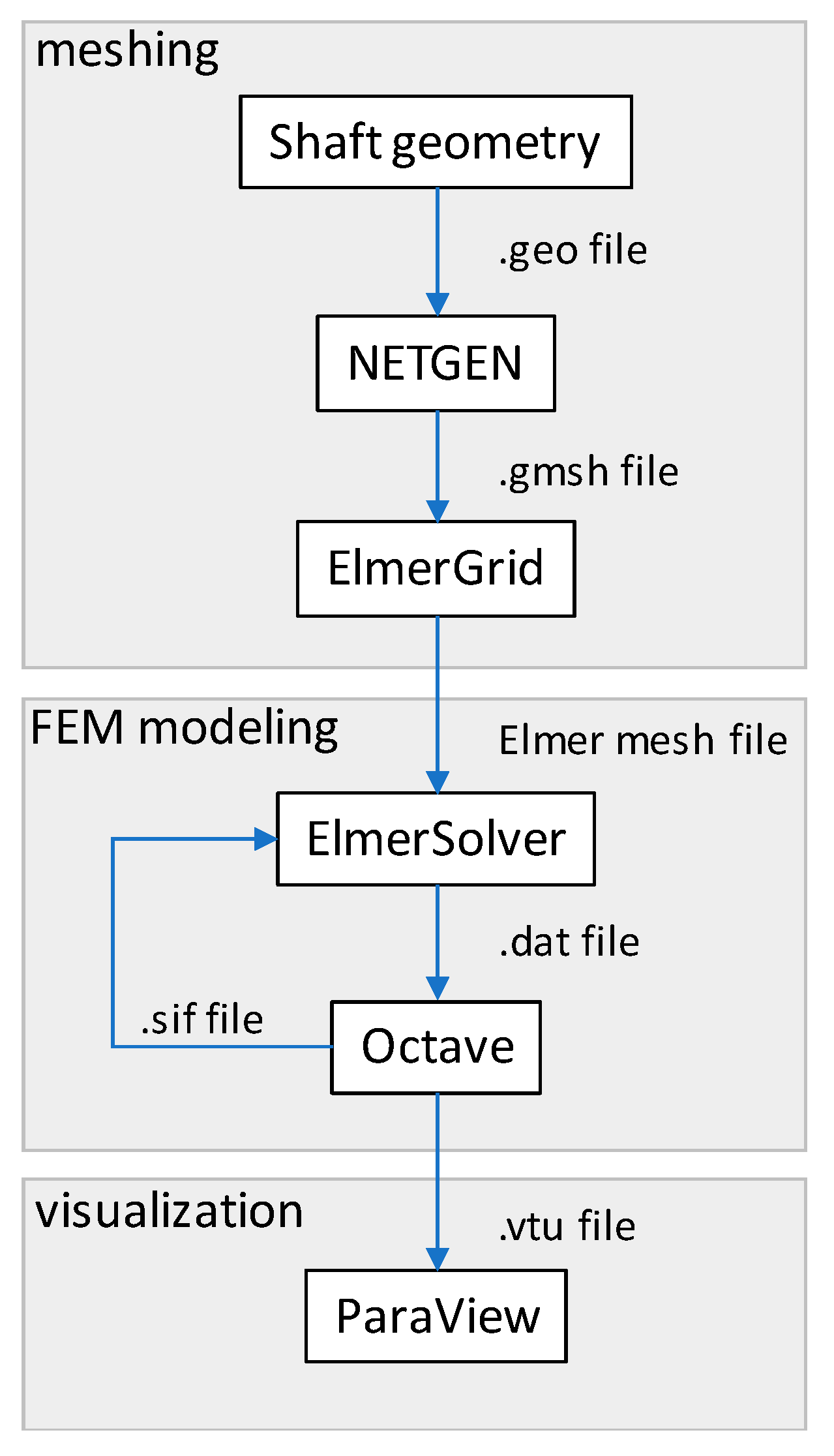
3. Implementation of Proposed Model in Open-Source FEM-Oriented Software
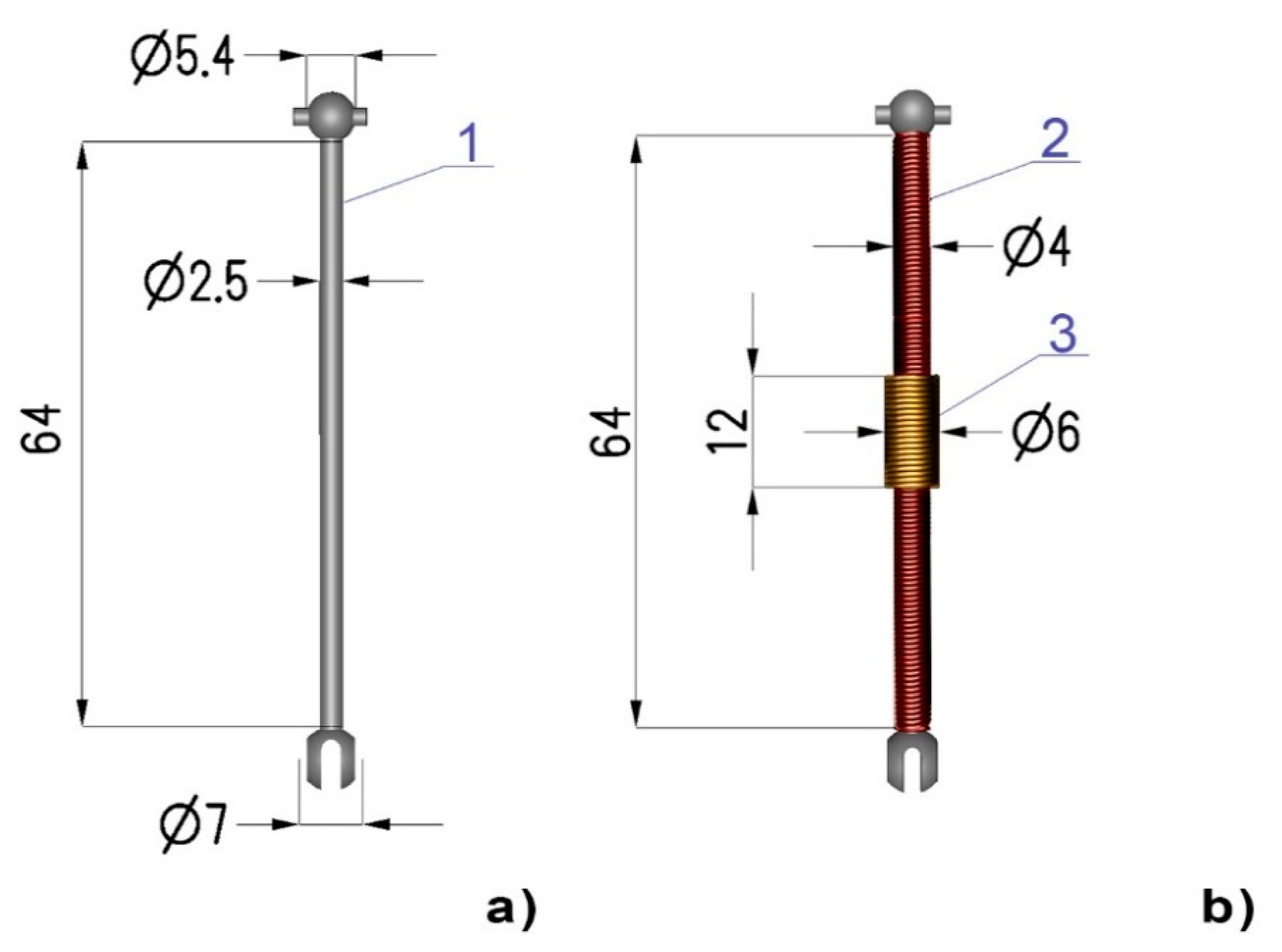
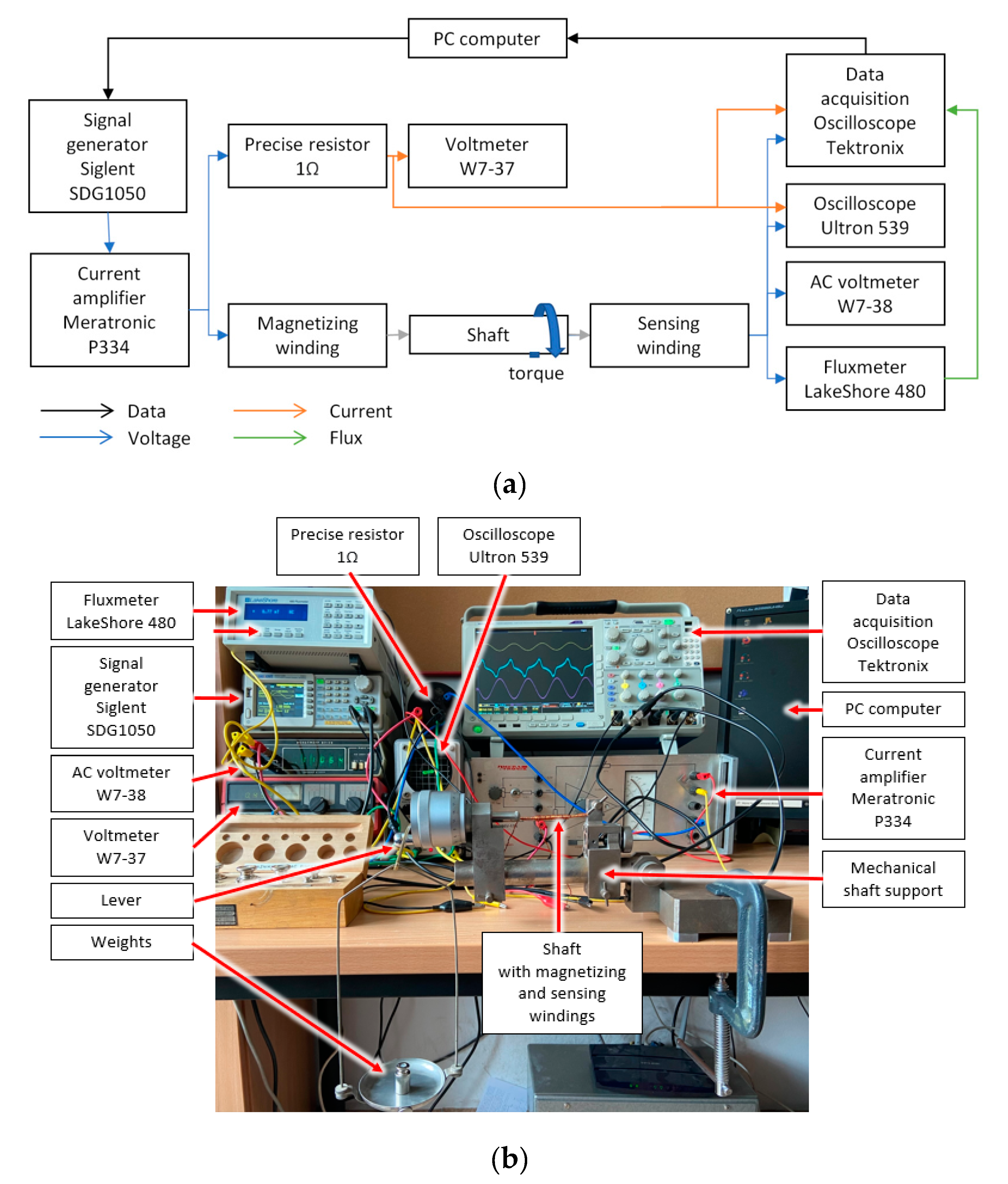
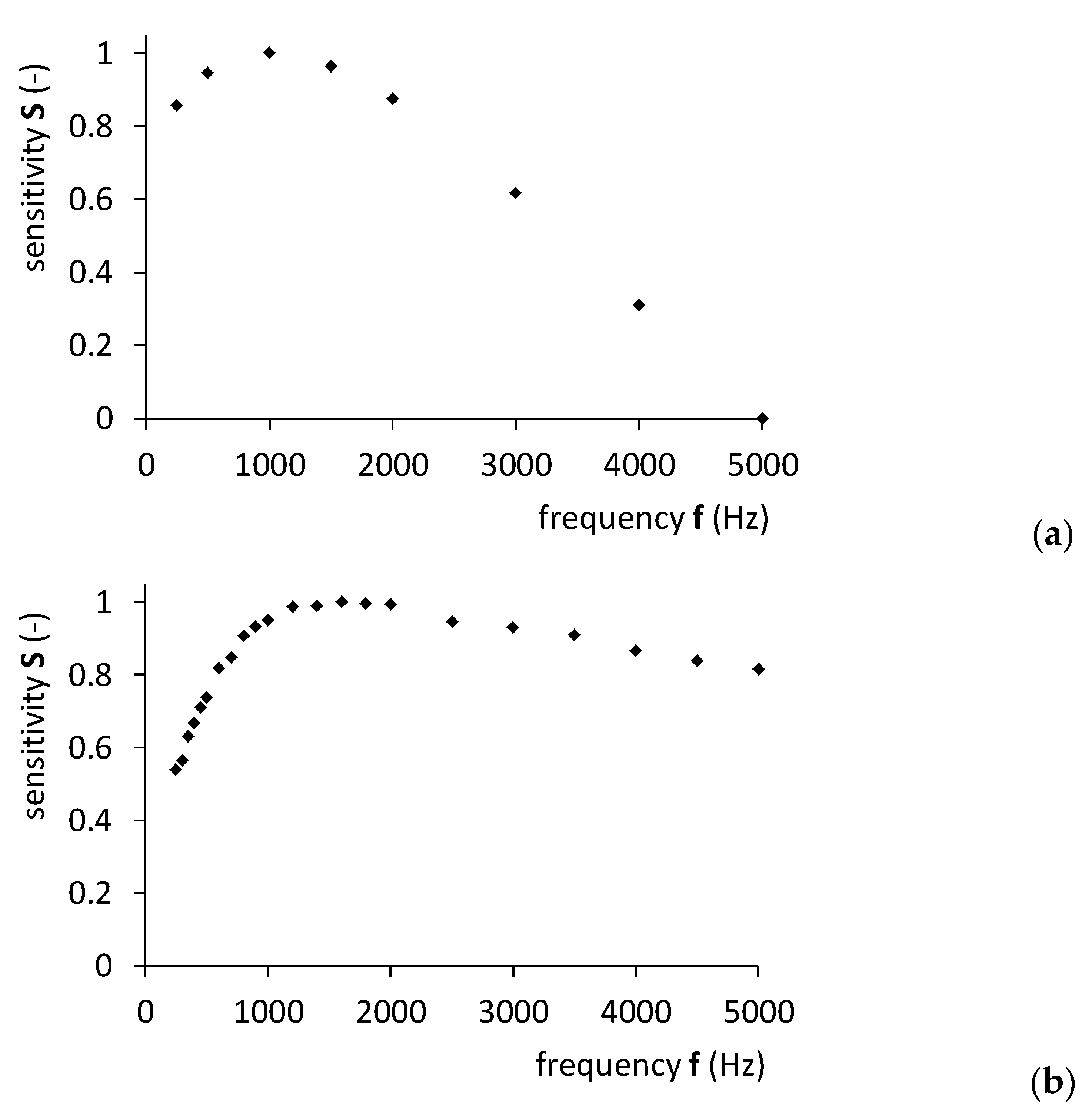
4. Experimental Validation of Proposed Model
- -
- SDG1050 signal generator (Siglent, Helmond, The Netherlands);
- -
- P334 current amplifier (Meratronic, Warsaw, Poland);
- -
- Precise resistor 1 kΩ (INCO, Warsaw, Poland);
- -
- Voltmeter W7-37 (Petersburg, Russia);
- -
- Fluxmeter LakeShore 480 (Lake Shore Cryotronics, Inc., Westerville, OH, USA);
- -
- AC voltmeter W7-38 (Leningrad, USSR);
- -
- Oscilloscope Ultron 539 (Munchen, Germany);
- -
- Oscilloscope Tektronix MDO4024C (Beaverton, OR, USA);
- -
- PC computer (X-KOM, Warsaw, Poland).
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Džapo, H.; Stare, Z.; Bobanac, N. Digital Measuring System for Monitoring Motor Shaft Parameters on Ships. IEEE Trans. Instrum. Meas. 2009, 58, 3702–3712. [Google Scholar] [CrossRef]
- Bonisławski, M.; Hołub, M.; Borkowski, T.; Kowalak, P. A Novel Telemetry System for Real Time, Ship Main Propulsion Power Measurement. Sensors 2019, 19, 4771. [Google Scholar] [CrossRef]
- Hammons, T.J.; Chanal, L. Measurement of torque in steam turbine-generator shafts following severe disturbances on the electrical supply system-analysis and implementation. IEEE Trans. Energy Convers. 1991, 6, 193–203. [Google Scholar] [CrossRef]
- Zhang, H.; Wenske, J.; Reuter, A.; Neshati, M. Proposals for a practical calibration method for mechanical torque measurement on the wind turbine drive train under test on a test bench. Wind Energy 2020, 23, 1048–1062. [Google Scholar] [CrossRef]
- Zhang, H.; De Luna, R.O.; Pilas, M.; Wenske, J. A study of mechanical torque measurement on the wind turbine drive train-ways and feasibilities. Wind Energy 2018, 21, 1406–1422. [Google Scholar] [CrossRef]
- Khan, H.; D’Imperio, M.; Cannella, F.; Caldwell, D.G.; Cuschieri, A.; Semini, C. Towards Scalable Strain Gauge-Based Joint Torque Sensors. Sensors 2017, 17, 1905. [Google Scholar] [CrossRef] [PubMed]
- Joubair, A.; Zhao, L.F.; Bigras, P.; Bonev, I.A. Use of a Force-Torque Sensor for Self-Calibration of a 6-DOF Medical Robot. Sensors 2016, 16, 798. [Google Scholar] [CrossRef]
- Tang, T.; Lin, H.-C.; Zhao, Y.; Chen, W.; Tomizuka, M. Autonomous alignment of peg and hole by force/torque measurement for robotic assembly. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016. [Google Scholar]
- O’Neill, J.J.; Stephens, T.K.; Kowalewski, T.M. Evaluation of Torque Measurement Surrogates as Applied to Grip Torque and Jaw Angle Estimation of Robotic Surgical Tools. IEEE Robot. Autom. Lett. 2018, 3, 3027–3034. [Google Scholar] [CrossRef]
- Jung, B.-J.; Kim, B.; Koo, J.C.; Choi, H.R.; Moon, H. Joint Torque Sensor Embedded in Harmonic Drive Using Order Tracking Method for Robotic Application. IEEE/ASME Trans. Mechatron. 2017, 22, 1594–1599. [Google Scholar] [CrossRef]
- Fleming, W. Automotive torque measurement: A summary of seven different methods. In Proceedings of the 32nd IEEE Vehicular Technology Conference, San Diego, CA, USA, 23–26 March 1982; pp. 71–78. [Google Scholar]
- Gao, B.; Chen, H.; Ma, Y.; Sanada, K. Design of nonlinear shaft torque observer for trucks with Automated Manual Transmission. Mechatronics 2011, 21, 1034–1042. [Google Scholar] [CrossRef]
- Kim, W.; Kang, C.M.; Son, Y.-S.; Chung, C.C. Nonlinear Steering Wheel Angle Control Using Self-Aligning Torque with Torque and Angle Sensors for Electrical Power Steering of Lateral Control System in Autonomous Vehicles. Sensors 2018, 18, 4384. [Google Scholar] [CrossRef]
- Bitar, S.; Probst, J.S.; Garshelis, I.J. Development of a Magnetoelastic Torque Sensor for Formula 1 and CHAMP Car Racing Applications. SAE Tech. Pap. Ser. 2000, 1, 85. [Google Scholar] [CrossRef]
- Stahl, K.; Höhn, B.-R.; Otto, H.-P.; Bäumler, R.; Hasl, C. Electro Mechanically Actuated Torque Sensing Multi-Disc. Clutch for Automatic Transmissions–Electro Mechanic Powershift Clutch; Springer: Berlin, Germany, 2013; pp. 85–104. [Google Scholar]
- Zhao, Z.; Chen, H.; Yang, Y. Fuzzy Determination of Target Shifting Time and Torque Control of Shifting Phase for Dry Dual Clutch Transmission. Math. Probl. Eng. 2014, 2014, 347490. [Google Scholar] [CrossRef]
- Zhao, Z.-G.; Chen, H.-J.; Yang, Y.-Y.; He, L. Torque coordinating robust control of shifting process for dry dual clutch transmission equipped in a hybrid car. Veh. Syst. Dyn. 2015, 53, 1269–1295. [Google Scholar] [CrossRef]
- Petreus, D.; Farca, C.; Dobra, P.; Moga, D. Torque measurement system design. In Proceedings of the 2008 IEEE International Conference on Automation, Quality and Testing, Robotics, Pasadena, CA, USA, 19–23 May 2008; pp. 174–177. [Google Scholar]
- Jin, H.; Lu, W.-Y. Strain Measurement of Microsamples Using Laser Interferometry. In Proceedings of the ASME 2006 International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006; pp. 563–567. [Google Scholar]
- Zupan, M.; Hemker, K.J. Application of fourier analysis to the laser based interferometric strain/displacement gage. Exp. Mech. 2002, 42, 214–220. [Google Scholar] [CrossRef]
- Zi, X.; Geng, S.; Zhao, S.; Shu, F. Measurement of short shaft power based on a digital speckle correlation method. Meas. Sci. Technol. 2015, 26, 045001. [Google Scholar] [CrossRef]
- Zi, X.; Geng, S.; Zhao, S.; Wang, Y.; Qin, W. Research on Principle of Saft Dynamic Torque Measurement Based on Digital Industrial Photogrammetry Technology. Chin. J. Lasers 2015, 42, 208002. [Google Scholar] [CrossRef][Green Version]
- Kruger, L.; Swart, P.L.; Chtcherbakov, A.A.; van Wyk, A.J. Non-contact torsion sensor using fibre Bragg gratings. Meas. Sci. Technol. 2004, 15, 1448–1452. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, L.; Yuan, Y.; Xu, G.; Liu, F. A Two Fiber Bragg Gratings Sensing System to Monitor the Torque of Rotating Shaft. Sensors 2016, 16, 138. [Google Scholar] [CrossRef]
- Silva, D.; Mendes, J.C.; Pereira, A.B.; Gégot, F.; Alves, L.N. Measuring Torque and Temperature in a Rotating Shaft Using Commercial SAW Sensors. Sensors 2017, 17, 1547. [Google Scholar] [CrossRef] [PubMed]
- Bieńkowski, A.; Szewczyk, R.; Salach, J. Industrial Application of Magnetoelastic Force and Torque Sensors. Acta Phys. Pol. A 2010, 118, 1008–1009. [Google Scholar] [CrossRef]
- Bieńkowski, A.; Szewczyk, R. The possibility of utilizing the high permeability magnetic materials in construction of magnetoelastic stress and force sensors. Sens. Actuators A Phys. 2004, 113, 270–276. [Google Scholar] [CrossRef]
- Dahle, O. The pressductor and the torductor—Two heavy-duty transducers based on magnetic stress sensitivity. IEEE Trans. Commun. Electron. 1964, 83, 752–758. [Google Scholar] [CrossRef]
- Salach, J.; Bieńkowski, A.; Szewczyk, R. The ring-shaped magnetoelastic torque sensors utilizing soft amorphous magnetic materials. J. Magn. Magn. Mater. 2007, 316, e607–e609. [Google Scholar] [CrossRef]
- Jackiewicz, D. Stress assessment in steel truss structures on the basis of magnetoelastic effects. Adv. Mechatron. Solut. 2016, 393, 467–472. [Google Scholar]
- Jackiewicz, D.; Kachniarz, M.; Bieńkowski, A.; Szewczyk, R. Possibilities of Application of the Magnetoelastic Effect for Stress Assessment in Construction Elements Made of Steel Considering Rayleigh Region. Adv. Intell. Syst. Comput. 2017, 543, 689–697. [Google Scholar] [CrossRef]
- Jackiewicz, D.; Nowicki, M.; Szewczyk, R.; Bienkowski, A.; Kachniarz, M.; Salach, J.; Kaminski, M. Application of Magnetoelastic Effects for Stress Assesment and Risk Mitigation in Constructions. J. Eng. Stud. Res. 2015, 21, 65–70. [Google Scholar] [CrossRef]
- Bieńkowski, A. Magnetoelastic Villari effect in Mn–Zn ferrites. J. Magn. Magn. Mater. 2000, 215–216, 231–233. [Google Scholar] [CrossRef]
- Dapino, M.; Smith, R.; Flatau, A. Structural magnetic strain model for magnetostrictive transducers. IEEE Trans. Magn. 2000, 36, 545–556. [Google Scholar] [CrossRef]
- Ostaszewska-Liżewska, A.; Szewczyk, R.; Råback, P.; Malinen, M. Modelling the Characteristics of Ring-Shaped Magnetoelastic Force Sensor in Mohri’s Configuration. Sensors 2020, 20, 266. [Google Scholar] [CrossRef] [PubMed]
- Szewczyk, R. Generalization of the Model of Magnetoelastic Effect: 3D Mechanical Stress Dependence of Magnetic Permeability Tensor in Soft Magnetic Materials. Materials 2020, 13, 4070. [Google Scholar] [CrossRef]
- Aydin, U.; Rasilo, P.; Martin, F.; Belahcen, A.; Daniel, L.; Haavisto, A.; Arkkio, A. Effect of multi-axial stress on iron losses of electrical steel sheets. J. Magn. Magn. Mater. 2019, 469, 19–27. [Google Scholar] [CrossRef]
- Sablik, M. Modeling stress dependence of magnetic properties for NDE of steels. Nondestruct. Test. Eval. 1989, 5, 49–65. [Google Scholar] [CrossRef]
- Kaido, C.; Hirose, N.; Iwasa, S.; Hayashi, T.; Waki, Y. Stress Dependence of Magnetic Properties in Non-oriented Electrical Steel Sheets. J. Magn. Soc. Jpn. 2010, 34, 140–145. [Google Scholar] [CrossRef]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Mohri, K. Review on recent advances in the field of amorphous-metal sensors and transducers. IEEE Trans. Magn. 1984, 20, 942–947. [Google Scholar] [CrossRef]
- Kwun, H. Investigation of the dependence of Barkhausen noise on stress and the angle between the stress and magnetization directions. J. Magn. Magn. Mater. 1985, 49, 235–240. [Google Scholar] [CrossRef]
- Stuelpnagel, J. On the Parametrization of the Three-Dimensional Rotation Group. SIAM Rev. 1964, 6, 422–430. [Google Scholar] [CrossRef]
- Available online: https://linuxmint.com/ (accessed on 8 April 2020).
- GNU Octave (Version 5.2.0). Available online: https://octave.org/doc/v5.2.0/ (accessed on 25 April 2020).
- Netgen/NGSolve. Available online: https://ngsolve.org/ (accessed on 23 November 2020).
- Elmer. Available online: https://www.csc.fi/web/elmer (accessed on 1 November 2020).
- Paraview. Available online: https://www.paraview.org/ (accessed on 1 November 2020).
- Salach, J.; Bienskowski, A.; Szewczyk, R. Magnetoelastic, ring-shaped torque sensors with the uniform stress distribution. J. Autom. Mob. Robot. Intell. Syst. 2013, 1, 66–68. [Google Scholar]
- Nowak, P.; Nowicki, M.; Juś, A.; Szewczyk, R. Utilization of Eddy Current Tomography in Automotive Industry. Acta Phys. Pol. A 2017, 131, 1168–1170. [Google Scholar] [CrossRef]
- Silveyra, J.M.; Garrido, J.M.C. On the modelling of the anhysteretic magnetization of homogeneous soft magnetic materials. J. Magn. Magn. Mater. 2021, in press. [Google Scholar]


| Torque [Nm] | 0 | 1.3 | ||
|---|---|---|---|---|
| Frequency [Hz] | Voltage [mV] | Flux Density [mT] | Voltage [mV] | Flux Density [mT] |
| 50 | 11.2 | 101.57 | 9.54 | 86.6 |
| 60 | 13.29 | 100.59 | 11.38 | 85.91 |
| 70 | 15.36 | 99.55 | 13.17 | 85.24 |
| 80 | 17.38 | 98.63 | 14.9 | 84.6 |
| 90 | 19.39 | 97.79 | 16.68 | 83.92 |
| 100 | 21.37 | 96.94 | 18.4 | 83.28 |
| 120 | 25.24 | 95.42 | 21.78 | 82.07 |
| 140 | 29 | 93.93 | 25 | 80.88 |
| 160 | 32.64 | 92.47 | 28.2 | 79.71 |
| 180 | 36.16 | 91.06 | 31.3 | 78.59 |
| 200 | 39.57 | 89.7 | 34.2 | 77.48 |
| 250 | 47.6 | 86.5 | 41.4 | 74.98 |
| 300 | 55.25 | 83.63 | 48.1 | 72.63 |
| 350 | 62.37 | 81.01 | 54.44 | 70.52 |
| 400 | 69.12 | 78.64 | 60.42 | 68.55 |
| 450 | 75.49 | 76.43 | 66.1 | 66.73 |
| 500 | 81.57 | 74.37 | 71.5 | 65.04 |
| 600 | 92.8 | 70.69 | 81.6 | 61.98 |
| 700 | 103.26 | 67.45 | 90.9 | 59.26 |
| 800 | 112.8 | 64.57 | 99.54 | 56.82 |
| 900 | 121.7 | 61.99 | 107.5 | 54.62 |
| 1000 | 130.1 | 59.66 | 115 | 52.64 |
| 1200 | 145.5 | 55.64 | 128.8 | 49.16 |
| 1400 | 159.5 | 52.28 | 141.2 | 46.22 |
| 1600 | 172.3 | 49.44 | 152.6 | 43.72 |
| 1800 | 184.3 | 47.02 | 163.2 | 41.57 |
| 2000 | 195.6 | 44.92 | 173.2 | 39.7 |
| 2500 | 221.9 | 40.74 | 196.1 | 35.96 |
| 3000 | 245.7 | 37.6 | 217 | 33.14 |
| 3500 | 268 | 35.15 | 236.5 | 30.94 |
| 4000 | 289 | 33.18 | 254.6 | 29.176 |
| 4500 | 309.3 | 31.55 | 272.2 | 27.72 |
| 5000 | 328.7 | 30.18 | 289 | 26.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostaszewska-Liżewska, A.; Nowicki, M.; Szewczyk, R.; Malinen, M. A FEM-Based Optimization Method for Driving Frequency of Contactless Magnetoelastic Torque Sensors in Steel Shafts. Materials 2021, 14, 4996. https://doi.org/10.3390/ma14174996
Ostaszewska-Liżewska A, Nowicki M, Szewczyk R, Malinen M. A FEM-Based Optimization Method for Driving Frequency of Contactless Magnetoelastic Torque Sensors in Steel Shafts. Materials. 2021; 14(17):4996. https://doi.org/10.3390/ma14174996
Chicago/Turabian StyleOstaszewska-Liżewska, Anna, Michał Nowicki, Roman Szewczyk, and Mika Malinen. 2021. "A FEM-Based Optimization Method for Driving Frequency of Contactless Magnetoelastic Torque Sensors in Steel Shafts" Materials 14, no. 17: 4996. https://doi.org/10.3390/ma14174996
APA StyleOstaszewska-Liżewska, A., Nowicki, M., Szewczyk, R., & Malinen, M. (2021). A FEM-Based Optimization Method for Driving Frequency of Contactless Magnetoelastic Torque Sensors in Steel Shafts. Materials, 14(17), 4996. https://doi.org/10.3390/ma14174996







