Next Article in Journal
First-Principle Calculation on Inelastic Electron Scattering in Diamond and Graphite
Next Article in Special Issue
The Two-Domain Model Utilizing the Effective Pinning Energy for Modeling the Strain-Dependent Magnetic Permeability in Anisotropic Grain-Oriented Electrical Steels
Previous Article in Journal
Design and Validation of Additively Manufactured Metallic Cellular Scaffold Structures for Bone Tissue Engineering
Previous Article in Special Issue
A FEM-Based Optimization Method for Driving Frequency of Contactless Magnetoelastic Torque Sensors in Steel Shafts
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 15
Issue 9
10.3390/ma15093311
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

First-Principles Study on Possible Half-Metallic Ferrimagnetism in Double Perovskites Pb2XX′O6 (X = Ti, Zr, Hf, V, Nb and Ta, X′ = Tc, Ru, Os and Rh)

by
Bo-Yu Chen
1,
Po-Han Lee
1,2,* and
Yin-Kuo Wang
3,*
1
Affiliated Senior High School of National Taiwan Normal University, Taipei 10658, Taiwan
2
Department of Electro-Optical Engineering, National Taipei University of Technology, Taipei 10608, Taiwan
3
Center for General Education and Department of Physics, National Taiwan Normal University, Taipei 10610, Taiwan
*
Authors to whom correspondence should be addressed.
Materials 2022, 15(9), 3311; https://doi.org/10.3390/ma15093311
Submission received: 13 April 2022 / Revised: 2 May 2022 / Accepted: 2 May 2022 / Published: 5 May 2022
(This article belongs to the Collection Magnetoelastic Materials)
Browse Figures
Versions Notes

Abstract

:
Pb-based double perovskite compounds with chemical formula Phey have abundant physical properties in the spintronic field. Among all the features, the spin interaction of half-metallic (HM) is regarded as an important performance measure because of its high potential in spintronic devices. In this research study, we calculate density of state (DOS) to investigate possible half-metal candidates by executing structural optimization based on the method of generalized gradient approximation (GGA) and strong correlation effect (GGA + U). Furthermore, following the earlier methods by calculating and comparing energy difference of various compounds with the four initial magnetic states: ferromagnetic, ferrimagnetic, antiferromagnetic and nonmagnetic, we can determine which magnetic state is more stable. Results indicate that there are 13 possible ferrimagnetic HM candidates in these combinations, including Pb2NbTcO6, Pb2TaTcO6, Pb2TiRuO6, Pb2ZrRuO6, Pb2HfRuO6, Pb2VRuO6, Pb2NbRuO6, Pb2TadRuO6, Pb2ZrOsO6, Pb2HfOsO6, Pb2VOsO6, Pb2ZrRhO6 and Pb2HfRhO6 under GGA and GGA + U schemes. The stability of analysis by analyzing the energy gap illustrates that all 13 possible candidates are half metals and ferrimagnetic states, so our studies could provide guidelines for scientists to fabricate new double perovskites in future.

1. Introduction

Half metals (HMs) are potential and popular materials in the field of spintronics device research [1,2,3,4,5,6,7,8] owing to their function of inducing 100% spin polarization. With an aim to discover more HMs, the group of double perovskites is an ideal selection because they account for an enormous majority of known HMs, including Sr2FeMoO6 [5,9,10,11], Sr2FeReO6 [9,12], La2VTcO6 [12], La2VCuO6 [12], La2MoTcO6 [13], La2WReO6 [14], BiPbVRuO6 [15], Bi2CrCoO6 [16] and Bi2FeNiO6 [16], mixed valance perovskite structures manganese oxide Ln0.5Ca0.5MnO3 [17] and Ln0.7Sr0.3MnO3 [18,19], spinel FeCr2S4 [20,21] and Mn-doping GaAs [22,23]. On the other hand, the topic of magnetism has also received significant attention in the discussion of double perovskites family, the magnetic state ranging from antiferromagnetic [24,25,26,27,28,29] to ferrimagnetic [30,31,32] and ferromagnetic [33,34,35]. Among them, ferrimagnetic materials are widely used in non-volatile memory devices such as hard drives, which utilize their ability to easily switch the spins of electrons and be magnetized.
Due to the structural and compositional flexibility of the double perovskites structure, many researchers are continually disclosing new HM materials from the group of double perovskites A2XX′O6, where A is a relatively large cation [36,37,38], and X and X′ are metal ions. It is anticipated that study of the replacement of the large lead(II) cation in A site element [39] could provide opportunities to find stable HM candidates in related research, because Pb2+ has a suitable size to be combined with smaller X and X′ site cations to satisfy the tolerance criterion (t) noted by Goldschmidt [40], with t having a value close to unity for stable perovskite structures. In this regard, some compounds of Pb2XX′O6 in previous studies were experimentally synthesized [41,42,43], in which there are indeed some HM materials, i.e., Pb2TcReO6 [44], Pb2MoOsO6 [44], Pb2FeRuO6 [45], Pb2FeMoO6 [45], Pb2CrRuO6 [46] and Pb2CrOsO6 [46]. It is evident that the choice to select X and X′ allows one to decide the physical properties of double perovskites because of their cation size and valance distribution of d (or f) orbitals [47,48,49].
However, in the strictest sense, perfect half-metallicity is limited to ideal crystals at zero Kelvin temperature; real HMs mainly exhibit dramatic decreases in the spin polarization due to thermal effects and intrinsic crystal and surface imperfection [50], which are ignored by the calculation of density functional theory (DFT) [51]. Nevertheless, for conquering the implicated synthesis processes of double perovskite compounds, some researchers indeed found good agreement of experimental synthesized results about HMs with the theory predictions such as Sr2FeReO6 [52,53]. For the magnetic property of Pb2MnWO6 [54], Ivanov et al. used DFT-based calculations to predict the presence of a low-temperature magnetic ordering, which matches their experimental results. Consequently, the DFT calculation also makes it possible to predict the properties of some compounds in the condition of zero Kelvin temperature, and provides limited but useful information at finite temperature.
Following the solid work that shows that some cyclical behaviors could be determined by the XX′ pairs [55,56], we will focus here on the transition metal combination of IVB/VB group and VIIB/VIIIB group and attempt to thoroughly investigate potential HM candidates in the group of Pb2XX′O6. The method with which we calculate these double perovskites is based on DFT and the procedure is shown as follows: First, we optimize our structure by the method of generalized gradient approximation (GGA) [57]. After that, through the process of optimization, we determine whether or not the material is an HM candidate by two rules: one is the integer spin magnetic moment from compounds, and the other one is the energy gap existing in the single-side channel provided by density of states (DOS). In other words, the band gap of either spin-up or spin-down is indeed observed and exists in the single channel. Next, the consideration of strong correlation effect (GGA + U) [58,59,60] is also checked to make sure that there is stability of the energy gap, which is then computationally convenient for accurate calculations of electronic structures. Last, the same method is executed repeatedly with four initial states, i.e., ferromagnetic (FM), ferrimagnetic (FiM), antiferromagnetic (AF) and nonmagnetic (NM). Finally, magnetic states of these double perovskites are then verified by the energetic comparison of these results.

2. Materials and Methods

The Pb-based double perovskites consist of Pb, IVB/VB transition metals (Ti, Zr, Hf, V, Nb and Ta) paired with VIIB/VIIIB transition metals (Tc, Ru, Os and Rh) and oxygen, as shown in Figure 1. In total, there are 24 kinds of compounds counted upon which structural optimization is executed in order to check which one is the more stable HM material candidate. Furthermore, this study begins with the four types of initial magnetic states, i.e., ferromagnetic (FM), ferrimagnetic (FiM), antiferromagnetic (AF) and nonmagnetic (NM) for each compound, as shown in Figure 2. Accordingly, based on results, comparison between each state can provide information about the stable situation for all compounds. Lastly, density of states (DOS) is analyzed for d-orbital electrons to confirm not only magnetic but also half-metallic properties. By doing so, HM candidates could be picked up through protracted and complex processes. Last, all candidates are examined in consideration of the strong correlation effect (GGA + U).
Next, we determine whether the structures are stable or not after full structural optimization, implying two structures being discussed. One is the tetragonal structure (space group of I4/mmm, No. 139), and it is made of two non-equivalent types of oxygen atoms, in which the locations of O1 atoms are on the z-axis and there are four O2 atoms existing on the xy-plane, as shown in Figure 1. Accordingly, they are the cases of F(i)M state. The other one is the tetragonal structure (space group of P4/mmm, No. 123) with non-equivalent types of oxygen atoms, in which the angle of X-O1-X′ is maintained at 180 ° and the angle of X-O2-X′ has been changed a little but is still near 180 ° during the process of structural optimization. This means that the symmetry reduction is deemed rather minor and the c/a ratio is very close to the value of 2 . These features could be found in the AF state.
In the FM and FiM states, each X and X′ ion has similar spin states (that is, (X, X, X′, X′) = (m, m, m′, m′) = FM or (m, m, −m′, −m′) = FiM), which can cause the assumption of the half-metallicity of the double perovskite. By the self-consistent process, most of the initial FM and FiM states all converge into one of the states. In the AF states, the spin state of (X, X, X′, X′) can be noted as (m, −m, m′, −m′). The induced equivalence in the charge is Q↑[X(X′)] = Q↓[X(X′)], which can be observed from the symmetry of the spin-up and spin-down in the total figure of density of state (DOS). No spin polarization is observed in the NM state. Calculation results for all four magnetic phases are performed to find the most stable magnetic phase. (However, when we put spin polarization into consideration, the calculation results show that the compounds become more stable.) The self-consistent process with high convergence requirement is also performed to guarantee the accuracy of the result.
In this research, we present electronic structure calculations with generalized gradient approximation (GGA) plus on-site coulomb interaction (GGA + U). Structural optimization calculations are carried out through the full-potential projector-augmented wave [61] (PAW) method by using the code of the Vienna Ab Initio Simulation Package (VASP) [62,63,64] to determine the theoretical lattice constraints and atomic positions. The calculation for the Brillouin zone is conducted using 8 × 8 × 6 Monkhorst–Pack k-grid sampling. The cut-off energy of the plane wave basis is set to 450 eV. The energy convergence criteria for the full structure optimization and self-consistent calculations are set to 1 × 10 − 5 and 1 × 10 − 7 eV, respectively. The Wigner–Seitz radius of the Pb atom is set as 3.3 atomic units (a.u.), 1.6 a.u. for O atom and 2.7 a.u. for X(X′) ion. For the final and equilibrium structures, the forces and stresses acting on all the atoms are less than 0.3 eV/Å and 0.9 kBar, respectively.

3. Results and Discussion

After calculation under the GGA scheme, we find that 13 out of the 24 compounds in the Pb2XX′O6 are categorized as HMs, including Pb2NbTcO6, Pb2TaTcO6, Pb2TiRuO6, Pb2ZrRuO6, Pb2HfRuO6, Pb2VRuO6, Pb2NbRuO6, Pb2TaRuO6, Pb2ZrOsO6, Pb2HfOsO6, Pb2VOsO6, Pb2ZrRhO6 and Pb2HfRhO6. Based on these results, Tc, Ru, Os and Rh are suitable for substitute X′ site element, and we follow this order to systemically discuss all possible HM candidates. For clearer description with the GGA scheme, Figure 3a–d describe the DOS of Pb2NbTcO6, Pb2TaTcO6 and PDOS of d-orbital in Pb2NbTcO6 and Pb2TaTcO6, respectively. In comparison with these figures, Figure 4a–d illustrate the same compounds just under the GGA + U scheme. Following the figure arrangement of GGA and GGA + U, Figure 5a–l and Figure 6a–l, Figure 7a–f and Figure 8a–f and Figure 9a–d and Figure 10a–d illustrate the DOS and PDOS of Pb2XRuO6 (X = Ti, Zr, Hf, V, Nb and Ta), Pb2XOsO6 (X = Zr, Hf and V) and Pb2XRhO6 (X = Zr and Hf), respectively.

3.1. FiM-HM Compounds: Pb2XTcO6 (X = Nb and Ta)

In Table 1, it shows the energy difference between AF and FiM states; note that ΔE = FiM—AF and their values are −21 and −96 meV/f.u. for Pb2NbTcO6 and Pb2TaTcO6, respectively. Furthermore, with the GGA + U scheme, the values of ΔE decrease to −26 and −178 meV/f.u., indicating a more stable state of FiM for these compounds, thus illustrating direct evidence that these materials are ferrimagnetic. Table 2 lists all the energy of AF and FiM states in detail.
As shown in Figure 3a,b, the band gaps of Pb2NbTcO6 and Pb2TaTcO6 occur in the spin-up channel, while some electrons occupy the Fermi level of the spin-down channel, which provides obvious evidence for HM materials. As to the second indicator for half-metal compound, it is the integer value of mtot. Here, the values of mtot are 2.000 μB/f.u. in the case of Pb2NbTcO6 and Pb2TaTcO6, which illustrates HM property for these compounds. In addition, Pb2TaTcO6 still maintains the possibility of being HM material under the GGA + U scheme with a little fluctuation of magnetism because the mtot value of Pb2TaTcO6 changes from 2.000 to 2.011 μB/f.u.
However, these variations (+U, the coulomb interaction potential) do not change the magnetic states of compounds; instead, the tendency of being FiM material under the GGA + U scheme is more stable than that under the GGA scheme. In addition, under these two schemes, the distributions of electrons whose energy is higher than Fermi energy are almost the same.
Next, we discuss the electronic configuration of the two compounds. For Pb2NbTcO6, the ideal electronic distributions of Nb and Tc we expected are Nb5+ (3d104s24p6: t02ge0g) at S = 0 and Tc3+(4d45s0:t42ge0g) at S = 1. From the result of calculations with the GGA method, the electron distributions are Nb2.9+(4d2.1) and Tc2.4+(4d4.6), and those with the GGA + U scheme are Nb3.1+(4d1.9) and Tc2.5+(4d4.5).
In the case of Pb2TaTcO6, the valance states are Ta5+ (4f145d06s0:t02ge0g) at S = 0 and Tc3+ (4d45s0:t42ge0g) at S = 1. After the GGA calculation, we find that the actual valance states of Ta and Tc are 2.1 and 4.6, as shown in Table 1. We notice Ta2.8+ (5d2.2) and Tc2.4+ (4d4.6). With the GGA + U scheme, the d orbital electrons of Ta and Tc are 2.2 and 4.5, which imply the electronic configurations are Ta2.9+(5d2.1) and Tc2.4+(4d4.6).
The significant feature of this group is Pb2TaTcO6, also illustrating half-metallic property under the GGA scheme and GGA + U scheme, while it is considered to be a little fluctuation of magnetism under the GGA + U scheme. This phenomenon may be confirmed through experiments in the future; our calculations just provide an accurate answer about whether this compound is a possible HM candidate.

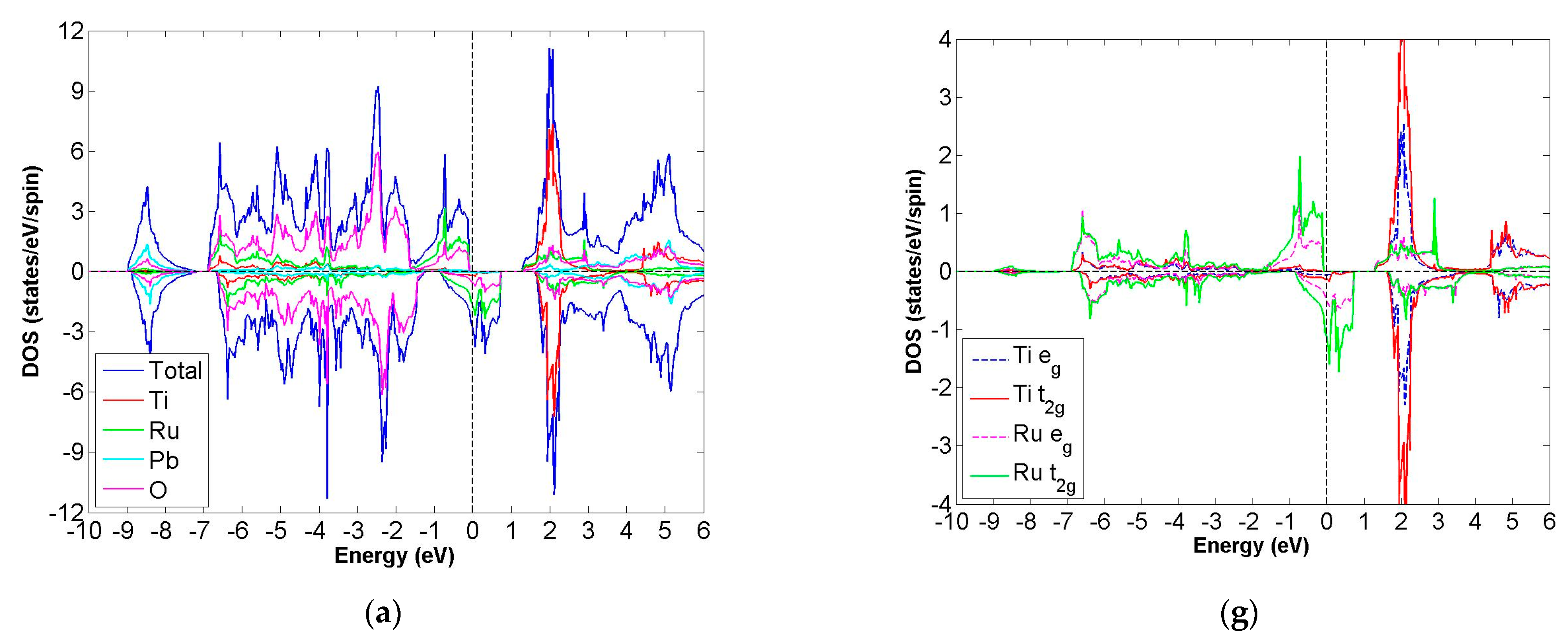
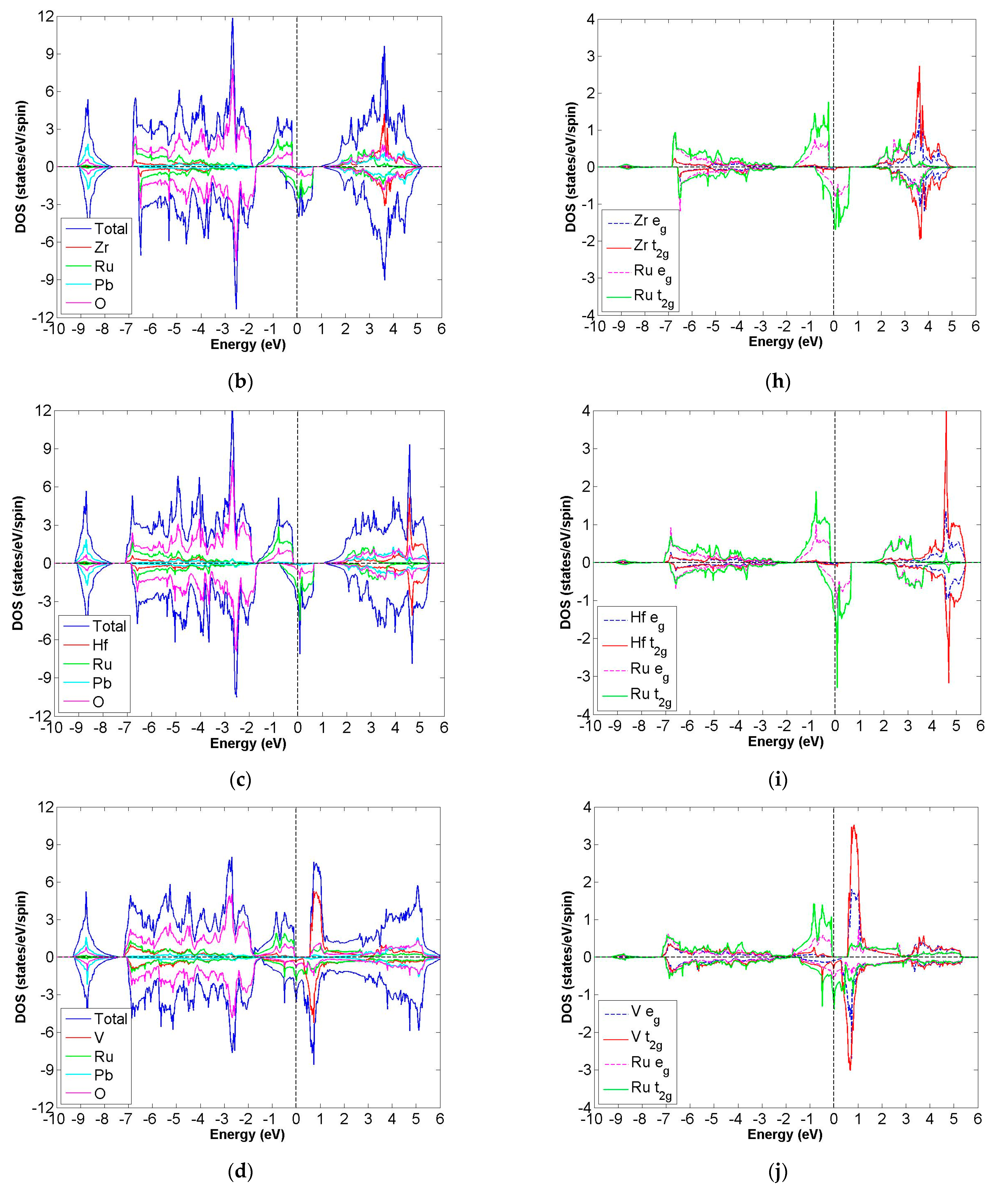
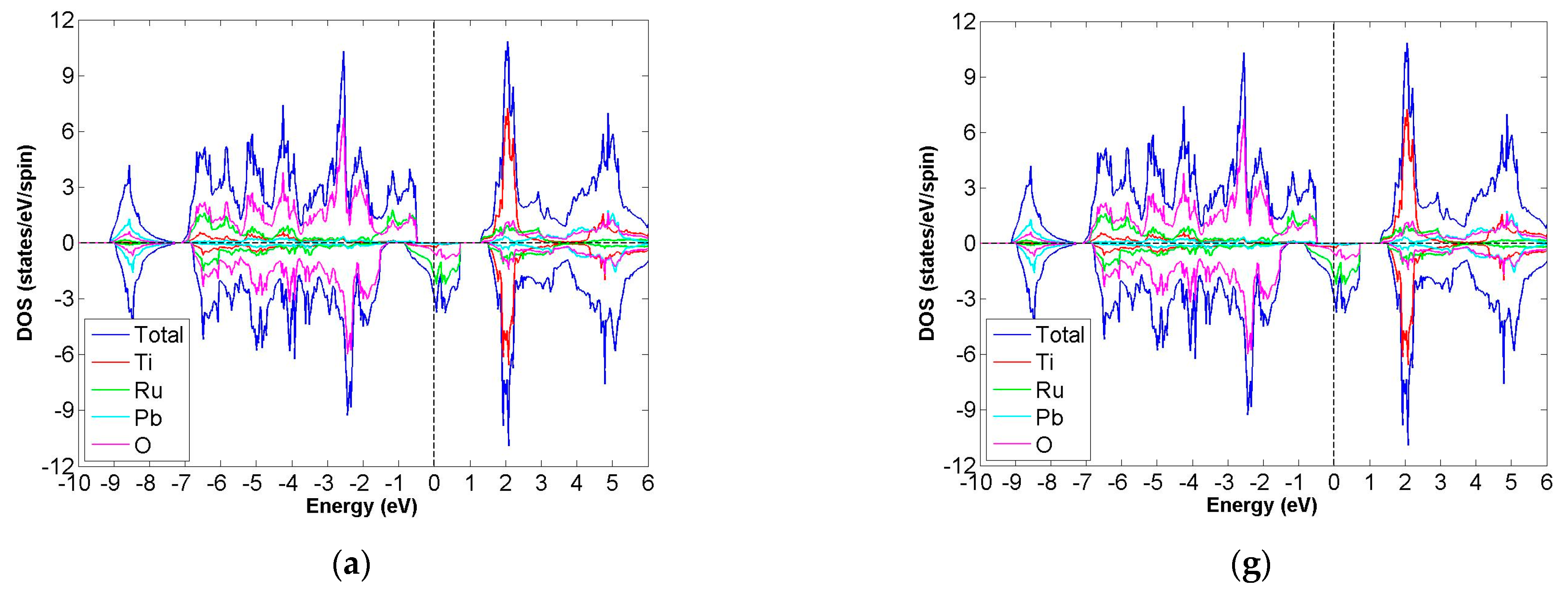
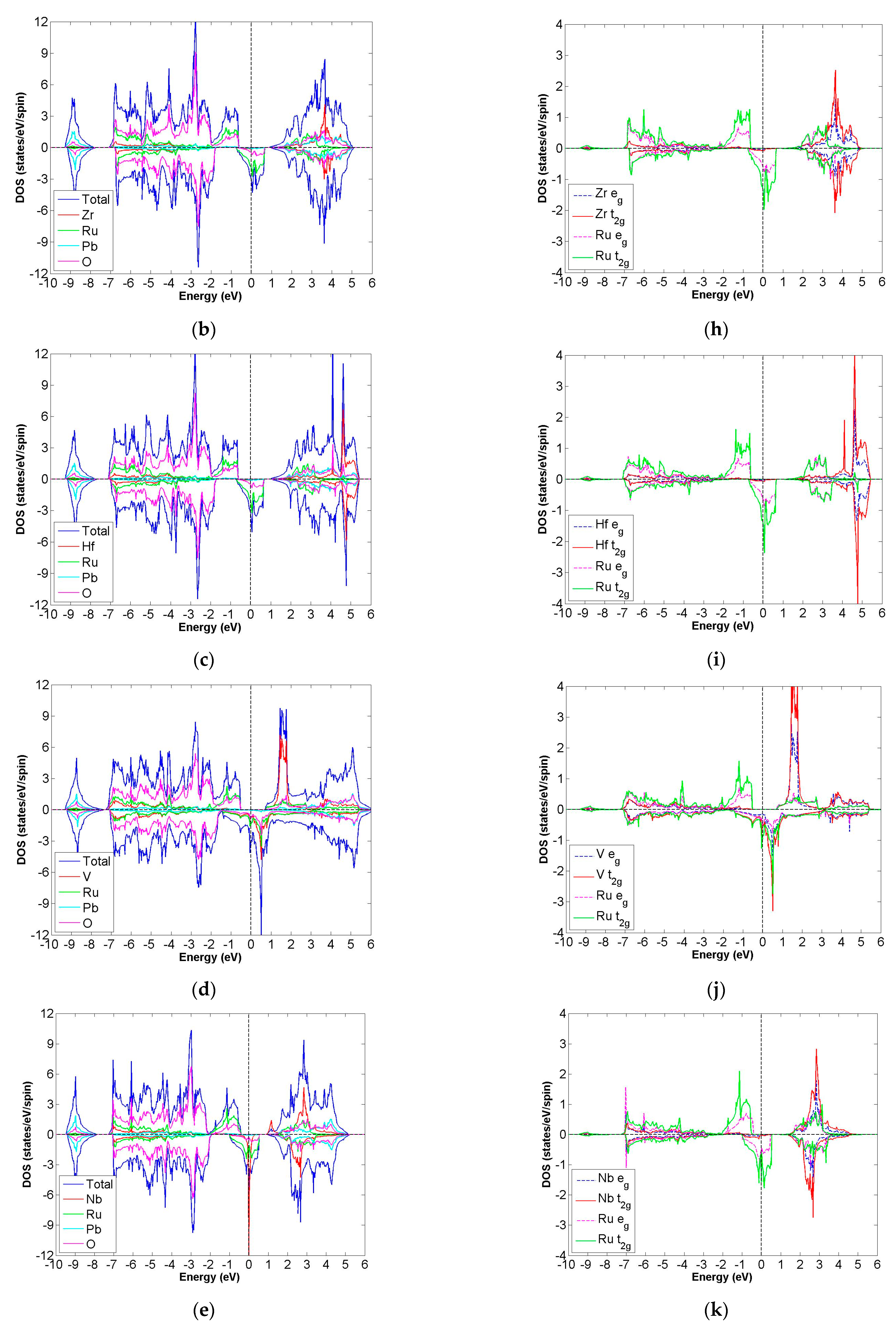
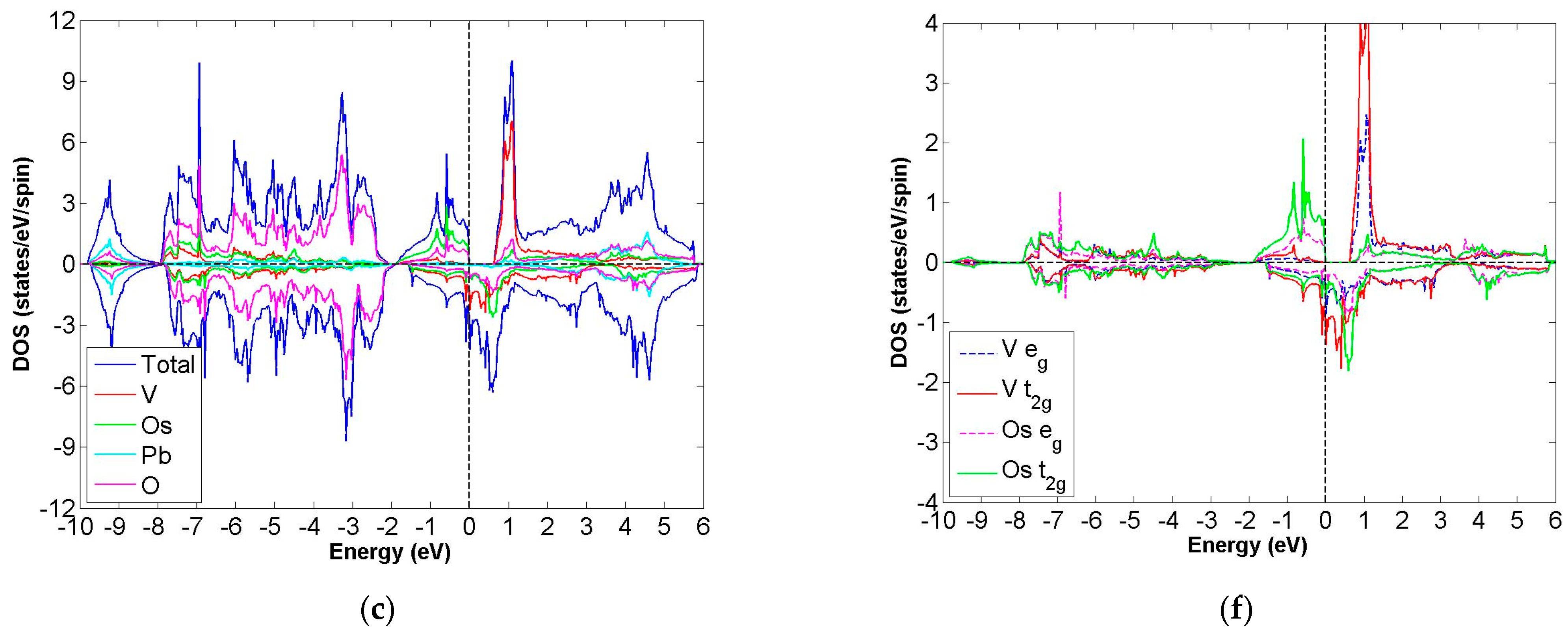
3.2. FiM-HM Compounds: Pb2XRuO6 (X = Ti, Zr, Hf, V, Nb and Ta)

In the case of Pb2XRuO6, all combinations can be categorized into the half-metal family, namely Pb2TiRuO6, Pb2ZrRuO6, Pb2HfRuO6, Pb2VRuO6, Pb2NbRuO6 and Pb2TaRuO6. All of them are FiM materials, indicated by ΔE values, which are −43, −55, −50, −18, −49 and −22 meV/f.u. for these compounds, respectively. With examination of the cases under the GGA + U scheme, they also remain in the same magnetic state; ΔE values of them are −24, −106, −92, −139, −115 and −60 meV/f.u., respectively. As a result, all compounds in this group are FiM materials under these schemes.
As seen in Table 1, mtot for Pb2TiRuO6, Pb2ZrRuO6 and Pb2HfRuO6 are 2.000 μB/f.u., but those of the others are maintained at 1.000 μB/f.u. Even though their values are not the same, all of them are FiM-HM materials because their mtot are integers except zero. The other evidence for half-metal property is provided by Figure 5a–l. The band gaps of these compounds only occur in the spin-up channel, while the spin-down channel is conductive.
When we monitor electrons near Fermi energy, the distribution of Pb2TiRuO6 is like the cases of Pb2ZrRuO6 and Pb2HfRuO6, and DOS of Pb2VRuO6 is analogous to those of Pb2NbRuO6 and Pb2TaRuO6. The difference between them is the DOS of X site element in the spin-up channel. PDOS of Ti, Ru and Hf are almost concentrated, ranging from about 2 to 5 eV, and in the case of V, Nb and Ta, PDOS of them ranges from about 1 to 5 eV. When compared with Table 1, this phenomenon leads to the band gap values of Pb2VRuO6, Pb2NbRuO6 and Pb2TaRuO6 being 1.35, 1.18 and 1.25 eV, larger than those of Pb2VRuO6, Pb2NbRuO6 and Pb2TaRuO6, which are 0.62, 1.00 and 0.85 eV, respectively.
When using the nominal valance states, the ordered double perovskites point to the state of Pb22+(XX′)8+O6. In this paragraph, we will discuss the ideal valance configurations of Pb2TiRuO6, Pb2ZrRuO6 and Pb2HfRuO6, and then compare them with the calculation results of both GGA and GGA + U schemes. First, the transition metal elements (X, X′) of Pb2TiRuO6 are Ti and Ru, in which Ti and Ru have valance configurations of Ti4+(3d0) and Ru4+(3d4), so the valance states are Ti4+(3d0:t02ge0g) at S = 0 and Ru4+(4d44s0: t42ge0g) at S = 1. Nevertheless, the valance configurations were simplified based on the ideal ionic model. Therefore, the electronic number of elements that would be redistributed in consideration of the process of hybridization among Ti 3d, Ru 4d and oxygen 2p orbitals is ignored in this model. The redistribution results of the electronic number indicate Ti and Ru having total electron numbers of 2.0 and 6.0 for d orbitals, showing the valance states of Ti2+(3d2) and Ru2+(4d6). In the consideration of GGA + U schemes, Ti and Ru have 1.9 and 6 electrons for d orbitals, so the valance states are Ti2.1+(3d1.9) and Ru2+(4d6).
In the ionic picture of Pb2ZrRuO6, the formal valance of ZrRu is +8, and the electronic configurations are Zr4+ (4d0:t62ge4g), S = 0 and Ru4+(4d44s0: t42ge0g) at S = 1. According to the calculation results, we found Zr and Ru total electron numbers of 1.5 and 6.0 for d orbitals, showing the valance states of Zr2.5+(4d1.5) and Ru2+(4d6); in the case of Pb2HfRuO6, the electronic configurations are Hf4+(5d0:t02ge0g) at S = 0 and Ru4+(4d44s0: t42ge0g) at S = 1, and the actual situations are Hf2.4+(4d1.6) and Ru2+(4d6). With the GGA+U scheme, as in the case of GGA, the valance states are Zr2.5+(4d1.5) and Ru2+(4d6), just differences in Hf2.5+(4d1.5).
In the ionic picture of Pb2VRuO6, the formal valance of VRu is +8, and the electronic configurations are V5+ (3d0:t02ge0g), S = 0 and Ru3+(4d54s0: t52ge0g) at S = 1/2. According to the calculation result, we found V and Ru total electron numbers of 3.6 and 6.1 for d orbitals, showing the valance states of V1.4+(3d3.6) and Ru1.9+(4d6.1). With GGA + U scheme, there are 3.6 and 6.1 electrons for d orbitals of V and Ru, which implies the valance states are V1.5+(3d3.5) and Ru1.9+(4d6.1).
In the case of Pb2NbRuO6, the electron configurations are Nb5+(3d104s24p6: t02ge0g) at S = 0 and Ru3+(4d54s0: t52ge0g) at S = 1/2. The result provides that the valance states of double perovskites are Nb2.8+(4d2.2) and Ru1.9+(4d6.1) with the GGA scheme. On the other hand, the distribution with the GGA + U scheme of electron number is Nb3.0+(4d2) and Rh1.9+(4d6.1).
Last, Pb2TaRuO6 consists of Ti and Ru, which have valance configurations Ta5+(4f145d06s0:t02ge0g) at S = 0 and Ru4+(4d44s0: t42ge0g) at S = 1. The redistribution of electronic number provided by calculation with the GGA method indicates Ta and Ru having total electron numbers of 2.2 and 6.2 for d orbitals, showing the valance states of Ta2.8+(5d2.2) and Ru1.8+(4d6.2). In the consideration of GGA + U schemes, Ta and Ru have 2.1 and 6.2 electrons for d orbitals, so electron distributions are Ta2.9+(5d2.1) and Ru2+(4d6.2).
In this group, here, the most important result is that these combinations provide an assortment of HM candidates, with all double perovskites including the Ru element presenting half-metallic property. In the aspect of magnetic state, these six compounds belong to the FiM phase category, and ΔE of them are significant enough to determine it.

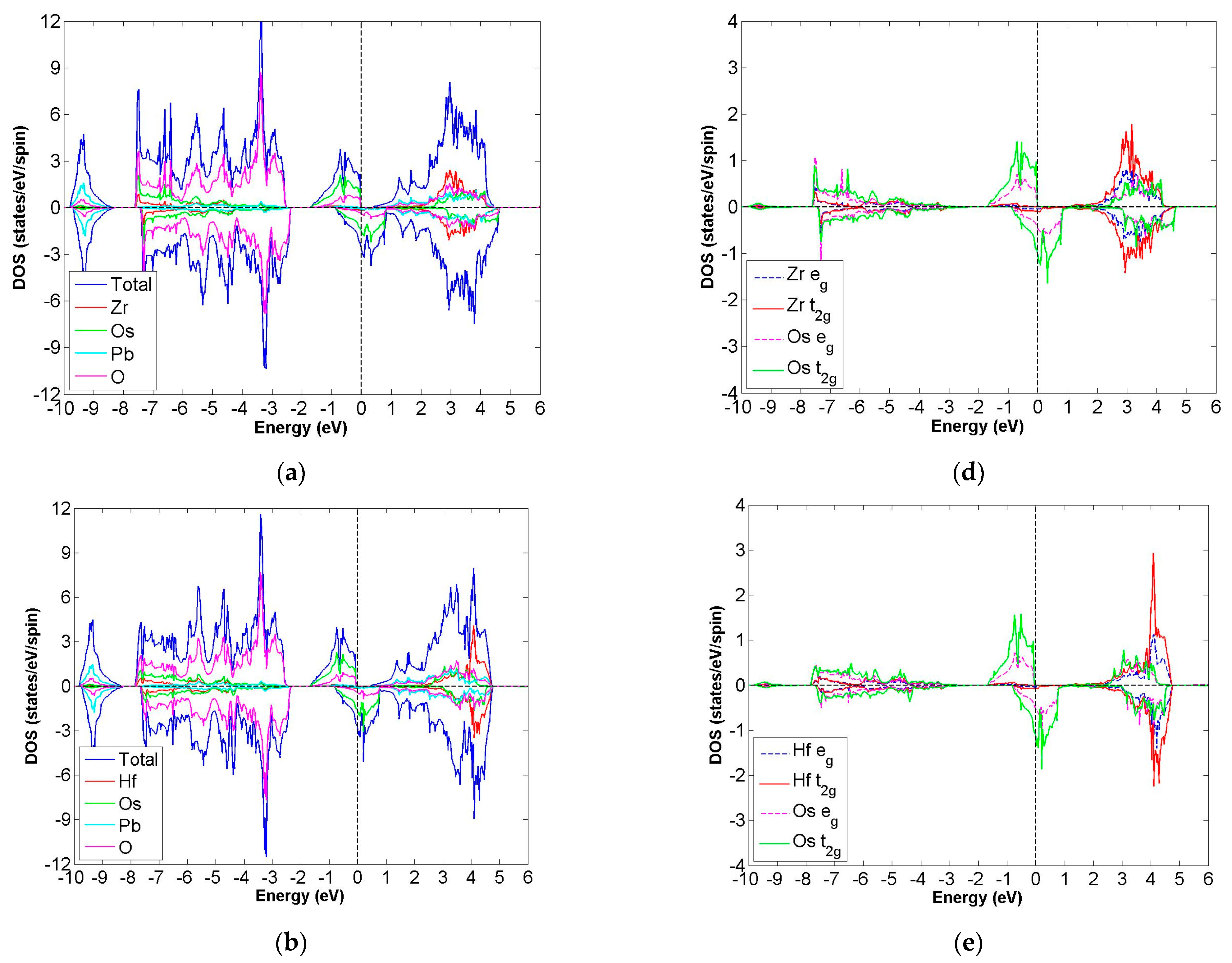
3.3. FiM-HM Compounds: Pb2XOsO6 (X = Zr, Hf and V)

After full structural optimization, the magnetic states for Pb2ZrOsO6, Pb2HfOsO6 and Pb2VOsO6 converge to FiM state. Under the GGA scheme, ΔE for these compounds are −27, −28 and −30 meV/f.u., and with the GGA + U scheme, they decrease to −112, −97 and −309 meV/f.u., respectively. All the evidence illustrates a greater tendency for the FiM state.
As seen in Table 1, mtot for Pb2ZrOsO6 and Pb2HfOsO6 is 2.000 μB/f.u., and mtot for Pb2VOsO6 is 1.000 μB/f.u. Table 1 also shows the energy gaps for these compounds, which are 0.38, 0.47 and 0.65 eV. When we refer to Figure 7a,b, a few electrons occupy the energy range of 0.5 to 1 eV, so this phenomenon makes the band gaps of the group compounds narrower than others. These results also provide direct evidence indicating that these compounds belong to the FiM-HM family.
Next, we investigate ideal electron configuration with covalent electron theory. For Pb2ZrOsO6, it has electron configuration Zr4+(4d0:t62ge4g) at S = 0 and Os4+(4f145d45s0:t42ge0g) at S = 1. Table 1 shows the electron configurations of Pb2ZrOsO6, describing Zr2.5+(4d1.5) and Os2.6+(5d5.4) under the GGA scheme, which indicates that Zr and Os contribute almost the same electron numbers for the bond. With the GGA + U scheme, the results are similar to previous results; with the GGA scheme, the electron configurations are also Zr2.5+(4d1.5) and Os2.6+(5d5.4). In the case of Pb2HfOsO6, we assume the electron configurations are Hf4+(5d0:t02ge0g) at S = 0 and Os4+(4f145d45s0:t42ge0g) at S = 1. Then, calculation results provide that the valance states are Hf2.4+(4d1.6) and Os2.6+(5d5.4). With the GGA+U scheme, the valance states are also Hf2.4+(4d1.6) and Os2.6+(5d5.4), which are similar to the case under the GGA scheme. The valance states of Pb2VOsO6 could be represented by V5+ (3d0:t02ge0g), S = 0 and Os3+(4f145d56s0:t5ge02g) at S = 1/2. According to our calculation results, they imply the true valance states are V1.5+(3d3.5) and Os2.6+(5d5.4) based on the GGA method. With the GGA+U scheme, electrons of d orbital are 3.5 and 5.4 for V1.5+(3d3.5) and Os2.6+(5d5.4), suggesting that the distribution is identical to results with the GGA scheme.
In the cases of Pb2ZrOsO6, Pb2HfOsO6 and Pb2VOsO6, they not only have half-metallic property, but also boast narrower band gap when compared with other HMs in this paper. Under the GGA + U scheme, the gaps of compounds become wider; however, they are still remarkably smaller than those of others under the same scheme.

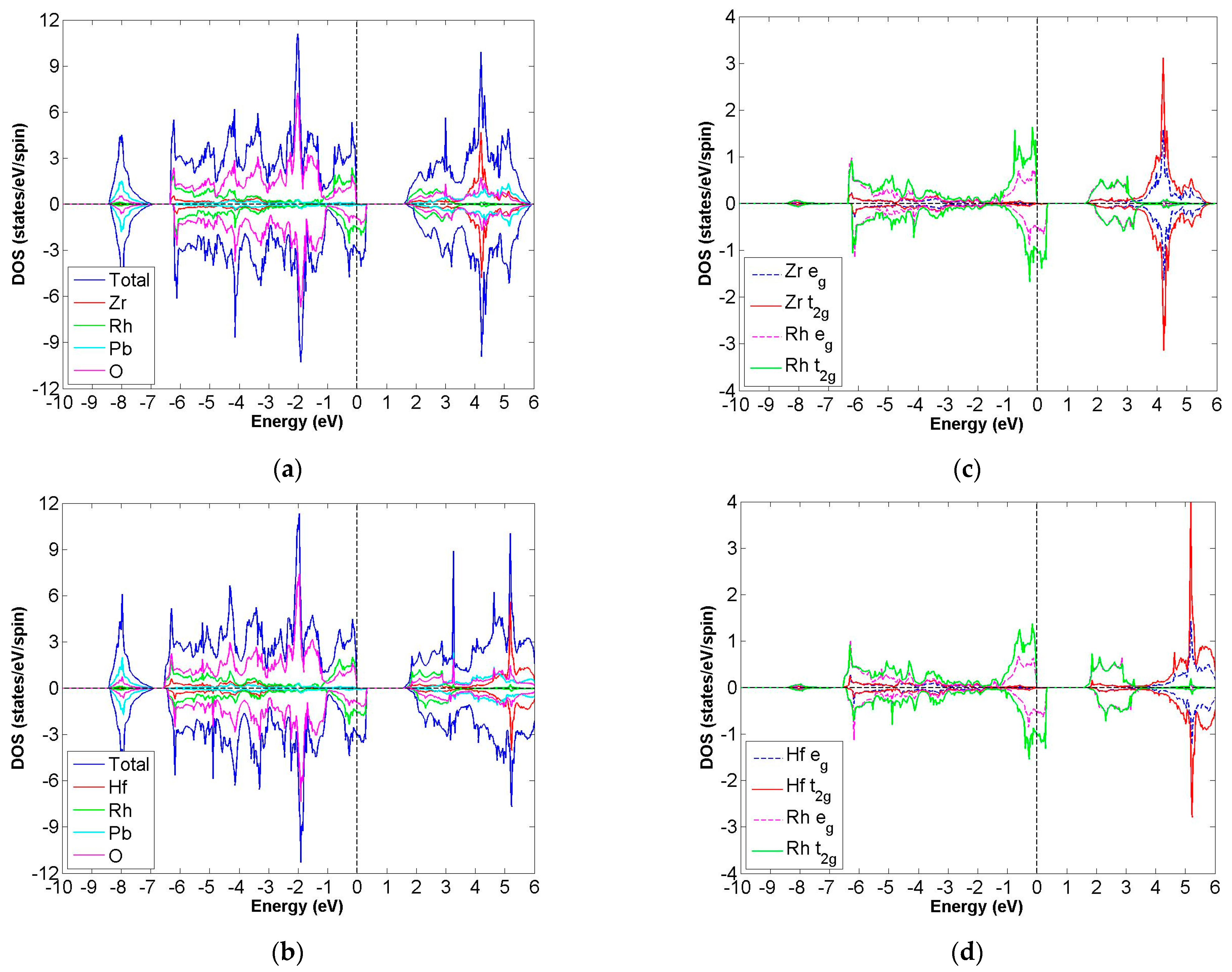
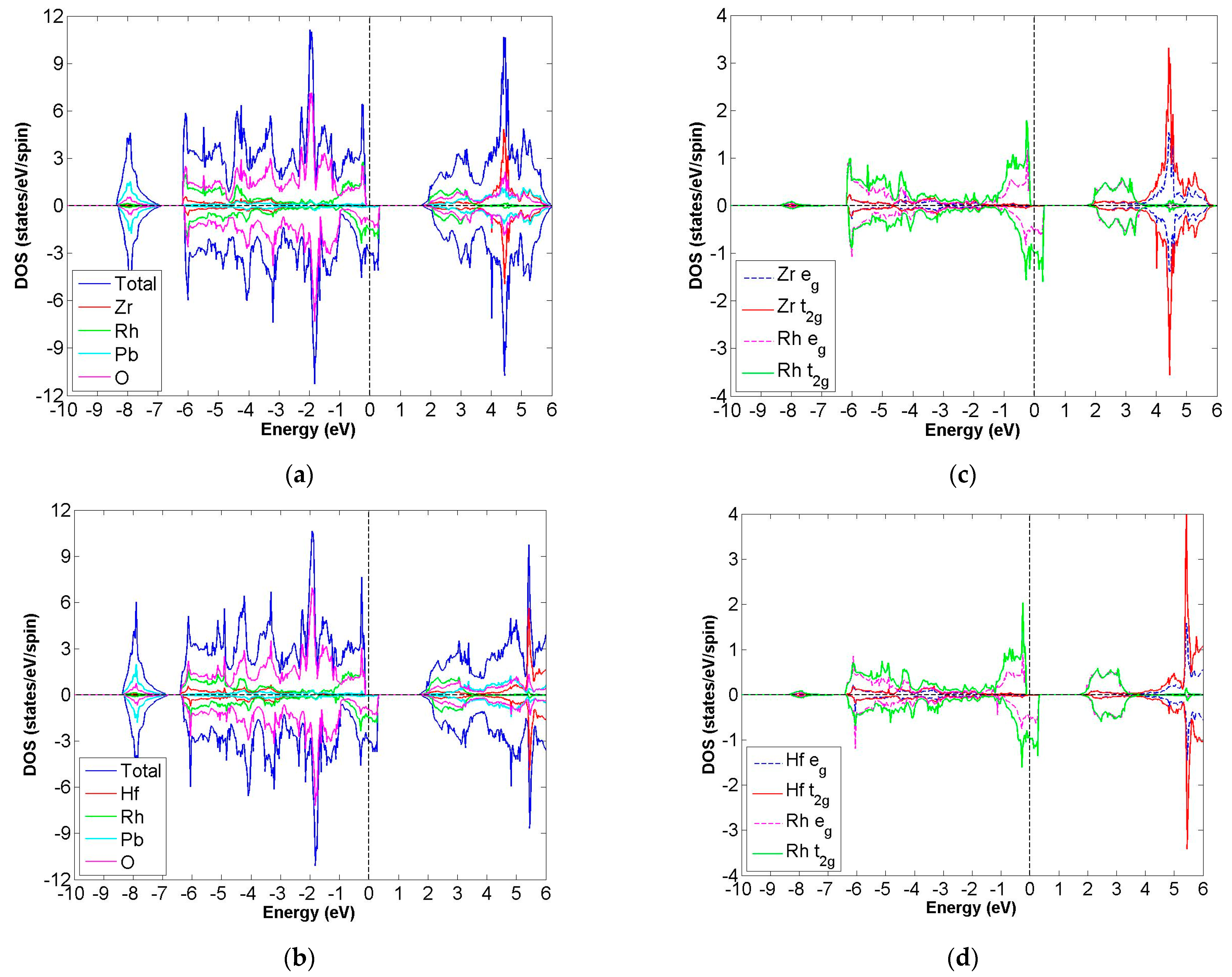
3.4. FiM-HM Compounds: Pb2XRhO6 (X = Zr and Hf)

In this group of compounds, there are two HM candidates, namely, Pb2ZrRhO6 and Pb2HfRhO6. With the GGA and GGA + U scheme, their final stable states belong to FiM rather than AF, as shown by the ΔE listed in Table 1. However, ΔE values of them are very small, at −8 and −10 meV/f.u. under the GGA scheme. The values of ΔE are too small to distinguish the preferred state of Pb2ZrRhO6 and Pb2HfRhO6, although they are negative. Nevertheless, the situation disappears while the calculation is in consideration of the GGA + U scheme. The results mean Pb2ZrRhO6 and Pb2HfRhO6 are considered as possible FiM-HM candidates.
Last, for Pb2ZrRhO6, the electron configurations are Zr4+(4d0:t62ge4g) at S = 0 and Rh4+(4d55s0: t52ge0g) at S = 1/2. After calculation, the results showing the real valance states are Zr2.5+(4d1.5) and Rh2.2+(4d6.8) with the GGA scheme. With the GGA + U scheme, the distributions of electron number are Zr2.5+(4d1.5) and Rh1.9+(4d7.1). In the case of Pb2HfRhO6, the electron configurations we expected are Hf4+(5d0:t02ge0g) at S = 0 and Rh4+(4d55s0: t52ge0g) at S = 1/2. Calculation results point out that the valance states of Pb2HfRhO6 are Hf2.4+(5d1.6) and Rh2.3+(4d6.7), while with the GGA + U scheme, the valance states are Hf2.6+(5d1.4) and Rh2.1+(4d6.9).
In the last group, the properties of Pb2ZrRhO6 and Pb2HfRhO6 studied here imply that they are the possible HM candidates. When the magnetic state is discussed, ΔE of Pb2ZrRhO6 and Pb2HfRhO6 are so small that we cannot determine whether they are in the FiM state or not under the GGA scheme. In consideration of the scheme with GGA + U, the ΔE decreases to −36 and −34 meV/f.u., and therefore we still categorize this group of compounds into FiM materials.

4. Conclusions

By the calculations with the GGA and GGA + U schemes, our work provides 13 possible FiM-HM candidates, namely Pb2NbTcO6, Pb2TaTcO6,Pb2TiRuO6, Pb2ZrRuO6, Pb2HfRuO6, Pb2VRuO6, Pb2NbRuO6, Pb2TaRuO6, Pb2ZrOsO6, Pb2HfOsO6, Pb2VOsO6, Pb2ZrRhO6 and Pb2HfRhO6. Then, we categorize these compounds in four groups according to X′ site element. We first analyze the case of the group of Pb2XTcO6. Omitting the small fluctuation of magnetic moment, Pb2TaTcO6 still remains with a possibility of being HM material when the strong correlation effect (GGA + U) is considered in the calculation, so it is still categorized in HM families. Fortunately, Pb2NbTcO6 retains its half-metallic property under the GGA + U scheme. Then, we also discuss the significant features for other groups. In the case of Pb2XRuO6, this group contains an abundance of HM candidates, which account for half of HM materials. Groups Pb2XOsO6, Pb2ZrOsO6, Pb2HfOsO6 and Pb2VOsO6 have a narrower band gap in comparison with other compounds. Compounds in the category of Pb2XRhO6 converge to an uncertain magnetic state (AF or FiM) and the ΔE decreases to −36 and −34 meV/f.u. under the scheme with GGA + U. Therefore, we still categorize this group of compounds into FiM materials. In short, the calculation within DFT provides 13 possible FiM-HM candidates, and we hope this result for the prediction of Pb-based double perovskites could provide systematic guidelines for future research on high-potential spintronics devices.

Author Contributions

Conceptualization, B.-Y.C., P.-H.L. and Y.-K.W.; Methodology, B.-Y.C., P.-H.L. and Y.-K.W.; Software, P.-H.L. and Y.-K.W.; Validation, B.-Y.C., P.-H.L. and Y.-K.W.; Formal Analysis, B.-Y.C., P.-H.L. and Y.-K.W.; Investigation, B.-Y.C., P.-H.L. and Y.-K.W.; Resources, Y.-K.W.; Data Curation, B.-Y.C. and P.-H.L.; Writing—Original Draft Preparation, B.-Y.C. and P.-H.L.; Writing—Review and Editing, P.-H.L. and Y.-K.W.; Visualization, B.-Y.C., P.-H.L. and Y.-K.W.; Supervision, P.-H.L. and Y.-K.W.; Project Administration, Y.-K.W.; Funding Acquisition, Y.-K.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data supporting this study’s findings are available from the corresponding author upon reasonable request.

Acknowledgments

Y.-K.W. acknowledges the support by Taiwan Ministry of Science and Technology (MOST) through Grant No. MOST 109-2224-E-003-001. The calculations were conducted at the National Center for High-Performance Computing (NCHC) of Taiwan. The authors gratefully acknowledge the resource support from NCHC and the Computational Materials Research Focus Group. B.-Y.C. also genuinely acknowledges the helpful and indispensable discussion with Yi-Chih Wu.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Prinz, G.A. Magnetoelectronics. Science 1998, 282, 1660–1663. [Google Scholar] [CrossRef] [PubMed]
  2. Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; von Molnár, V.S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A spin-based electronics vision for the future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Žutić, I.; Fabian, J.; Sarma, S.D. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323. [Google Scholar] [CrossRef] [Green Version]
  4. De Groot, R.A.; Mueller, F.M.; Van Engen, P.G.; Buschow, K.H.J. New class of materials: Half-metallic ferromagnets. Phys. Rev. Lett. 1983, 50, 2024. [Google Scholar] [CrossRef] [Green Version]
  5. Kobayashi, K.I.; Kimura, T.; Sawada, H.; Terakura, K.; Tokura, Y. Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure. Nature 1998, 395, 677–680. [Google Scholar] [CrossRef]
  6. Pickett, W.E.; Moodera, J.S. Half metallic magnets. Phys. Today 2001, 54, 39–45. [Google Scholar] [CrossRef]
  7. Lewis, S.P.; Allen, P.B.; Sasaki, T. Band structure and transport properties of CrO2. Phys. Rev. B 1997, 55, 10253. [Google Scholar] [CrossRef] [Green Version]
  8. Jedema, F.J.; Filip, A.T.; Van Wees, B.J. Electrical spin injection and accumulation at room temperature in an all-metal mesoscopic spin valve. Nature 2001, 410, 345–348. [Google Scholar] [CrossRef]
  9. Jeng, H.T.; Guo, G.Y. First-principles investigations of orbital magnetic moments and electronic structures of the double perovskites Sr2FeMoO6, Sr2FeReO6, and Sr2CrWO6. Phys. Rev. B 2003, 67, 094438. [Google Scholar] [CrossRef]
  10. Chan, T.S.; Liu, R.S.; Guo, G.Y.; Hu, S.F.; Lin, J.G.; Chen, J.M.; Chang, C.R. Effects of B′-site transition metal on the properties of double perovskites Sr2FeMO6 (M = Mo, W): B′ 4d–5d system. Solid State Commun. 2005, 133, 265–270. [Google Scholar] [CrossRef]
  11. Wu, H. Electronic structure study of double perovskites A2FeReO6 (A = Ba, Sr, Ca) and Sr2MMoO6 (M = Cr, Mn, Fe, Co) by LSDA and LSDA+U. Phys. Rev. B 2001, 64, 125126. [Google Scholar] [CrossRef] [Green Version]
  12. Kato, H.; Okuda, T.; Okimoto, Y.; Tomioka, Y.; Oikawa, K.; Kamiyama, T.; Tokura, Y. Structural and electronic properties of the ordered double perovskites A2MReO6 (A = Sr, Ca; M = Mg, Sc, Cr, Mn, Fe, Co, Ni, Zn). Phys. Rev. B 2004, 69, 184412. [Google Scholar] [CrossRef]
  13. Wang, Y.K.; Lee, P.H.; Guo, G.Y. Half-metallic antiferromagnetic nature of La2VTcO6 and La2VCuO6 from ab initio calculations. Phys. Rev. B 2009, 80, 224418. [Google Scholar] [CrossRef]
  14. Chen, S.H.; Xiao, Z.R.; Liu, Y.P.; Wang, Y.K. Investigation of possible half-metallic antiferromagnets on double perovskites LaABB′O6 (A = Ca, Sr, Ba; B, B′ = transition elements). J. Appl. Phys. 2010, 108, 093908. [Google Scholar] [CrossRef]
  15. Weng, K.C.; Wang, Y.K. Electronic structure of half-metal antiferromagnetism in double-perovskite BiPbVRuO6 and BiPbVOsO6. J. Phys. Soc. Jpn. 2014, 83, 054715. [Google Scholar] [CrossRef]
  16. Lin, H.Z.; Hu, C.Y.; Lee, P.H.; Yan, A.Z.Z.; Wu, W.F.; Chen, Y.F.; Wang, Y.K. Half-Metallic Property Induced by Double Exchange Interaction in the Double Perovskite Bi2BB′O6 (B, B′ = 3d Transitional Metal) via First-Principles Calculations. Materials 2019, 12, 1844. [Google Scholar] [CrossRef] [Green Version]
  17. Coey, J.M.D.; Viret, M.; Von Molnár, S. Mixed-valence manganites. Adv. Phys. 1999, 48, 167–293. [Google Scholar] [CrossRef]
  18. Park, J.H.; Vescovo, E.; Kim, H.J.; Kwon, C.; Ramesh, R.; Venkatesan, T. Magnetic properties at surface boundary of a half-metallic ferromagnet La0.7Sr0.3MnO3. Phys. Rev. Lett. 1998, 81, 1953. [Google Scholar] [CrossRef]
  19. Kronik, L.; Jain, M.; Chelikowsky, J.R. Electronic structure and spin polarization of MnxGa1-xN. Phys. Rev. B 2002, 66, 041203. [Google Scholar] [CrossRef]
  20. Chen, Z.; Tan, S.; Yang, Z.; Zhang, Y. Evidence for a non-double-exchange mechanism in FeCr2S4. Phys. Rev. B 1999, 59, 11172. [Google Scholar] [CrossRef]
  21. Park, M.S.; Kwon, S.K.; Youn, S.J.; Min, B.I. Half-metallic electronic structures of gaint magnetoresistive spinels: Fe1-xCuxCr2S4 (x = 0.0, 0.5, 1.0). Phys. Rev. B 1999, 59, 10018. [Google Scholar] [CrossRef] [Green Version]
  22. Shirai, M.; Ogawa, T.; Kitagawa, I.; Suzuki, N. Band structures of zinc-blende-type MnAs and (MnAs)1(GaAs)1 superlattice. J. Magn. Magn. Mater. 1998, 177, 1383–1384. [Google Scholar] [CrossRef]
  23. Park, J.H.; Kwon, S.K.; Min, B.I. Electronic structures of III–V based ferromagnetic semiconductors: Half-metallic phase. Phys. B Condens. Matter 2000, 281, 703–704. [Google Scholar] [CrossRef]
  24. Battle, P.D.; Goodenough, J.B.; Price, R. The crystal structures and magnetic properties of Ba2LaRuO6 and Ca2LaRuO6. J. Solid State Chem. 1983, 46, 234–244. [Google Scholar] [CrossRef]
  25. Battle, P.D.; Jones, C.W. The crystal and magnetic structures of Sr2LuRuO6, Ba2YRuO6, and Ba2LuRuO6. J. Solid State Chem. 1989, 78, 108–116. [Google Scholar] [CrossRef]
  26. Ortega-San Martin, L.; Chapman, J.P.; Lezama, L.; Sánchez-Marcos, J.; Rodríguez-Fernández, J.; Arriortua, M.I.; Rojo, T. Factors determining the effect of Co (ii) in the ordered double perovskite structure: Sr2CoTeO6. J. Mater. Chem. 2005, 15, 183–193. [Google Scholar] [CrossRef]
  27. Izumiyama, Y.; Doi, Y.; Wakeshima, M.; Hinatsu, Y.; Shimojo, Y.; Morii, Y. Magnetic properties of the antiferromagnetic double perovskite Ba2PrRuO6. J. Phys. Condens. Matter 2001, 13, 1303–1313. [Google Scholar] [CrossRef]
  28. Li, M.R.; Hodges, J.P.; Retuerto, M.; Deng, Z.; Stephens, P.W.; Croft, M.C.; Deng, X.; Kotliar, G.; Sánchez-Benítez, J.; Walker, D.; et al. Mn2MnReO6: Synthesis and magnetic structure determination of a new transition-metal-only double perovskite canted antiferromagnet. Chem. Mater. 2016, 28, 3148–3158. [Google Scholar] [CrossRef]
  29. Zhu, W.K.; Lu, C.K.; Tong, W.; Wang, J.M.; Zhou, H.D.; Zhang, S.X. Strong ferromagnetism induced by canted antiferromagnetic order in double perovskite iridates (La1-xSrx)2ZnIrO6. Phys. Rev. B 2015, 91, 144408. [Google Scholar] [CrossRef] [Green Version]
  30. Li, M.R.; Retuerto, M.; Deng, Z.; Stephens, P.W.; Croft, M.; Huang, Q.; Wu, H.; Deng, X.; Kotliar, G.; Sánchez-Benítez, J.; et al. Giant Magnetoresistance in the Half-Metallic Double-Perovskite Ferrimagnet Mn2FeReO6. Angew. Chem. Int. Ed. 2015, 54, 12069–12073. [Google Scholar] [CrossRef]
  31. Arévalo-López, A.M.; McNally, G.M.; Attfield, J.P. Large Magnetization and Frustration Switching of Magnetoresistance in the Double-Perovskite Ferrimagnet Mn2FeReO6. Angew. Chem. Int. Ed. 2015, 54, 12074–12077. [Google Scholar] [CrossRef] [PubMed]
  32. Wang, H.; Zhu, S.; Ou, X.; Wu, H. Ferrimagnetism in the double perovskite Ca2FeOsO6: A density functional study. Phys. Rev. B 2014, 90, 054406. [Google Scholar] [CrossRef] [Green Version]
  33. Demazeau, G.; Siberchicot, B.; Matar, S.; Gayet, C.; Largeteau, A. A new ferromagnetic oxide La2MnIrO6: Synthesis, characterization, and calculation of its electronic structure. J. Appl. Phys. 1994, 75, 4617–4620. [Google Scholar] [CrossRef]
  34. Serrate, D.; De Teresa, J.M.; Ibarra, M.R. Double perovskites with ferromagnetism above room temperature. J. Phys. Condens. Matter 2006, 19, 023201. [Google Scholar] [CrossRef]
  35. Attfield, J.P. Structure–property relations in doped perovskite oxides. Int. J. Inorg. Mater. 2001, 3, 1147–1152. [Google Scholar] [CrossRef]
  36. Karppinen, M.; Yamauchi, H. Chemistry of halfmetallic and related cation-ordered double perovskites. In Frontiers in Magnetic Materials; Narlikar, A.V., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 153–184. [Google Scholar]
  37. King, G.; Woodward, P.M. Cation ordering in perovskites. J. Mater. Chem. 2010, 20, 5785–5796. [Google Scholar] [CrossRef]
  38. Kwon, O.; Kim, Y.I.; Kim, K.; Kim, J.C.; Lee, J.H.; Park, S.S.; Han, J.W.; Kim, Y.M.; Kim, G.; Jeong, H.Y. Probing One-Dimensional Oxygen Vacancy Channels Driven by Cation–Anion Double Ordering in Perovskites. Nano Lett. 2020, 20, 8353–8359. [Google Scholar] [CrossRef]
  39. Artner, C.; Weil, M. Lead (II) oxidotellurates (VI) with double perovskite structures. J. Solid State Chem. 2019, 276, 75–86. [Google Scholar] [CrossRef]
  40. Goldschmidt, V.M. Die gesetze der krystallochemie. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
  41. Liu, Y.P.; Fuh, H.R.; Wang, Y.K. First-principles study of half-metallic materials in double-perovskite A2FeMO6 (M = Mo, Re, and W) with IVA group elements set on the A-site position. J. Phys. Chem. C 2012, 116, 18032–18037. [Google Scholar] [CrossRef]
  42. Fuh, H.R.; Weng, K.C.; Liu, Y.P.; Wang, Y.K. Theoretical prediction of a new type of half-metallic materials in double derovskite Pb2BB′O6 (B, B′= 3d Transition Metal) via first-principle calculations. Spin 2014, 4, 1450001. [Google Scholar] [CrossRef]
  43. Shimakawa, Y.; Azuma, M.; Ichikawa, N. Multiferroic compounds with double-perovskite structures. Materials 2011, 4, 153–168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Fuh, H.R.; Liu, Y.P.; Wang, Y.K. First principle research of possible HM-AFM in double perovskites A2MoOsO6 and A2TcReO6 (A = Si, Ge, Sn, and Pb) with group IVA elements set on the A-site position. Solid State Sci. 2013, 19, 94–98. [Google Scholar] [CrossRef]
  45. Rached, H.; Bendaoudia, S.; Rached, D. Investigation of Iron-based double perovskite oxides on the magnetic phase stability, mechanical, electronic and optical properties via first-principles calculation. Mater. Chem. Phys. 2017, 193, 453–469. [Google Scholar] [CrossRef]
  46. Fuh, H.R.; Liu, Y.P.; Chen, S.H.; Wang, Y.K. Electronic structures of compensated magnetism in double perovskites A2CrRu(Os)O6 (A = Si, Ge, Sn, and Pb) from ab initio calculations. J. Alloys Compd. 2013, 547, 126–131. [Google Scholar] [CrossRef]
  47. Anderson, M.T.; Greenwood, K.B.; Taylor, G.A.; Poeppelmeier, K.R. B-cation arrangements in double perovskites. Prog. Solid State Chem. 1993, 22, 197–233. [Google Scholar] [CrossRef]
  48. Deng, Z.Q.; Smit, J.P.; Niu, H.J.; Evans, G.; Li, M.R.; Xu, Z.L.; Claridge, J.B.; Rosseinsky, M.J. B cation ordered double perovskite Ba2CoMo0.5Nb0.5O6-δ as a potential SOFC cathode. Chem. Mater. 2009, 21, 5154–5162. [Google Scholar] [CrossRef]
  49. Glazer, A.M. Simple ways of determining perovskite structures. Acta Crystallogr. A 1975, 31, 756–762. [Google Scholar] [CrossRef] [Green Version]
  50. Dowben, P.A.; Skomski, R. Are half metallic ferromagnets half metals? J. Appl. Phys. 2004, 95, 7453. [Google Scholar] [CrossRef] [Green Version]
  51. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef] [Green Version]
  52. Fuoco, L.; Rodriguez, D.; Peppel, T.; Maggard, P.A. Molten-Salt-Mediated Syntheses of Sr2FeReO6, Ba2FeReO6, and Sr2CrReO6: Particle Sizes, B/B′ Site Disorder, and Magnetic Properties. Chem. Mater. 2011, 23, 5409–5414. [Google Scholar] [CrossRef]
  53. Rai, D.P.; Shankar, A.; Ghimire, M.P.; Sandeep; Thapa, R.K. The electronic, magnetic and optical properties of double perovskite A2FeReO6 (A = Sr, Ba) from first principles approach. Comput. Mater. Sci. 2015, 101, 313–320. [Google Scholar] [CrossRef]
  54. Ivanov, S.A.; Bush, A.A.; Stash, A.I.; Kamentsev, K.E.; Shkuratov, V.Y.; Kvashnin, Y.O.; Autieri, C.; Marco, I.D.; Sanyal, B.; Eriksson, O.; et al. Polar Order and Frustrated Antiferromagnetism in Perovskite Pb2MnWO6 Single Crystals. Inorg. Chem. 2016, 55, 2791–2805. [Google Scholar] [CrossRef] [PubMed]
  55. Galasso, F.; Pyle, J. Ordering in compounds of the A(B’0.33Ta0.67) O3 type. Inorg. Chem. 1963, 2, 482–484. [Google Scholar] [CrossRef]
  56. Nakamura, T.; Choy, J.H. Determination of ionic valency pairs via lattice constants in ordered perovskites (ALa)(Mn2+ Mo5+) O6 (A= Ba, Sr, Ca) with applications to (ALa)(Fe3+Mo4+) O6, Ba2(Bi3+Bi5+) O6 and Ba2(Bi3+Sb5+) O6. J. Solid State Chem. 1977, 20, 233–244. [Google Scholar] [CrossRef]
  57. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  58. Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner, I. Phys. Rev. B 1991, 44, 943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  59. Solovyev, I.V.; Dederichs, P.H.; Anisimov, V.I. Corrected atomic limit in the local-density approximation and the electronic structure of d impurities in Rb. Phys. Rev. B 1994, 50, 16861. [Google Scholar] [CrossRef]
  60. Zener, C. Interaction between the d-shells in the transition metals. II. Ferromagnetic compounds of manganese with perovskite structure. Phys. Rev. 1951, 82, 403. [Google Scholar] [CrossRef]
  61. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [Green Version]
  62. Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115. [Google Scholar] [CrossRef] [PubMed]
  63. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  64. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
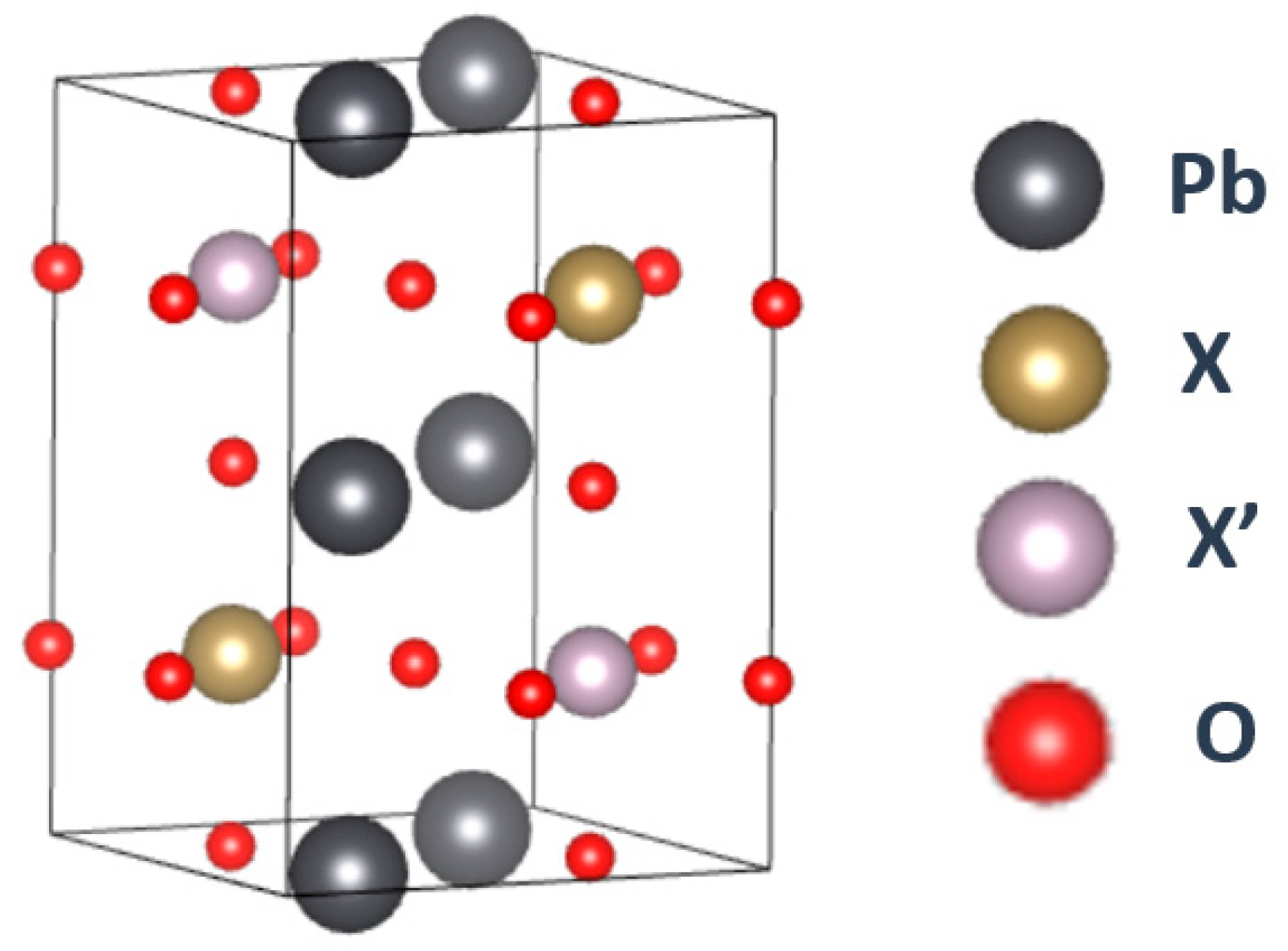
Materials 15 03311 g001 550
Figure 1. An ideal ordered double perovskite structure of Pb2XX′O6.
Figure 1. An ideal ordered double perovskite structure of Pb2XX′O6.
Materials 15 03311 g001
Materials 15 03311 g002 550
Figure 2. The schematic diagram of four magnetic states: FM, FiM, AF and NM.
Figure 2. The schematic diagram of four magnetic states: FM, FiM, AF and NM.
Materials 15 03311 g002
Materials 15 03311 g003 550
Figure 3. Based on the GGA calculation, the calculated total and partial DOS values of (a) Pb2NbTcO6 and (b) Pb2TaTcO6 and the partial DOS of eg and t2g spin orbitals for (c) Nb and Tc and (d) Ta and Tc.
Figure 3. Based on the GGA calculation, the calculated total and partial DOS values of (a) Pb2NbTcO6 and (b) Pb2TaTcO6 and the partial DOS of eg and t2g spin orbitals for (c) Nb and Tc and (d) Ta and Tc.
Materials 15 03311 g003
Materials 15 03311 g004 550
Figure 4. Under GGA + U (U of Nb, Ta and Tc set up as 2) schemes, the calculated total and partial DOS values of (a) Pb2NbTcO6, (b) Pb2TaTcO6 and the partial DOS of eg and t2g spin orbitals for (c) Nb and Tc and (d) Ta and Tc.
Figure 4. Under GGA + U (U of Nb, Ta and Tc set up as 2) schemes, the calculated total and partial DOS values of (a) Pb2NbTcO6, (b) Pb2TaTcO6 and the partial DOS of eg and t2g spin orbitals for (c) Nb and Tc and (d) Ta and Tc.
Materials 15 03311 g004
Materials 15 03311 g005a 550Materials 15 03311 g005b 550Materials 15 03311 g005c 550
Figure 5. Based on the GGA calculation, the calculated total and partial DOS values of (a) Pb2TiRuO6, (b) Pb2ZrRuO6, (c) Pb2HfRuO6, (d) Pb2TiRuO6, (e) Pb2ZrRuO6 and (f) Pb2HfRuO6 and partial DOS of eg and t2g spin orbitals for (g) Ti and Ru, (h) Zr and Ru, (i) Hf and Ru, (j) V and Ru, (k) Nb and Ru, (l) Ta and Ru.
Figure 5. Based on the GGA calculation, the calculated total and partial DOS values of (a) Pb2TiRuO6, (b) Pb2ZrRuO6, (c) Pb2HfRuO6, (d) Pb2TiRuO6, (e) Pb2ZrRuO6 and (f) Pb2HfRuO6 and partial DOS of eg and t2g spin orbitals for (g) Ti and Ru, (h) Zr and Ru, (i) Hf and Ru, (j) V and Ru, (k) Nb and Ru, (l) Ta and Ru.
Materials 15 03311 g005aMaterials 15 03311 g005bMaterials 15 03311 g005c
Materials 15 03311 g006a 550Materials 15 03311 g006b 550Materials 15 03311 g006c 550
Figure 6. Under GGA + U (U of Ti, Zr, Hf, V, Nb, Ta and Ru set up as 2) schemes, the calculated total and partial DOS values of (a) Pb2TiRuO6, (b) Pb2ZrRuO6, (c) Pb2HfRuO6, (d) Pb2VRuO6, (e) Pb2NbRuO6 and (f) Pb2TaRuO6 and the partial DOS of eg and t2g spin orbitals for (g) Ti and Ru, (h) Zr and Ru, (i) Hf and Ru, (j) V and Ru, (k) Nb and Ru, (l) Ta and Ru.
Figure 6. Under GGA + U (U of Ti, Zr, Hf, V, Nb, Ta and Ru set up as 2) schemes, the calculated total and partial DOS values of (a) Pb2TiRuO6, (b) Pb2ZrRuO6, (c) Pb2HfRuO6, (d) Pb2VRuO6, (e) Pb2NbRuO6 and (f) Pb2TaRuO6 and the partial DOS of eg and t2g spin orbitals for (g) Ti and Ru, (h) Zr and Ru, (i) Hf and Ru, (j) V and Ru, (k) Nb and Ru, (l) Ta and Ru.
Materials 15 03311 g006aMaterials 15 03311 g006bMaterials 15 03311 g006c
Materials 15 03311 g007a 550Materials 15 03311 g007b 550
Figure 7. Based on the GGA calculation, the calculated total and partial DOS values of (a) Pb2ZrOsO6, (b) Pb2HfOsO6 and (c) Pb2VOsO6 and the partial DOS of eg and t2g spin orbitals for (d) Zr and Os, (e) Hf and Os and (f) V and Os.
Figure 7. Based on the GGA calculation, the calculated total and partial DOS values of (a) Pb2ZrOsO6, (b) Pb2HfOsO6 and (c) Pb2VOsO6 and the partial DOS of eg and t2g spin orbitals for (d) Zr and Os, (e) Hf and Os and (f) V and Os.
Materials 15 03311 g007aMaterials 15 03311 g007b
Materials 15 03311 g008a 550Materials 15 03311 g008b 550
Figure 8. Under GGA + U (U of Zr, Hf, V and Os set up as 2) schemes, the calculated total and partial DOS values of (a) Pb2ZrOsO6, (b) Pb2HfOsO6 and (c) Pb2VOsO6 and the partial DOS of eg and t2g spin orbitals for (d) Zr and Os and (e) Hf and Os and (f) V and Os.
Figure 8. Under GGA + U (U of Zr, Hf, V and Os set up as 2) schemes, the calculated total and partial DOS values of (a) Pb2ZrOsO6, (b) Pb2HfOsO6 and (c) Pb2VOsO6 and the partial DOS of eg and t2g spin orbitals for (d) Zr and Os and (e) Hf and Os and (f) V and Os.
Materials 15 03311 g008aMaterials 15 03311 g008b
Materials 15 03311 g009 550
Figure 9. Based on the GGA calculation, the calculated total and partial DOS values of (a) Pb2ZrRhO6 and (b) Pb2HfRhO6 and partial DOS of eg and t2g spin orbitals for (c) Zr and Rh and (d) Hf and Rh.
Figure 9. Based on the GGA calculation, the calculated total and partial DOS values of (a) Pb2ZrRhO6 and (b) Pb2HfRhO6 and partial DOS of eg and t2g spin orbitals for (c) Zr and Rh and (d) Hf and Rh.
Materials 15 03311 g009
Materials 15 03311 g010 550
Figure 10. Under GGA + U (U of Zr, Hf and Rh set up as 2) schemes, the calculated total and partial DOS values of (a) Pb2ZrRhO6, (b) Pb2HfRhO6 and the partial DOS of eg and t2g spin orbitals for (c) Zr and Rh and (d) Hf and Rh.
Figure 10. Under GGA + U (U of Zr, Hf and Rh set up as 2) schemes, the calculated total and partial DOS values of (a) Pb2ZrRhO6, (b) Pb2HfRhO6 and the partial DOS of eg and t2g spin orbitals for (c) Zr and Rh and (d) Hf and Rh.
Materials 15 03311 g010
Table
Table 1. Physical properties of the selected FiM-HM family of Pb2XX′O6 (X = IVB/VB X′ = Rh, Hf, Os and Tc) in double perovskite structure by GGA and GGA + U calculations. The parenthesis behind U presents the on-site coulomb parameters: 3 eV for UV, and 2 eV for UIVB, UNb, UTa, URh, UHf, UOs and UTc. (0,0) denotes the absence of GGA + U calculations. ΔE refers to the energy difference between FiM and AF states. The spin magnetic moments for X, X′ and the total moment are listed in the table as mX, mX′ and mtot, respectively. The number of electrons in the spin-up and spin-down orbitals is recorded for X(X′) element.
Table 1. Physical properties of the selected FiM-HM family of Pb2XX′O6 (X = IVB/VB X′ = Rh, Hf, Os and Tc) in double perovskite structure by GGA and GGA + U calculations. The parenthesis behind U presents the on-site coulomb parameters: 3 eV for UV, and 2 eV for UIVB, UNb, UTa, URh, UHf, UOs and UTc. (0,0) denotes the absence of GGA + U calculations. ΔE refers to the energy difference between FiM and AF states. The spin magnetic moments for X, X′ and the total moment are listed in the table as mX, mX′ and mtot, respectively. The number of electrons in the spin-up and spin-down orbitals is recorded for X(X′) element.
Materials Pb2XX′O6 ( U X , U X ′ ) Spin Magnetic Moment (μB/f.u.)d Orbital
Electrons ↑/↓		Band Gap (eV)ΔE
(meV/f.u.)
FiM-AF
mXmX′mtotXX′
NbTc(0,0)−1.5271.8462.0001.016/1.1123.200/1.3750.47/0.00−21
(2,2)−1.8861.9802.0000.913/1.0343.251/1.2920.95/0.00−26
TaTc(0,0)−0.0721.5882.0001.054/1.1193.099/1.5270.30/0.00−96
(2,2)−0.1161.6912.0111.004/1.1153.141/1.4670.80/0.00−178
TiRu(0,0)−0.0721.3482.0000.955/1.0193.675/2.3411.35/0.00−43
(2,2)−0.0981.3782.0000.916/1.0083.691/2.3291.80/0.00−24
ZrRu(0,0)−0.0311.3862.0000.747/0.7713.696/2.3251.18/0.00−55
(2,2)−0.0361.4062.0000.720/0.7503.708/2.3171.52/0.00−106
HfRu(0,0)−0.0281.3792.0000.784/0.8023.690/2.3261.25/0.00−50
(2,2)−0.0291.3942.0000.758/0.7803.699/2.3211.60/0.00−92
VRu(0,0)−0.3640.9061.0001.614/1.9643.492/2.5980.62/0.00−18
(3,2)−0.8751.1741.0001.341/2.1933.613/2.4521.23/0.00−139
NbRu(0,0)−1.2830.9991.0001.046/1.1503.549/2.5621.00/0.00−49
(2,2)−1.5311.0521.0000.960/1.0813.578/2.5381.30/0.00−115
TaRu(0,0)−0.0410.7611.0001.062/1.0993.453/2.7000.85/0.00−22
(2,2)−0.0510.7671.0001.029/1.0773.466/2.7061.12/0.00−60
ZrOs(0,0)−0.0301.3722.0000.746/0.7723.386/2.0320.38/0.00−27
(2,2)−0.0441.4622.0000.714/0.7563.442/1.9980.75/0.00−112
HfOs(0,0)−0.0251.3722.0000.782/0.8003.386/2.0320.47/0.00−28
(2,2)−0.0321.4522.0000.752/0.7793.436/2.0020.82/0.00−97
VOs(0,0)−0.8371.2181.0001.366/2.1823.310/2.1090.65/0.00−30
(3,2)−1.4571.6291.0001.050/2.4753.492/1.8841.65/0.00−309
ZrRh(0,0)−0.0210.5571.0000.752/0.7693.700/3.1471.60/0.00−10
(2,2)−0.0210.5291.0000.728/0.7463.968/3.1721.82/0.00−36
HfRh(0,0)−0.0200.5481.0000.788/0.8023.695/3.1501.57/0.00−8
(2,2)−0.0190.5171.0000.764/0.7793.690/3.1751.82/0.00−34
Table
Table 2. In the table below, total energy of possible HM candidates with each magnetic state is presented. UX(X′) are the effective parameters used in GGA + U calculations for X(X′).
Table 2. In the table below, total energy of possible HM candidates with each magnetic state is presented. UX(X′) are the effective parameters used in GGA + U calculations for X(X′).
Materials
Pb2XX′O6		 ( U X , U X ′ ) Final StatesE (eV/f.u.)Materials
Pb2XX′O6		 ( U X , U X ′ ) Final StatesE (eV/f.u.)
NbTc(0,0)AF−74.269TaRu(0,0)AF−74.610
(2,2)AF−72.512 (2,2)AF−72.606
(0,0)FiM−74.290 (0,0)FiM−74.632
(2,2)FiM−72.538 (2,2)FiM−72.666
TaTc(0,0)AF−76.443ZrOs(0,0)AF−73.595
(2,2)AF−74.486 (2,2)AF−71.755
(0,0)FiM−76.539 (0,0)FiM−73.622
(2,2)FiM−74.664 (2,2)FiM−71.867
TiRu(0,0)AF−70.600HfOs(0,0)AF−75.677
(2,2)AF−68.628 (2,2)AF−73.851
(0,0)FiM−70.643 (0,0)FiM−75.705
(2,2)FiM−68.752 (2,2)FiM−73.948
ZrRu(0,0)AF−71.763VOs(0,0)AF−71.377
(2,2)AF−69.993 (3,2)AF−67.913
(0,0)FiM−71.818 (0,0)FiM−71.407
(2,2)FiM−70.099 (3,2)FiM−68.222
HfRu(0,0)AF−73.897ZrRh(0,0)AF−69.142
(2,2)AF−72.119 (2,2)AF−67.422
(0,0)FiM−73.947 (0,0)FiM−69.152
(2,2)FiM−72.211 (2,2)FiM−67.458
VRu(0,0)AF−69.729HfRh(0,0)AF−71.277
(3,2)AF−66.201 (2,2)AF−69.542
(0,0)FiM−69.747 (0,0)FiM−71.285
(3,2)FiM−66.340 (2,2)FiM−69.576
NbRu(0,0)AF−72.123
(2,2)AF−70.084
(0,0)FiM−72.172
(2,2)FiM−70.199
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Chen, B.-Y.; Lee, P.-H.; Wang, Y.-K. First-Principles Study on Possible Half-Metallic Ferrimagnetism in Double Perovskites Pb2XX′O6 (X = Ti, Zr, Hf, V, Nb and Ta, X′ = Tc, Ru, Os and Rh). Materials 2022, 15, 3311. https://doi.org/10.3390/ma15093311

AMA Style

Chen B-Y, Lee P-H, Wang Y-K. First-Principles Study on Possible Half-Metallic Ferrimagnetism in Double Perovskites Pb2XX′O6 (X = Ti, Zr, Hf, V, Nb and Ta, X′ = Tc, Ru, Os and Rh). Materials. 2022; 15(9):3311. https://doi.org/10.3390/ma15093311

Chicago/Turabian Style

Chen, Bo-Yu, Po-Han Lee, and Yin-Kuo Wang. 2022. "First-Principles Study on Possible Half-Metallic Ferrimagnetism in Double Perovskites Pb2XX′O6 (X = Ti, Zr, Hf, V, Nb and Ta, X′ = Tc, Ru, Os and Rh)" Materials 15, no. 9: 3311. https://doi.org/10.3390/ma15093311

APA Style

Chen, B. -Y., Lee, P. -H., & Wang, Y. -K. (2022). First-Principles Study on Possible Half-Metallic Ferrimagnetism in Double Perovskites Pb2XX′O6 (X = Ti, Zr, Hf, V, Nb and Ta, X′ = Tc, Ru, Os and Rh). Materials, 15(9), 3311. https://doi.org/10.3390/ma15093311

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop