Magnetic Properties of Novel Layered Disulfides CuCr0.99Ln0.01S2 (Ln = La…Lu)
Abstract
:1. Introduction
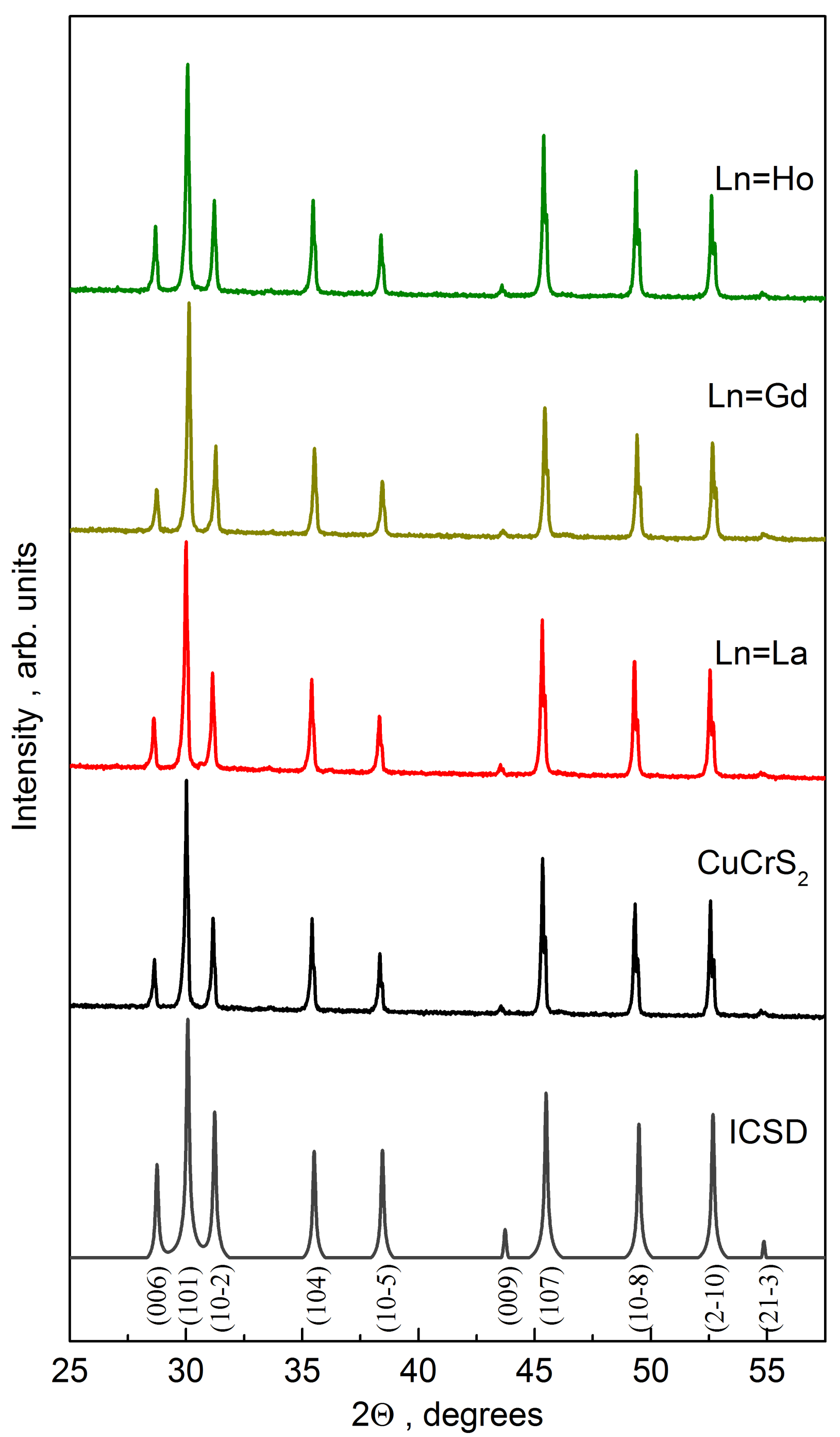
2. Experimental
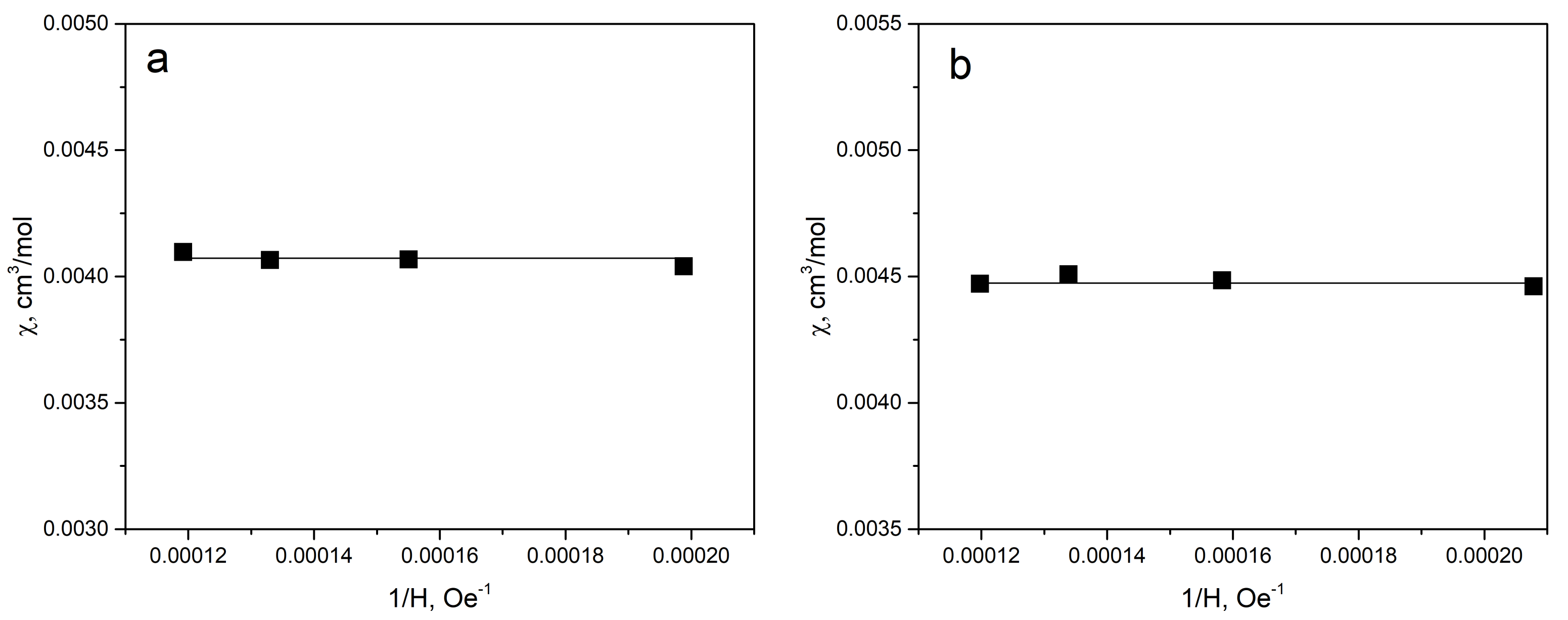
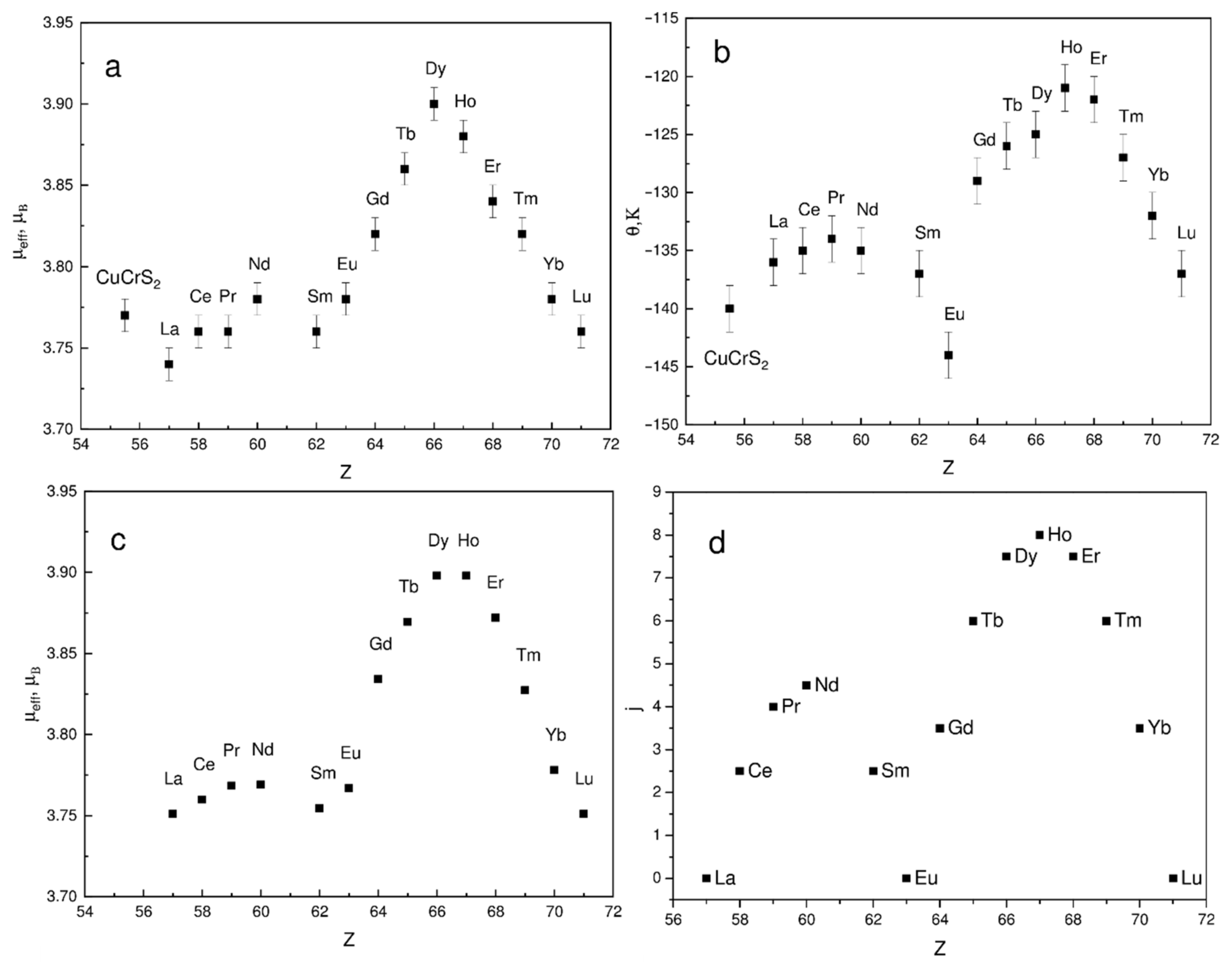
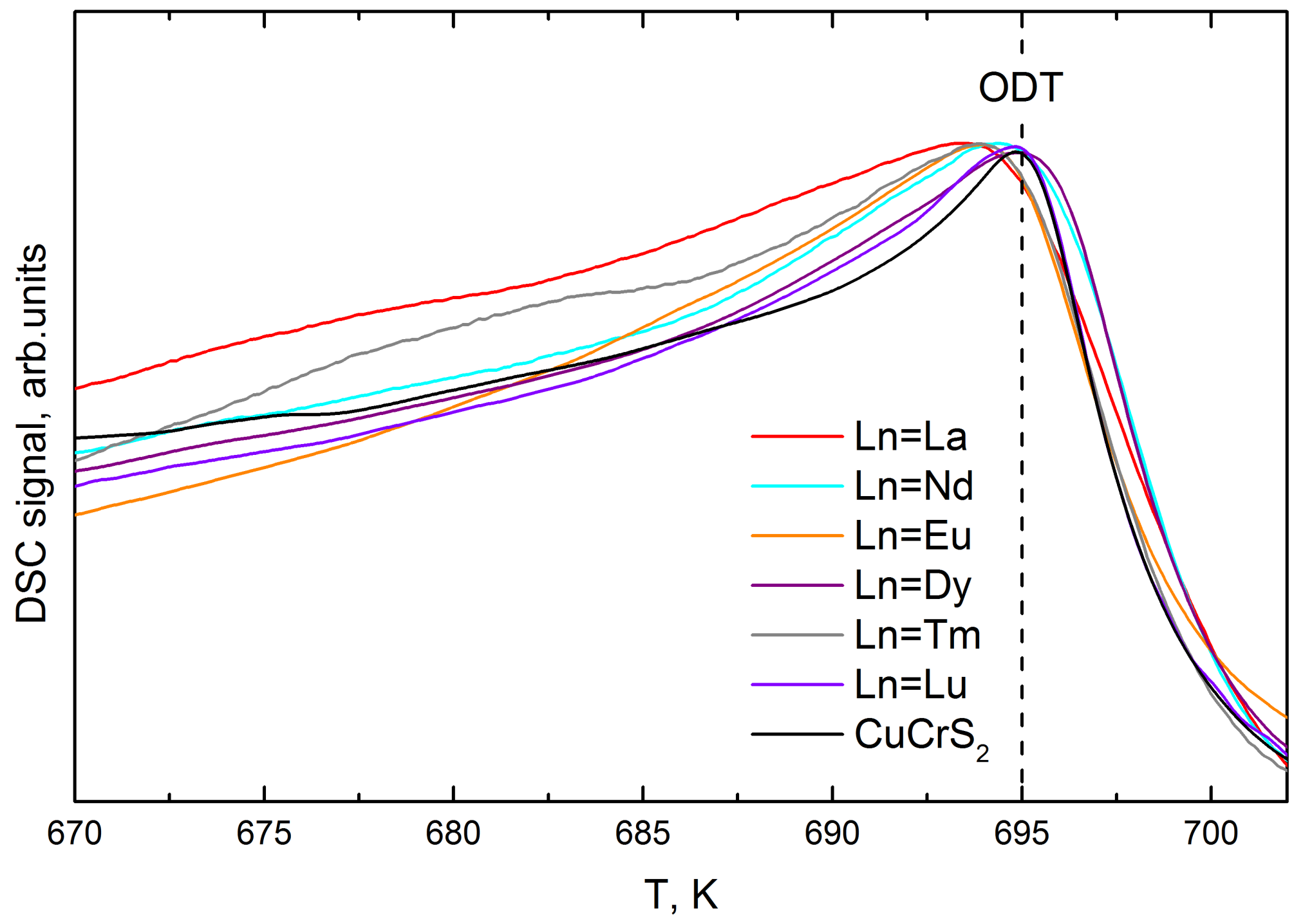
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Engelsman, F.M.R.; Wiegers, G.A.; Jellinek, F.; Van Laar, B. Crystal structures and magnetic structures of some metal(I) chromium(III) sulfides and selenides. J. Solid State Chem. 1973, 6, 574–582. [Google Scholar] [CrossRef]
- Bongers, P.F.; Van Bruggen, C.F.; Koopstra, J.; Omloo, W.P.F.A.M.; Wiegers, G.A.; Jellinek, F. Structures and magnetic properties of some metal (I) chromium (III) sulfides and selenides. J. Phys. Chem. Solids 1968, 29, 977–984. [Google Scholar] [CrossRef]
- Korotaev, E.V.; Syrokvashin, M.M.; Filatova, I.Y.; Sotnikov, A.V. Effect of the Order-Disorder Transition on the Electronic Structure and Physical Properties of Layered CuCrS2. Materials 2021, 14, 2729. [Google Scholar] [CrossRef]
- Rasch, J.C.E.; Boehm, M.; Ritter, C.; Mutka, H.; Schefer, J.; Keller, L.; Abramova, G.M.; Cervellino, A.; Löffler, J.F. Magnetoelastic coupling in the triangular lattice antiferromagnet CuCrS2. Appl. Phys. Lett. 2009, 80, 104431. [Google Scholar]
- Karmakar, A.; Dey, K.; Chatterjee, S.; Majumdar, S.; Giri, S. Spin correlated dielectric memory and rejuvenation in multiferroic CuCrS2. Appl. Phys. Lett. 2014, 104, 052906. [Google Scholar] [CrossRef] [Green Version]
- Almukhametov, R.F.; Yakshibayev, R.A.; Gabitov, E.V.; Abdullin, A.R.; Kutusheva, R.M. Structural properties and ionic conductivities of CuCr1–xVxS2 solid solutions. Phys. Status Solidi 2003, 236, 29–33. [Google Scholar] [CrossRef]
- Korotaev, E.V.; Syrokvashin, M.M.; Filatova, I.Y.; Pelmenev, K.G.; Zvereva, V.V.; Peregudova, N.N. Seebeck Coefficient of Cation-Substituted Disulfides CuCr1−xFexS2 and Cu1−xFexCrS2. J. Electron. Mater. 2018, 47, 3392–3397. [Google Scholar] [CrossRef]
- Korotaev, E.V.; Syrokvashin, M.M.; Filatova, I.Y.; Trubina, S.V.; Nikolenko, A.D.; Ivlyushkin, D.V.; Zavertkin, P.S.; Sotnikov, A.V.; Kriventsov, V.V. XANES investigation of novel lanthanide-doped CuCr0.99Ln0.01S2 (Ln = La, Ce) solid solutions. Appl. Phys. A 2020, 126, 537. [Google Scholar] [CrossRef]
- Hansen, A.-L.; Dankwort, T.; Groß, H.; Etter, M.; König, J.; Duppel, V.; Kienle, L.; Bensch, W. Structural properties of the thermoelectric material CuCrS2 and of deintercalated CuxCrS2 on different length scales: X-ray diffraction, pair distribution function and transmission electron microscopy studies. J. Mater. Chem. C 2017, 5, 9331–9338. [Google Scholar] [CrossRef]
- Al’mukhametov, R.F.; Yakshibaev, R.A.; Gabitov, É.V.; Abdullin, A.R. Investigation of superionic phase transition in the CuCr1-xVxS2 system by X-ray diffraction and magnetic methods. Phys. Solid State 2000, 42, 1508–1511. [Google Scholar] [CrossRef]
- Tsujii, N.; Kitazawa, H.; Kido, G. Insulator to metal transition induced by substitution in the nearly two-dimensional compound CuCr1-xVxS2. Phys. Status Solidi Curr. Top. Solid State Phys. 2006, 3, 2775–2778. [Google Scholar]
- Al’mukhametov, R.F.; Yakshibaev, R.A.; Gabitov, E.V.; Abdullin, A.R. Synthesis and X-ray diffraction study of CuCr1-xVxS2. Inorg. Mater. 2000, 36, 437–440. [Google Scholar] [CrossRef]
- Wu, D.; Huang, S.; Feng, D.; Li, B.; Chen, Y.; Zhang, J.; He, J. Revisiting AgCrSe2 as a promising thermoelectric material. Phys. Chem. Chem. Phys. 2016, 18, 23872–23878. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Basu, R.; Bhatt, R.; Pitale, S.; Singh, A.; Aswal, D.K.; Gupta, S.K.; Navaneethan, M.; Hayakawa, Y. CuCrSe2: A high performance phonon glass and electron crystal thermoelectric material. J. Mater. Chem. A 2013, 1, 11289–11294. [Google Scholar] [CrossRef]
- Guy, D.R.P.; Marseglia, E.A.; Guy, S.C. Electron Spin Resonance in CuCrS2 and CuCrSe2 Single Crystals. Mol. Cryst. Liq. Cryst. 1985, 121, 165–168. [Google Scholar] [CrossRef]
- Akmanova, G.R.; Davletshina, A.D. Ionic conductivity and diffusion in superionic conductors CuCrS2-AgCrS2. Lett. Mater. 2013, 3, 76–78. [Google Scholar] [CrossRef] [Green Version]
- Abramova, G.M.; Petrakovskii, G.A. Metal-insulator transition, magnetoresistance, and magnetic properties of 3d-sulfides (Review). Low Temp. Phys. 2006, 32, 725–734. [Google Scholar] [CrossRef]
- Tsujii, N.; Kitazawa, H. Substitution effect on the two-dimensional triangular-lattice system CuCrS2. J. Phys. Condens. Matter 2007, 19, 145245. [Google Scholar] [CrossRef]
- Al’mukhametov, R.F.; Yakshibaev, R.A.; Gabitov, É.V. Magnetic and transport properties of CuCr1−xVxS2 compounds. Phys. Solid State 1999, 41, 1327–1328. [Google Scholar] [CrossRef]
- Vasilyeva, I.G. Chemical aspect of the structural disorder in CuCrS2 and CuCr1–xVxS2 solid solutions. J. Struct. Chem. 2017, 58, 1009–1017. [Google Scholar] [CrossRef]
- Korotaev, E.V.; Syrokvashin, M.M.; Filatova, I.Y.; Zvereva, V.V. Vanadium doped layered copper-chromium sulfides: The correlation between the magnetic properties and XES data. Vacuum 2020, 179, 109390. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Zhu, J.H.; You, L.; Guo, K.; Li, Z.L.; Lin, W.G.; Huang, J.; Luo, J. Enhanced and stabilized n-type thermoelectric performance in α-CuAgSe by Ni doping. Mater. Today Phys. 2019, 10, 100095. [Google Scholar] [CrossRef]
- Tewari, G.C.; Tripathi, T.S.; Rastogi, A.K. Thermoelectric properties of layer-antiferromagnet CuCrS2. J. Electron. Mater. 2010, 39, 1133–1139. [Google Scholar] [CrossRef] [Green Version]
- Abramova, G.M.; Petrakovskǐ, G.A.; Vorotynov, A.M.; Velikanov, D.A.; Kiselev, N.I.; Bovina, A.F.; Szymczak, R.; Al’mukhametov, R.F. Phase transitions and colossal magnetoresistance in CuVxCr1−xS2 layered disulfides. JETP Lett. 2006, 83, 118–121. [Google Scholar] [CrossRef]
- Inorganic Crystal Structure Database, Version 2.1.0. Leibniz Institute for Information Infrastructure, FIZ Karlsruhe, Eggenstein- Leopoldshafen, Germany, (n.d.). Available online: https://icsd.products.fiz-karlsruhe.de/ (accessed on 17 August 2021).
- Vassilieva, I.G.; Kardash, T.Y.; Malakhov, V.V. Phase transformations of CuCrS2: Structural and chemical study. J. Struct. Chem. 2009, 50, 288–295. [Google Scholar] [CrossRef]
- Selwood, P. Magnetochemistry, 2nd ed.; Interscience Publishers: New York, NY, USA, 1956. [Google Scholar]
- Le Nagard, N.; Collin, G.; Gorochov, O. Etude structurale et proprietes physiques de CuCrS2. Mater. Res. Bull. 1979, 14, 1411–1417. [Google Scholar] [CrossRef]
- Moeller, T. The Chemistry of the Lanthanides; Elsevier: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Korotaev, E.V.; Syrokvashin, M.M.; Filatova, I.Y.; Trubina, S.V.; Nikolenko, A.D.; Ivlyushkin, D.V.; Zavertkin, P.S.; Kriventsov, V.V. The conduction band of the lanthanide doped chromium disulfides CuCr0.99Ln0.01S2 (Ln=La, Ce, Gd): XANES investigations. In Proceedings of the AIP Conference, Novosibirsk, Russian, 13–16 July 2020; Volume 2299, p. 080004. [Google Scholar]
- Adachi, H.; Ino, H. A ferromagnet having no net magnetic moment. Nature 1999, 401, 148–150. [Google Scholar] [CrossRef]
- Murphy, D.W.; Chen, H.S.; Tell, B. Superionic Conduction in AgCrS2 and AgCrSe2. J. Electrochem. Soc. 1977, 124, 1268–1271. [Google Scholar] [CrossRef]
- Korotaev, E.V.; Syrokvashin, M.M.; Peregudova, N.N.; Kanazhevskii, V.V.; Mazalov, L.N.; Sokolov, V.V. Effects of the nearest-neighbor environment of copper atoms on the XANES spectra of layered chromium-copper disulfides. J. Struct. Chem. 2015, 56, 596–600. [Google Scholar] [CrossRef]
- Korotaev, E.V.; Kanazhevskiy, V.V.; Peregudova, N.N.; Syrokvashin, M.M.; Mazalov, L.N.; Sokolov, V.V.; Filatova, I.Y.; Pichugin, A.Y. Xanes of X-ray absorbtion K edges of chromium dichalcogenides CuCr1-x M′xS2 and MCrX2. J. Struct. Chem. 2016, 57, 1355–1361. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korotaev, E.V.; Syrokvashin, M.M.; Filatova, I.Y.; Zvereva, V.V. Magnetic Properties of Novel Layered Disulfides CuCr0.99Ln0.01S2 (Ln = La…Lu). Materials 2021, 14, 5101. https://doi.org/10.3390/ma14175101
Korotaev EV, Syrokvashin MM, Filatova IY, Zvereva VV. Magnetic Properties of Novel Layered Disulfides CuCr0.99Ln0.01S2 (Ln = La…Lu). Materials. 2021; 14(17):5101. https://doi.org/10.3390/ma14175101
Chicago/Turabian StyleKorotaev, Evgeniy V., Mikhail M. Syrokvashin, Irina Yu. Filatova, and Valentina V. Zvereva. 2021. "Magnetic Properties of Novel Layered Disulfides CuCr0.99Ln0.01S2 (Ln = La…Lu)" Materials 14, no. 17: 5101. https://doi.org/10.3390/ma14175101
APA StyleKorotaev, E. V., Syrokvashin, M. M., Filatova, I. Y., & Zvereva, V. V. (2021). Magnetic Properties of Novel Layered Disulfides CuCr0.99Ln0.01S2 (Ln = La…Lu). Materials, 14(17), 5101. https://doi.org/10.3390/ma14175101





