Stress-Based FEM in the Problem of Bending of Euler–Bernoulli and Timoshenko Beams Resting on Elastic Foundation
Abstract
:1. Introduction
2. Stress-Based Formulation of the Euler–Bernoulli Beam on Elastic Foundation
2.1. Governing Equations
2.2. The Complementary Work Principle
2.3. Matrix Form of the Equilibrium-Based Fe Method
2.4. Interelement Equilibrium
2.5. Applied Element
3. Stress-Based Formulation for the Timoshenko Beam on Elastic Foundation
3.1. Governing Equations and Weak Formulation
3.2. The Complementary Work Principle
3.3. Finite Element Formulation of the Stress-Based Approach
4. The Stress-Based Beam Element with Linear Interpolation of Foundation Response
5. Error Estimation of the Approximate Solution
6. Numerical Examples
6.1. Two-Span Symmetric Beam Loaded Uniformly
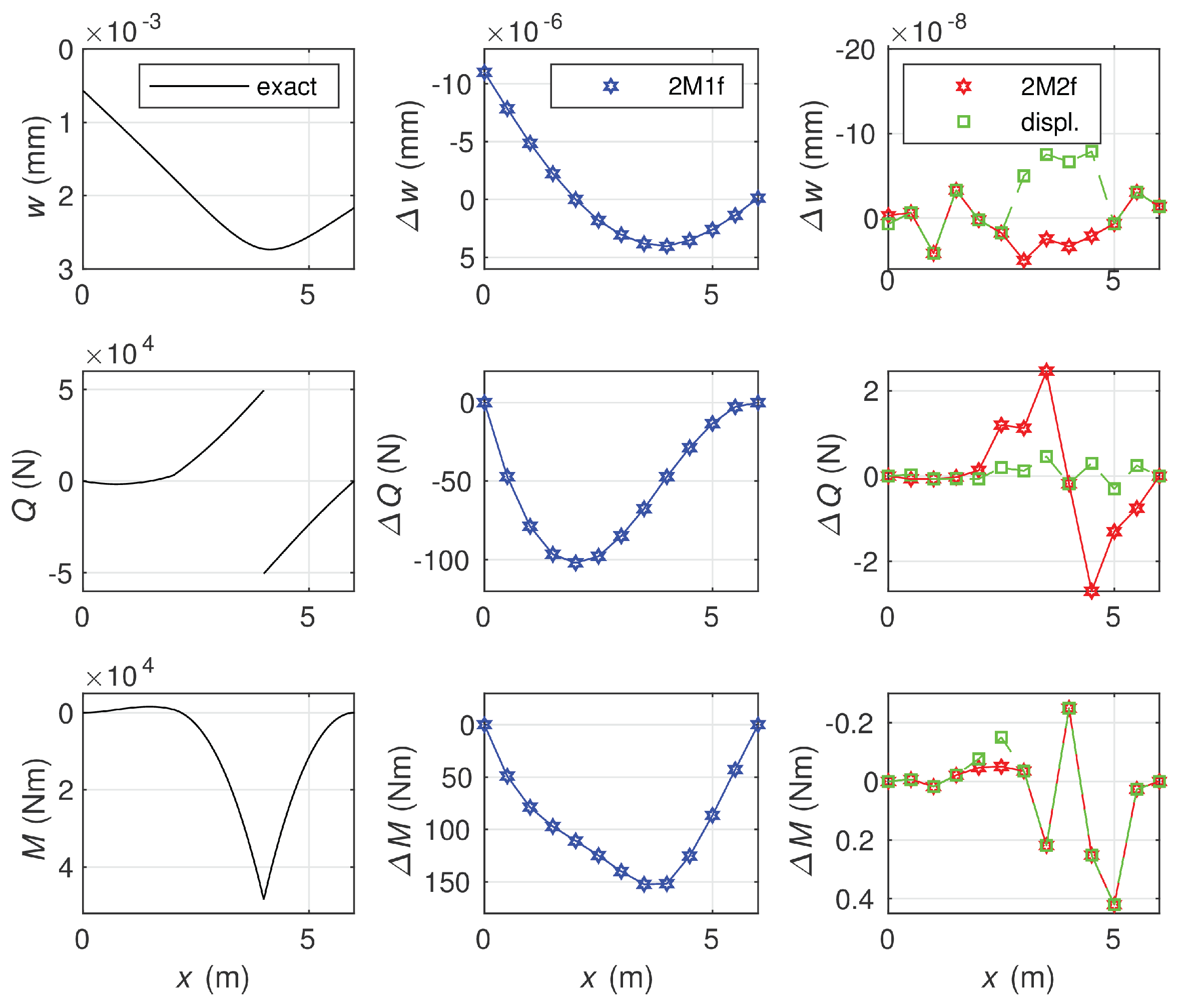
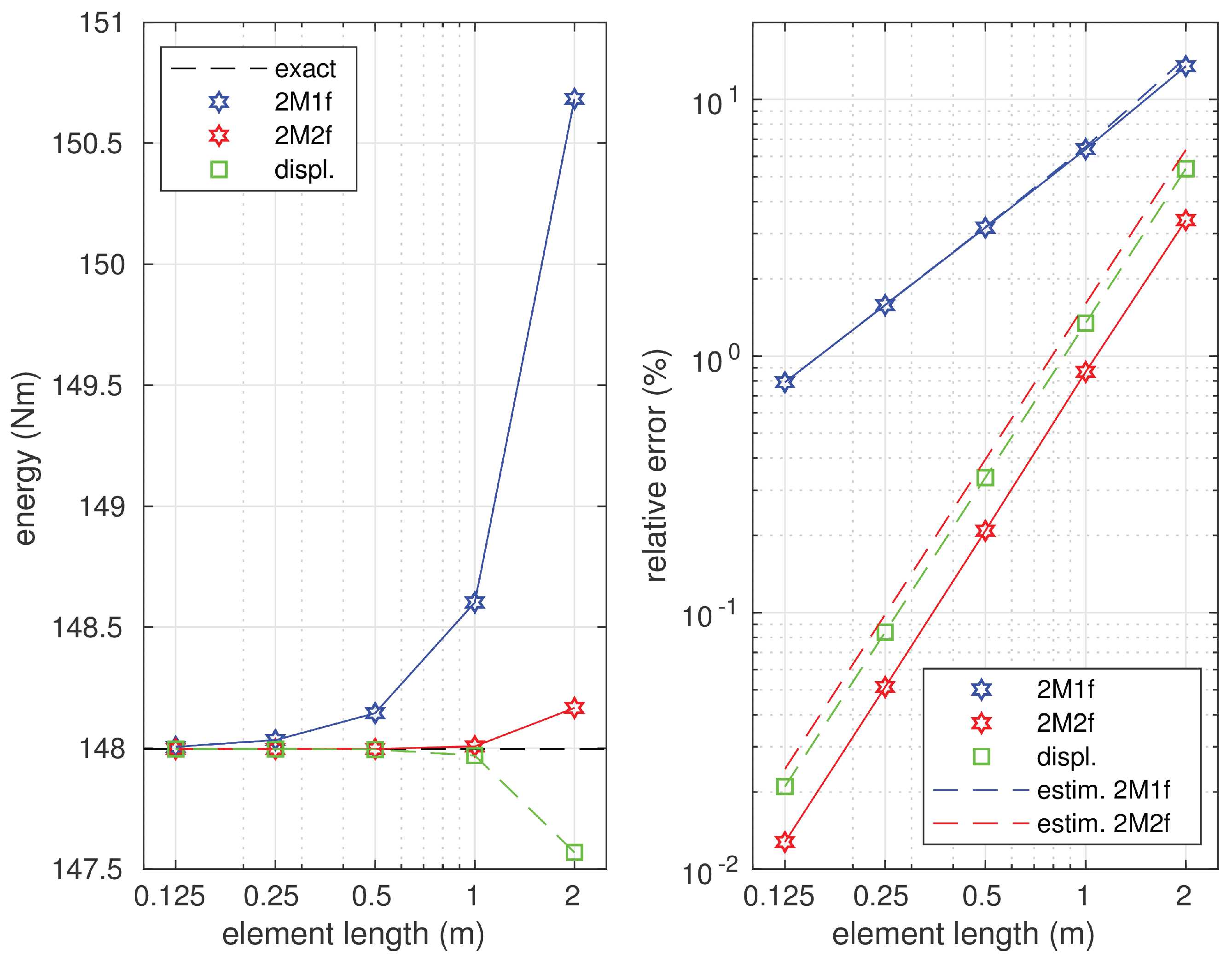
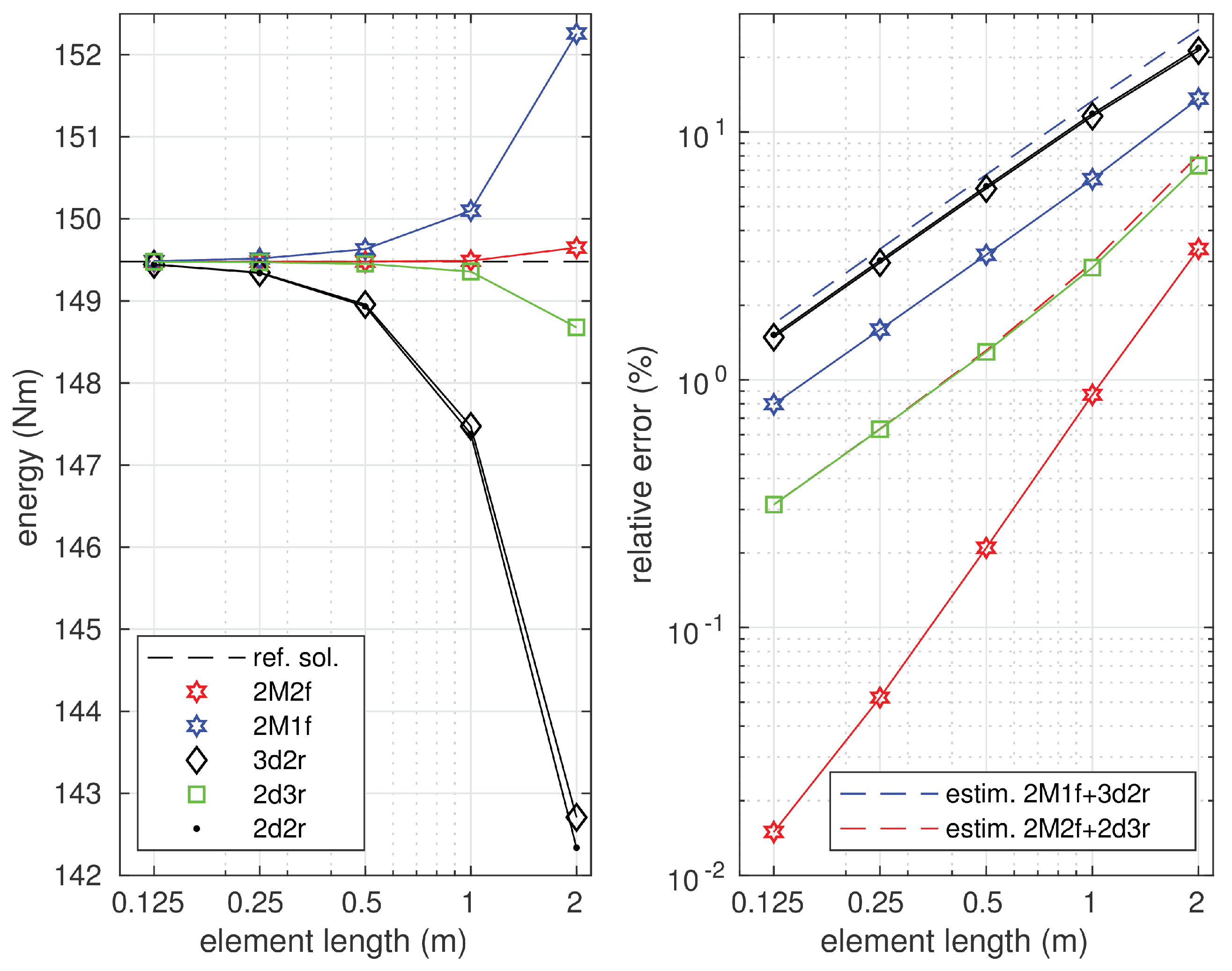
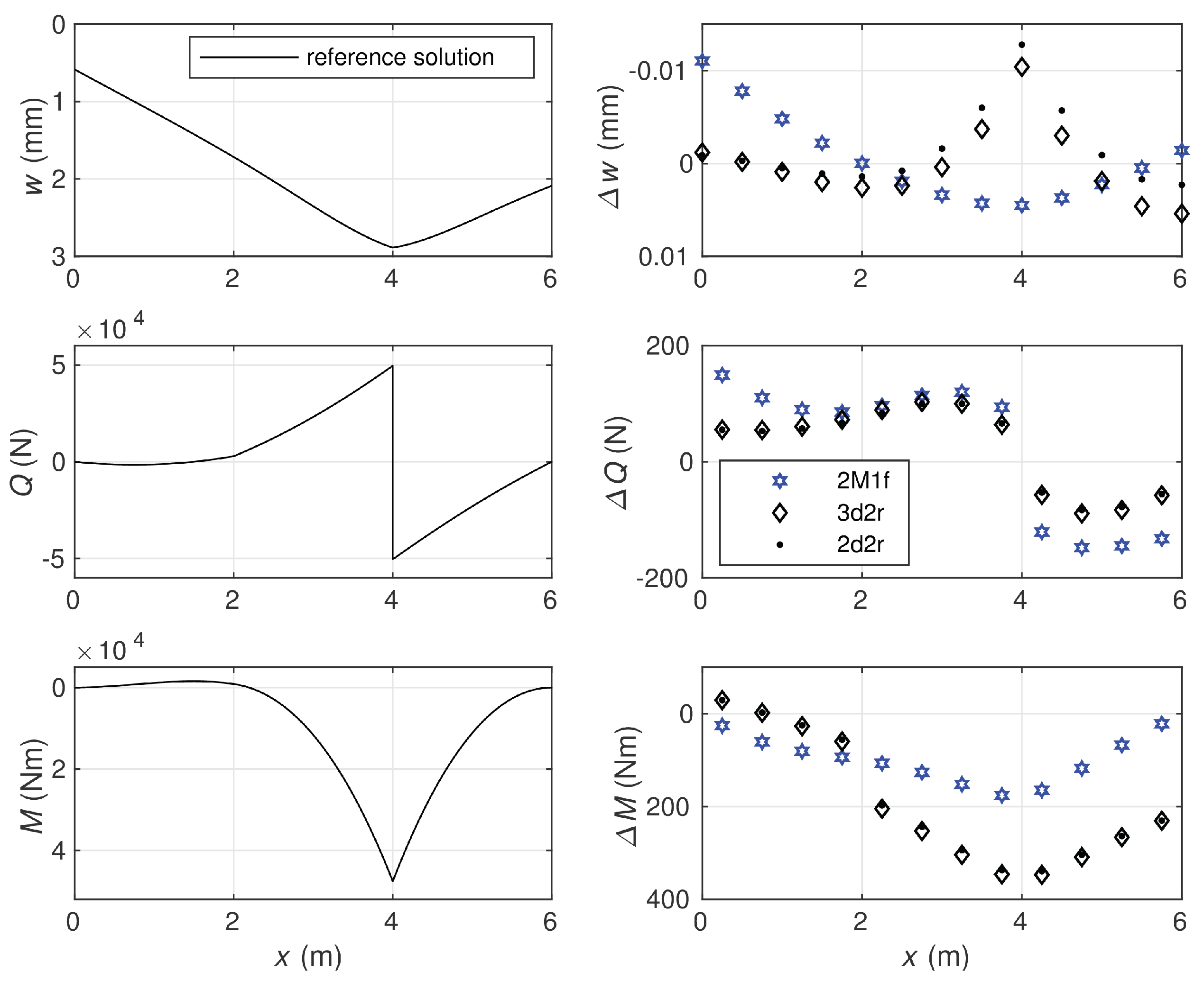
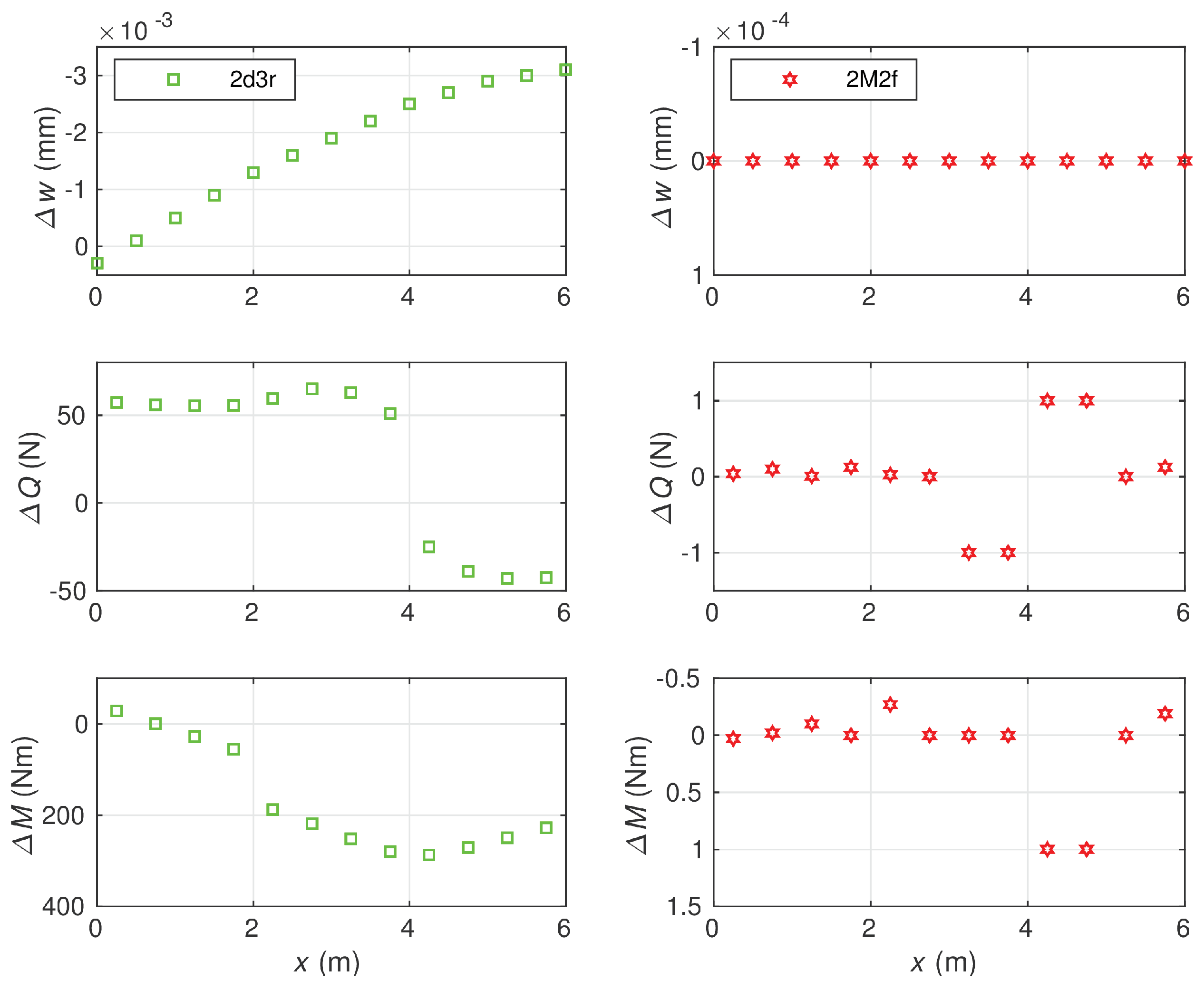
6.2. Euler–Bernoulli Beam on Elastic Foundation
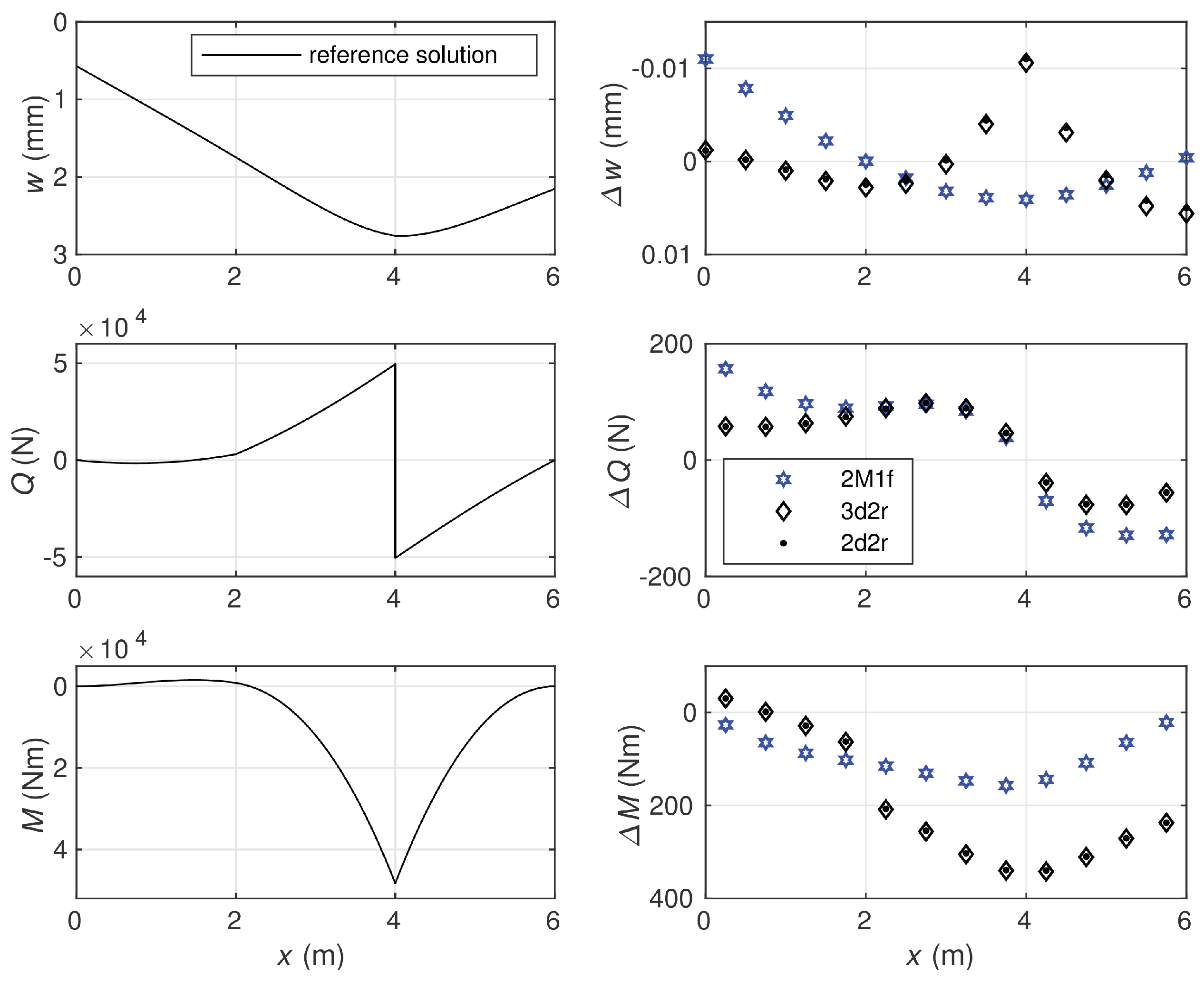
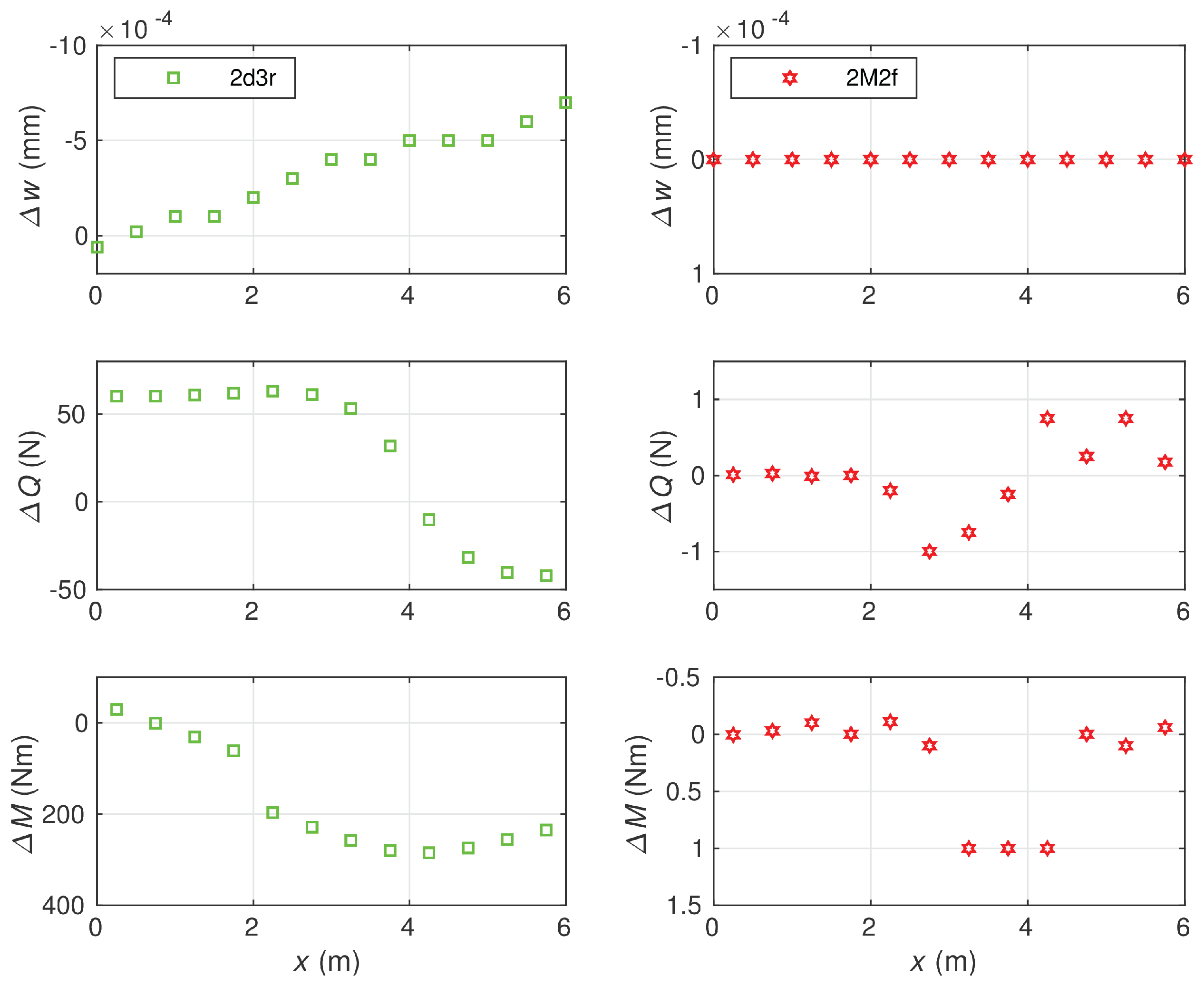
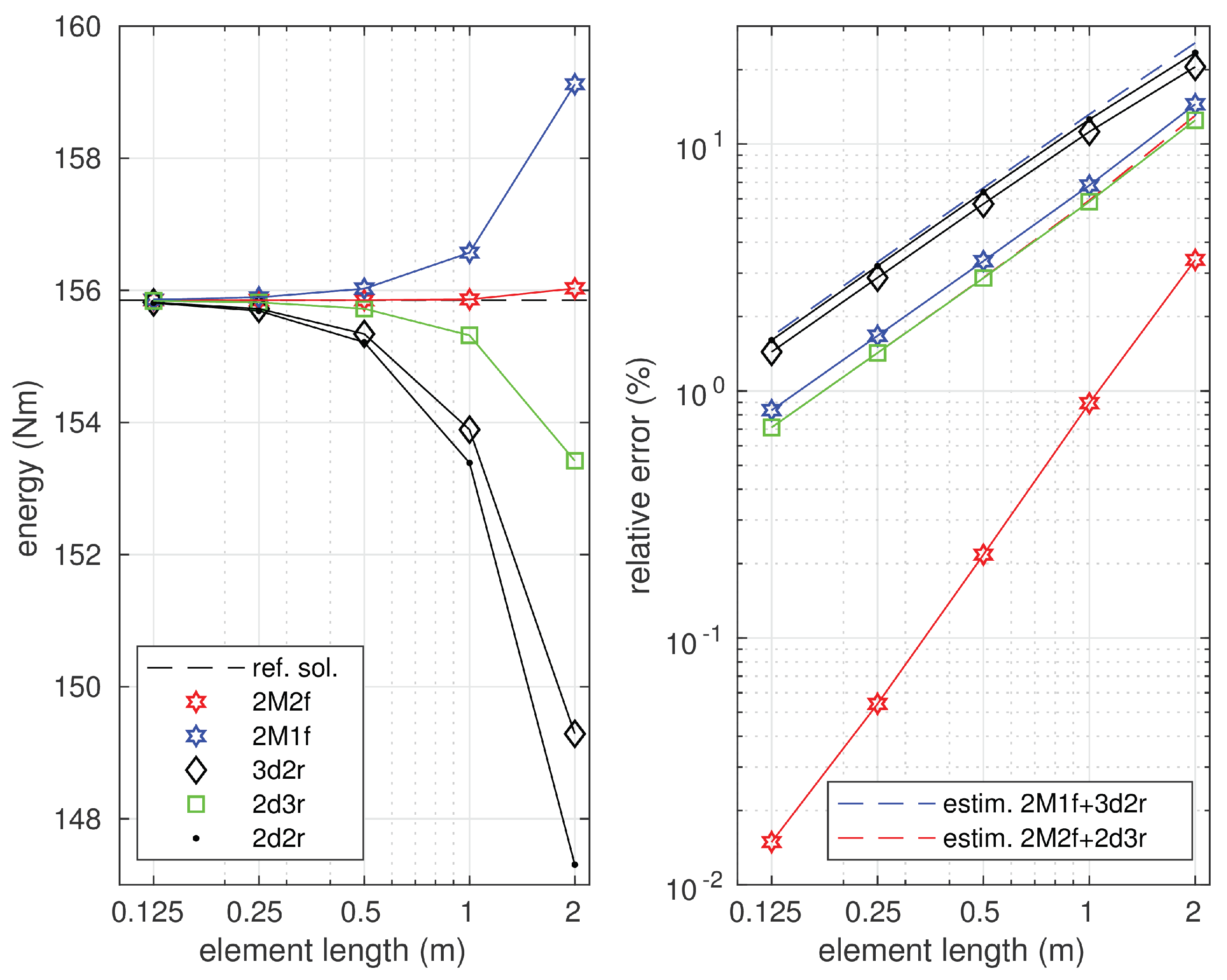
6.3. Timoshenko Beam on Elastic Foundation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cowper, G.R. The shear coefficient in Timoshenko’s beam theory. J. Appl. Mech. 1966, 33, 335–340. [Google Scholar] [CrossRef]
- Wang, C.M.; Reddy, J.N.; Lee, K.H. Shear Deformable Beams and Plates. Relationships with Classical Solutions; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Fraeijs de Veubeke, B. Displacemet and equilibrium models in finite element method. In Stress Analysis; Zienkiewicz, O.C., Holister, G.S., Eds.; John Wiley: Hoboken, NJ, USA, 1965; Chapter 9; pp. 145–197. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method for Solid and Structural Mechanics; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Too, J.M. Reduced integration technique in general analysis of plates and shells. Int. J. Numer. Methods Eng. 1971, 3, 275–290. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Taylor, R.L.; Kanoknukulchai, W. A simple and efficient finite element for plate bending. Int. J. Numer. Methods Eng. 1977, 11, 1529–1543. [Google Scholar] [CrossRef]
- Yokoyama, T. A reduced integration Timoshenko beam element. Thin Walled Struct. 1994, 411–418. [Google Scholar] [CrossRef]
- Reddy, J.N.; Wang, C.M.; Lee, K.H. Relationships between bending solutions of classical and shear deformation beam theories. Int. J. Solids Struct. 1997, 34, 3373–3384. [Google Scholar] [CrossRef]
- Mukherjee, S.; Reddy, J.N.; Krishnamoorthy, C.S. Convergence properties and derivative extraction of the superconvergent Timoshenko beam finite element. Comput. Methods Appl. Mech. Eng. 2001, 190, 3475–3500. [Google Scholar] [CrossRef]
- Więckowski, Z.; Golubiewski, M. Improvement in accuracy of the finite element method in analysis of stability of Euler–Bernoulli and Timoshenko beams. Thin Walled Struct. 2007, 45, 950–954. [Google Scholar] [CrossRef]
- Oñate, E. Beams, Plates and Shells. In Structural Analysis with the Finite Element Method. Linear Statics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2. [Google Scholar]
- Kanok-Nukulchai, W.; Barry, W.; Saran-Yasoontorn, K.; Bouillard, P.H. On elimination of shear locking in the element-free Galerkin method. Int. J. Numer. Meth. Eng. 2001, 52, 705–725. [Google Scholar] [CrossRef]
- Beissel, S.; Belytschko, T. Nodal integration of the element-free Galerkin method. Comput. Methods Appl. Mech. Eng. 1996, 139, 49–74. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.; Gu, L. Element-free Galerkin methods. Int. J. Num. Meth. Eng. 1996, 37, 229–256. [Google Scholar] [CrossRef]
- Xiao, J.R.; McCarthy, M.A. Meshless analysis of Timoshenko beams based on a locking-free formulation and variational approaches. Comput. Methods Appl. Mech. Eng. 2003, 192, 4403–4424. [Google Scholar] [CrossRef]
- Feng, H.; Cui, X.; Li, G. Static and dynamic analysis of Timoshenko beam using nodal integration technique. Int. J. Appl. Mech. 2012, 4, 1250045. [Google Scholar] [CrossRef]
- Reddy, J. An Introduction to Nonlinear Finte Element Analysis with Application to Heat Transfer, Fluid Mechanics, and Solid Mechanics; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Beirão de Veiga, L.; Lovadina, C.; Reali, A. Avoiding shear locking for the Timoshenko beam problem via isogeometric collocation methods. Comput. Methods Appl. Mech. Eng. 2012, 241–244, 38–51. [Google Scholar] [CrossRef]
- Auricchio, F.; Beirão de Veiga, L.; Kiendl, J.; Lovadina, C.; Reali, A. Locking-free isogeometric collocation methods for spatial Timoshenko rods. Comput. Methods Appl. Mech. Eng. 2013, 263, 113–126. [Google Scholar] [CrossRef]
- Kiendl, J.; Auricchio, F.; Reali, A. A displacement-free formulation for the Timoshenko beam problem and a corresponding isogeometric collocation approach. Meccanica 2018, 53, 1403–1413. [Google Scholar] [CrossRef]
- Balobanov, V.; Niiranen, J. Locking-free variational formulations and isogeometric analysis for the Timoshenko beam models of strain gradient and classical elasticity. Comput. Methods Appl. Mech. Eng. 2018, 339, 137–159. [Google Scholar] [CrossRef]
- Zhang, B.; Yuming, H.; Dabiao, L.; Zhipeng, G.; Shen, L. Non-classical Timoshenko beam element based on the strain gradient elasticity theory. Finite Elem. Anal. Des. 2014, 79, 22–39. [Google Scholar] [CrossRef]
- Wong, F.T.; Sugianto, S. Study of the discrete shear gap technique in Timoshenko beam elements. Civ. Eng. Dimens. 2017, 19, 54–62. [Google Scholar] [CrossRef] [Green Version]
- Heteneyi, M. Beams on Elastic Foundation. Theory with Applications in the Fields od Civil and Mechanical Engineering; University of Michigan Press: Ann Arbor, MI, USA, 1946. [Google Scholar]
- Kuo, Y.; Cleghorn, W.; Behdinan, K. Stress-based finite element method for Euler–Bernoulli beams. Trans. Can. Soc. Mech. Eng. 2006, 30. [Google Scholar] [CrossRef]
- Synge, J. The Hypercircle in Mathematical Physics; Cambridge University Press: Cambridge, UK, 1957. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Więckowski, Z.; Świątkiewicz, P. Stress-Based FEM in the Problem of Bending of Euler–Bernoulli and Timoshenko Beams Resting on Elastic Foundation. Materials 2021, 14, 460. https://doi.org/10.3390/ma14020460
Więckowski Z, Świątkiewicz P. Stress-Based FEM in the Problem of Bending of Euler–Bernoulli and Timoshenko Beams Resting on Elastic Foundation. Materials. 2021; 14(2):460. https://doi.org/10.3390/ma14020460
Chicago/Turabian StyleWięckowski, Zdzisław, and Paulina Świątkiewicz. 2021. "Stress-Based FEM in the Problem of Bending of Euler–Bernoulli and Timoshenko Beams Resting on Elastic Foundation" Materials 14, no. 2: 460. https://doi.org/10.3390/ma14020460
APA StyleWięckowski, Z., & Świątkiewicz, P. (2021). Stress-Based FEM in the Problem of Bending of Euler–Bernoulli and Timoshenko Beams Resting on Elastic Foundation. Materials, 14(2), 460. https://doi.org/10.3390/ma14020460




