Analytical Compliance Equations of Generalized Elliptical-Arc-Beam Spherical Flexure Hinges for 3D Elliptical Vibration-Assisted Cutting Mechanisms
Abstract
:1. Introduction
2. Analytical Compliance Equations of Elliptical-Arc-Beam Spherical Flexure Hinges
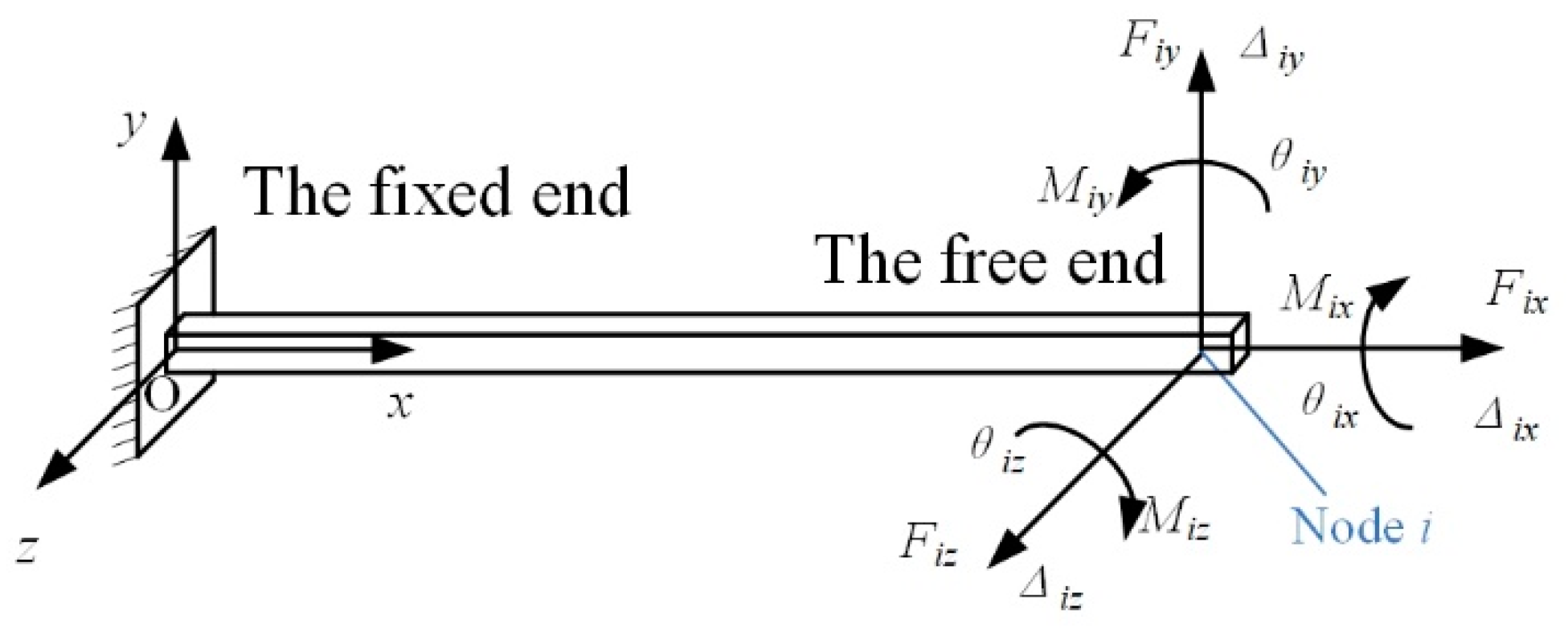
2.1. Compliance Equations of Generalized Spatial Flexure Hinges
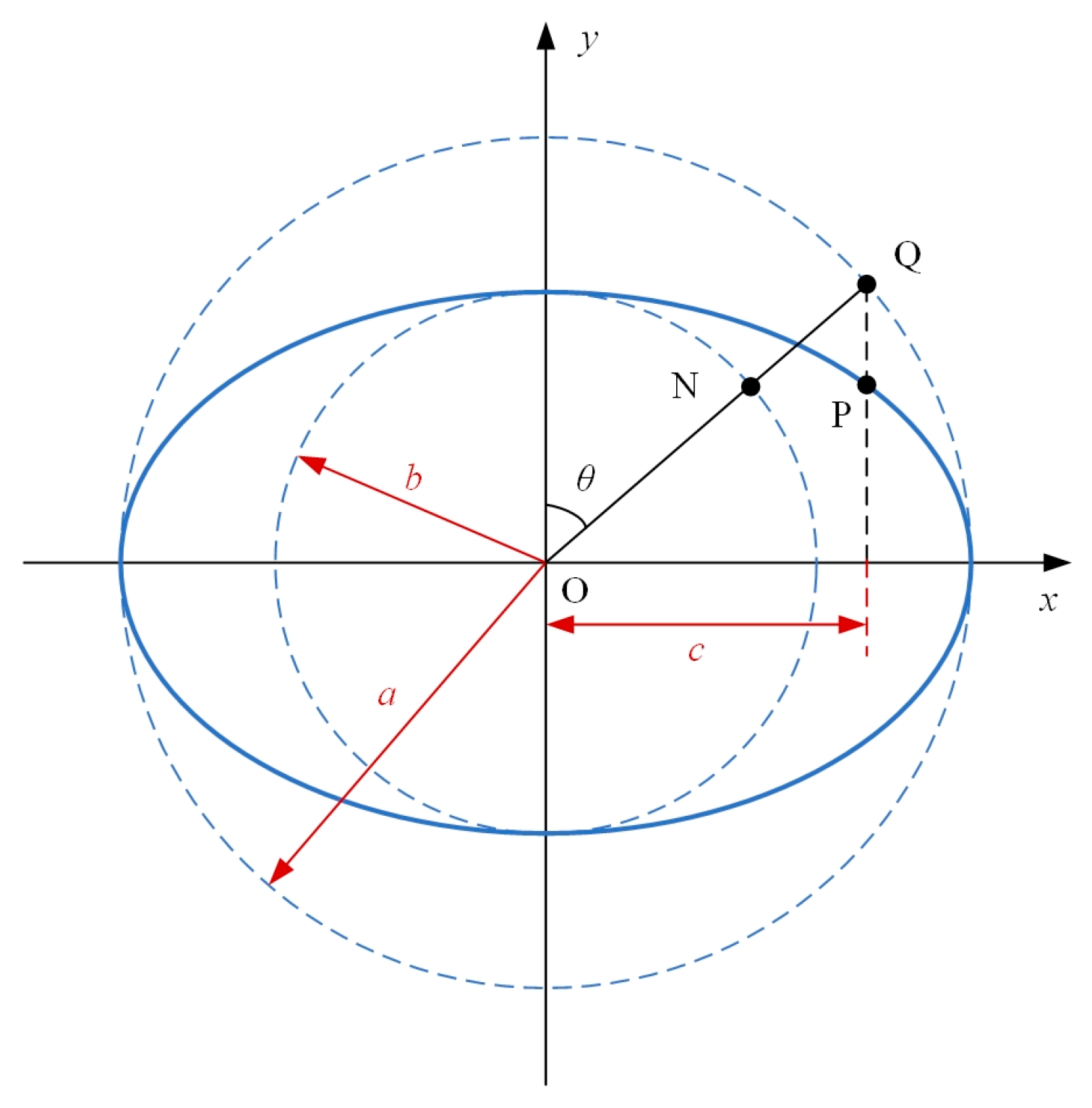
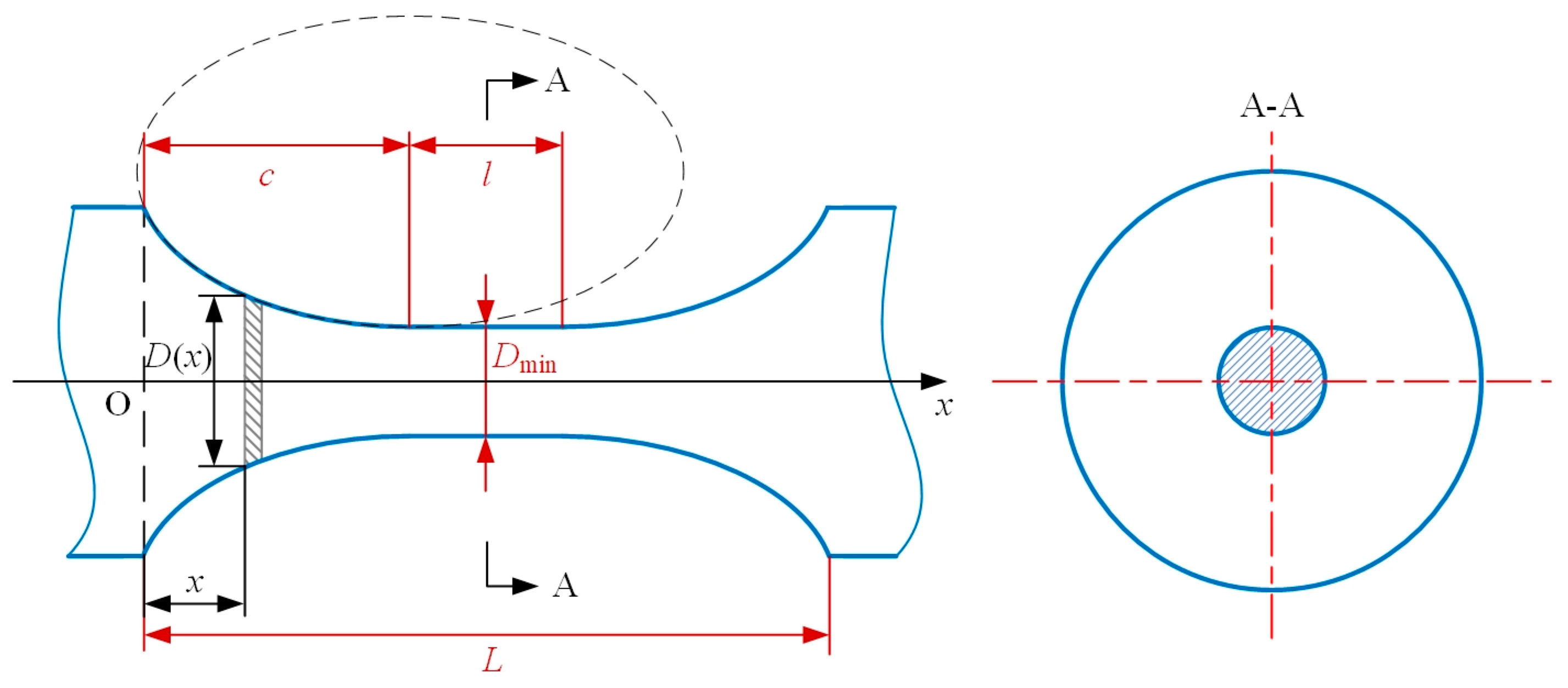
2.2. The Notch Profile of Generalized Elliptical-Arc-Beam Spherical Flexure Hinges
2.3. Analytical Equations of the Factors in the Compliance Matrix
3. Results
3.1. Compliance Factors of Spherical Elliptical-Arc Flexure Hinges
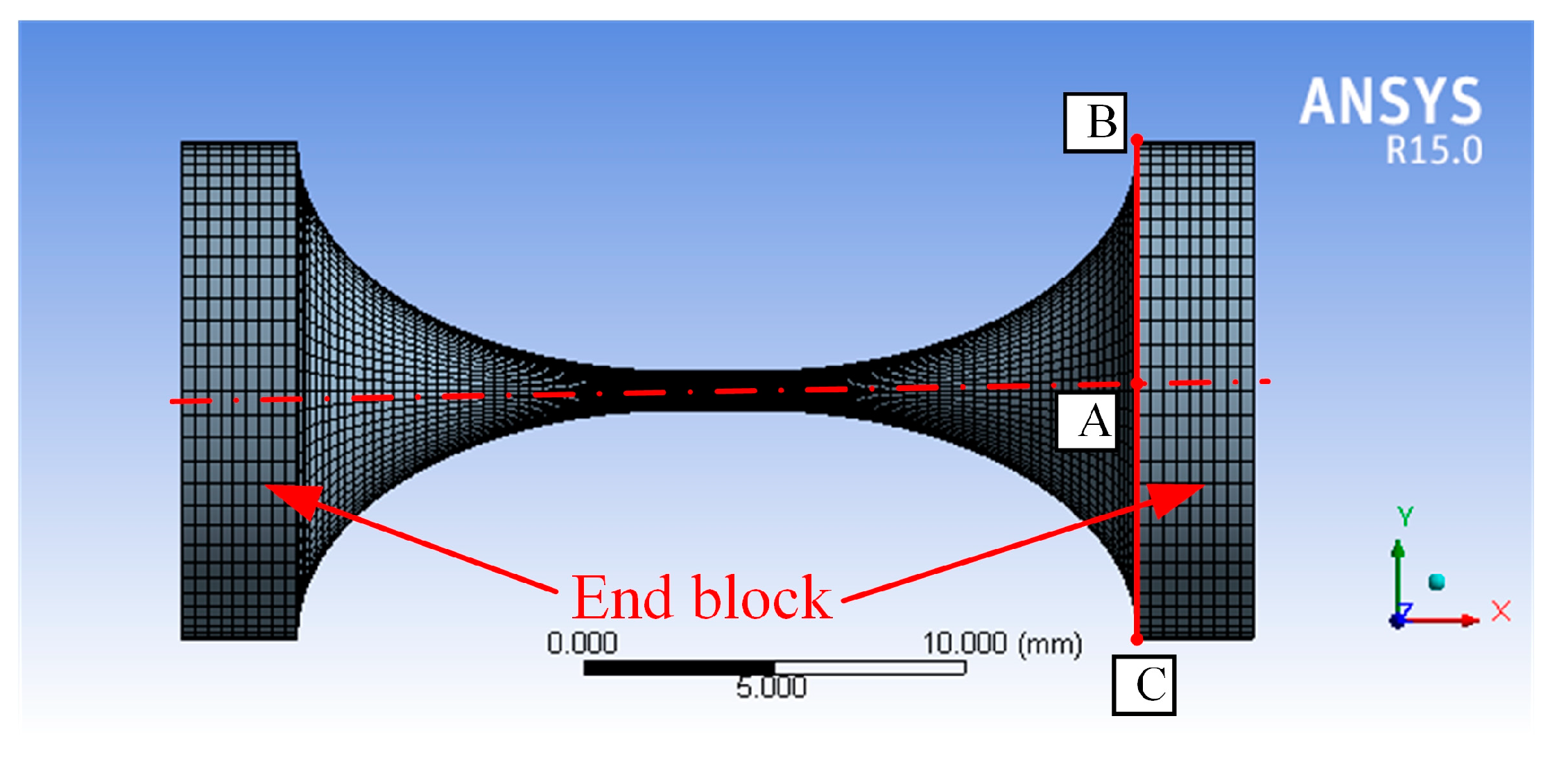
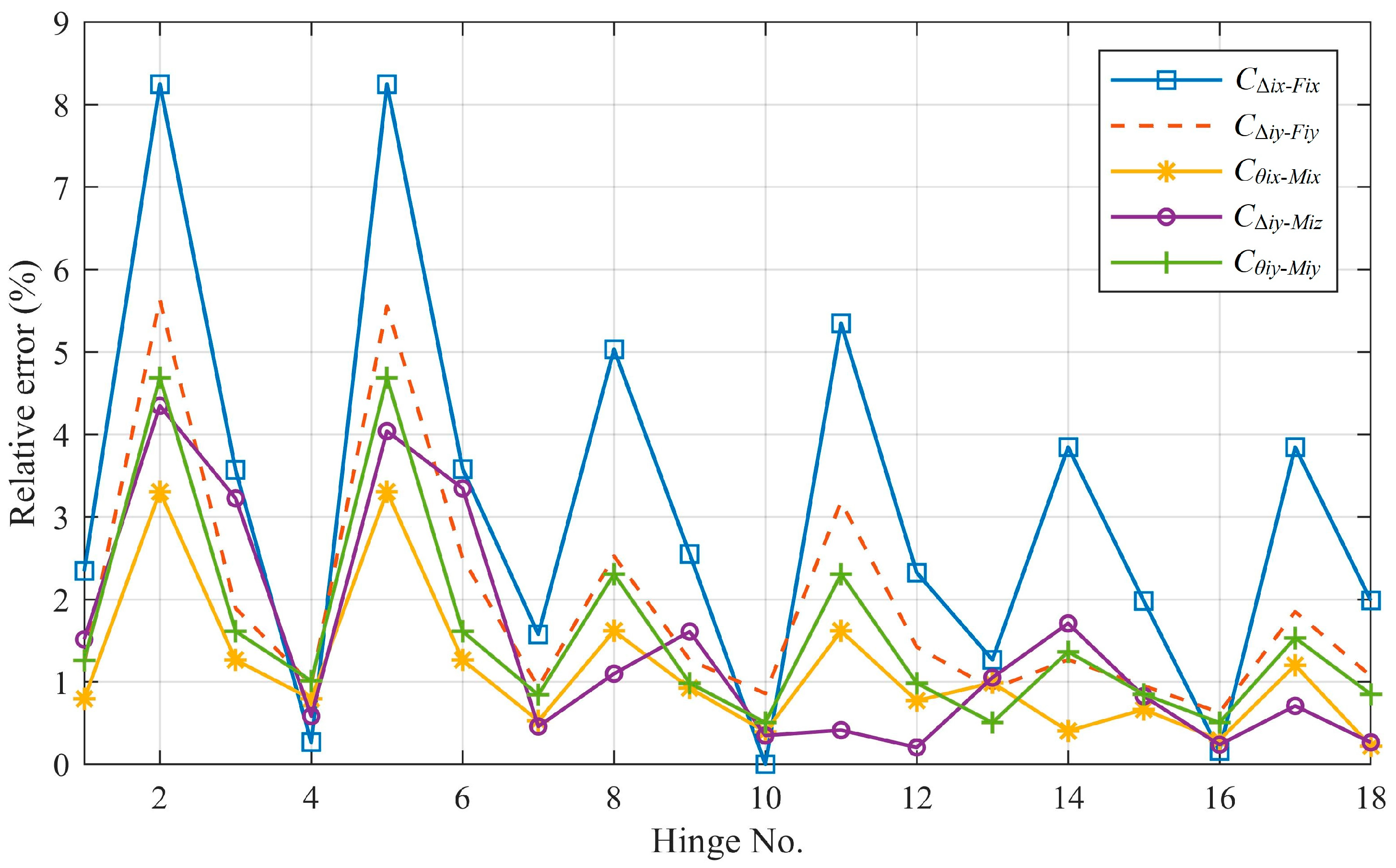
3.2. Simulation Validation by FEA
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Fi | External load vector acts on node i at the free end of the flexure hinge |
| Fik | External force component of Fi with subscript k denoting its direction, k = x, y, z |
| Mik | External moment component of Fi with subscripts k denoting its direction, k = x, y, z |
| ∆i | Displacement vector of node i at the free end of the flexure hinges resulted by Fi |
| ∆ik | Translation component of ∆i with subscript k denoting its direction |
| θik | Rotation component of ∆i with subscript k denoting its direction |
| x | Position coordinate along the flexure hinge |
| L | Length of the flexure hinge |
| A(x) | Section area of the flexure hinge, a function of x |
| E | Young’s modulus of material |
| G | Shearing modulus of material |
| μ | Shearing coefficient for a short beam with circular section |
| Fx(x) | Axial force along x-axis of the flexure hinge, a function of x |
| Fk(x) | Shear force along k-axis of the flexure hinge, a function of x, k = y, z |
| Mk(x) | Moment around k-axis of the flexure hinge, a function of x, k = x, y, z |
| U | Strain energy of the flexure hinge acted by Fi |
| Ci | Compliance matrix of the flexure hinge at node i |
| Cm-n | Compliance in the direction of m caused by the external load n, m = ∆ix, ∆iy, ∆iz, θix, θiy, θiz and n = Fix, Fiy, Fiz, Mix, Miy, Miz |
| D(x) | Diameter variation of circular section, a function of x |
| a | Length of semi-major axis of ellipse |
| b | Length of semi-minor axis of ellipse |
| θ | Eccentric angle of ellipse |
| xp | Horizontal coordinate of point P on the ellipse |
| yp | Vertical coordinate of point P on the ellipse |
| Dmin | Diameter of the middle beam |
| l | Notch length of the middle beam part |
| c | Notch length of the elliptical -arc part |
| θm | Maximum eccentric angle |
| ζ | Intermediate variable, ζ = Dmin/2b |
| Nj | Intermediate variables for integral simplification, j = 1, 2, 3, 4 |
Appendix A
References
- Gao, W.; Han, H.; Zhang, F.Z.; Leach, R.; Linares, J.M. On-machine and in-process surface metrology for precision manufacturing. CIRP Ann. Manuf. Technol. 2019, 68, 843–866. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Liu, S.; Wang, L. Surface modification of biomedical titanium alloy: Micromorphology, microstructure evolution and biomedical applications. Coatings 2019, 9, 249. [Google Scholar] [CrossRef] [Green Version]
- Boidi, G.; Grützmacher, P.G.; Kadiric, A.; Profito, F.J.; Machado, I.F.; Gachot, C.; Dini, D. Fast laser surface texturing of spherical samples to improve the frictional performance of elasto-hydrodynamic lubricated contacts. Friction 2021, 9, 1227–1241. [Google Scholar] [CrossRef]
- Wang, Y.K.; Wang, J.J.; Chen, A.; Kwok, N.; Guo, P. Structural coloration using face turning and variable tool vibration frequency. J. Manuf. Process. 2020, 56, 1392–1396. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, L.; Huang, P.; Schonemann, L.; Zhu, W.L. Design and control of a piezoelectrically actuated fast tool servo for diamond turning of microstructured surfaces. IEEE Trans. Ind. Electron. 2019, 67, 6688–6697. [Google Scholar] [CrossRef]
- Chen, Y.L.; Cai, Y.; Tohyama, K.; Shimizu, Y.; Ito, S.; Gao, W. Autotracking single point diamond cutting on nonplanar brittle material substrates by a high-rigidity force controlled fast tool servo. Precis. Eng. 2017, 49, 253–261. [Google Scholar] [CrossRef]
- Zhao, D.; Zhu, Z.; Huang, P.; Guo, P.; Zhu, L.; Zhu, Z. Development of a piezoelectrically actuated dual-stage fast tool servo. Mech. Syst. Signal Pract. 2020, 144, 106873. [Google Scholar] [CrossRef]
- Huang, H.; Pan, Y.; Pang, Y.; Shen, H.; Sun, L. Piezoelectric Ultrasonic Biological Microdissection Device Based on a Novel Flexure Mechanism for Suppressing Vibration. Micromachines 2021, 12, 196. [Google Scholar] [CrossRef] [PubMed]
- Hussein, R.; Sadek, A.; Elbestawi, M.; Attia, M. Chip morphology and delamination characterization for vibration-assisted drilling of carbon fiber-reinforced polymer. J. Manuf. Mater. Process. 2019, 3, 23. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Shao, Z.; Su, H.; Fu, H. An energy-based approach for kinetostatic modeling of general compliant mechanisms. Mech. Mach. Theory 2019, 142, 103588. [Google Scholar] [CrossRef]
- Chen, G.; Wu, H.; Li, B.; Wang, M.Y. Fully compliant bistable mechanisms with enhanced pitch stiffness. Mech. Syst. Signal Pract. 2021, 161, 107926. [Google Scholar] [CrossRef]
- Chen, F.; Dong, W.; Yang, M.; Sun, L.; Du, Z. A PZT actuated 6-DOF positioning system for space optics alignment. IEEE-ASME Trans. Mech. 2019, 24, 2827–2838. [Google Scholar] [CrossRef]
- Zhang, S.J.; Zhou, Y.P.; Zhang, H.J.; Xiong, Z.W. Advances in ultra-precision machining of micro-structured functional surfaces and their typical applications. Int. J. Mach. Tool. Manu. 2019, 142, 16–41. [Google Scholar] [CrossRef]
- Zheng, L.; Qin, P.; Lv, D.; Wei, W.; Dong, X.; Park, S. Low-frequency axial vibration drilling of Al2O3/GFRP laminated composite plate by diamond trepanning bit. Compos. Struct. 2020, 245, 112374. [Google Scholar] [CrossRef]
- Paros, J.M.; Weisbord, L. How to Design Flexure Hinges. Mach. Design 1965, 37, 151–156. [Google Scholar]
- Smith, S.T.; Badami, V.G.; Dale, J.S. Elliptical flexure hinges. Rev. Sci. Instrum. 1997, 68, 1474. [Google Scholar] [CrossRef]
- Chen, G.; Liu, X.; Gao, H.; Jia, J. A generalized model for conic flexure hinges. Rev. Sci. Instrum. 2009, 80, 151. [Google Scholar] [CrossRef]
- Chen, G.; Liu, X.; Du, Y. Elliptical-arc-fillet flexure hinges: Toward a generalized model for commonly used flexure hinges. J. Mech. Design 2011, 133, 081002. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.; Cui, Z.; Chen, X.F. Fuzzy multi-objective optimization for movement performance of deep-notch elliptical flexure hinges. Rev. Sci. Instrum. 2015, 86, 065005. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.S.N.; Garcia, E.; Goldfarb, M. Design of circular cross-section corner-filleted flexure hinges for three-dimensional compliant mechanisms. Mech. Mach. Theory 2002, 37, 477–498. [Google Scholar] [CrossRef]
- Lobontiu, N.; Garcia, E.; Hardau, M.; Bal, N. Stiffness characterization of corner-filleted flexure hinges. Rev. Sci. Instrum. 2004, 75, 4896–4905. [Google Scholar] [CrossRef]
- Shi, R.C.; Dong, W.; Du, Z.J. Design methodology and performance analysis of application-oriented flexure hinges. Rev. Sci. Instrum. 2013, 84, 075005. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Lee, M.Y.; Kim, J.S.; Lee, D.Y. Compliance matrix of a single-bent leaf flexure for a modal analysis. Shock Vib. 2015, 2015, 672831. [Google Scholar] [CrossRef]
- Smith, S.T.; Chetwynd, D.G.; Bowen, D.K. Design and assessment of monolithic high precision translation mechanisms. J. Phys. E Sci. Instrum. 1987, 20, 977. [Google Scholar] [CrossRef]
- Tian, Y.; Shirinzadeh, B.; Zhang, D.; Zhong, Y. Three flexure hinges for compliant mechanism designs based on dimensionless graph analysis. Precis. Eng. 2010, 34, 92–100. [Google Scholar] [CrossRef]
- Li, T.M.; Zhang, J.L.; Jiang, Y. Derivation of empirical compliance equations for circular flexure hinge considering the effect of stress concentration. Int. J. Precis. Eng. Man. 2015, 16, 1735–1743. [Google Scholar] [CrossRef]
- Tuo, W.; Li, X.; Ji, Y.; Wu, T.; Xie, Z. Analytical compliance model for right circle flexure hinge considering the stress concentration effect. Int. J. Precis. Eng. Man. 2020, 21, 1–10. [Google Scholar] [CrossRef]
- Zhang, C.; Song, Y.; Ehmann, K.F. Design and experimental investigation of a parallel flexure hinge-based 3D elliptical vibration-assisted cutting mechanism. J. Micromech. Microeng. 2020, 30, 085008. [Google Scholar] [CrossRef]
- Wei, H.; Shirinzadeh, B.; Tang, H.; Niu, X. Closed-form compliance equations for elliptic-revolute notch type multiple-axis flexure hinges. Mech. Mach. Theory 2021, 156, 104154. [Google Scholar] [CrossRef]
- Yong, Y.K.; Lu, T.F.; Handley, D.C. Review of circular flexure hinge design equations and derivation of empirical formulations. Precis. Eng. 2008, 32, 63–70. [Google Scholar] [CrossRef]

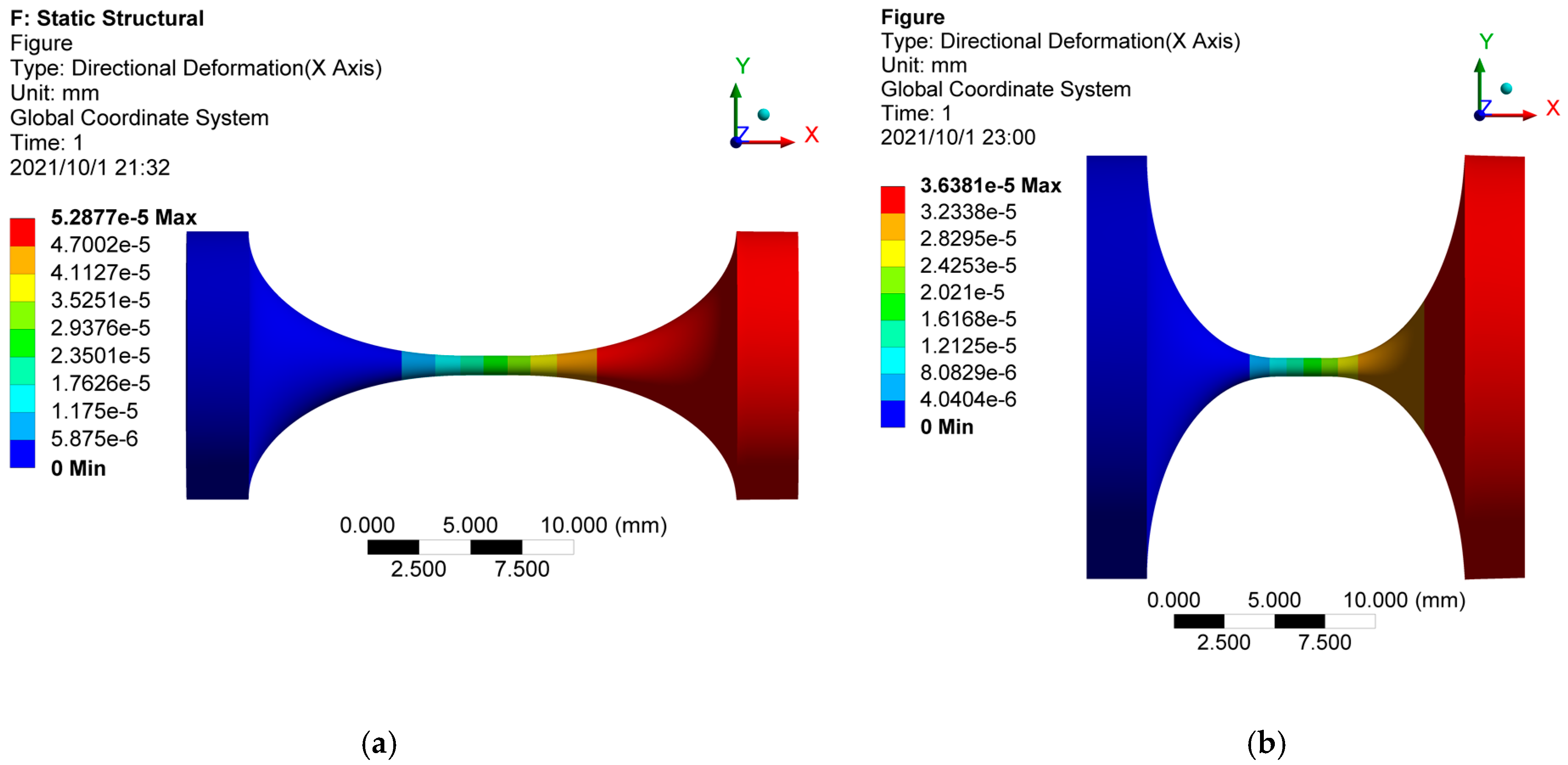
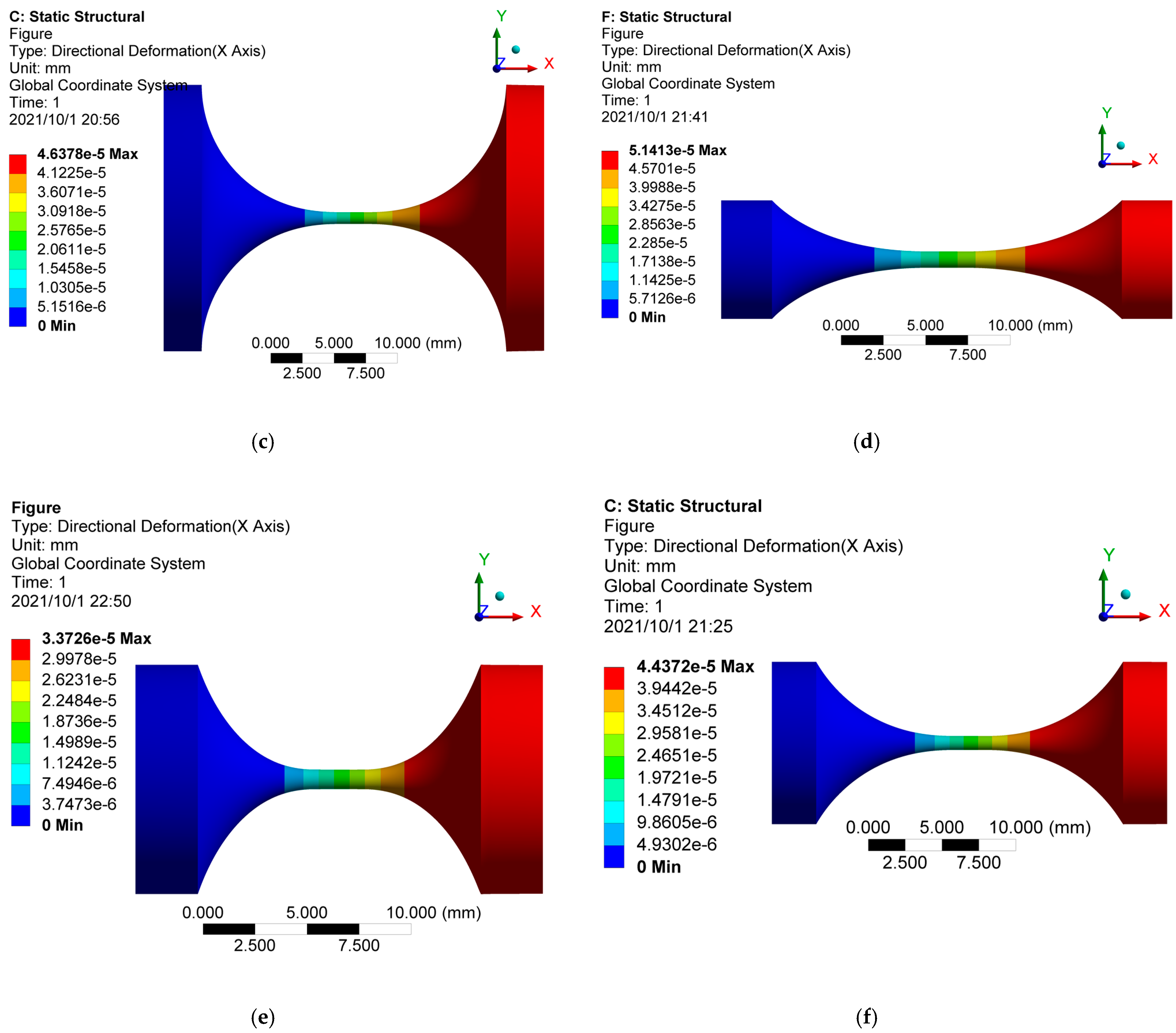
| Hinge No. | a (mm) | b (mm) | c (mm) | θm (°) | Dmin (mm) | Notch Type |
|---|---|---|---|---|---|---|
| 1 | 8.25 | 4 | 8.25 | 90 | 0.5 | Elliptical |
| 2 | 5 | 7 | 5 | 90 | 0.4 | Elliptical |
| 3 | 7 | 4 | 6.76 | 75 | 0.5 | Elliptical-arc |
| 4 | 4.5 | 6 | 3.90 | 60 | 0.4 | Elliptical-arc |
| 5 | 4 | 4 | 3.86 | 75 | 0.5 | Circular |
| 6 | 6 | 6 | 5.20 | 60 | 0.4 | Circular |
| 7 | 4 | 4 | 4 | 90 | 0.5 | Right-circular |
| 8 | 7 | 7 | 7 | 90 | 0.4 | Right-circular |
| 9 | 1 | 0.1 | 1 | 90 | 0.5 | Elliptical |
| 10 | 1 | 0.5 | 1 | 90 | 0.6 | Elliptical |
| 11 | 0.875 | 0.3 | 0.875 | 90 | 0.75 | Elliptical |
| Hinge No. | CΔix-Fix (×10−8 m/N) | CΔiy-Fiy (10−5 m/N) | Cθix-Mix (rad/Nm) | CΔiy-Miz (10−3 m/N) | Cθiy-Miy (rad/Nm) |
|---|---|---|---|---|---|
| 1 | 11.19 | 32.23 | 6.01 | 38.10 | 4.62 |
| 2 | 7.32 | 11.77 | 6.04 | 23.20 | 4.65 |
| 3 | 9.49 | 18.41 | 5.10 | 26.50 | 3.92 |
| 4 | 7.08 | 7.00 | 5.87 | 17.60 | 4.52 |
| 5 | 5.42 | 3.44 | 2.91 | 8.70 | 2.24 |
| 6 | 9.45 | 16.56 | 7.83 | 31.3 | 6.02 |
| 7 | 5.42 | 3.68 | 2.91 | 9.00 | 2.24 |
| 8 | 10.25 | 32.27 | 8.46 | 45.60 | 6.51 |
| 9 | 4.40 | 0.32 | 3.23 | 2.50 | 2.48 |
| 10 | 2.28 | 0.09 | 1.00 | 0.76 | 0.76 |
| 11 | 1.53 | 0.04 | 0.46 | 0.31 | 0.36 |
| Hinge No. | a (mm) | b (mm) | c (mm) | θm (°) | Dmin (mm) | l (mm) | Notch Type |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 6 | 10 | 90 | 1 | 0 | Elliptical |
| 2 | 6 | 10 | 6 | 90 | 1 | 0 | Elliptical |
| 3 | 10 | 10 | 10 | 90 | 1 | 0 | Right-circular |
| 4 | 10 | 6 | 8.66 | 60 | 1 | 0 | Elliptical-arc |
| 5 | 6 | 10 | 5.20 | 60 | 1 | 0 | Elliptical-arc |
| 6 | 10 | 10 | 8.66 | 60 | 1 | 0 | Circular |
| 7 | 10 | 6 | 10 | 90 | 1 | 2 | Elliptical-beam |
| 8 | 6 | 10 | 6 | 90 | 1 | 2 | Elliptical-beam |
| 9 | 10 | 10 | 10 | 90 | 1 | 2 | Circular-beam |
| 10 | 10 | 6 | 8.66 | 60 | 1 | 2 | Elliptical-arc-beam |
| 11 | 6 | 10 | 5.20 | 60 | 1 | 2 | Elliptical-arc-beam |
| 12 | 10 | 10 | 8.66 | 60 | 1 | 2 | Circular-arc-beam |
| 13 | 10 | 6 | 10 | 90 | 1 | 4 | Elliptical-beam |
| 14 | 6 | 10 | 6 | 90 | 1 | 4 | Elliptical-beam |
| 15 | 10 | 10 | 10 | 90 | 1 | 4 | Circular-beam |
| 16 | 10 | 6 | 8.66 | 60 | 1 | 4 | Elliptical-arc-beam |
| 17 | 6 | 10 | 5.20 | 60 | 1 | 4 | Elliptical-arc-beam |
| 18 | 10 | 10 | 8.66 | 60 | 1 | 4 | Circular-arc-beam |
| Hinge No. | CΔix-Fix (×10−8 m/N) | CΔiy-Fiy (10−5 m/N) | Cθix-Mix (rad/Nm) | CΔiy-Miz (10−3 m/N) | Cθiy-Miy (rad/Nm) |
|---|---|---|---|---|---|
| 1 (Analytical) | 3.75 | 4.04 | 5.01 | 3.90 | 3.91 |
| 1 (FEA) | 3.84 | 4.09 | 5.05 | 3.96 | 3.96 |
| 2 (Analytical) | 1.78 | 0.67 | 2.34 | 1.10 | 1.83 |
| 2 (FEA) | 1.94 | 0.71 | 2.42 | 1.15 | 1.92 |
| 3 (Analytical) | 2.97 | 3.11 | 3.90 | 3.00 | 3.05 |
| 3 (FEA) | 3.08 | 3.17 | 3.95 | 3.10 | 3.10 |
| 4 (Analytical) | 3.73 | 3.06 | 5.01 | 3.40 | 3.91 |
| 4 (FEA) | 3.74 | 3.09 | 5.05 | 3.42 | 3.95 |
| 5 (Analytical) | 1.78 | 0.51 | 2.34 | 0.95 | 1.83 |
| 5 (FEA) | 1.94 | 0.54 | 2.42 | 0.99 | 1.92 |
| 6 (Analytical) | 2.96 | 2.34 | 3.90 | 2.60 | 3.05 |
| 6 (FEA) | 3.07 | 2.40 | 3.95 | 2.69 | 3.10 |
| 7 (Analytical) | 4.99 | 7.40 | 7.54 | 6.50 | 5.89 |
| 7 (FEA) | 5.07 | 7.47 | 7.58 | 6.53 | 5.94 |
| 8 (Analytical) | 3.02 | 1.93 | 4.87 | 2.70 | 3.81 |
| 8 (FEA) | 3.18 | 1.98 | 4.95 | 2.73 | 3.90 |
| 9 (Analytical) | 4.20 | 6.24 | 6.43 | 5.50 | 5.03 |
| 9 (FEA) | 4.31 | 6.32 | 6.49 | 5.59 | 5.08 |
| 10 (Analytical) | 4.97 | 5.77 | 7.54 | 5.70 | 5.89 |
| 10 (FEA) | 4.97 | 5.82 | 7.57 | 5.72 | 5.92 |
| 11 (Analytical) | 3.01 | 1.52 | 4.87 | 2.40 | 3.81 |
| 11 (FEA) | 3.18 | 1.57 | 4.95 | 2.41 | 3.90 |
| 12 (Analytical) | 4.20 | 4.85 | 6.43 | 4.90 | 5.03 |
| 12 (FEA) | 4.30 | 4.92 | 6.48 | 4.91 | 5.08 |
| 13 (Analytical) | 6.23 | 11.9 | 1.00 | 9.40 | 7.87 |
| 13 (FEA) | 6.31 | 12.01 | 1.01 | 9.50 | 7.91 |
| 14 (Analytical) | 4.25 | 3.89 | 7.40 | 4.60 | 5.78 |
| 14 (FEA) | 4.42 | 3.94 | 7.43 | 4.68 | 5.86 |
| 15 (Analytical) | 5.44 | 10.40 | 8.96 | 8.40 | 7.00 |
| 15 (FEA) | 5.55 | 10.50 | 9.02 | 8.47 | 7.06 |
| 16 (Analytical) | 6.20 | 9.48 | 1.007 | 8.40 | 7.87 |
| 16 (FEA) | 6.21 | 9.54 | 1.01 | 8.42 | 7.91 |
| 17 (Analytical) | 4.25 | 3.18 | 7.40 | 4.20 | 5.78 |
| 17 (FEA) | 4.42 | 3.24 | 7.49 | 4.23 | 5.87 |
| 18 (Analytical) | 5.43 | 8.32 | 9.00 | 7.50 | 7.00 |
| 18 (FEA) | 5.54 | 8.41 | 9.02 | 7.52 | 7.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wu, S.; Shao, Z. Analytical Compliance Equations of Generalized Elliptical-Arc-Beam Spherical Flexure Hinges for 3D Elliptical Vibration-Assisted Cutting Mechanisms. Materials 2021, 14, 5928. https://doi.org/10.3390/ma14205928
Wang H, Wu S, Shao Z. Analytical Compliance Equations of Generalized Elliptical-Arc-Beam Spherical Flexure Hinges for 3D Elliptical Vibration-Assisted Cutting Mechanisms. Materials. 2021; 14(20):5928. https://doi.org/10.3390/ma14205928
Chicago/Turabian StyleWang, Han, Shilei Wu, and Zhongxi Shao. 2021. "Analytical Compliance Equations of Generalized Elliptical-Arc-Beam Spherical Flexure Hinges for 3D Elliptical Vibration-Assisted Cutting Mechanisms" Materials 14, no. 20: 5928. https://doi.org/10.3390/ma14205928
APA StyleWang, H., Wu, S., & Shao, Z. (2021). Analytical Compliance Equations of Generalized Elliptical-Arc-Beam Spherical Flexure Hinges for 3D Elliptical Vibration-Assisted Cutting Mechanisms. Materials, 14(20), 5928. https://doi.org/10.3390/ma14205928






