Analysis and Optimization of Machining Hardened Steel AISI 4140 with Self-Propelled Rotary Tools
Abstract
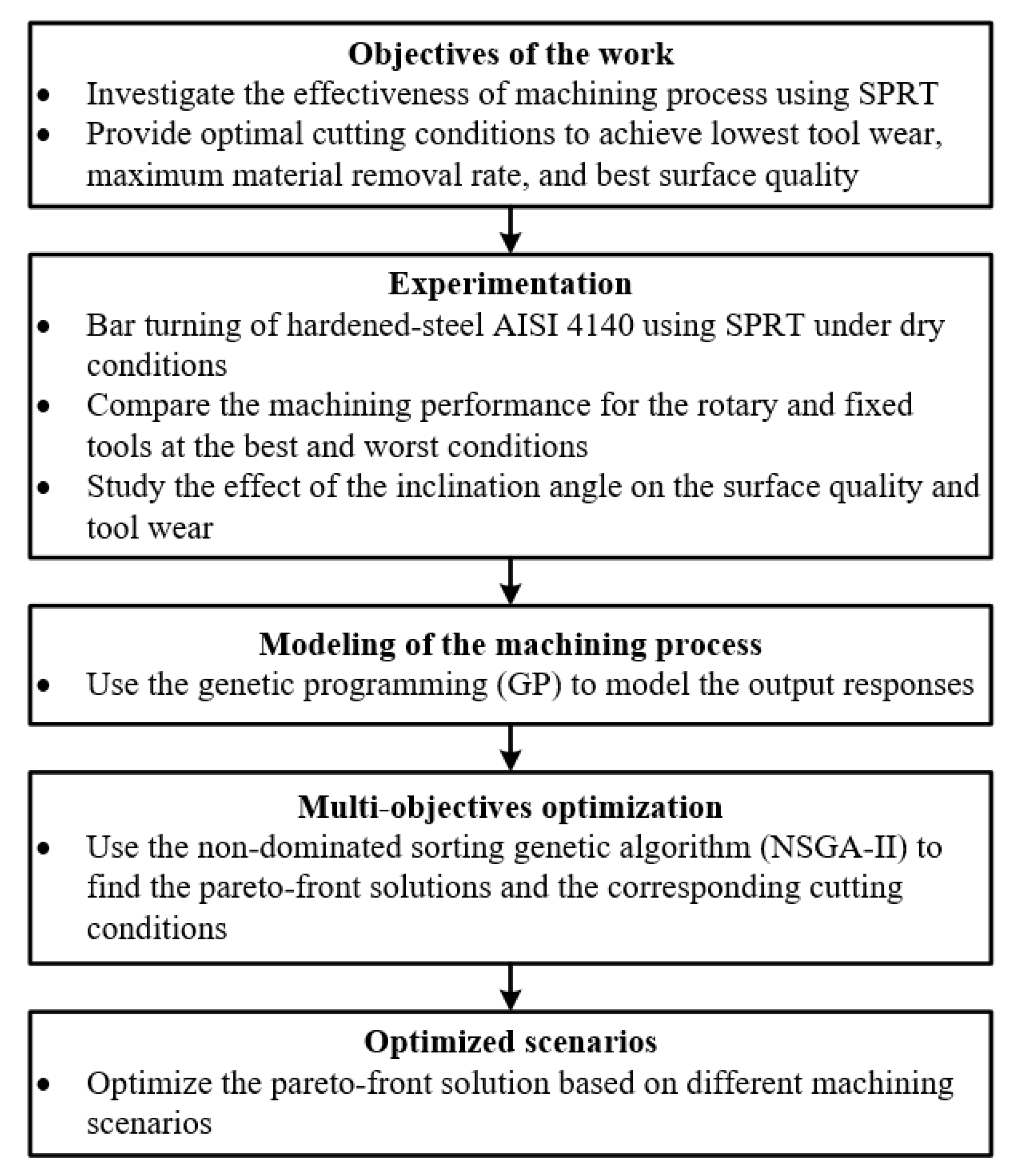
:1. Introduction
2. Materials and Methods
3. Results and Discussion
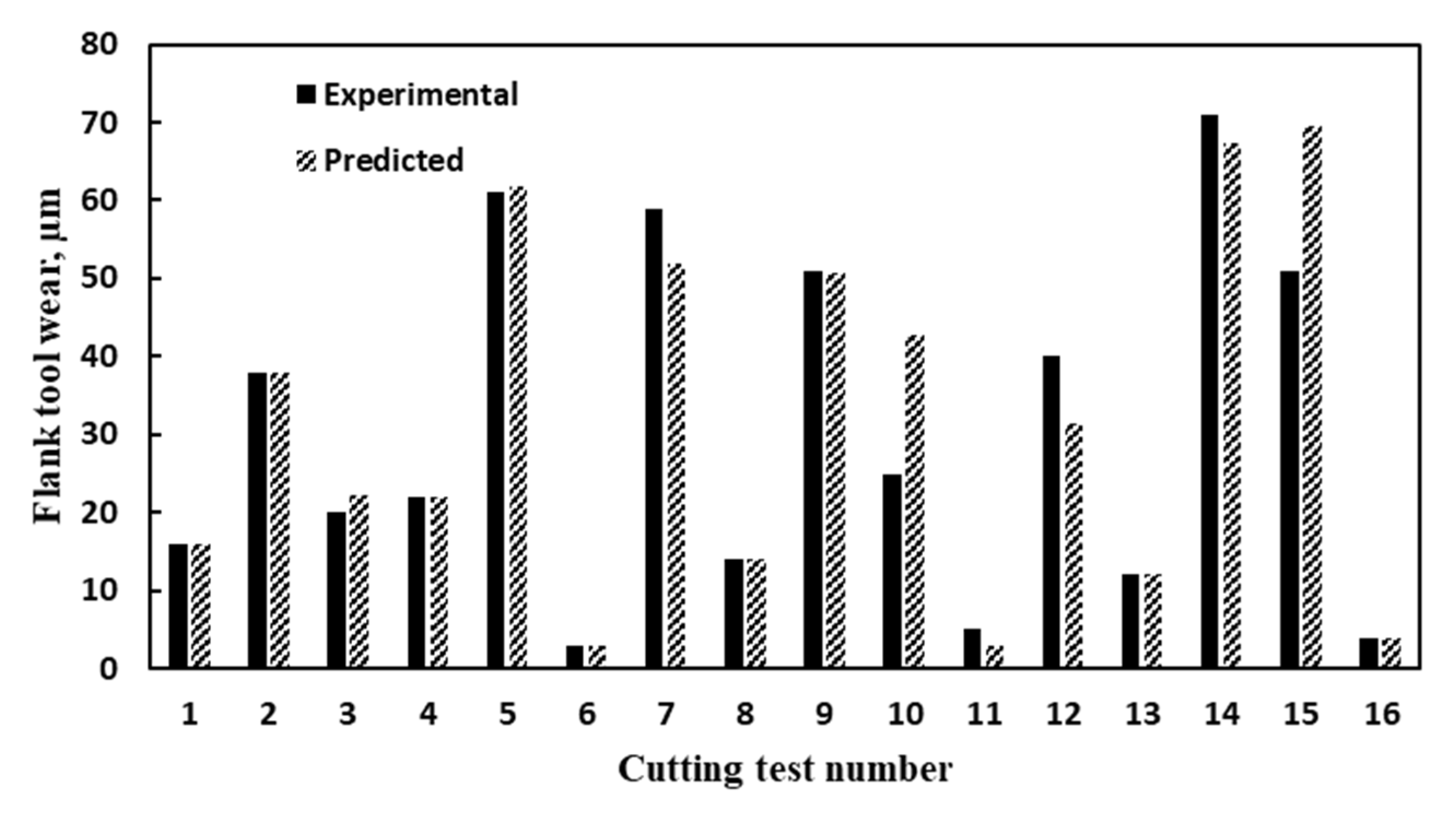
4. Modeling of the Machining Characteristics
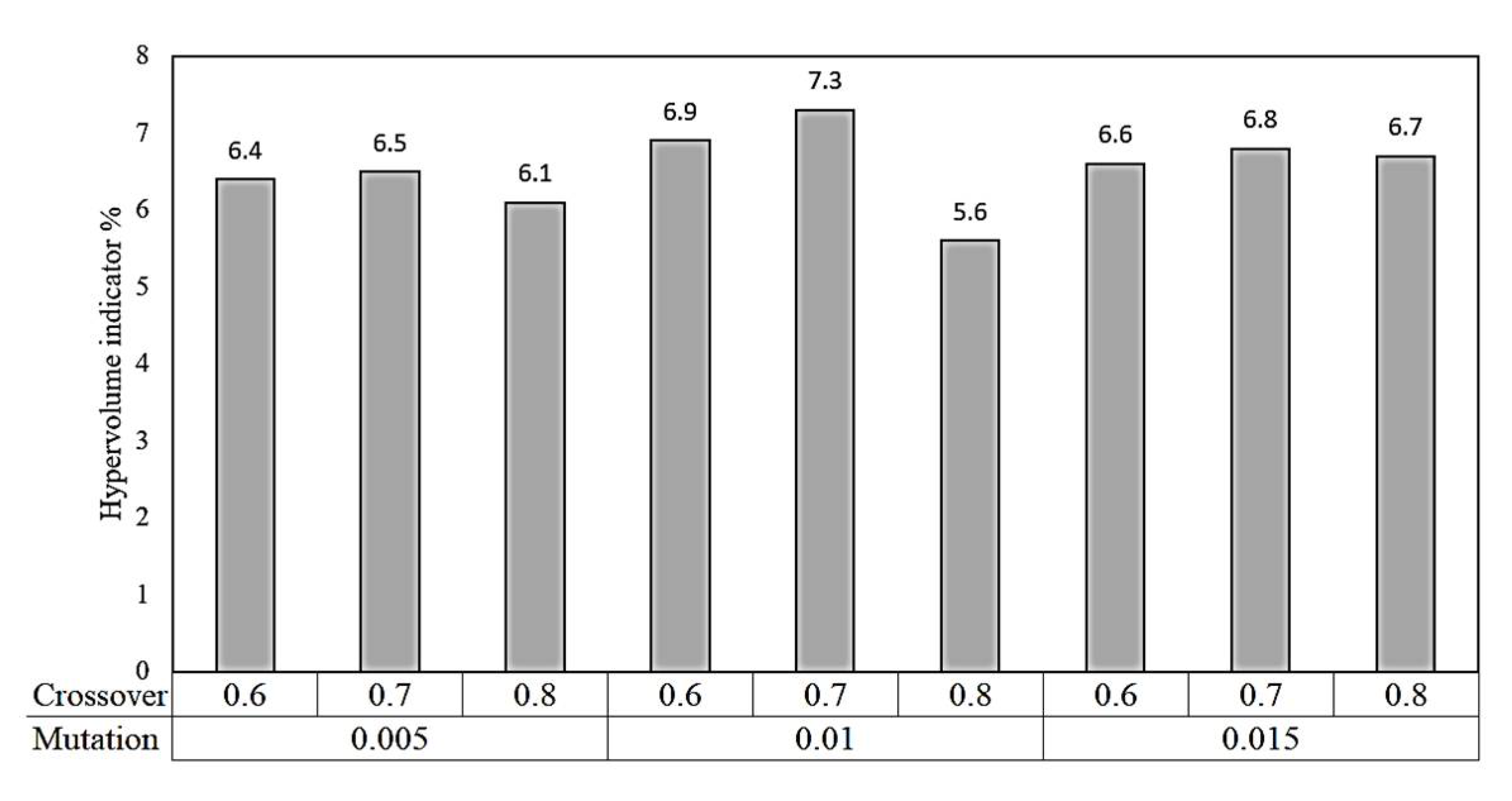
5. Multi-Objective Optimization
- Select the size of the population based on the constraints and their range;
- Perform non-dominated sort for the initialized populations;
- Assign crowding distance values for the population of individuals;
- Select the individuals based on the rank and the crowding distance;
- Apply the genetic algorithm crossover and mutation operators;
- Recombine and select an individual for the next generation until the population size exceeds the current size.
6. Optimized Scenarios
7. Conclusions and Future Work
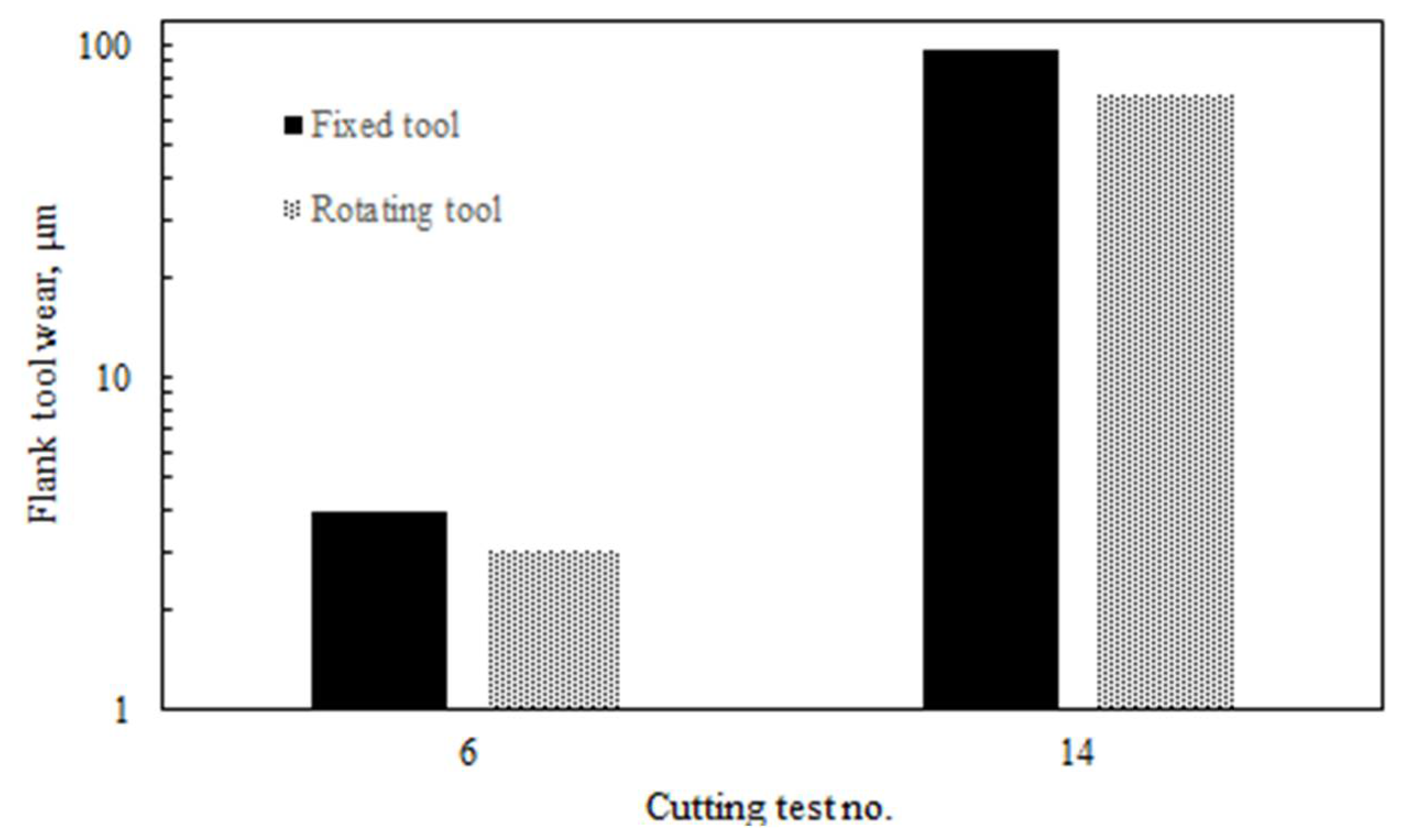
- Using a self-propelled rotary tool reduced the flank tool wear by 37% and 22% at the worst and best cutting conditions, respectively, compared to the fixed tool;
- Unlike conventional cutting, increasing the feed rate led to a decrease in the flank tool wear;
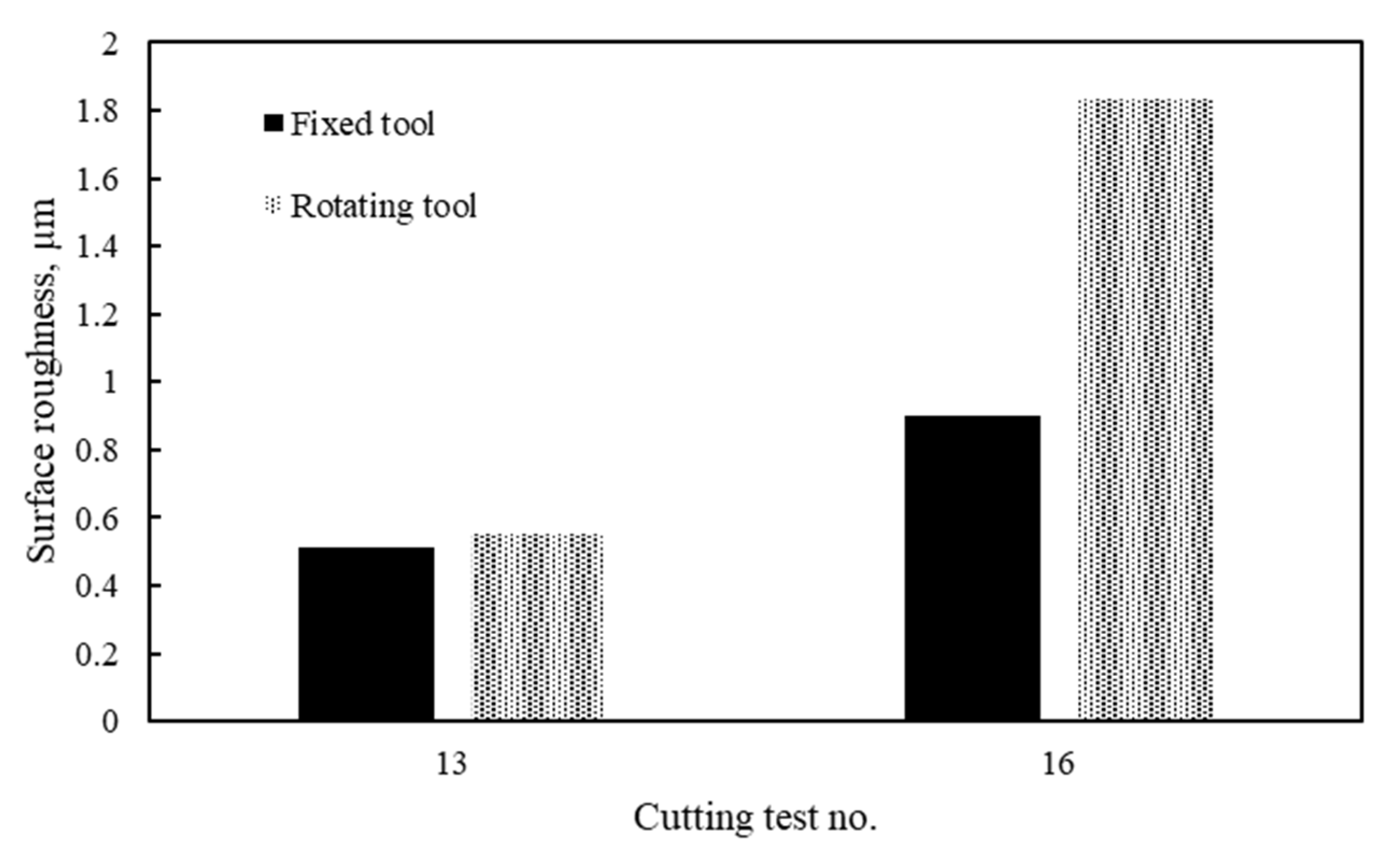
- A comparison between the self-propelled rotary tool and the fixed tool shows that the fixed tool provided better surface roughness;
- A comparison between two cutting tests with different inclination angles shows that there were no chips adhesion observed in the machined surface at 20° inclination angle, and accordingly, lower tool wear was obtained compared to the case of 5° inclination angle;
- The surface roughness values of rotary tools are relatively low compared to conventional tools (i.e., single point) due to the large radius of the round insert compared to the nose radius of the conventional tool. However, better surface roughness was provided by fixed round tools compared to the round tools under rotational motion;
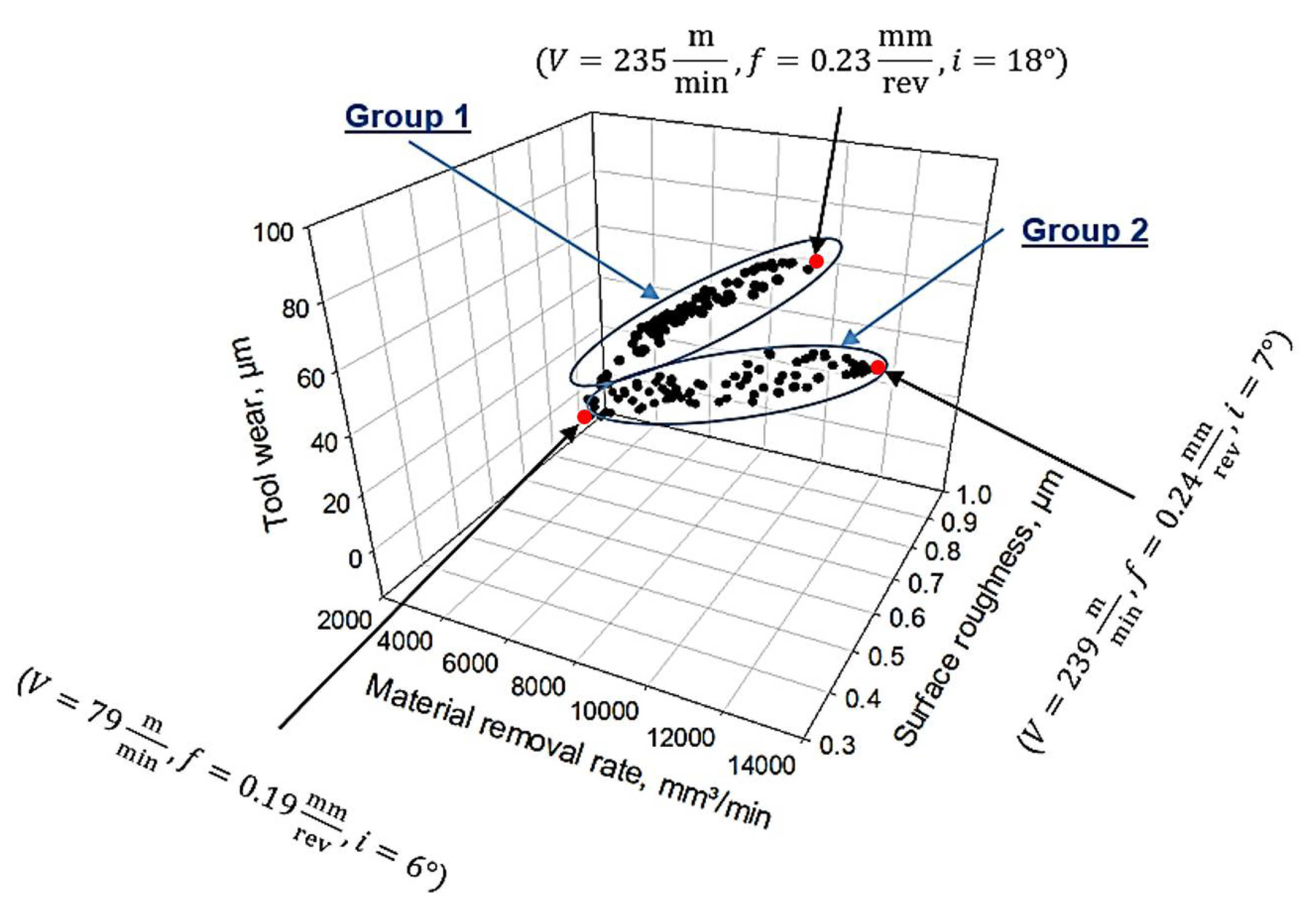
- Based on the optimized scenarios of multi-objective optimization (NSGA-II), the optimal cutting variable levels for the equal-weighted scenario were found at a cutting velocity of 98 m/min, a feed rate of 0.23 mm/rev, and an inclination angle of 7°. Besides, the optimal cutting conditions for the productivity scenario were obtained at the highest cutting velocity and feed rate (i.e., V = 240 m/min and f = 0.25 mm/rev), and an inclination angle of 7°. While the optimum conditions for the finishing scenario were found at a cutting velocity of 235 m/min, a feed rate of 0.19 mm/rev, and an inclination angle of 19°;
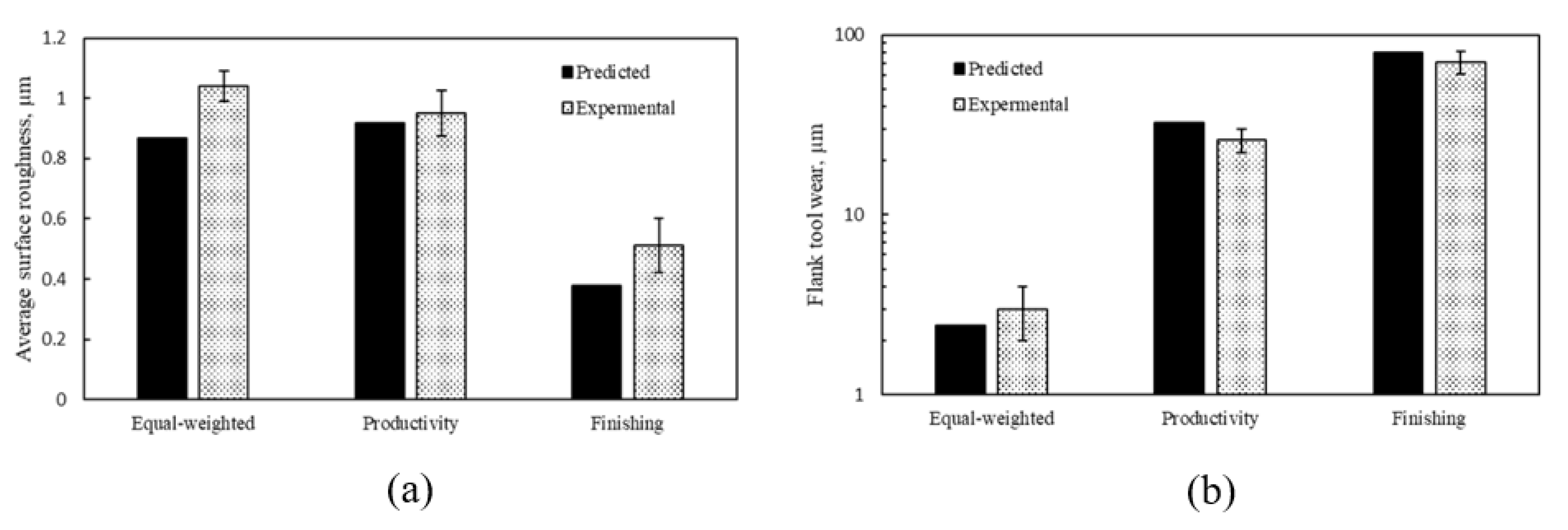
- To validate the effectiveness of the three studied scenarios, confirmation experimental tests have been conducted, and the results showed a good agreement with the predicted values.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kishawy, H.; Elbestawi, M.A. Effects of edge preparation and cutting speed on surface integrity of die materials in hard machining. Proc. Int. Mech. Eng. Congr. Exp. Med. 1998, 8, 269–276. [Google Scholar]
- Kishawy, H. An experimental evaluation of cutting temperatures during high speed machining of hardened D2 tool steel. Mach. Sci. Technol. 2002, 6, 67–79. [Google Scholar] [CrossRef]
- Shokrani, A.; Dhokia, V.; Newman, S.T. Environmentally conscious machining of difficult-to-machine materials with regard to cutting fluids. Int. J. Mach. Tools Manuf. 2012, 57, 83–101. [Google Scholar] [CrossRef] [Green Version]
- Marksberry, P. Micro-flood (MF) technology for sustainable manufacturing operations that are coolant less and occupationally friendly. J. Clean. Prod. 2007, 15, 958–971. [Google Scholar] [CrossRef]
- Ahmed, W.; Hegab, H.; Mohany, A.; Kishawy, H. Sustainability assessment of difficult-to-cut materials using rotary tools: A step towards sustainable machining environment. Procedia Manuf. 2021, 53, 92–98. [Google Scholar] [CrossRef]
- Kishawy, H.; Pang, L.; Balazinski, M. Modeling of tool wear during hard turning with self-propelled rotary tools. Int. J. Mech. Sci. 2011, 53, 1015–1021. [Google Scholar] [CrossRef]
- Khan, M.A.; Jaffery, S.H.I.; Khan, M.; Younas, M.; Butt, S.I.; Ahmad, R.; Warsi, S. Multi-objective optimization of turning titanium-based alloy Ti-6Al-4V under dry, wet, and cryogenic conditions using gray relational analysis (GRA). Int. J. Adv. Manuf. Technol. 2020, 106, 3897–3911. [Google Scholar] [CrossRef]
- Azom AISI 4140 Alloy Steel (UNS G41400). Available online: https://www.azom.com/article.aspx?ArticleID=6769 (accessed on 13 August 2021).
- Chen, P.; Hoshi, T. High-Performance Machining of SiC whisker-reinforced aluminium composite by self-propelled rotary tools. CIRP Ann. 1992, 41, 59–62. [Google Scholar] [CrossRef]
- Ezugwu, E.O. Improvements in the machining of aero-engine alloys using self-propelled rotary tooling technique. J. Mater. Process. Technol. 2007, 185, 60–71. [Google Scholar] [CrossRef]
- Wang, Z.; Ezugwu, E.; Gupta, A. Evaluation of a self-propelled rotary tool in the machining of aerospace materials. Tribol. Trans. 1998, 41, 289–295. [Google Scholar] [CrossRef]
- Lei, S.; Liu, W. High-speed machining of titanium alloys using the driven rotary tool. Int. J. Mach. Tools Manuf. 2002, 42, 653–661. [Google Scholar] [CrossRef]
- Harun, S.; Shibasaka, T.; Moriwaki, T. Cutting temperature measurement in turning with actively driven rotary tool. Key Eng. Mater. 2009, 389–390, 138–143. [Google Scholar] [CrossRef]
- Karaguzel, U.; Olgun, U.; Uysal, E.; Budak, E.; Bakkal, M. Increasing tool life in machining of difficult-to-cut materials using nonconventional turning processes. Int. J. Adv. Manuf. Technol. 2015, 77, 1993–2004. [Google Scholar] [CrossRef]
- Kishawy, H.; Gerber, A. A model for the tool temperature during machining with a rotary tool. In Proceedings of the International Mechanical Engineers Congress and Exposition, IMECE2001/MED23312. New York, NY, USA, 11–16 November 2001; pp. 1–8. [Google Scholar]
- El-Mounayri, H.; Razak, A.L.; Kessler, M. Investigating turning of hard-to-cut material using self-propelled rotary tool. In Proceedings of the International Manufacturing Science and Engineering Conference, Corvallis, OR, USA, 13–17 June 2011; pp. 331–338. [Google Scholar]
- Kishawy, H.; Li, L.; El-Wahab, A. Prediction of chip flow direction during machining with self-propelled rotary tools. Int. J. Mach. Tools Manuf. 2006, 46, 1680–1688. [Google Scholar] [CrossRef]
- Li, L.; Kishawy, H. A model for cutting forces generated during machining with self-propelled rotary tools. Int. J. Mach. Tools Manuf. 2006, 46, 1388–1394. [Google Scholar] [CrossRef]
- Kishawy, H.; Ahmed, W.; Mohany, A. Analytical modeling of metal cutting process with self-propelled rotary tools. CIRP J. Manuf. Sci. Technol. 2021, 33, 115–122. [Google Scholar] [CrossRef]
- Kishawy, H.; Wilcox, J. Tool wear and chip formation during hard turning with self-propelled rotary tools. Int. J. Mach. Tools Manuf. 2003, 43, 433–439. [Google Scholar] [CrossRef]
- Thellaputta, G.R.; Bose, P.; Rao, C.; Raju, C. Effect of machining variables on cutting temperature while rotary milling of inconel 625. In Recent Advances in Material Sciences; Springer: Singapore, 2019; pp. 27–36. [Google Scholar]
- Nieslony, P.; Krolczyk, G.; Chudy, R.; Wojciechowski, S.; Maruda, R.; Biłous, P.; Lipowczyk, M.; Stachowiak, L. Study on physical and technological effects of precise turning with self-propelled rotary tool. Precis. Eng. 2020, 66, 62–75. [Google Scholar] [CrossRef]
- Ahmed, W.; Hegab, H.; Kishawy, H.; Mohany, A. Estimation of temperature in machining with self-propelled rotary tools using finite element method. J. Manuf. Process. 2021, 61, 100–110. [Google Scholar] [CrossRef]
- Ahmed, W.; Hegab, H.; Mohany, A.; Kishawy, H. On machining hardened steel AISI 4140 with self-propelled rotary tools: Experimental investigation and analysis. Int. J. Adv. Manuf. Technol. 2021, 113, 3163–3176. [Google Scholar] [CrossRef]
- Abbas, A.T.; Benyahia, F.; El Rayes, M.M.; Pruncu, C.; Taha, M.A.; Hegab, H. Towards optimization of machining performance and sustainability aspects when turning AISI 1045 Steel under different cooling and lubrication strategies. Materials 2019, 12, 3023. [Google Scholar] [CrossRef] [Green Version]
- Sangwan, K.S.; Saxena, S.; Kant, G. Optimization of machining parameters to minimize surface roughness using integrated ANN-GA approach. Procedia CIRP 2015, 29, 305–310. [Google Scholar] [CrossRef]
- Pawar, P.; Khalkar, M. Multi-objective optimization of wire-electric discharge machining process using multi-objective artificial bee colony algorithm. In Advanced Engineering Optimization through Intelligent Techniques; Springer: Singapore, 2020; pp. 39–46. [Google Scholar]
- Dabade, U.A.; Joshi, S.; Ramakrishnan, N. Analysis of surface roughness and chip cross-sectional area while machining with self-propelled round inserts milling cutter. J. Mater. Process. Technol. 2003, 132, 305–312. [Google Scholar] [CrossRef]
- Hao, W.; Zhu, X.; Li, X.; Turyagyenda, G. Prediction of cutting force for self-propelled rotary tool using artificial neural networks. J. Mater. Process. Technol. 2006, 180, 23–29. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Duong, Q.-D.; Mia, M. Sustainability-based optimization of the rotary turning of the hardened steel. Metals 2020, 10, 939. [Google Scholar] [CrossRef]
- Rao, T.B.; Krishna, A.G.; Katta, R.K.; Krishna, K.R. Modeling and multi-response optimization of machining performance while turning hardened steel with self-propelled rotary tool. Adv. Manuf. 2015, 3, 84–95. [Google Scholar] [CrossRef]
- Gurgen, S.; Sofuoglu, M.A.; Cakir, F.H.; Orak, S.; Kushan, M.C. Multi response optimization of turning operation with self-propelled rotary tool. Procedia Soc. Behav. Sci. 2015, 195, 2592–2600. [Google Scholar] [CrossRef] [Green Version]
- Gangil, M.; Pradhan, M. Modeling and optimization of electrical discharge machining process using RSM: A review. Mater. Today Proc. 2017, 4, 1752–1761. [Google Scholar] [CrossRef]
- Kishawy, H.; Becze, C.; McIntosh, D. Tool performance and attainable surface quality during the machining of aerospace alloys using self-propelled rotary tools. J. Mater. Process. Technol. 2004, 152, 266–271. [Google Scholar] [CrossRef]
- Yamamoto, H.; Satake, K.; Narita, T.; Sasahara, H.; Tsutsumi, M.; Muraki, T. Thermal behavior and chip formation on rotary cutting of difficult-to-cut materials utilizing multi tasking lathe and MQL. In Proceedings of the International Conference on Leading Edge Manufacturing in 21st Century, LEM 2009, The Japan Society of Mechanical Engineers, Tokyo, Japan, 4 December 2009; pp. 661–666. [Google Scholar]
- Banzhaf, W.; Nordin, P.; Keller, R.E.; Francone, F.D. Genetic Programming; Springer: Boston, MA, USA, 1998. [Google Scholar]
- Brezocnik, M.; Kovacic, M.; Ficko, M. Prediction of surface roughness with genetic programming. J. Mater. Process. Technol. 2004, 157, 28–36. [Google Scholar] [CrossRef]
- Kök, M.; Kanca, E.; Eyercioğlu, Ö. Prediction of surface roughness in abrasive waterjet machining of particle reinforced MMCs using genetic expression programming. Int. J. Adv. Manuf. Technol. 2011, 55, 955–968. [Google Scholar] [CrossRef]
- Garg, A.; Tai, K. Review of genetic programming in modeling of machining processes. In Proceedings of the International Conference on Modelling, Identification and Control, Wuhan, China, 24–26 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 653–658. [Google Scholar]
- Hegab, H.; Salem, A.; Rahnamayan, S.; Kishawy, H. Analysis, modeling, and multi-objective optimization of machining Inconel 718 with nano-additives based minimum quantity coolant. Appl. Soft Comput. 2021, 108, 107416. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Chen, J. Multi-objective optimization of cutting parameters with improved NSGA-II. In Proceedings of the International Conference on Management and Service Science, Wuhan, China, 16–18 September 2009; IEEE: Piscataway, NJ, USA, 2012; pp. 1–4. [Google Scholar]
- Zitzler, E. Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications. Ph.D. Thesis, Institut für Technische Informatik und Kommunikationsnetze Computer Engineering and Networks Laboratory, Zurich, Switzerland, 1999. [Google Scholar]
- Armarego, E.; Katta, R. Predictive cutting model for forces and power in self-propelled rotary tool turning operations. CiRP Ann. 1997, 46, 19–24. [Google Scholar] [CrossRef]




| Property | Material | |||
|---|---|---|---|---|
| Ti-6Al-4 V | Inconel 718 | Titanium | AISI 4140 | |
| Density (g/cm3) | 4.43 | 8.22 | 4.5 | 7.85 |
| Ultimate tensile strength (MPa) | 950 | 1350 | 220 | 729.5 |
| Yield strength (MPa) | 880 | 1170 | 140 | 379.2 |
| Modulus of elasticity (GPa) | 113.8 | 200 | 116 | 198 |
| Ductility (%) | 14 | 16 | 54 | 25.7 |
| Fracture toughness (MPa m1/2) | 75 | 96.4 | 70 | 66 |
| Thermal conductivity (W/mK) | 6.7 | 11.4 | 17 | 42.7 |
| C | SI | Mn | Cr | Mo | Fe |
|---|---|---|---|---|---|
| 0.38%–0.43% | 0.15%–0.3% | 0.7%–1% | 0.8%–1.1% | 0.15%–0.25% | 96.75%–97.84% |
| Test No | Inclination Angle Levels | Feed Rate Levels | Cutting Speed Levels |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 |
| 3 | 1 | 3 | 3 |
| 4 | 1 | 4 | 4 |
| 5 | 2 | 1 | 2 |
| 6 | 2 | 2 | 1 |
| 7 | 2 | 3 | 4 |
| 8 | 2 | 4 | 3 |
| 9 | 3 | 1 | 3 |
| 10 | 3 | 2 | 4 |
| 11 | 3 | 3 | 1 |
| 12 | 3 | 4 | 2 |
| 13 | 4 | 1 | 4 |
| 14 | 4 | 2 | 3 |
| 15 | 4 | 3 | 2 |
| 16 | 4 | 4 | 1 |
| Test No | i (°) | f (mm/rev) | V (m/min) | VB (µm) | Ra (µm) |
|---|---|---|---|---|---|
| 1 | 5 | 0.1 | 70 | 16 | 0.83 |
| 2 | 5 | 0.15 | 127 | 38 | 1.08 |
| 3 | 5 | 0.2 | 167 | 20 | 0.78 |
| 4 | 5 | 0.25 | 240 | 22 | 0.95 |
| 5 | 10 | 0.1 | 127 | 61 | 1.00 |
| 6 | 10 | 0.15 | 70 | 3 | 1.13 |
| 7 | 10 | 0.2 | 240 | 59 | 0.84 |
| 8 | 10 | 0.25 | 167 | 14 | 0.90 |
| 9 | 15 | 0.1 | 167 | 51 | 1.18 |
| 10 | 15 | 0.15 | 240 | 25 | 0.93 |
| 11 | 15 | 0.2 | 70 | 5 | 1.17 |
| 12 | 15 | 0.25 | 127 | 40 | 1.48 |
| 13 | 20 | 0.1 | 240 | 12 | 0.56 |
| 14 | 20 | 0.15 | 167 | 71 | 0.94 |
| 15 | 20 | 0.2 | 127 | 51 | 1.11 |
| 16 | 20 | 0.25 | 70 | 4 | 1.83 |
| Scenario | Machining Outputs | ||
|---|---|---|---|
| (Ra) | (VB) | (MRR) | |
| (A): Equal-weighted | 33.33% | 33.33% | 33.33% |
| (B): Productivity | 10% | 30% | 60% |
| (C): Finishing | 70% | 20% | 10% |
| Scenario | Machining Outputs | ||
|---|---|---|---|
| Ra (µm) | VB (µm) | MRR (mm3/min) | |
| (A): Equal-weighted | 0.87 | 2.42 | 4580 |
| (B): Productivity | 0.92 | 32.56 | 11,851 |
| (C): Finishing | 0.38 | 79.93 | 9156 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, W.; Hegab, H.; Mohany, A.; Kishawy, H. Analysis and Optimization of Machining Hardened Steel AISI 4140 with Self-Propelled Rotary Tools. Materials 2021, 14, 6106. https://doi.org/10.3390/ma14206106
Ahmed W, Hegab H, Mohany A, Kishawy H. Analysis and Optimization of Machining Hardened Steel AISI 4140 with Self-Propelled Rotary Tools. Materials. 2021; 14(20):6106. https://doi.org/10.3390/ma14206106
Chicago/Turabian StyleAhmed, Waleed, Hussien Hegab, Atef Mohany, and Hossam Kishawy. 2021. "Analysis and Optimization of Machining Hardened Steel AISI 4140 with Self-Propelled Rotary Tools" Materials 14, no. 20: 6106. https://doi.org/10.3390/ma14206106
APA StyleAhmed, W., Hegab, H., Mohany, A., & Kishawy, H. (2021). Analysis and Optimization of Machining Hardened Steel AISI 4140 with Self-Propelled Rotary Tools. Materials, 14(20), 6106. https://doi.org/10.3390/ma14206106








