Differential Entropy: An Appropriate Analysis to Interpret the Shape Complexity of Self-Similar Organic Islands
Abstract
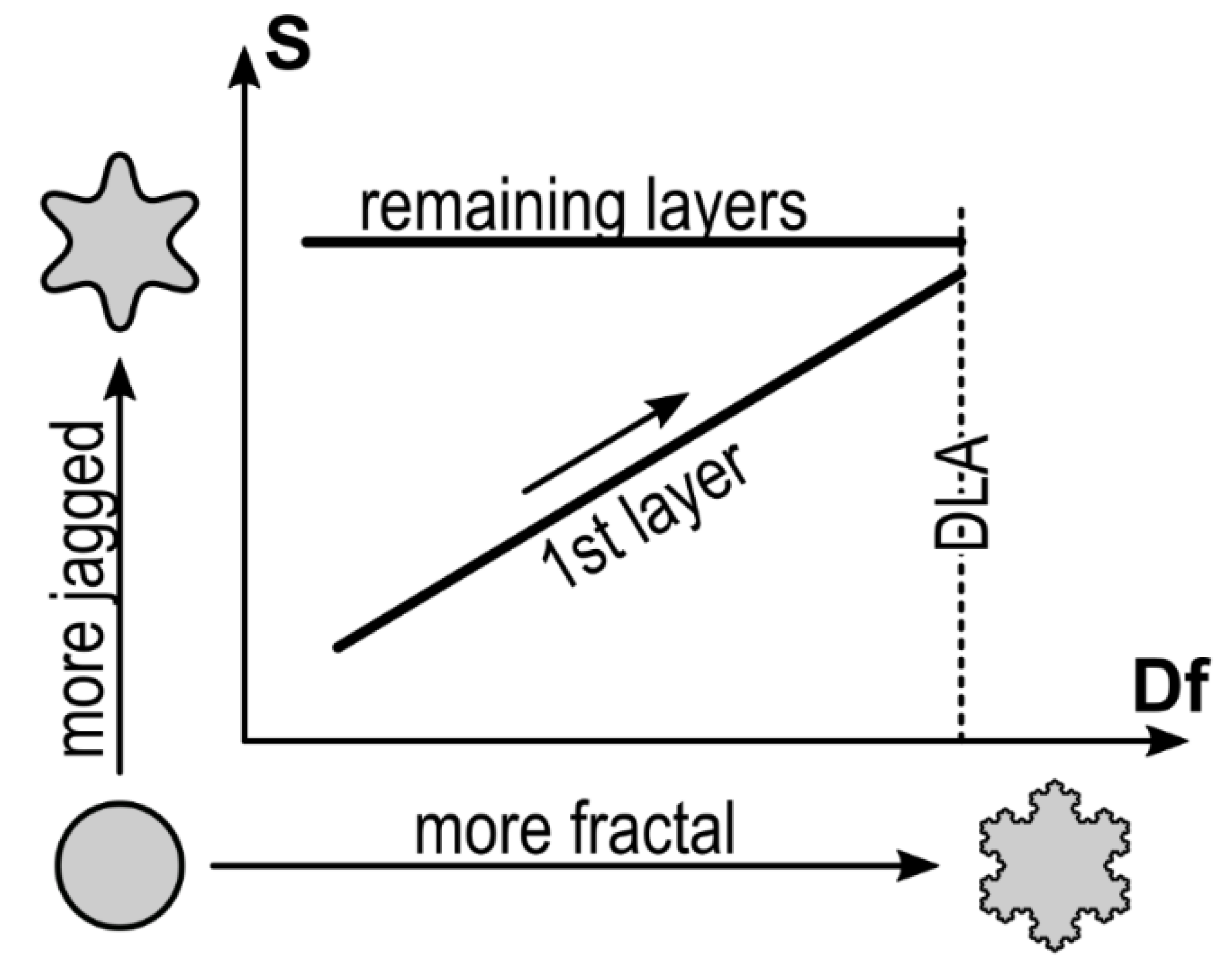
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. AFM Imaging
2.3. Image Processing and Data Analysis
3. Results
4. Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dürr, A.C.; Schreiber, F.; Ritley, K.A.; Kruppa, V.; Krug, J.; Dosch, H.; Struth, B. Rapid Roughening in Thin Film Growth of an Organic Semiconductor (Diindenoperylene). Phys. Rev. Lett. 2003, 90, 16104. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.N.; Barrena, E.; de Oteyza, D.G.; Dosch, H. Transition from layer-by-layer to rapid roughening in the growth of DIP on SiO2. Surf. Sci. 2007, 601, 2420–2425. [Google Scholar] [CrossRef]
- Frank, C.; Novák, J.; Banerjee, R.; Gerlach, A.; Schreiber, F.; Vorobiev, A.; Kowarik, S. Island size evolution and molecular diffusion during growth of organic thin films followed by time-resolved specular and off-specular scattering. Phys. Rev. B 2014, 90, 45410. [Google Scholar] [CrossRef] [Green Version]
- Ehrlich, G.; Hudda, F.G. Atomic View of Surface Self-Diffusion: Tungsten on Tungsten. J. Chem. Phys. 1966, 44, 1039–1049. [Google Scholar] [CrossRef]
- Schwoebel, R.L. Step Motion on Crystal Surfaces. II. J. Appl. Phys. 1969, 40, 614–618. [Google Scholar] [CrossRef]
- Hlawacek, G.; Puschnig, P.; Frank, P.; Winkler, A.; Ambrosch Draxl, C.; Teichert, C. Characterization of step edge barriers in organic thin-film growth. Science 2008, 321, 108–111. [Google Scholar] [CrossRef]
- Fendrich, M.; Krug, J. Ehrlich-Schwoebel effect for organic molecules: Direct calculation of the step-edge barrier using empirical potentials. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 76, 2–4. [Google Scholar] [CrossRef] [Green Version]
- Goose, J.E.; First, E.L.; Clancy, P. Nature of step-edge barriers for small organic molecules. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 81, 10–12. [Google Scholar] [CrossRef]
- Zhang, X.; Barrena, E.; Goswami, D.; de Oteyza, D.G.; Weis, C.; Dosch, H. Evidence for a Layer-Dependent Ehrlich-Schwobel Barrier in Organic Thin Film Growth. Phys. Rev. Lett. 2009, 103, 136101. [Google Scholar] [CrossRef]
- Biscarini, F.; Zamboni, R.; Samori, P.; Ostoja, P.; Taliani, C.; Samorí, P.; Ostoja, P.; Taliani, C. Growth of conjugated oligomer thin films studied by atomic-force microscopy. Phys. Rev. B 1995, 52, 14868–14877. [Google Scholar] [CrossRef]
- Virkar, A.A.; Mannsfeld, S.; Bao, Z.; Stingelin, N. Organic Semiconductor Growth and Morphology Considerations for Organic Thin-Film Transistors. Adv. Mater. 2010, 22, 3857–3875. [Google Scholar] [CrossRef]
- Verlaak, S.; Steudel, S.; Heremans, P.; Heremans, P.; Janssen, D.; Janssen, D.; Deleuze, M.S. Nucleation of organic semiconductors on inert substrates. Phys. Rev. B 2003, 68, 195409. [Google Scholar] [CrossRef]
- Riede, M.; Mueller, T.; Tress, W.; Schueppel, R.; Leo, K. Small-molecule solar cells—Status and perspectives. Nanotechnology 2008, 19, 424001. [Google Scholar] [CrossRef]
- Fratini, S.; Nikolka, M.; Salleo, A.; Schweicher, G.; Sirringhaus, H. Charge transport in high-mobility conjugated polymers and molecular semiconductors. Nat. Mater. 2020, 19, 491–502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dinelli, F.; Murgia, M.; Levy, P.; Cavallini, M.; Biscarini, F.; de Leeuw, D.M. Spatially Correlated Charge Transport in Organic Thin Film Transistors. Phys. Rev. Lett. 2004, 92, 90–93. [Google Scholar] [CrossRef] [PubMed]
- Shehu, A.; Quiroga, S.D.; D’Angelo, P.; Albonetti, C.; Borgatti, F.; Murgia, M.; Scorzoni, A.; Stoliar, P.; Biscarini, F. Layered Distribution of Charge Carriers in Organic Thin Film Transistors. Phys. Rev. Lett. 2010, 104, 246602. [Google Scholar] [CrossRef] [PubMed]
- Kyndiah, A.; Cramer, T.; Albonetti, C.; Liscio, F.; Chiodini, S.; Murgia, M.; Biscarini, F. Charge Transfer and Percolation in C60/Pentacene Field-Effect Transistors. Adv. Electron. Mater. 2015, 1, 1400036. [Google Scholar] [CrossRef]
- Liscio, F.; Albonetti, C.; Broch, K.; Shehu, A.; Quiroga, S.D.; Ferlauto, L.; Frank, C.; Kowarik, S.; Nervo, R.; Gerlach, A.; et al. Molecular reorganization in organic field-effect transistors and its effect on two-dimensional charge transport pathways. ACS Nano 2013, 7, 1257–1264. [Google Scholar] [CrossRef] [PubMed]
- Chiodini, S.; Straub, A.; Donati, S.; Albonetti, C.; Borgatti, F.; Stoliar, P.; Murgia, M.; Biscarini, F. Morphological Transitions in Organic Ultrathin Film Growth Imaged by In Situ Step-by-Step Atomic Force Microscopy. J. Phys. Chem. C 2020, 124, 14030–14042. [Google Scholar] [CrossRef]
- Brillante, A.; Bilotti, I.; Della Valle, R.G.; Venuti, E.; Girlando, A.; Masino, M.; Liscio, F.; Milita, S.; Albonetti, C.; D’angelo, P.; et al. Structure and dynamics of pentacene on SiO2: From monolayer to bulk structure. Phys. Rev. B 2012, 85, 195308. [Google Scholar] [CrossRef] [Green Version]
- Hlawacek, G.; Teichert, C. Nucleation and growth of thin films of rod-like conjugated molecules. J. Phys. Condens. Matter 2013, 25, 143202. [Google Scholar] [CrossRef] [Green Version]
- Moulin, J.-F.F.; Dinelli, F.; Massi, M.; Albonetti, C.; Kshirsagar, R.; Biscarini, F. In situ X-ray synchrotron study of organic semiconductor ultra-thin films growth. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2006, 246, 122–126. [Google Scholar] [CrossRef]
- Albonetti, C.; Barbalinardo, M.; Milita, S.; Cavallini, M.; Liscio, F.; Moulin, J.-F.; Biscarini, F. Selective Growth of alpha-Sexithiophene by Using Silicon Oxides Patterns. Int. J. Mol. Sci. 2011, 12, 5719–5735. [Google Scholar] [CrossRef] [Green Version]
- Fritz, S.E.; Martin, S.M.; Frisbie, C.D.; Ward, M.D.; Toney, M.F. Structural Characterization of a Pentacene Monolayer on an Amorphous SiO2 Substrate with Grazing Incidence X-ray Diffraction. J. Am. Chem. Soc. 2004, 126, 4084–4085. [Google Scholar] [CrossRef]
- Mayer, A.C.; Ruiz, R.; Headrick, R.L.; Kazimirov, A.; Malliaras, G.G. Early stages of pentacene film growth on silicon oxide. Org. Electron. 2004, 5, 257–263. [Google Scholar] [CrossRef]
- Mayer, A.C.; Ruiz, R.; Zhou, H.; Headrick, R.L.; Kazimirov, A.; Malliaras, G.G. Growth dynamics of pentacene thin films: Real-time synchrotron x-ray scattering study. Phys. Rev. B 2006, 73, 205307. [Google Scholar] [CrossRef]
- Ruiz, R.; Choudhary, D.; Nickel, B.; Toccoli, T.; Chang, K.C.; Mayer, A.C.; Clancy, P.; Blakely, J.M.; Headrick, R.L.; Iannotta, S.; et al. Pentacene thin film growth. Chem. Mater. 2004, 16, 4497–4508. [Google Scholar] [CrossRef]
- Krug, J.; Spohn, H. Universality classes for deterministic surface growth. Phys. Rev. A 1988, 38, 4271–4283. [Google Scholar] [CrossRef] [PubMed]
- Valle, F.; Brucale, M.; Chiodini, S.; Bystrenova, E.; Albonetti, C. Nanoscale morphological analysis of soft matter aggregates with fractal dimension ranging from 1 to 3. Micron 2017, 100, 60–72. [Google Scholar] [CrossRef] [PubMed]
- Kowarik, S.; Gerlach, A.; Sellner, S.; Schreiber, F.; Cavalcanti, L.; Konovalov, O. Real-Time Observation of Structural and Orientational Transitions during Growth of Organic Thin Films. Phys. Rev. Lett. 2006, 96, 125504. [Google Scholar] [CrossRef] [Green Version]
- Krause, B.; Dürr, A.C.; Ritley, K.; Schreiber, F.; Dosch, H.; Smilgies, D. Structure and growth morphology of an archetypal system for organic epitaxy: PTCDA on Ag(111). Phys. Rev. B 2002, 66, 235404. [Google Scholar] [CrossRef] [Green Version]
- Yim, S.; Jones, T.S. Anomalous scaling behavior and surface roughening in molecular thin-film deposition. Phys. Rev. B 2006, 73, 161305. [Google Scholar] [CrossRef]
- Zorba, S.; Shapir, Y.; Gao, Y. Fractal-mound growth of pentacene thin films. Phys. Rev. B 2006, 74, 245410. [Google Scholar] [CrossRef] [Green Version]
- Evans, J.W.; Thiel, P.A.; Bartelt, M.C. Morphological evolution during epitaxial thin film growth: Formation of 2D islands and 3D mounds. Surf. Sci. Rep. 2006, 61, 1–128. [Google Scholar] [CrossRef]
- Biscarini, F.; Samorí, P.; Greco, O.; Zamboni, R. Scaling Behavior of Anisotropic Organic Thin Films Grown in High Vacuum. Phys. Rev. Lett. 1997, 78, 2389–2392. [Google Scholar] [CrossRef]
- Ţălu, Ş. Micro and Nanoscale Characterization of Three Dimensional Surfaces: Basics and Applications; Napoca Star: Cluj-Napoca, Romania, 2015; ISBN 6066903497. [Google Scholar]
- Chiodini, S.; D’Avino, G.; Muccioli, L.; Bartolini, L.; Gentili, D.; Toffanin, S.; Albonetti, C. Self-organization of complete organic monolayers via sequential post-deposition annealing. Prog. Org. Coat. 2020, 138, 105408. [Google Scholar] [CrossRef]
- Pratontep, S.; Brinkmann, M.; Nüesch, F.; Zuppiroli, L. Correlated growth in ultrathin pentacene films on silicon oxide: Effect of deposition rate. Phys. Rev. B 2004, 69, 165201. [Google Scholar] [CrossRef]
- Brinkmann, M.; Pratontep, S.; Contal, C. Correlated and non-correlated growth kinetics of pentacene in the sub-monolayer regime. Surf. Sci. 2006, 600, 4712–4716. [Google Scholar] [CrossRef]
- Pratontep, S.; Nüesch, F.; Zuppiroli, L.; Brinkmann, M. Comparison between nucleation of pentacene monolayer islands on polymeric and inorganic substrates. Phys. Rev. B 2005, 72, 85211. [Google Scholar] [CrossRef]
- Ruiz, R.; Nickel, B.; Koch, N.; Feldman, L.C.; Haglund, R.F.; Kahn, A.; Family, F.; Scoles, G.; Haglund, R.F., Jr.; Kahn, A.; et al. Dynamic Scaling, Island Size Distribution, and Morphology in the Aggregation Regime of Submonolayer Pentacene Films. Phys. Rev. Lett. 2003, 91, 136102. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, R.; Nickel, B.; Koch, N.; Feldman, L.C.; Haglund, R.F.; Kahn, A.; Scoles, G. Pentacene ultrathin film formation on reduced and oxidized Si surfaces. Phys. Rev. B Condens. Matter Mater. Phys. 2003, 67, 125406. [Google Scholar] [CrossRef]
- Meyer zu Heringdorf, F.-J.J.; Reuter, M.C.; Tromp, R.M. Growth dynamics of pentacene thin films. Nature 2001, 412, 517–520. [Google Scholar] [CrossRef]
- Bales, G.S.; Chrzan, D.C. Transition from Compact to Fractal Islands during Submonolayer Epitaxial Growth. Phys. Rev. Lett. 1995, 74, 4879–4882. [Google Scholar] [CrossRef]
- Amar, J.G.; Semaan, M. Island nucleation and growth with anomalous diffusion. Phys. Rev. E 2016, 93, 062805. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Lin, Z.; Zhigilei, L.V.; Reinke, P. Fractal structures in fullerene layers: Simulation of the growth process. J. Phys. Chem. C 2008, 112, 4687–4695. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, G.; Theobald, J.A.; Beton, P.H. Fractal-compact island transition and self-limiting growth of pentacene on polymers. Surf. Sci. 2003, 537, 241–246. [Google Scholar] [CrossRef]
- Royston, J.; Amar, J.G. Island-size distribution and capture numbers in three-dimensonal nucleation: Dependence on island morphology. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 041602. [Google Scholar] [CrossRef]
- Huang, W.J.; Li, B.Q.; Zuo, J.M. Diffusion-limited submonolayer pentacene thin film growth on hydrogen-passivated Si(1 1 1) substrates. Surf. Sci. 2005, 595, 157–164. [Google Scholar] [CrossRef]
- Zhu, W.; Mohammadi, E.; Diao, Y. Quantitative Image Analysis of Fractal-Like Thin Films of Organic Semiconductors. J. Polym. Sci. Part B Polym. Phys. 2019, 57, 1622–1634. [Google Scholar] [CrossRef]
- Chambers, E.; Emerson, T.; Grimm, C.; Leonard, K. Exploring 2D Shape Complexity BT. In Research in Shape Analysis: WiSH2, Sirince, Turkey, June 2016; Genctav, A., Leonard, K., Tari, S., Hubert, E., Morin, G., El-Zehiry, N., Chambers, E., Eds.; Springer International Publishing: New York, NY, USA, 2018; pp. 61–83. ISBN 9783319770666. [Google Scholar]
- Chen, Y.; Sundaram, H. Estimating Complexity of 2D Shapes. In Proceedings of the 2005 IEEE 7th Workshop on Multimedia Signal Processing, Shanghai, China, 30 October–2 November 2005; pp. 1–4. [Google Scholar]
- Su, H.; Bouridane, A.; Crookes, D. Scale Adaptive Complexity Measure of 2D Shapes. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; Volume 2, pp. 134–137. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. Communication In The Presence Of Noise. Proc. IEEE 1998, 86, 447–457. [Google Scholar] [CrossRef]
- Kish, L.B.; Ferry, D.K. Information entropy and thermal entropy: Apples and oranges. J. Comput. Electron. 2018, 17, 43–50. [Google Scholar] [CrossRef] [Green Version]
- Çengel, Y.A. On Entropy, Information, and Conservation of Information. Entropy 2021, 23, 779. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T. Information Theory and Statistical Mechanics. II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Castro-Alvaredo, O.A.; Doyon, B. Entanglement Entropy of Highly Degenerate States and Fractal Dimensions. Phys. Rev. Lett. 2012, 108, 120401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dahlsten, O.C.O. Non-Equilibrium Statistical Mechanics Inspired by Modern Information Theory. Entropy 2013, 15, 5346–5361. [Google Scholar] [CrossRef]
- Main, I.G.; Al-Kindy, F.H. Entropy, energy, and proximity to criticality in global earthquake populations. Geophys. Res. Lett. 2002, 29, 24–25. [Google Scholar] [CrossRef] [Green Version]
- Arzate-Vázquez, I.; Chanona-Pérez, J.J.; Calderón-Domínguez, G.; Terres-Rojas, E.; Garibay-Febles, V.; Martínez-Rivas, A.; Gutiérrez-López, G.F. Microstructural characterization of chitosan and alginate films by microscopy techniques and texture image analysis. Carbohydr. Polym. 2012, 87, 289–299. [Google Scholar] [CrossRef]
- Sitges, C.; Bornas, X.; Llabrés, J.; Noguera, M.; Montoya, P. Linear and nonlinear analyses of EEG dynamics during non-painful somatosensory processing in chronic pain patients. Int. J. Psychophysiol. 2010, 77, 176–183. [Google Scholar] [CrossRef]
- Nemcsics, Á.; Nagy, S.; Mojzes, I.; Schwedhelm, R.; Woedtke, S.; Adelung, R.; Kipp, L. Investigation of the surface morphology on epitaxially grown fullerene structures. Vacuum 2009, 84, 152–154. [Google Scholar] [CrossRef]
- Zmeskal, O.; Dzik, P.; Vesely, M. Entropy of fractal systems. Comput. Math. Appl. 2013, 66, 135–146. [Google Scholar] [CrossRef]
- Tumbek, L.; Gleichweit, C.; Zojer, K.; Winkler, A. Origin of the bimodal island size distribution in ultrathin films of para-hexaphenyl on mica. Phys. Rev. B 2012, 86, 85402. [Google Scholar] [CrossRef] [Green Version]
- Pulker, H.; Pulker, H.K. Coatings on Glass; Elsevier: Amsterdam, The Netherlands, 1999; Volume 20, ISBN 0080525555. [Google Scholar]
- Nanbu, K.; Watanabe, Y. Thickness distribution of films fabricated by the molecular beam epitaxy technique. Vacuum 1986, 36, 349–354. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1982; ISBN 9780716711865. [Google Scholar]
- Avnir, D.; Biham, O.; Lidar, D.; Malcai, O. Is the Geometry of Nature Fractal? Science 1998, 279, 39–40. [Google Scholar] [CrossRef] [Green Version]
- Imre, A.R. Artificial fractal dimension obtained by using perimeter—Area relationship on digitalized images. Appl. Math. Comput. 2006, 173, 443–449. [Google Scholar] [CrossRef]
- Douketis, C.; Wang, Z.; Haslett, T.L.; Moskovits, M. Fractal character of cold-deposited silver films determined by low-temperature scanning tunneling microscopy. Phys. Rev. B 1995, 51, 11022–11031. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Cent. Eur. J. Phys. 2012, 10, 181–188. [Google Scholar] [CrossRef]
- Amar, J.G.; Family, F.; Lam, P.-M. Dynamic scaling of the island-size distribution and percolation in a model of submonolayer molecular-beam epitaxy. Phys. Rev. B 1994, 50, 8781–8797. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Michalowicz, J.V.; Nichols, J.M.; Bucholtz, F. Calculation of Differential Entropy for a Mixed Gaussian Distribution. Entropy 2008, 10, 200–206. [Google Scholar] [CrossRef] [Green Version]
- Marsh, C. Introduction to Continuous Entropy. Dep. Comput. Sci. Princet. Univ. 2013. Available online: https://www.crmarsh.com/static/pdf/Charles_Marsh_Continuous_Entropy.pdf (accessed on 25 August 2021).
- Inkscape Project Inkscape. Inkscape Project. Inkscape, 2020. Available online: https://inkscape.org (accessed on 25 August 2021).
- Pratontep, S.; Brinkmann, M.; Nüesch, F.; Zuppiroli, L. Nucleation and growth of ultrathin pentacene films on silicon dioxide: Effect of deposition rate and substrate temperature. Synth. Met. 2004, 146, 387–391. [Google Scholar] [CrossRef]
- Venables, J.A. Introduction to Surface and Thin Film Processes; Cambridge University Press: Cambridge, UK, 2000; ISBN 9780521785006. [Google Scholar]
- Hwang, R.Q.; Schröder, J.; Günther, C.; Behm, R.J. Fractal growth of two-dimensional islands: Au on Ru(0001). Phys. Rev. Lett. 1991, 67, 3279–3282. [Google Scholar] [CrossRef] [PubMed]
- Bérubé, D.; Jébrak, M. High precision boundary fractal analysis for shape characterization. Comput. Geosci. 1999, 25, 1059–1071. [Google Scholar] [CrossRef]
- Bensimon, D.; Domany, E.; Aharony, A. Crossover of Fractal Dimension in Diffusion-Limited Aggregates. Phys. Rev. Lett. 1983, 51, 1394. [Google Scholar] [CrossRef]
- Brune, H.; Bromann, K.; Kern, K.; Jacobsen, J.; Stoltze, P.; Jacobsen, K.; Nørskov, J. Fractal and Dendritic Growth of Surface Aggregates. MRS Online Proc. Libr. 1995, 407, 379–389. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wang, T.; Wang, H.; Zhu, F.; Li, G.; Yan, D. Ultrathin-film growth of para-sexiphenyl (II): Formation of large-size domain and continuous thin film. J. Phys. Chem. B 2008, 112, 7821–7825. [Google Scholar] [CrossRef]
- Batabyal, R.; Mahato, J.C.; Das, D.; Roy, A.; Dev, B.N. Self-organized one-atom thick fractal nanoclusters via field-induced atomic transport. J. Appl. Phys. 2013, 114, 64304. [Google Scholar] [CrossRef]
- Yang, J.; Wang, T.; Wang, H.; Zhu, F.; Li, G.; Yan, D. Ultrathin-film growth of para-sexiphenyl (I): Submonolayer thin-film growth as a function of the substrate temperature. J. Phys. Chem. B 2008, 112, 7816–7820. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Toccoli, T.; Zhang, J.; Koch, N.; Iacob, E.; Pallaoro, A.; Iannotta, S.; Rudolf, P. Key role of molecular kinetic energy in early stages of pentacene island growth. Appl. Phys. A 2009, 95, 21–27. [Google Scholar] [CrossRef] [Green Version]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation. Phys. Rev. B 1983, 27, 5686–5697. [Google Scholar] [CrossRef] [Green Version]
- Garbaczewski, P. Differential Entropy and Dynamics of Uncertainty. J. Stat. Phys. 2006, 123, 315. [Google Scholar] [CrossRef] [Green Version]
- Michalowicz, J.V.; Nichols, J.M.; Bucholtz, F. Handbook of Differential Entropy; CRC Press: Boca Raton, FL, USA, 2013; ISBN 1466583169. [Google Scholar]
- Mac Fhionnlaoich, N.; Guldin, S. Information Entropy as a Reliable Measure of Nanoparticle Dispersity. Chem. Mater. 2020, 32, 3701–3706. [Google Scholar] [CrossRef]
- Lazo, A.V.; Rathie, P. On the entropy of continuous probability distributions (Corresp.). IEEE Trans. Inf. Theory 1978, 24, 120–122. [Google Scholar] [CrossRef]
- Li, Z.; Costa, L.D.F. Investigating shape and function relationship in retinal ganglion cells. J. Integr. Neurosci. 2002, 01, 195–215. [Google Scholar] [CrossRef]
- Vařenka, J.; Kubinek, R. Image analysis tools of dendritic structure classification. Pattern Recognit. Image Anal. 2006, 16, 651–655. [Google Scholar] [CrossRef]
- Andrle, R. Complexity and scale in geomorphology: Statistical self-similarity vs. characteristic scales. Math. Geol. 1996, 28, 275–293. [Google Scholar] [CrossRef]
- Chiodini, S. In-Situ and Real Time Scanning Probe Microscopy of Organic Ultra THIN films. Ph.D. Thesis, Università di Bologna, Bologna, Italy, 2015. [Google Scholar]
- Mulheran, P.A.; Blackman, J.A. The origins of island size scaling in heterogeneous film growth. Philos. Mag. Lett. 1995, 72, 55–60. [Google Scholar] [CrossRef]
- 3M Science Applied to Life. Hydrophilicity and Surface Energy, a Little of the Science behind the Test Strip; 3M Science Applied to Life: Saint Paul, MN, USA, 2018. [Google Scholar]
- Dinelli, F.; Moulin, J.-F.; Loi, M.A.; Da Como, E.; Massi, M.; Murgia, M.; Muccini, M.; Biscarini, F.; Wie, J.; Kingshott, P. Effects of Surface Chemical Composition on the Early Growth Stages of α-Sexithienyl Films on Silicon Oxide Substrates. J. Phys. Chem. B 2006, 110, 258–263. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Toccoli, T.; Koch, N.; Iacob, E.; Pallaoro, A.; Rudolf, P.; Iannotta, S. Controlling the Early Stages of Pentacene Growth by Supersonic Molecular Beam Deposition. Phys. Rev. Lett. 2007, 98, 076601. [Google Scholar] [CrossRef] [Green Version]
- Tonezzer, M.; Rigo, E.; Gottardi, S.; Bettotti, P.; Pavesi, L.; Iannotta, S.; Toccoli, T. Role of kinetic energy of impinging molecules in the α-sexithiophene growth. Thin Solid Film. 2011, 519, 4110–4113. [Google Scholar] [CrossRef]
- Huang, L.; Liu, C.; Yu, B.; Zhang, J.; Geng, Y.; Yan, D. Evolution of 2,5-Bis(4-biphenylyl)bithiophene Thin Films and Its Effect on the Weak Epitaxy Growth of ZnPc. J. Phys. Chem. B 2010, 114, 4821–4827. [Google Scholar] [CrossRef]
- Lee, S.B. Measure of the fractal dimension of islands in epitaxial thin film growth. J. Korean Phys. Soc. 2005, 47, 577. [Google Scholar]
- Bartolini, L.; Malferrari, M.; Lugli, F.; Zerbetto, F.; Paolucci, F.; Pelicci, P.G.; Albonetti, C.; Rapino, S. Interaction of Single Cells with 2D Organic Monolayers: A Scanning Electrochemical Microscopy Study. ChemElectroChem 2018, 5, 2975–2981. [Google Scholar] [CrossRef]
- Pimpinelli, A.; Villain, J.; Wolf, D.E. Fractal terraces in MBE growth. J. Phys. I 1993, 3, 447–457. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Feng, J. Understanding the Fractal Dimensions of Urban Forms through Spatial Entropy. Entropy 2017, 19, 600. [Google Scholar] [CrossRef] [Green Version]
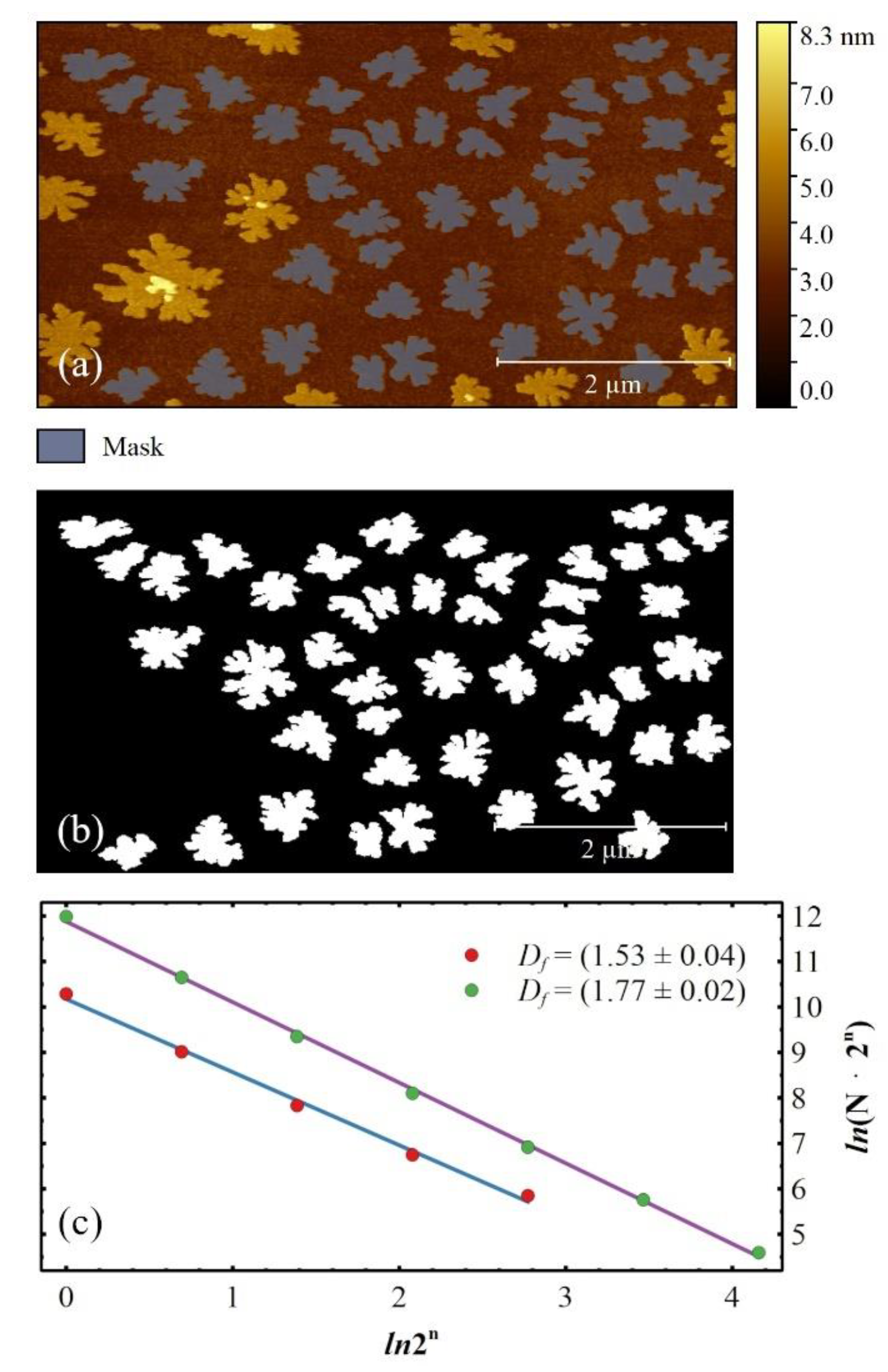



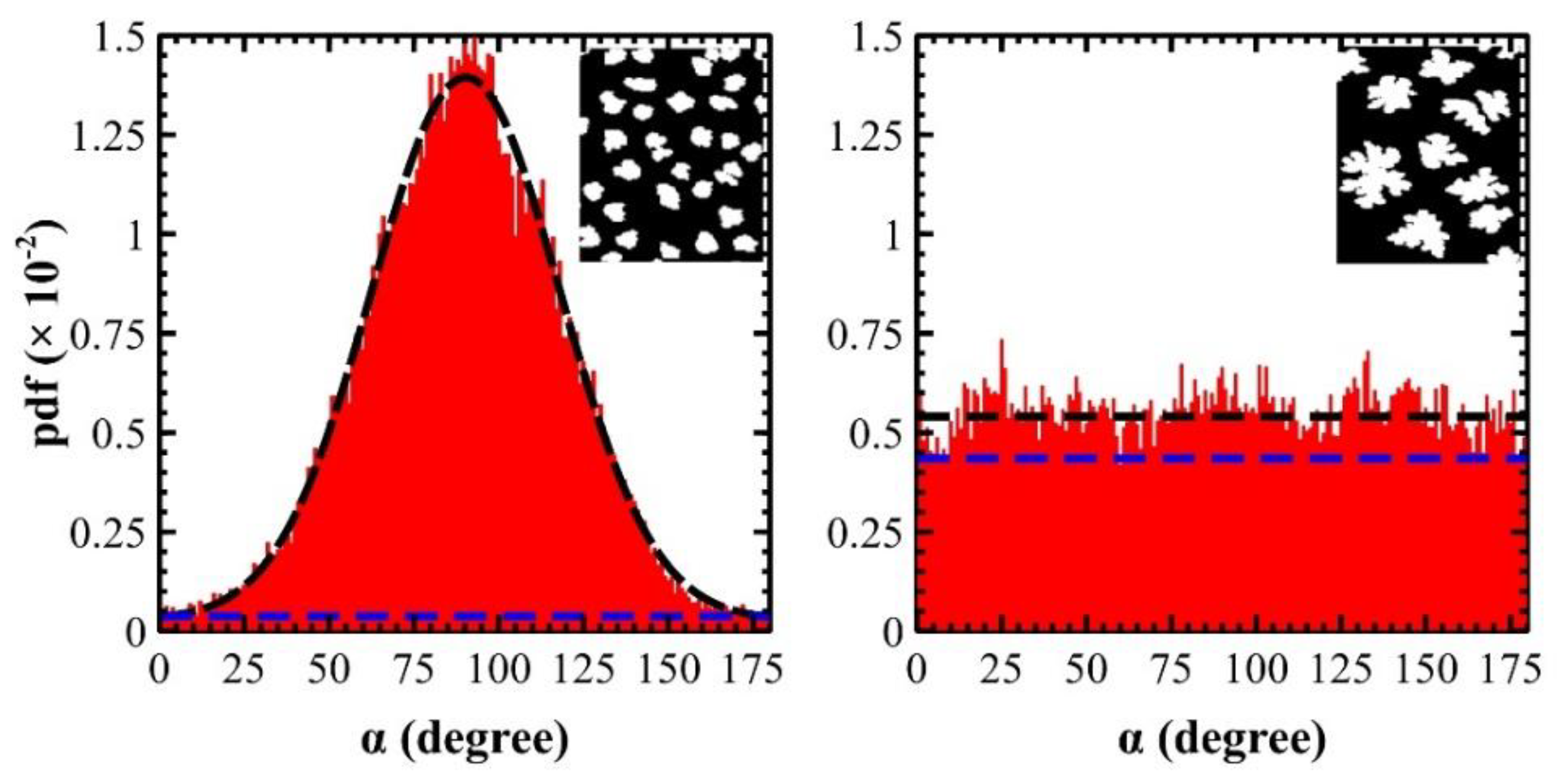
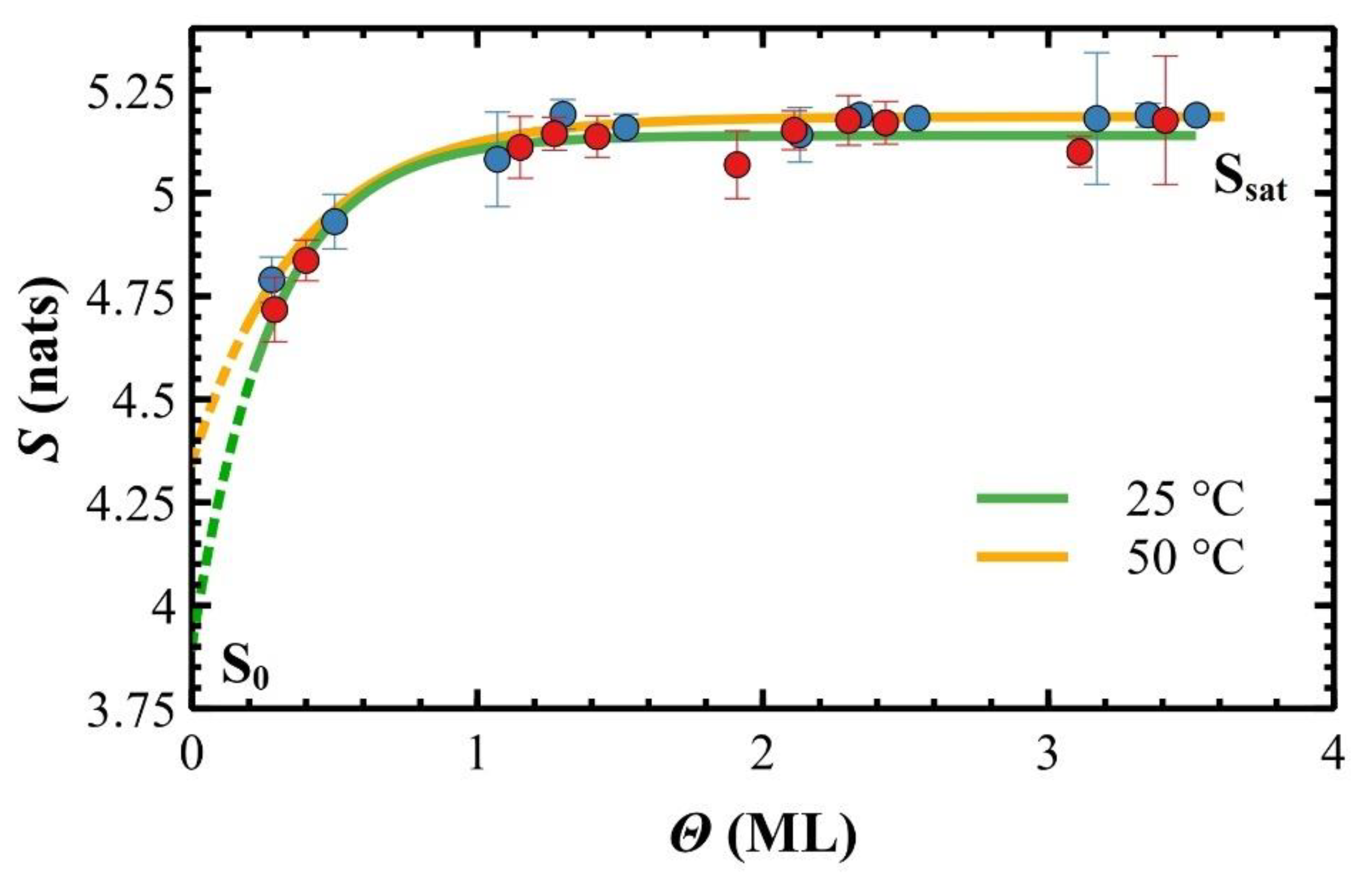
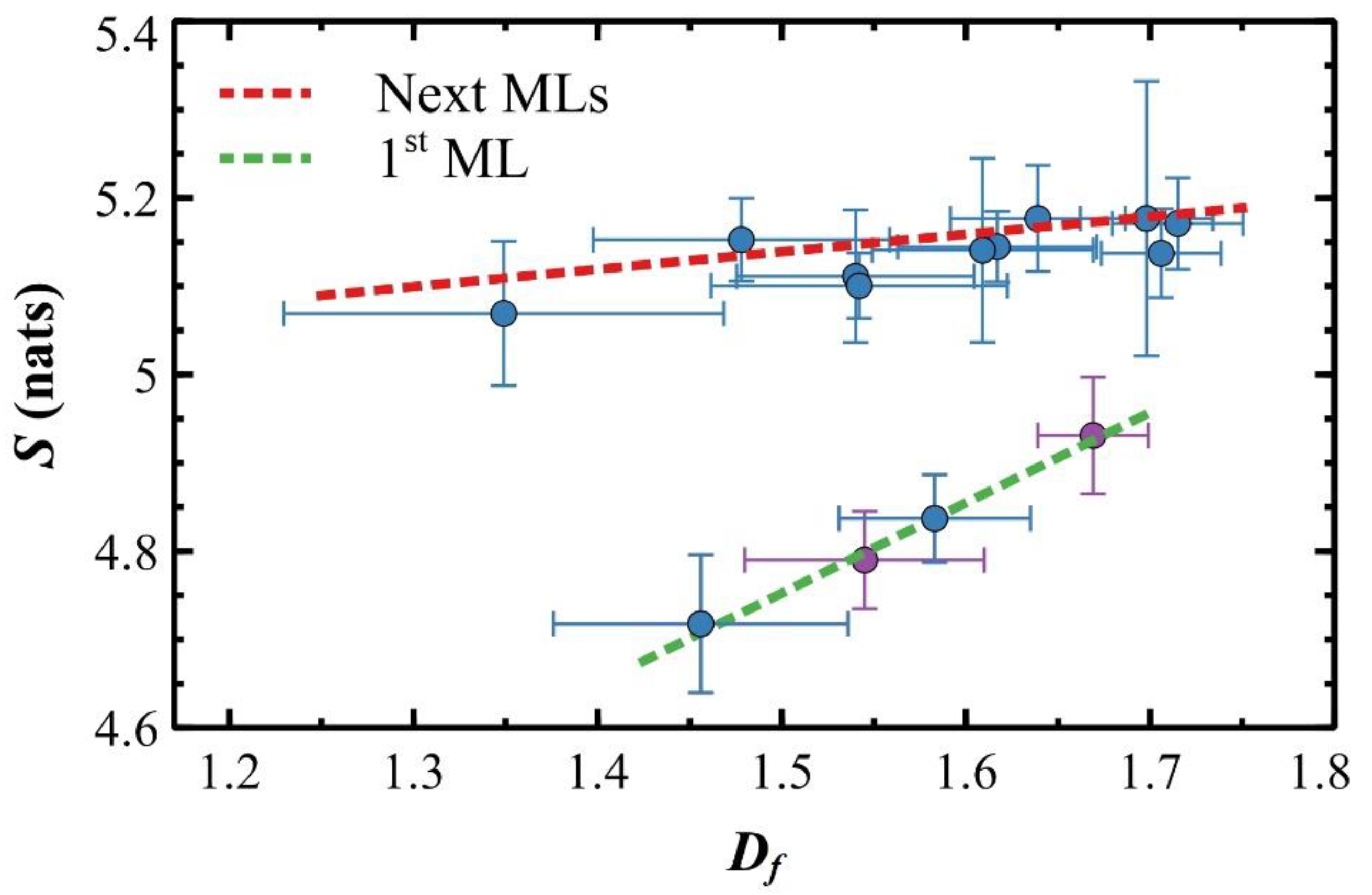
| TS (°C) | Ssat (Nats) | S0 (Nats) | ΘC (ML) |
|---|---|---|---|
| 25 | (5.14 ± 0.02) | ~3.80 | (0.28 ± 0.08) |
| 50 | (5.186 ± 0.004) | ~4.35 | (0.38 ± 0.07) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiodini, S.; Stoliar, P.; Garrido, P.F.; Albonetti, C. Differential Entropy: An Appropriate Analysis to Interpret the Shape Complexity of Self-Similar Organic Islands. Materials 2021, 14, 6529. https://doi.org/10.3390/ma14216529
Chiodini S, Stoliar P, Garrido PF, Albonetti C. Differential Entropy: An Appropriate Analysis to Interpret the Shape Complexity of Self-Similar Organic Islands. Materials. 2021; 14(21):6529. https://doi.org/10.3390/ma14216529
Chicago/Turabian StyleChiodini, Stefano, Pablo Stoliar, Pablo F. Garrido, and Cristiano Albonetti. 2021. "Differential Entropy: An Appropriate Analysis to Interpret the Shape Complexity of Self-Similar Organic Islands" Materials 14, no. 21: 6529. https://doi.org/10.3390/ma14216529
APA StyleChiodini, S., Stoliar, P., Garrido, P. F., & Albonetti, C. (2021). Differential Entropy: An Appropriate Analysis to Interpret the Shape Complexity of Self-Similar Organic Islands. Materials, 14(21), 6529. https://doi.org/10.3390/ma14216529







