Model of Ploughing Cortical Bone with Single-Point Diamond Tool
Abstract
:1. Introduction
2. Modeling on Bone Cutting Force for SPDT
2.1. Modeling on Normal Force
2.2. Modeling on Tangential Force
3. Experimental Setup and Method
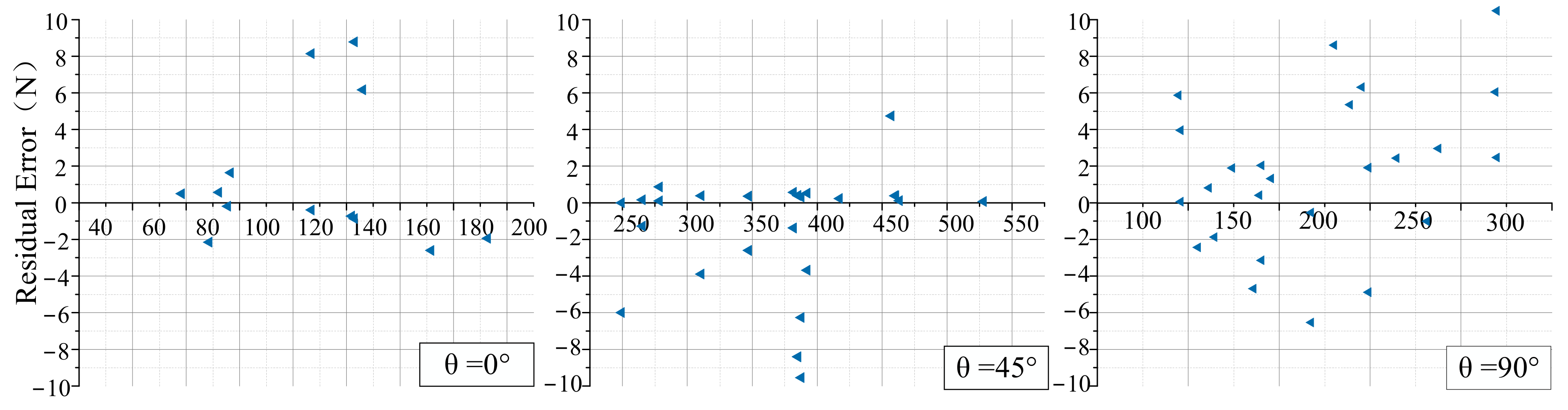
4. Results and Discussion
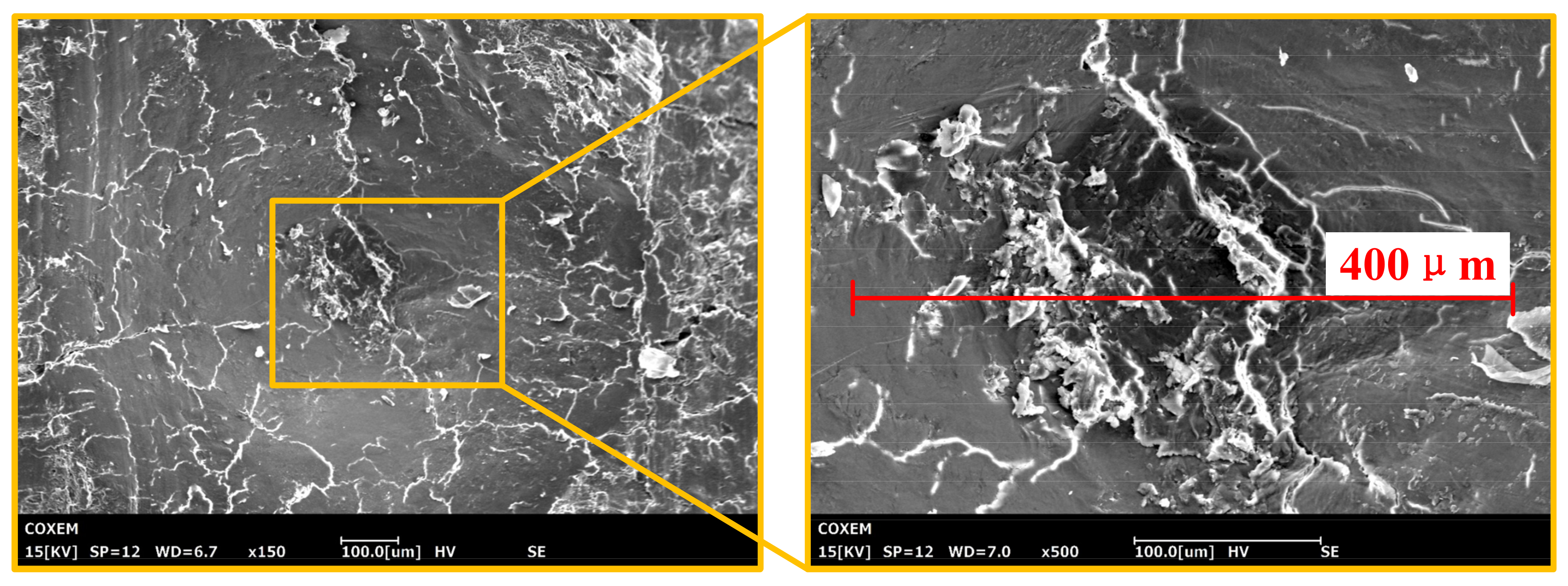
4.1. Morphology of Bone Sample
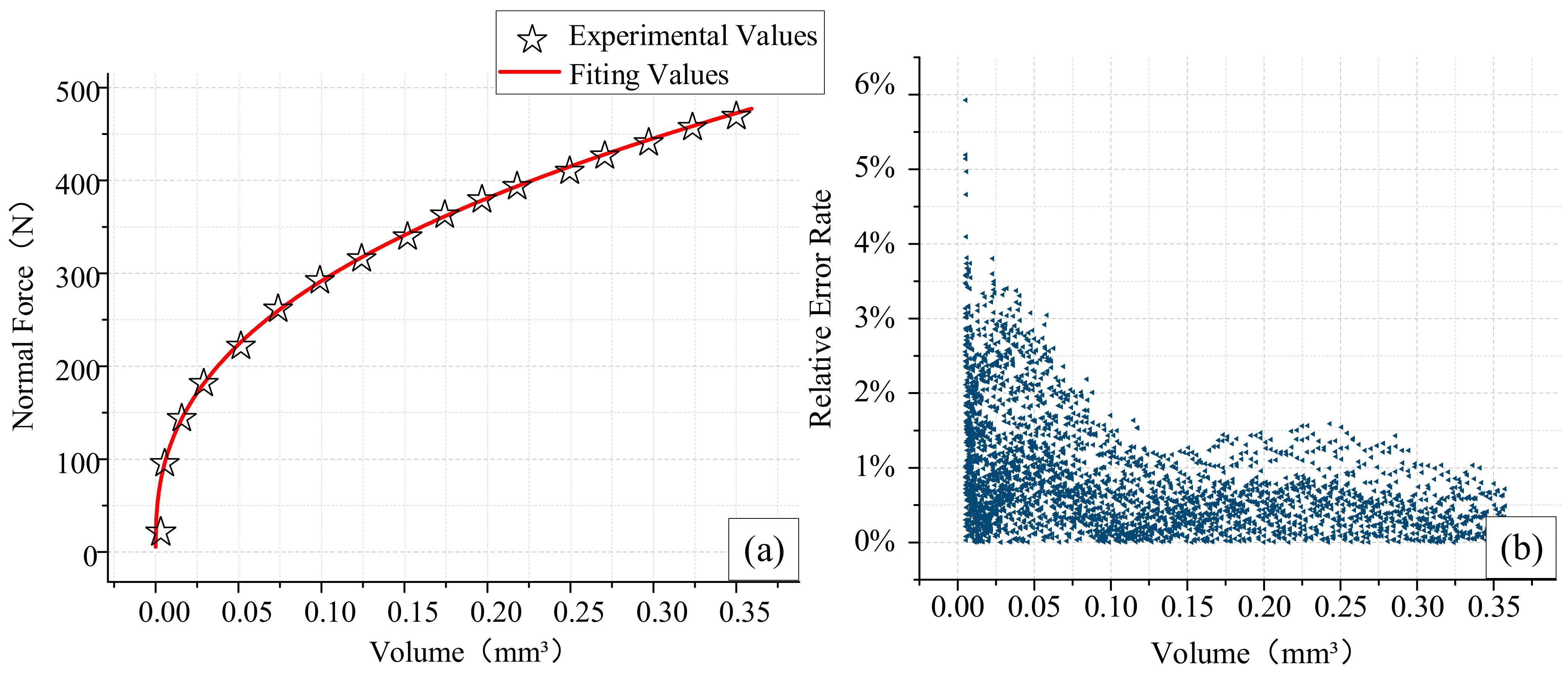
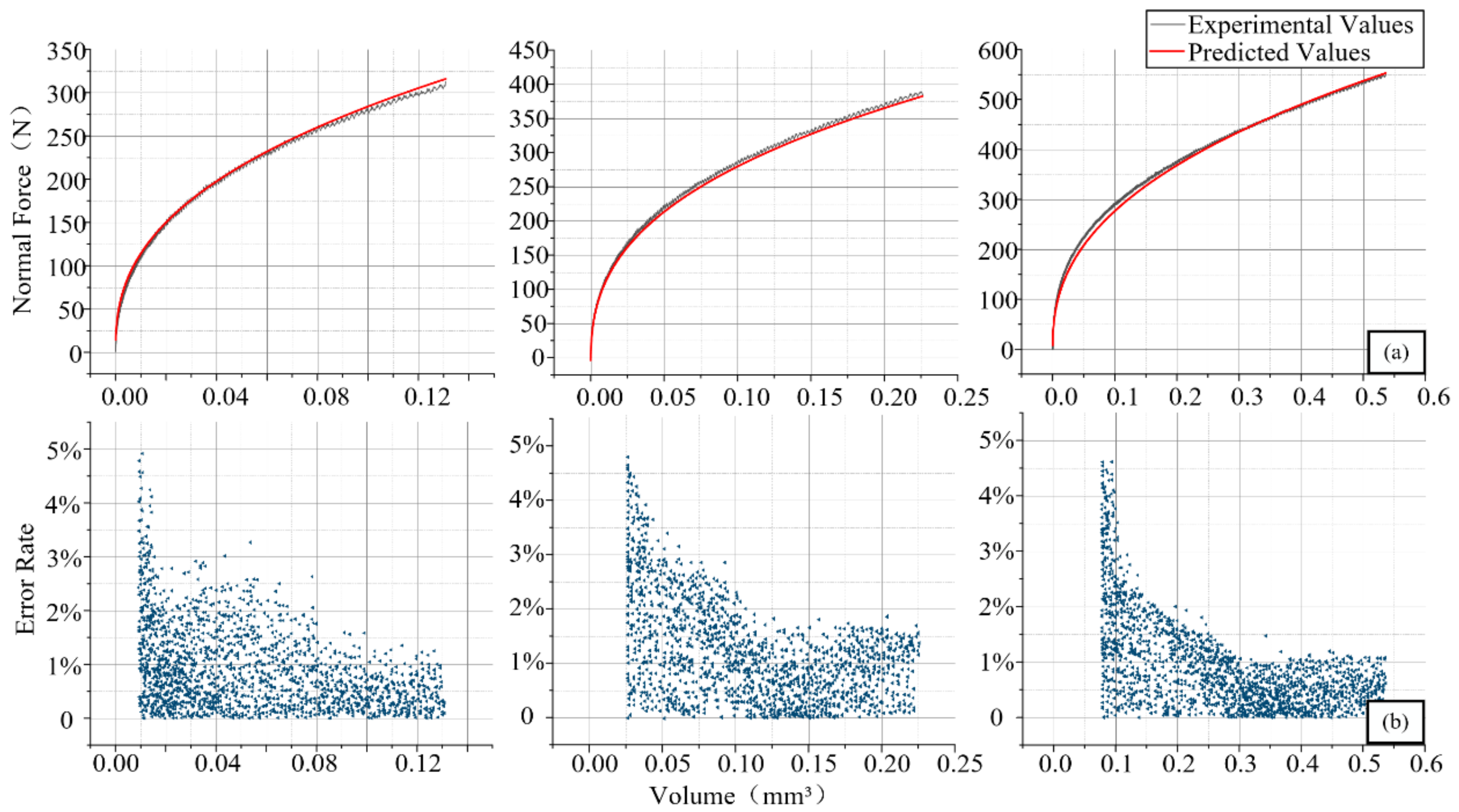
4.2. Normal Force Validation
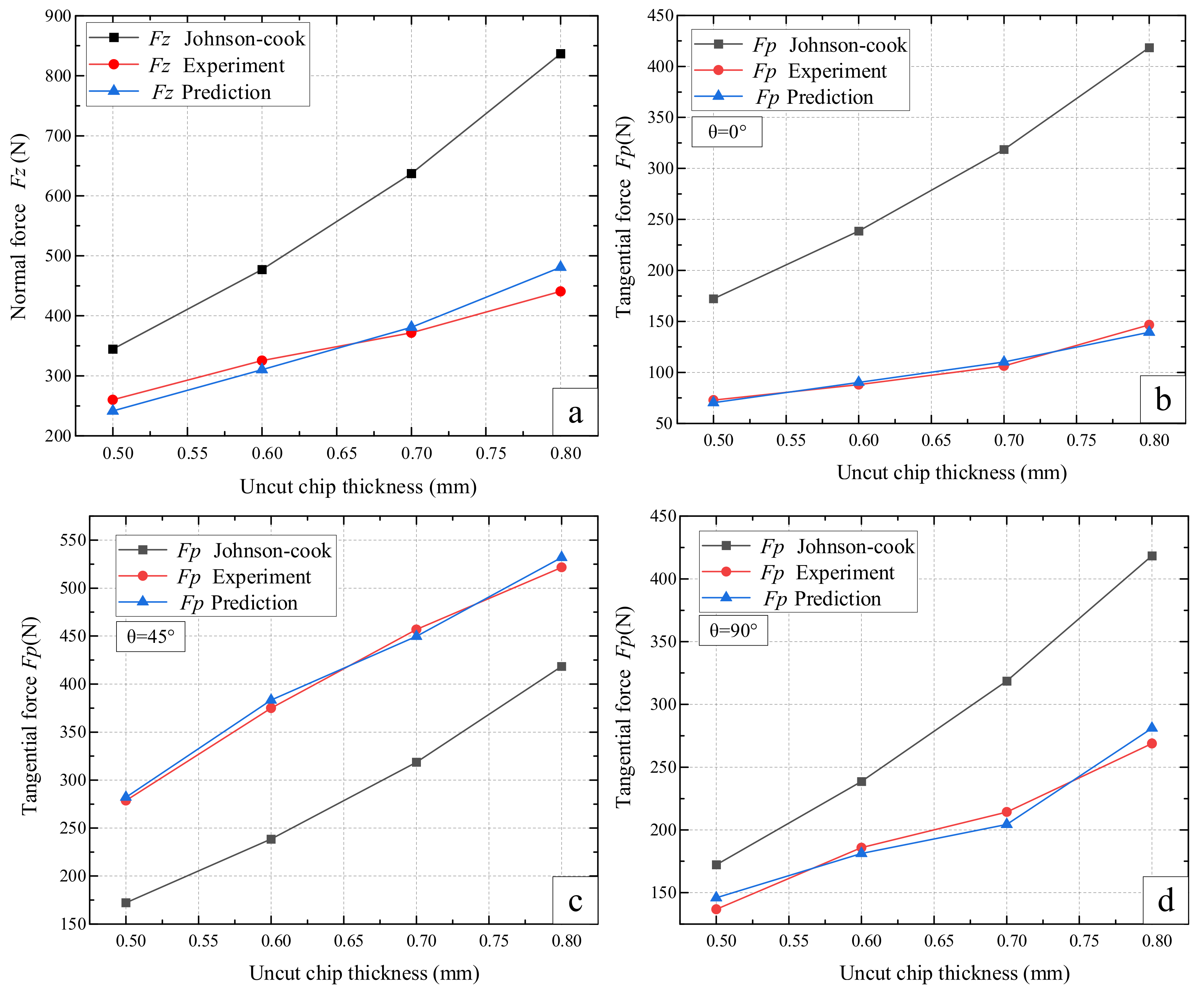
4.3. Tangential Force Validation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Langer, R.; Vacanti, J.P. Tissue Engineering. Science 1993, 260, 920–926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alison, G.H.; Ernie, W.H. Designing implant surface topography for improved biocompatibility. Expert Rev. Med. Devic. 2013, 10, 257–267. [Google Scholar]
- Kunzler, T.P.; Drobek, T. Systematic study of osteoblast and fibroblast response to roughness by means of surface-morphology gradients. Biomaterials 2007, 8, 2175–2182. [Google Scholar] [CrossRef]
- Eisenbarth, E.; Meyle., J. Influence of the surface structure of titanium materials on the adhesion of fibroblasts. Biomaterials 1996, 17, 1399–1403. [Google Scholar] [CrossRef]
- Cook, G.; Timms, P.L. Exact Replication of Biological Structures by Chemical Vapor Deposition of Silica. Angew. Chem. Int. Ed. Engl. 2010, 42, 557–559. [Google Scholar] [CrossRef]
- Ni, J.; Lv, J.J. Load-reduction mechanism of microstructure broach inspired by dung beetle surface. Manuf. Process. 2021, 64, 758–765. [Google Scholar] [CrossRef]
- Chen, C.C.A.; Pham., Q.P. Study on quasi-orthogonal machining of elastomer pad by single-point diamond tool. Int. J. Adv. Manuf. Technol. 2018, 95, 2555–2565. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Zhang, Z. Surface damage mechanics of WC/Co composites investigated by indentation and diamond scratch. Mater. Res. Express 2018, 6, 016514. [Google Scholar] [CrossRef]
- Jasinevicius, R.G. Influence of cutting conditions scaling in the machining of semiconductors crystals with single point diamond tool. J. Mater. Process. Technol. 2006, 179, 111–116. [Google Scholar] [CrossRef]
- Curreym, J.D. Strength of bone. Nature 1989, 195, 513–514. [Google Scholar] [CrossRef]
- Dempsterm, W.T.; Liddicoatm, R.T. Compact bone as a non-isotropic material. Am. J. Ana. 1952, 91, 331–362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Q.S.; Dai, L. A cortical bone milling force model based on orthogonal cutting distribution method. Adv. Manuf. 2020, 8, 204–215. [Google Scholar] [CrossRef]
- Liao, Z.R.; Axinte, D. On modelling of cutting force and temperature in bone milling. J. Mater. Process. Technol. 2019, 266, 627–638. [Google Scholar] [CrossRef]
- Bai, X.F.; Hou., S.J. Analysis of machining process and thermal conditions during vibration-assisted cortical bone drilling based on generated bone chip morphologies. Med. Eng. Phys. 2020, 83, 73–81. [Google Scholar] [CrossRef]
- Babbar, A.; Jain, V. In vivo evaluation of machining forces, torque, and bone quality during skull bone grinding. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2020, 234, 095441192091149. [Google Scholar]
- Santiuste, C.; Rodriguez-Millan, M. The influence of anisotropy in numerical modeling of orthogonal cutting of cortical bone. Compos. Struct. 2014, 116, 423–431. [Google Scholar] [CrossRef] [Green Version]
- Hage, I.S.; Hamade., R.F. Micro-FEM Orthogonal Cutting Model for Bone Using Microscope Images Enhanced Via Artificial Intelligence. J. Procedia CIRP 2013, 8, 385–390. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.W.; Zhang, Z.Y. Mechanism for material removal in diamond turning of reaction-bonded silicon carbide. Int. J. Mach. Tool Manuf. 2009, 49, 366–374. [Google Scholar] [CrossRef]
- Ayomoh, M.; Abou-El-Hossein, K.A. Cutting force prediction for single point diamond tool-tip. In Proceedings of the 2013 6th Robotics and Mechatronics Conference (RobMech), Durban, South Africa, 30–31 October 2013. [Google Scholar]
- Heamawatanachai, S.; Bamberg, E. Cutting force model of orbital single-point micromachining tool. Int. J. Mach. Tool Manuf. 2010, 50, 815–823. [Google Scholar] [CrossRef]
- Jumare, A.I.; Khaled, A. Prediction model for single-point diamond tool-tip wear during machining of optical grade silicon. Int. J. Adv. Manuf. Technol. 2018, 98, 2519–2529. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Li, C.H. Analysis of single-grain interference mechanics based on material removal and plastic stacking mechanisms in nanofluid minimum quantity lubrication grinding. Procedia CIRP 2018, 71, 116–121. [Google Scholar] [CrossRef]
- Yang, M.; Li, C.H. Predictive model for minimum chip thickness and size effect in single diamond grain grinding of zirconia ceramics under different lubricating conditions. Ceram. Int. 2019, 45, 14908–14920. [Google Scholar] [CrossRef]
- Barber, J.R.; Ciavarella, M. Contact mechanics. Int. J. Solids Struct. 2000, 37, 29–43. [Google Scholar] [CrossRef]
- Xu, X.P.; Li, Y. Force ratio in the circular sawing of granites with a diamond segmented blade. J. Mater. Process. Technol. 2003, 139, 281–285. [Google Scholar] [CrossRef]
- Tahmasbi, V.; Ghoreishi, M. Investigation, sensitivity analysis, and multi-objective optimization of effective parameters on temperature and force in robotic drilling cortical bone. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2017, 231, 1012. [Google Scholar] [CrossRef]
- Singh, G.; Jain, V. Optimization of process parameters for drilled hole quality characteristics during cortical bone drilling using Taguchi method. Mech. Behav. Biomed. 2016, 62, 355–365. [Google Scholar] [CrossRef]
- Lomax, R.G.; Hahs-vaughn, D.L. Statistical Concepts (A Second Course); Routledge: New York, NY, USA, 2012; pp. 11–14. [Google Scholar]
- Liu, H.; Shah, S. On-line outlier detection and data cleaning. Comput. Chem. Eng. 2004, 28, 1635–1647. [Google Scholar] [CrossRef]




| Performance Parameter | Bone Type | |
|---|---|---|
| Bovine | Human | |
| Tensile strength (MPa) | 140–250 | 130–200 |
| Compressive strength (MPa) | 45–150 | 40–145 |
| Young’s modulus (GPa) | 10–22 | 10–17 |
| Shear modulus (MPa) | 3 | 3 |
| Density (kg/m3) | 1950–2100 | 1800–2000 |
| Poisson’s ratio | 0.33 | 0.4 |
| Specific heat (J/kg K) | 1300 | 1330 |
| Thermal conductivity (W/m K) | 0.1–0.3 | 0.1–0.43 |
| NO | Uncut Chip Thickness (mm) | Cutting Angle |
|---|---|---|
| 1 | 0.5 | 0°/45°/90° |
| 2 | 0.6 | 0°/45°/90° |
| 3 | 0.7 | 0°/45°/90° |
| 4 | 0.8 | 0°/45°/90° |
| Level: 0.7 mm Fitting: Fz = 707.53 V 0.39 R-Squared R2: 0.99977 | |||||
|---|---|---|---|---|---|
| DOF | Sum of Square | Mean-Square | F-Measure | Confidence Level | |
| Regression Coefficient | 2 | 2.89 × 108 | 1.45 × 108 | 1.44 × 10−7 | 95% |
| Residual Error | 4111 | 41,283.57 | 10.04 | ||
| Coefficient | fp(θ0) | C1 | C2 | C3 | θ0 |
|---|---|---|---|---|---|
| Optimized value | 0.29 | 0.294 | 0.934 | 0.45 | 0 |
| fp (0°) | Error Rate | fp (90°) | Error Rate | fp (45°) | Error Rate |
|---|---|---|---|---|---|
| 0.29 | 1.36% | 0.55 | 1.99% | 1.23 | 2.49% |
| 0.29 | 1.42% | 0.55 | 1.02% | 1.21 | 1.06% |
| 0.29 | 2.26% | 0.55 | 1.00% | 1.21 | 1.05% |
| 0.30 | 1.00% | 0.58 | 1.07% | 1.22 | 1.46% |
| 0.30 | 1.95% | 0.58 | 1.06% | 1.22 | 1.83% |
| 0.5 mm | 0.6 mm | 0.8 mm | |||
| Fp (0°) (N) | Error Rate | Fp (0°) (N) | Error Rate | Fp (0°) | Error Rate |
| 64.35 | 6.23% | 88.61 | 2.43% | 126.84 | 0.31% |
| 80.04 | 3.02% | 95.58 | 0.19% | 146.06 | 4.22% |
| 60.56 | 5.29% | 92.24 | 0.62% | 142.96 | 0.61% |
| 71.70 | 3.15% | 96.63 | 1.69% | 141.90 | 0.05% |
| 75.46 | 3.84% | 78.30 | 0.64% | 171.60 | 1.51% |
| 0.5 mm | 0.6 mm | 0.8 mm | |||
| Fp (45°) | Error Rate | Fp (45°) | Error Rate | Fp (45°) | Error Rate |
| 314.57 | 1.25% | 374.95 | 1.61% | 528.01 | 1.58% |
| 277.75 | 0.31% | 383.11 | 0.36% | 528.79 | 0.68% |
| 266.73 | 0.48% | 393.6 | 2.18% | 542.52 | 0.50% |
| 296.38 | 1.18% | 349.87 | 0.75% | 534.53 | 0.23% |
| 255.31 | 0.1% | 395.99 | 0.94% | 525.84 | 1.94% |
| 0.5 mm | 0.6 mm | 0.8 mm | |||
| Fp (90°) | Error Rate | Fp (90°) | Error Rate | Fp (90°) | Error Rate |
| 145.83 | 0.04% | 172.33 | 1.09% | 282.28 | 0.36% |
| 136.02 | 11.06% | 194.27 | 0.68% | 299.33 | 3.75% |
| 164.39 | 1.13% | 188.69 | 0.22% | 266.69 | 4.36% |
| 155.29 | 1.57% | 190.56 | 2.52% | 244.23 | 4.54% |
| 128.36 | 17.79% | 160.52 | 0.50% | 312.95 | 1.89% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, J.; Wang, Y.; Meng, Z.; Cai, J.; Feng, K.; Zhang, H. Model of Ploughing Cortical Bone with Single-Point Diamond Tool. Materials 2021, 14, 6530. https://doi.org/10.3390/ma14216530
Ni J, Wang Y, Meng Z, Cai J, Feng K, Zhang H. Model of Ploughing Cortical Bone with Single-Point Diamond Tool. Materials. 2021; 14(21):6530. https://doi.org/10.3390/ma14216530
Chicago/Turabian StyleNi, Jing, Yang Wang, Zhen Meng, Jun Cai, Kai Feng, and Hongwei Zhang. 2021. "Model of Ploughing Cortical Bone with Single-Point Diamond Tool" Materials 14, no. 21: 6530. https://doi.org/10.3390/ma14216530
APA StyleNi, J., Wang, Y., Meng, Z., Cai, J., Feng, K., & Zhang, H. (2021). Model of Ploughing Cortical Bone with Single-Point Diamond Tool. Materials, 14(21), 6530. https://doi.org/10.3390/ma14216530






