Creep-Fatigue Crack Initiation Simulation of a Modified 12% Cr Steel Based on Grain Boundary Cavitation and Plastic Slip Accumulation
Abstract
:1. Introduction
2. Model
2.1. Crystal Plasticity Model
2.2. Grain Boundary Cavitation Model
2.2.1. Cavity Nucleation
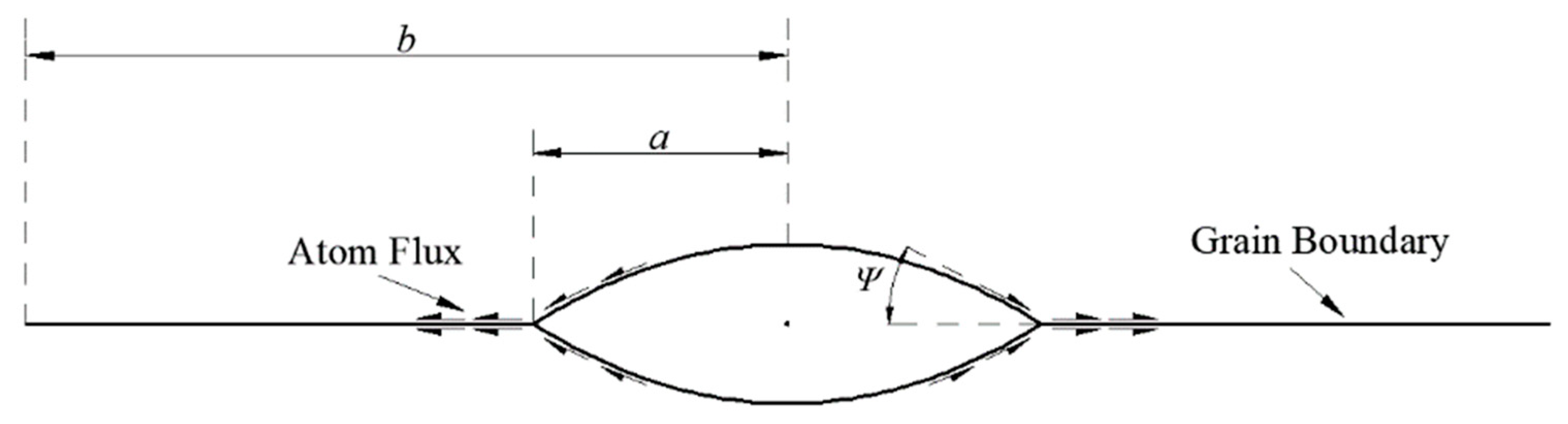
2.2.2. Cavity Growth
2.3. Fatigue Crack Initiation Model
3. Finite Element Implementation
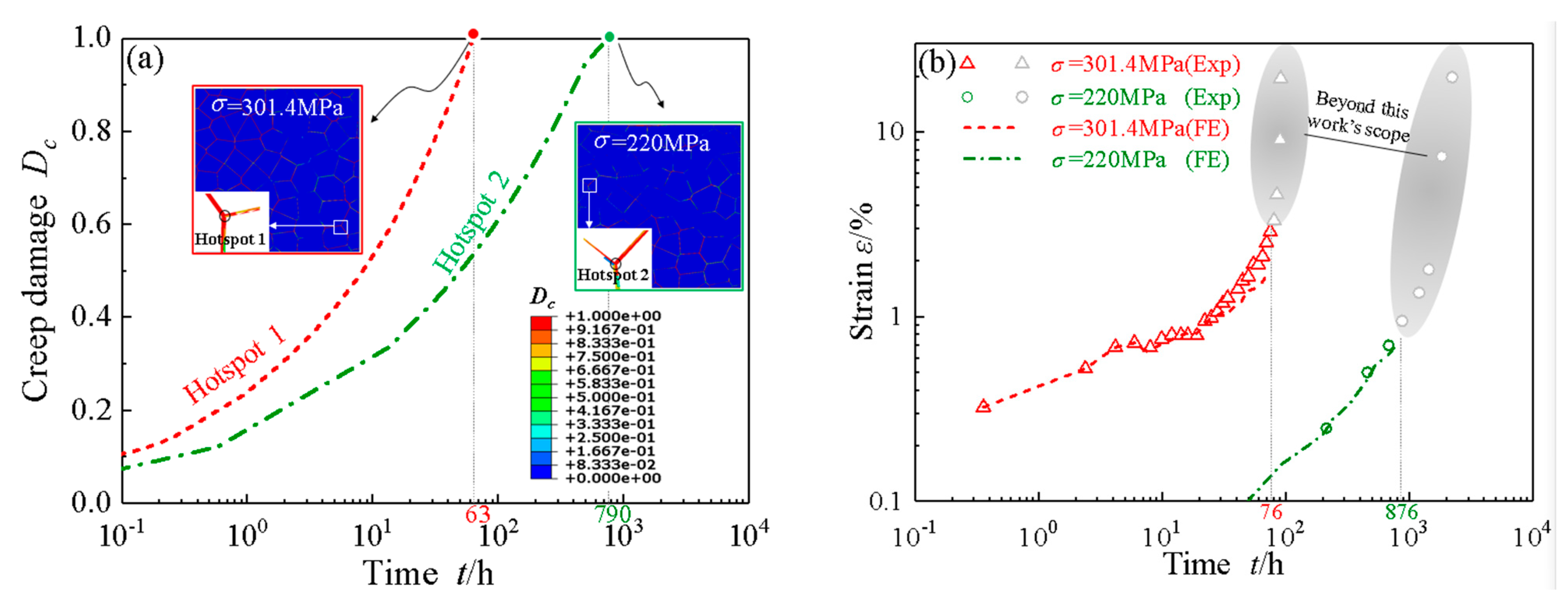
3.1. Validation of Model Parameters
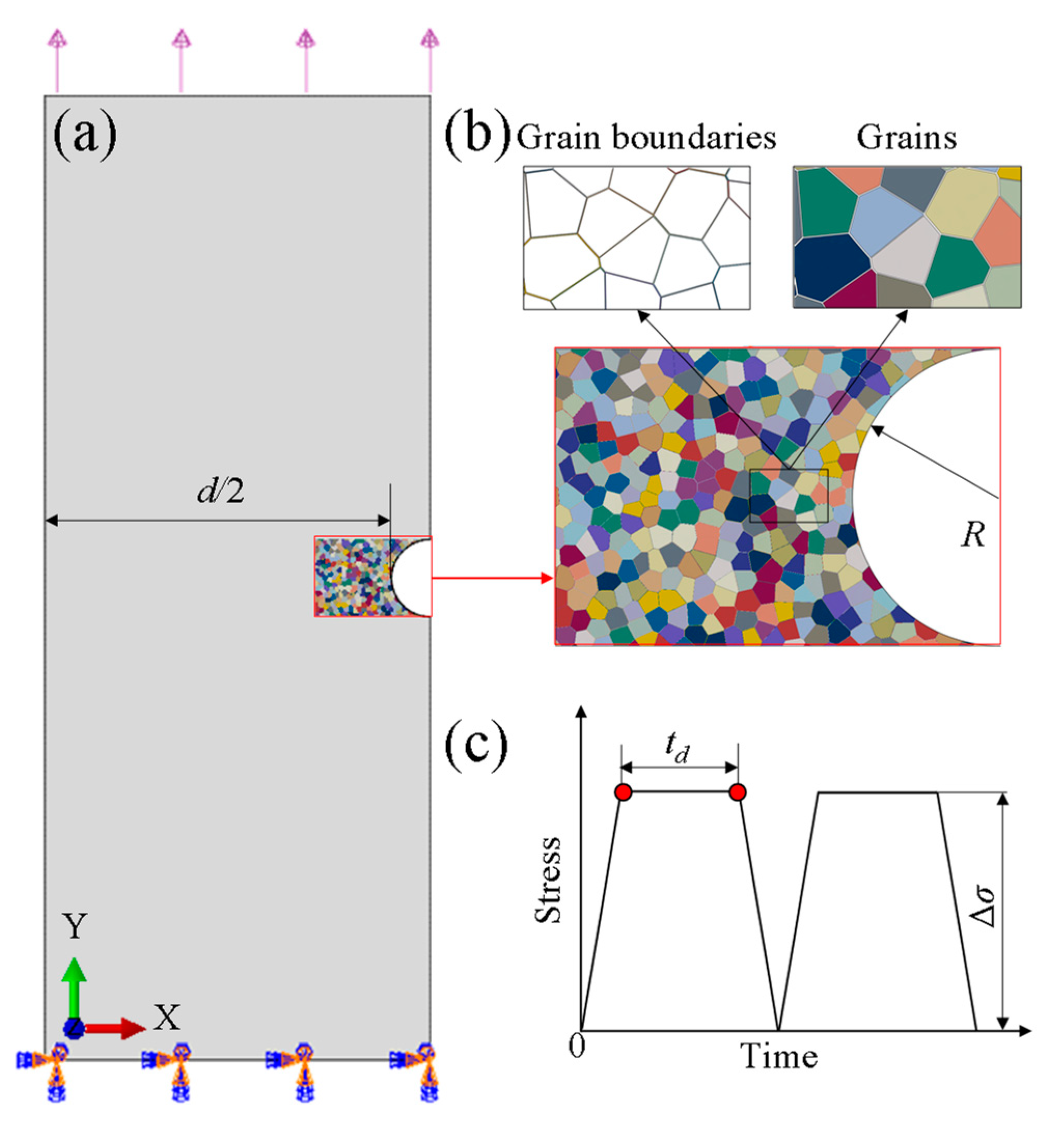
3.2. Simulation of Crack Initiation of Notched Specimens under Creep-Fatigue Loading
4. Results and Discussion
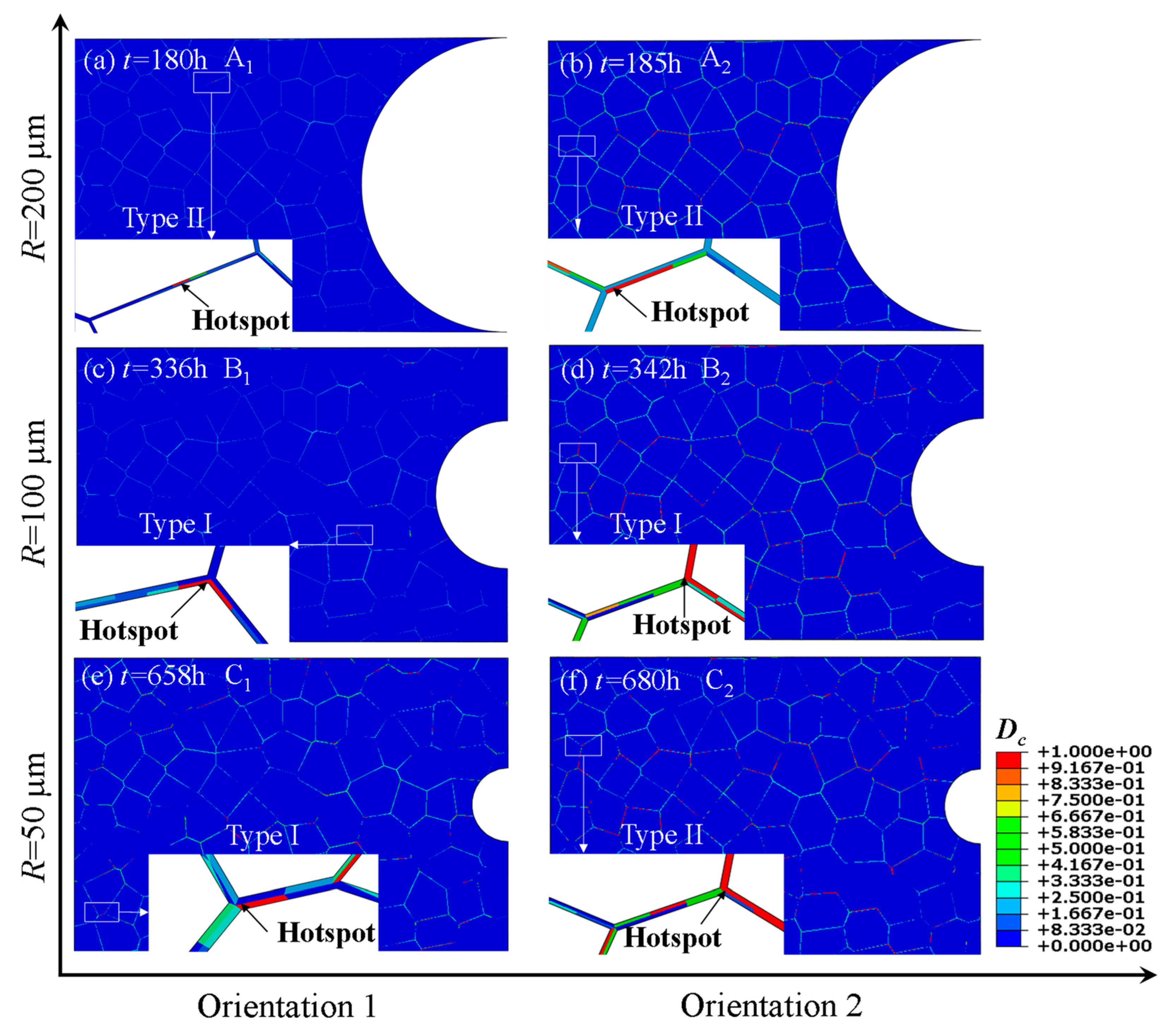
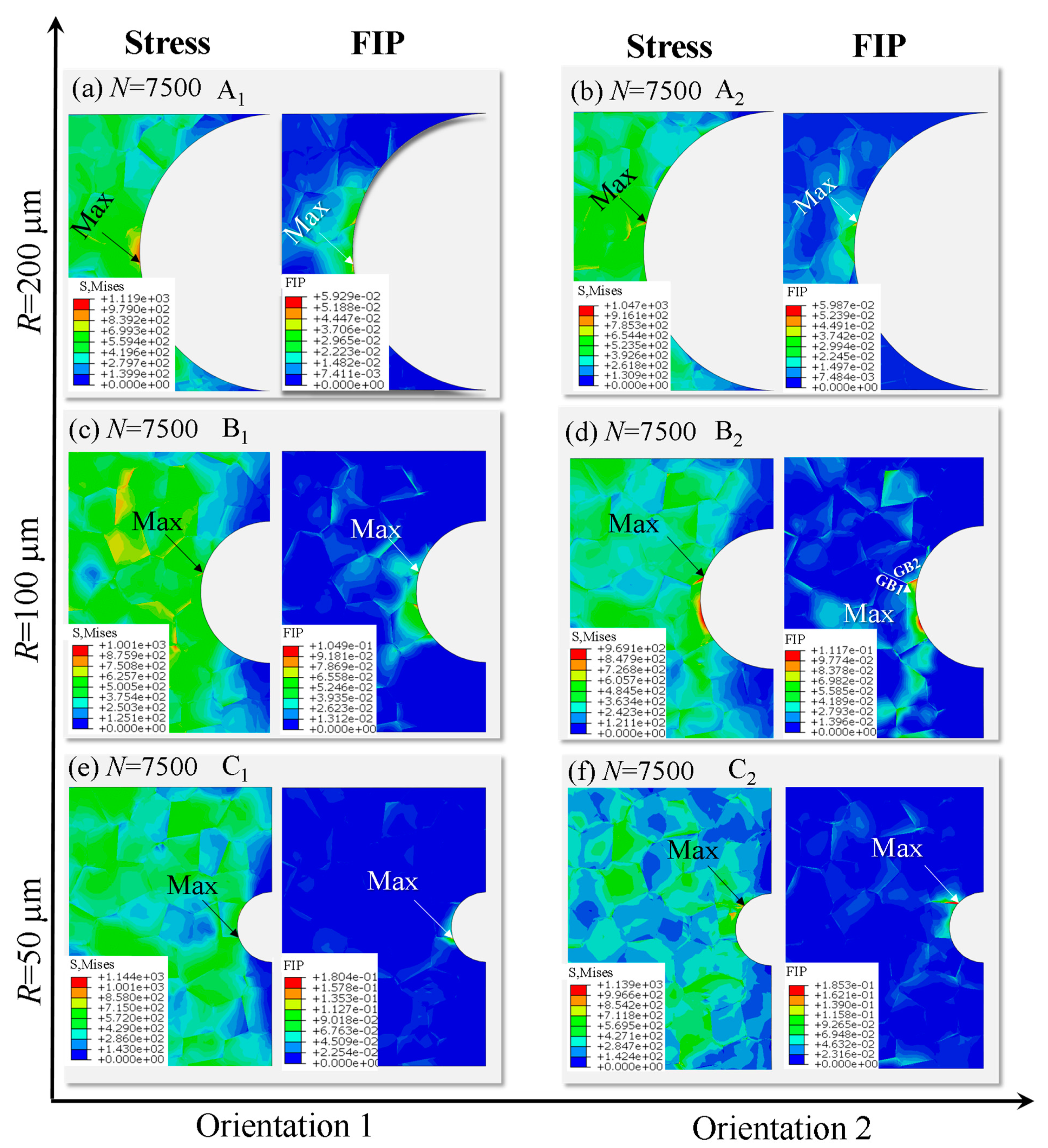
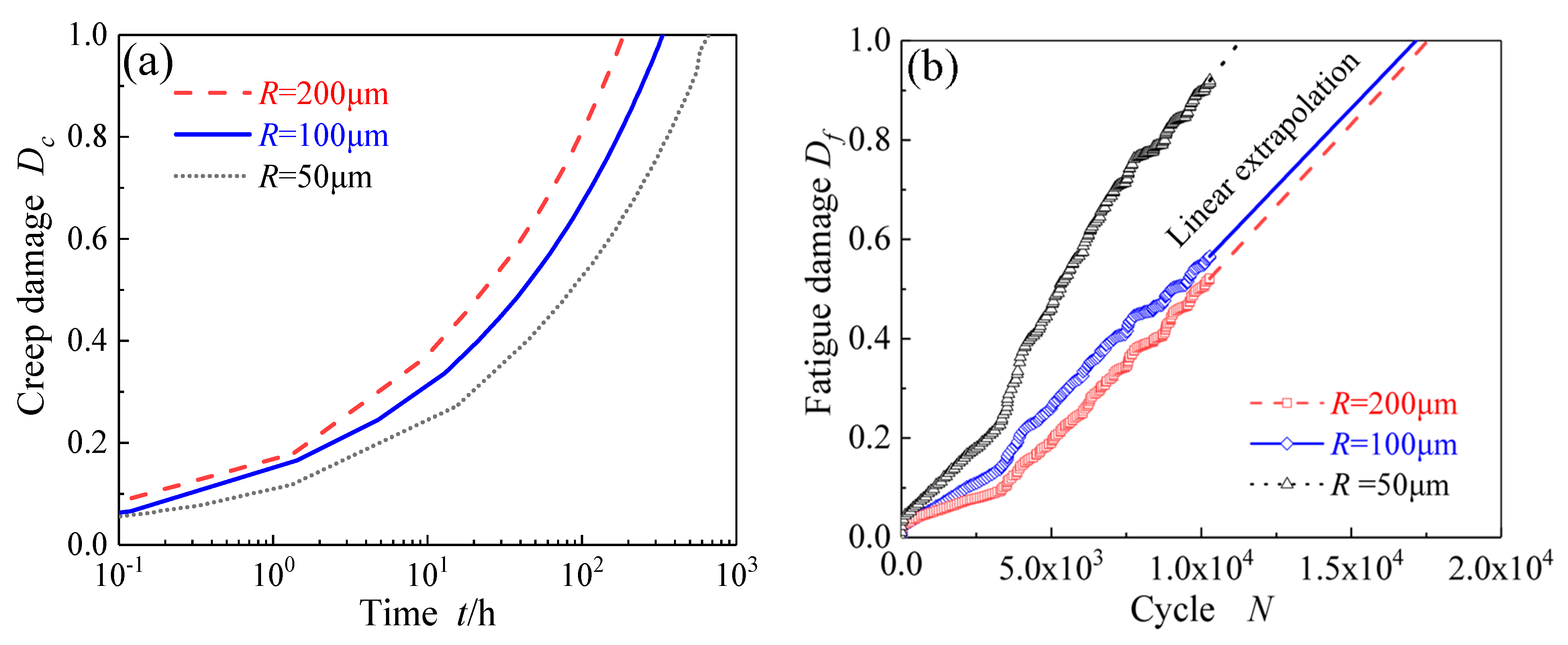
4.1. Effect of Initial Notch Size on Creep and Fatigue Crack Initiations
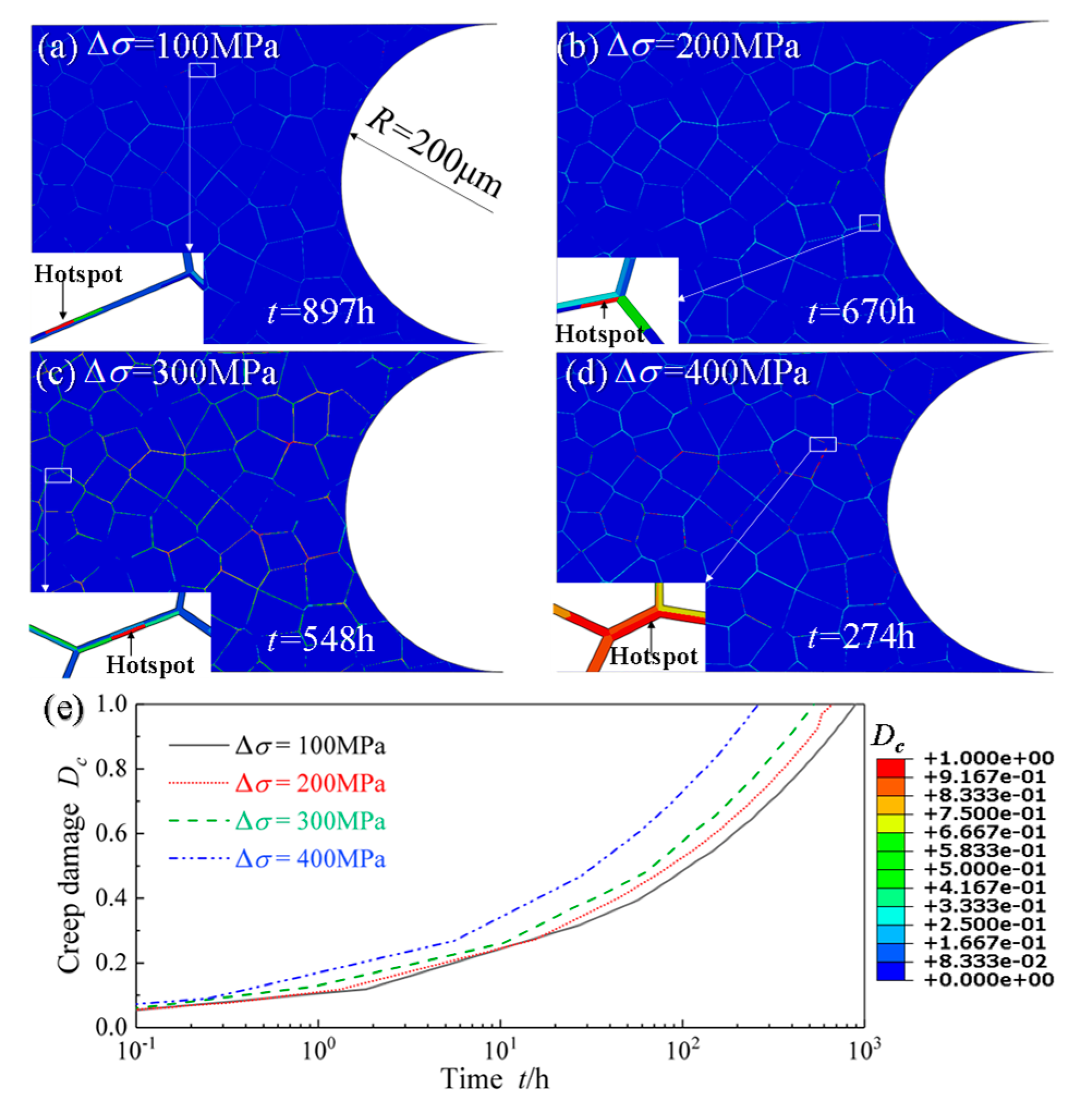
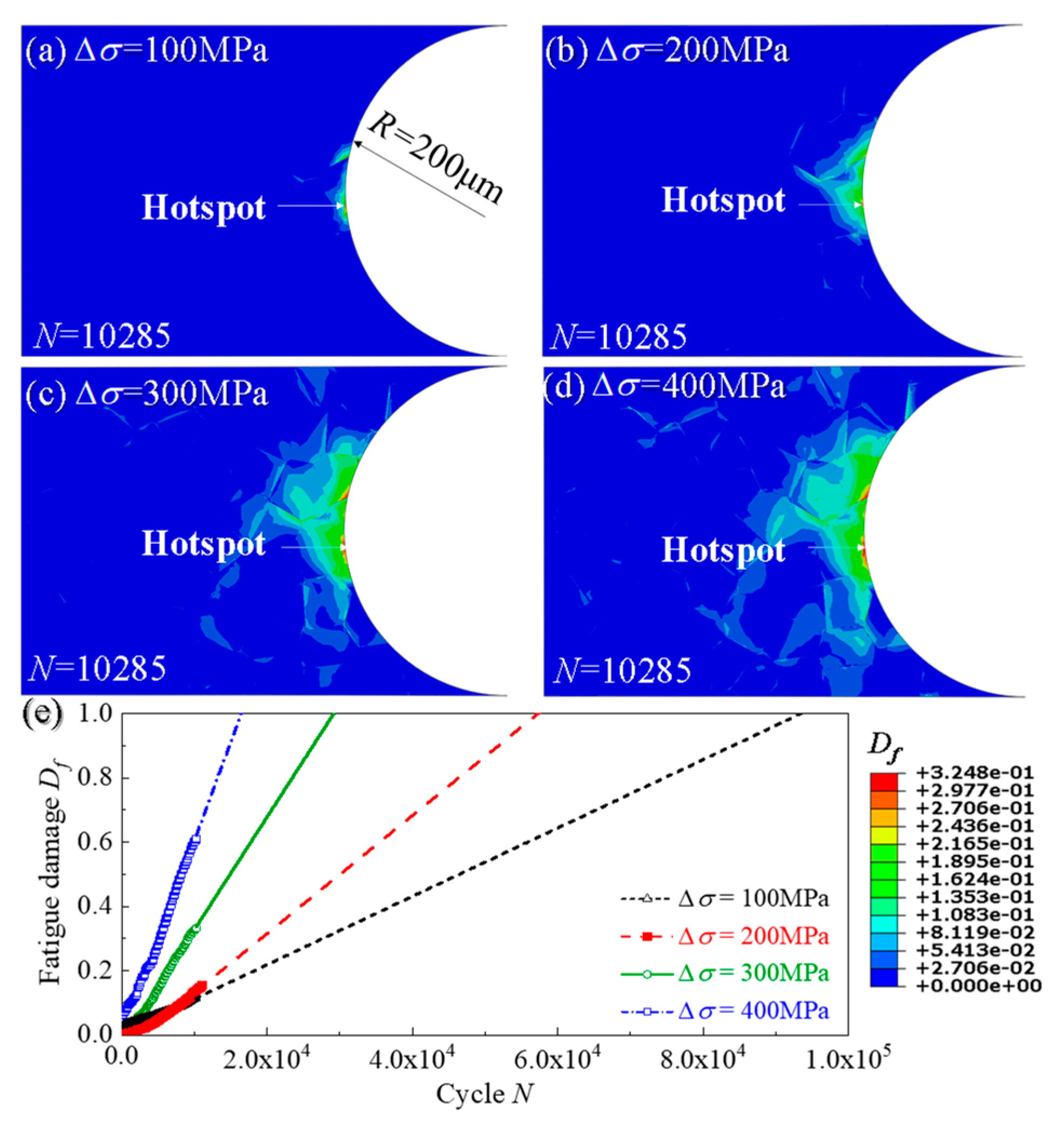
4.2. Effect of Stress Range on Creep and Fatigue Crack Initiations
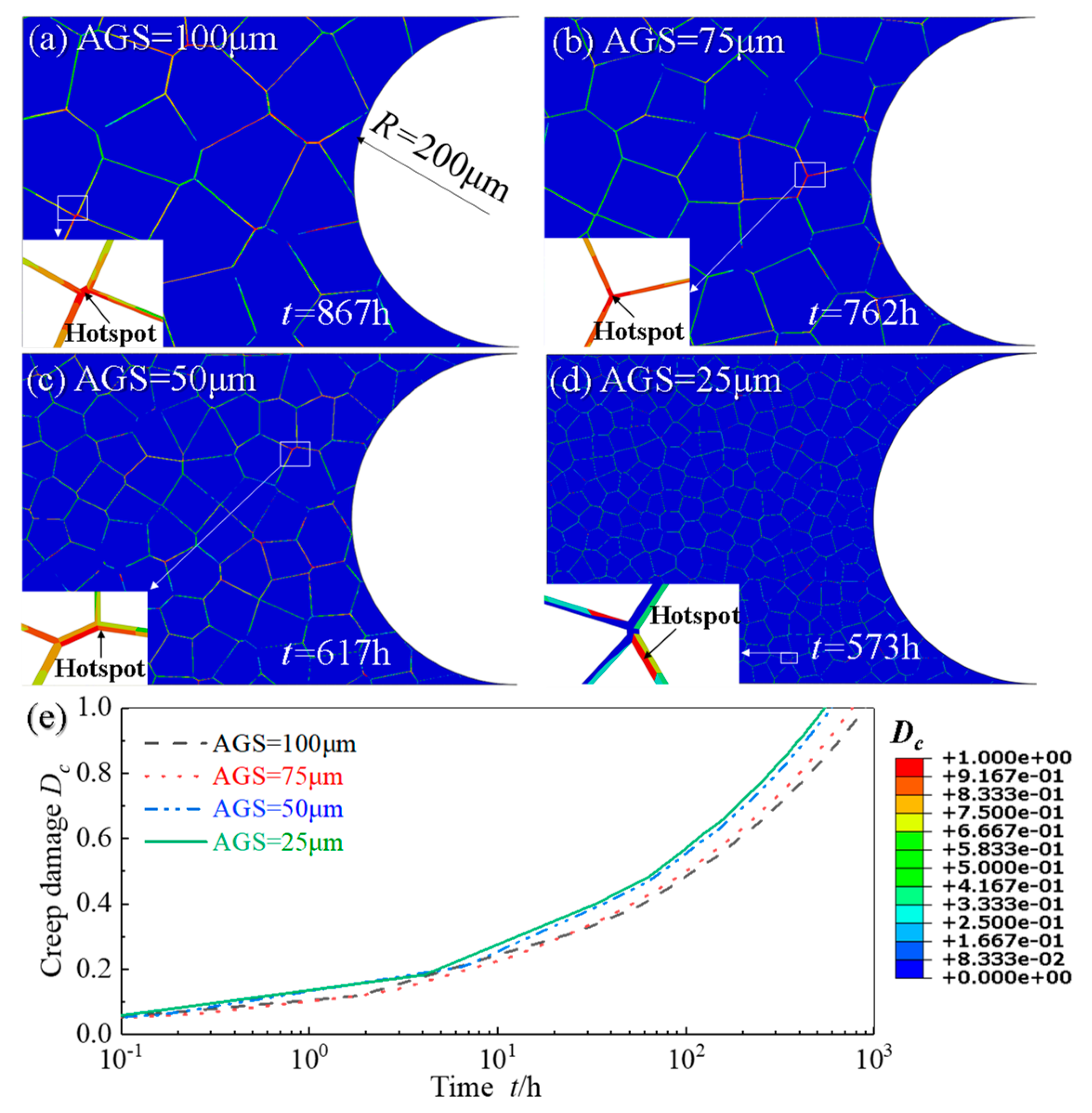
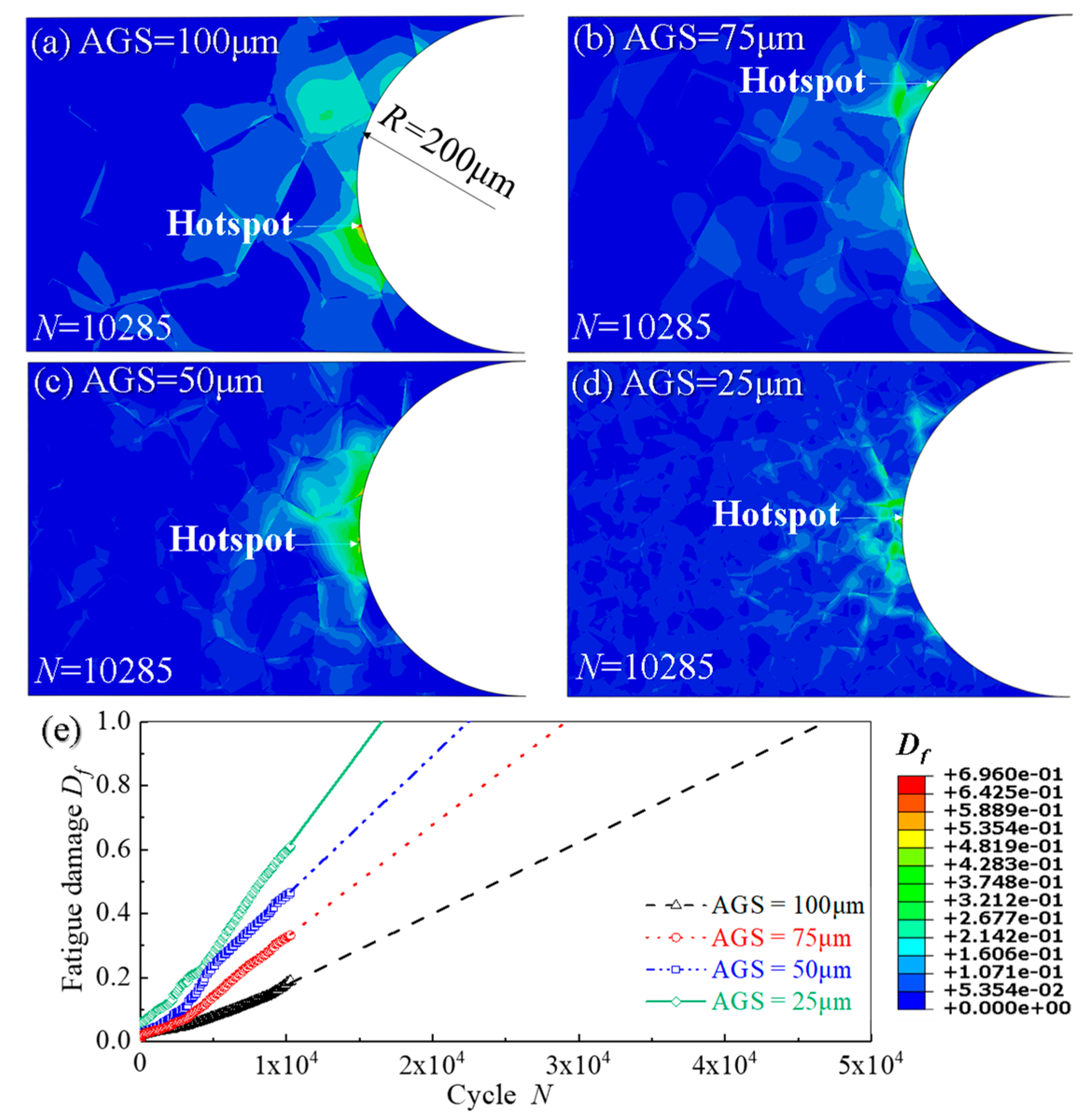
4.3. Effect of Average Grain Size on Creep and Fatigue Crack Initiations
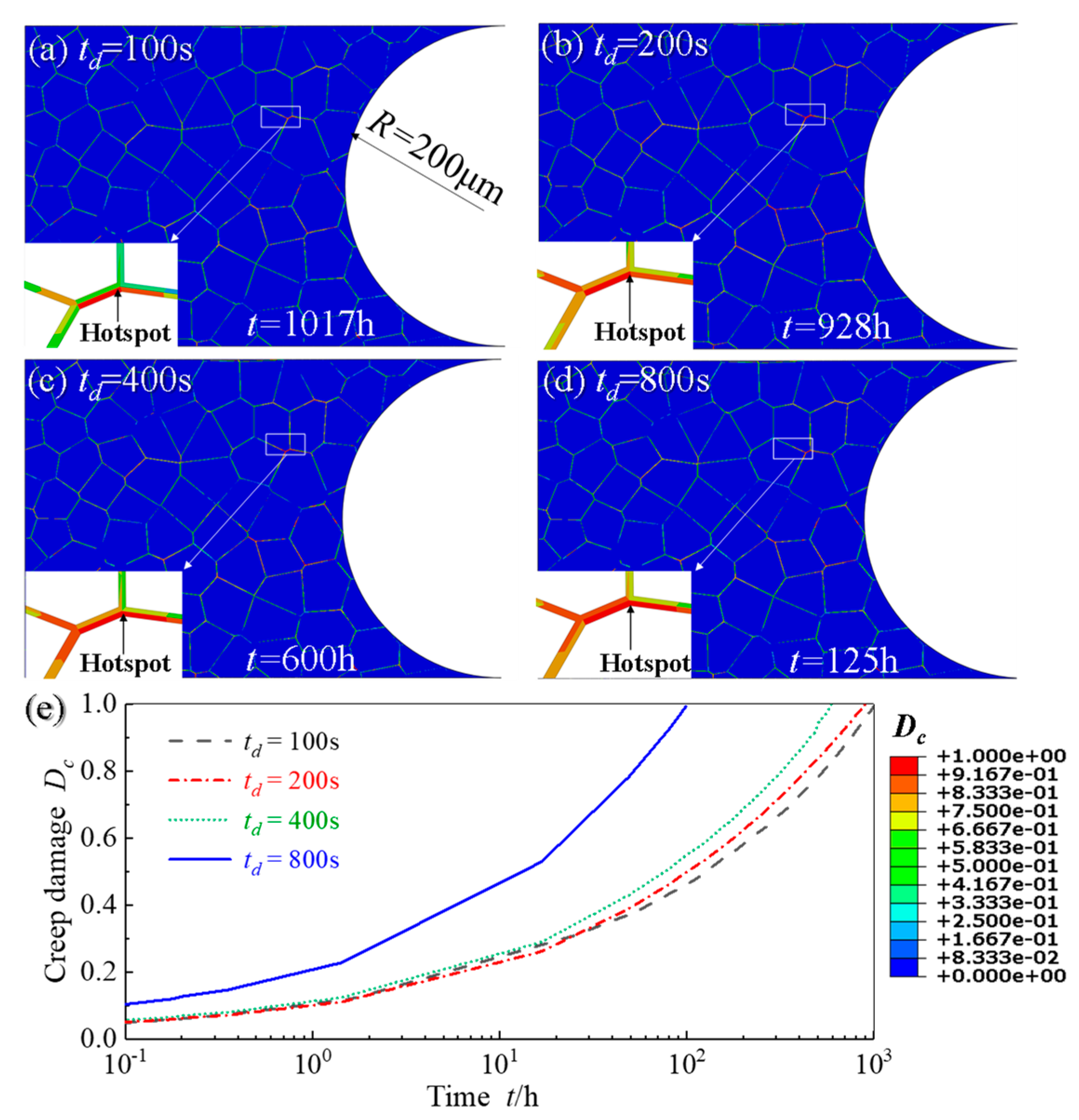
4.4. Effect of Holding Time on Creep and Fatigue Crack Initiations
5. Conclusions
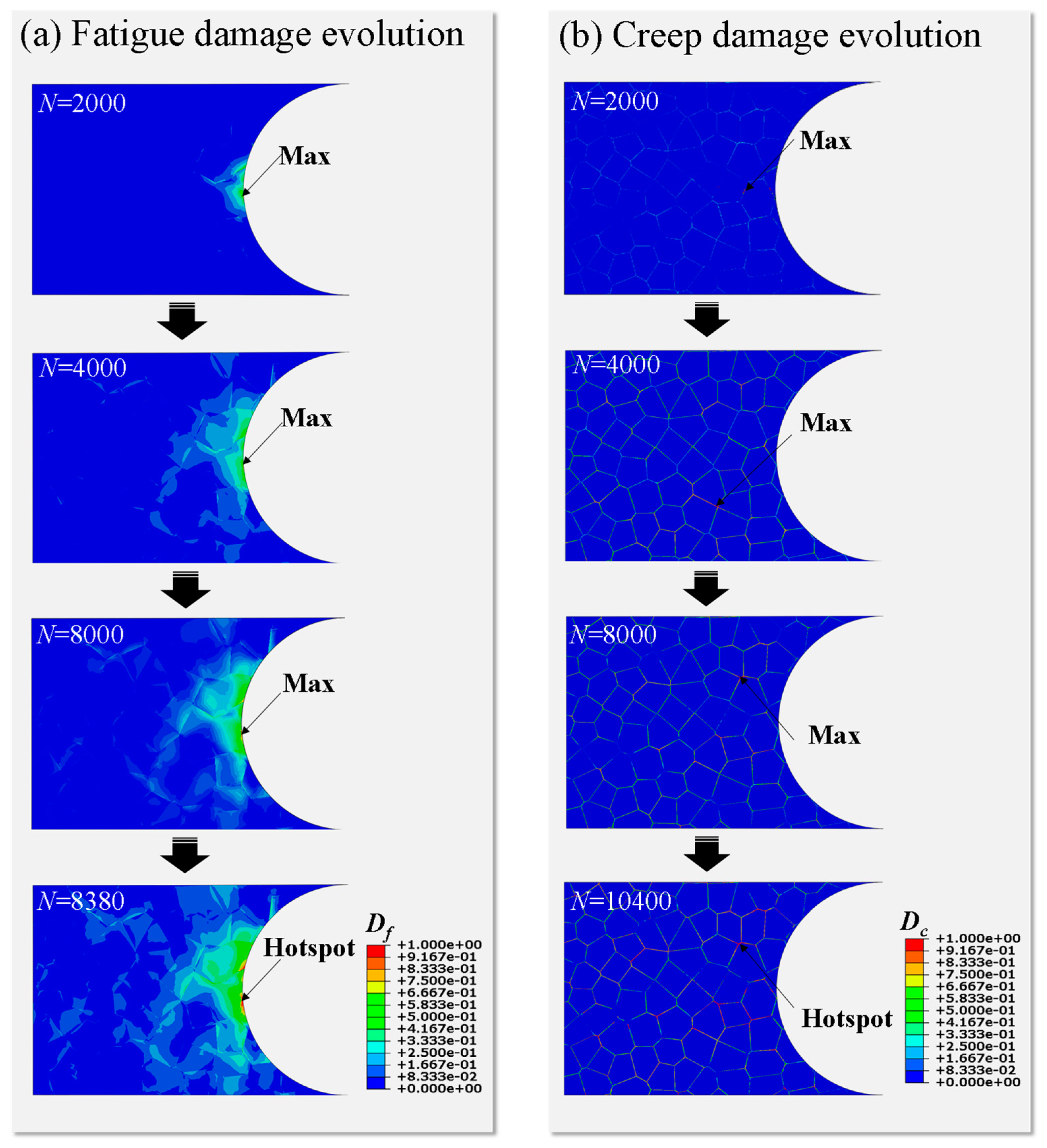
- Fatigue crack initiation occurs on the surface of the notch root during the whole lifetime. The creep crack initiation is basically located at a distance of 2~8 grains from the surface of the notch, at the triple grain boundary junction or at the grain boundary approximately perpendicular to the loading direction;
- For specimens with a notch root radius from 50 μm to 200 μm, the fatigue initiation time is shortened with the decrease of the root radius of the notch, while the creep crack initiation time becomes longer with the increase of the notch acuity ratio due to the reinforcement effect of the notch;
- As the stress range increases, the initiation times of creep and fatigue crack initiations are shortened. Meanwhile, with the decrease of AGS and the increase of holding time, the initiations of creep and fatigue cracks also accelerate;
- For specimens with the same notch size and stress range, both creep and fatigue crack initiation sites are insensitive to the holding times ranging from 100 s to 800 s.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tu, S.T.; Xuan, F.Z.; Wang, W.Z. Some critical issues in creep and fracture assessment at high temperature. Acta Metall. Sin. 2009, 45, 781–787. [Google Scholar]
- Viswanathan, R.; Stringer, J. Failure mechanisms of high temperature components in power plants. J. Eng. Mater. Technol. 2000, 122, 246–255. [Google Scholar] [CrossRef]
- Liu, W. The dynamic creep rupture of a secondary superheater tube in a 43 MW coal-fired boiler by the decarburization and multilayer oxide scale buildup on both sides. Eng. Fail. Anal. 2015, 53, 1–14. [Google Scholar] [CrossRef]
- Mourya, R.K.; Banerjee, A.; Sreedhar, B.K. Effect of creep on the failure probability of bolted flange joints. Eng. Fail. Anal. 2015, 50, 71–87. [Google Scholar] [CrossRef]
- Khodamorad, S.H.; Fatmehsari, D.H.; Rezaie, H.; Sadeghipour, A. Analysis of ethylene cracking furnace tubes. Eng. Fail. Anal. 2012, 21, 1–8. [Google Scholar] [CrossRef]
- Ejaz, N.; Qureshi, I.N.; Rizvi, S.A. Creep failure of low pressure turbine blade of an aircraft engine. Eng. Fail. Anal. 2011, 18, 1407–1414. [Google Scholar] [CrossRef]
- Ahmad, J.; Purbolaksono, J.; Beng, L.C. Failure analysis on high temperature superheater Inconel® 800 tube. Eng. Fail. Anal. 2010, 17, 328–333. [Google Scholar] [CrossRef]
- Wang, P.; Cui, L.; Scholz, A.; Linn, S.; Oechsner, M. Multiaxial thermomechanical creep-fatigue analysis of heat-resistant steels with varying chromium contents. Int. J. Fatigue 2014, 67, 220–227. [Google Scholar] [CrossRef]
- Cui, L.; Wang, P.; Hoche, H.; Scholz, A.; Berger, C. The influence of temperature transients on the lifetime of modern high-chromium rotor steel under service-type loading. Mater. Sci. Eng. C 2013, 560, 767–780. [Google Scholar] [CrossRef]
- Di Gianfrancesco, A. Materials for Ultra-Supercritical and Advanced Ultra-Supercritical Power Plants; Woodhead Publishing: Cambridge, UK, 2016; pp. 652–775. [Google Scholar]
- Aslan, O.; Quilici, S.; Forest, S. Numerical modeling of fatigue crack growth in single crystals based on microdamage theory. Int. J. Damage Mech. 2011, 20, 681–705. [Google Scholar] [CrossRef]
- Henaff, G.; Odemer, G.; Benoit, G.; Koffi, E.; Journet, B. Prediction of creep–fatigue crack growth rates in inert and active environments in an aluminium alloy. Int. J. Fatigue 2009, 31, 1943–1951. [Google Scholar] [CrossRef]
- Wen, J.F.; Tu, S.T. A multiaxial creep-damage model for creep crack growth considering cavity growth and microcrack interaction. Eng. Fract. Mech. 2014, 123, 197–210. [Google Scholar] [CrossRef]
- Carlsson, K. Modeling of Three Dimensional Microstructures Including Grain Boundary Mechanisms. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, December 2013. [Google Scholar]
- Ghazvinian, E.; Kalenchuk, K.S.; Diederichs, M.S. Three-dimensional random Voronoi models for simulation of brittle rock damage around underground excavations in laminated ground. In Deep Mining 2017: Proceedings of the Eighth International Conference on Deep and High Stress Mining; Australian Centre for Geomechanics: Perth, Australia, 2017; pp. 277–288. [Google Scholar]
- Weyer, S.; Fröhlich, A.; Riesch-Oppermann, H.; Cizelj, L.; Kovac, M. Automatic finite element meshing of planar Voronoi tessellations. Eng. Fract. Mech. 2002, 69, 945–958. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Karimpour, M.; Balint, D.; Lin, J. Cohesive zone representation and junction partitioning for crystal plasticity analyses. Int. J. Numer. Meth. Eng. 2012, 92, 715–733. [Google Scholar] [CrossRef]
- Danilov, V.I.; Konovalov, S.V.; Zhuravleva, S.V.; Zuev, L.B.; Gromov, V.E. Macrolocalization of plastic strain in creep of fine-grain aluminum. Tech. Phys. 2005, 50, 376–379. [Google Scholar] [CrossRef]
- Yasniy, P.; Maruschak, P.; Lapusta, Y. Experimental study of crack growth in a bimetal under fatigue and fatigue-creep conditions. Int. J. Fract. 2006, 139, 545–552. [Google Scholar] [CrossRef]
- Busso, E.P.; Meissonnier, F.T.; O’dowd, N.P. Gradient-dependent deformation of two-phase single crystals. J. Mech. Phys. Solids 2000, 48, 2333–2361. [Google Scholar] [CrossRef]
- Sauzay, M.; Jourdan, T. Polycrystalline microstructure, cubic elasticity, and nucleation of high-cycle fatigue cracks. Int. J. Fract. 2006, 141, 431–446. [Google Scholar] [CrossRef]
- Simonovski, I.; Nilsson, K.F.; Cizelj, L. The influence of crystallographic orientation on crack tip displacements of microstructurally small, kinked crack crossing the grain boundary. Comput. Mater. Sci. 2007, 39, 817–828. [Google Scholar] [CrossRef]
- McDowell, D.L.; Dunne, F.P.E. Microstructure-sensitive computational modeling of fatigue crack formation. Int. J. Fatigue 2010, 32, 1521–1542. [Google Scholar] [CrossRef]
- Li, D.F.; Barrett, R.A.; O’Donoghue, P.E.; O’Dowd, N.P.; Leen, S.B. A multi-scale crystal plasticity model for cyclic plasticity and low-cycle fatigue in a precipitate-strengthened steel at elevated temperature. J. Mech. Phys. Solids 2017, 101, 44–62. [Google Scholar] [CrossRef] [Green Version]
- Tang, B.; Zhang, M.; Yang, R.; Chen, W.; Li, J. Microplasticity behavior study of equiaxed near-β titanium alloy under high-cycle fatigue loading: Crystal plasticity simulations and experiments. J. Mater. Res. Technol. 2019, 8, 6146–6157. [Google Scholar] [CrossRef]
- Efthymiadis, P.; Pinna, C.; Yates, J.R. Fatigue crack initiation in AA2024: A coupled micromechanical testing and crystal plasticity study. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 321–338. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Pons, D.J. Crack propagation mechanisms for creep fatigue: A consolidated explanation of fundamental behaviours from initiation to failure. Metals 2018, 8, 623. [Google Scholar] [CrossRef] [Green Version]
- Luo, C.; Chattopadhyay, A. Prediction of fatigue crack initial stage based on a multiscale damage criterion. Int. J. Fatigue 2011, 33, 403–413. [Google Scholar] [CrossRef]
- Luo, C.; Wei, J.; Parra-Garcia, M.; Chattopadhyay, A.; Peralta, P. Fatigue damage prediction in metallic materials based on multiscale modeling. AIAA J. 2009, 47, 2567–2576. [Google Scholar] [CrossRef]
- Luo, C. Multiscale Modeling & Virtual Sensing for Structural Health Monitoring. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2011. [Google Scholar]
- Zhao, N.; Roy, A.; Wang, W.; Zhao, L.; Silberschmidt, V.V. Coupling crystal plasticity and continuum damage mechanics for creep assessment in Cr-based power-plant steel. Mech. Mater. 2019, 130, 29–38. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Xuan, F.Z.; Zhao, P. A dislocation-based constitutive model for the cyclic response of nanolath strengthened steels. Int. J. Mech. Sci. 2019, 155, 475–487. [Google Scholar] [CrossRef]
- Liu, Z.G.; Wong, W.H.; Guo, T.F. Void behaviors from low to high triaxialities: Transition from void collapse to void coalescence. Int. J. Plast. 2016, 84, 183–202. [Google Scholar] [CrossRef]
- Hu, J.D.; Xuan, F.Z.; Liu, C.J. A void growth model of multiaxial power-law creep rupture involving the void shape changes. Int. J. Mech. Sci. 2018, 144, 723–730. [Google Scholar] [CrossRef]
- Wang, T.C.; Shih, C.F.; Needleman, A. Crack growth by grain boundary cavitation in the transient and extensive creep regimes. Int. J. Fract. 1991, 52, 159–189. [Google Scholar] [CrossRef]
- Hu, J.D.; Xuan, F.Z.; Liu, C.J.; Chen, B. Modelling of cavity nucleation under creep-fatigue interaction. Mech. Mater. 2021, 156, 103799. [Google Scholar] [CrossRef]
- Tvergaard, V. On the creep constrained diffusive cavitation of grain boundary facets. J. Mech. Phys. Solids 1984, 32, 373–393. [Google Scholar] [CrossRef]
- Onck, P.; van der Giessen, E. Microstructurally-based modelling of intergranular creep fracture using grain elements. Mech. Mater. 1997, 26, 109–126. [Google Scholar] [CrossRef]
- Onck, P.; van der Giessen, E. Micromechanics of creep fracture: Simulation of intergranular crack growth. Comp. Mater Sci. 1998, 13, 90–102. [Google Scholar] [CrossRef]
- Needleman, A.; Rice, J.R. Plastic Creep Flow Effects in the Diffusive Cavitation of Grain Boundaries. In Perspectives in Creep Fracture; Pergamon: Oxford, UK, 1983; pp. 107–124. [Google Scholar]
- Wen, J.F.; Liu, Y.; Srivastava, A.; Tu, S.T.; Needleman, A. Environmentally enhanced creep crack growth by grain boundary cavitation under cyclic loading. Acta Mater. 2018, 153, 136–146. [Google Scholar] [CrossRef]
- Van der Giessen, E.; Tvergaard, V. Micromechanical studies of cyclic creep fracture under stress-controlled loading. J. Phys. IV 1996, 6, 449–459. [Google Scholar] [CrossRef] [Green Version]
- Messner, M.C.; Truster, T.J.; Cochran, K.B.; Parks, D.M.; Sham, T.L. FY17 Status Report on the Micromechanical Finite Element Modeling of Creep Fracture of Grade 91 Steel; Argonne National Lab. (ANL): Argonne, IL, USA, 2017. [Google Scholar]
- Zhang, W.; Wang, X.; Wang, Y.; Yu, X.; Gao, Y.; Feng, Z. Type IV failure in weldment of creep resistant ferritic alloys: I. Micromechanical origin of creep strain localization in the heat affected zone. J. Mech. Phys. Solids 2020, 134, 103774. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, X.; Wang, Y.; Yu, X.; Gao, Y.; Feng, Z. Type IV failure in weldment of creep resistant ferritic alloys: II. Creep fracture and lifetime prediction. J. Mech. Phys. Solids 2020, 134, 103775. [Google Scholar] [CrossRef]
- Li, K.S.; Wang, R.Z.; Yuan, G.J.; Zhu, S.P.; Zhang, X.C.; Tu, S.T.; Miura, H. A crystal plasticity-based approach for creep-fatigue life prediction and damage evaluation in a nickel-based superalloy. Int. J. Fatigue 2021, 143, 106031. [Google Scholar] [CrossRef]
- Schäfer, B.J.; Sonnweber-Ribic, P.; Hartmaier, A. Micromechanical modeling of fatigue crack nucleation around non-metallic inclusions in martensitic high-strength steels. Metals 2019, 9, 1258. [Google Scholar] [CrossRef] [Green Version]
- Manonukul, A.; Dunne, F. High– and low–cycle fatigue crack initiation using polycrystal plasticity. Proc. R. Soc. Lond. Ser. A. 2004, 460, 1881–1903. [Google Scholar] [CrossRef]
- Li, R.; Yang, G.; Yang, M.X.; Yin, F.S.; Chen, Z. Microstructure and mechanical properties analysis of imported X12CrMoWVNbN10-1-1 steel for turbine. Spec. Steel Technol. 2013, 19, 6–10. [Google Scholar]
- Gaffard, V.; Besson, J.; Gourgues-Lorenzon, A.F. Creep failure model of a tempered martensitic stainless steel integrating multiple deformation and damage mechanisms. Int. J. Fract. 2005, 133, 139–166. [Google Scholar] [CrossRef]
- Tan, J.P.; Tu, S.T.; Wang, G.Z.; Xuan, F.Z. Effect and mechanism of out-of-plane constraint on creep crack growth behavior of a Cr–Mo–V steel. Eng. Fract. Mech. 2013, 99, 324–334. [Google Scholar] [CrossRef]
- Goyal, S.; Laha, K.; Das, C.R.; Panneerselvi, S.; Mathew, M.D. Effect of constraint on creep behavior of 9Cr-1Mo steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2014, 45, 619–632. [Google Scholar] [CrossRef]
- Xu, X.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T. Effects of creep ductility and notch constraint on creep fracture behavior in notched bar specimens. Mater. High Temp. 2016, 33, 198–207. [Google Scholar] [CrossRef]
- Schäfer, B.J.; Sonnweber-Ribic, P.; Hartmaier, A. Micromechanical modelling of the influence of strain ratio on fatigue crack initiation in a martensitic steel-a comparison of different fatigue indicator parameters. Materials 2019, 12, 2852. [Google Scholar] [CrossRef] [Green Version]
- Yuan, G.J.; Zhang, X.C.; Chen, B.; Tu, S.T.; Zhang, C.C. Low-cycle fatigue life prediction of a polycrystalline nickel-base superalloy using crystal plasticity modelling approach. J. Mater. Sci. Technol. 2020, 38, 28–38. [Google Scholar] [CrossRef]
- Darling, K.A.; Rajagopalan, M.; Komarasamy, M.; Bhatia, M.A.; Hornbuckle, B.C.; Mishra, R.S.; Solanki, K.N. Extreme creep resistance in a microstructurally stable nanocrystalline alloy. Nature 2016, 537, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Shi, H. Effects of grain size distribution on the creep damage evolution of polycrystalline materials. J. Phys. D 2010, 43, 6–7. [Google Scholar] [CrossRef]
- Qin, C.H.; Ye, S.; Zhang, X.C.; Tu, S.T. Effects of grain sizes on small fatigue crack growth of GH4169 ni-base alloy. Mater. Mech. Eng. 2016, 40, 11–20. [Google Scholar]
- Bache, M.R. A review of dwell sensitive fatigue in titanium alloys: The role of microstructure, texture and operating conditions. Int. J. Fatigue 2003, 25, 1079–1087. [Google Scholar] [CrossRef]
- Kim, B.J.; Lim, B.S. Effect of creep holding time on the fatigue behavior in P92 steel weldment at high temperature. In Materials Science Forum; Trans Tech Publications Ltd.: Kapellweg, Switzerland, 2005; Volume 475, pp. 4211–4214. [Google Scholar]
- Carroll, L.J.; Cabet, C.; Carroll, M.C.; Wright, R.N. The development of Microstructural damage during high temperature creep–fatigue of a nickel alloy. Int. J. Fatigue 2013, 47, 115–125. [Google Scholar] [CrossRef]


| Category | Parameter | Unit | Value |
|---|---|---|---|
| Elastic modulus | C11 | GPa | 167.2 |
| C12 | GPa | 140.5 | |
| C44 | GPa | 74.9 | |
| Material parameters in flow rule | Reference strain rate, | s−1 | 0.001 |
| Flow rule power law exponent, m | / | 30 | |
| Material parameters in self- and latent-isotropic hardening for the main slip systems | Initial hardening modulus, | MPa | 1340 |
| Initial slip system strength, | MPa | 150 | |
| Critical shear stress, | MPa | 270 | |
| Material parameters in self- and latent-isotropic hardening for the secondary slip systems | Initial hardening modulus, | MPa | 6700 |
| Initial slip system strength, | MPa | 1350 | |
| Critical shear stress, | MPa | 750 | |
| Material parameters in kinematic hardening | Direct hardening coefficient, c | MPa | 5800 |
| Dynamic response coefficient, d | / | 2 | |
| Critical value of FIPp | FIPp,crit | / | 0.23 |
| Parameter | Unit | Value |
|---|---|---|
| Initial cavity radius, | mm | 5 × 10−5 |
| Half initial distance between cavities, | mm | 6 × 10−2 |
| Atomic volume, | m3 | 1.18 × 10−29 |
| Grain boundary diffusion parameter, | mm5/N/min | 4.75 × 10−15 |
| Activation energy for grain boundary diffusion, | kJ/mol | 174 |
| pre-exponent diffusion coefficient, | mm3/s | 1.35 × 10−20 |
| Traction normalization parameter, | MPa | 100 |
| Equilibrium cavity tip half-angle, | ° | 75 |
| Nucleation rate constant, | mm−2 | 5.6 × 10−16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.; Wang, R.-Z.; Shu, Y.; Fei, J.-W.; Wen, J.-F.; Tu, S.-T. Creep-Fatigue Crack Initiation Simulation of a Modified 12% Cr Steel Based on Grain Boundary Cavitation and Plastic Slip Accumulation. Materials 2021, 14, 6565. https://doi.org/10.3390/ma14216565
Jin X, Wang R-Z, Shu Y, Fei J-W, Wen J-F, Tu S-T. Creep-Fatigue Crack Initiation Simulation of a Modified 12% Cr Steel Based on Grain Boundary Cavitation and Plastic Slip Accumulation. Materials. 2021; 14(21):6565. https://doi.org/10.3390/ma14216565
Chicago/Turabian StyleJin, Xin, Run-Zi Wang, Yang Shu, Jia-Wen Fei, Jian-Feng Wen, and Shan-Tung Tu. 2021. "Creep-Fatigue Crack Initiation Simulation of a Modified 12% Cr Steel Based on Grain Boundary Cavitation and Plastic Slip Accumulation" Materials 14, no. 21: 6565. https://doi.org/10.3390/ma14216565
APA StyleJin, X., Wang, R.-Z., Shu, Y., Fei, J.-W., Wen, J.-F., & Tu, S.-T. (2021). Creep-Fatigue Crack Initiation Simulation of a Modified 12% Cr Steel Based on Grain Boundary Cavitation and Plastic Slip Accumulation. Materials, 14(21), 6565. https://doi.org/10.3390/ma14216565







