Cold Rolling Texture Prediction Using Finite Element Simulation with Zooming Analysis
Abstract
:1. Introduction
2. FE Modeling of Cold Rolling Process
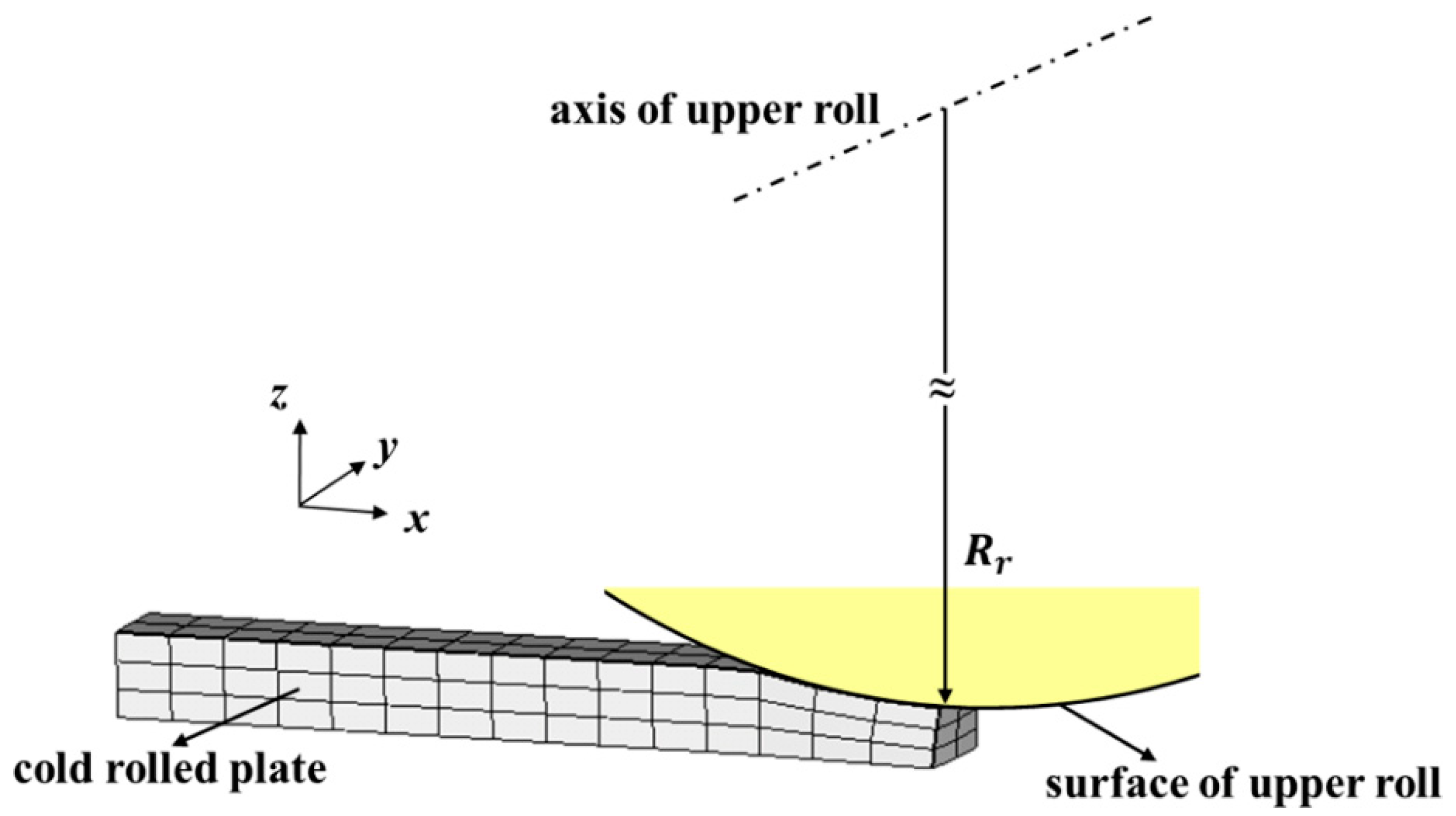
2.1. Modeling of Rolls and Cold-Rolled Plate
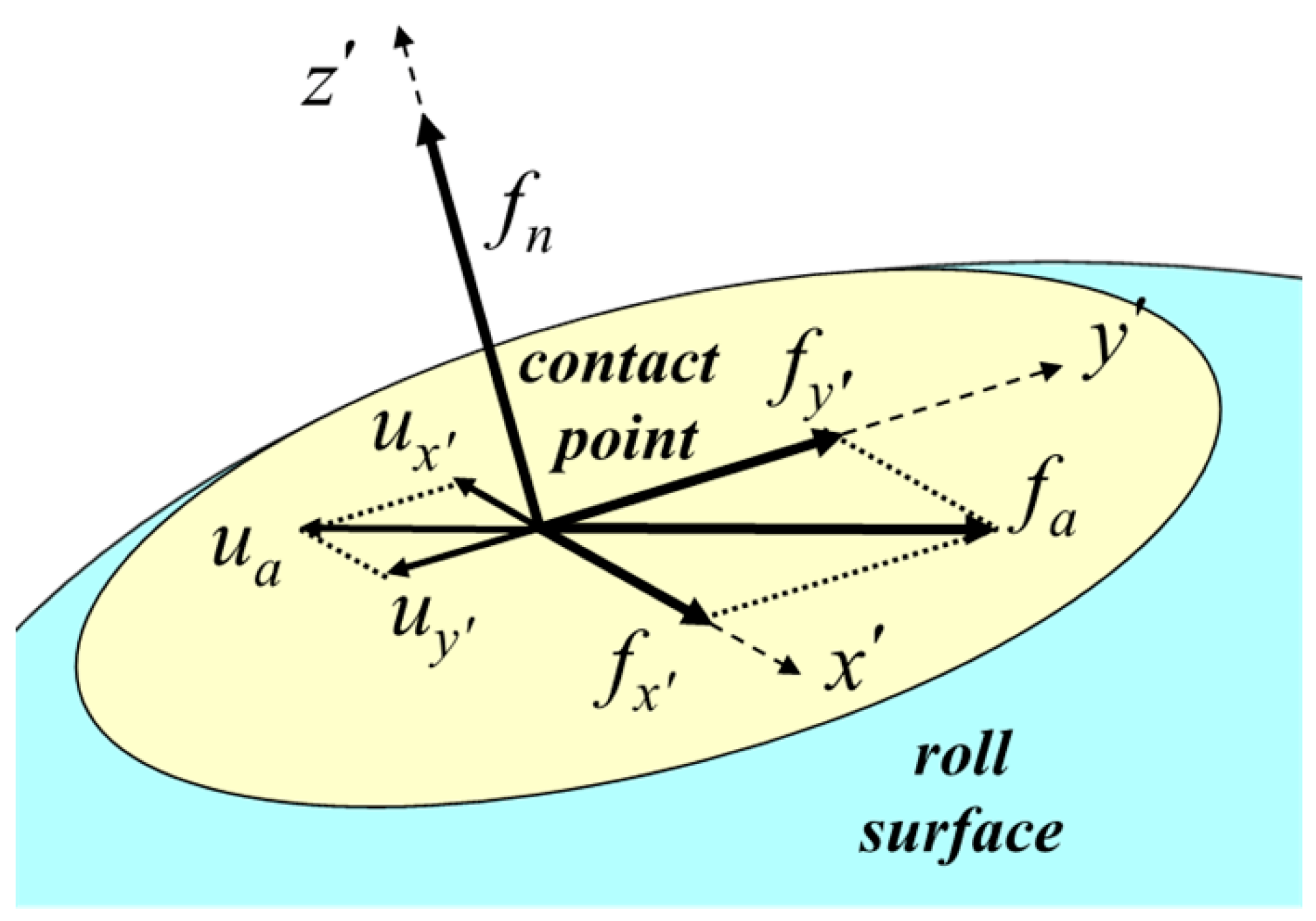
2.2. Modeling of Contact
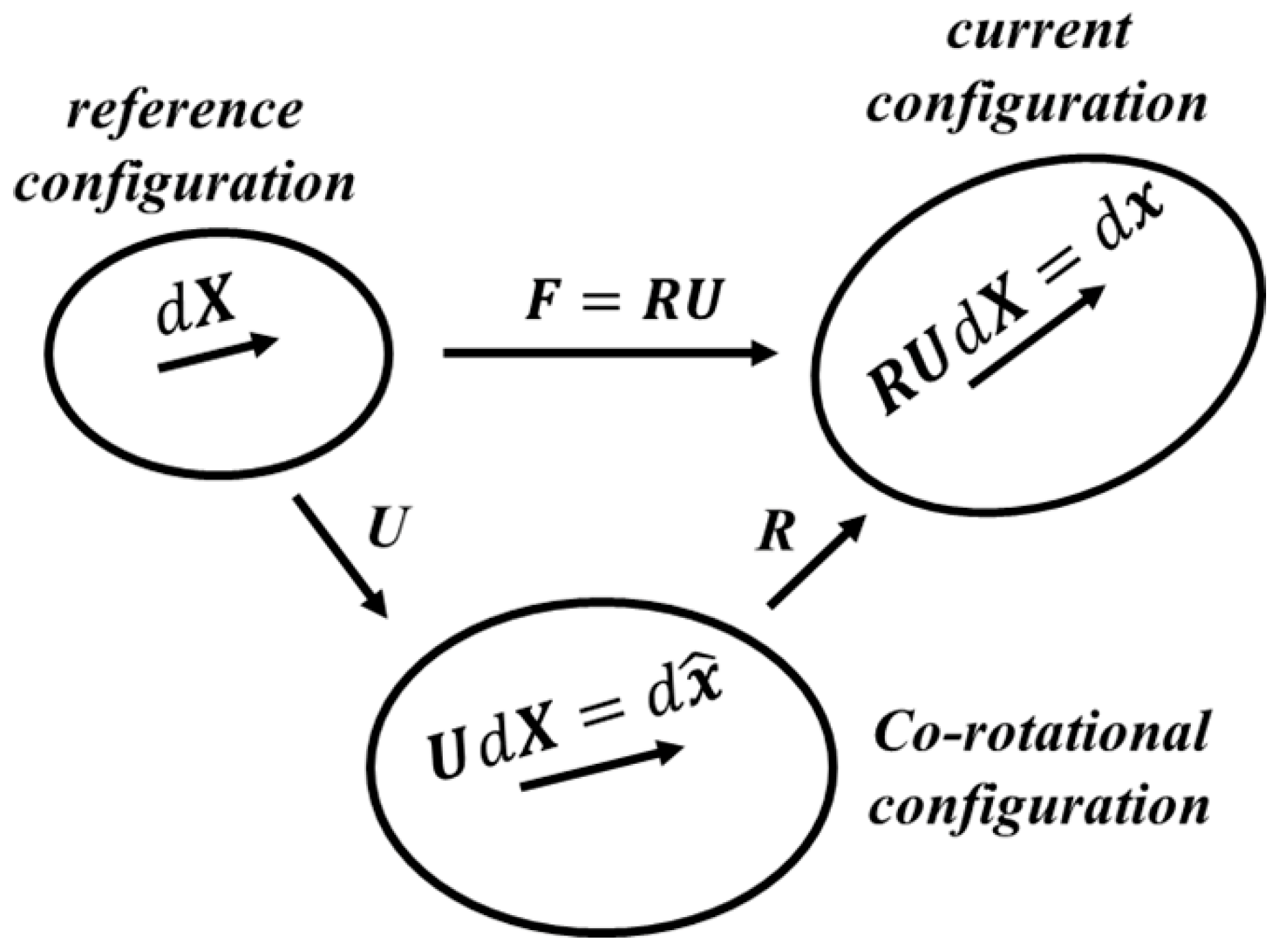
2.3. Co-Rotational Formulation
3. Macro-Scale and Micro-Scale Material Constitutive Modeling
3.1. Macro-Scale Phenomenological Constitutive Model for Stress and Strain Calculation
3.2. Micro-Scale Crystal Plasticity Constitutive Model for Lattice Orientation Calculation
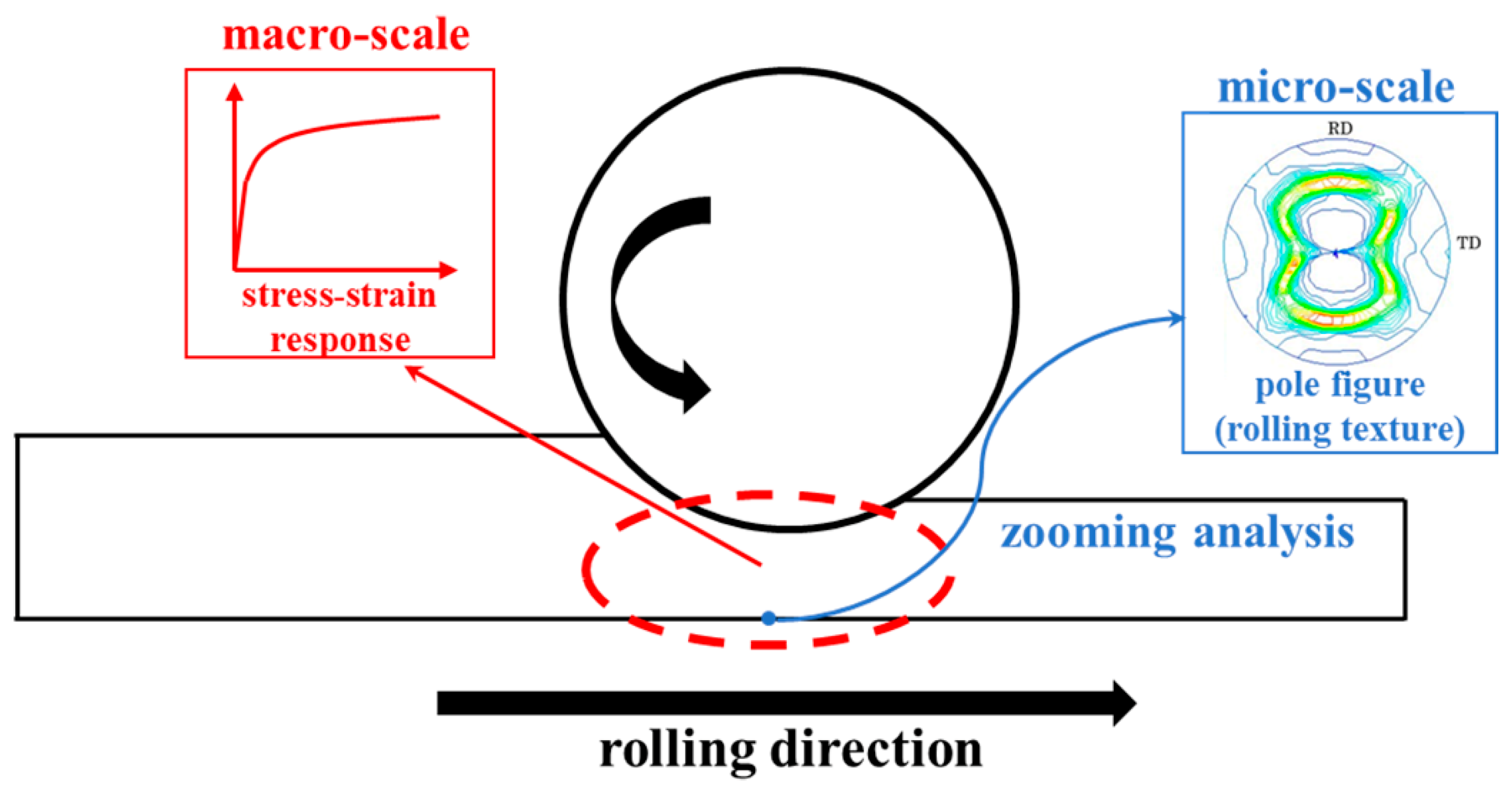
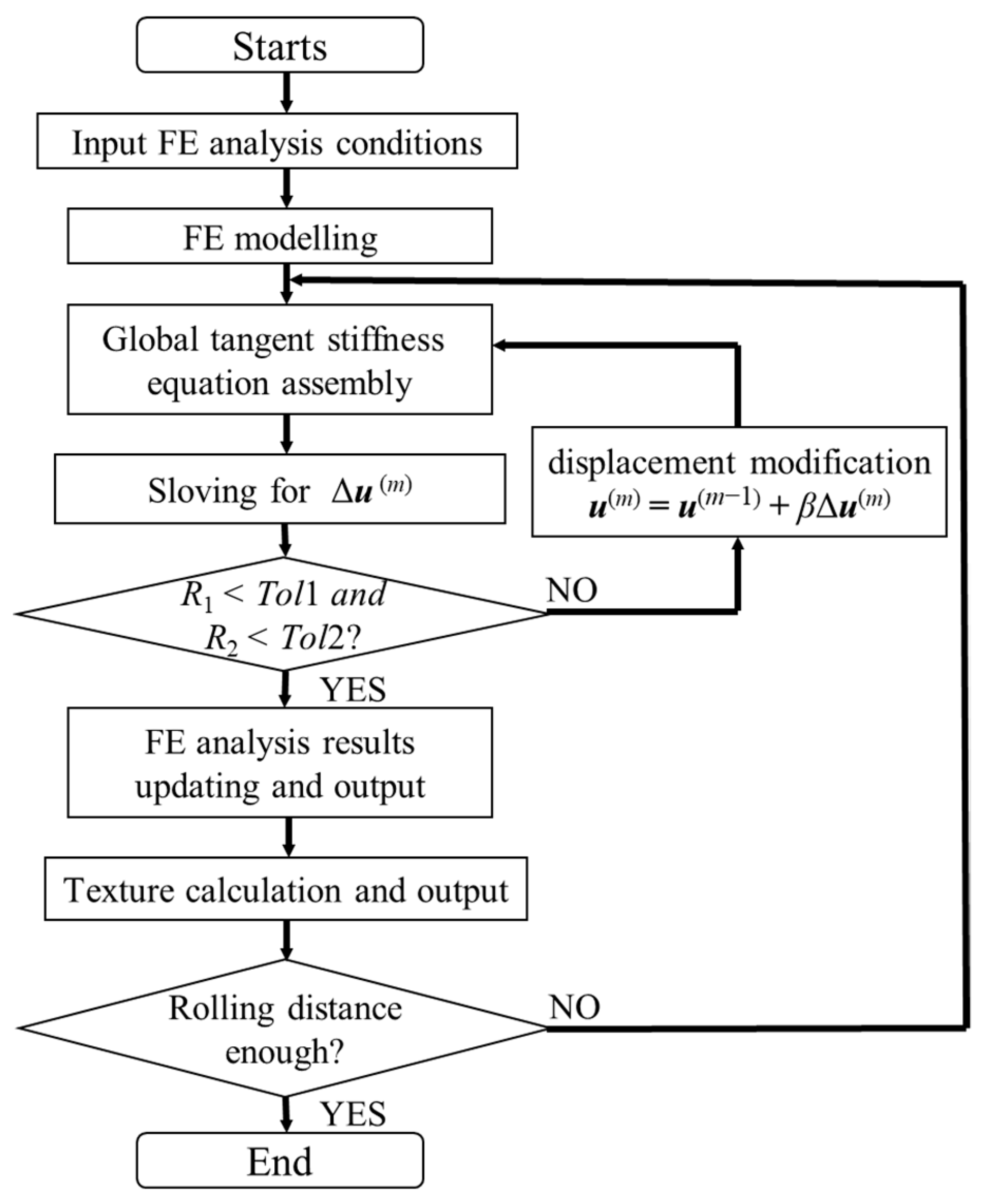
4. FE and Zooming Analysis Method for Cold Rolling Texture Prediction
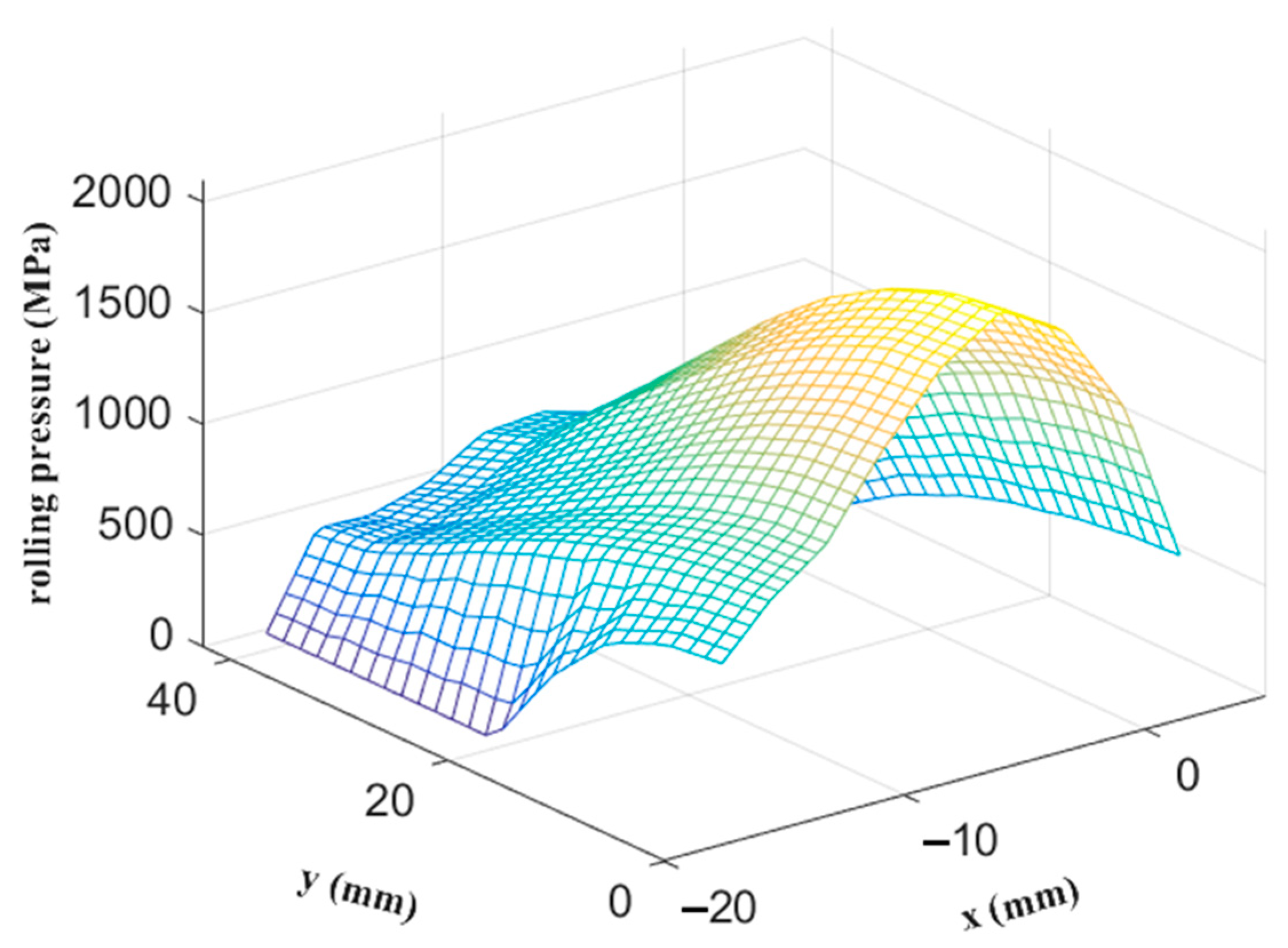
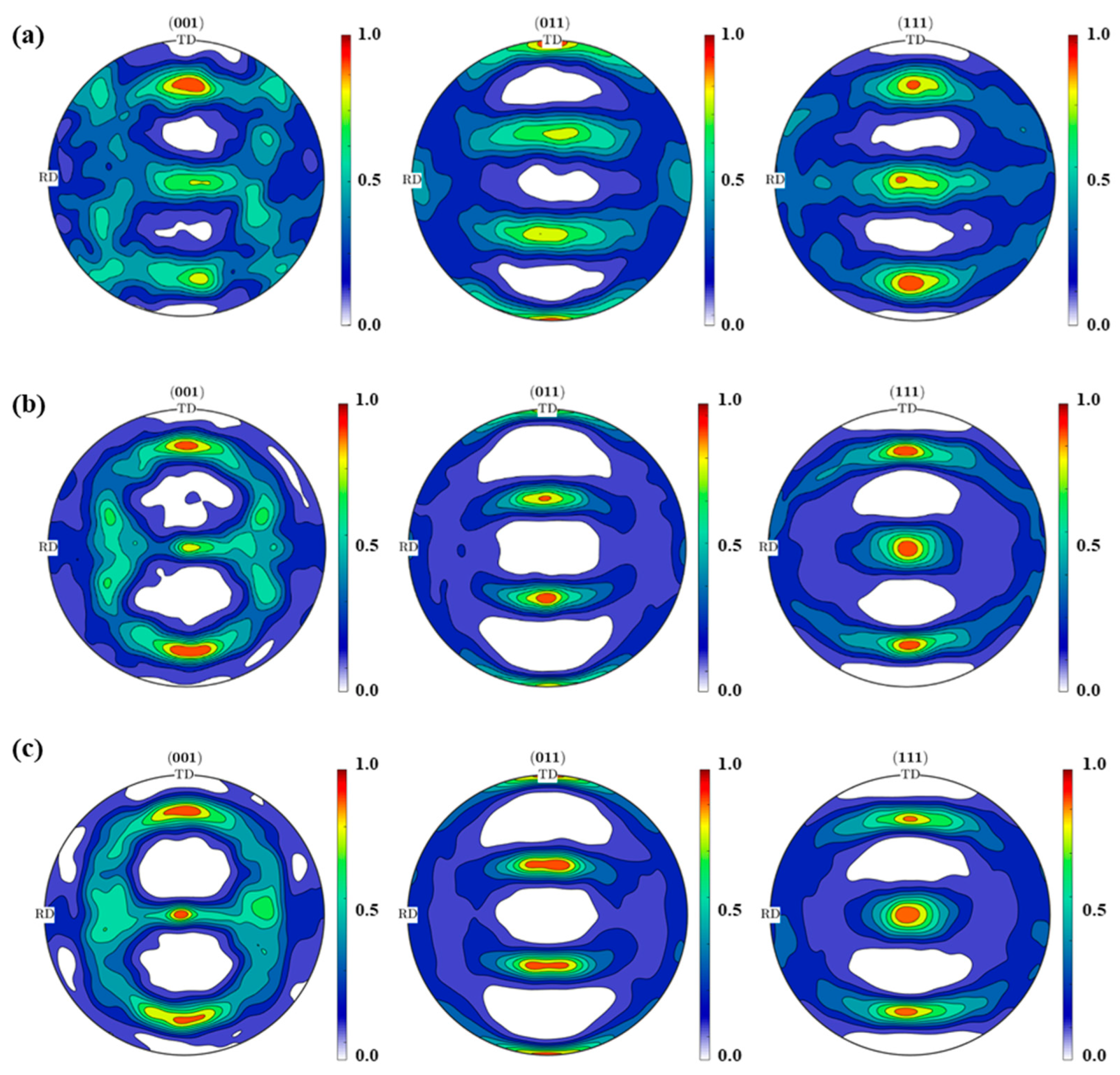
5. Validation of Current Analysis Framework
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
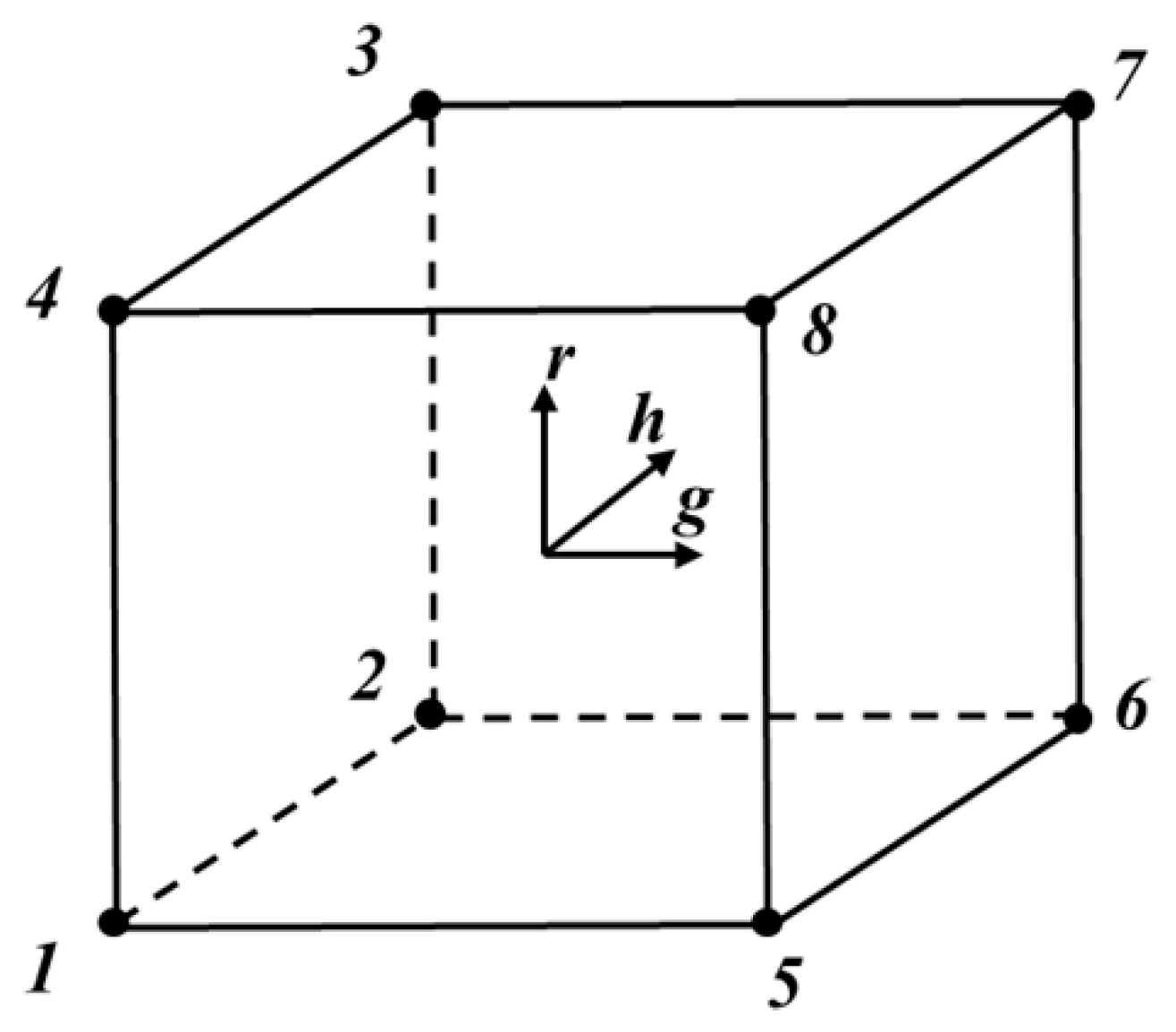
Appendix A. Shape Function of the First-Order Brick Element
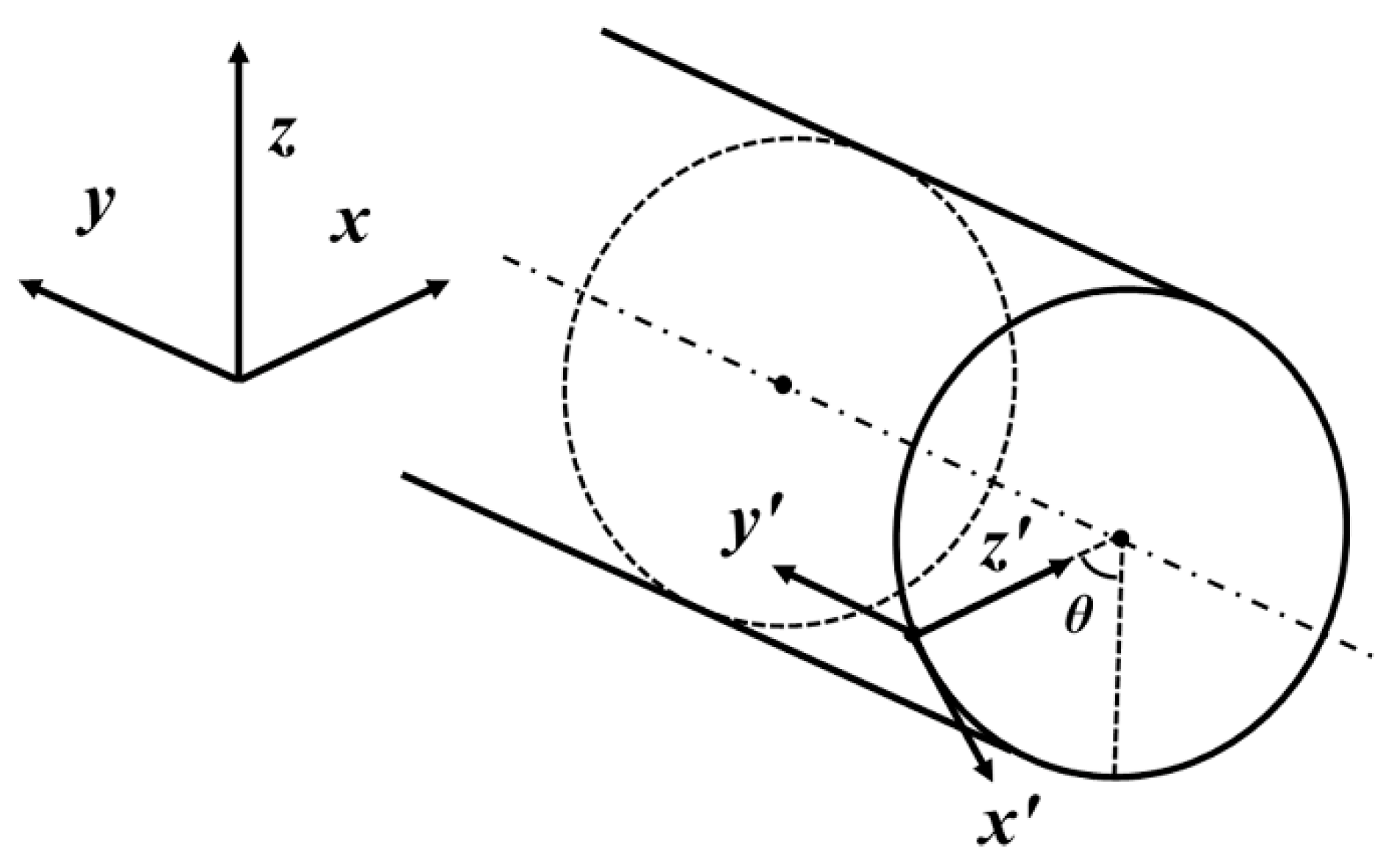
Appendix B. Local Coordinate System for Contact Calculation
References
- Pustovoytov, D.; Pesin, A.; Tandon, P. Asymmetric (Hot, Warm, Cold, Cryo) Rolling of Light Alloys: A Review. Metals 2021, 11, 956. [Google Scholar] [CrossRef]
- Mo, T.; Chen, Z.; Zhou, Z.; Liu, J.; He, W.; Liu, Q. Enhancing of mechanical properties of rolled 1100/7075 Al alloys laminated metal composite by thermomechanical treatments. Mater. Sci. Eng. A 2021, 800, 140313. [Google Scholar] [CrossRef]
- Wang, H.; Wu, B.; Higuchi, T.; Yanagimoto, J. Tension Leveling Using Finite Element Analysis with Different Constitutive Relations. ISIJ Int. 2020, 60, 1273–1283. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Ito, K.; Mori, N.; Oya, T.; Taylor, T.; Yanagimoto, J. Constitutive Equations Based on Non-associated Flow Rule for the Analysis of Forming of Anisotropic Sheet Metals. Int. J. Precis. Eng. Manuf. Technol. 2020, 7, 465–480. [Google Scholar] [CrossRef]
- Friedman, P.A.; Pan, J. Effects of plastic anisotropy and yield criteria on prediction of forming limit curves. Int. J. Mech. Sci. 2000, 42, 29–48. [Google Scholar] [CrossRef]
- Tekkaya, A.E.; Allwood, J.M.; Bariani, P.F.; Bruschi, S.; Cao, J.; Gramlich, S.; Groche, P.; Hirt, G.; Ishikawa, T.; Löbbe, C.; et al. Metal forming beyond shaping: Predicting and setting product properties. CIRP Ann. -Manuf. Technol. 2015, 64, 629–653. [Google Scholar] [CrossRef]
- Bate, P.S.; Quinta da Fonseca, J. Texture development in the cold rolling of IF steel. Mater. Sci. Eng. A 2004, 380, 365–377. [Google Scholar] [CrossRef]
- Yanagimoto, J. FE-based analysis for the prediction of inner microstructure in metal forming. Model. Simul. Mater. Sci. Eng. 2002, 10, R111–R134. [Google Scholar] [CrossRef]
- Morimoto, T.; Yoshida, F.; Kusumoto, Y.; Yanagida, A. Development of Recrystallization Texture Prediction Method Linking with Deformation Texture Prediction Model. ISIJ Int. 2012, 52, 592–600. [Google Scholar] [CrossRef]
- Das, A. Calculation of Crystallographic Texture of BCC Steels During Cold Rolling. J. Mater. Eng. Perform. 2017, 26, 2708–2720. [Google Scholar] [CrossRef]
- Fujita, N.; Igi, S.; Diehl, M.; Roters, F.; Raabe, D. The through-process texture analysis of plate rolling by coupling finite element and fast Fourier transform crystal plasticity analysis. Model. Simul. Mater. Sci. Eng. 2019, 27, 085005. [Google Scholar] [CrossRef]
- Després, A.; Zecevic, M.; Lebensohn, R.A.; Mithieux, J.D.; Chassagne, F.; Sinclair, C.W. Contribution of intragranular misorientations to the cold rolling textures of ferritic stainless steels. Acta Mater. 2020, 182, 184–196. [Google Scholar] [CrossRef]
- Amini, A.M.; Dureisseix, D.; Cartraud, P. Multi-scale domain decomposition method for large-scale structural analysis with a zooming technique: Application to plate assembly. Int. J. Numer. Methods Eng. 2009, 79, 417–443. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, T.; Okuda, H. Zooming method for FEA using a neural network. Comput. Struct. 2021, 247, 106480. [Google Scholar] [CrossRef]
- Llau, A.; Jason, L.; Dufour, F.; Baroth, J. Adaptive zooming method for the analysis of large structures with localized nonlinearities. Finite Elem. Anal. Des. 2015, 106, 73–84. [Google Scholar] [CrossRef]
- Katagiri, H.; Sano, H.; Semba, K.; Mimura, N.; Yamada, T. Fast Calculation of AC Copper Loss for High Speed Machines by Zooming Method. IEEJ J. Ind. Appl. 2017, 6, 395–400. [Google Scholar] [CrossRef] [Green Version]
- Wriggers, P. Contact Boundary Value Problem and Weak Form. In Computational Contact Mechanics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 109–156. [Google Scholar]
- Kobayashi, S.; Oh, S.-I.; Altan, T. Metal Forming and the Finite-Element Method; Oxford University Press: New York, NY, USA, 1989; ISBN 9780195044027. [Google Scholar]
- Yanagimoto, J.; Nakano, M.; Higuchi, T.; Izumi, R.; Wang, F. Elastic-Plastic Finite Element Analysis of Sheet Rolling Using Co-Rotational Formulation. Steel Res. Int. 2006, 77, 576–582. [Google Scholar] [CrossRef]
- Pham, Q.T.; Lee, M.-G.; Kim, Y.-S. New procedure for determining the strain hardening behavior of sheet metals at large strains using the curve fitting method. Mech. Mater. 2021, 154, 103729. [Google Scholar] [CrossRef]
- Hemmerich, E.; Rolfe, B.; Hodgson, P.D.; Weiss, M. The effect of pre-strain on the material behaviour and the Bauschinger effect in the bending of hot rolled and aged steel. Mater. Sci. Eng. A 2011, 528, 3302–3309. [Google Scholar] [CrossRef]
- Taylor, G.I. The distortion of crystals of aluminium under compression. Part II.—Distortion by double slipping and changes in orientation of crystals axes during compression. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1927, 116, 16–38. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, H. Polycrystal Plasticity. Trans. Jpn. Soc. Mech. Eng. Ser. A 1999, 65, 201–209. [Google Scholar] [CrossRef]
- Chapuis, A.; Liu, Q. Simulations of texture evolution for HCP metals: Influence of the main slip systems. Comput. Mater. Sci. 2015, 97, 121–126. [Google Scholar] [CrossRef]
- Zhang, Y. Solving large-scale linear programs by interior-point methods under the Matlab ∗ Environment †. Optim. Methods Softw. 1998, 10, 1–31. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Tieu, A.K. Modelling of the rolling processes by a 3-D rigid plastic/visco-plastic finite element method with shifted ICCG method. Comput. Struct. 2001, 79, 2727–2740. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Y.; Zhang, Z.; Zhong, W. A new reduced integration solid-shell element based on EAS and ANS with hourglass stabilization. Int. J. Numer. Methods Eng. 2015, 104, 805–826. [Google Scholar] [CrossRef]
- Richelsen, A.B.; Tvergaard, V. 3D Analysis of cold rolling using a constitutive model for interface friction. Int. J. Mech. Sci. 2004, 46, 653–671. [Google Scholar] [CrossRef]
- Du, C.; Maresca, F.; Geers, M.G.D.; Hoefnagels, J.P.M. Ferrite slip system activation investigated by uniaxial micro-tensile tests and simulations. Acta Mater. 2018, 146, 314–327. [Google Scholar] [CrossRef]
- Lee, D.N.; Oh, K.H. Calculation of plastic strain ratio from the texture of cubic metal sheet. J. Mater. Sci. 1985, 20, 3111–3118. [Google Scholar] [CrossRef]
- Daniel, D.; Jonas, J.J. Measurement and prediction of plastic anisotropy in deep-drawing steels. Metall. Trans. A 1990, 21, 331–343. [Google Scholar] [CrossRef]



| Material | S45C |
|---|---|
| Roll radius | 180 mm |
| Plate dimensions | 320 mm (length) × 84 mm (width) × 6 mm (thickness) |
| Plate mesh size | 2.00 mm (length) × 5.25 mm (width) × 1.00 mm (thickness) |
| Thickness reduction | 28.33% |
| Young’s modulus | 210 GPa |
| Poisson’s ratio | 0.3 |
| Flow stress | MPa |
| Friction coefficient | 0.3 |
| Width Spread Ratio | Rolling Force | Rolling Torque | |
|---|---|---|---|
| Experiment | 1.19% | 2058 kN | 17.7 kN·m |
| Simulation | 1.19% | 1870 kN | 13.8 kN·m |
| {110}<111> | {112}<111> | {123}<111> | |
|---|---|---|---|
| ( 1 1 0)[−1 1 1] | ( 1 1 2)[−1−1 1] | ( 1 2 3)[ 1 1−1] | ( 2 3 1)[ 1−1 1] |
| ( 1 1 0)[ 1−1 1] | (−1−1 2)[ 1 1 1] | (−1 2 3)[ 1−1 1] | (−2 3 1)[ 1 1−1] |
| (−1 1 0)[ 1 1−1] | (−1 1 2)[ 1−1 1] | ( 1−2 3)[−1 1 1] | ( 2−3 1)[ 1 1 1] |
| (−1 1 0)[ 1 1 1] | ( 1−1 2)[−1 1 1] | ( 1 2−3)[ 1 1 1] | ( 2 3−1)[−1 1 1] |
| ( 1 0 1)[ 1 1−1] | ( 1 2 1)[−1 1−1] | ( 2 1 3)[ 1 1−1] | ( 3 2 1)[−1 1 1] |
| ( 1 0 1)[−1 1 1] | (−1 2−1)[ 1 1 1] | (−2 1 3)[ 1−1 1] | (−3 2 1)[ 1 1 1] |
| (−1 0 1)[ 1−1 1] | ( 1 2−1)[ 1 1 1] | ( 2−1 3)[−1 1 1] | ( 3−2 1)[ 1 1−1] |
| (−1 0 1)[ 1 1 1] | (−1 1 2)[ 1 1−1] | ( 2 1−3)[ 1 1 1] | ( 3 2−1)[ 1−1 1] |
| ( 0 1 1)[ 1 1−1] | ( 2 1 1)[ 1−1−1] | ( 1 3 2)[ 1−1 1] | ( 3 1 2)[−1 1 1] |
| ( 0 1 1)[ 1−1 1] | ( 2−1−1)[ 1 1 1] | (−1 3 2)[ 1 1−1] | (−3 1 2)[ 1 1 1] |
| ( 0−1 1)[ 1 1 1] | ( 2−1 1)[ 1 1−1] | ( 1−3 2)[ 1 1 1] | ( 3−1 2)[ 1 1−1] |
| ( 0−1 1)[−1 1 1] | ( 2 1−1)[ 1−1 1] | ( 1 3−2)[−1 1 1] | ( 3 1−2)[ 1−1 1] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Ding, S.; Taylor, T.; Yanagimoto, J. Cold Rolling Texture Prediction Using Finite Element Simulation with Zooming Analysis. Materials 2021, 14, 6909. https://doi.org/10.3390/ma14226909
Wang H, Ding S, Taylor T, Yanagimoto J. Cold Rolling Texture Prediction Using Finite Element Simulation with Zooming Analysis. Materials. 2021; 14(22):6909. https://doi.org/10.3390/ma14226909
Chicago/Turabian StyleWang, Honghao, Sheng Ding, Tom Taylor, and Jun Yanagimoto. 2021. "Cold Rolling Texture Prediction Using Finite Element Simulation with Zooming Analysis" Materials 14, no. 22: 6909. https://doi.org/10.3390/ma14226909





