Identification of the Fractional Zener Model Parameters for a Viscoelastic Material over a Wide Range of Frequencies and Temperatures
Abstract
:1. Introduction
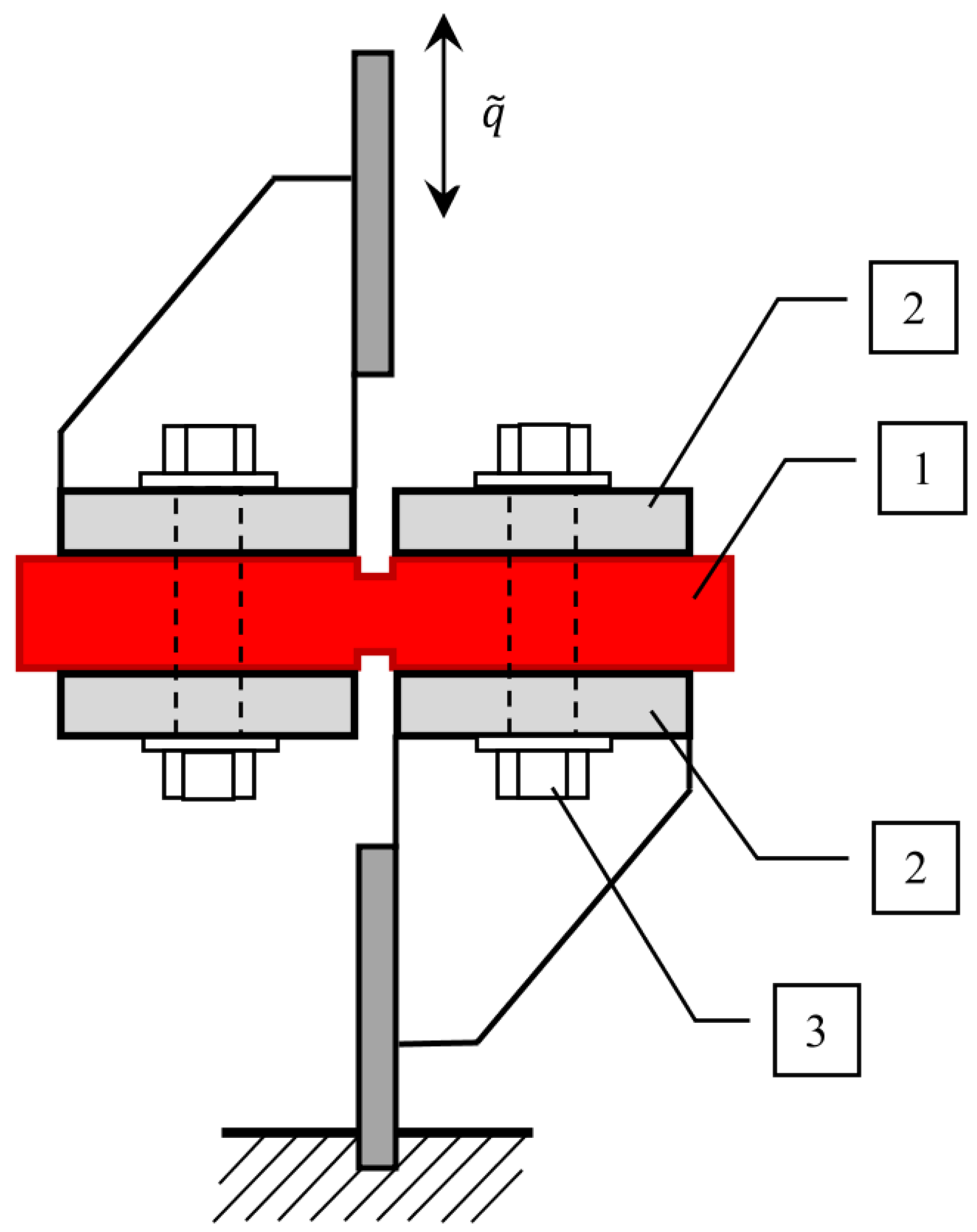
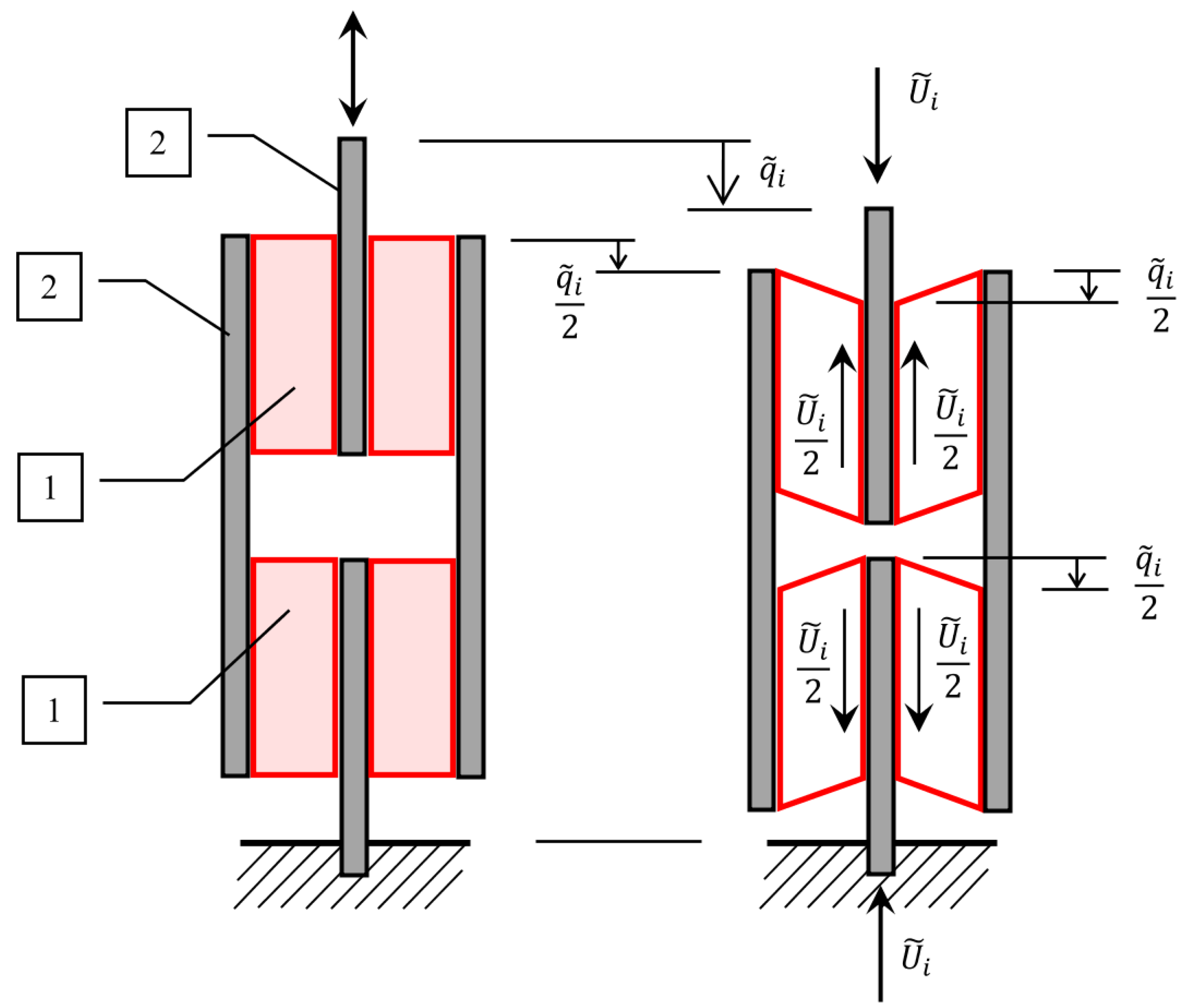
2. Materials and Methods
2.1. Description of the Viscoelastic Material Properties
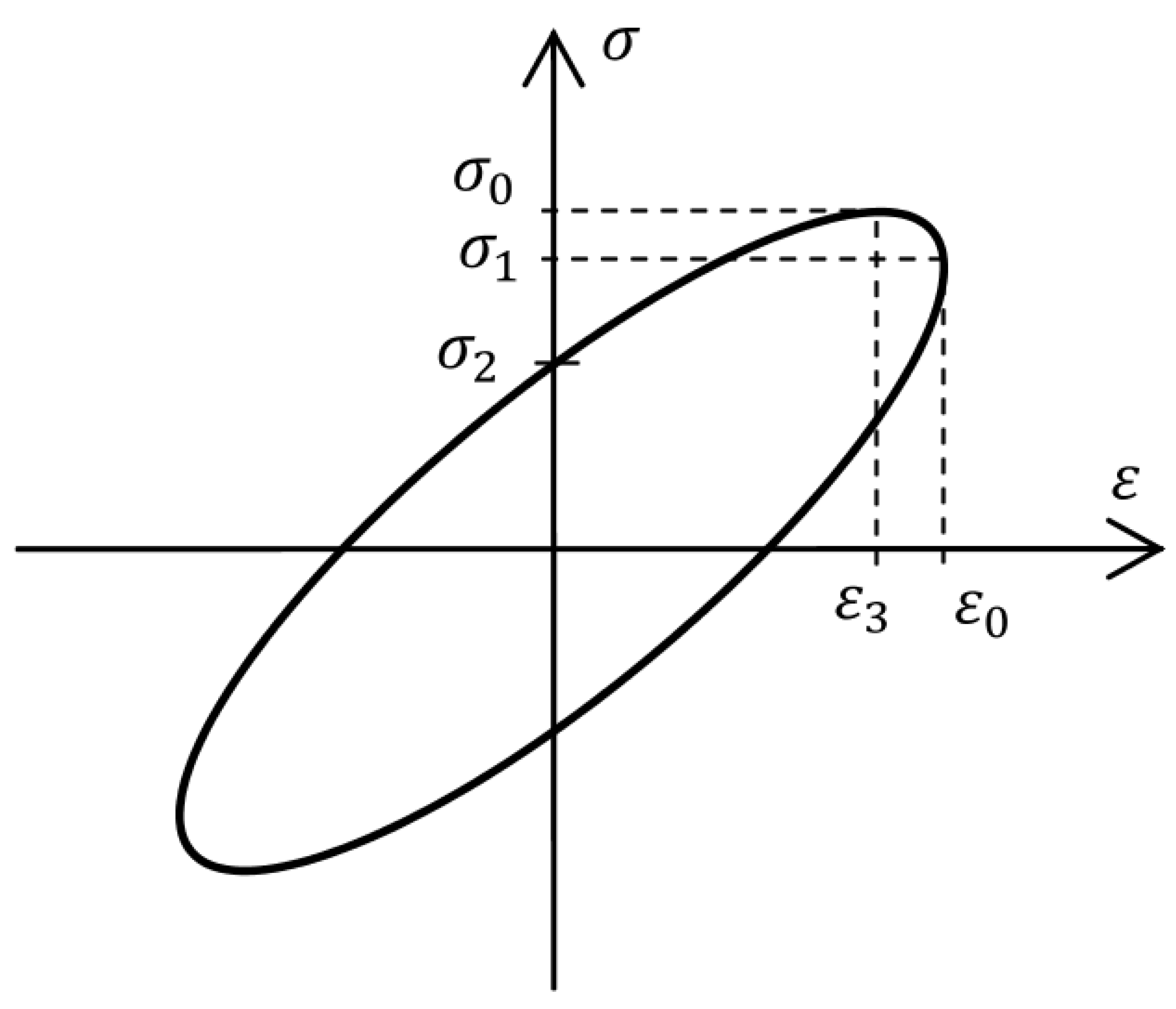
2.1.1. Hysteresis Loop
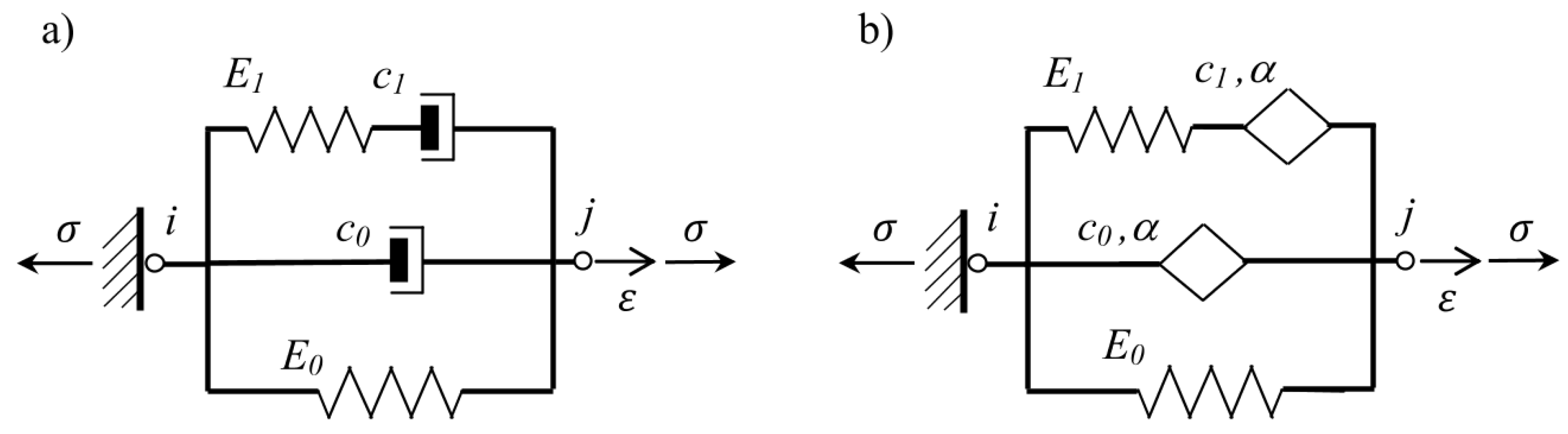
2.1.2. Rheological Model of VE Material
2.1.3. Complex Modulus
- for the fractional Kelvin model:
- for the fractional Maxwell model:
2.2. Identification Method
2.2.1. Functional Relationships for the Zener Model
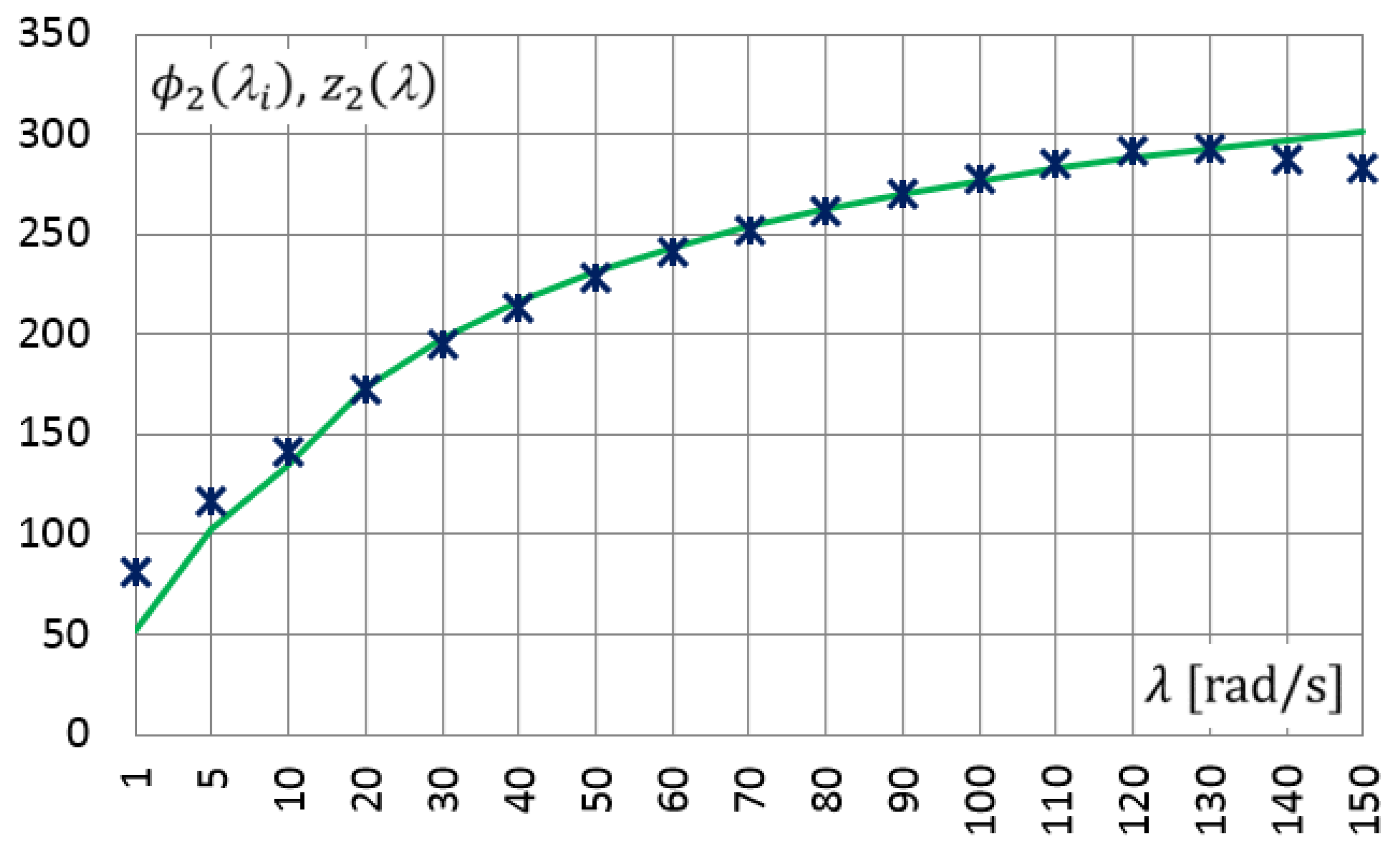
2.2.2. Experimental Data Approximation
2.2.3. Functional Relations for Measured Data
2.2.4. Identification of Model Parameters
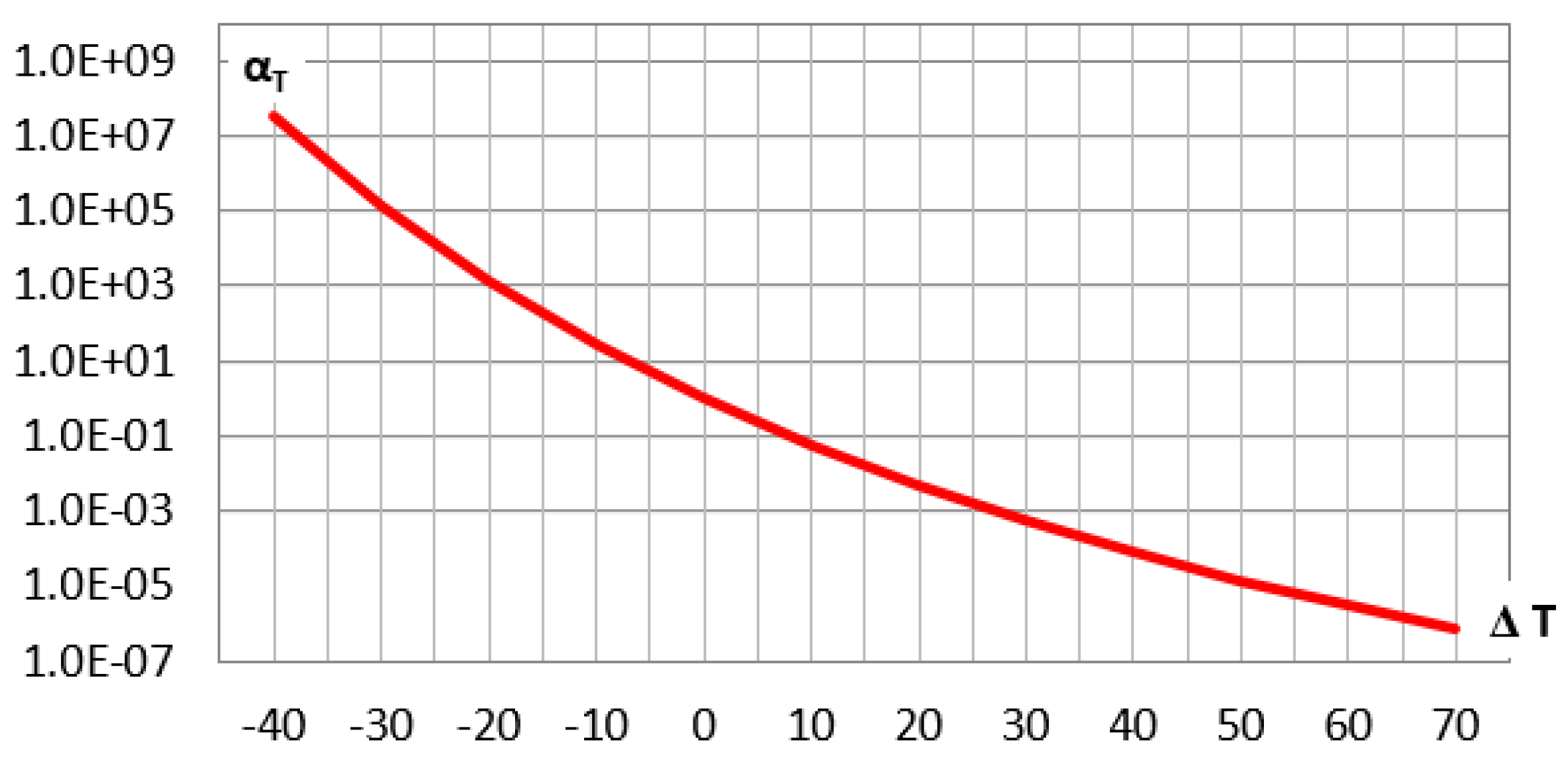
2.3. Temperature Influence
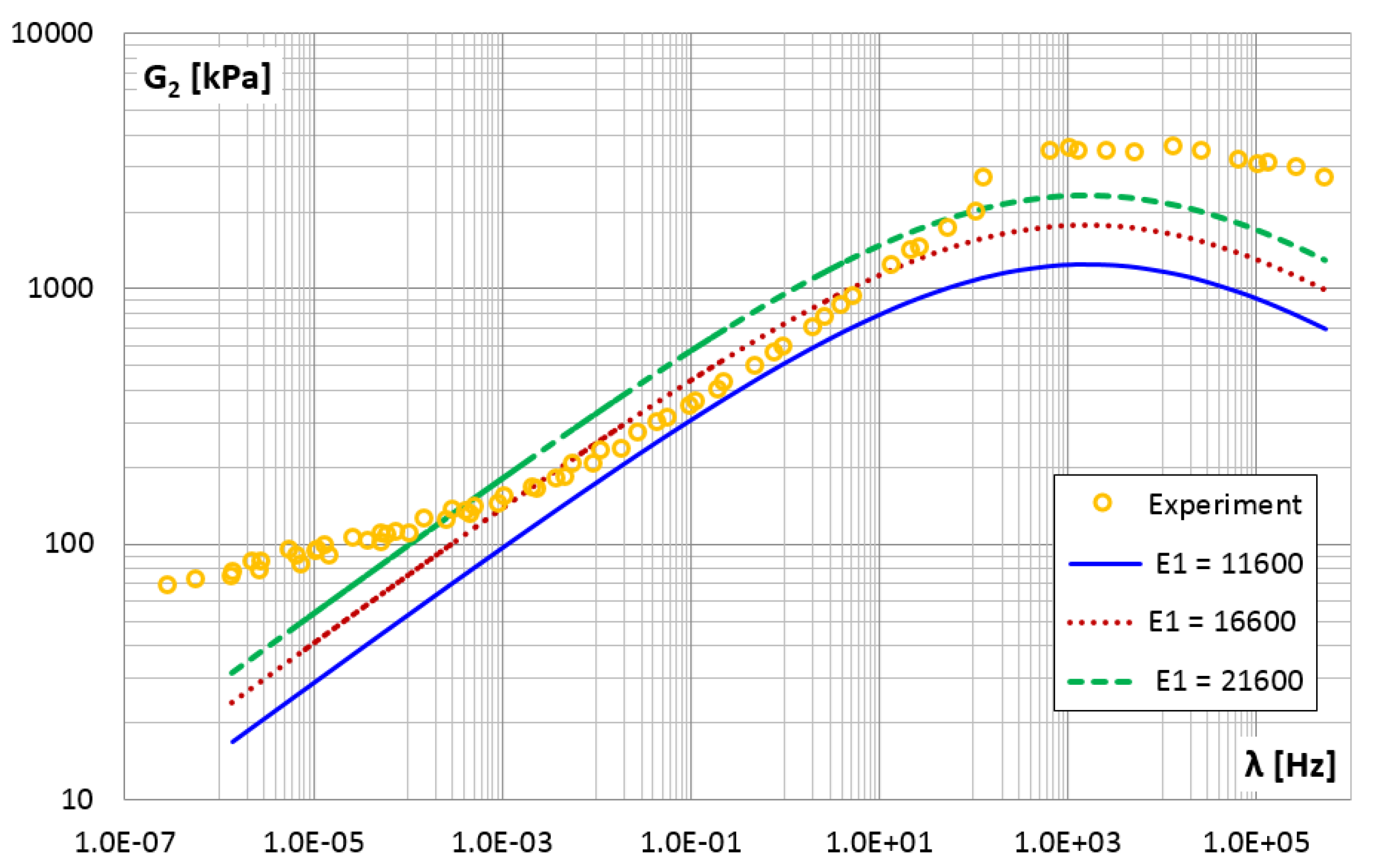
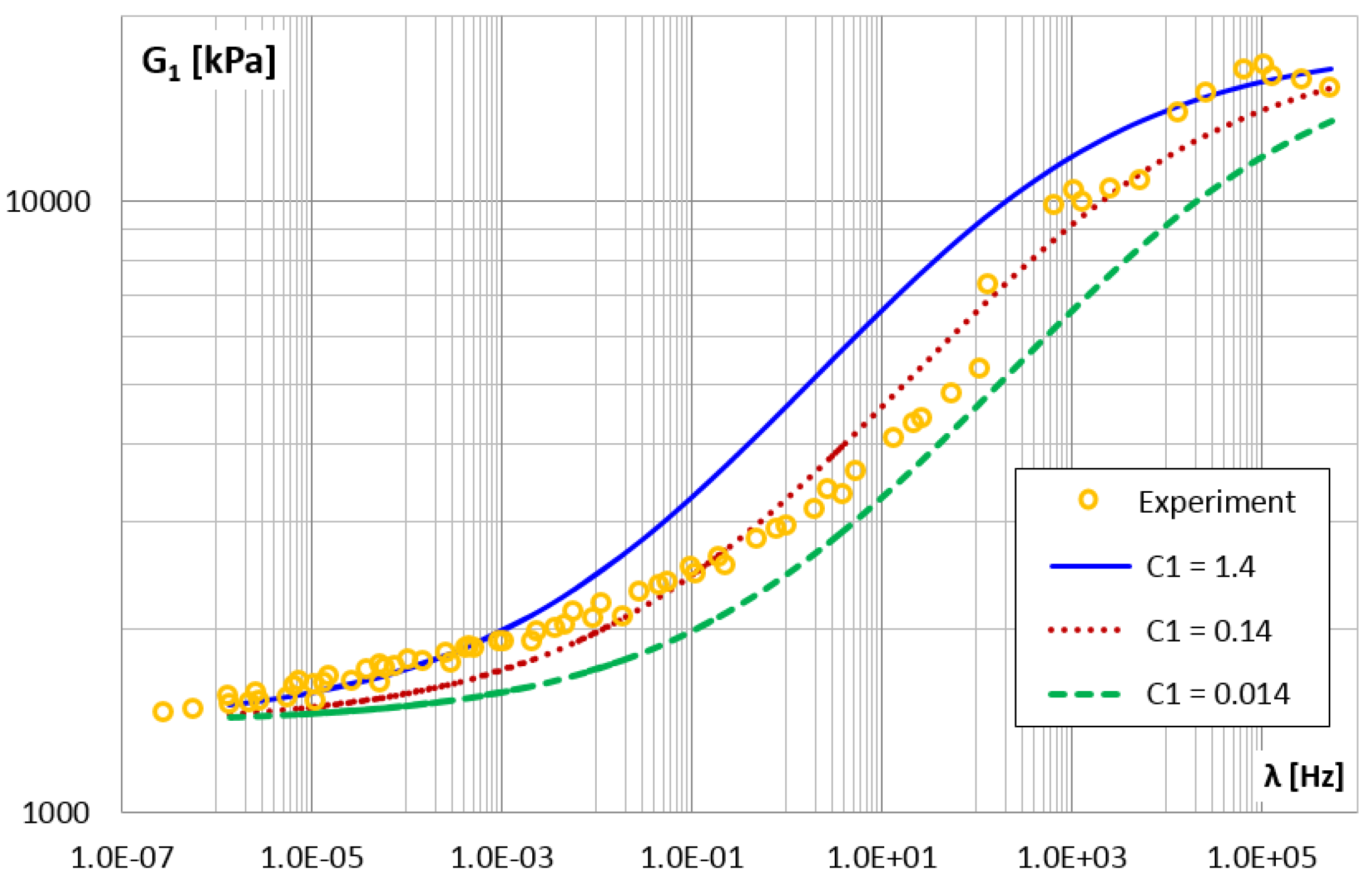
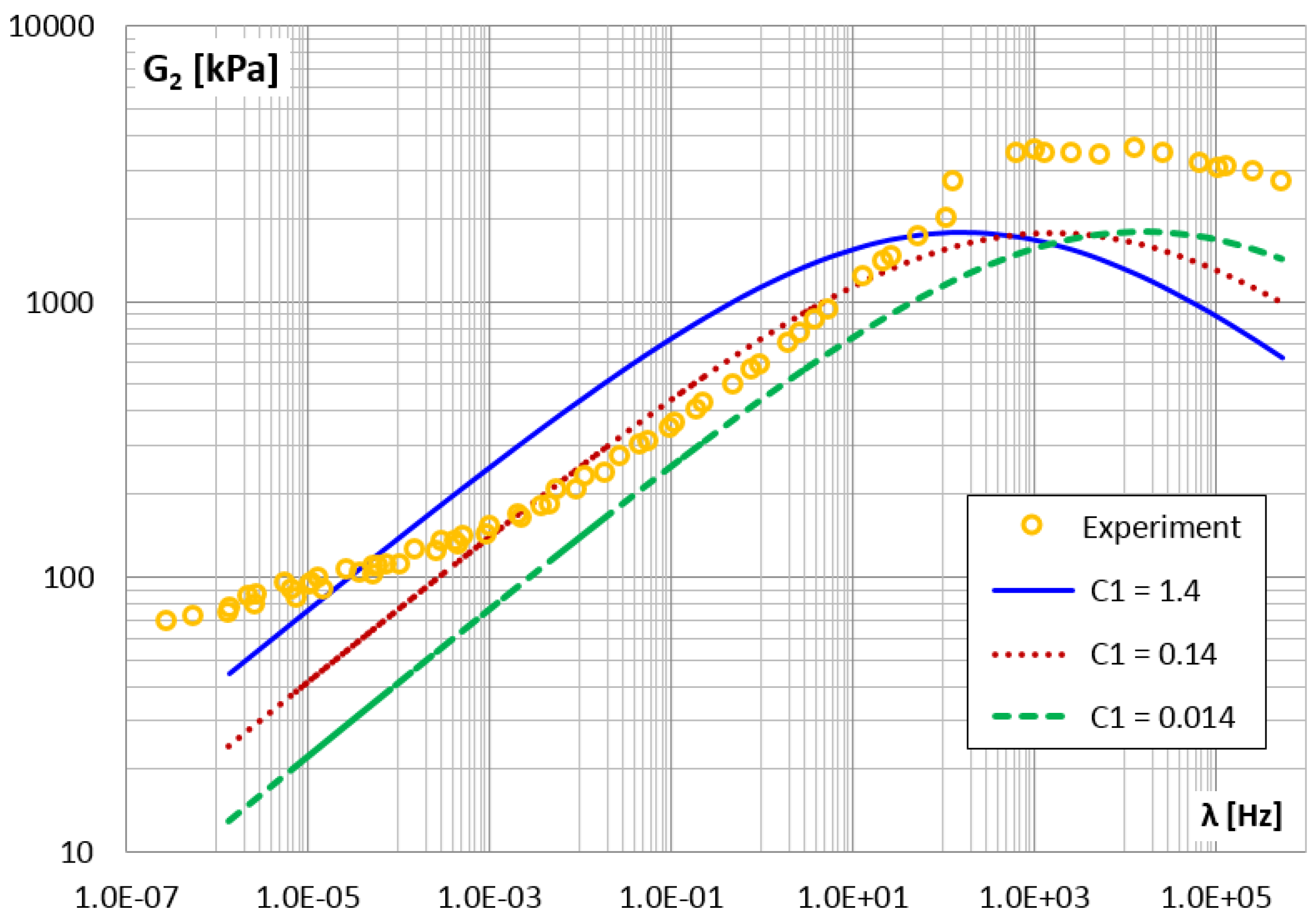
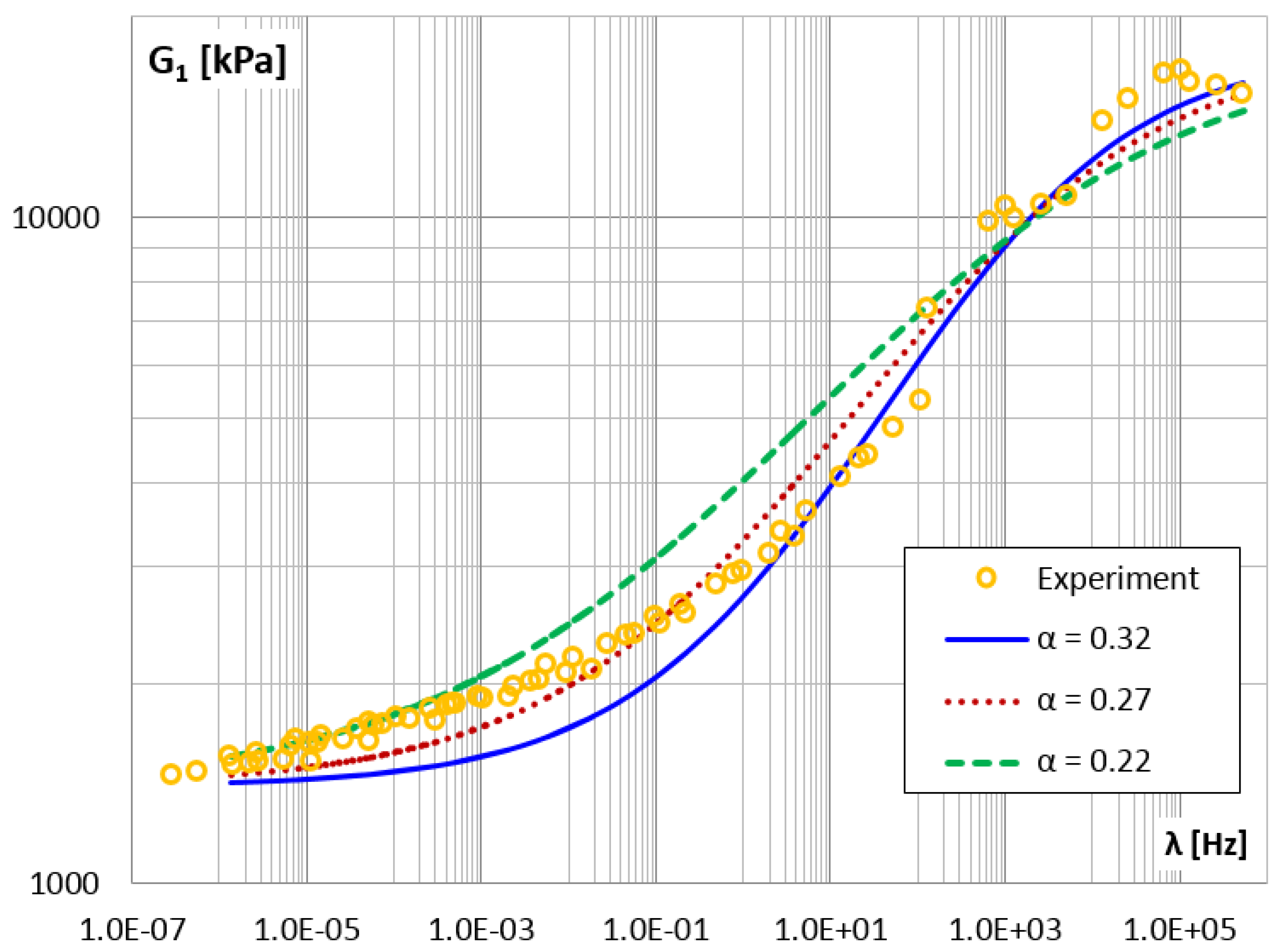
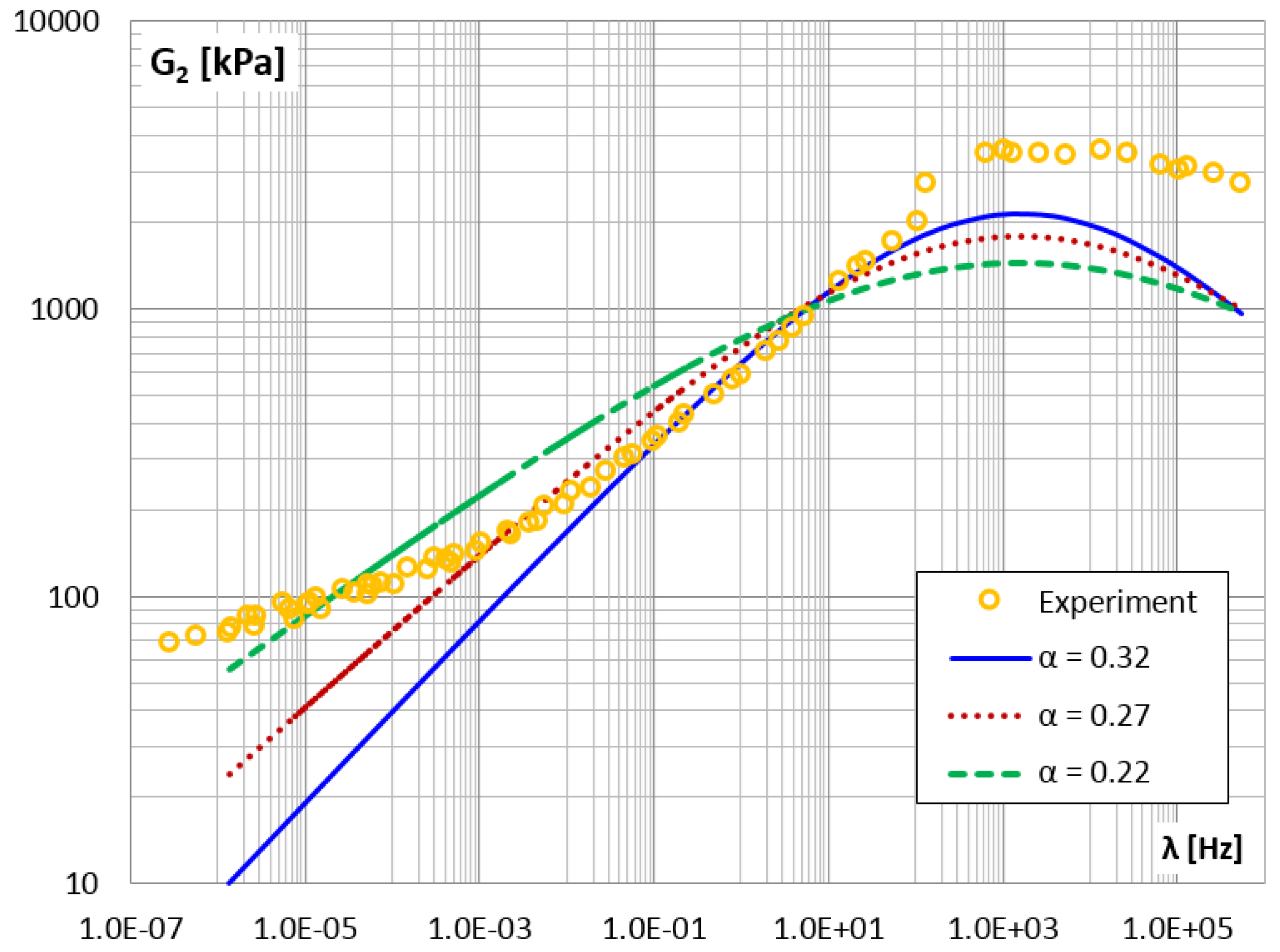
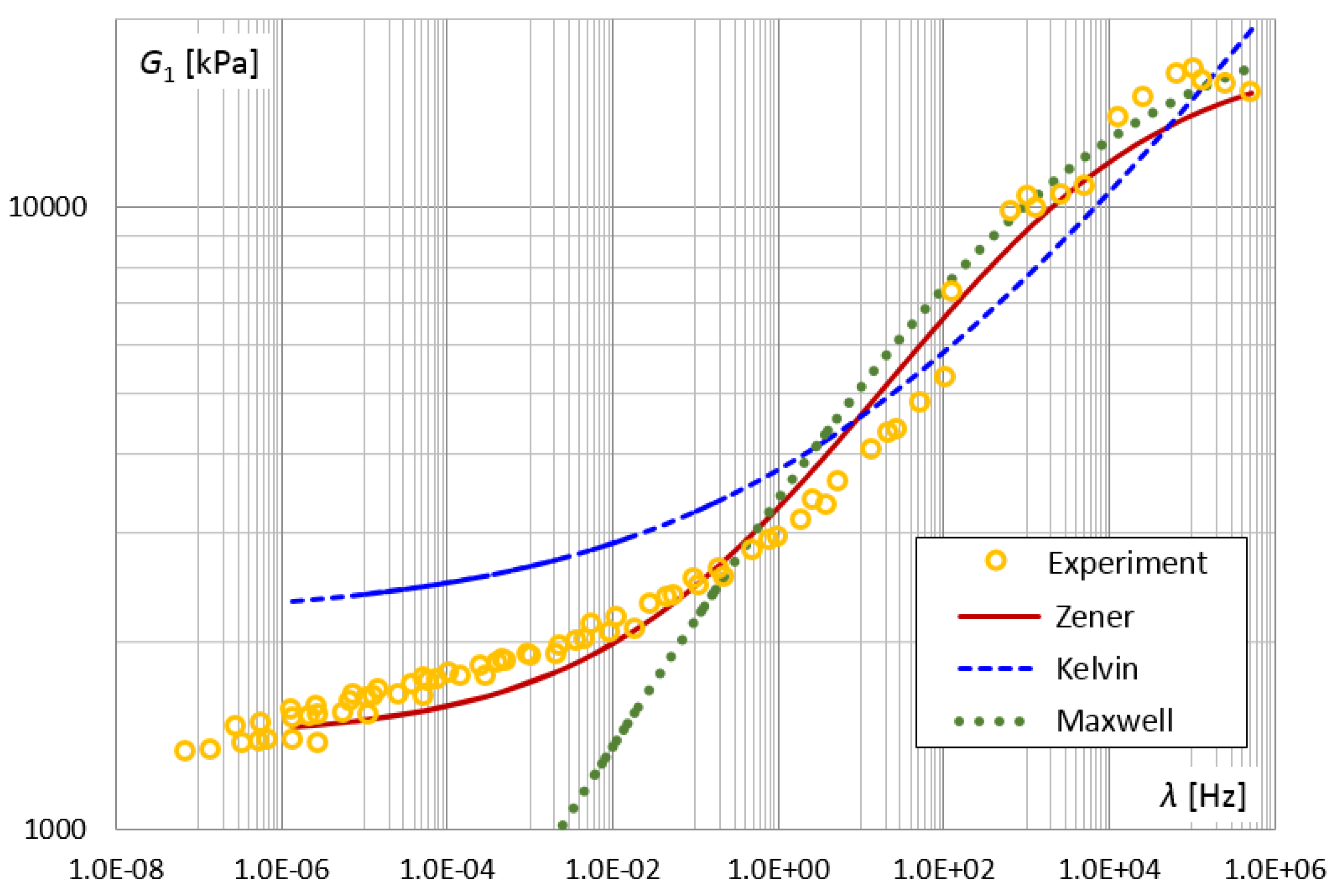
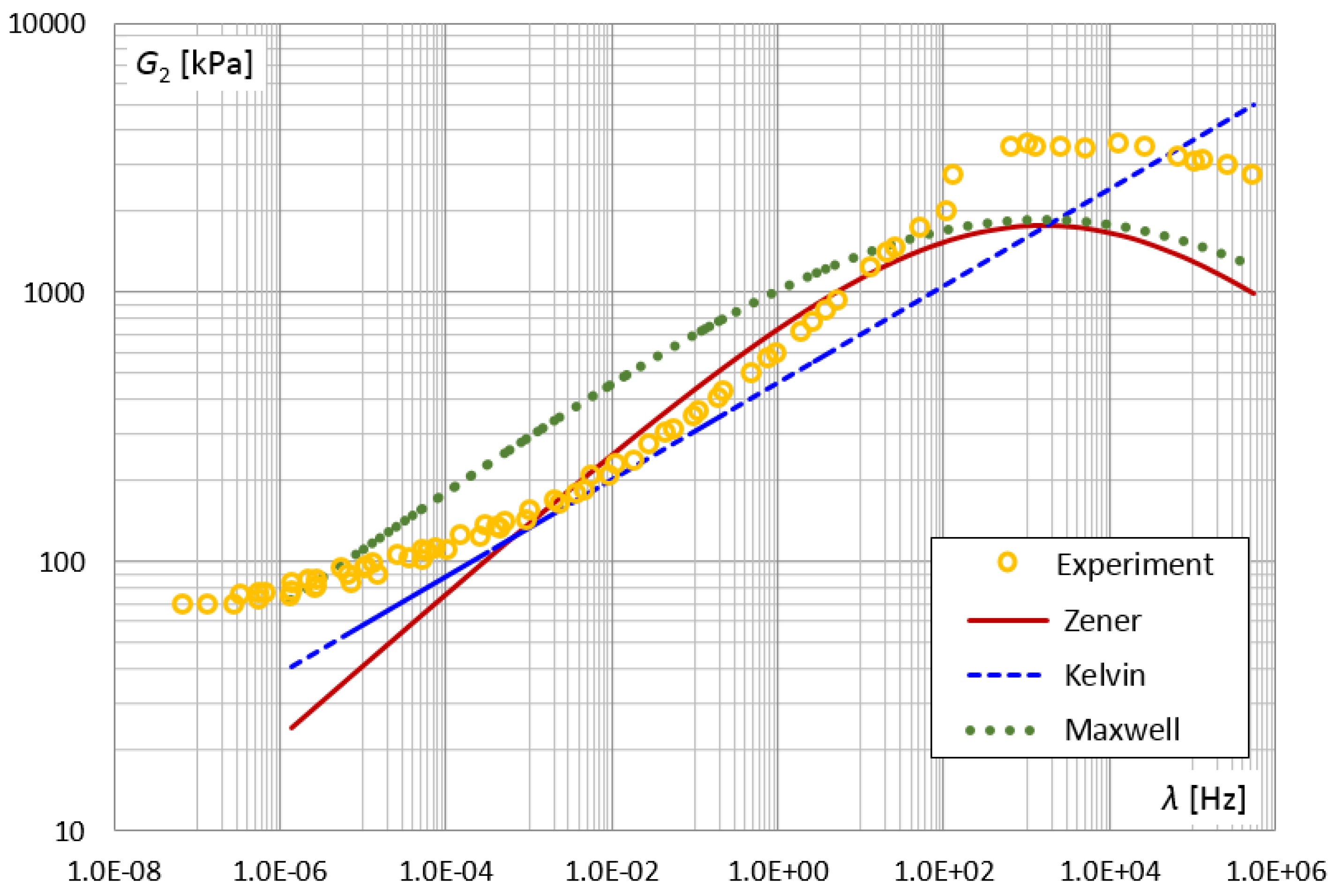
3. Results and Discussion
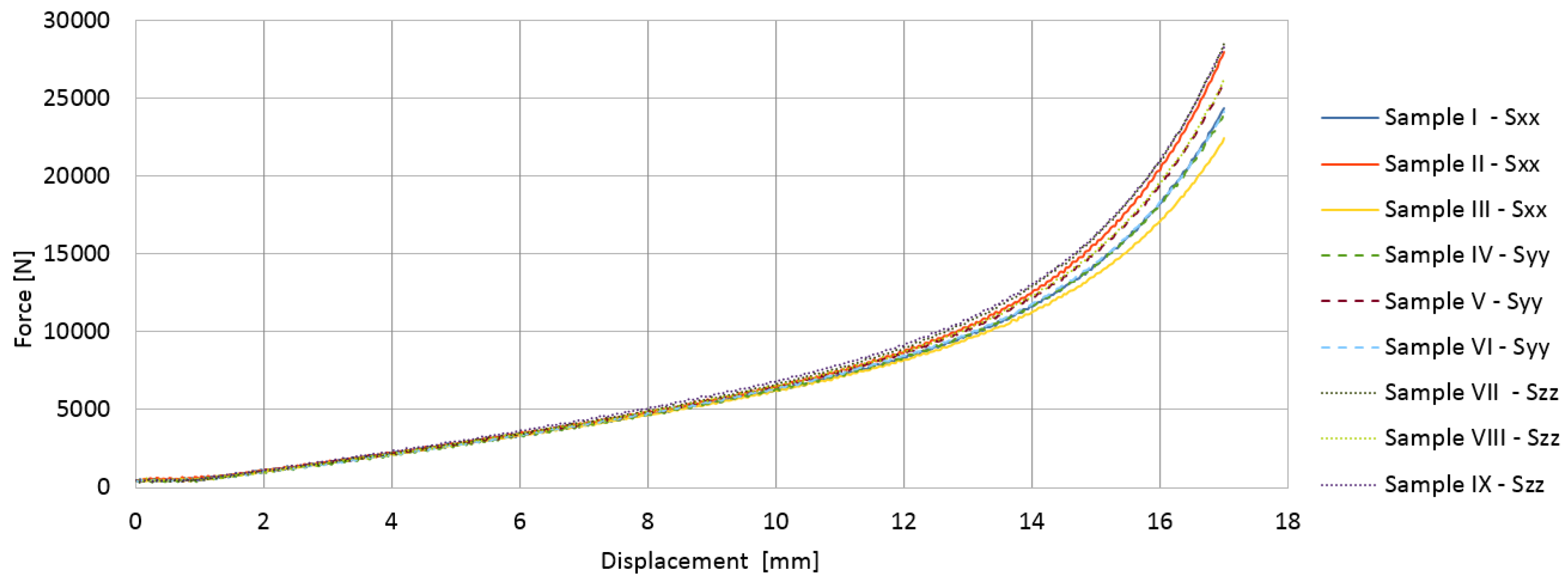
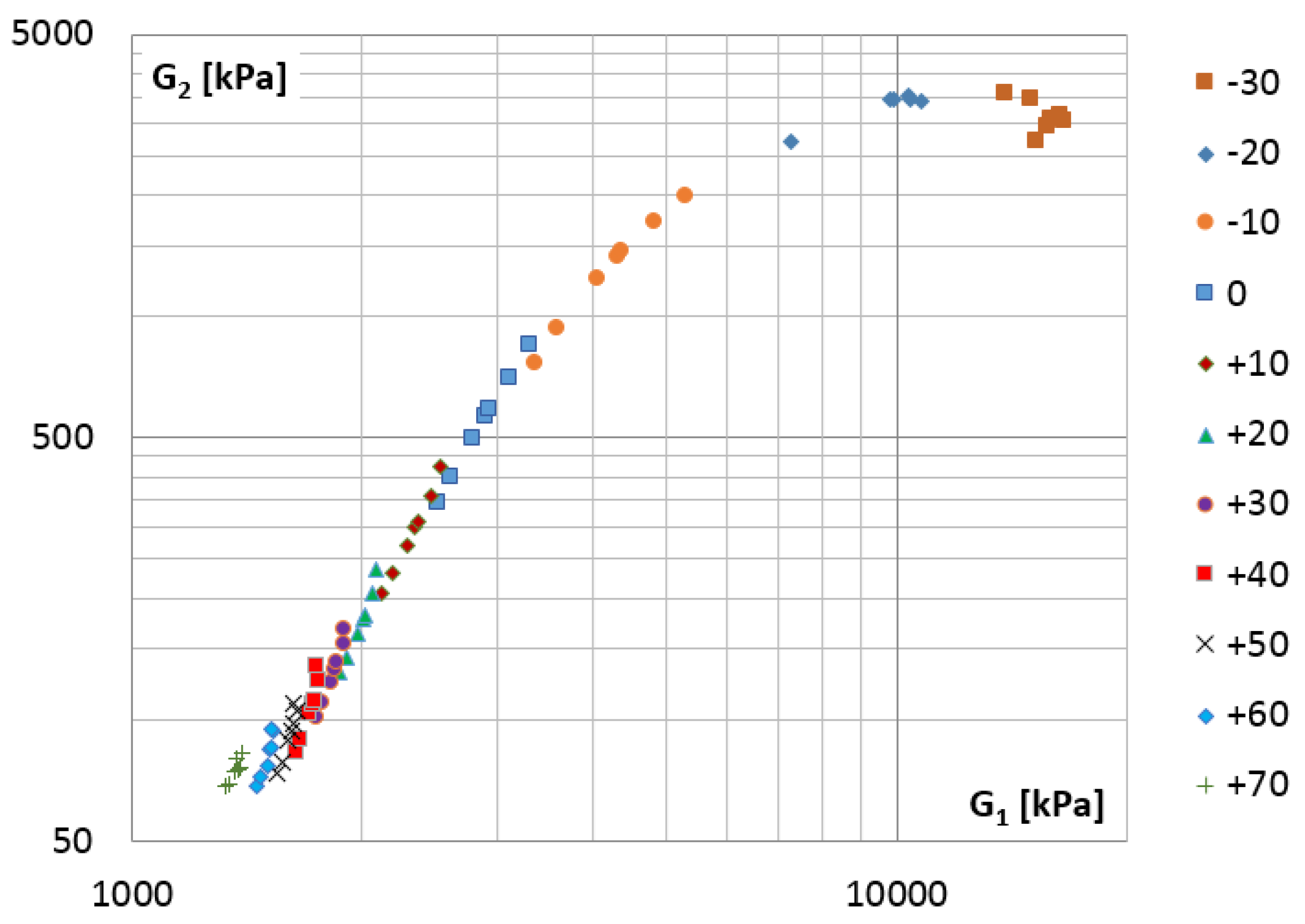
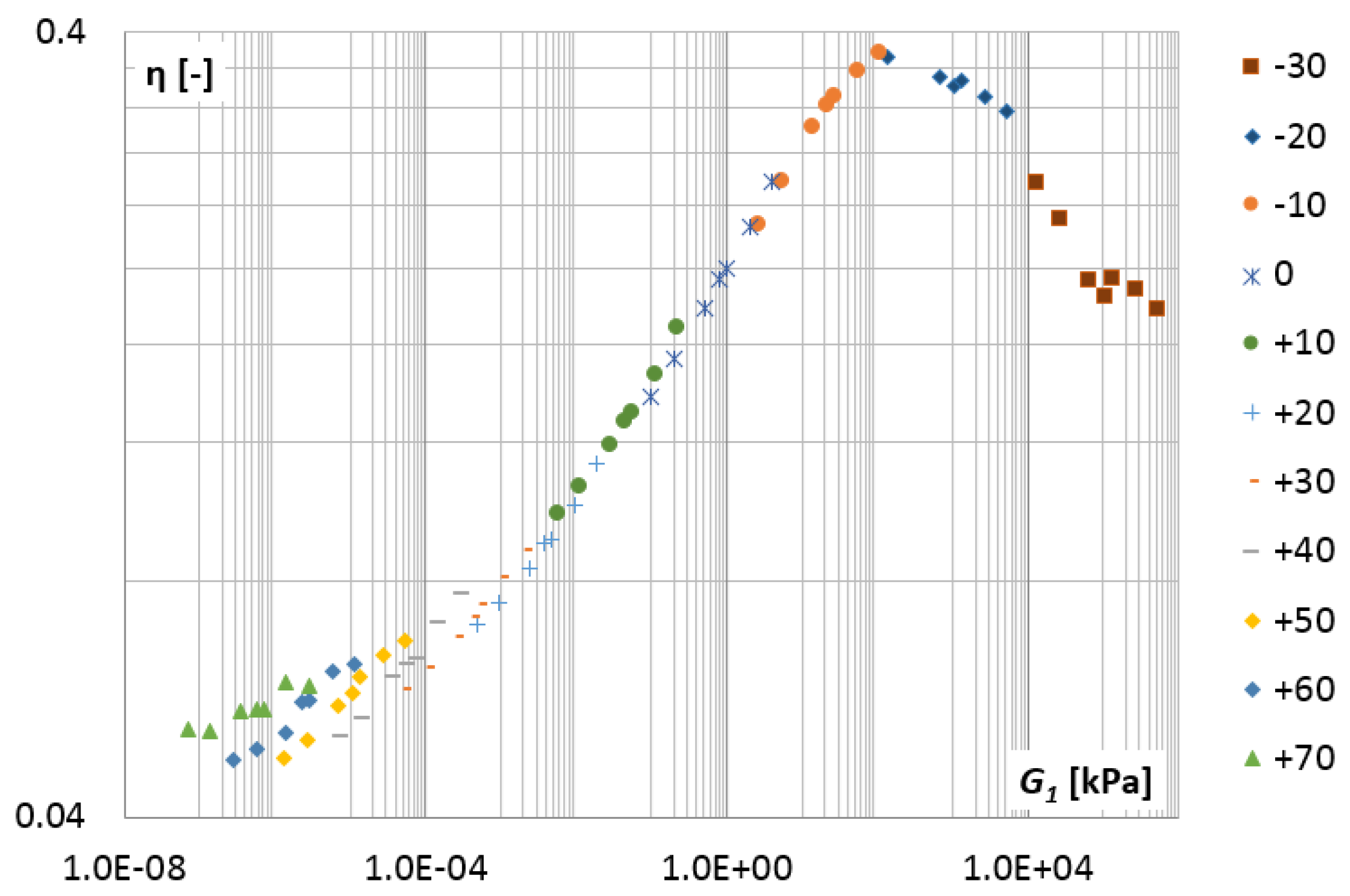
3.1. Test Results for Selected VE Materials
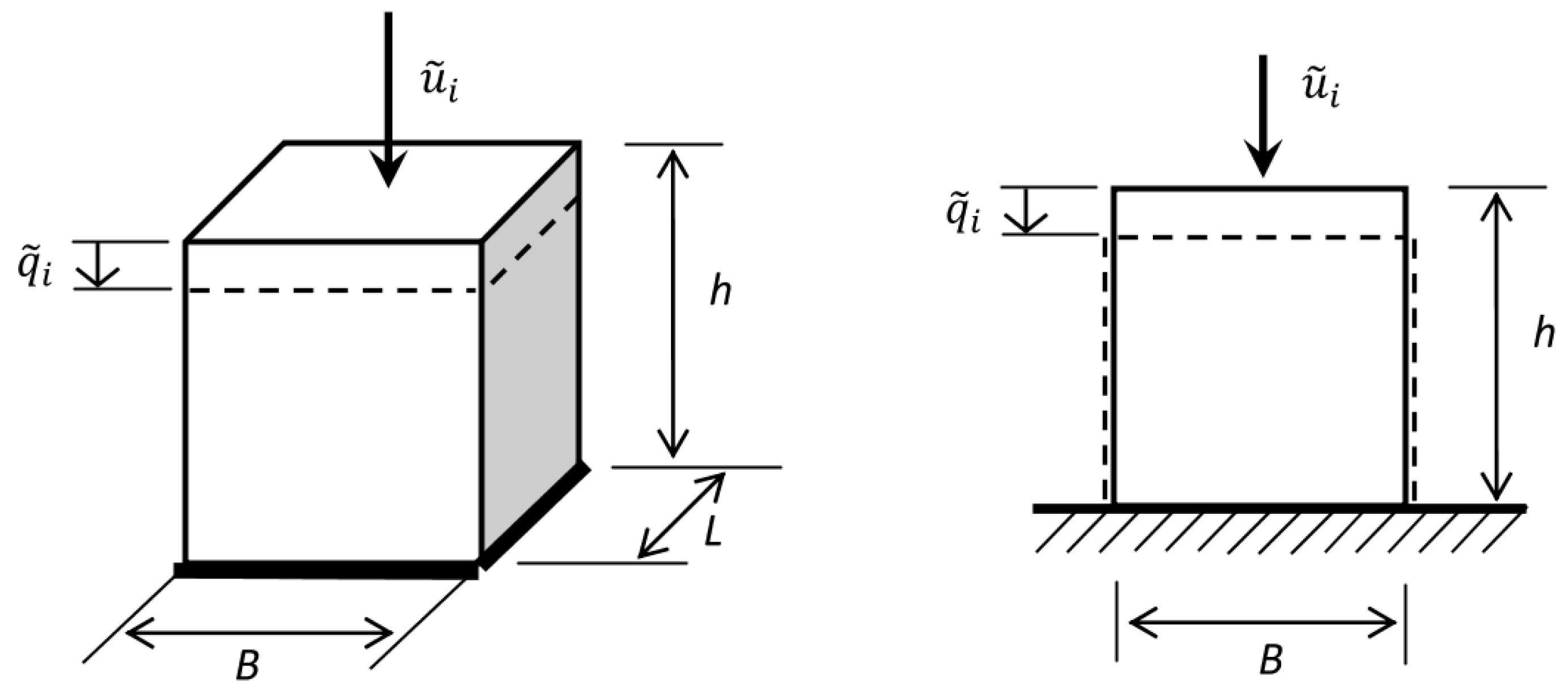
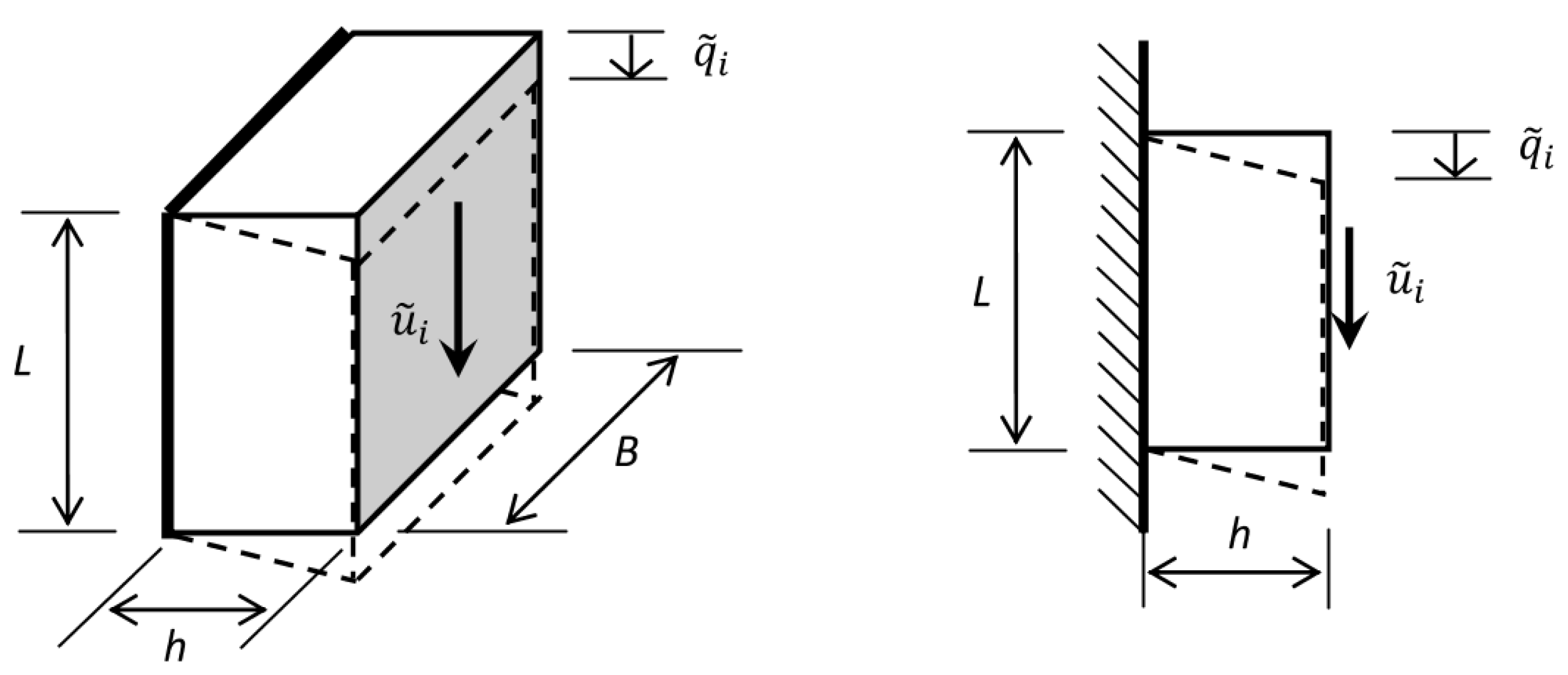
3.1.1. Transverse Shear Test
3.1.2. Longitudinal Shear Test
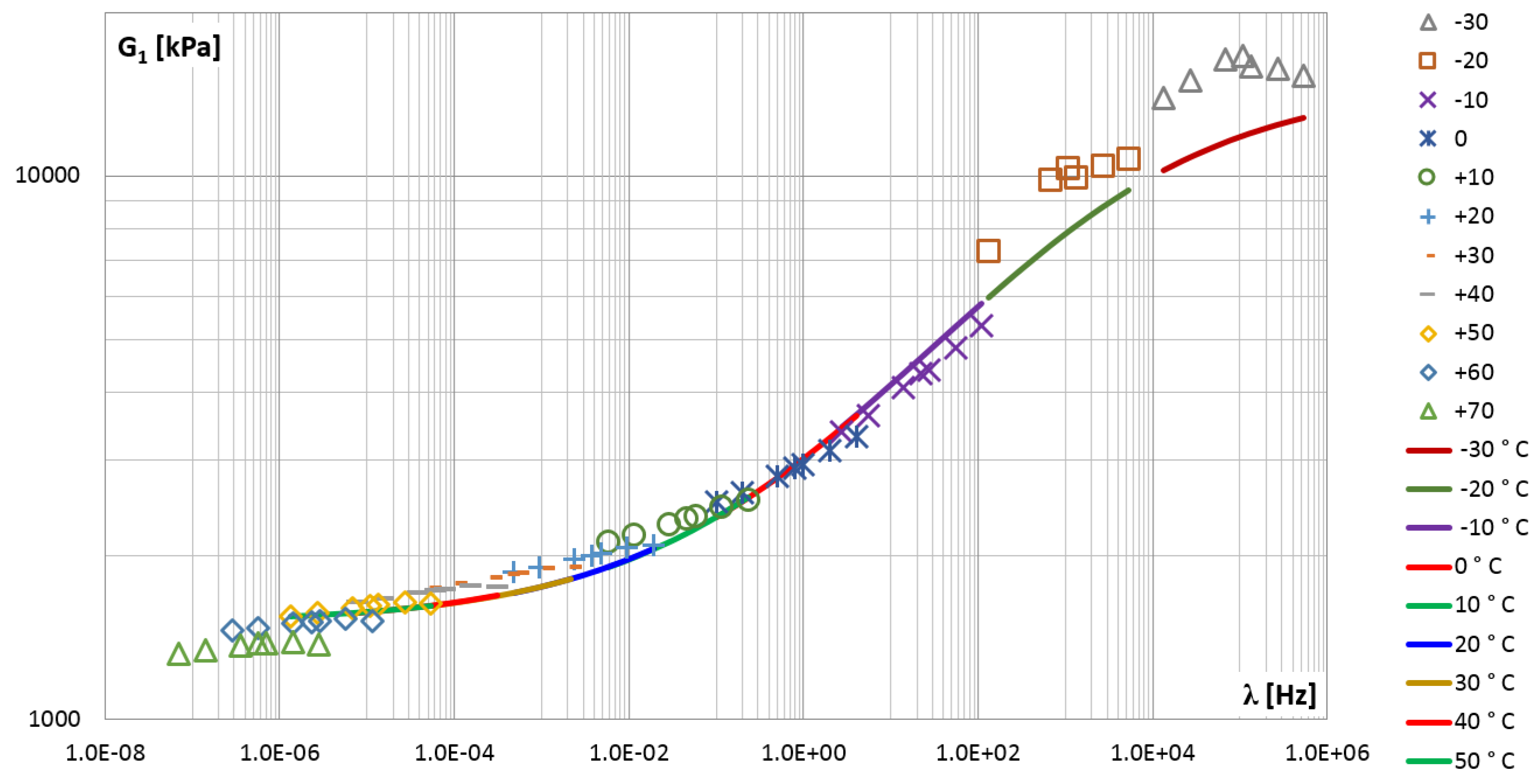
3.1.3. Construction of a Master Curve Diagram
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soong, T.T.; Spencer, B.F. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Christopoulos, C.; Filiatrault, A. Principles of Passive Supplemental Damping and Seismic Isolation; IUSS Press: Pavia, Italy, 2006. [Google Scholar]
- Zelleke, D.H.; Elias, S.; Matsagar, V.A.; Jain, A.K. Supplemental dampers in base-isolated buildings to mitigate large isolator displacement under earthquake excitations. Bull. N. Z. Soc. Earthq. Eng. 2015, 48, 100–117. [Google Scholar]
- Talyan, N.; Elias, S.; Matsagar, V.A. Earthquake Response Control of Isolated Bridges Using Supplementary Passive Dampers. Pract. Period. Struct. Des. Constr. 2021, 26, 04021002. [Google Scholar] [CrossRef]
- Naranjo-Pérez, J.; Jiménez-Alonso, J.F.; Díaz, I.M.; Quaranta, G.; Sáez, A. Motion-Based Design of Passive Damping Systems to Reduce Wind-Induced Vibrations of Stay Cables under Uncertainty Conditions. Appl. Sci. 2020, 10, 1740. [Google Scholar] [CrossRef] [Green Version]
- Pawlak, Z.M.; Lewandowski, R. Effectiveness of the Passive Damping System Combining the Viscoelastic Dampers and Inerters. Int. J. Struct. Stab. Dyn. 2020, 20, 2050140. [Google Scholar] [CrossRef]
- Ge, T.; Huang, X.H.; Guo, Y.Q.; He, Z.F.; Hu, Z.W. Investigation of Mechanical and Damping Performances of Cylindrical Viscoelastic Dampers in Wide Frequency Range. Actuators 2021, 10, 71. [Google Scholar] [CrossRef]
- Bergman, D.M.; Hanson, R.D. Viscoelastic mechanical damping devices tested at real earthquake displacements. Earthq. Spectra 1993, 9, 389–417. [Google Scholar] [CrossRef]
- Tsai, C.S. Temperature effect of viscoelastic dampers during earthquakes. J. Struct. Eng. 1994, 120, 394–409. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus—A different approach to the analysis of viscoelastically damped structures. AIAA J. 1983, 27, 1412–1417. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. A new method for solving dynamic problems of fractional derivative viscoelasticity. Int. J. Eng. Sci. 2001, 39, 149–176. [Google Scholar] [CrossRef]
- Chang, T.; Singh, M.P. Seismic analysis of structures with a fractional derivative model of viscoelastic dampers. Earthq. Eng. Eng. Vib. 2002, 1, 251–260. [Google Scholar] [CrossRef]
- Lewandowski, R.; Bartkowiak, A.; Maciejewski, H. Dynamic analysis of frames with viscoelastic dampers: A comparison of damper models. Struct. Eng. Mech. 2012, 41, 113–137. [Google Scholar] [CrossRef] [Green Version]
- Lewandowski, R.; Pawlak, Z. Dynamic analysis of frames with viscoelastic dampers modelled by rheological models with fractional derivatives. J. Sound Vib. 2011, 330, 923–936. [Google Scholar] [CrossRef]
- Li, H.; Gomez, D.; Dyke, S.J.; Xu, Z. Fractional differential equation bearing models for base-isolated buildings: Framework development. J. Struct. Eng. 2020, 146, 04019197. [Google Scholar] [CrossRef]
- Lewandowski, R.; Chorążyczewski, B.; Wasilewicz, P. Evaluation of parameters of viscous fluid and viscoelastic dampers. Vib. Phys. Syst. 2006, 22, 223–228. [Google Scholar]
- Chang, T.S.; Singh, M.P. Mechanical model parameters for viscoelastic dampers. J. Eng. Mech. 2009, 135, 581–584. [Google Scholar] [CrossRef]
- Lewandowski, R.; Chorążyczewski, B. Identification of the parameters of the Kelvin–Voigt and the Maxwell fractional models, used for modeling of viscoelastic dampers. Comput. Struct. 2010, 88, 1–17. [Google Scholar] [CrossRef]
- Xu, Z.D.; Xu, C.; Hu, J. Equivalent fractional Kelvin model and experimental study on viscoelastic damper. J. Vib. Control 2015, 21, 2536–2552. [Google Scholar] [CrossRef]
- Fan, W.; Jiang, X.; Qi, H. Parameter estimation for the generalized fractional element network Zener model based on the Bayesian method. Stat. Mech. Appl. 2015, 427, 40–49. [Google Scholar] [CrossRef]
- Pritz, T. Five-parameter fractional derivative model for polymeric damping materials. J. Sound Vib. 2003, 265, 935–952. [Google Scholar] [CrossRef]
- Lewandowski, R.; Słowik, M.; Przychodzki, M. Parameters identification of fractional models of viscoelastic dampers and fluids. Struct. Eng. Mech. 2017, 63, 181–193. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Emri, I. Rheology of Solid Polymers; Technical Report; The British Society of Rheology. 2005. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.361.7111&rep=rep1&type=pdf (accessed on 7 November 2021).
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Barbero, E.J.; Ford, K.J. Equivalent Time Temperature Model for Physical Aging and Temperature Effects on Polymer Creep and Relaxation. J. Eng. Mater. Technol. 2004, 126, 413–419. [Google Scholar] [CrossRef]
- Gergesova, M.; Zupancic, B.; Saprunov, I.; Emri, I. The closed form t-T-P shifting (CFS) algorithm. J. Rheol. 2011, 55, 1–16. [Google Scholar] [CrossRef]
- Litewka, P.; Lewandowski, R. Influence of elastic supports on non-linear steady-state vibrations of Zener material plates. In Computer Methods in Mechanics (CMM2017), Proceedings of the 22nd International Conference on Computer Methods in Mechanics, Lublin, Poland, 13–16 September 2017; AIP Publishing: New York, NY, USA, 2018. [Google Scholar]
- Podlubny, I. Fractional Differential Equation; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Lewandowski, R.; Pawlak, Z. Optimal Placement of Viscoelastic Dampers Represented by the Classical and Fractional Rheological Models. In Design Optimization of Active and Passive Structural Control Systems; Lagaros, N., Plevris, V., Mitropoulou, C., Eds.; IGI Global: Hershey, PA, USA, 2013; pp. 50–84. [Google Scholar]
- Moreira, R.A.S.; Corte-Real, J.D.; Dias Rodrigues, J. A generalized frequency–temperature viscoelastic model. Shock Vib. 2010, 17, 407–418. [Google Scholar] [CrossRef]
- Lewandowski, R.; Przychodzki, M. Approximate method for temperature- dependent characteristics of structures with viscoelastic dampers. Arch. Appl. Mech. 2018, 88, 1695–1711. [Google Scholar] [CrossRef] [Green Version]
- Rouleau, L.; Deü, J.F.; Legay, A.; Le Lay, F. Application of Kramers–Kronig relations to time–temperature superposition for viscoelastic materials. Mech. Mater. 2013, 65, 66–75. [Google Scholar] [CrossRef]
- Gaisford, S. Principles of Thermal Analysis and Calorimetry; The Royal Society of Chemistry: Cambridge, UK, 2016. [Google Scholar]






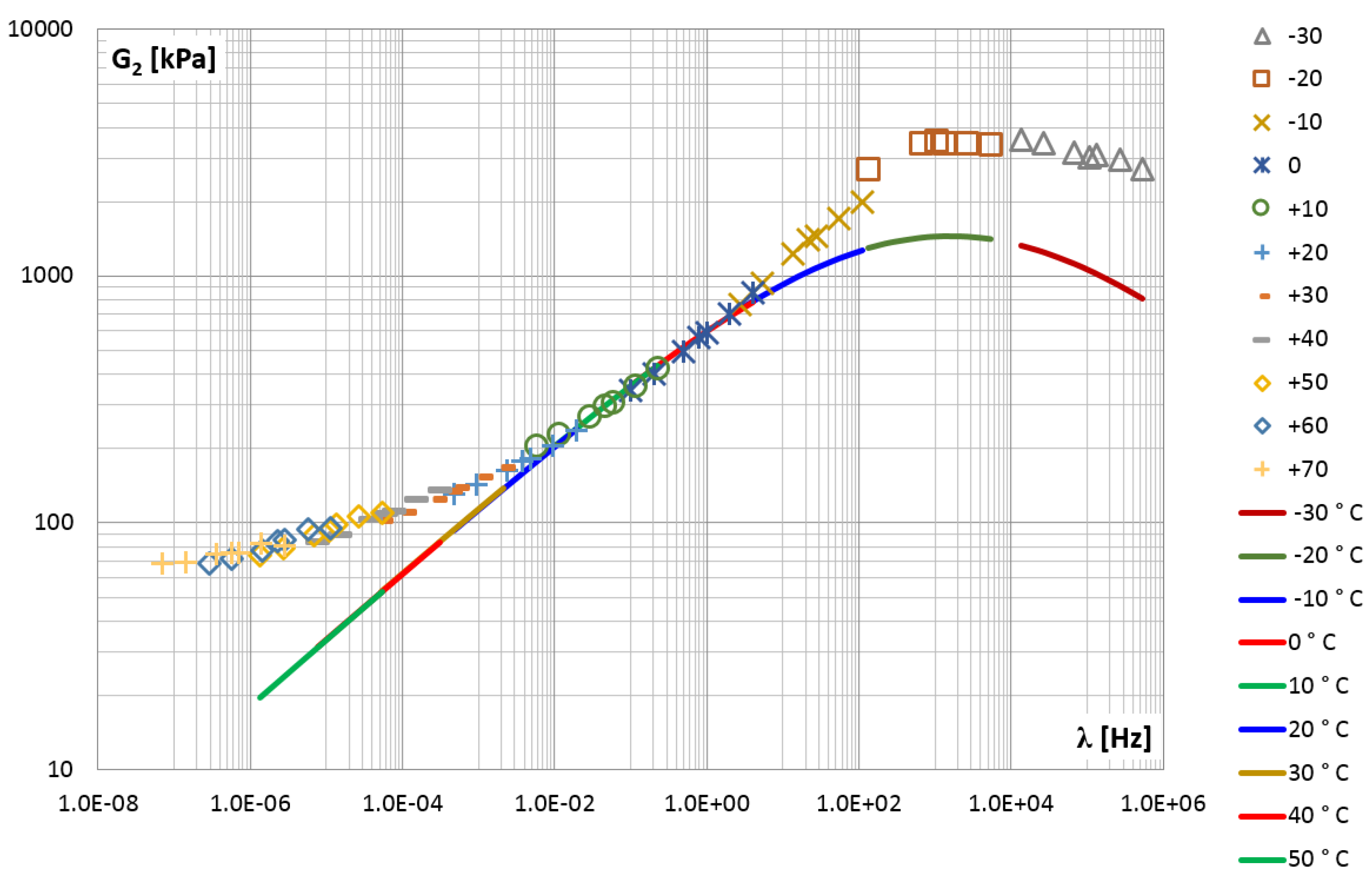
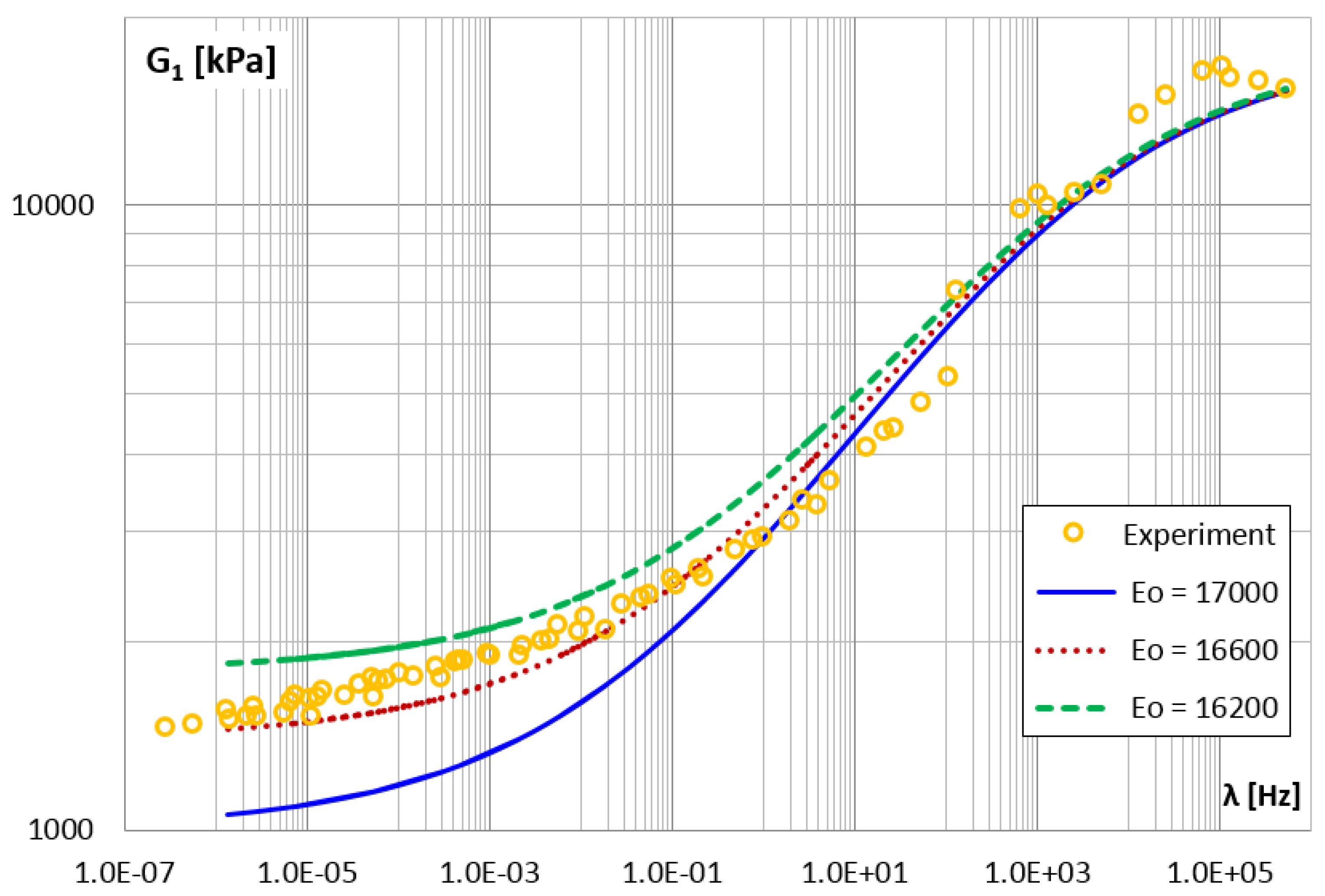
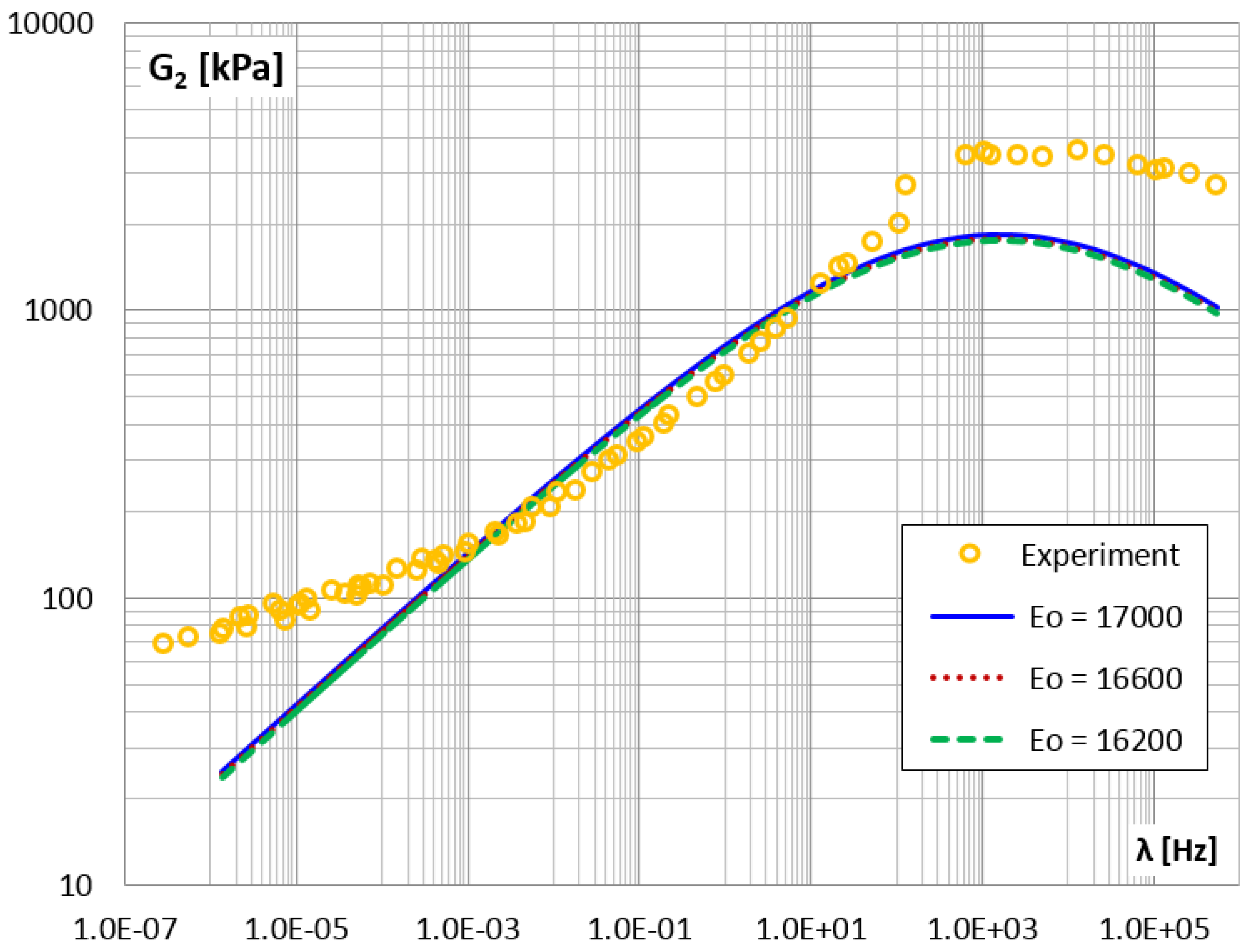
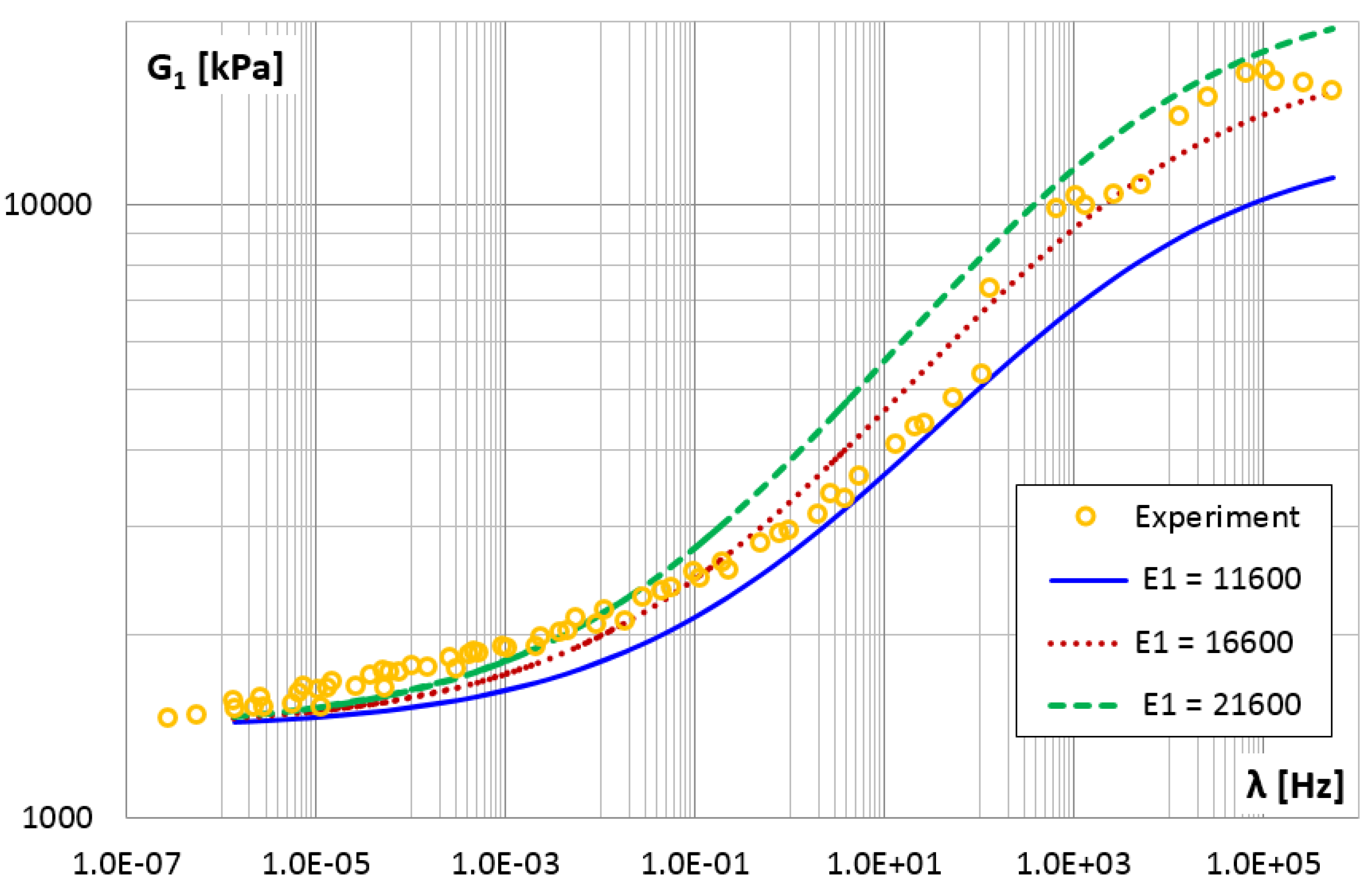
| Amplitudes of Approximating Functions | Functional Relationships | ||
|---|---|---|---|
| [mm] | 0.00556 | 349,503 | |
| [mm] | 0.88536 | ||
| 37.98 | 40,700 | ||
| 309.21 | |||
| Amplitudes of Approximating Functions | Functional Relationships | ||
|---|---|---|---|
| 0.00116 | [kPa] | 2454.02 | |
| 0.18445 | |||
| [Pa] | 55,551 | [kPa] | 285.78 |
| [Pa] | 452,313 | ||
| Model Parameter | Mean Relative Error | |||
|---|---|---|---|---|
| [%] | [%] | |||
| 1000 | 18.59 | 16.23 | ||
| 1400 | 10.75 | 15.37 | ||
| 1800 | 16.97 | 14.52 | ||
| 11,600 | 17.45 | 37.99 | ||
| 16,600 | 10.75 | 15.37 | ||
| 21,600 | 32.38 | 73.82 | ||
| 0.014 | 11.65 | 25.64 | ||
| 0.14 | 10.75 | 15.37 | ||
| 1.40 | 18.52 | 38.46 | ||
| 0.22 | 22.36 | 40.97 | ||
| 0.27 | 10.75 | 15.37 | ||
| 0.32 | 13.25 | 22.39 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawlak, Z.M.; Denisiewicz, A. Identification of the Fractional Zener Model Parameters for a Viscoelastic Material over a Wide Range of Frequencies and Temperatures. Materials 2021, 14, 7024. https://doi.org/10.3390/ma14227024
Pawlak ZM, Denisiewicz A. Identification of the Fractional Zener Model Parameters for a Viscoelastic Material over a Wide Range of Frequencies and Temperatures. Materials. 2021; 14(22):7024. https://doi.org/10.3390/ma14227024
Chicago/Turabian StylePawlak, Zdzisław M., and Arkadiusz Denisiewicz. 2021. "Identification of the Fractional Zener Model Parameters for a Viscoelastic Material over a Wide Range of Frequencies and Temperatures" Materials 14, no. 22: 7024. https://doi.org/10.3390/ma14227024







